DOI:10.32604/iasc.2021.013009
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.013009 | |
| Article |
Low Complexity Decoding Algorithm for Uplink SCMA Based on Aerial Spherical Decoding
1Qinghai Nationalities University, Xining, 810007, China
2Science and Technology on Micro-system Laboratory, Shanghai Institute of Micro-System and Information Technology, Chinese Academy of Sciences, Shanghai, 201800, China
3University of Chinese Academy of Sciences, Beijing, 100049, China
*Corresponding Author: Guoqing Jia. Email: guoqing.jia@qhmu.edu.cn
Received: 30 August 2020; Accepted: 13 October 2020
Abstract: As a new non-orthogonal multiple access technology for 5G massive machine type communication scenario, the sparse code multiple access (SCMA) has greatly improved the spectrum efficiency due to the high connection density. SCMA combines QAM (Quadrature Amplitude Modulation) modulation and sparse spreading into a codebook set to obtain forming gain. The user binary bit data is directly mapped into multi-dimensional codewords in the transmitter. The receiver uses the message passing algorithm (MPA) for multi-user detection to achieve efficient decoding. However, MPA is a good solution for SCMA, though its high complexity limits the application in practical systems. In order to reduce the complexity of MPA, this paper proposed a low-complexity decoding algorithm based on the serial spherical decoding message passing algorithm (SSD-MPA), which greatly enhanced the practicability of the SCMA system. The SSD-MPA took into account the distribution characteristics of the Gaussian noise and the reliability of the constellation points, and only updates the trusted constellation point messages of nodes within the spherical radius. At the same time, it used a serial strategy to speed up the convergence rate. The simulation results have shown that when the radius sets properly, the algorithm reduces the complexity by about 2/3 compared with the original MPA, and the performance was almost lossless.
Keywords: 5G; sparse code multiple access; MPA; spherical decoding; serial strategy
The massive machine type communication (mMTC) is the main application scenario of 5G, and its main feature is the high connection density. The sparse code multiple access (SCMA) is a new type of non-orthogonal multiple access technology in the code domain [1–3], which evolves from the low density spread spectrum (LDS). It combines the quadrature amplitude modulation (QAM) and the sparse spreading into a codebook set, in so a ‘forming gain’ [4,5] is obtained. In a SCMA system, the binary bit data of a user is directly mapped into the multi-dimensional codewords, and the receiver uses the message passing algorithm (MPA) to achieve efficient decoding. In a MPA, the sparseness of the codeword is used to effectively reduce the decoding complexity, and the performance is close to the optimal MPA. Therefore, the MPA is the most commonly used decoding algorithm in a SCMA. The SCMA can increase the spectral efficiency more than 150% and is expected to become a candidate technology for mMTC [6,7].
Although MPA has reduced the decoding complexity, the latter is is still high, which limits the application of SCMA in practical communication systems [8–10]. To this end, Mu et al. [11] proposed a partially marginalized MPA (PM-MPA) which reduced the number of update nodes and fixed the complexity of MPA by marginalizing some users. However, the performance of the PM-MPA was significantly reduced, especially in the case of high signal-to-noise ratio (SNR). Du et al. [12] proposed a message passing algorithm (S-MPA) based on a serial strategy. The S-MPA converted the parallel calculations in the original MPA to the serial calculations, thereby, reducing the number of iterations required. Yang et al. [13] used the thresholds to control the iterative process, in order to reduce the complexity, but its performance also decreased. Klimentyev et al. [14] simplified the decoding process and reduced the number of iterations to 2–3 times based on the characteristics of the codeword in the codebook. Wei et al. [15] proposed a low-complexity decoding algorithm based on the list ball decoding (LSD). This algorithm only considered the signals in the hypersphere, and did not need to traverse all possible combinations, and thereby reduced the complexity. Wei et al. [16] introduced two low-complexity algorithms. One is the sign flip algorithm (SFA), which performed hard decisions and flipped the unreliable signals during the resource node updating. The other was a dynamic partial marginalized MPA, which dynamically determined the marginalized users through the reliability defined by SFA. Ma et al. [17] proposed a low-complexity MPA detector based on the dynamic factor graph (DFG-MPA). The DFG-MPA dynamically updated the factor graph by judging the size of the user codeword confidence level, where the larger value of the confidence level did not participate in the current and subsequent updates. And Miao et al. [18] proposed a continuously updated dynamic factor graph algorithm, which could speed up the convergence, and reduce the external information. Shen et al. [19] also introduced a dynamic subgraph MPA (DS-MPA) algorithm, which had a slow convergence and high complexity. Yuan et al. [20] proposed a hybrid message passing algorithm, which limited the user state to a Gaussian state based on the energy minimization approximation. Yang et al. [21] proposed a spherical decoding MPA (SD-MPA), which only updated the constellation point messages within the radius, though the convergence rate was slow.
In this context, the major contribution of this paper is to propose a serial spherical decoding MPA (SSD-MPA) algorithm, which can further reduce its complexity. Specifically, according to the relationship between the Gaussian noise distribution characteristics and the reliability of the constellation points, this algorithm chooses to update the trusted constellation points in the spherical range, and accelerates the convergence speed through a serial strategy. When the sphere radius sets properly, SSD-MPA reduces the computational complexity by about two-thirds, with almost no loss in the bit error rate (BER) performance. The rest of this paper is organized as follows. Firstly, the system model of SCMA is reviewed and analyzed in Section 2. Then, a serial spherical decoding MPA is proposed in Section 3. Furthermore, the numerical simulation and analysis are discussed in Section 4. Finally, the conclusions are drawn in Section 5.
We assume that, in an uplink SCMA system, J users share K with same resources. The system has L codebooks of dimension M × K, where M represents the number of constellation points of the codebooks, K represents the number of resources of the codebook. In this system, each user has an exclusive codebook, the system overload rate is defined as λ = J/K, where J > K.
The uplink SCMA system model of J = 6, L = 6, K = 4, and M = 4 is shown in Fig. 1.
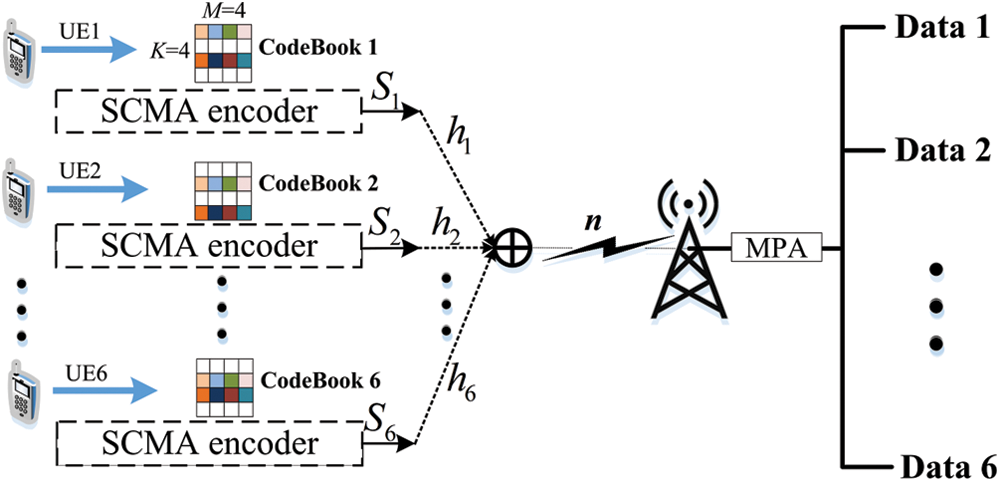
Figure 1: Uplink SCMA system model
At the user’s transmitter, each user j uses the SCMA encoder to map a lb(M) bit data stream into the N(N < K) dimensional codewords according to the codebook allocated by the base station (BS), then N-dimensional codewords are sparsely mapped to the K resources according to the resource mapping relationship of the codebooks, and each user j finally outputs a K-dimensional codeword Sj. In the end, the data of these J users can be superimposed on the same K resources in a non-orthogonal manner, and transmitted to the BS.
The factor graph shows the non-orthogonal superposition of multiple users in Fig. 2. This graph contains two types of nodes: ones are resource nodes (FNs), the others are user nodes (VNs). Among them, the connection represents the payload relationship between the FNs and VNs.
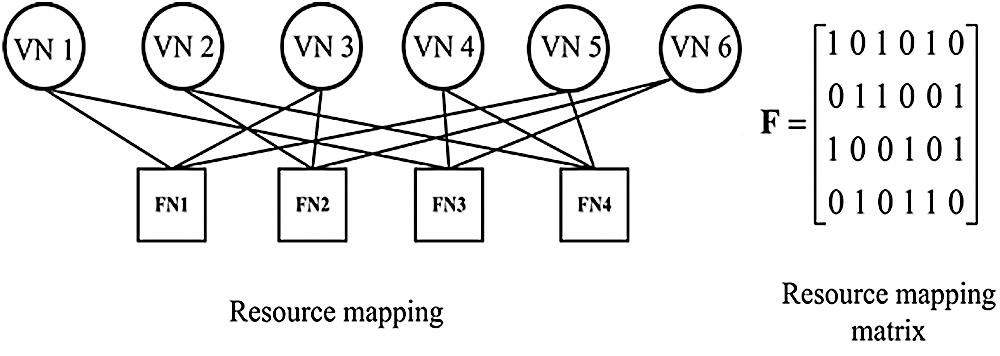
Figure 2: Uplink SCMA system factor graph
Therefore, the received signal of the receiver in a BS is expressed as follows:
where, Sj = (S1,j,S2,j,…SK,j)T represents the codeword of user j on K resources. hj = (h1,j,h2,j,…hK,j)T is the channel coefficient, and n~CN(0,σ2I) is K-dimensional Gaussian noise.
According to the factor graph, the codewords of df users are superimposed on the same resource. So, the received signal on the k-th resource can be expressed as follows:
where, N(k) = {j|Sk,j≠ 0} is the user set whose data is superimposed on the k-th resource, and the base is df.
As a typical multi-user detection algorithm, MPA is widely applied in a SCMA. It uses the sparse features of codewords to model the receivers based on the factor graph. The decoding process consists of two parts: iteratively updating node messages and codewords decisions.
1. Iteratively updating node messages
Firstly, an iteratively updating the node messages of resource node k and user node j can be expressed as follows:
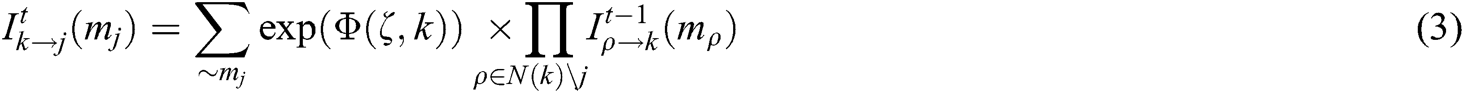
where, V(j) = {k|Sk,j ≠ 0} is the set of resources mapped by the j-th user, norm(●) indicates the normalization, and the modulus value is dv. Φ(ζ,k) represents the Euclidean Distance between the received signal and the constellation point. It is expressed as follows:
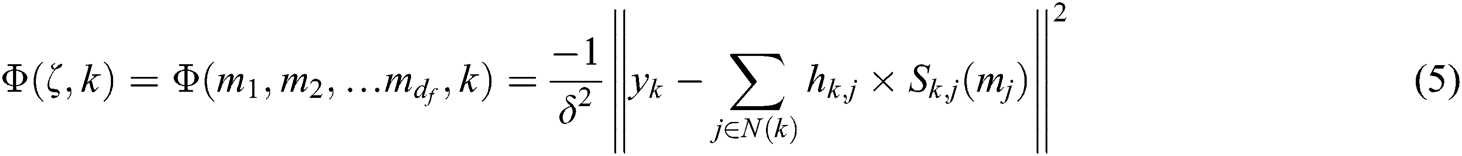
It is worth noting that the message updated by the resource node in Eq. (3), and it needs to be used in Eq. (4) until the next iteration.
2. Codewords decisions
Then, after the iteration is completed, the codeword probability is calculated according to the log-likelihood ratio (LLR). And then the user bit data is judged, it is expressed as follows:
3 Serial Spherical Decoding MPA (SSD-MPA)
Although the MPA can reduce the complexity to the order of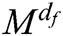 
, its complexity increases exponentially with the number of superimposed users df and the size of codebook M. The complexity of MPA is mainly concentrated on the process of the iteratively updating node messages and iterative convergence. Considering these two process, in this paper, we propose a low-complexity decoding algorithm based on serial spherical decoding, which called SSD-MPA.
In SSD-MPA, the influence of Gaussian noise on the received signal is considered, that is to say, the Euclidean Distance between the constellation point and the received signal determines the credibility of the constellation point. When the Euclidean Distance is smaller, the credibility of the constellation point is higher, and the correct probability of the codeword corresponding to the constellation point is greater. Therefore, according to the requirements of the actual scenario, setting an appropriate spherical radius (i.e., Euclidean Distance) can achieve a trade-off between the performance and the complexity of BER.
At the same time, the SSD-MPA uses a serial strategy to update the nodes message, in order to further reduce the complexity. In this serial update strategy, the updated message of a resource node is directly passed to the user node without waiting for the next iteration, so the user node can use the message of the resource node in time. The SSD-MPA can speed up the convergence speed by serial updating. The steps of SSD-MPA are shown in Algorithm 1:
The complexity of the MPA focuses on the process of the iteratively updating node messages. The original MPA traverses all constellation point sets with each iteration, so the complexity is high. The SSD-MPA limits the update range to a spherical radius, and it does not need to update all node messages. Tab. 1 gives the convergence complexity formula of the SSD-MPA and other algorithms. Among them, NMPA, NS-MPA, NSD-MPA, NDS-MPA, and NSSD-MPA indicate the number of iterations required for the corresponding algorithm to converge, and |Φ*(k) | represents the number of nodes on the resource k that fall in a spherical range.
Table 1: Comparison of convergence complexity
4 Simulations and Numerical Analysis
In this section, we use the MATLAB simulation platform to numerically simulate the SSD-MPA. The convergence speed, BER, and complexity performance of several algorithms are analyzed. The simulation parameters are shown in Tab. 2.
Table 2: Simulation parameters settings
In Fig. 3, the convergence performance of several algorithms is shown at SNR = 12 dB. According to the simulation results of Fig. 3, it can be known that the DS-MPA has the slowest convergence speed, and it requires approximately 7 iterations. While the MPA requires approximately 5–6 iterations. In contrast, the S-MPA, SD-MPA and SSD-MPA converge faster, requiring only 2–3 iterations to converge. It should be noted that although SD-MPA with a radius of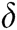 
has converged in 3 iterations, however the performance is poor. However, 5 iterations are required for SD-MPA with a radius of 
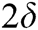. From the analysis in Fig. 3, it can be concluded that SSD-MPA has the fastest convergence speed.
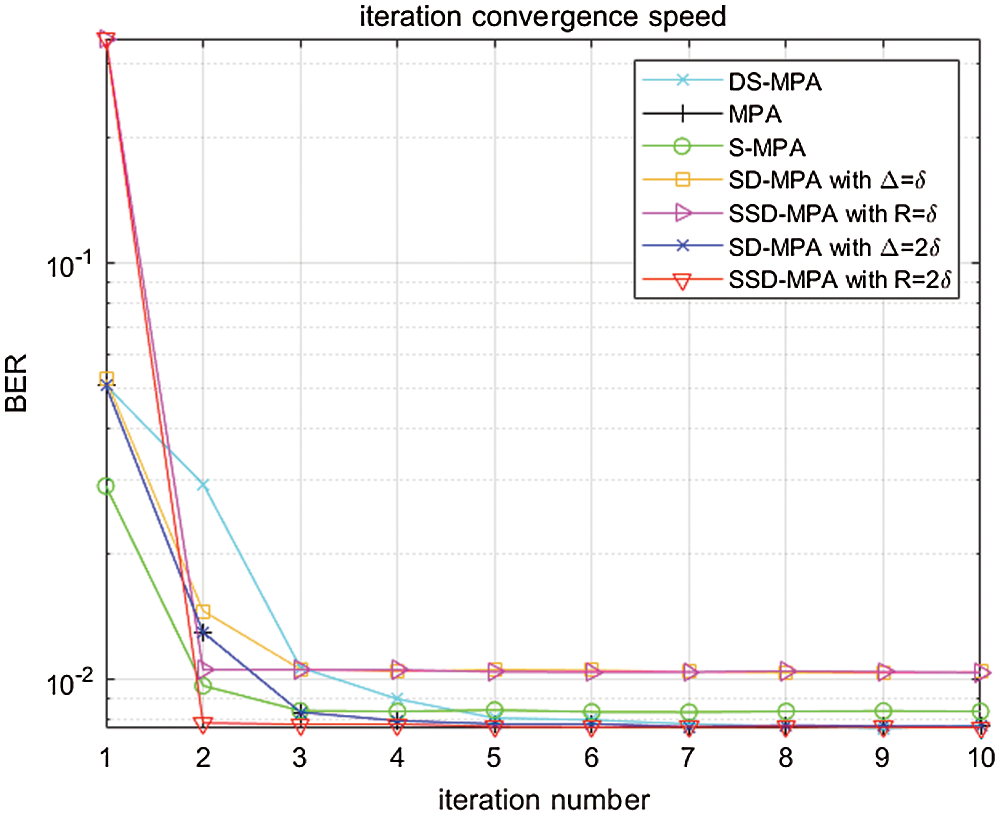
Figure 3: Comparison of convergence speed
According to the simulation results obtained in Fig. 3, the SSD-MPA only needs 2 iterations to converge, and the number of iterations that is required by the algorithm does not exceed 10 times. Therefore, the BER performance simulations at N = 2 and N = 10 are given in Figs. 4 and 5.
Figure 4: BER performance comparison graph for N = 2
Figure 5: BER performance comparison graph for N = 10
In Fig. 4, the BER performance comparison of various algorithms is given, when N is 2. It can be seen from Fig. 4 that when the SNR is low, the performance of SD-MPA and SSD-MPA with a radius of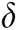 
is the lowest, and the performance of S-MPA and SSD-MPA with a radius of 
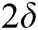is the best. With the increase of SNR, the performance of several algorithms is gradually approaching, but the performance of DS-MPA becomes the worst, and the performance of SSD-MPA with radius 
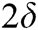is always optimal.
In Fig. 5 the BER performance comparison of various algorithms is given, when N is 10, in which all the algorithms are converged. The performance of the SD-MPA and SSD-MPA with a radius of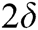 
is similar to the performance of the S-MPA and MPA, while the performance of the SD-MPA and SSD-MPA with a 
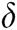radius is consistent. Therefore, it can be concluded from the analysis in Fig. 5 that the performance of the SSD-MPA with a radius of 
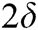has no loss.
Although the complexity formulas of several algorithms have been given in Tab. 1, as the number of constellation points falling in a spherical range is unknown, so the actual calculation amount of the SD-MPA and SSD-MPA cannot give specific formulas. Therefore, in Fig. 6 the actual operation amount of several algorithms is plotted in the simulation process.
In Fig. 6, the calculations of addition, multiplication, and comparison of several algorithms are respectively counted. Although the MPA does not have a comparison operation, the addition and multiplication operations are very large. In contrast, the amount of the SSD-MPA operation is only about 1/3 of the MPA.
Figure 6: Comparison of complexity
As a new non-orthogonal multiple access technology for 5G, the SCMA has greatly improved spectrum efficiency. However, the SCMA’s complexity is high, which limits its application in practical communication systems. This paper proposed a low complexity decoding algorithm based on serial spherical decoding, and verified the BER performance and complexity of the proposed algorithm through MATLAB simulation platform. The results show that, when the sphere radius sets properly, the SSD-MPA can reduce the complexity of MPA by about 2/3, and the performance is almost lossless. The practicability of the MPA is greatly enhancedTherelationship between sphere radius and performance will be researched in the further work.
Funding Statement: This work is supported by the National Natural Science Foundation of Qinghai Province, China (No. 2020-ZJ-724).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Agiwal, A. Roy and N. Saxena. (2016). “Next generation 5G wireless networks: A comprehensive survey,” IEEE Communications Surveys & Tutorials, vol. 18, no. 3, pp. 1617–1655. [Google Scholar]
2. W. Zhang, W. Fang, Q. Zhao, X. Ji and G. Jia. (2020). “Energy efficiency in Internet of Things: An overview,” Computers Materials & Continua, vol. 63, no. 2, pp. 787–811. [Google Scholar]
3. H. Nikopour and H. Baligh. (2013). “Sparse code multiple access,” in Proc. PIMRC, London, UK, pp. 332–336. [Google Scholar]
4. W. Fang, N. Cui, W. Chen, W. Zhang and Y. Chen, “A trust-based security system for data collecting in smart city,” IEEE Transactions on Industrial Informatics. (Early Access). [Google Scholar]
5. R. Hoshyar, F. P. Wathan and R. Tafazolli. (2008). “Novel low-density signature for synchronous CDMA systems over AWGN channel,” IEEE Transactions on Signal Processing, vol. 56, no. 4, pp. 1616–1626. [Google Scholar]
6. F. Bi, X. Fu, W. Chen, W. Fang, X. Miao et al. (2020). , “Fire detection method based on improved fruit fly optimization-based SVM,” Computers, Materials & Continua, vol. 62, no. 1, pp. 199–216. [Google Scholar]
7. W. Fang, W. Zhang, Q. Zhao, X. Ji, W. Chen et al. (2019). , “Comprehensive analysis of secure data aggregation scheme for industrial wireless sensor network,” Computers, Materials & Continua, vol. 61, no. 2, pp. 583–599. [Google Scholar]
8. X. F. Li, Y. B. Zhuang and S. X. Yang. (2017). “Cloud computing for big data processing,” Intelligent Automation & Soft Computing, vol. 23, no. 4, pp. 545–546. [Google Scholar]
9. J. Peng, M. Tang, M. Li and Z. Zha. (2017). “A load balancing method for massive data processing under cloud computing environment,” Intelligent Automation & Soft Computing, vol. 23, no. 4, pp. 547–553. [Google Scholar]
10. W. Wu, Y. Chen and D. Seng. (2017). “Implementation of web mining algorithm based on cloud computing,” Intelligent Automation & Soft Computing, vol. 23, no. 4, pp. 599–604. [Google Scholar]
11. H. Mu, Z. Ma, M. Alhaji, P. Fan and D. Chen. (2015). “A fixed low complexity message pass algorithm detector for up-link SCMA system,” IEEE Wireless Communications Letters, vol. 4, no. 6, pp. 585–588. [Google Scholar]
12. Y. Du, B. Dong, Z. Chen, J. Fang and L. Yang. (2016). “Shuffled multiuser detection schemes for uplink sparse code multiple access aystems,” IEEE Communications Letters, vol. 20, no. 6, pp. 1231–1234. [Google Scholar]
13. L. Yang, Y. Liu and Y. Siu. (2016). “Low complexity message passing algorithm for SCMA system,” IEEE Communications Letters, vol. 20, no. 12, pp. 2466–2469. [Google Scholar]
14. V. P. Klimentyev and A. B. Sergienko. (2016). “A low-complexity SCMA detector for AWGN channel based on solving overdetermined systems of linear equations,” in Proc. REDUNDANCYSt. Petersburg, pp. 61–65. [Google Scholar]
15. F. Wei and W. Chen. (2017). “Low complexity iterative receiver design for sparse code multiple access,” IEEE Transactions on Communications, vol. 65, no. 2, pp. 621–634. [Google Scholar]
16. L. Wei, B. Huang and J. Zheng. (2018). “Low-complexity detectors for uplink SCMA: Symbol flipping and dynamic partial marginalization-based MPA,” in Proc. VTC Spring, Porto, pp. 1–5. [Google Scholar]
17. X. Ma, L. Yang, Z. Chen and Y. Siu. (2017). “Low complexity detection based on dynamic factor graph for SCMA systems,” IEEE Communications Letters, vol. 21, no. 12, pp. 2666–2669. [Google Scholar]
18. J. Miao, X. Hu and Z. Zhao. (2019). “A low complexity multiuser detection scheme with dynamic factor graph for uplink SCMA systems,” in Proc. ICCC, Changchun, China, pp. 846–851. [Google Scholar]
19. M. Shen, J. Li and Y. He. (2019). “Dynamic subgraph detection algorithm for uplink SCMA system,” Telecommunication Engineering, vol. 59, no. 7, pp. 749–754. [Google Scholar]
20. W. Yuan, N. Wu, A. Zhang, X. Huang, Y. Li et al. (2020). , “Iterative receiver design for FTN signaling aided sparse code multiple access,” IEEE Transactions on Wireless Communications, vol. 19, no. 2, pp. 915–928. [Google Scholar]
21. L. Yang, X. Ma and Y. Siu. (2017). “Low complexity MPA detector based on sphere decoding for SCMA,” IEEE Communications Letters, vol. 21, no. 8, pp. 1855–1858. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |