DOI:10.32604/iasc.2021.013541
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.013541 | |
| Article |
A Fast and Accurate Vascular Tissue Simulation Model Based on Point Primitive Method
1Jiangsu Engineering Center of Network Monitoring, Engineering Research Center of Digital Forensics, Ministry of Education, School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing, 210044, China
3State Key Laboratory of Bioelectronics, Jiangsu Key Lab of Remote Measurement and Control, School of Instrument Science and Engineering, Southeast University, Nanjing, 210096, China
4Faculty of Information Technology, University of Information Technology and Management in Rzeszow, Rzeszow, 35-225, Poland
*Corresponding Author: Xiaorui Zhang. Email: zxr365@126.com
Received: 30 August 2020; Accepted: 14 February 2021
Abstract: Virtual surgery simulation is indispensable for virtual vascular interventional training system, which provides the doctor with visual scene between catheter and vascular. Soft tissue deformation, as the most significant part, determines the success or failure of the virtual surgery simulation. However, most soft tissue deformation model cannot simultaneously meet the requirement of high deformation accuracy and real-time interaction. To solve the challenge mentioned above, this paper proposes a fast and accurate vascular tissue simulation model based on point primitive method. Firstly, the proposed model simulates a deformation of the internal structure of the vascular tissue by adopting a point primitive method. Besides, the stretching constraint and elastic potential energy constraint are introduced to control and correct node motion. Furthermore, a mapping function from the interior to the surface of the vascular tissue is constructed based on moving least squares algorithm to render the visual effect of deformation. Finally, a training system based on the proposed model is set up on the PHANTOM OMNI force-tactile feedback device to realize the deformation simulation of the virtual vascular tissue. Experimental results shows that the proposed model can enhance real-time performance of the training system under the premise of ensuring deformation accuracy, as well as simulate the elasticity of soft tissue.
Keywords: Soft tissue deformation; virtual vascular interventional training system; point primitive method; elastic potential energy constraint; mapping function
Due to the development of the social economy and the improvement of people’s living standards, vascular diseases occur frequently in the middle-aged and elderly population in China. So far, minimally invasive vascular interventional surgery is the most direct and effective treatment method for vascular diseases [1]. Minimally invasive vascular interventional surgery has been widely used as it has the advantages, such as little traumas and pain, as well as short postoperative recovery time compared with traditional surgery [2]. But the existing vascular interventional surgeries do not meet the requirement of patients for minimally invasive surgeries, resulting in a low rescue-rate and high mortality in vascular diseases. With the advance of virtual surgery, the virtual vascular interventional training system provides a promising application prospect for vascular interventional surgery. It provides surgeons with a good training platform and assistance in visual and tactile sense, and enables repeated surgical trials, thus improving surgeons’ technical level. Meanwhile, the usage of virtual vascular interventional training systems can save training costs on real corpses and help in avoiding some ethical issues [3,4].
Although the virtual vascular interventional training system has many advantages for the treatment of vascular diseases, there are still some challenges that need to be solved or balanced when it is set up. At present, the mass-spring model [5–8], finite element model [9–13], mesh-less model [14–18], and tensor-mass method [19] are major physical modeling methods. Many researchers have paid more attention to the vascular model based on these four methods and obtained certain achievements. Wang et al. [20] have used vascular mechanical properties to determine spring coefficients in the mass-spring model, thereby improving the deformation accuracy but reducing the real-time performance. Wu et al. [21] have considered relations between the forces and spring deformation such as elongation and bending based on a traditional mass-spring model, and simulated vascular deformation by optimizing the model parameters with the help of Gaussian processes. This method improves the model stable but degrades the deformation accuracy. Hu et al. [22] have proposed a new mass-spring model based on domain constraint. It achieves a real-time performance but cannot meet the deformation accuracy. Liu et al. [23] have put forward an optimized finite element model, where the Quasi-Newton algorithm is used to accelerate deformation computation, thereby improving the real-time performance of the model. Ye et al. [24] have adopted a spatial adaptive acceleration algorithm in the context of a mesh-less model to accelerate the deformation computation for the vascular model. This algorithm enables a real-time operation but fails in the deformation accuracy. Guo et al. [25] have employed the implicit Euler solver and CG-linear solver to accelerate the deformation computation for the triangular tensor-mass model. This method enhances real-time performance of the model, but the deformation accuracy is not high because it only simulates the surface of the vascular tissue. One year later, they proposed a tetrahedral tensor-mass model to simulate the interior structure of vascular tissue. This model effectively improves the deformation accuracy but fails to improve its real-time performance [26]. As is stated above, accurate vascular deformation effects can be obtained only using high-precision physical modeling methods, but this kind of method will reduce the real-time performance of the training system to some extent. Therefore, how to effectively balance the accuracy and real-time performance during simulating deformation of soft tissues is still a challenge.
To address above challenges, this study proposes a fast and accurate vascular tissue simulation model based on a point primitive method. The proposed model can trade off the deformation accuracy against real-time performance during virtual surgery simulation. During the simulation, a deformation model is constructed based on a point primitive method to capture the motion of nodes modeled inside the vascular tissue. Moreover, stretching constraint and elastic potential energy constraint are employed to simulate the elasticity of vascular tissue by adjusting the node motion. And then a mapping function from interior to the surface of vascular tissue is built to render the deformation with the help of the moving least square algorithm.
The rest part of the paper is organized as follows. Section 2 elaborates on the vascular tissue simulation model based on point primitive method. Then, experimental results and analysis to verify the performance of the proposed vascular tissue simulation model are presented and discussed in Section 3. Finally, the conclusion is presented in Section 4.
The framework of our proposed model in the virtual vascular interventional training system is shown in Fig. 1. The framework includes virtual environment establishment, vascular tissue deformation and interaction between doctors and virtual vascular tissue through PHANTOM OMNI. The vascular tissue deformation is be made up of the deformation model constructing, constraints conducting and mapping function building.
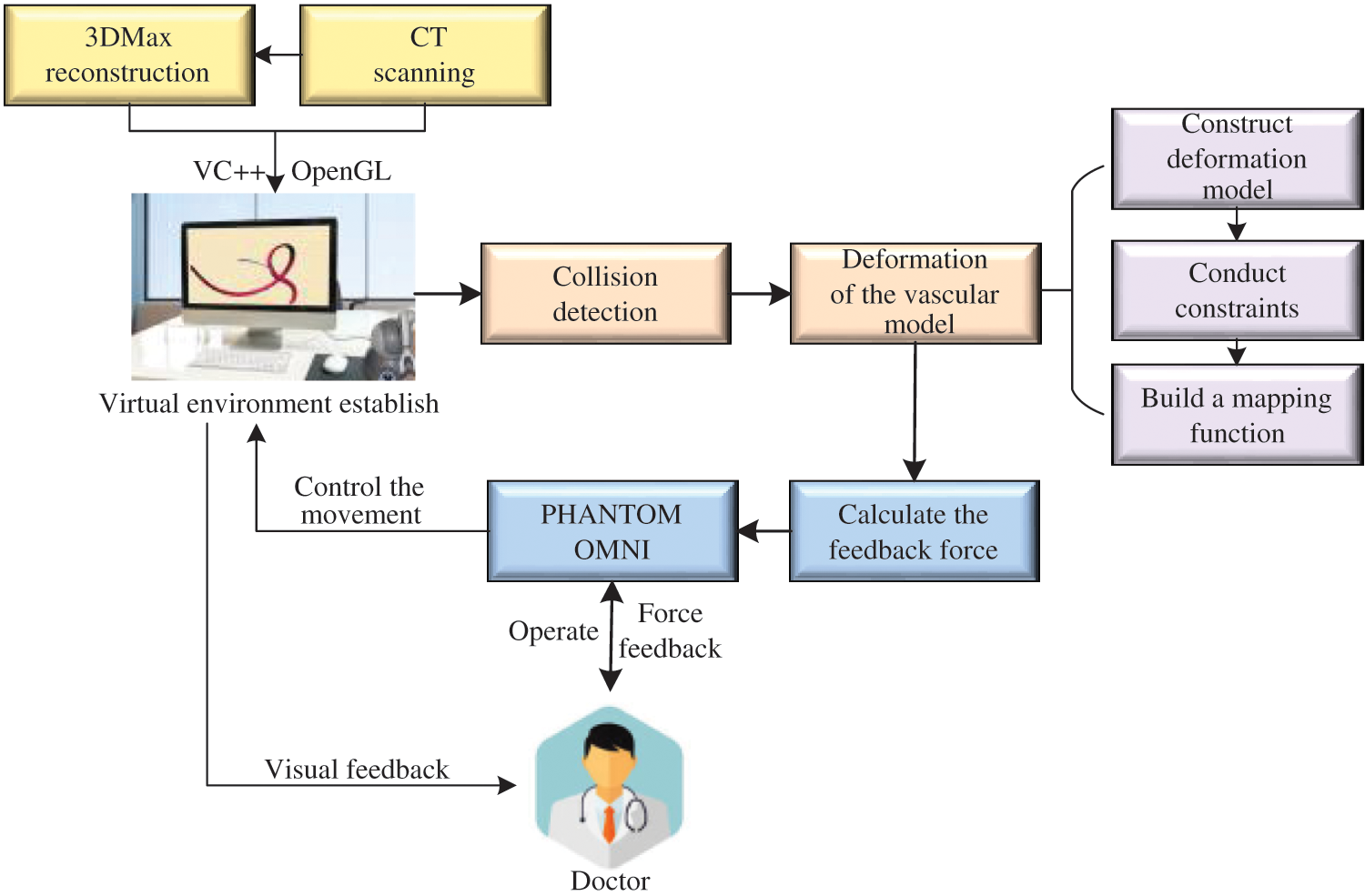
Figure 1: Framework of our proposed model
This study uses the point primitive method to construct a deformation model. The main idea of the method is to use a set of discrete nodes to calculate the stress and strain generated by the soft tissue deformation. Then, based on the obtained stress and strain values, displacement of each node is calculated in deformation, thereby capturing vascular tissue deformation.
Assuming that the internal structure of the vascular tissue can be discretized into N nodes, and each node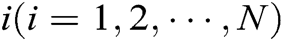 
has two physical properties including mass 
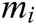and volume 
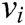. Fig. 2 shows the node support domains inside deformation model. The blue line represents the boundary of vascular tissue surface, the black dots represent the internal nodes, the red area represents the support domain 
of nodes, and node i is the center node of the support domain, therefore, the rest nodes are neighbors of node i.
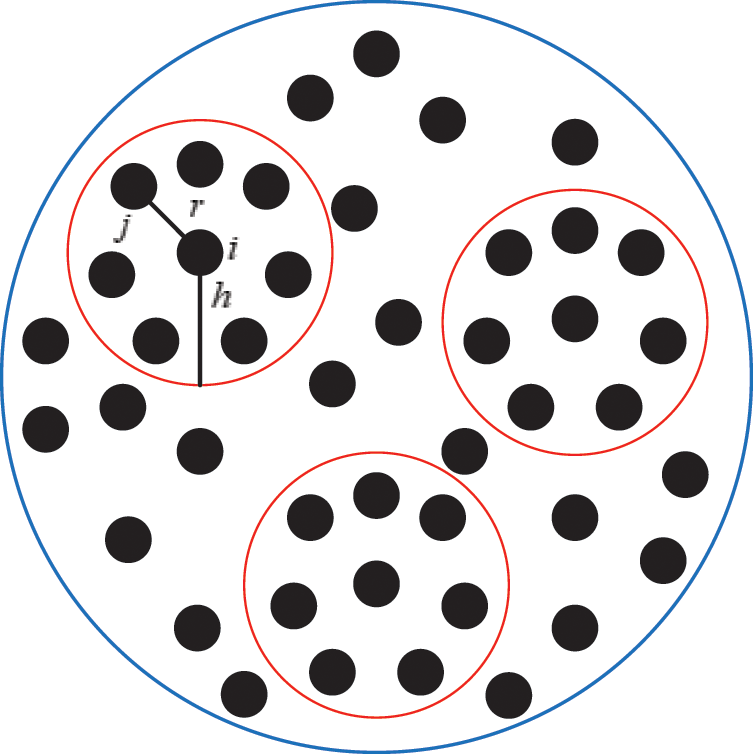
Figure 2: Schematic diagram of node support domains inside vascular tissue
The properties of each node are obtained from a kernel function in the support domain. Generally, the smaller the distance between the neighbor nodes and the center node is, the larger effect they have. Therefore, in order to measure the effect of the center node i on its neighbor node j, we used a kernel function to express the relationship as
where h is the support radius of the node i and r is the distance between them. Then the spatial derivatives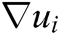 
of the displacement vector 
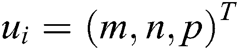are calculated at node i as
where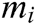 
, 
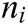, and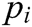 
are the x-component, y-component, and z-component of 
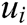respectively. And 
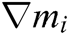can be computed according to Eq. (3)
where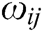 
is the mass weight between node i and j which is obtained by Eq. (1), 
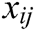is the difference vector between node i and j, i.e., 
, 
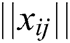is the modulus of the vector 
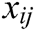, and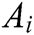 
is the moment matrix. Moreover, 
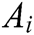can be described as follows
Similarly, 
and 
are also computed by the mentioned method, to achieve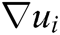 
. Furthermore, the strain 
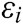and the stress 
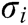at node i are obtained based on Eq. (2) as follows
where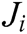 
is the Jacobi matrix at node i, I is the identity matrix, and C is the elastic matrix, which is determined by Young’s modulus and Poisson’s ratio.
If the vascular tissue has an elastic deformation under external force, the strain energy will be generated in it. Therefore, we estimate the strain energy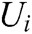 
stored around node i based on 
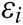and 
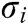as
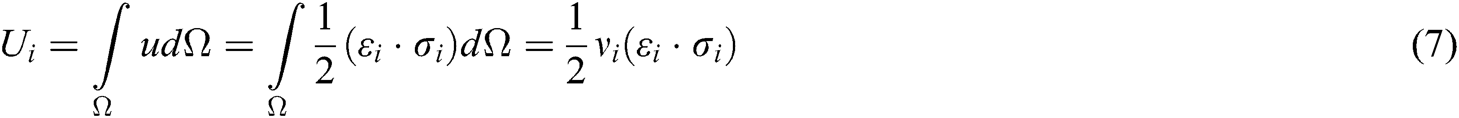
The strain energy is a function of displacement vector 
and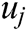 
. Taking the derivative with respect to these displacement vectors yields the force acting on node i and j
It turns out that the force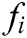 
acting on node i is equal to the sum of all 
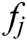acting on its neighbor nodes in magnitude but opposite direction.
Finally, the deformation displacement vector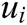 
inside the vascular tissue can be solved by Eq. (10) using integration method
where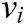 
and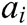 
express the velocity and acceleration of node i, respectively, 
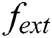and 
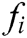are the external force and internal force, respectively, and t is the iteration time.
Since the earlier deformation model fails to simulate the biomechanical property of vascular tissue, we added stretching constraint and elastic potential energy constraint in this model using position-based dynamics method. As a result, we can realistically characterize the properties of real vascular tissue.
With the position-based dynamics method, the node positions determined by Eq. (10) is projected to a valid position so that it satisfies the defined constraints, that is, move the node and find a correction factor to modify the deformation position of the node. And the correction factor must meet the following Eq. (11)
where C is the constraint function. The correction factor of a single node obtained from Eq. (11) is as follows
where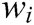 
is the reciprocal of mass 
.
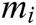As shown in Fig. 3, if the distance between nodes is not equal to their original length, the nodes are pulled or pushed by adjusting the stretching constraint to make sure their distance returns to the original length. This solves the problem of mutual penetration between nodes caused by the projection operation. Therefore, the stretching constraint function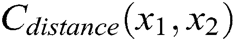 
between any two nodes is defined as
where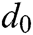 
is the original length between node 
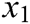and node 
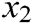. The derivatives of the function 
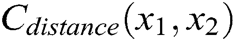are described as
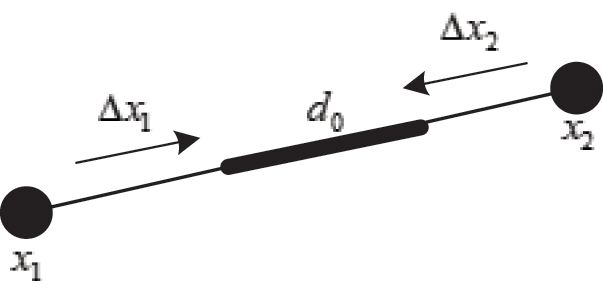
Figure 3: Stretching constraint
Hence, the correction factor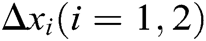 
of the node under the function of stretching constraint can be derived as follows
2.2.2 Elastic Potential Energy Constraint
The internal structure of the vascular tissue is divided into a set of virtual tetrahedrons based on discrete nodes. Here, an elastic potential energy constraint is designed to describe the elasticity of objects using the spring potential of each tetrahedron with elastic coefficients. As shown in Fig. 4, if the vascular tissue deforms, the spring potential of each deformed tetrahedron will also change correspondingly. Therefore, four nodes of the tetrahedron need to adjust their positions under the function of elastic potential energy constraint to ensure that the vascular model achieves elastic potential energy conservation during simulating the elasticity. Supposing that any two nodes in the tetrahedron are connected by a virtual spring, the elastic potential energy constraint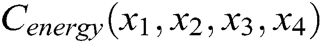 
is defined as
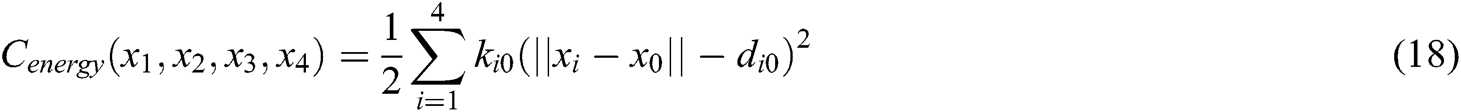
where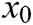 
is the barycenter of tetrahedron 
, 
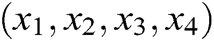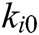is the elastic coefficient of virtual spring 
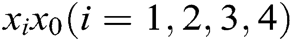connecting node 
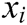and node 
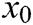, and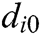 
is the original length of 
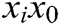. The derivatives of the function 
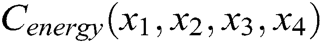are described as
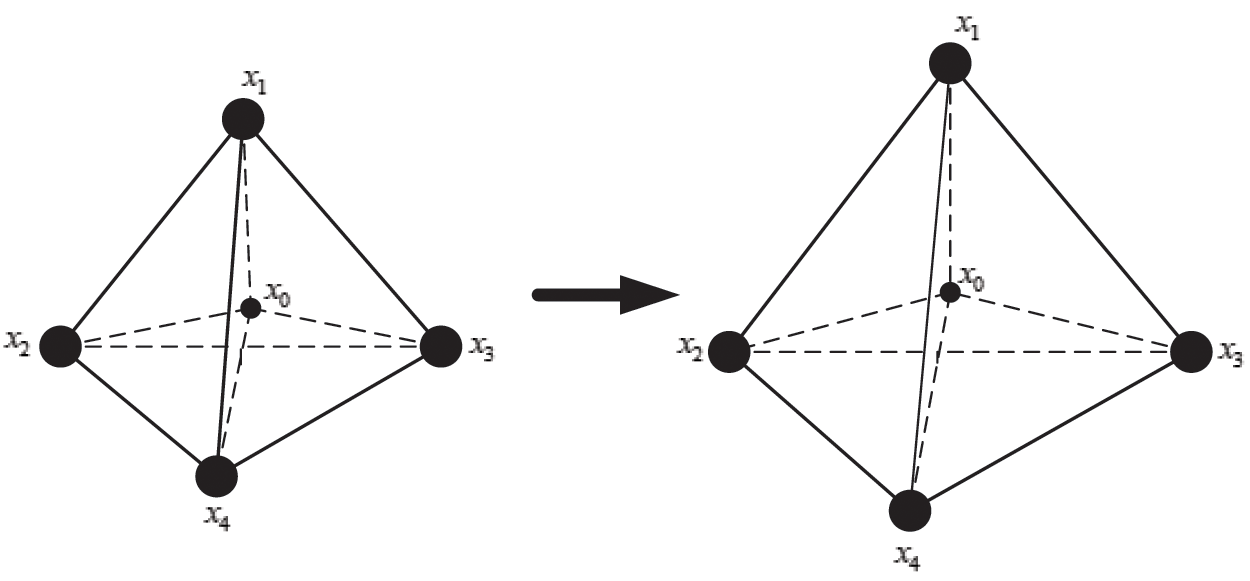
Figure 4: Elastic potential energy constraint
Hence, the correction factor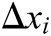 
, i=1, 2, 3, 4 of each node of the tetrahedron under the function of elastic potential energy constraint can be derived as follows
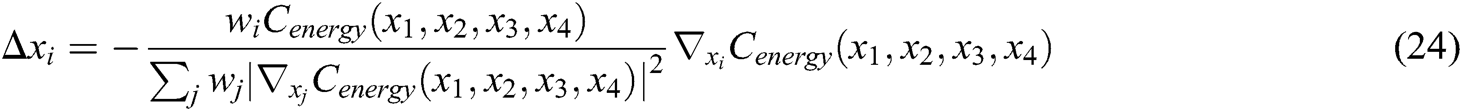
The final deformation position of the node that satisfies the stretching constraint and the elastic potential energy constraint is determined by using Eqs. (16), (17), and (24), which guarantees the elasticity of vascular tissue.
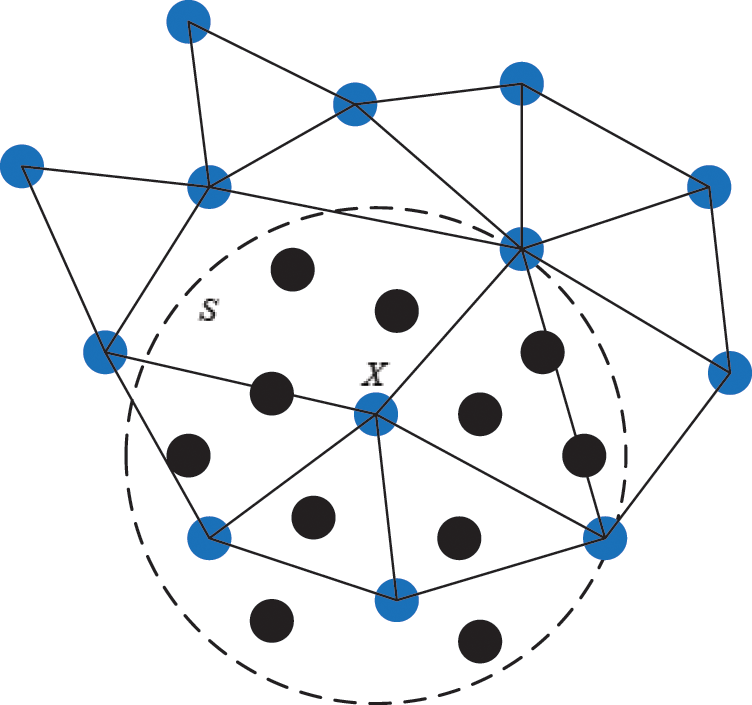
Figure 5: The support domain of surface particle X
As illustrated in Section 2.1, the motion of vascular tissue is analyzed with the internal nodes. Thus, we need to establish a mapping function from the interior to the surface of vascular tissue to visualize the deformation process and render the deformation effect based on moving least square algorithm. A set of discrete particles is used to describe the surface structure of vascular tissue, and each surface particle can be represented by the internal nodes in its support domain. The support domain of surface particle X is shown in Fig. 5, in which the blue dots represent the surface particles, the black dots represent the internal nodes, and the circular area represents the support domain S of the surface particle X. Therefore, the mapping function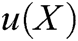 
is defined as
where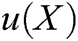 
is the field function, which represents the displacement of particle X, 
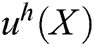is the approximation function of 
, 
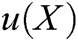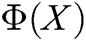is the shape function of particle X, n is the number of internal nodes in the support domain, and 
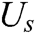is an n-dimensional vector containing the value of the deformation displacement at each node in the support domain.
The approximation function of the field function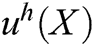 
is constructed based on moving least square algorithm and 
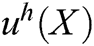is used to express the displacement of particle X. 
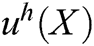is defined as follows
where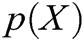 
is the polynomial basis function and 
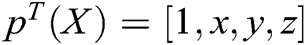, m is the number of basis function, and 
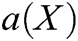is the coefficient vector, where 
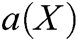can be derived by minimizing the weighted 
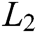norm as
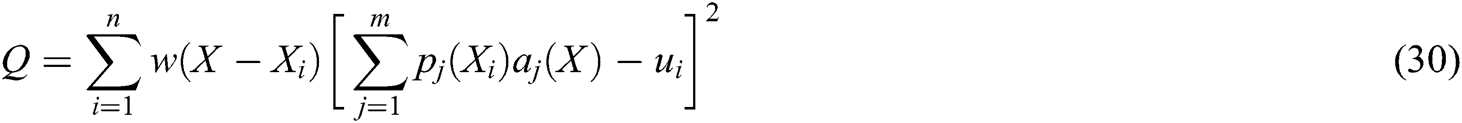
where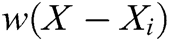 
is the weight function, 
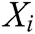is the node in support domain, and 
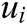is the deformation displacement of node 
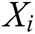. Besides, we rewrite Eq. (30) in the matrix form as
where P is the matrix of basis function and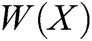 
is the matrix of weight function. Note that P and 
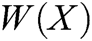are represented as follows
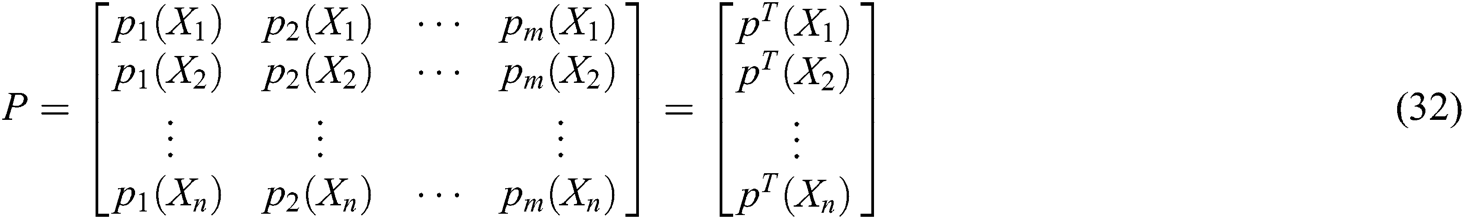
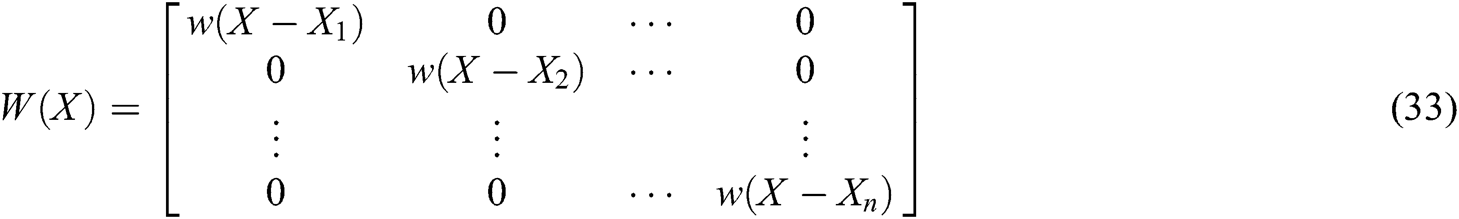
Finally, derived Eq. (31) with respect to X to obtain the coefficient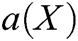 
as
where
It can be seen that the weight function plays an important role in constructing the approximate function. Therefore, the cubic spline function is adopted as the weight function, which is defined as
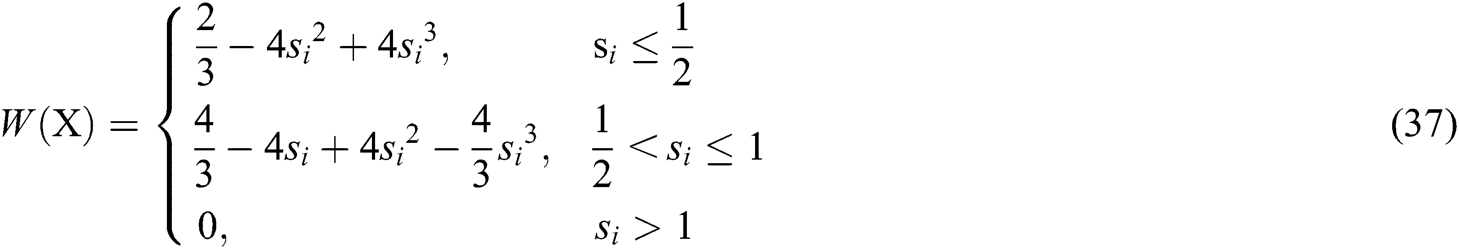
where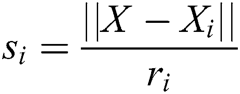 
and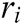 
is the radius of support domain of particle 
.
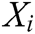Therefore, the displacement of surface particle X, is obtained, i.e., the field function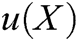 
. The field function based on moving least square algorithm can be expressed as follows
where the shape function is described as
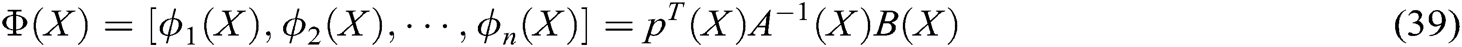
All the experiments are based on a desktop with NVIDA GeForce RTX 2080Ti, Intel(R) Core(TM) i9-9900K CPU (3.60 GHz, 8 cores) and 32G RAM, and run on the Windows 10 operating platform. We adopt VC++ 2019, 3Dmax 2019, and OpenGL 4.6 to program the proposed algorithm and model, and use PHANTOM OMNI hand controller to perform force-tactile interaction operation, which realizes the deformation simulation of the virtual aortic vessels as shown in Fig. 6.
Figure 6: Simulation environment
During the simulation, we firstly used 3Dmax software to reconstruct the 3D geometric model of vascular tissue according to the medical CT image. Besides, we employed OpenGL to visually render the vascular model and virtual surgical scene with illumination and texture mapping. Then the operator used the PHANTOM OMNI to interact with vascular tissue through a virtual surgical instrument, resulting in producing deformation under the action of an external force. Finally, the feedback force generated by the deformation is output to PHANTOM OMNI, making the operator feels the feedback force.
To verify the effectiveness of the proposed model and the stability of the virtual vascular interventional training system, we built a straight, bent, and twice bent deformation simulation process for a hand dorsal vein, aortic vessels, and retinal artery vessels, respectively, as shown in Figs. 7, 8, and 9. It can be seen that the deformation process is continuous and the fluent, the deformation effect is realistic when the operator applies the stress to vascular tissues using a virtual catheter.
Figure 7: The deformation of hand dorsal vein
Figure 8: The deformation of bent aortic vessels
Figure 9: The deformation of retinal artery vessels under bent twice state
This study added the same stress force to real and virtual hand dorsal vein, computed their displacement, and compared the force-displacement curves to verify the accuracy of the proposed model. The mass-spring model [8], the finite element model [23], the tensor-mass method [26], the filling model [27], the position-based dynamics method [16], and the proposed model in this paper are used to conduct the deformation simulation of virtual hand dorsal vein. Fig. 10 shows the force-displacement curves of real hand dorsal vein and virtual hand dorsal vein based on six different models. From seen Fig. 10, it is obvious that the virtual hand dorsal vein based on the proposed model has a similar force-displacement curve with the real hand dorsal vein, which matches the real curve better than based on other five models.
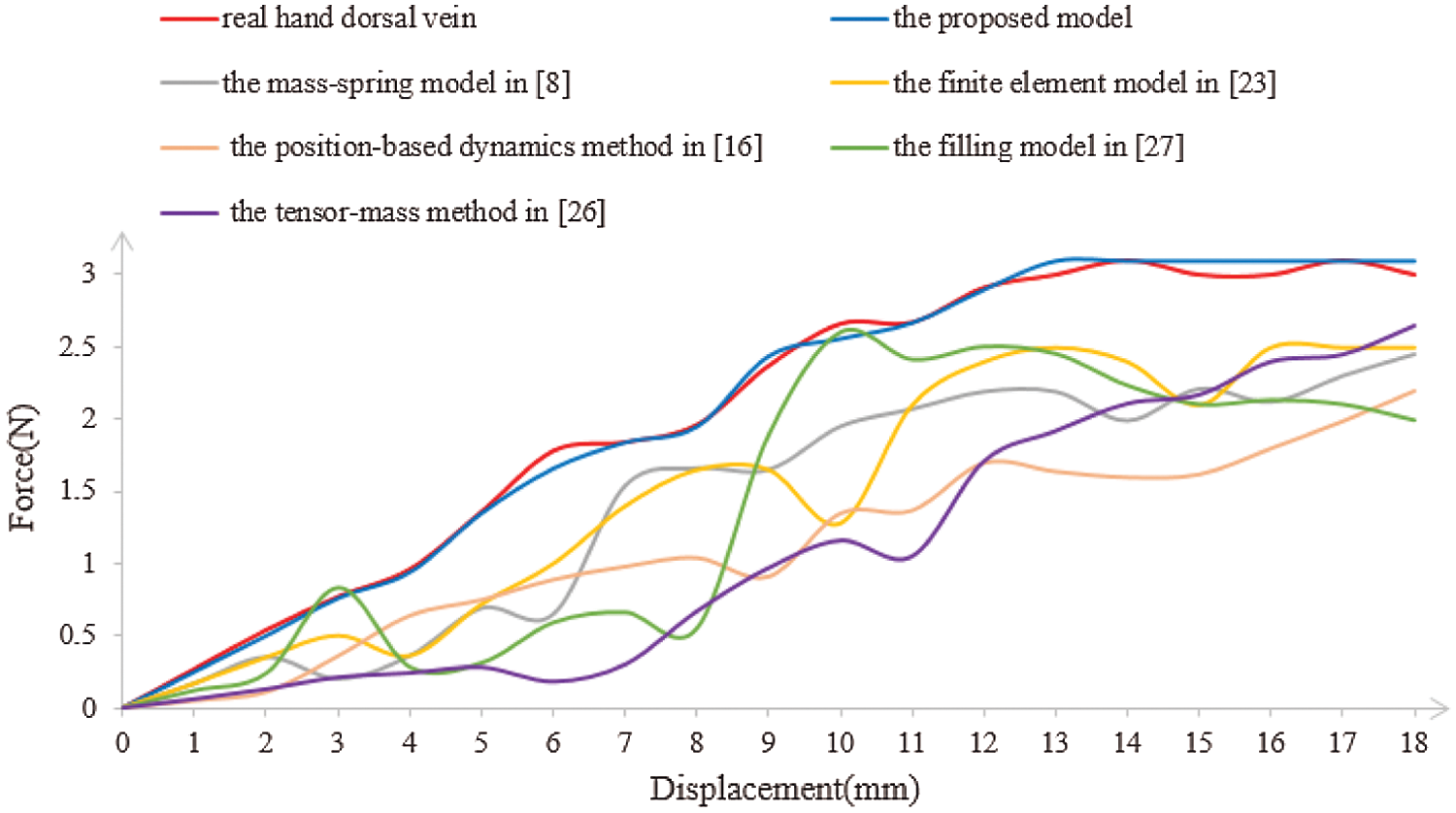
Figure 10: The force-displacement curves of real and virtual hand dorsal veins
3.3.2 Real-time Performance of Model
Real-time performance is a key factor in virtual surgery, because it directly affects the authenticity of a virtual vascular interventional training system. Frames per second (FPS) is an important indicator to measure real-time performance. Commonly, 30 frames can meet the demand for virtual surgery training. Also, the larger the FPS is, the higher the visual refresh rate is, and the better the real-time performance is [28]. Therefore, we used the mass-spring model [8], the finite element model [23], the tensor-mass method [26], the filling model [27], the position-based dynamics method [16], and the proposed model to simulate the deformation based on a different number of vascular nodes. Then, we compared the frames and the deformation time to verify the real-time performance. The deformation time and the frames of different cases are shown in Figs. 11 and 12, from which the proposed model has the least deformation time and the largest frames than the other five models based on same vascular node size. Therefore, the conclusion can be drawn that the real-time performance of the proposed model outperforms the other five models.
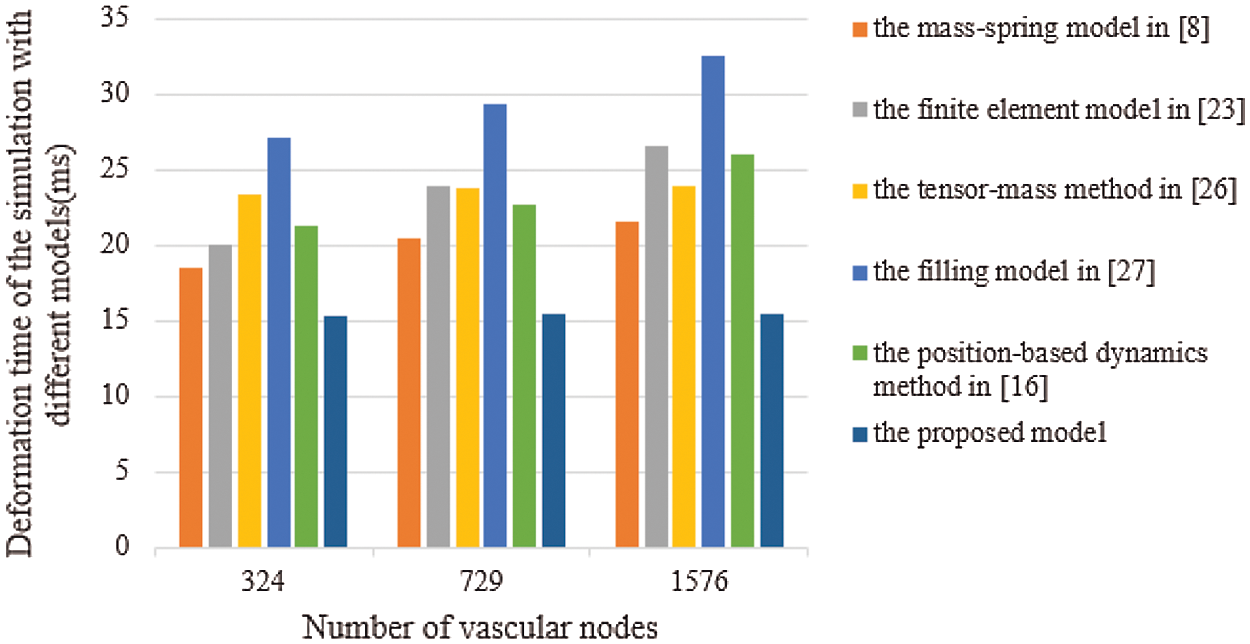
Figure 11: Deformation time of the simulation with six different models
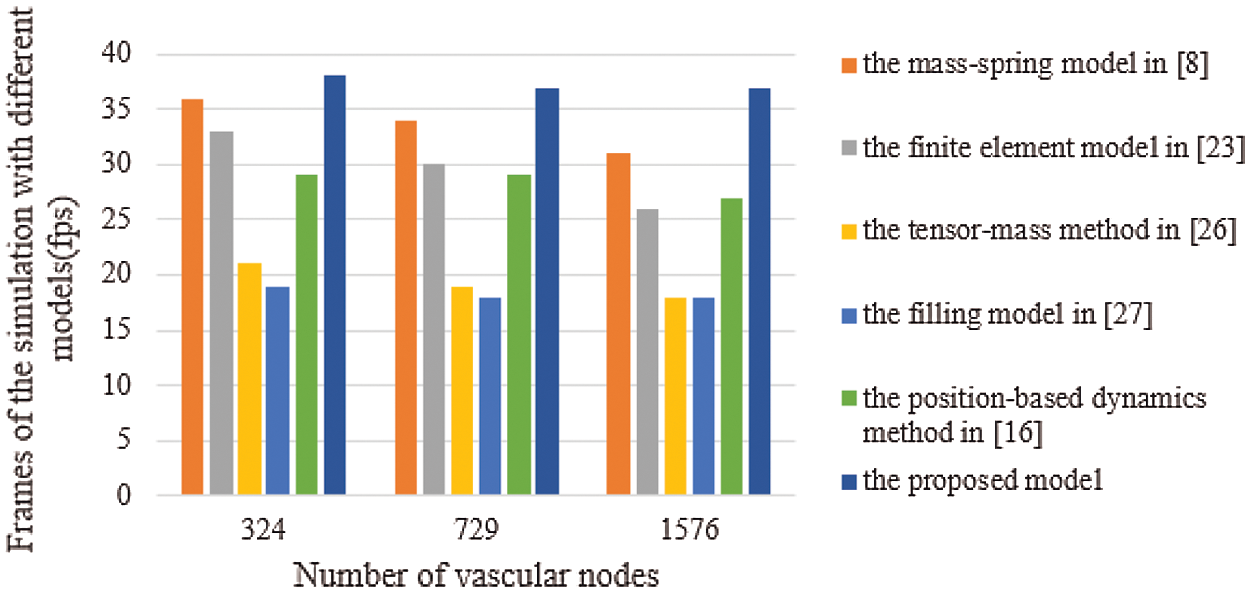
Figure 12: Frames of the simulation with six different models
3.3.3 Comprehensive Evaluation of Model
The visual characteristic, operational characteristic, and tactile characteristic of the virtual vascular interventional training system directly influence its force-tactile perception performance and friendliness of human-computer interaction. Therefore, the analytic hierarchy process [29] is utilized to verify the force-tactile perception performance of the proposed model by comparing the performance of six different models on the basis of earlier three characteristics. The six models includes the mass-spring model [8], the finite element model [23], the tensor-mass method [26], the filling model [27], the position-based dynamics method [16], and the proposed model.
Analytic hierarchy process, which evaluates the force-tactile perception performance of the simulation system based on the proposed model, is mainly divided into the following three steps:
(1) Establish the hierarchical structure of the evaluation system
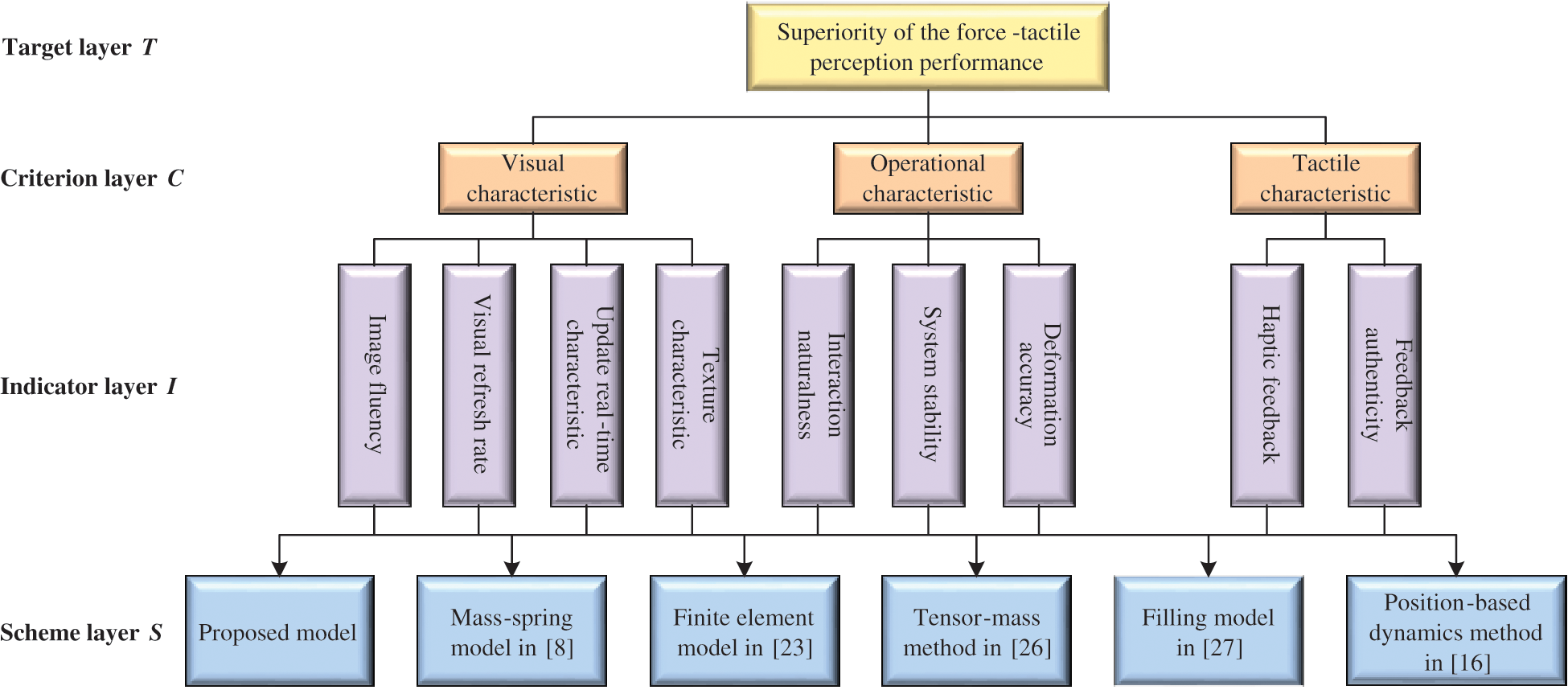
Figure 13: Evaluation system of the force-tactile perception performance
The force-tactile perception performance of the simulation system is taken as the evaluated object, and its characteristics are hierarchized to build a hierarchical structure, including the target layer, criterion layer, indicator layer, and scheme layer, which is constructed as shown in Fig. 13. The target layer T indicates the superiority of force-tactile perception performance. The criterion layer C is the first-level evaluation indicator, including visual characteristic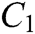 
, operational characteristic 
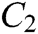, and tactile characteristic 
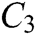. The indicator layer I is the second-level evaluation indicator, including the image fluency 
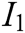, visual refresh rate 
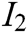, update real-time characteristic 
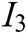, texture characteristic 
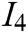, interaction naturalness 
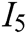, system stability 
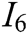, deformation accuracy 
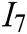, haptic feedback 
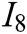, and feedback authenticity 
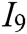. The scheme layer S is the six models mentioned previously.
(2) Determine the weight of evaluation indicator
Table 1: Weight assignment for force-tactile perception performance evaluation
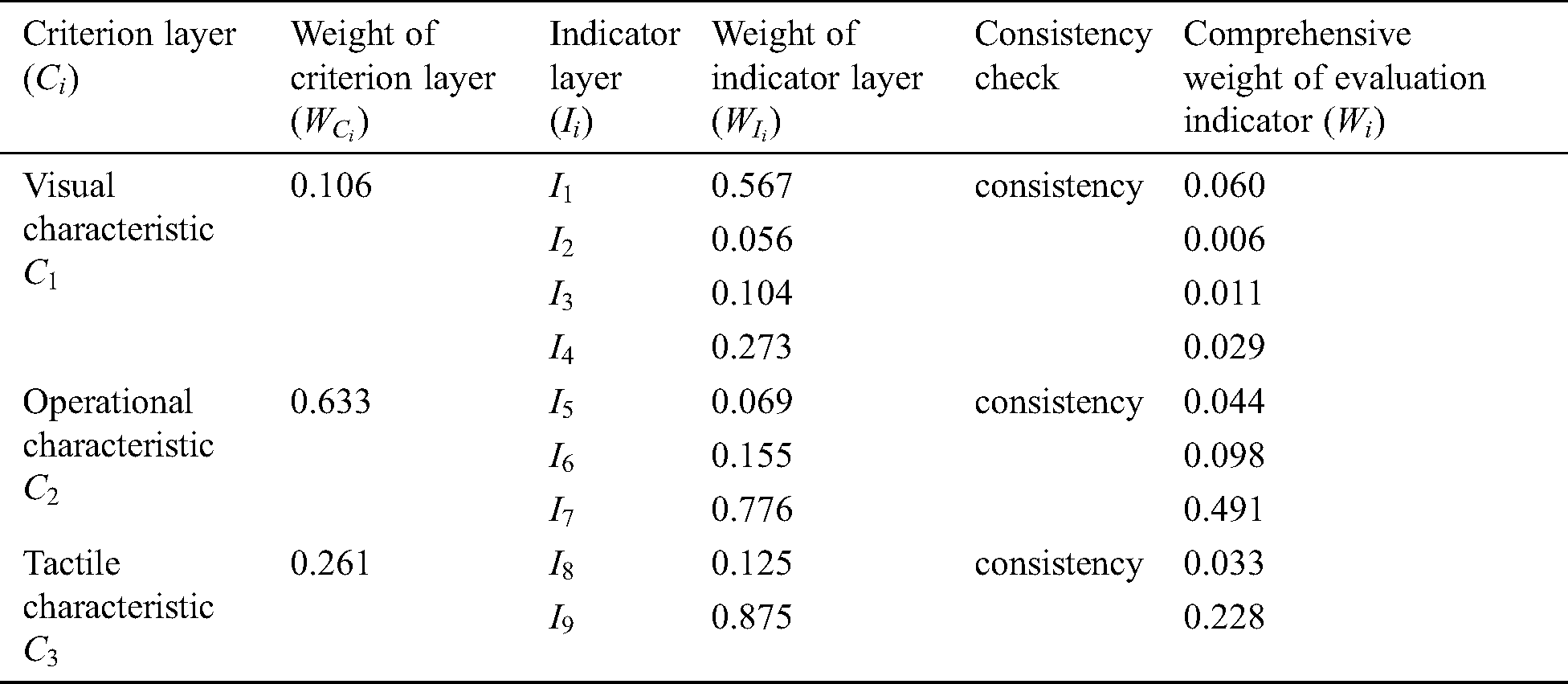
Eighteen doctors have been participating in the study from the first affiliated hospital of Nanjing Medical University, including 8 interns, 3 residents, 4 associate chief physicians, and 3 chief physicians. The doctors score each evaluation indicator based on the 1–9 ratio scale [30] according to the influence of different evaluation indicators on the force-tactile perception performance. The comparison matrix is constructed by combining the opinions of doctors on the score of the evaluation indicator, so that the weight of each evaluation indicator can be calculated and the consistency of the comparison matrix can be checked, as shown in Tab. 1.
(3) Comprehensive evaluation result
Table 2: Evaluation standard of the force-tactile perception performance
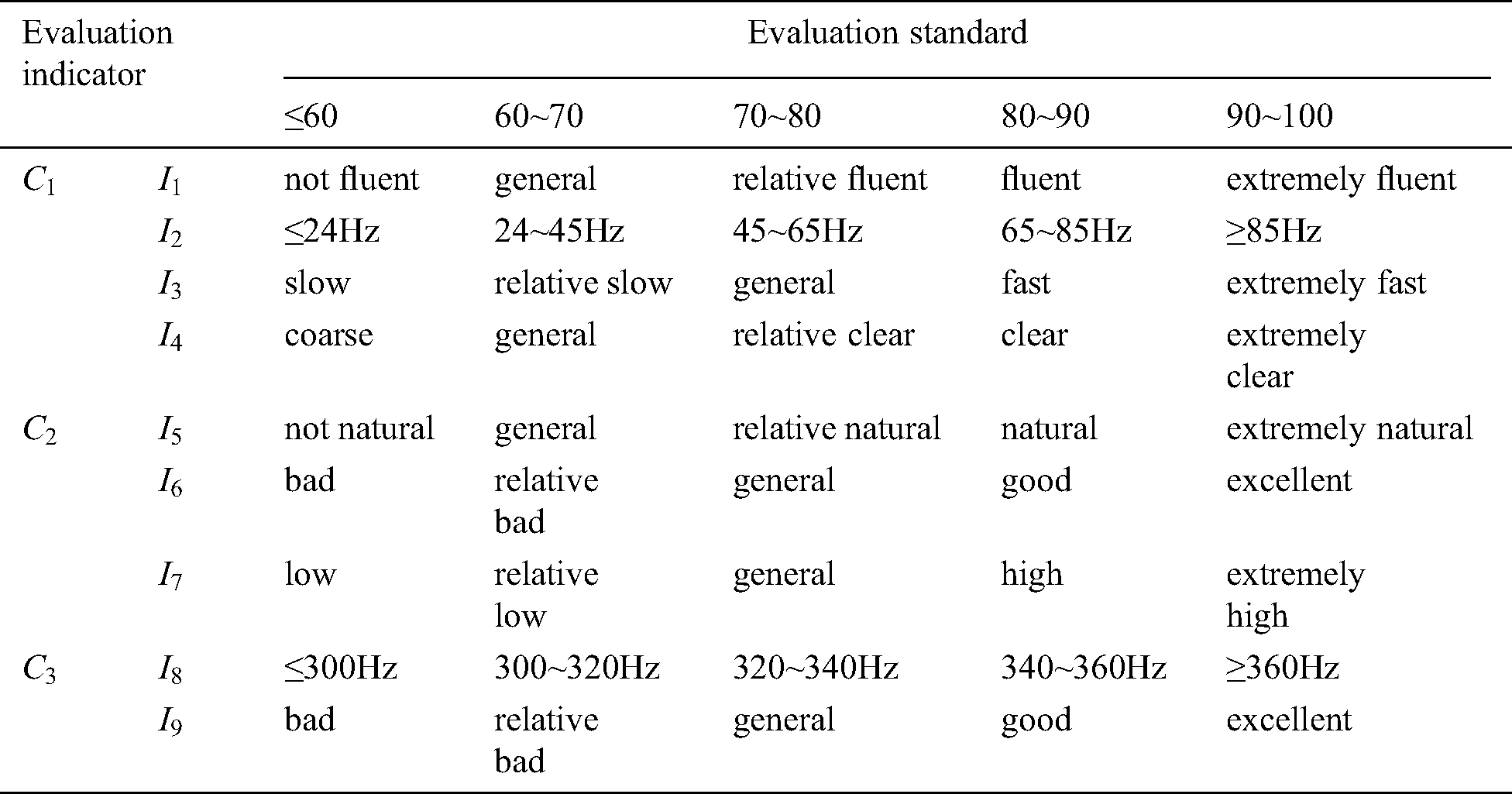
Firstly, doctors are invited to interact with the virtual vascular tissue simulation system based on the six different models through PHANTOM OMNI. Secondly, please they observe the visual characteristics, operational characteristics, and tactile characteristics carefully and define the evaluation standard of the force-tactile perception performance according to the interaction results, shown in Tab. 2. Thirdly, they grade each evaluation indicator, and finally, the comprehensive score of the force-tactile perception performance of the simulation system is obtained by multiplying each evaluation indicator score and its corresponding weight, as calculated in Eq. (40)
where G is the comprehensive score, k is the number of the evaluation indicator in the indicator layer,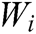 
is the comprehensive weight of evaluation indicator 
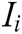, and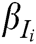 
is the score of evaluation indicator 
.
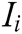The comprehensive evaluation results of the force-tactile perception performance of the simulation system is summarized in Tab. 3.
Table 3: Comparison of the comprehensive evaluation results
Tab. 3 indicates that the proposed model achieved the highest comprehensive score. It means the virtual vascular interventional training system based on our model has the best force-tactile perception performance, better visual characteristics, operational characteristics, and tactile characteristics.
In this paper, we proposed a fast and accurate vascular tissue simulation model based on point primitive method in a virtual vascular interventional training system. The deformation simulation is built on PHANTOM OMNI force-tactile feedback device with 3Dmax 2019, VC++ 2019, and OpenGL 4.6. This method establishes a deformation model to control the motion of the nodes using the point primitive method inside the vascular tissue. Besides, in this deformation model, the stretching constraint and elastic potential energy constraint are added to characterize the elasticity of soft tissue. In addition, the mapping function from the interior to surface of the vascular tissue is constructed to render the deformation effect. Experimental results show that the proposed model not only provides high deformation accuracy, but also has a fast real-time performance.
To apply the proposed model to a virtual vascular interventional training system, the force feedback needs to provide high fidelity. Follow-up research will focus to more accurate calculation, high-efficiency data processing. Furthermore, this study only simulated the deformation of vascular tissue due to the limitation of CPU computational power, which did not consider further interactions and simulations after deformation, such as constructing the cutting and bleeding simulations. In the future, we will attempt to study the cutting simulation of the vascular tissue by accelerating the deformation computation with the aid of GPU.
Funding Statement: This work was supported, in part, by the National Natural Science Foundation of China (No. 61304205, 61502240); in part, by the Natural Science Foundation of Jiangsu Province (BK20191401, BK20201136); in part, by the Innovation and Entrepreneurship Training Project of College Students (202010300290, 202010300211, 202010300116E).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Guo and S. X. Guo. (2017). “Design and characteristics evaluation of a novel VR-based robot-assisted catheterization training system with force feedback for vascular interventional surgery,” Microsystem Technologies, vol. 23, no. 8, pp. 3107–3116. [Google Scholar]
2. S. Lee, S. Shim, H. Ha, H. Lee and J. Hong. (2020). “Simultaneous optimization of patient-image registration and hand-eye calibration for accurate augmented reality in surgery,” IEEE Transactions on Biomedical Engineering, vol. 67, no. 9, pp. 2669–2682. [Google Scholar]
3. B. Martin-Perez, H. Bennis and A. M. Lacy. (2018). “Virtual reality simulation for surgery: From video games to transanal total mesorectal excision,” Techniques in Coloproctology, vol. 22, no. 1, pp. 5–6. [Google Scholar]
4. D. Luo, Y. Zhang and R. Y. Zhao. (2018). “Study on deformation technology of virtual surgery simulator based on liver puncture,” in Proc. ICRAE, Guangzhou, China, pp. 176–179. [Google Scholar]
5. X. R. Zhang, X. F. Yu, W. Sun and A. G. Song. (2020). “An optimized model for the local compression deformation of soft tissue,” KSII Transactions on Internet and Information Systems, vol. 14, no. 2, pp. 671–686. [Google Scholar]
6. X. R. Zhang, J. L. Duan, W. Sun and S. K. Jha. (2019). “A tumour perception system based on a multi-layer mass-spring model,” International Journal of Sensor Networks, vol. 31, no. 1, pp. 24–32. [Google Scholar]
7. X. R. Zhang, J. L. Duan, J. Liu and N. I. Badler. (2019). “An integrated suture simulation system with deformation constraint under a suture control strategy,” Computers, Materials & Continua, vol. 60, no. 3, pp. 1055–1071. [Google Scholar]
8. C. Q. Li, J. J. Ding, Z. C. Hong, Y. C. Pan and P. X. Liu. (2018). “A surface mass-spring model with new flexion springs and collision detection Algorithms based on volume structure for real-time soft-tissue deformation interaction,” IEEE Access, vol. 6, pp. 75572–75597. [Google Scholar]
9. W. H. Kim, E. S. Song, K. W. Ju, J. H. Lee, M. Y. Kim et al. (2019). , “Finite element analysis of novel separable fixture for easy retrievement in case with peri-implantitis,” Materials, vol. 12, no. 2, pp. 235. [Google Scholar]
10. R. Q. Fuentes-Aguilar, J. C. Bello-Robles and J. Ruiz-León. (2018). “Modeling of soft object deformation using finite element differential neural networks,” IFAC PapersOnLine, vol. 51, no. 13, pp. 474–478. [Google Scholar]
11. W. G. Hou, P. X. Liu and M. H. Zheng. (2019). “A new model of soft tissue with constraints for interactive surgical simulation,” Computer Methods and Programs in Biomedicine, vol. 175, no. Suppl. 1, pp. 35–43. [Google Scholar]
12. J. N. Zhang and S. Chauhan. (2020). “Fast computation of soft tissue thermal response under deformation based on fast explicit dynamics finite element algorithm for surgical simulation,” Computer Methods and Programs in Biomedicine, vol. 187, no. 6–8, pp. 105244. [Google Scholar]
13. P. G. M. Knoops, A. Borghi, R. W. F. Breakey, J. Ong, N. U. O. Jeelani et al. (2019). , “Three-dimensional soft tissue prediction in orthognathic surgery: A clinical comparison of Dolphin, ProPlan CMF, and probabilistic finite element modelling,” International Journal of Oral and Maxillofacial Surgery, vol. 48, no. 4, pp. 511–518. [Google Scholar]
14. S. A. Heredia-Perez, K. Harada, M. A. Padilla-Castaneda, M. Marques-Marinho and J. A. Marquez-Flores. (2019). “Virtual reality simulation of robotic transsphenoidal brain tumor resection: Evaluating dynamic motion scaling in a master-slave system,” International Journal of Medical Robotics and Computer Assisted Surgery, vol. 15, no. 1, pp. e1953. [Google Scholar]
15. Y. N. Zou, P. X. Liu, Q. Q. Cheng, P. H. Lai and C. Q. Li. (2017). “A new deformation model of biological tissue for surgery simulation,” IEEE Transactions on Cybernetics, vol. 47, no. 11, pp. 3494–3503. [Google Scholar]
16. L. Xu, Y. H. Lu and Q. Liu. (2018). “Integrating viscoelastic mass spring dampers into position-based dynamics to simulate soft tissue deformation in real time,” Royal Society Open Science, vol. 5, no. 2, pp. 171587. [Google Scholar]
17. J. J. Pan, S. Z. Yan, H. Qin and A. Hao. (2018). “Real-time dissection of organs via hybrid coupling of geometric metaballs and physics-centric mesh-free method,” Visual Computer, vol. 34, no. 1, pp. 105–116. [Google Scholar]
18. Y. J. Peng, Q. L. Li, Y. Y. Yan and Q. Wang. (2019). “Real-time deformation and cutting simulation of cornea using point based method,” Multimedia Tools and Applications, vol. 78, no. 2, pp. 2251–2268. [Google Scholar]
19. B. Gao, L. Shang, X. Cai, Y. Jiang and S. Yang. (2019). “Blood flow simulation of virtual simulation system for vascular interventional surgery,” in Proc. ICMA, Tianjin, China, pp. 2245–2250. [Google Scholar]
20. Y. Wang, S. X. Guo and B. F. Gao. (2015). “Vascular elasticity determined mass-spring model for virtual reality simulators,” International Journal of Mechatronics and Automation, vol. 5, no. 1, pp. 1–10. [Google Scholar]
21. D. M. Wu, C. S. Lv and Y. D. Bao. (2016). “An improved vascular model based on mass spring model and parameters optimization by Gaussian Processes,” in Proc. ICMA, Harbin, China, pp. 2425–2430. [Google Scholar]
22. J. Q. Hu, Y. J. Feng, S. Q. Zhou, L. P. Huang, Q. R. Zeng et al. (2017). , “An improved mass spring model based on internal point set domain constraint,” in Proc. CCDC, Chongqing, China, pp. 6826–6831. [Google Scholar]
23. X. H. Liu and J. F. Yao. (2018). “Modelling and simulation of vascular tissue based on finite element method,” in Proc. ICISCE, Zhengzhou, China, pp. 336–340. [Google Scholar]
24. X. F. Ye, J. G. Zhang, P. Li, T. Wang and S. X. Guo. (2016). “A fast and stable vascular deformation scheme for interventional surgery training system,” BioMedical Engineering OnLine, vol. 15, no. 1, pp. 572. [Google Scholar]
25. S. X. Guo, X. J. Cai, B. F. Gao, Q. X. Yang, Y. Zhao et al. (2017). , “Tensor-mass model based real-time simulation of vessels deformation and force feedback for the interventional surgery training system,” in Proc. ICMA, Takamatsu, Japan, pp. 433–438. [Google Scholar]
26. S. X. Guo, X. J. Cai and B. F. Gao. (2018). “A tensor-mass method-based vascular model and its performance evaluation for interventional surgery virtual reality simulator,” International Journal of Medical Robotics and Computer Assisted Surgery, vol. 14, no. 6, pp. e1946. [Google Scholar]
27. X. F. Ye, X. K. Mei and S. G. Xiao. (2018). “Filling model based soft tissue deformation model,” in Proc. ICMA, Changchun, China, pp. 1655–1659. [Google Scholar]
28. Y. J. Peng, Y. R. Ma, Y. H. Wang and J. L. Shan. (2017). “The application of interactive dynamic virtual surgical simulation visualization method,” Multimedia Tools and Applications, vol. 76, no. 23, pp. 25197–25214. [Google Scholar]
29. G. Guidi, M. Sliskovic, A. C. Violante and L. Vukic. (2020). “Application of the analytic hierarchy process (AHP) to select the best oil spill cleanup method in marine protected areas for calm sea condition,” Global Nest Journal, vol. 22, no. 7, pp. 354–360. [Google Scholar]
30. S. Lina. (2019). “Analysis of factors affecting investment efficiency based on analytic hierarchy process and support vector machine (SVM) model,” Cluster Computing, vol. 22, no. S2, pp. 4367–4374. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |