DOI:10.32604/iasc.2021.015793
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.015793 | |
| Article |
PTS-PAPR Reduction Technique for 5G Advanced Waveforms Using BFO Algorithm
1Department of Electronics and Communication Engineering, JECRC University, Jaipur 303905, India
2Institute of Research and Development, Duy Tan University, Danang550000, Vietnam
3Faculty of Information Technology, Duy Tan University, Danang550000, Vietnam
4Department of Mechanical Engineering, College of Engineering, Taif University, P. O. Box 11099, Taif21944, Saudi Arabia
*Corresponding Author: Dac-Nhuong Le. Email: ledacnhuong@duytan.edu.vn
Received: 01 December 2020; Accepted: 02 January 2021
Abstract: Non-orthogonal multiple access (NOMA) will play an imperative part in an advanced 5G radio arrangement, owing to its numerous benefits such as improved spectrum adeptness, fast data rate, truncated spectrum leakage, and, so on. So far, NOMA undergoes from peak to average power ratio (PAPR) problem, which shrinks the throughput of the scheme. In this article, we propose a hybrid method, centered on the combination of advanced Partial transmission sequence (PTS), Selective mapping (SLM), and bacteria foraging optimization (BFO), known as PTS-BFO and SLM-PTS. PTS and SLM are utilized at the sender side and divide the NOMA into several sub-blocks. An optimal phase factor is achieved by the BFA and combined with the NOMA sub-block, where a low peak power value is obtained. Further, we estimate the bit error rate (BER) and PAPR of BFA in the SLM and PTS technique. The simulation outputs reveal that the PTS-BFO outperforms the traditional peak power minimization approaches and moderates the complexity of the system. It is concluded that the proposed algorithm is not explored for the NOMA waveform.
Keywords: 5G; non-orthogonal multiple access (NOMA); peak to average power ratio (PAPR); partial transmission sequence (PTS); bacterial foraging optimization (BFO)
Orthogonal frequency division multiplexing (OFDM) is currently employed in 4G radio, but it is not considered for the 5G radio system due to its several disadvantages mentioned in [1–3]. FBMC is one of the best standard advanced wave form schemes that can be envisaged for 5G radio. The NOMA is one of the most promising advances for the state-of-the-art portable matching framework because of its efficient transmission capacity. One of the most significant qualities of NOMA is the use of power space to understand numerous inputs simultaneously [4]. Accordingly, it is prescribed to utilize Successive Interference cancelation method (SIC) at the sender side to upgrade the exhibition of the framework. NOMA likewise expands the limit of the 5G organize a framework allowing a few client gadgets to share indistinguishable assets. The efficiency of NOMA with versatile power portion is examined [5]. The investigation results uncover that the limit of the framework dependent on NOMA is 70% more prominent than the OFDM framework. Nevertheless, there are some obstacles in the NOMA [6,7].
The PAPR is among the few obstacles to its regularization. PAPR hampers the exhibition of the framework because the usage of the OFDM transmission conspires at the sender of the framework PAPR is regarded as one of the significant concerns in designing the FBMC framework. An escalation in PAPR decreases the excellence of the system by increasing the PAPR and bit error rate (BER) of FBMC. The design of FBMC is built in filters; Inverse Fast Fourier transforms (IFFTs) and, FFTs. The cluster of filters reduces the spectrum outflow and improves the bandwidth shaping [8,9]. BFA is regarded as the latest developments optimizer algorithm, centered on the rummage behavior of the E. coli bacteria. The principal persistence of BFA is to produce a perfect phase factor for SLM [10]. The authors of [11] described that the FBMC waveform cannot employ OFDM's conservative PAPR practices because of its uncommon configuration.
In [12], a hybrid system grounded on SLM and circular transformation (CT) is considered for the advanced waveform. The simulation fallouts show an enhanced PAPR enactment, while an upsurge in the BER factor is observed. In [13], the Genetic algorithm-bilayer partial transmission sequence (GA-BPTS) is implemented for FBMC. The unitary layer of the PTS is converted to double-layered and phase factor is derived from GA, which optimized the peak power of the structure. The bit error rate (BER) execution of the framework is improved by spreading the sign over the whole range. Also, PAPR is decreased by executing a network pre-coding pinnacle control decrease method [14]. The work in [15] proposed a survey of future generation wireless communication systems, dynamic spectrum access, and CRN, which contain many spectrum sensing methods for CRN. This improves dynamic spectrum usage and minimizes intrusion for authorized users. The best possible solutions for multiple-band joint detection are analyzed in a practical environment. An experimental result reveals that prediction spectrum detection techniques can significantly improve system efficiency. The work in [16] gave their contemplations towards range seeing in the advanced radio. Architects advance the synergistic vision system through the introduction of importance and NOMA. The results of the reconstruction and examination indicate that the system can reasonably update the probability of opening the range of vision. A sincere and key test of wireless systems is to offer the cell some assistance with edging profit, execution, and ampleness and attract multi-stream transmissions to cell edge customers. Obstacle engagement systems based on various radio wires and inter-cell coordination are now strongly oriented towards synthesis. In the current work, the NOMA PAPR implementation is explored. In this paper, we propose and demonstrate a novel and suitable method for the NOMA framework relying upon various radio wires at the transmitter of the transmitting module and the recipient. The traditional reduction methods and proposed BFA reduction methods have not been contemplated. Also, it eliminates the problem of adjacent channel interference in the QAM modulated communication system. To the best of our understanding and the work presented, it should be noted that the suggested SLM-BFA and PTS-BFA are not currently under consideration for the NOMA waveform.
In this work, we integrate PTS-BFO and SLM-BFO. Initially, PTS and SLM are applied to the NOMA, and subsequently the BFO phase elements are multiplied by the PTS and SLM-OMA symbols. The diverse combinations of phase factors and sub-blocks are applied to decrease the PAPR of the structure.
The schematic of NOMA is given in Fig. 1.
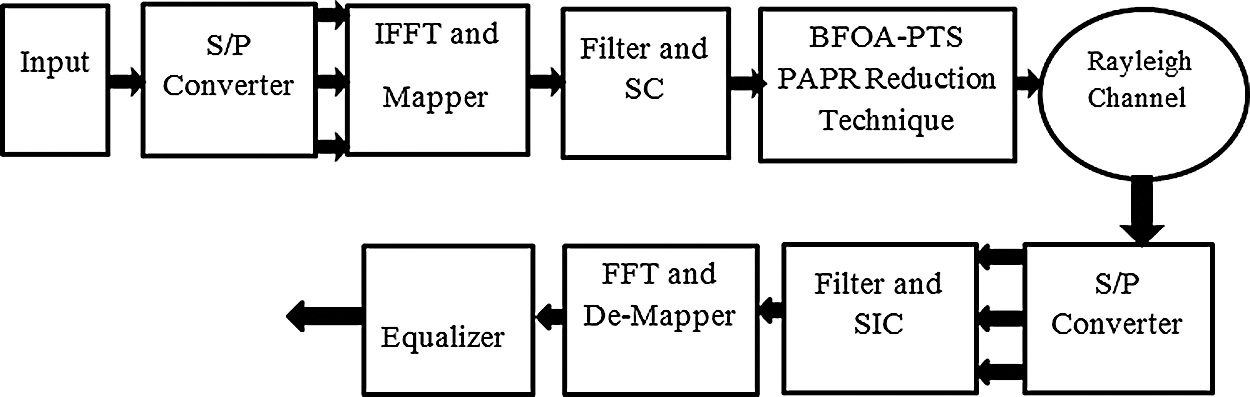
Figure 1: NOMA
The NOMA signal can be represented as [17]:
where k = 0, 1, 2…N-1. The Eq. (1) after the PHYDYAS filter can be represented as:
where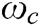 
is the carrier frequency, and 
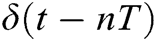is the PHYYDAS filter.
From, Eq. (2), the PAPR of the NOMA signal can be written as:
where E {} is the expected value.
Traditionally, PAPR is defined in terms of dB:
To analyze the effect of the reduction method, it is imperative to evaluate the complementary cumulative distribution function (CCDF) of PAPR. The CCDF of NOMA waveform is presented every bit:
2.1 Bacterial Foraging Optimization Algorithm (BFOA)
BFA is extensively employed as a novel optimization technique. It is based on the nature of E. coli bacteria. It is one of the universally adopted algorithms for analyzing the difficulties that arise in the process of optimizing the real environment [18]. There are three stages to a BFO:
a) Chemotaxis: It is a procedure to perform a run and tumble and final estimates the fitness value of bacterium,
b) Reproduction: It estimates the health position and classifies the bacterium in descending sequence in accordance with the health rank of the bacterium and
c) Termination: It involves eliminating the bacterium that has a poor health [19]. The bacterium with high fitness condition indicates the ideal location in the environment.
In the proposed algorithm, the main concern is to find the ideal value of the phase factor which can be multiplied by the NOMA symbols for an optimal peak power [20]. The schematic of the proposed model is illustrated in Fig. 2.
The objective of the projected work is attained in dualistic phases. In the first stage, the advanced SLM and PTS are used for the NOMA signal. It pursues the division of all sub-blocks. SLM and PTS also upsurge the computational intricacy due to the use of IFFTS. In the second phase, we use a BFA to identify an enhanced phase element for SLM, which reduces the PAPR and system complexity.
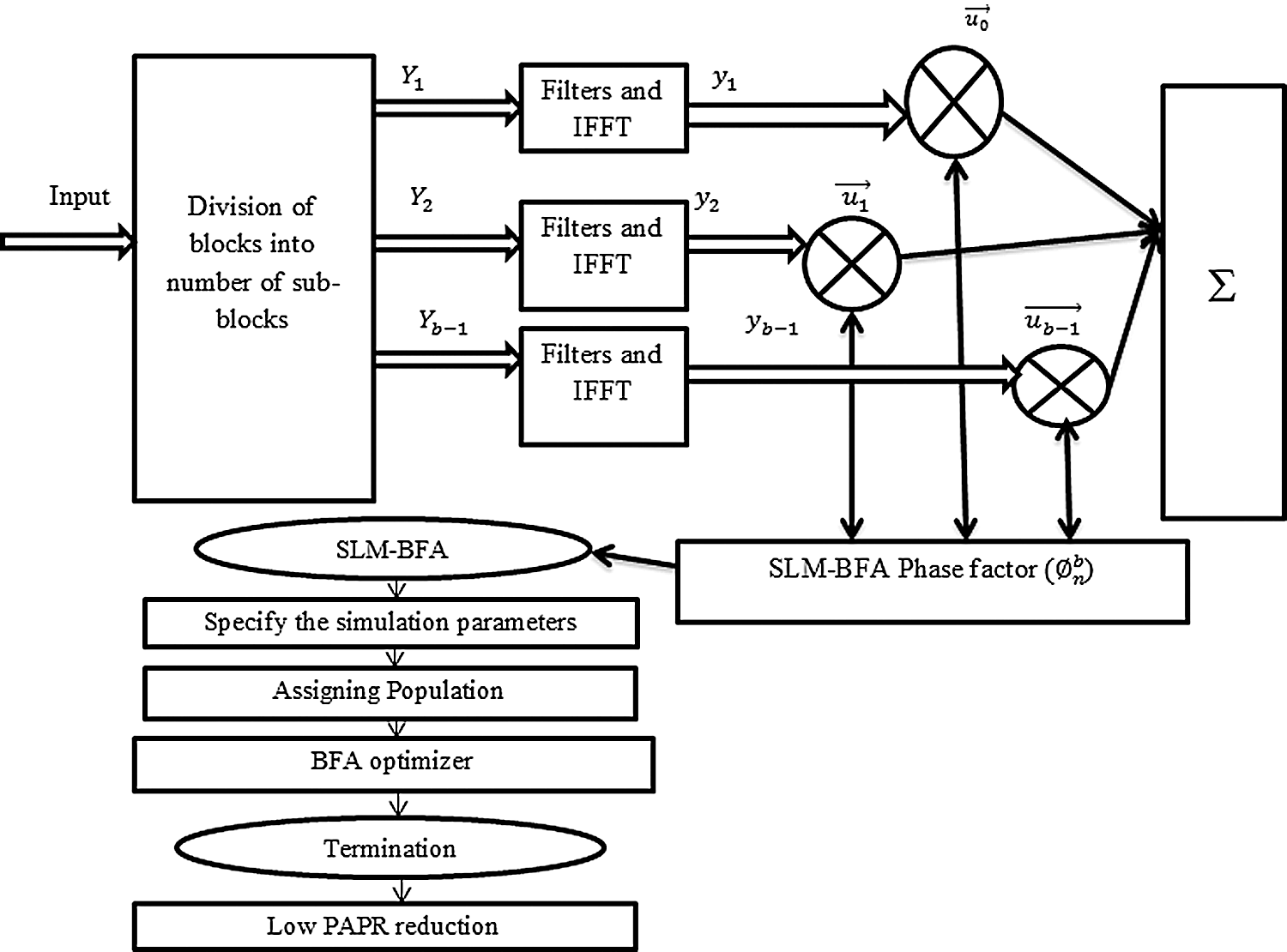
Figure 2: Proposed model
The NOMA may be represented by equation [21] as follows:
where b is the sub-blocks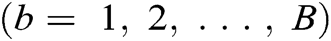 
and n is the number of sub-carriers. The real 
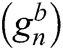and imaginary 
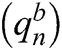FBMC symbols for 
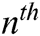sub-carriers can be expressed as:
A cluster of the filter is applied on Eq. (7), resulting:
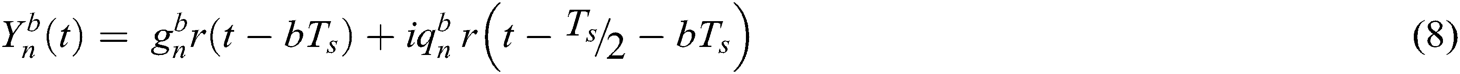
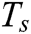is the phase period of the NOMA symbol and r is the characteristic of the filter. The IFFT of 
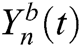is expressed as [22]:
Now, the BFA is applied to obtain an optimal phase sequence for SLM and PTS. The composite phase aspect is expressed as:
where 
are generated to integrate with SLM. The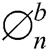 
is characterized in terms of vector U is given as:
The NOMA symbol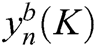 
with BFA optimal phase factor 
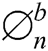is expressed as:
The preeminent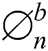 
incorporation of 
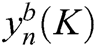with the lowest PAPR is picked as:
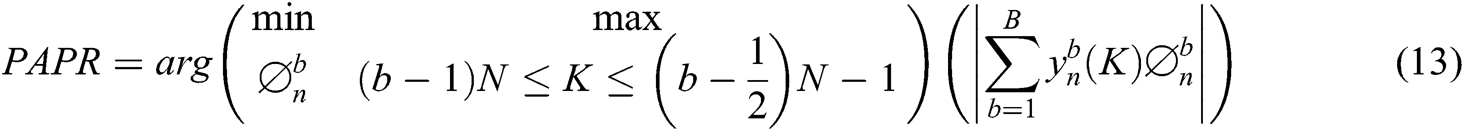
From Eq. (13), it is noted that the SLM-PTS-BFO familiarized two crucial constraints U, and b, hence PAPR of the NOMA signal can be diminished by choosing different values of U, and b.
The present work is analyzed by using Matlab-2014. The constraints used in the model are shown in Tab. 1.
Table 1: Simulation Parameters
In the presented simulation, we have selected N = 256, 64-QAM transmission scheme, PHYDYAS filter with roll-off factor (α = 1), b = 8, 16, 32, U = 2, and 4. The proposed approach is rigorously reviewed with a Matlab-2014. Considering the complexity, the number of multiplications required by the SLM-BFA are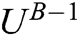 
in comparison to the SLM [23] (4N2 V + 8V2), where N is total sub-carriers and V is sub-blocks. The multiplications requisite in the PTS-BFA are 
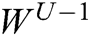whereas the PTS and SLM-CT [19] needs 4N (NV+ 2VV, 4 (N + 2V) multiplications and 2 (2N + 2U + 2 × 2UU − V − U), 2N (2NV + U) additions, where V is the sub-blocks, N is the total number of sub-carriers and W and b is phase factors. In terms of complexity, the BFO surpasses conventional techniques. Tab. 1 indicates the constraints utilized in the present computer simulation.
Fig. 3 represents the PAPR performance of SLM-BFO and conventional SLM. The best PAPR performance is accomplished by changing the values of U and b. For the CCDF of 0.1%, the PAPR is reduced to 10 dB, 7.9 dB, 5.8 dB, 5.2 dB, 3.9 dB, 3.1 dB and 2.1 dB for SLM, U = 2 b = 8, U = 2 b = 16, U = 2 b = 32, U = 4 b = 8, U = 4 b = 16 and U = 8 b = 32. It has been established that peak performance can be achieved through two constraints.
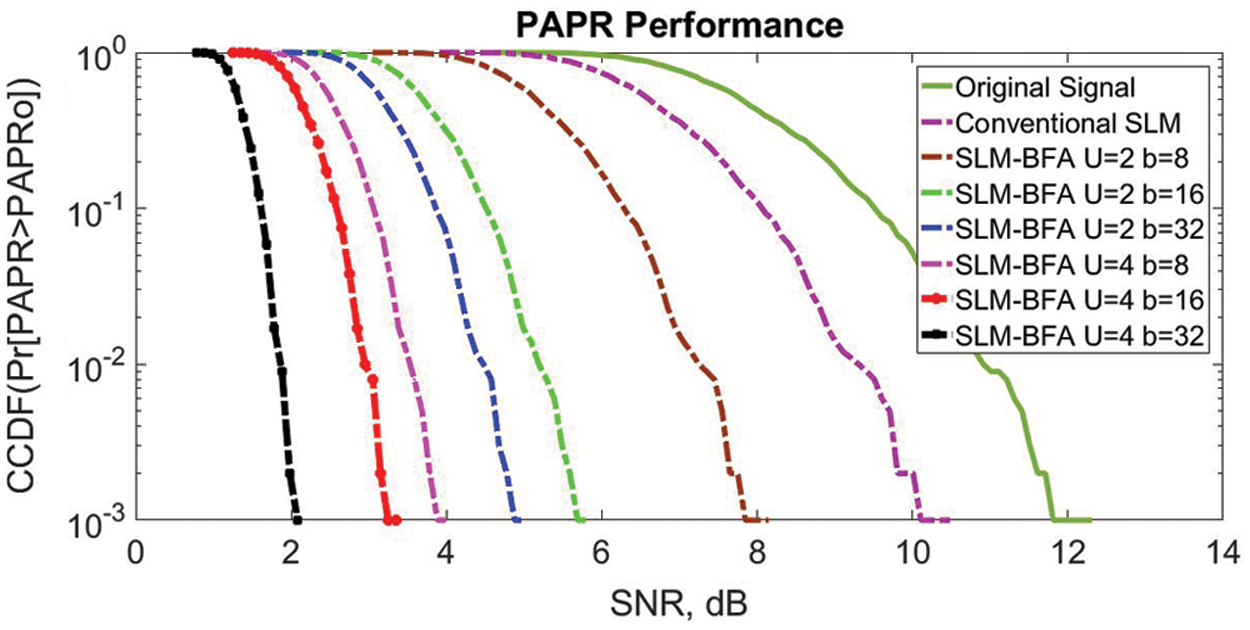
Figure 3: PAPR performance
Fig. 4. illustrates the BER performance of SLM-BFA and SLM. In order to obtain a BER of 0.010%, the signal to noise ratio (SNR) are 12 dB, 9.7 dB, 8.8 dB, 8.2 dB, 7.2 dB, 5.4 dB and 4.3 dB for SLM, U = 2 b = 8, U = 2 b = 16, U = 2 b = 32, U = 4 b = 8, U = 4 b = 16 and U = 8 b = 32.
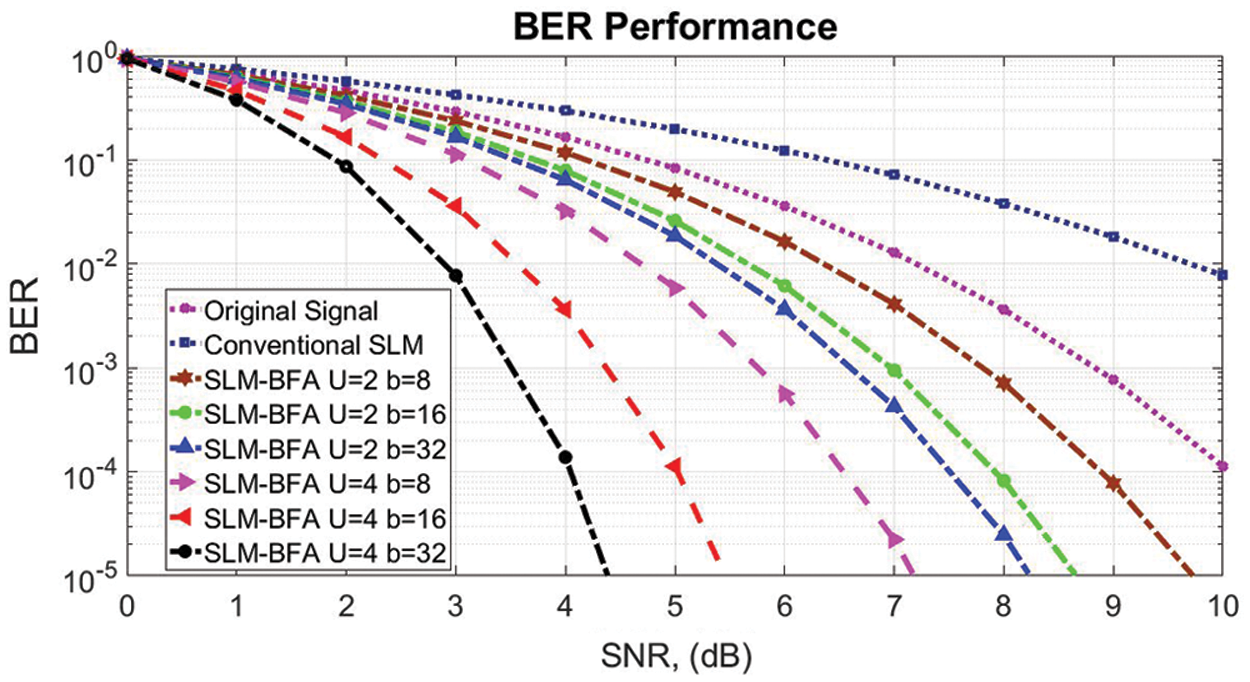
Figure 4: BER performance
The CCDF for NOMA PAPR is illustrated in the Fig. 5. The gain of 17 dB in the PAPR is achieved by the PTS. It is seen that the gain of 4 dB, 37 dB, 44 dB, 63 dB, 68 dB for the diverse value of u and W, respectively. The ideal PAPR performance has resulted in u = 4 and b = 32.
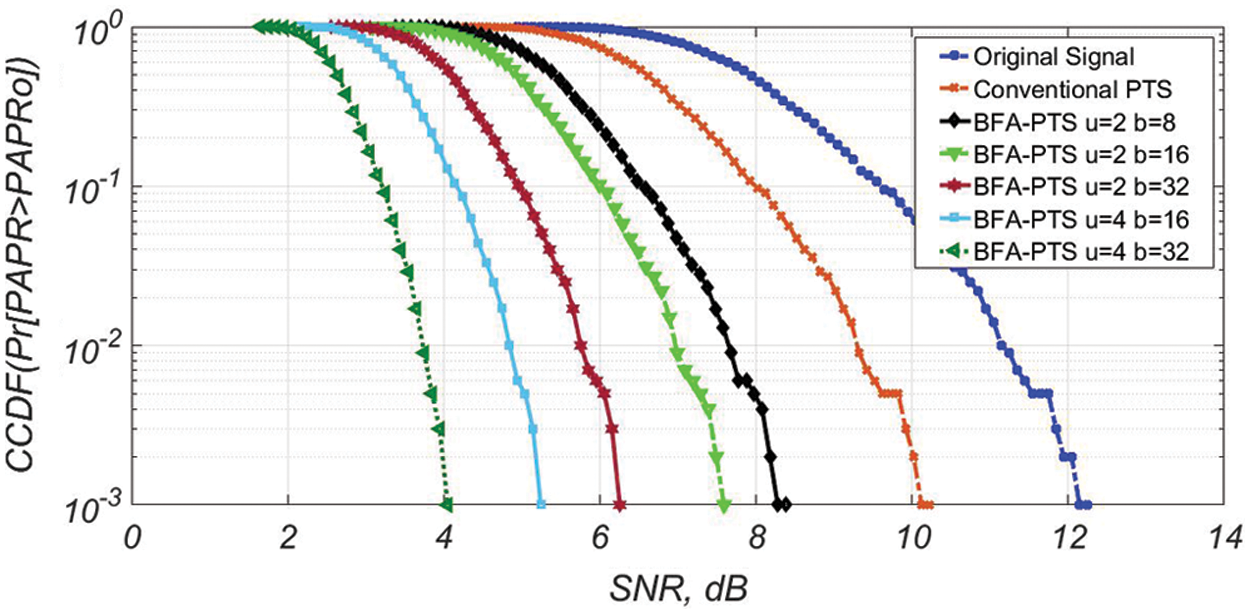
Figure 5: PAPR BFA-PTS
The BER curve is shown in Fig. 6. It is seen that the reduction algorithms obtained a gain of 18 dB, 36 dB, 43 dB, 49 dB, 72 dB, and 79 dB, for diverse ideals of sub-blocks and phase factors, respectively. The best possible PAPR performance is seen for u = 4 and b = 32.
Figure 6: BER BFA-PTS
To analyze the throughput of the OFDM and NOMA waveform, the BER performance estimation is shown in Fig. 7. The SNRs of the OFDM and NOMA are 12 dB and 14.5 dB, for BER of 10−3 dB. It indicates that the NOMA obtained a gain of 2.5 dB as compared to the OFDM structure [24]. In addition, the NOMA throughput is improved in an efficient manner by applying a proposed BFO-PTS and BFO-SLM.
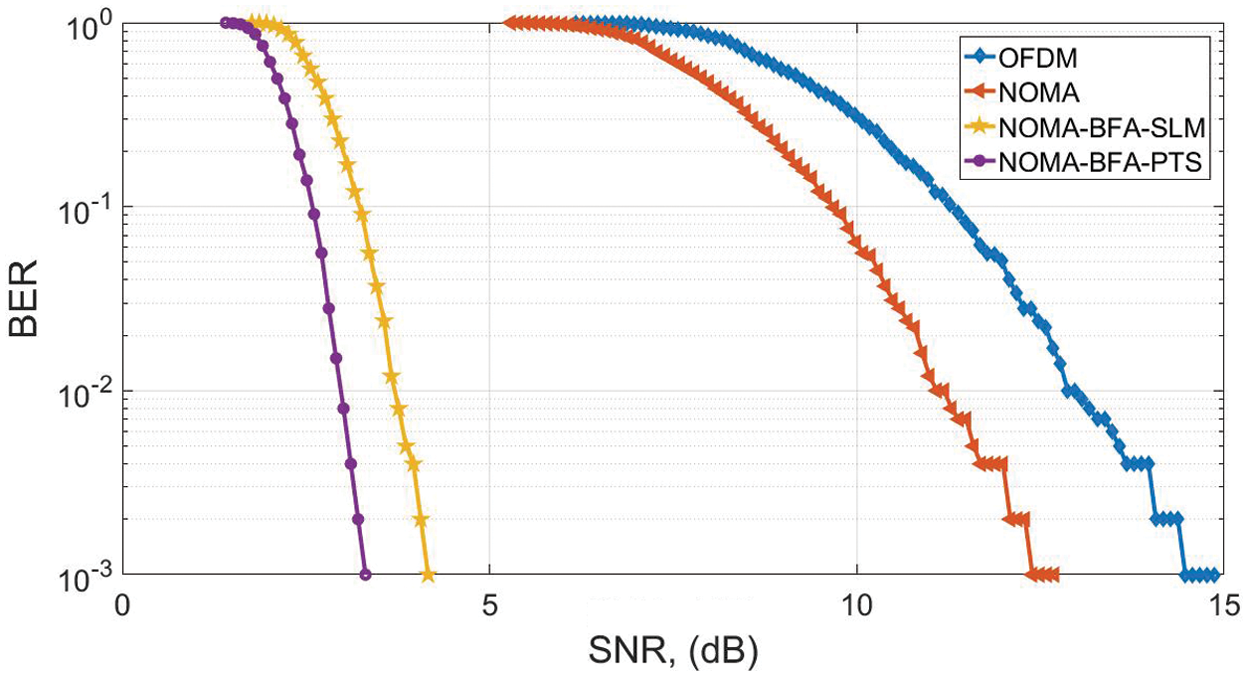
Figure 7: BER NOMA & OFDM
The conventional OFDM and proposed NOMA waveform schemes are examined to calculate the peak power performance, indicated in Fig. 8. The CCDF of 10−3 is obtained at the SNR of 10.5 dB and 13.5 dB for the OFDM and NOMA waveform. Hence, it is concluded that the peak power efficiency of NOMA is better than the conventional OFDM structure.
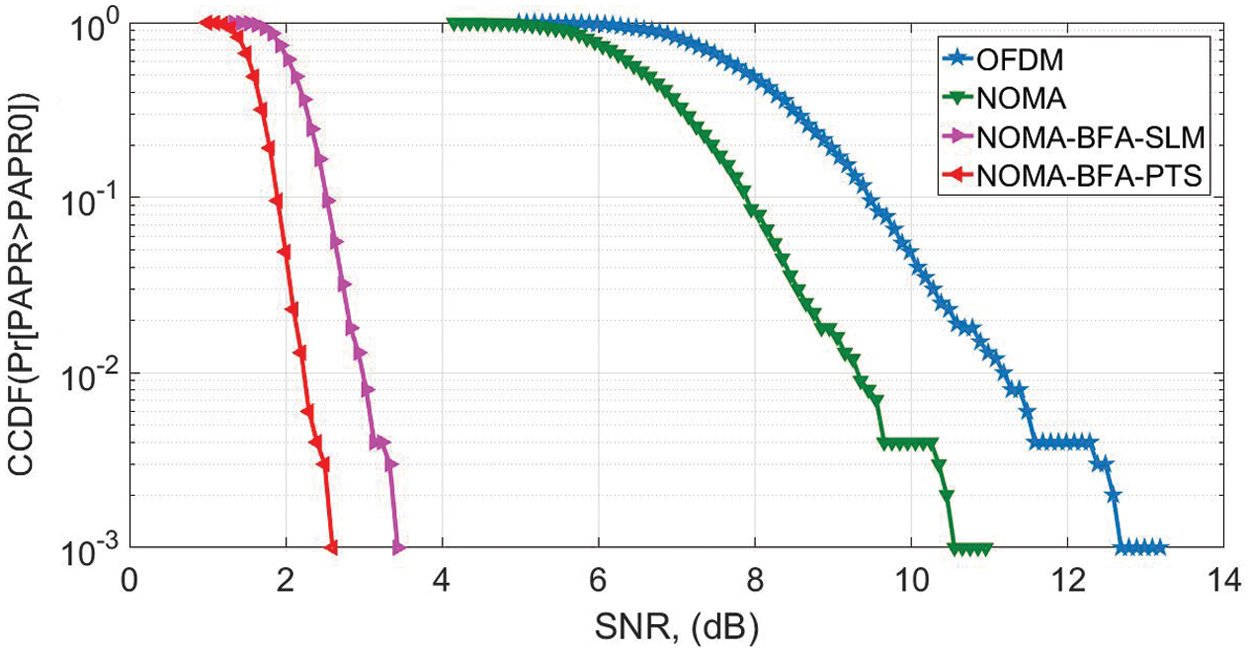
Figure 8: PAPR NOMA & OFDM
The Power spectrum density (PSD) of NOMA is demonstrated in Fig. 9. It is observed that the out of band spectrum leakage performance of the NOMA waveform is efficient and guarantees the high spectral access of the framework.
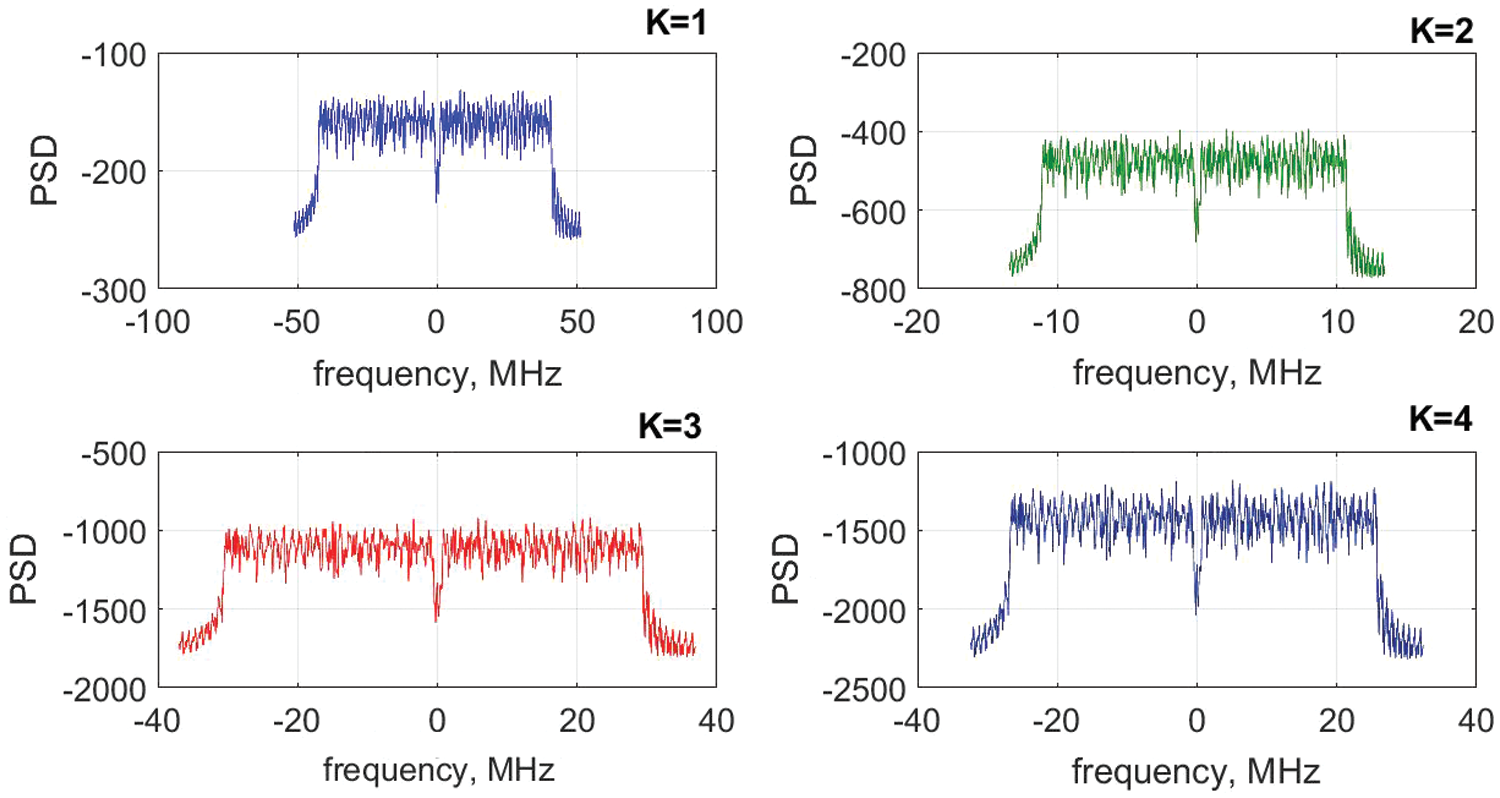
Figure 9: PSD of NOMA
In this work, the hybrid PAPR algorithms are implemented for the 256-QAM-NOMA structure. PTS and SLM are regarded as one of the most dynamic methods to decrease the PAPR of the waveforms. It also prompts high computational intricacy. Further, a BFO is implemented to find a suitable phase element for which an optimal PAPR is attained. The conclusions of the simulation reveal that the NOMA with SLM-BFO and PTS-BFO performed better than the traditional PAPR procedures and in particular reduced the complexity of the NOMA structure. In the future, BFA can be combined with a number of advanced PAPR methods for 5G waveform.
Funding Statement: Taif University Researchers Supporting Project number (TURSP-2020/77), Taif university, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Arun, B. Shikha and G. Manisha. (2019). “FBMC vs. OFDM: 5G mobile communication system,” International Journal of Systems, Control and Communications, vol. 10, no. 3, pp. 250–264. [Google Scholar]
2. A. Kumar, M. A. Albreem, M. Gupta, M. H. Alsharif and S. Kim. (2020). “Future 5G network based smart hospitals: hybrid detection technique for latency improvement,” IEEE Access, vol. 8, pp. 153240–153249. [Google Scholar]
3. S. Chen and J. Zhao. (2014). “The requirements challenges and technologies for 5G of terrestrial mobile telecommunication,” IEEE Commun. Magazine, vol. 52, no. 5, pp. 36–43. [Google Scholar]
4. A. Kumar and M. Gupta. (2015). “A novel modulation technique for 5G mobile communication system,” American Journal of Applied Sciences, vol. 12, no. 9, pp. 601–605. [Google Scholar]
5. I. Baig and V. Jeoti. (2011). “A new discrete Hartley transform precoding based interleaved-OFDMA uplink system with reduced PAPR from 4G cellular networks,” Journal of Engineering Science and Technology, vol. 6, no. 6, pp. 685–694. [Google Scholar]
6. I. Baig, N. ulHasan, M. Zghaibeh, I. U. Khan and A. S. Saand. (2017). “A DST precoding based uplink NNOMA scheme for PAPR reduction in 5G wireless network,” in 2017 7th Int. Conf. on Modeling, Simulation, and Applied Optimization (ICMSAOSharjah, pp. 1–4. [Google Scholar]
7. Y. Saito, Y. Kishiyama, A. Benjebbour, T. Nakamura, A. Li et al. (2013). , “Non-orthogonal multiple access (NNOMA) for cellular future radio access,” in Proc. of IEEE 77th Vehicular Technology Conf. (VTCpp. 1–5. [Google Scholar]
8. D. Na and K. Choi. (2018). “Low PAPR FBMC,” IEEE Transactions on Wireless Communications, vol. 17, no. 1, pp. 182–193. [Google Scholar]
9. H. Liang and H. Jiang. (2019). “The modified artificial bee colony-based SLM scheme for PAPR reduction in OFDM systems,” in 2019 Int. Conf. on Artificial Intelligence in Information and Communication (ICAIIC). Okinawa, Japan, 504–508. [Google Scholar]
10. Q. Zhang, H. Chen, J. Luo, Y. Xu and C et al. (2018). , “Wu etal, Chaos enhanced bacterial foraging optimization for global optimization,” IEEE Access, vol. 6, pp. 64905–64919. [Google Scholar]
11. F. Sandoval, G. Poitau and F. Gagnon. (2017). “Hybrid peak-to-average power ratio reduction techniques: Review and performance comparison,” IEEE Access, vol. 5, pp. 27145–27161. [Google Scholar]
12. K. Arun. (2019). “Novel hybrid PAPR reduction technique for NOMA and FBMC system and its impact in power amplifiers,” IETE Journal of Research, vol. 65, no. 5, pp. 1–17. [Google Scholar]
13. L. V. Siying and Z. Junhui. (2019). “Genetic Algorithm Based Bilayer PTS scheme for peak-to-average power ratio reduction of FBMC/OQAM signal,” IEEE Access, vol. 8, pp. 17945–17955. [Google Scholar]
14. I. F. Akyildiz, W. V. Lee and S. Mohanty. (2006). “Next generation/dynamic spectrum access cognitive radio wireless network-A survey, Computer Networks,” Elsevier, vol. 50, no. 13, pp. 2127–2159. [Google Scholar]
15. C. C. Tu and B. Champagne. (2010). “Subspace-Based Blind Channel Estimation for MIMO-OFDM systems with reduced time averaging,” IEEE Transactions on Vehicular Technology and Advancements, vol. 59, no. 3, pp. 1539,1544. [Google Scholar]
16. J. Tong, L. Ping and X. Ma. (2009). “Superposition coded modulation with peak-power limitation,” IEEE Transactions on information Theory, vol. 55, no. 6, pp. 2562–2576. [Google Scholar]
17. I. Baig, U. Farooq, N. U. Hasan, M. Zghaibeh, U. M. Rana et al. (2018). , “On the PAPR reduction: A novel filtering based Hadamard transform precoded uplink MC-NOMA scheme for 5G cellular networks,” in 2018 1st IEEE International Conference on Computer Applications & Information Security (ICCAISpp. 1–4. [Google Scholar]
18. K. Arun and M. Gupta. (2020). “Peak average power reduction in NOMA by using PTSCT technique,” Recent Advances in Computer Science and Communications, vol. 13, no. 3, pp. 502–507. [Google Scholar]
19. S. Das, A. Biswas, S. Dasgupta and A. Abraham. (2009). “Bacterial foraging optimization algorithm: theoretical foundations, analysis, and applications,” in Foundations of Computational Intelligence, vol. 3. Studies in Computational Intelligence, vol. 203, Berlin, Heidelberg: Springer, pp. 23–55. [Google Scholar]
20. S. Mishra and C. N. Bhende. (2007). “Bacterial foraging technique-based optimized active power filter for load compensation,” IEEE Transactions on Power Delivery, vol. 22, no. 1, pp. 457–465. [Google Scholar]
21. M. Humayun, N. Jhanjhi, M. Alruwaili, S. S. Amalathas, V. Balasubramanian et al. (2020). , “Privacy Protection and Energy Optimization for 5G-Aided Industrial Internet of Things,” IEEE Access, vol. 8, pp. 183665–183677. [Google Scholar]
22. A. Kumar, M. A. Albreem, M. Gupta, M. H. Alsharif and S. Kim. (2020). “Future 5G network based smart hospitals: Hybrid detection technique for latency improvement,” IEEE Access, vol. 8, pp. 153240–153249. [Google Scholar]
23. A. Kumar and M. Gupta. (2020). “A comprehensive study of PAPR reduction techniques: design of DSLM-CT joint reduction technique for advanced waveform,” Soft Computing, vol. 24, no. 16, pp. 11893–11907. [Google Scholar]
24. A. Kumar. (2020). “Detection in 5G mobile communication system using hybrid technique,” National Academy Science Letters, vol. 30, no. 1, pp. 40. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |