DOI:10.32604/iasc.2021.015460

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.015460 |  |
| Article |
Filter-Based Feature Selection and Machine-Learning Classification of Cancer Data
College of Computer Science and Engineering, Taibah University, Yanbu, Saudi Arabia
*Corresponding Author: Mohammed Farsi. Email: mailto: Mafarsi@taibahu.edu.sa
Received: 22 November 2020; Accepted: 02 February 2021
Abstract: Microarray cancer data poses many challenges for machine-learning (ML) classification including noisy data, small sample size, high dimensionality, and imbalanced class labels. In this paper, we propose a framework to address these problems by properly utilizing feature-selection techniques. The most important features of the cancer datasets were extracted with Logistic Regression (LR), Chi-2, Random Forest (RF), and LightGBM. These extracted features served as input columns in an applied classification task. This framework’s main advantages are reducing time complexity and the number of irrelevant features for the dataset. For evaluation, the proposed method was compared to models using Support Vector Machine (SVM), k-Nearest Neighbor (KNN), Decision Tree (DT), LR, and RF. To prove the proposed framework’s efficiency, all the experiments were performed on four standard datasets, encompassing two binary and two multiclass imbalanced-microarray cancer datasets: Lung (5-class dataset), Small Round Blue Cell Tumors (SRBCT; 4-class dataset), and Ovarian and Breast Cancer 2-class datasets). The experimental results of our comparison showed that the proposed framework achieved the highest predictive performance. A comparative study of our framework, using accuracy and F1 as metrics, was performed against state-of-the-art approacheswhich illustrated that the proposed method presented a better result for two of the selected datasets.
Keywords: Artificial intelligence; classification; feature selection; linear support vector machine; learning model
The analysis of microarray data involves such challenges as small sample size, high dimensionality, and multiclass-imbalance problems [1]. In real-world datasets, the multiclass-imbalance problem is a known issue where the number of samples of one or some classes are larger than the others. This results in a reduction of the performance of the classification model for minority classes [2]. Several machine-learning (ML) algorithms expect the dataset to have a balanced class distribution [3]. Feature-selection techniques are used to reduce issues related to this and the high rate of cancer-data dimensionality. Consequently, conducting research in this area is required and possible for different disciplines, such as statistics, computational biology, and ML [4].
When building a ML model, it is hard to identify what distinguishes between important and unimportant features, as shown in Fig. 1 [5]. Removing unimportant features has many benefits, such as reducing memory and computational cost, maximizing accuracy, and avoiding the overfitting problem during the training stage [6,7]. A few features can be useful for one algorithm (for example, Decision Tree [DT]), but they may not be helpful for another model, such as a regression model. Moreover, irrelevant features can negatively affect the model’s performance. Data preprocessing and feature selection are the most significant steps in designing and selecting the best model for a specific problem [8].
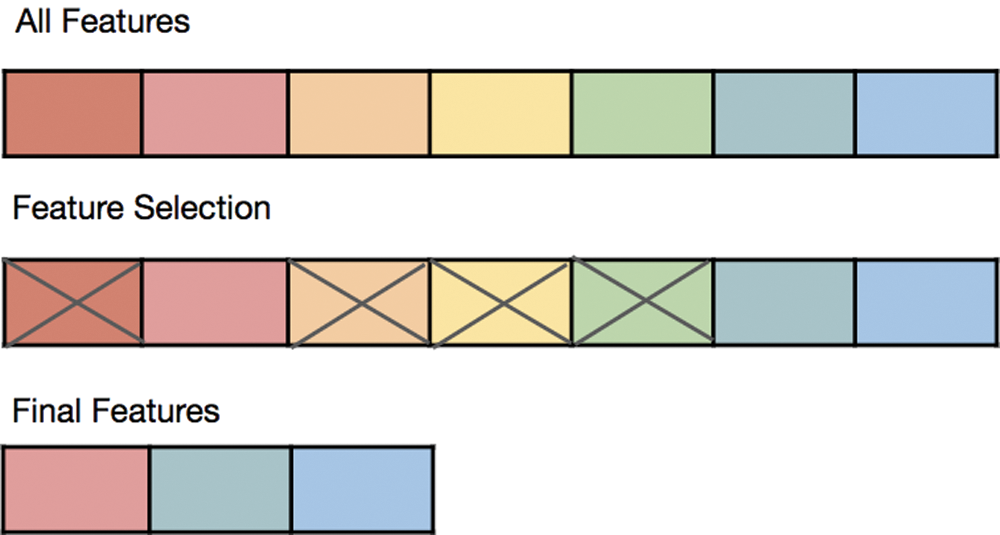
Figure 1: Removing noise features from the whole parts set
The feature-selection technique is applied to carefully choose the best subset of features to attain an identical or higher classification performance [9]. The primary types of feature-selection techniques are filter, wrapper, embedded, feature shuffling, and hybrid. The main goals for these methods are to increase the model’s performance, reduce training time, avoid overfitting problems, and decrease the input datas dimensionality. Although feature selection has certain disadvantages, it is an essential preprocessing technique ML because it generates extra information and provides an intuitive understanding of the typical pattern before the proposed classifier is used [10,11].
ML feature-selection techniques can be broadly classified into the following common method categories, as shown in Tab. 1: filter, wrapper, embedded, and hybrid [12]. Each method has its weaknesses and strengths, depending on the shape of the data and the classifier used to solve the problem at hand. The main differences between the filter and wrapper methods are presented in Fig. 2.
Four microarray cancer datasets were used in this work—the Small Round Blue Cell Tumors (SRBCT) dataset is a 4-class dataset, the Lung dataset is a 5-class dataset, and the Ovarian and Breast Cancer datasets are 2-class datasets [13]. These data were used to carry out a series of tests, and the empirical results were used to determine how the suggested method compares to state-of-the-art systems. The most commonly used metrics—namely, accuracy, confusion matrix, precision, recall, and F1 score—were used to assess the performance of the classification model.
Table 1: Feature-selection methods

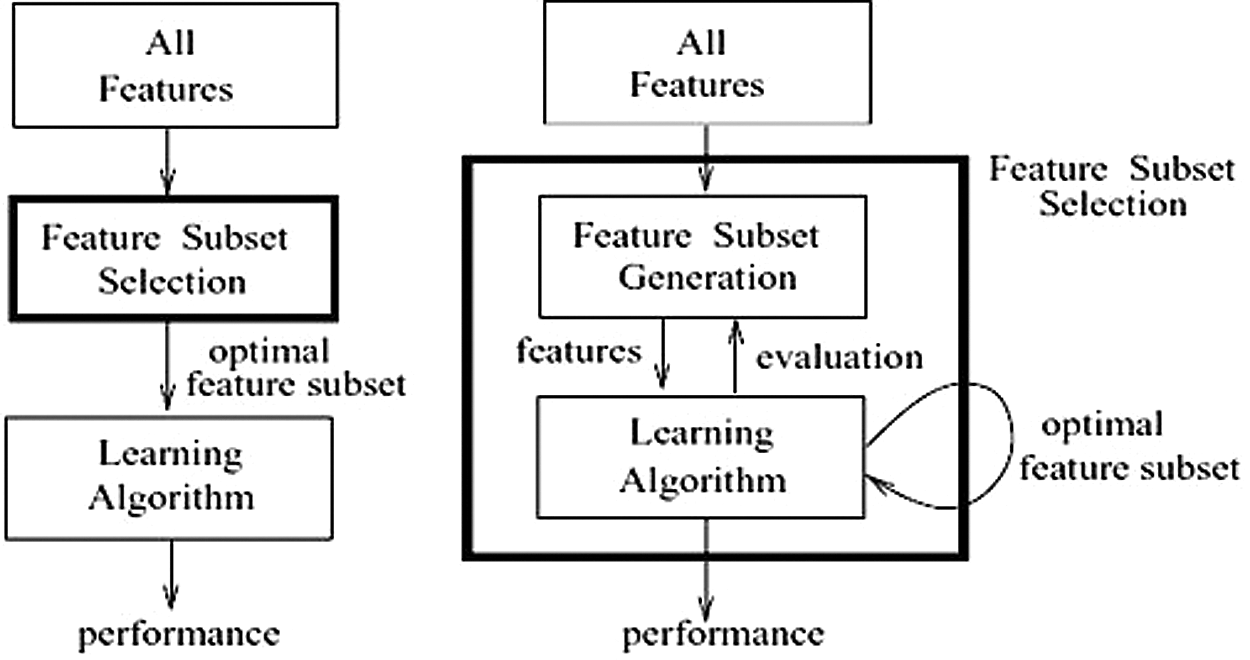
Figure 2: Main differences between filter and wrapper methods [10] (a) Filter method (b) Wrapper method
The main contributions of this paper are as follows:
• Development of a framework based on LR with wrapper-based feature selection that outperforms many state-of-the-art works
• Finding that the features selected by the wrapper-based approach improve the performance of the classifiers
• Setting the main goals of the proposed model as increasing performance, reducing training time, avoiding the overfitting problem, and decreasing the dimensionality of the input data
In this section, state-of-the-art feature-selection and classification models for microarray cancer data are investigated. Recently, many researchers have proposed efficient feature-selection and classification models. Garro et al. [14] introduced an optimization framework that uses the artificial bee-colony algorithm for feature selection. Chen et al. [15] proposed the particle-swarm-optimization algorithm with a DT classifier to improve the performance of ridge-regression classification methods. Liu et al. [16] developed a hybrid method to address the multiclass imbalance problem of the microarray cancer dataset. Aziz et al. [17] introduced an aggregate of fuzzy-backward feature-elimination and independent-component analysis for feature selection.
Guo et al. [18] developed an efficient two-step L1-regularization framework to classify microarray cancer data. Ebrahimpour et al. [19] proposed an ensemble model with a Maximum Relevancy and Minimum Redundancy-based feature-selection technique using Hesitant Fuzzy Sets. Shekar and Guesh [4] proposed a hybrid ensemble approach for multiclass cancer classification. Al-Rajab et al. [20] introduced a three-phase approach, which includes feature detection, classification, and performance evaluation.
The previous pieces of literature attempted to develop novel feature-selection techniques and classification models to achieve higher accuracy and lower running times for cancer-data classification tasks. They involve some limitations however—for example, the predictive model guarantees less accuracy in some cancer datasets.
In this section, the proposed framework is described. The ensemble ML models based on the robust classifiers for microarray-cancer-data classification are presented. Generally, in any classification problem, the model uses the collected dataset for training and testing. The k-fold cross-validation (CV) technique was used to measure the classifier’s average performance in order to address the problem of overfitting during the training phase; the basic idea of the k-fold CV technique is that it iteratively trains each sample four times and tests at the fifth iteration. A grid-search technique, which selected the best parameters based on the k-fold CV, was used to increase the ML models’ performance, and the range of parameter values was set. The proposed framework’s workflow is presented in Fig. 3, which depicts the cancer data, feature-selection methods, and classifiers trained using the original and reduced feature sets. Model evaluation was applied to the test samples.
In this section, a summarized description of the selected cancer dataset is presented. The four multiclass cancer datasets used to test the framework’s efficiency are available for download from the Shenzhen University data repository [13]. The complete description is presented in Tab. 2. The SRBCT dataset is the 4-class dataset, Lung is the 5-class dataset, Ovarian and Breast Cancer are 2-class datasets.
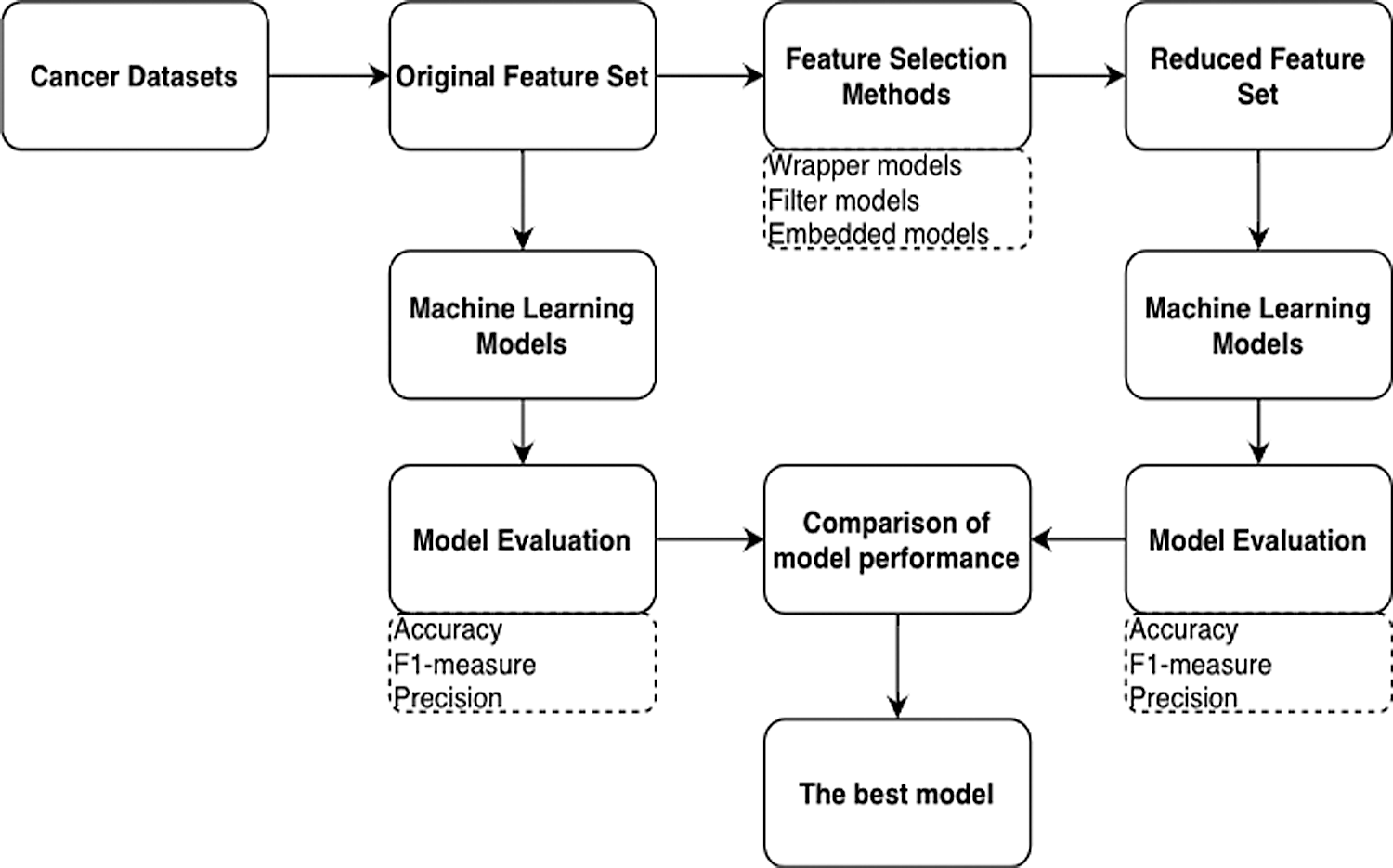
Figure 3: Process steps for applying the feature selection methods and machine learning models

Recently, feature-selection techniques have taken on a primary role in assisting with microarray-dataset classification. These methods are used to handle many problems, such as long running time, overfitting, and memory usage. Information gain is an important technique to use with filter methods that calculate each feature’s importance by ranking pertaining to class label [4]. With this method, which quantifies the information obtained from each feature, important features receive a higher value and rank, whereas irrelevant features receive a rank of zero [21].The focus is to find an attribute that provides the largest amount of information gain by ranking the features in accordance with their relevance. Information gain is a measure of the change in entropy, which is calculated with Eq. (1):
S represents the set of samples, X is a feature, |S| is the size of S instances, and Sv stands for a subset of S, such that Xv = v and Values(X) refers to the set of all possible values of the X attribute. Entropy is a measure used to compute how pure or mixed a given attribute is in the distribution. The entropy of each feature is mathematically computed, as shown in Eq. (3):
E represents the entropy value, S denotes the sample size, X is a feature, and pi is the probability.
Generally, to evaluate a proposed-framework’s performance, several standard classification performance metrics are used, including accuracy, recall, precision, F1 score, and confusion matrix. Eqs. (4)–(7) show the mathematical formulas for accuracy, recall, precision, and F1 score, which are calculated based on True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN) [22–25].
4 Experimental Results and Analysis
In this section, the experimental results are discussed. All experiments were performed using the four known binary and multiclass-microarray datasets. To measure the performance of the ML model, a five-fold CV technique was used to calculate the mean accuracy and standard deviation of the five-fold evaluation results.
Tab. 3 presents the top-10 features of the Breast Cancer datasetthe amount of times each was selected, and the results of different feature-selection models applied to the dataset. A value of “True” means the feature was selected using the corresponding algorithm; for example, NM_020974 was selected by all the algorithms.
Table 3: The top 10 features of Brest Cancer dataset and the count of the selected times for each features

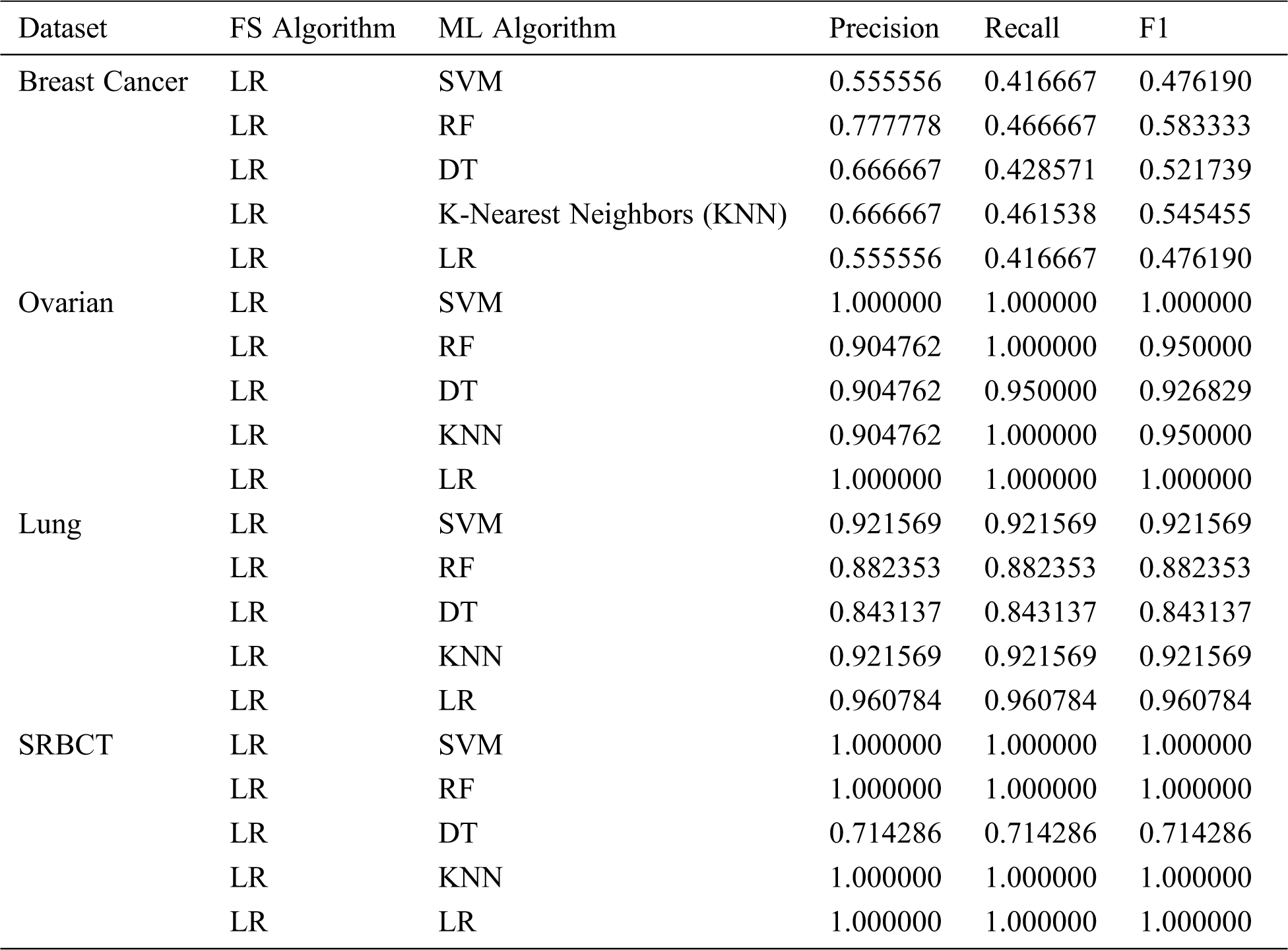
Tab. 4 shows the classification report of the ML models for all the datasets, in which themodels are evaluated by precision, recall, and F1. The results show that 100 percent precision, recall, and F1 were achieved with two datasets—Ovarian and SRBCT. For the Breast Cancer dataset, the Random Forest (RF) model performed the best, scoring 0.777778 and 0.466667 for precision and recall, respectively. For the Ovarian dataset, the Support Vector Machine (SVM) and Logistic Regression (LR) models outperformed the other algorithms, scoring 1.000000 for precision, recall, and F1. The LR model was the best algorithm for the Lung dataset, scoring 0.960784 for precision, recall, and F1. Finally, for the SRBCT dataset, all the models scored 1.000000 for precision, recall, and F1, except DT, as shown in Tab. 4.
Table 4: ML-model classification report for all datasets
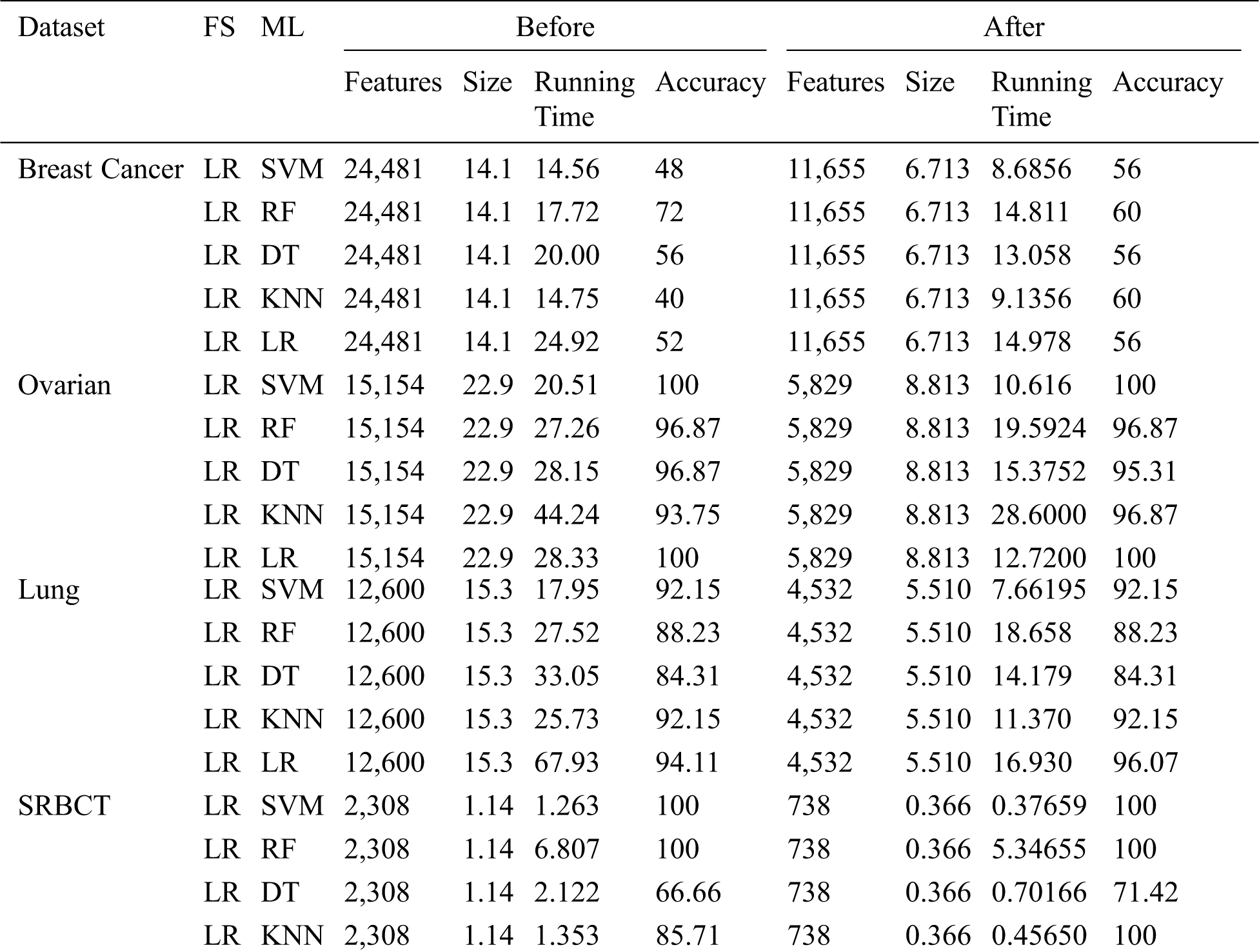
Tab. 5 shows the huge improvement in performance after LR feature selection was performed. For the Breast Cancer dataset, the accuracy of SVM increased from 48 percent to 56 percent and the running time decreased from 14.563 to 8.685 seconds after feature selection. With the SRBCT dataset, the performance of DT increased from 66.66 percent to 71.42 percent with the feature-selected dataset.
Table 5: ML-model classification reportbefore and after feature selection
A comparative study was performed against state-of-the-art models, and the best results in terms of accuracy were seen with two of the selected datasetsSRBCT and Ovarian with each model scoring 100 percent. The works of Liu et al. [16] and Shekar et al. [26] scored 99 percent and 100 percent in accuracy, respectively, as presented in Tab. 6.
Table 6: Comparative study of the proposed method against state-of-the-art models

The paper addresses the challenges prevalent in cancer-microarray datasets, such as high dimensionality, small sample size, and imbalanced class labels. Feature-selection techniques based on the ML models were introduced. In the framework, the most important features of the cancer datasets were extracted with LR, Chi-2, RF, and LightGBM. They were then used as input columns in the classification task. The main advantage of this framework is reducing the time complexity and the number of irrelevant features in the dataset. The proposed method was compared with KNN, SVM, DT, LR, and RF in experiments performed on four standard multiclass-microarray cancer datasets. The results showed that the proposed method is more effective in predictive capability. A comparative studymeasuring the accuracy and F1 of our framework against state-of-the-art approaches demonstrated that the proposed method achieved a better result with four datasets.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
1. M. A. Hambali, T. O. Oladele and K. S. Adewole. (2020). “Microarray cancer feature selection: Review, challenges, and research directions,” International Journal of Cognitive Computing in Engineering, vol. 1, pp. 78–97. [Google Scholar]
2. S. Wang and X. Yao. (2012). “Multiclass imbalance problems: Analysis and potential solutions,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 42, no. 4, pp. 1119–1130. [Google Scholar]
3. Y. Sun, A. K. C. Wong and M. S. Kamel. (2011). “Classification of imbalanced data: A review,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 23, no. 04, pp. 687–719. [Google Scholar]
4. B. H. Shekar and G. Dagnew. (2018). “Classification of multiclass microarray cancer data using ensemble learning method,” Data Analytics and Learning. Singapore: Springer, 279–292. [Google Scholar]
5. V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione et al. (2018). , “Machine learning modeling of superconducting critical temperature,” npj Computational Materials, vol. 4, pp. 1–14. [Google Scholar]
6. X. Ying. (2019). “An overview of overfitting and its solutions,” Journal of Physics: Conference Series, vol. 11168, no. 2, pp. 022022. [Google Scholar]
7. D. Jain and V. Singh. (2018). “Feature selection and classification systems for chronic disease prediction: A review,” Egyptian Informatics Journal, vol. 19, no. 3, pp. 179–189. [Google Scholar]
8. I. Gad and D. Hosahalli. (2020). “A comparative study of prediction and classification models on NCDC weather data,” International Journal of Computers and Applications, pp. 1–12, published online: 20 May. [Google Scholar]
9. R.-C. Chen, C. Dewi, S.-W. Huang and R. E. Caraka. (2020). “Selecting critical features for data classification based on machine learning methods,” Journal of Big Data, vol. 7, no. 52, pp. 26. [Google Scholar]
10. M. S. Saini and R. Alfred. (2011). “A genetic-based wrapper feature selection approach using nearest neighbor distance matrix,” in 3rd Conference on Data Mining and Optimization (DMOPutrajaya, Malaysia: IEEE. [Google Scholar]
11. A. Subasi. (2020). Data preprocessing, in practical machine learning for data analysis using python. Elsevier, pp. 27–89. [Google Scholar]
12. P. Kalapatapu, S. Goli, P. Arthum and A. Malapati. (2016). “A study on feature selection and classification techniques of Indian music,” Procedia Computer Science, vol. 98, no. 5, pp. 125–131. [Google Scholar]
13. Z. Zhu, Y. S. Ong and J. M. Zurada. (2010). “Identification of full and partial class relevant genes,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 7, no. 2, pp. 263–277. [Google Scholar]
14. B. A. Garro, K. Rodríguez and R. A. Vázquez. (2016). “Classification of DNA microarrays using artificial neural networks and ABC algorithm,” Applied Soft Computing, vol. 38, pp. 548–560. [Google Scholar]
15. K. H. Chen, K. J. Wang, K. M. Wang and M. A. Angelia. (2014). “Ap-plying particle swarm optimization-based decision tree classifier for cancer classification on gene expression data,” Applied Soft Computing, vol. 24, no. 7, pp. 773–780. [Google Scholar]
16. Z. Liu, D. Tang, Y. Cai, R. Wang and F. Chen. (2017). “A hybrid method based on ensemble WELM for handling multiclass imbalance in cancer microarray data,” Neurocomputing, vol. 266, pp. 641–650. [Google Scholar]
17. R. Aziz, C. Verma and N. Srivastava. (2016). “A fuzzy-based feature selection from independent component subspace for machine learning classification of microarray data,” Genomics Data, vol. 8, pp. 4–15. [Google Scholar]
18. S. Guo, D. Guo, L. Chen and Q. Jiang. (2017). “An L1-regularized feature selection method for local dimension reduction on microarray data,” Computational Biology and Chemistry, vol. 67, no. 7, pp. 92–101. [Google Scholar]
19. M. K. Ebrahimpour and M. Eftekhari. (2017). “Ensemble of feature selection methods: A hesitant fuzzy sets approach,” Applied Soft Computing, vol. 50, pp. 300–312. [Google Scholar]
20. M. Al-Rajab, J. Lu and Q. Xu. (2017). “Examining applying high-performance genetic data feature selection and classification algorithms for colon cancer diagnosis,” Computer Methods and Programs in Biomedicine, vol. 146, no. February (2), pp. 11–24. [Google Scholar]
21. V. Bolón-Canedo, N. Sánchez-Maroño, A. Alonso-Betanzos, J. Benítez and F. Herrera. (2014). “A review of microarray datasets and applied feature selection methods,” Information Sciences, vol. 282, no. 3, pp. 111–135. [Google Scholar]
22. Z. Malki, E. S. Atlam, A. E. Hassanien, G. Dag-new, M. A. Elhosseini et al. (2020). , “Association between weather data and COVID-19 pandemic predicting mortality rate: Machine learning approaches,” Chaos, Solitons & Fractals, vol. 138, no. 10223, pp. 110–137. [Google Scholar]
23. Z. Malki, E. S. Atlam, A. Ewis, G. Dagnew, A. R. Alzighaibi et al. (2020). , “ARIMA models for predicting the end of COVID-19 pandemic and the risk of second re-bound,” Neural Computing and Applications, pp. 1–20, published online: 23 October. [Google Scholar]
24. Z. Malki, E. Atlam, G. Dagnew, A. R. Alzighaibi, E. Ghada et al. (2020). , “Bidirectional residual LSTM-based human activity recognition,” Computer and Information Science, vol. 13, no. 3, pp. 40. [Google Scholar]
25. G. Doreswamy, I. Gad and B. R. Manjunatha. (2018). “Multi-label classification of big NCDC weather data using deep learning model,” Soft Computing Systems, Singapore: Springer, pp. 232–241. [Google Scholar]
26. B. H. Shekar and G. Dagnew. (2019). “Grid search-based hyperparameter tuning and classification of microarray cancer data,” 2019 Second Int. Conf. on Advanced Computational and Communication Paradigms (ICACCPGangtok, India: IEEE, pp. 1–8. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |