DOI:10.32604/iasc.2021.018252

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.018252 |  |
| Article |
Paralleling Collision Detection on Five-Axis Machining
1Department of Computer Science and Information Engineering, Advanced Institute of Manufacturing with High-Tech Innovations, National Chung Cheng University, Chiayi, 621005, Taiwan
2Department of Computer Science and Information Management, Providence University, Taichung, 433303, Taiwan
*Corresponding Author: Ting-Hsuan Chien. Email: thchien0616@pu.edu.tw
Received: 02 March 2021; Accepted: 05 April 2021
Abstract: With the rapid growth of the Fourth Industrial Revolution (or Industry 4.0), five-axis machining has played an important role nowadays. Due to the expensive cost of five-axis machining, how to solve the collision detection for five-axis machining in real-time is very critical. In this paper, we present a parallel method to detect collision for five-axis machining. Moreover, we apply the bounding volume hierarchy technique with two-level bounding volume represent the surface or solid of the object to reduce triangle meshes inside each axis of the five-axis machine tool, and then matching the operating range limit of the five-axis machine tool itself, delete the no colliding triangle mesh. Additionally, we also propose some optimization with loop unrolling and prefetching techniques to improve performance of collision detection. Our approach can reduce the execution time significantly by computing six separating axes in plan and eleven separating axis in non-plan between two triangle meshes based on the characteristic of GPUs (Graphics Processing Units) for program acceleration. Our proposed work consists of kinematic analysis and interpolation for axes to save the numerous collision detection for five-axis machining computations. In this experiment, the result shows that using the proposed approach above can achieve approximately 37.1 times speedup than that of CPU.
Keywords: Collision detection; five-axis machining; graphics processing units
As Industry 4.0 has become the focus of industrial manufacturing, the Computer Numerically Controlled (CNC) machine tools have played an essential role the industry. More advanced machining technologies use five-axis CNC machining for complicated part fabrication. The Five-axis machine has two rotary tables that improve the machining capability and quality. However, five-axis machining has high axial table colliding chances due to the coordinated motion for rotating and translating tables. If the machine tool differs during machining, it damages the machine itself and delays the productions. Therefore, how to prevent axial table collisions during machining is very important for five-axis machining processes. Owing to the expensive cost of machine tools, avoiding collision detection has become a critical issue.
There are three types commonly used for five-axis machine tools: table tilting type, spindle tilting type, and table/spindle tilting type. Although the table tilting type is used in this paper for theorem derivation and explanation, the proposed approach can be applied to other types. Fig. 1 is an example of a commercially available table tilting type for five-axis machines.

Figure 1: (a) The table tilting type for five-axis machines, (b) The STL model of the machine
The machine design is usually modeled as STL format that uses triangular facets to describe designed objects. Each triangular element contains three vertices and a normal facial vector. Most of the commercially available Computer-Aided Design (CAD) software provide STL format for object design output, as shown in Fig. 1(b).
In this paper, we propose a work about the real-time anti-detection to solve the issue mentioned earlier. To achieve this objective, the proposed work consists of the following steps. We first perform the kinematics analyses for five-axis motions. The format of the machine structure is modeled as STL used commonly in CAD software. The input is the g-code that represents the tool motions to produce the surface of an object. Since three-dimensional surface objects are modeled as triangle meshes for digital holography, they are the primitive elements of three-dimensional objects in computers [1]. Hence, the intersection test for two triangles will determine if the collision will occur. To improve performance, we try to eliminate the triangle meshes that never collide based on the bounding volume hierarchy [2]. In this manner, we can reduce the computation amount to save the computation time and thus obtain an ideal speedup. As the GPUs have been used widely for many applications, we propose a parallel method to determine whether two objects in a three-dimension space intersect or not in parallel. Compared with the traditional way, the proposed similar approach can improve the performance again. Besides, with our domain knowledge and experiences on GPU and CUDA (Compute Unified Device Architecture) programming, we apply some optimization techniques such as loop unrolling, prefetching, alignment, strode access, and interchanging the bounding volume to improve performance further.
The remainder of the paper is organized as follows. We describe the previous work related to our work in Section 2. Then we present how to reduce the number of triangle meshes based on the bounding volume hierarchy technique in Section 3. Next, we explain how to parallel the collision detection for two objects on the GPU in Section 4. In Section 5, we show the results of our numerical experiments regarding our proposed algorithm’s performance on GPUs. Finally, we summarize our findings with some concluding remarks in Section 6.
Möller [3] designed an efficient algorithm to detect collision for two triangles. Held [4] also presented a similar algorithm but in a different way. Both of them computed the signed distance of three vertices of a triangle from the plane containing the other triangle. If all the values are the same sign, they do not intersect. Otherwise, they may cross, and the problem is then reduced to an overlap test of two line segments positioned on the same line of corner between the two planes containing the triangles. Moller computed a parametric equation of the intersection of two planes, found the intervals for the line that lays inside each triangle, and performed a one-dimensional interval overlap test. In contrast, Held reduced the problem to a two-dimensional triangle/line-segment test after projecting to a convenient plane. Guigue et al. [5] then followed Moller by using an orientated decision defined by a determinant of a 4 × 4 matrix to predict and compute the signed distance of each vertex from orientated decision. The intersection test is then reduced to check the signs of orientated decision. Tropp et al. [6] presented an algebraic approach similar to that of Held, while the key observation is that the set of equations are strongly related to each other. They reused some computation results for certain variables based on linear algebra. Then, the common elements of the different equations can be applied to speed up the solution whilst exploiting the linearity of the matrix operations. Chang et al. [7] adopted Moller’s algorithm based on OBB-based collision detection to improve it. Instead, we use the splitting axis theorem and induce six separating axes in plan and 11 separating line axes in non-plan between two triangle meshes to address this issue, as shown in Fig. 2.

Figure 2: Six separating lines in the plane and 11 splitting axes in the non-plane between two triangle
The idea of decreasing the execution time is to reduce the number of triangle meshes. Ritter proposed the bounding sphere [8] to wrap any irregular object in the form of a sphere. This work can calculate efficiently with few parameters. Cohen et al. proposed a collision detection method using AABB for the wrapped volume [9] and projected X, Y, and Z axes of the object. Their work was convenient to set up the wrapping by wrapping the thing with each X, Y, Z projection amount. Later, OBB was proposed by Gottschalk et al. [10] to use the covariance matrix to calculate the three principal axis directions according to the appearance of the object and then project the three main axis directions, respectively. In this way, the bounding object was similar to the original one, and the number of bounding bodies was significantly reduced. A k-DOP [11] was a convex polygon in a two-dimensional space or a convex polyhedron in a three-dimensional space that contains an object. It is obtained by moving a set of infinitely distant oriented planes to intersect the object. In addition, bounding this group of points and the smallest shell must be convex in theory. The convex hull [12] was proposed to bound an object with the smallest surface area and volume among all the shells. The advantage was that any graph can be simplified into a convex hull of a group of points. are common bounding volume techniques.
3 Reducing Triangles Meshes with Two-Level Bounding Volume
In general, although it is better to bound an object from left to right, the rough collision detection time becomes much longer and the memory size must be larger. The AABB is the bounding box aligned with the axes of the coordinate system. In this paper, we will use AABB to represent a bounding object. For an AABB, min and max mean the left top and the right down of a bounding object. When the object is rotated, the min-max must be computed again. For the collision detection of two AABBs, O1 and O2, O1 and O2 will collide if and only if !(O1.max.x < O2.min.x || O1.min.x > O2.max.x), !(O1.max.y < O2.min.y || O1.min.y > O2.max.y), and !(O1.max.z < O2.min.z || O1.min.z > O2.max.z).
Considering into this concern account, we choose the AABB bounding volume in this paper because the others are too complicated during the computation for bounding volume hierarchies. The advantages of AABB are using less memory size, computing bounding sub-volume simply, and achieving a better performance. We also use bounding volume hierarchies with AABB to reduce triangle meshes of two objects in the fetching stage while using GPU. Moreover, the reduction of triangle meshes can save time to find separating axis numbers. Thus, we first illustrate the AABB bounding volume technique and continue displaying the n level bounding volume hierarchies with AABB. Because there are many multiprocessors and blocks in GPU, the hardware can schedule blocks to multiprocessors in any order and thus the numerous blocks will be time consuming. For this goal, the collision detection will be performed the rough collision detection based on the bounding volume technique first and then compute the detailed collision detection stage.
The idea of the n level bounding volume hierarchies with AABB is the rough collision detection in levels. In other words, we are not concerned whether triangle meshes are overlapping or not. In Fig. 3, there are many sub-AABBs (R2, R3, R4, R5, R6, R7, …) by segmenting the AABB (R1) between object1 and object2. Finding the collision regions of two objects is from the maximum size region to the minimum size region. Regions R2, R4, R5 and the regions in R4 and R5 of object1 are not found, because the regions do not collide with the regions of the object2. The order relation of finding the areas can be presented by using breadth-first search (BFS) to search a tree structure. A tree node presents a region, where the bigger areas is the parent node and the smaller areas in it are child nodes. In this manner, the bounding volume hierarchies are models as an n-level tree. In BFS, if R2 in object1 does not be searched depending on whether it collides with R2 and R3 in object2 or not, the child and offspring nodes of R2 in object1 are not searched for them either.

Figure 3: The n-level bounding volume hierarchies with AABB
In our design, we use a two level bounding volume hierarchies with AABB. For an example shown in Fig. 4, O1 contains two sub-AABBs named S1_O1 and S2_O1 and O2 contains two sub-AABBs named S1_O2 and S2_O2. In the rough collision detection stage, to check whether the two objects collide or not, we only detect the collision of O1 and O2. Moreover, if O1 and O2 collide, four cases must be checked: the collision detection of S1_O1 and S1_O2, S1_O1 and S2_O2, S2_O1 and S1_O2, and S2_O1 and S2_O2. If S2_O1 and S1_O2 collide, the threads of GPU will be assigned in a CUDA program to detect the collision of triangle meshes in S2_O1 and S1_O2 in the detailed collision detection stage (see Section 4). As a result, the rough collision detection cannot make sure if two AABBs really collide. The detailed collision detection must be performed to check it precisely.

Figure 4: An example for the rough collision detection and the detailed collision detection
Fig. 5 is the overview that a simulator replicates the five-axis machine tool’s motion and the collision detection system is implemented on the GPU to meet the real-time constraint. This section fist depicts the CUDA programming model and then presents how to perform optimization techniques to parallelize collision detection on GPU. We also show a paralleling algorithm to improve collision detection performance on the SIMD (Single Instruction Multiple Data) architecture.

Figure 5: The simulator is implemented on CPU and the collision detector is implemented on GPU
CUDA is a parallel computing platform and programming model created by NVIDIA [13]. In Fig. 3, a kernel function is composed of the parallel subroutine and the memory model. Implementation of every thread in the grid is the kernel function. A grid is a collection of blocks, and a block is a collection of threads. A wrap is a group of 32 threads executed physically in parallel. Two designs need to be noted. Firstly, the wrap-based execution is the effective method on the SIMD architecture. Designing a warp to execute the same thread effectively uses the SIMD architecture, Otherwise, the performance will decrease. As an example, because the divergent thread design causes a reduction of parallelism, it is possible not to use this design. Secondly, the thread number in a block is a multiple of 32. That is a better design for the performance because the hardware does not need to add more warps to execute. If the thread number in a block is not multiple of 32, it will add more warps to execute and decrease performance.
To improve collision detection performance, we perform loop unrolling and prefetch to exploit instruction level parallelism and loop level parallelism.
Loop unrolling can extend the paralleling space by replicating the loop body many times, only adjusting the loop termination code. We then can find threads enough to be assigned to GPU via dependence analysis. If loops are independent, then they can be executed in parallel. Fig. 6 shows that the loop unrolling technique is used to increase the parallel degree.

Figure 6: Loop unrolling can increase the parallelism
If there are n triangle meshes on object1, and m triangle meshes on the object2, there are m × n threads in total assigned to execute in parallel. Developers can avoid the thread divergence as much as possible. Therefore, if there are the six separating lines or the 11 separating lines depending on whether they are in a plane or not, they must be checked sequentially whether they can separate two triangle meshes in a thread. If there are no separating lines to separate two triangle meshes in a thread, these two objects may collide. This may result in different execution time for every thread because just finding a separating line to check collision depends on which separating line can ensure if the collision happen. For a real-time system, we considered the worst-case execution time as the performance issue. With the aid of loop unrolling, we can exploit more parallelism to improve performance by executing more threads.
To improve the memory bandwidth, we propose a prefetching mechanism to solve this problem. Normally, we can use CUDA API (cudaMalloc (), cudaMemcpy ()) to load data from the memory of CPU to the global memory of GPU. When the simulator’s cutter of the five-axis machine tool is moved or rotated by motion control, the data in the global memory of GPU must be updated by GPU to detect collision. Therefore, there is not a bottleneck during collision detection. In Fig. 7, there are six axes X, Y, Z, A, B and Cutter. If the number of triangle meshes of the X axis and Y axis are N and M, N × M threads must fetch different data from the X axis and Y axis of GPU’s global memory to execute in parallel.

Figure 7: A data prefetching model from global memory to execute
4.2.3 Alignment and Stride Access
Based on the hardware’s warp-based execution, the maximum number of the threads is 1024 (32 × 32) for a GPU block [14]. A thread will fetch data from the X axis and Y axis and design a data structure with a two-dimensional block and a two-dimensional thread. The size of the two-dimensional block is (N/32+1) × (M/32+1). The row index and the column index of the two-dimensional block ae from 0 to N/32+1 and from 0 to M/32+1, respectively. The size of the two-dimensional thread is 32 × 32, where the row index and the column index are from 0 to 32. Thus, there are 1024 threads in every block. The thread (ti,tj) in the block (bi,bj) fetches data from the index of X axis data is 32 × bi + ti and the index of Y axis data is 32 × bj + tj. Thus, it is possible to avoid thread divergence and result in a higher parallel degree on GPU because of this design. If the execution result of thread (ti,tj) in the block (bi,bj) is true, the colliding flag in global memory will be set to indicate that the two objects will collide. Therefore, because kth thread in a block fetches kth data in GPU’s global memory, the misaligned access pattern and stridden access problems do not occur. Thus, GPU can use the coalesced memory technique to improve the performance of the fetching data.
4.2.4 Interchanging the Bounding Volume
Unfortunately, a problem will occur while using two-level bounding volume hierarchies in the rough collision detection stage. In Fig. 8, all sub-regions of O1 overlap with sub-regions of O2, S1_O1 overlaps with S1_O2, and S2_O1 coincides with S2_O2. In this case, since GPU’s threads will fetch all triangle meshes in O1 and O2 in the detailed collision detection stage, the performance does not improve. We propose a solution by interchanging the sub-regions in two level bounding volume hierarchies to solve this problem. Regions R_S1_O1, R_S2_O1, R_S1_O2 and R_S2_O2 are designated as the new regions after the interchanging. In this way, the threads can fetch R_S2_O1 and R_S1_O2 to execute the detailed collision detection on GPU and the performance will be improved.

Figure 8: The problem and solution of the two-level bounding volume hierarchy in the rough collision detection stage
This section implements the proposed collision detection system and measures execution time on CPU and GPU. We also simulate the motion of the five-axis machine tool to perform collision detection.
Tab. 1 shows the test platform. The simulator and the collision detection system of the five-axis machine tool have been implemented on CPU and GPU.

To measuring time and displaying the execution results of our parallel collision detection algorithm, we ensure the following. (1) Write an interpreter simply to interpret G-codes that are the most widely used numerical control (NC) programming language. (2) Convert the five-axis machine tool into digital data represented as triangle meshes. (3) Display the digital data on the computer screen with OpenGL. (4) Write motion control simply with the sample time = 0.1 ms and the federate = 10000 mm/min. (5) Simulate the motion of the five-axis machine tool. For example, if the cutter moves a unit toward the X direction, the five-axis machine tool must move the X axis first and then move Z axis. (6) Perform the collision detection for the eight cases: Cutter-X, Cutter-Y, Cutter-A, Cutter-C, Z-X, Z-Y, Z-A and Z-C.

Figure 9: The five-axis CNC machine tool and its simulator
In Fig. 9, we can begin to simulate the five-axis machine tool’s motion in the computer. When the cutter moves a minimum unit, the program performs the collision detection for the eight cases above. If the two objects collide, the program stops running.
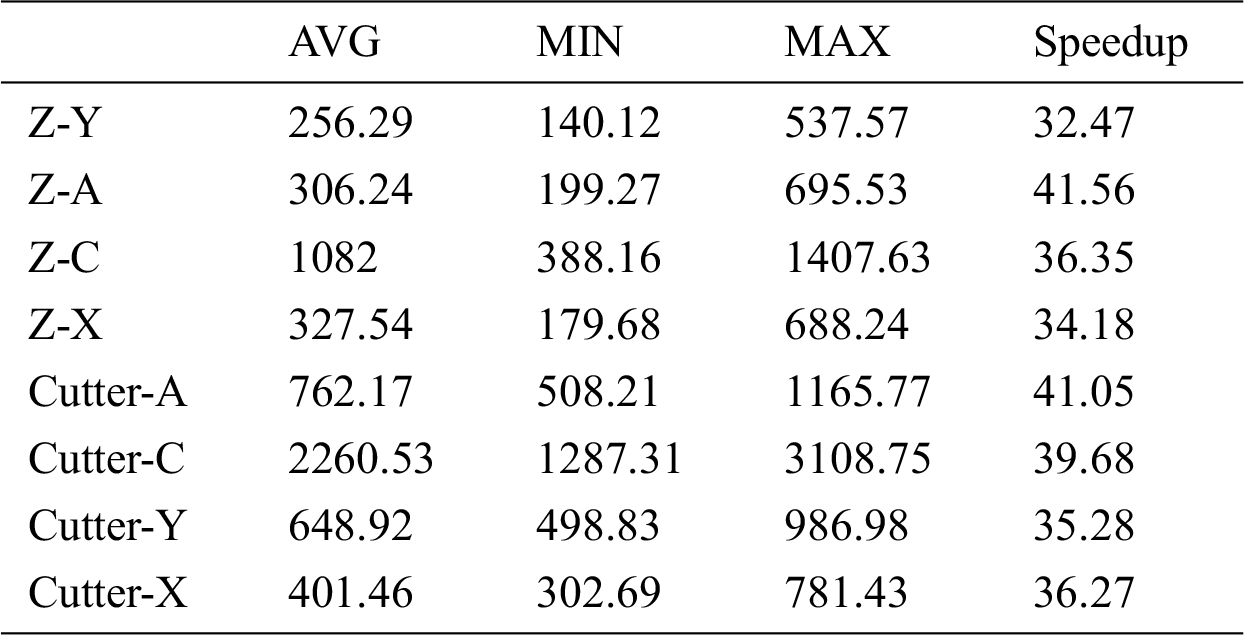
We measure the execution time of the eight cases mentioned above on GPU and CPU. The execution time on GPU is the CUDA profiling tools. The numbers of triangle meshes of X, Y, and Z axes are 44,136, and 180. The numbers of triangle meshes of A, C, and the cutter are 164, 548, and 716. The execution time for CPU and GPU are shown in Tabs. 2 and 3. From the result, we can see that the Cutter-C case takes more execution time than the others because there are more numbers of triangle meshes. Moreover, using our parallel method on GPU, the proposed work can improve the performance by 37.1 times compared to CPU in terms of average execution time.
Table 2: Execution time on CPU (us)

Table 3: Execution time on CPU (us) and speedup of average execution time compared to CPU
We have presented an efficient method for axial table collision detection on five-axis machining in this paper. Our approach includes analyzing machine kinematics and interpolating for separating axes that get rid of complicated cross-product computation. The performance result shows that the proposed approach is very efficient with GPU compared with the conventional detection method. Besides, there is usually a tiny embedded system in machine tools. Our parallel method on GPU is workable. Therefore, the performance of our parallel method is adjustable based on the limitation of a real-time system.
Acknowledgement: The authors would like to acknowledge the financial support of the National Science Council, Taiwan, ROC under the grant of project MOST 108-2218-E-194-007.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Gottschalk, M. C. Lin and D. Manocha, “OBBTree: A hierarchical structure for rapid interference detection,” in Proc. SIGGRAPH, New York, NY, USA, pp. 171–180, 1996. [Google Scholar]
2. J. Huynh, “Separating axis theorem for oriented bounding boxes,” Beersheva, Israel: Ben-Gurion University of the Negev, 2009. [Online]. Available: https://www.cs.bgu.ac.il/~vgp182/wiki.files/Separating%20Axis%20Theorem%20for%20Oriented%20Bounding%20Boxes.pdf. [Google Scholar]
3. T. Möller, “A fast triangle-triangle intersection test,” Journal of Graphics Tools, vol. 2, no. 2, pp. 25–30, 1997. [Google Scholar]
4. M. Held, “ERIT–A collection of efficient and reliable intersection tests,” Journal of Graphics Tools, vol. 2, no. 4, pp. 25–44, 1997. [Google Scholar]
5. G. Philippe and O. Devillers, “Fast and robust triangle-triangle overlap test using orientation predicates,” Journal of Graphics Tools, vol. 8, no. 1, pp. 25–32, 2003. [Google Scholar]
6. O. Tropp, A. Tal and I. Shimshoni, “A fast triangle to triangle intersection test for collision detection,” Computer Animation and Virtual Worlds, vol. 17, no. 5, pp. 527–535, 2006. [Google Scholar]
7. J. W. Chang and M. S. Kim, “Efficient triangle-triangle intersection test for OBB-based collision detection,” Computers & Graphics, vol. 33, no. 3, pp. 235–240, 2009. [Google Scholar]
8. J. Ritter, An efficient bounding sphere. Santa Clara, CA, USA: Academic Press Professional, 1990.[Online]. Available:https://www.researchgate.net/profile/Jack_Ritter/publication/242453691_An_Efficient_Bounding_Sphere/links/56e9d24e08ae95bddc2a2358/An-Efficient-Bounding-Sphere. [Google Scholar]
9. J. D. Cohen, M. Lin, D. Manocha and M. K. Ponamgi, “I-collide: An interactive and exact collision detection system for large-scale environments,” in Proc. I3D, New York, NY, USA, pp. 189-ff, 1995. [Google Scholar]
10. S. Gottschalk, “Collision queries using oriented bounding boxes,” Ph.D. dissertation. University of North Carolina at Chapel Hill, USA, 2000. [Google Scholar]
11. J. T. Klosowski, M. Held, J. S. B. Mitchell, H. Sowizral and K. Zikan, “Efficient collision detection using bounding volume hierarchies of k-DOPs,” IEEE transactions on Visualization and Computer Graphics, vol. 4, no. 1, pp. 21–36, 1998. [Google Scholar]
12. B. Chazelle, “An optimal convex hull algorithm in any fixed dimension,” Discrete & Computational Geometry, vol. 10, no. 4, pp. 337–409, 1993. [Google Scholar]
13. J. Cheng, M. Grossman and T. McKercher, Professional CUDA C programming. Hoboken, NJ, USA: John Wiley & Sons, 2014[Online]. Available:https://books.google.com.tw/books?hl=zh-TW&lr=&id=q3DvBQAAQBAJ&oi=fnd&pg=PR17&dq=NVIDIA+CUDA+C+Programming+Guide&ots=Kil1-mqyJ-&sig=TAhBbhb774M6HgS-uIhVuVPPxKM&redir_esc=y#v=onepage&q=NVIDIA%20CUDA%20C%20Programming%20Guide&f=false. [Google Scholar]
14. V. A. Dudnik, V. I. Kudryavtsev, S. A. Us and M. V. Shestakov, “Advanced features of NVIDIA Kepler architecture and parallel computation platform CUDA for developing scientific compute-intensive applications,” Problems of Atomic Science and Technology, vol. 71, no. 121, pp. 105–108, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |