Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.016589
Article

AttEF: Convolutional LSTM Encoder-Forecaster with Attention Module for Precipitation Nowcasting

Wei Fang1,2,*, Lin Pang1, Weinan Yi1 and Victor S. Sheng3

1School of Computer & Software, Engineering Research Center of Digital Forensics, Ministry of Education, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou, 215325, China
3Texas Tech University, Lubbock, TX79409, United States
*Corresponding Author: Wei Fang. Email: hsfangwei@sina.com
Received: 05 January 2021; Accepted: 19 April 2021

Abstract: Precipitation nowcasting has become an essential technology underlying various public services ranging from weather advisories to citywide rainfall alerts. The main challenge facing many algorithms is the high non-linearity and temporal-spatial complexity of the radar image. Convolutional Long Short-Term Memory (ConvLSTM) is appropriate for modeling spatiotemporal variations as it integrates the convolution operator into recurrent state transition functions. However, the technical characteristic of encoding the input sequence into a fixed-size vector cannot guarantee that ConvLSTM maintains adequate sequence representations in the information flow, which affects the performance of the task. In this paper, we propose Attention ConvLSTM Encoder-Forecaster(AttEF) which allows the encoder to encode all spatiotemporal information in a sequence of vectors. We design the attention module by exploring the ability of ConvLSTM to mergespace-time features and draw spatial attention. Specifically, several variants of ConvLSTM are evaluated: (a) embedding global-channel attention block (GCA-block) in ConvLSTM Encoder-Decoder, (b) embedding GCA-block in FconvLSTM Encoder-Decoder, (c) embedding global-channel-spatial attention block (GCSA-block) in ConvLSTM Encoder-Decoder. The results of the evaluation indicate that GCA-ConvLSTM produces the best performance of all three variants. Based on this, a new frame work which integrates the global-channel attention into the ConvLSTM encoder-forecaster is derived to model the complicated variations. Experimental results show that the main reason for the blurring of visual performance is the loss of crucial spatiotemporal information. Integrating the attention module can resolve this problem significantly.

Keywords: Convolutional LSTM; attention mechanism; sequence-to-sequence model; precipitation nowcasting

1  Introduction

Precipitation nowcasting involves providing accurate and timely forecasts of precipitation intensity in a local region. Radar echo extrapolation technology is the backbone of precipitation nowcasting. Extrapolation predicts future radar maps of fixed length, which strongly depend on the previously observed radar echo sequence. Lately, considerable progress has been made on the deep learning approach of radar echo extrapolation. Since the deep learning algorithm for radar echo extrapolation does not get any clues to understand the content of the input sequence, the biggest obstacle to accurately modelling the evolution process in this unsupervised situation is the way to learn the complex spatiotemporal correlations. As a result, establishing an effective precipitation forecasting model is always challenging.

The ongoing success of the sequence-to-sequence framework [1,2] has attracted widespread interest among researchers. However, it is not trivial to transfer this ability to precipitation nowcasting. On the one hand, the traditional encoder-decoder approach has to compress all the spatiotemporal information into a fixed-length vector. This may make it difficult for the network to address long-term spatiotemporal correlations [3]. On the other hand, it is unreasonable to assign the same weight to all inputs without discrimination. Motivated by these two deficiencies, we design AttEF for short- and long-term spatiotemporal modelling. The attention module in AttEF decides which parts of the input sequence to pay attention to depending on the preceding output of the decoder. By embedding the attention module in the forecaster, we relieve the encoder from the burden of having to encode all information in the input sequence into a vector of fixed length vector [3] and allow AttEF to focus on essential information. The attention moduleis obtained by exploring the ability for time-space feature fusion and the function of spatial attention of the convolution operators in ConvLSTM.

We carry out our work based on the previous studies [4,5]. The former research has pointed out that the convolution operators in the three gates of ConvLSTM scarcely contribute to the fusion of space-time feature. And extra spatial attention has no contribution to improving performance. With only the convolution operator of input-to-state transition, a new LSTM variant (FconvLSTM) is obtained. We integrate the global-channel attention in FconvLSTM encoder-decoder to buildvariant (b). Moreover, the viewpoint proposed by Woo et al. [5] indicates that the combination of channel attention and spatial attention can focus on the target object with more accuracy. Therefore, we integrate global-channel-spatial attention into the ConvLSTM encoder-decoder to construct variant (c).

Finally, we integrated global-channel attention into ConvLSTM encoder-decoder to build variant (a). In a nutshell, we have proposed and analyzed three structures. The overall design is shown in Fig. 1. The difference between the three variants is the choice of Att-block and LSTM block. Experiments between variant (a) and variant (b) demonstrate that convolution operators in the three gates of ConvLSTM have the ability to mergespace-time features. And experiments between variant (a) and variant (c) show that convolution operators have the function of spatial attention. By analyzing the experimental results in Section 4, we develop an AttEF structure based on the optimal variant GCA-ConvLSTM.

Figure 1: The overall architecture of the three variants

2  Related Work

Spatiotemporal sequence forecasting Precipitation nowcasting is an intrinsically spatiotemporal sequence forecasting problem. Spatiotemporal modelling has widely used in precipitation nowcasting [6,7], video prediction [8–18], robotics [19,20], and traffic flow prediction [21,22]. Lately, there is a tendency to replace the simple LSTM method [9] by the combination of CNN (convolution neural network) and LSTM networks [6,11,20,21,23] to model the spatiotemporal relationship. And this ConvLSTM type structure derives a variety of frameworks such asPredRNN [24], PredRNN++ [25], Memory in Memory [26], and EIDETIC 3D LSTM [27]. In addition, Fang et al. [28] proposed an LSTM and DCGAN based network. Brabandere et al. [29] designed a convolution kernel which changes with the input. Alahi et al. [30] proposed SocialLSTM to forecast the trajectory of pedestrians in the scene. Jain et al. [31] proposed a Structural-RNN to combine spatiotemporal graphs with RNN. Furthermore, the sequence-to-sequence model has been increasingly used in spatiotemporal modeling [7,9,32,33], which follows a paradigm: reconstruct future images from the internal state of the model. However, since the sequence-to-sequence model has to squash all the spatiotemporal information into a vector of fixed length, the predicted images are often blurry. Therefore, in this paper, we propose to design an attention module to assign different weights to different parts of the input sequence in order to focus only on the specific context vectors relevant to the generation of the next target image. Thereby our model can reduce the loss of important information and improve the clarity of the generated image.

Attention in encoder-decoder Some recent approaches [2,3] have sought to incorporate the attention mechanism into the sequence-to-sequence model. Mnih et al. [34] proposed a RAM that uses reinforcement learning to organize the perception location and scope. Ba et al. [35] further proposed DRAM for the identification of multiple targets in the images. Xu et al. [36] introduced the attention mechanism into the image captions and proposed soft attention and hard attention based on reinforcement learning. Luong et al. [37] proposed both local attention and global attention concepts. Yang et al. [38] proposed two levels of attention for document classification. Gehring et al. [39] proposed a sequence-to-sequence network entirely based on CNN and adopted a multilayer attention mechanism to obtain the relation between the encoder and the decoder. Fu et al. [40] proposed RA-CNN to solve the problem of fine-grained image classification. Chen et al. [41] proposed SCA-CNN that uses channel-wise attention and spatial attention to do image caption. Hu et al. [42] proposed SEnet to learn the correlation between the various channels. Woo et al. [5] applied the channel and spatial attention modules to learn what to pay attention to and where to pay attention to. Li et al. [43] proposed SKNet based on SENet to learn the importance of convolution kernels. The analysis in the study [4] showed that the convolution operators in the three gates of ConvLSTM barely contribute to the fusion of space-time feature, and ConvLSTM has no spatial attention function. In this paper, we integrate the global-channel attention into FconvLSTM encoder-decoder and ConvLSTM encoder-decoder and global-channel-spatial attention into ConvLSTM encoder-decoder to explore the importance of the convolution operator in ConvLSTM in the field of spatiotemporal sequence forecasting.

3  Exploring Model Structure for Precipitation Nowcasting

3.1 The Variants of ConvLSTM Encoder-Decoder

ConvLSTM, proposed by Shi et al. [7], uses convolution to perform four various transform operations on the input Xt and the hidden state Ht−1 , shown as Fig. 3A. And the main formulas are given as follows:

it=σ(Wxi∗Xt+Whi∗Ht−1+Wci∗Ct−1+bi) (1)

ft=σ(Wxf∗Xt+Whf∗Ht−1+Wcf∗Ct−1+bf) (2)

ot=σ(Wxo∗Xt+Who∗Ht−1+Wco∗Ct−1+bo) (3)

C~t=tanh⁡(Wxc∗Xt+Whc∗Ht−1+Wcc∗Ct−1+bc) (4)

Ct=ft∘Ct−1+it∘C~t (5)

Ht=ot∘tanh⁡(Ct) (6)

where σ is the sigmoid function, “*” and “ ∘ ” represent convolution operator and Hadamard product respectively. The parameter W is 2D convolution kernels. The input Xt , the cell state Ct , the hidden state Ht−1 , the candidate memory C~t , and the gates it , ft , ot are all 3D tensors. We build three variants of ConvLSTM, and the overall model architecture is presented in Fig. 1.

(a) Embedding global-channel attention block (GCA-block) in ConvLSTMEncoder-Decoder (GCA-ConvLSTM)

In this variant, the global-channel attention module (GCA-block)is embedded into ConvLSTM encoder-decoder, and we call the variant GCA-ConvLSTM. The structure first encodes the input sequence into N layers of encoder states: h¯j,Hlayer=Encoder(Xt−J+1,⋅⋅⋅,Xt),whereh¯j(j∈0,…,J) is the set of N-th hidden state for each input, Hlayer(layer∈0,…,N) is the output of the N-layer encoder. As shown in Fig. 1, N = 3, J = 4 can be expressed as h¯0,h¯1,h¯2,h¯3,H0,H1,H2=Encoder(Xt−J+1,⋅⋅⋅,Xt) . Then the decoder uses another N-layer ConvLSTM and GCA-block to generate predictions based on the encoder output: ht=Decoder(h~t,Hlayer) . At each time step of the decoder, h¯j(j∈0,…,J) and the hidden state ht−1 are input into the GCA-block to obtain the input of the decoder at the current time step: h~t=GCA−block(h¯j,ht−1) , h0=H2 . The main formulas of GCA-block are given as follows:

etj=conv3(conv1(ht−1)∗conv2(h¯j))dim∗h∗w,wherej∈0,…,J (7)

αtj=exp⁡(etj)∑k=1T⁡exp⁡(etk) (8)

ct=∑j=1J⁡αtjh¯j (9)

h~t=catnet(ct,ht−1) (10)

Formula (7) shows the alignment process we build. It measures the fit of the inputs around position j and the output at position t by multiplying h¯j and ht . And then divide by dim∗h∗w to decrease the saturation effect caused by excessive dimensions and sizes and divert attention. Then the weight αtj of each hidden state of the encoder h¯j is calculated by the softmax function as in formula (8). Finally, the context vector ct is computed, as in formula (9). As objects moving in the spatiotemporal sequence may undergo sudden changes and entanglements. This requires that the model learn short-term sequence dynamics and recall previous contexts before occlusion occurs. Therefore, both short- and long-term information is equally important. Thus, we design a Catnet-block for merging ct and ht−1 , which performs the fusion of short-and long-term information. The formula of the Catnet-block can be presented as follows:

h~t=σ(conv(ct))∗ct+ht (11)

Among them, σ is the sigmoid function. Formulas (7)–(11) jointly represent the GCA-block we constructed. The whole algorithm of GCA-block can be represented by formula (12). And the architecture of the GCA-block is shown in Fig. 2A.

Figure 2: Global-channel attention block(GCA-block). First, we apply an alignment process to the encoder’s hidden state h¯j and decoder’s hidden state ht−1 and obtain the output etj . Second, etj is entered into the softmax function to get the probabilities output αt . Third, the weight vector αt is multiplied by h¯j(j∈0,…,T) to obtain the context vector ct . Finally, ct and ht−1 are input into Catnet-block to get GCA-block output. The convolution kernels of conv1, conv2, and conv3 are 1 × 1, and the convolution kernel in Catnet-block is 3 × 3

h~t=GCA−block(h¯t,ht) (12)

(b) Embedding GCA-block in FconvLSTM Encoder-Decoder (GCA-FconvLSTM)

To verify the ability to merge the space-time features of the convolution operators in the three gates of ConvLSTM, we construct variant (b). The FconvLSTM removes the convolution operators of the gates in ConvLSTM as Fig. 3B. The main formulas of FconvLSTM are given as follows:

Figure 3: FconvLSTM applies the global average pooling operation to the input data Xt and Ht−1 , so the convolution operation is reduced to a fully connected operator

X¯t=GlobalAveragePooling(Xt) (13)

H¯t−1=GlobalAveragePooling(Ht−1) (14)

it=σ(Wxi∗X¯t+Whi∗H¯t−1+bi) (15)

ft=σ(Wxf∗X¯t+Whf∗H¯t−1+bf) (16)

ot=σ(Wxo∗X¯t+Who∗H¯t−1+bo) (17)

C~t=tanh⁡(Wxc∗Xt+Whc∗Ht−1+bc) (18)

Ct=ft∘Ct−1+it∘C~t (19)

Ht=ot∘tanh⁡(Ct) (20)

In this variant, the convolution operations of the three gates it , ft , and ot are transformed into fully connected operations, and only the convolution of the input-to-state transition is retained. he cell state Ct , the hidden state Ht and the candidate memory C~t are still 3D tensors. The pooled input X¯t , the pooled hidden state H¯t−1 , and the gates it , ft , ot are reduced to 1D tensors. Then, we build the GCA-FconvLSTM model that integrates GCA-block into FconvLSTM encoder-decoder.

(c) Embedding global-channel-spatial attention block (GCSA-block) in ConvLSTM Encoder-Decoder (GCSA-ConvLSTM)

To further verify the convolution operators in the gates of ConvLSTM play the role of spatial attention, we build variant (c). The difference compared to variant (a) is the alignment process. We combine global attention with channel attention and spatial attention to build a GCSA-block, which can be formulated as (21),where spatio_conv is a 3 × 3 convolution.

etj=spatio_conv(conv3(conv1(ht)∗conv2(h¯j))dim∗h∗w) (21)

3.2 Encoder-Forecaster Structure

In the previous section, we explored three variants of ConvLSTM encoder-decoder to design an attention module to capture short- and long-term spatiotemporal correlation. Experiments on Moving MNIST show that GCA-ConvLSTM outperforms other variants. The experimental results are shown in Section 4.

In this section, we build the encoder-forecaster structure based on the GCA-ConvLSTM explored above. There are two differences compared to the traditional encoder-decoder: Firstly, we insert downsampling and upsampling layers between the ConvLSTM, which are implemented by convolution and deconvolution with a stride; secondly, we reverse the link of the decoder network. This architecture is similar toTrajGRU [8], but the difference is the way we obtain information. AttEF would be able to select a subset of spatiotemporal information in an adaptive manner from all input and the generated images. The AttEF model integrates the GCA-block into the forecaster so that the forecaster input changes from void to GCA-block output. This enables our model to copewith sudden changes and model tangled movements by analyzing short- and long-term information. The model structure is presented in Fig. 4.

Figure 4: GCA-ConvLSTM Encoder-Forecaster (AttEF). The figure shows the prediction for the next three images X^3,X^4,X^5 based on the first three images X0,X1,X2 . The symbol ⊎ indicates the hidden states of the encoder is stacked out in one dimension

4  Experiments

In this section, we present experiments on two spatiotemporal datasets. First, we evaluate the performance of the three variants and the AttEF model on the Moving MNIST dataset. Then, we use another radar reflectivity dataset to further evaluate the performance of the AttEF model in the field of precipitation nowcasting. We train all models with PyTorch and optimize them using the ADAM optimizer with a starting learning rate of 10E−3. We define the loss function as L1 + L2 loss to simultaneously enhance the sharpness and the smoothness of the generated image.

4.1 Moving MNIST Dataset

The Moving MNIST dataset is a synthetic dataset, and each frame contains two hand-written digits that bouncing within a 64 × 64 patch. These hand-written numbers are randomly selected from the MNIST training set, and the start position and velocity direction are also randomly selected. A rebound occurs when a digit touches a border or another digit [10]. The random factors of these attributes increase the difficulty of the model prediction. This function serves to sample an unlimited size dataset. Each sequence has 20 images, and the model uses the first ten images to predict the next ten images. To evaluate the generalization and migration capabilities of the model, we also test on another Moving MNIST dataset with three digits.

Firstly, experimental comparisons are made on the three variants proposed in Section 3.1. GCA-ConvLSTM is superior to GCA-FconvLSTM and GCSA-ConvLSTM as shown in Fig. 5. The prediction examples selected in Fig. 5a have entangled digits in the input. The three variants can effectively separate the entangled targets, showing that the model can extract long-term information before the entanglement as a predictive reference. However, the predictive results of GCA-FconvLSTM and GCSA-ConvLSTM gradually deviate from the actual shape. The shape of the digit “5” in the GCSA-ConvLSTM prediction result in Fig. 5a has been gradually predicted to the incorrect shape of the digit “6”.

Figure 5: Prediction examples on the Moving MNIST-2 and Moving MNIST-3 test set (a) the Moving MNIST-2 test set (b) the Moving MNIST-3 test set

To evaluate the generalization ability of the model, we test the model trained on the two-digit dataset on the three-digit dataset. The test results of the three models are presented in Fig. 5b. As we can see, the last image in the outputs of GCA-ConvLSTM still has obvious digital shapes, while the outputs of other variants are blurry. Fig. 6 illustrates the frame-wise MSE results on the test set, and the lower curves indicate higher predictive accuracy.

Figure 6: Frame-wise MSE comparisons of three variances on the Moving MNIST test sets (a) MNIST-2 (b) MNIST-3

Based on the above experiments, we have concluded that the convolution operators in ConvLSTM play an essential role in dealing with spatiotemporal sequence problems. In the same condition for integrating the GCA-block, the performance of GCA-FconvLSTM is significantly lower than that of GCA-ConvLSTM. The reason is that it is difficult to capture the spatiotemporal motion pattern without the convolution operator. And the operation of global average pooling results in a large amount of loss of spatial information. The reason why GCA-ConvLSTM outperforms GCSA-ConvLSTM is that the convolution operator itself within ConvLSTM has the spatial attention function. As a result, the extra spatial attention not only does not contribute to the improvements of performance, but also further pares down he effective information, resulting in a distortion of the GCSA-ConvLSTM prediction.

we then carry out experimental comparisons between AttEF and other models. Fig. 7a provides a more specific frame-wise comparison. Both ConvLSTM and TrajGRU prediction is blurry. Although the predictive result of PredRNN is relatively clear, it gradually deviates from the correct shape of the digit “8” to the incorrect shape of the digit “2”. Such a phenomenon results from these three benchmark models which do not have a robust structure for adaptively updating an effective information flow. As well, we evaluate the generalization ability of the model in MNIST-3. As shown in Fig. 7b, AttEF achieves the best generalization results. And Fig. 8 illustrates the frame-wise MSE results.

Figure 7: Prediction examples on the Moving MNIST-2 and Moving MNIST-3 test set (a) the Moving MNIST-2 test set (b) the Moving MNIST-3 test set

Figure 8: Frame-wise MSE comparisons of different models on the Moving MNIST test sets (a) MNIST-2 (b) MNIST-3

4.2 Radar Echo Grid Dataset

The radar echo dataset used in this paper is a continuous sequence of mosaicked ground radar. And the single data is presented as 1000 × 1000 gridded data covering the Shaanxi Province. Each grid covers 0.01∘ of longitude and latitude corresponding to approximately 1 km2. And the value in the gridded data represents the radar reflectivity. The temporal resolution is 6 minutes. For pre-processing, we first set the negative values in the original data to zero. And then, we conduct a data normalization operation. Finally, the 1000 × 1000 radar grid data is stored in NumPy array format and resized to 500 × 500. We use a 20-frame-wide sliding window with a stride of 5 to extract samples (10 for the input and 10 for the prediction), and divide them into disjoint subsets of training, verification, and testing.

We set the patch size to 2 × 2 so that each 500 × 500 frame is represented by a 250 × 250 × 4 tensor. Also, we use precipitation nowcasting metrics to evaluate the results of the experiment. These indicators are: mean squared error (MSE), critical success index (CSI), probability of detection (POD), and false alarm rate (FAR). When calculating CSI, POD and FAR, we first convert the prediction and ground truth to a 0/1 matrix using a fixed threshold of radar reflectivity value and then calculate the hits (prediction = 1, truth = 1), misses (prediction = 0, The value of truth = 1) and false alarms (prediction = 1, truth = 0), these three skill scores are defined as CSI=hitshits+misses+falsealarms , POD=hitshits+misses , FAR=falsealarmshits+falsealarms . We choose two radar reflectivity values of 15 dBZ and 20 dBZ as the corresponding thresholds for binarization.

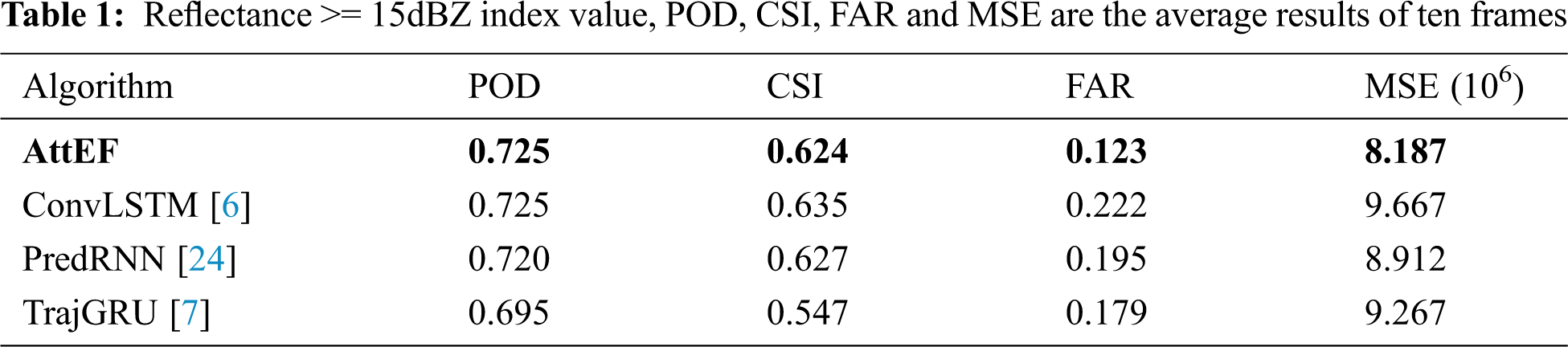
We take into account three benchmark models in this radar echo extrapolation experiment. ConvLSTM and TrajGRU are both proposed to address the precipitation nowcasting problem, but their predictions are blurry. AttEF performs the best, especially the short-term forecasts, and achieves the lowest MSE loss, as shown in Fig. 10. It is obvious from Fig. 9 that while all models tend to blur with the increase of forecasting steps, AttEF is more similar in shape to ground truth, with sharper edges and more details. Figs. 11 and 12 show the performance of the four models with thresholds of 15 dBZ and 20 dBZ on three skill scores. Tabs 1 and 2 evaluate the precipitation forecaste quality. Because filtering more information than 15 dBZ, the effect of 20 dBZ will naturally diminish. By analyzing the performance of the four models on the four evaluation indicators, we find that AttEF achieves the lowest FAR, and has the best performance on POD and CSI, especially the first few frames. Due to the inherent uncertainty of the future, AttEF generates increasingly blurry images from the first to the last time step. The reason why ConvLSTM performs well on POD and CSI is that the number of radar reflectivity values exceeding the threshold is relatively high. Therefore, ConvLSTM presents the worst performance on FAR and the lowest accuracy.

Figure 9: Visualize the result of callback extrapolation

Figure 10: The changing trends of the four models on MSE

Figure 11: Reflectance >= 20dBZ index value model three skill scores change trends

Figure 12: Reflectance >= 15dBZ index value model three skill scores change trends

5  Conclusion

In this paper, we have provided a new AttEF model with the ability to learn short- and long-term spatiotemporal correlations by intergrating a novel attention module in the forecaster. We design the attention model by exploring three variants of the ConvLSTM encoder-decoder. And these three variants confirm that the ConvLSTM convolution operators have the ability to merge spatio-temporal features and the spatial attention function. According to the exploration performances above on the Moving MNIST dataset, we have obtained the GCA-block attention module for the ConvLSTM encoder-decoder. Then the encoder-decoder is optimized to encoder-forecaster. And integrate the GCA-block into the forecaster to get our AttEF model. Finally, we carry out a comparative experiment with three mainstream algorithms using two spatiotemporal datasets. Experimental results show that the AttEF model can learn short- and long-term spatiotemporal dependencies adaptively and achieve the best performance on both datasets.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant No.42075007), the Open Project of Provincial Key Laboratory for Computer Information Processing Technology under Grant KJS1935, Soochow University, and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  I. Sutskever, O. Vinyals and Q. V. Le, “Sequence to sequence learning with neural networks,” Neural Information Processing Systems, vol. 27, pp. 3104–3112, 2014. [Google Scholar]

 2.  K. Cho, B. V. Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares et al., “Learning phrase representations using RNN encoder-decoder for statistical machine translation,” in Proc. EMNLP, Doha, Qatar, pp. 1724–1734, 2014. [Google Scholar]

 3.  D. Bahdanau, K. Cho and Y. Bengio, “Neural machine translation by jointly learning to align and translate,” in Proc. ICLR, San Diego, United States, 2015. [Google Scholar]

 4.  L. Zhang, G. Zhu, L. Mei, P. Shen, S. A. A. Shah et al., “Attention in convolutional LSTM for gesture recognition,” in Proc. NIPS, Montreal, Canada, pp. 1957–1966, 2018. [Google Scholar]

 5.  S. Woo, J. Park, J. Y. Lee and I. S. Kweon, “CBAM: Convolutional block attention module,” in Proc. ECCV, Munich, Germany, pp. 3–19, 2018. [Google Scholar]

 6.  X. Shi, Z. Chen, H. Wang, D. Y. Yeung, W. K. Wong et al., “Convolutional LSTM network: A machine learning approach for precipitation nowcasting,” in Proc. NIPS, Montreal, Canada, pp. 802–810, 2015. [Google Scholar]

 7.  X. Shi, Z. Gao, L. Lausen, H. Wang, D. Y. Yeung et al., “Deep learning for precipitation nowcasting: A benchmark and a new model,” in Proc. NIPS, Long Beach, CA, USA, pp. 5617–5627, 2017. [Google Scholar]

 8.  M. A. Ranzato, A. Szlam, J. Bruna, M. Mathieu, R. Collobert et al., “Video (language) modeling: A baseline for generative models of natural videos,” CoRR abs/1412.6604, 2014. [Google Scholar]

 9.  N. Srivastava, E. Mansimov and R. Salakhutdinov, “Unsupervised learning of video representations using lstms,” in Proc. ICML, Lille, France, 37, pp. 843–852, 2015. [Google Scholar]

10. H. Zhu, H. Fan, Z. Shu, C. You, X. Chen et al., “Optimal mode decision method for interframe prediction in h.264/avc,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2425–2439, 2020. [Google Scholar]

11. W. Lotter, G. Kreiman and D. Cox, “Deep predictive coding networks for video prediction and unsupervised learning,” in Proc. ICLR, Toulon, France, 2017. [Google Scholar]

12. T. Xue, J. Wu, K. Bouman and B. Freeman, “Visual dynamics: Probabilistic future frame synthesis via cross convolutional networks,” in Proc. NIPS, Barcelona, Spain, pp. 91–99, 2016. [Google Scholar]

13. C. Vondrick, H. Pirsiavash and A. Torralba, “Anticipating the future by watching unlabeled video,” CoRR abs/1504.08023, 2015. [Google Scholar]

14. C. Vondrick and A. Torralba, “Generating the future with adversarial transformers,” in Proc. CVPR, Honolulu, HI, pp. 2992–3000, 2017. [Google Scholar]

15. R. Villegas, J. Yang, Y. Zou, S. Sohn, X. Lin et al., “Learning to generate long-term future via hierarchical prediction,” in Proc. ICML, Sydney, NSW, Australia, vol.70, pp. 3560–3569, 2017. [Google Scholar]

16. J. V. Amersfoort, A. Kannan, M. A. Ranzato, A. Szlam, D. Tran et al., “Transformation-based models of video sequence,” arXiv:1701.08435, 2017. [Google Scholar]

17. E. Denton and R. Fergus, “Stochastic video generation with a learned prior,” in Proc. ICML, Stockholm, Sweden, pp. 1182–1191, 2018. [Google Scholar]

18. N. Wichers, R. Villegas, D. Erhan and H. Lee, “Hierarchical long-term video prediction without supervision,” in Proc. ICML, Stockholm, Sweden, pp. 6033–6041, 2018. [Google Scholar]

19. J. Oh, X. Guo, H. Lee, R. L. Lewis and S. Singh, “Action-conditional video prediction using deep networks in atari games,” in Proc.NIPS, Montreal, Canada, pp. 2863–2871, 2015. [Google Scholar]

20. C. Finn, I. Goodfellow and S. Levine, “Unsupervised learning for physical interaction through video prediction,” in Proc. NIPS, Barcelona, Spain, pp. 64–72, 2016. [Google Scholar]

21. J. Li, H. Li, G. Cui, Y. Kang, Y. Hu et al., “Gacnet: A generative adversarial capsule network for regional epitaxial traffic flow prediction,” Computers Materials & Continua, vol. 64, no. 2, pp. 925–940, 2020. [Google Scholar]

22. B. Yu, H. Yin and Z. Zhu, “Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting,” in Proc.IJCAI, Stockholm, Sweden, pp. 3634–3640, 2018. [Google Scholar]

23. V. Patraucean, A. Handa and R. Cipolla, “Spatio-temporal video autoencoder with differentiable memory,” CoRR abs/1511.06309, 2015. [Google Scholar]

24. Y. Wang, M. Long, J. Wang, Z. Gao and P. S. Yu, “PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs,” in Proc. NIPS, Long Beach, CA, USA, pp. 879–888, 2017. [Google Scholar]

25. Y. Wang, Z. Gao, M. Long, J. Wang and P. S. Yu, “PredRNN++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning,” in Proc. ICML, Stockholm, Sweden, pp. 5110–5119, 2018. [Google Scholar]

26. Y. Wang, J. Zhang, H. Zhu, M. Long, J. Wang et al., “Memory in memory: A predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics,” in Proc. CVPR, Long Beach, CA, USA, pp. 9146–9154, 2019. [Google Scholar]

27. Y. Wang, L. Jiang, M. H. Yang, L. J. Li, M. Long et al., “Eidetic 3D LSTM: A model for video prediction and beyond,” in Proc. ICLR, New Orleans, LA, USA2019. [Google Scholar]

28. W. Fang, F. Zhang, Y. Ding and J. Sheng, “A new sequential image prediction method based on lstm and dcgan,” Computers, Materials & Continua, vol. 64, no. 1, pp. 217–231, 2020. [Google Scholar]

29. B. D. Brabandere, X. Jia, T. Tuytelaars and L. V. Gool, “Dynamic filter networks,” in Proc. NIPS, Barcelona, Spain, pp. 667–675, 2016. [Google Scholar]

30. A. Alahi, K. Goel, V. Ramanathan, A. Robicquet, F. F. Li et al., “Social LSTM: Human trajectory prediction in crowded spaces,” in Proc. CVPR, Las Vegas, NV, pp. 961–971, 2016. [Google Scholar]

31. A. Jain, A. R. Zamir, S. Savarese and A. Saxena, “Structural-RNN: Deep learning on spatio-temporal graphs,” in Proc. CVPR, Las Vegas, NV, pp. 5308–5317, 2016. [Google Scholar]

32. C. Luo, C. Shi, X. Li, X. Wang, Y. Chen et al., “Multi-task learning using attention-based convolutional encoder-decoder for dilated cardiomyopathy cmr segmentation and classification,” Computers Materials & Continua, vol. 63, no. 2, pp. 995–1012, 2020. [Google Scholar]

33. Y. Wang, Z. Fu and X. Sun, “High visual quality image steganography based on encoder-decoder model,” Journal of Cyber Security, vol. 2, no. 3, pp. 115–121, 2020. [Google Scholar]

34. V. Mnih, N. Heess, A. Graves and K. Kavukcuoglu, “Recurrent models of visual attention,” in Proc. NIPS, Montreal, Quebec, Canada, vol.27, pp. 2204–2212, 2014. [Google Scholar]

35. J. Ba, V. Mnih and K. Kavukcuoglu, “Multiple object recognition with visual attention,” arXiv:1412.7755, 2014. [Google Scholar]

36. K. Xu, J. L. Ba, R. Kiros, K. Cho, A. Courville et al., “Show, attend and tell: Neural image caption generation with visual attention,” in Proc. ICLR, Lille, France, pp. 2048–2057, 2015. [Google Scholar]

37. M. T. Luong, H. Pham and C. D. Manning, “Effective approaches to attention-based neural machine translation,” in Proc. EMNLP, Lisbon, Portugal, pp. 1412–1421, 2015. [Google Scholar]

38. Z. Yang, D. Yang, C. Dyer, X. He, A. Smola et al., “Hierarchical attention networks for document classification,” in Proc. HLT-NAACL, San Diego, California, USA, pp. 1480–1489, 2016. [Google Scholar]

39. J. Gehring, M. Auli, D. Grangier, D. Yarats and Y. N. Dauphin, “Convolutional sequence to sequence learning,” in Proc. ICML, Sydney, NSW, Australia, pp. 1243–1252, 2017. [Google Scholar]

40. J. Fu, H. Zheng and T. Mei, “Look closer to see better: recurrent attention convolutional neural network for fine-grained image recognition,” in Proc. CVPR, Honolulu, HI, pp. 4476–4484, 2017. [Google Scholar]

41. L. Chen, H. Zhang, J. Xiao, L. Nie, J. Shao et al., “SCA-CNN: Spatial and channel-wise attention in convolutional networks for image captioning,” in Proc. CVPR, Honolulu, HI, pp. 6298–6306, 2017. [Google Scholar]

42. J. Hu, L. Shen, S. Albanie, G. Sun and E. Wu, “Squeeze-and-excitation networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 8, pp. 2011–2023, 2020. [Google Scholar]

43. X. Li, W. Wang, X. Hu and J. Yang, “Selective kernel networks,” in Proc. CVPR, Long Beach, CA, USA, pp. 510–519, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.