Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.017963
Article

Conveyor Belt Detection Based on Deep Convolution GANs

Xiaoli Hao1,*, Xiaojuan Meng1, Yueqin Zhang1, Jindong Xue2 and Jinyue Xia3

1College of Information and Computer, Taiyuan University of Technology, Jinzhong, 030600, China
2State Grid Taiyuan Power Supply Company, Taiyuan, 030012, China
3International Business Machines Corporation (IBM), New York, NY, USA
*Corresponding Author: Xiaoli Hao. Email: haoxiaoli@tyut.edu.cn
Received: 19 February 2021; Accepted: 23 May 2021

Abstract: The belt conveyor is essential in coal mine underground transportation. The belt properties directly affect the safety of the conveyor. It is essential to monitor that the belt works well. Traditional non-contact detection methods are usually time-consuming, and they only identify a single instance of damage. In this paper, a new belt-tear detection method is developed, characterized by two time-scale update rules for a multi-class deep convolution generative adversarial network. To use this method, only a small amount of image data needs to be labeled, and batch normalization in the generator must be removed to avoid artifacts in the generated images. The output of the discriminator uses a multi-classification softmax function to identify the scratches, cracks, and tears in the belt. In addition, we have improved the two time-scale update rule, by which the generator and discriminator use different learning rates, updated it according to α:β , and defined α:β as 2:1. It can strike a balance between the generator and discriminator, speed up discriminator training, and improve real-time damage detection. Experimental results show that the detection accuracy of tears reaches 100%, and the detection accuracy of non-serious damage is up to 97.1%.

Keywords: Two time-scale update rule; multi-class detection; deep convolution generative adversarial network; conveyor belt tear

1  Introduction

The belt conveyor is indispensable in underground transportation in coal mines, and its core component is the belt, whose state can directly affect the safe and stable operation of the conveyor [1–3]. However, in the complex environment of the pit, gangue and thin rods mixed with coal are likely to penetrate the conveyor belt and be caught on the roller, causing the belt to tear during the transport process [4–6]. In addition, if a conveyor belt works for a long time, its surface will be worn heavily and become covered in scratches and cracks because of uneven force. If these defects are not noticed, the belt may be torn [7–9]. Methods of tear detection are characterized as either contact [10–12] or non-contact [13–15]. Contact detection, such as swing roller detection [16–18] and tear pressure detection [19–21], often uses roller pressure for detection. These methods can quickly and simply detect whether a belt is torn according to force applied to the belt on the support roll, but the cost is relatively high. A large coal block passing through the blanking port and colliding with the buffer roller during transportation can easily cause false or missing detection. Most non-contact methods are based on non-destructive detection theory, such as ultrasound detection [22–25], which identifies tears according to the different states of sent and received ultrasonic waves produced by waveguides. However, there are complex noises in underground mining, making it difficult for the ultrasonic system to receive echoes of longitudinal tears, which results in low detection accuracy. With the development of computer vision, non-contact detection uses edge extraction to capture significant areas and detect acquired images. These methods only detect a single type of damage and have a long computation time, usually including preprocessing operations such as binarization, edge extraction, and image denoising.

Deep learning techniques, such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), and generative adversarial networks (GANs), have been widely applied in image segmentation and detection. Deep convolutional GANs (DCGANs) have been widely used in image processing, with their unsupervised learning methods. In a DCGAN, the multi-layer perceptron of the discriminator and generator in a GAN is replaced by a CNN. To make the entire network differentiable, the pooling layer in the CNN is removed and the fully connected layer is replaced by a global pooling layer to reduce calculation. However, for the batch normalization used in the extraction of upsampling features in DCGAN and its improved algorithms, the pixel space in the generator is not evenly covered and the generated image can easily produce artifacts. Moreover, the discriminator uses a binary classification function that can only output two categories: real and fake images. It cannot identify multiple types of damage. The discriminator and generator often use the same learning rate. The generator updates several times in training, while the discriminator only updates once, causing the discriminator to prematurely reach a local optimum, resulting in mode collapse. We propose an improved DCGAN and apply it to damage detection. We make the following innovations.

(1) The batch normalization of the generator can easily cause artifacts in the generated image and affect the accurate detection of conveyor belt damage. Furthermore, batch normalization is prone to long calculation times and significant memory use. We remove batch normalization to improve the accuracy of damage detection and reduce training time.

(2) The discriminator of DCGAN cannot be used to identify multiple types of damage. We adopt a multi-classification softmax function to transform the output vector into class probabilities. In this way, the scratches, cracks, and tears in the belt damage can be accurately identified.

(3) Since the discriminator and generator often use the same learning rate, the model is more likely to crash. We introduce a two-scale update rule under which the generator and discriminator use different learning rates, update according to α:β , and define α:β as 2:1. This maintains the balance between the generator and discriminator and improves the training speed of the discriminator, for better real-time damage detection.

The rest of this paper is organized as follows. Related work is presented in Section 2. Section 3 introduces the system design and the algorithm design in the detection subsystem. In Section 4, we propose our improved algorithm for belt damage detection based on a multi-class DCGAN. Experiments and analysis are discussed in Section 5.

2  Related Work

Yang et al. [26–28] proposed a conveyor belt tear warning method that captures an infrared image calculates a threshold value through a grey histogram, and obtains a binary image to determine whether the belt is torn. This method can detect only tears, since it merely binarizes the tearing area. Li et al. [29,30] developed a real-time detection method using edge detection and a single-scale image enhancement algorithm to extract edge and non-edge features to obtain a feature lattice array, whose numerical characteristics can be used to detect longitudinal tears. However, this method only extracts features for the area, fineness and rectangularity of the tear area and cannot detect other non-severe damage types in time. Qiao et al. [31–33] designed a binocular visual detection method using visible and infrared light to extract scene and edge features, respectively. The length, width, and area of longitudinal tears are obtained from the projection vectors of the acquired images on the X and Y axes. Hao et al. [34–36] devised a multi-class detection method based on visual salience, using support vector machine (SVM) to transform nonlinear separable samples of extracted seven-dimensional feature vectors into linear separable samples in a high-dimensional space. Test samples are classified using the radial basis function. Although this method can detect scratches, cracks, and tears, the collected images must be preprocessed by binarization and grey histograms to get the features of the damaged positions, which is time-consuming.

Deep learning has been widely applied in image segmentation [37–39] and detection [40,41], with its use of a massive data training network to extract object features. In practical application, however, people often obtain data that are not labeled. If we use the traditional CNN, it is time-consuming to manually label many images [42,43]. Goodfellow et al. [44,45] devised a generative adversarial network (GAN). Based on the idea of a zero-sum game, it extracts image features through competition between a discriminator and generator. The former tries to minimize the error through the identification of the generated image data, while the latter tries to maximize the error. Finally, the Nash balance is reached between the two and the foreground and background are segmented according to the differences of the features. Only a small amount of labeled data is needed, since the model can automatically learn the data distribution from the training samples and generate new sample data. However, network training usually adopts the gradient descent method, and the generator model may be trained along a certain feature all the time, resulting in non-convergence and model collapse. Radford et al. [46,47] worked out a DCGAN, replacing the upsampling layer with step convolution and the full connection layer with convolution. The model learns its own spatial downsampling, so the network can accurately obtain the image features. Batch normalization normalizes the input of each layer in the generator and discriminator to N(0,1), thus accelerating the training speed. However, the discriminator and generator usually adopt the same learning rate, so their updating speeds must be balanced carefully during training to avoid model collapse. For this reason, Heusel et al. [48] proposed a two time-scale update rule so that the generator and discriminator use different learning rates, so if the generator changes slowly enough, the discriminator still converges. When the two machines update at the rate of 1:1, the generative adversarial network will converge to a local Nash equilibrium. However, the discriminator updates much quicker than the generator, so the ratio of 1:1 cannot really solve the convergence problem.

3  Problem and Solution

We design a belt damage detection system including image acquisition, image detection, and a response subsystem. The image acquisition subsystem is composed of a surface light source and a charge coupled device (CCD) camera to collect damage images. The surface light source illuminates the belt surface vertically to improve the brightness of the image. The CCD camera is placed at an appropriate angle to collect belt images. The image detection subsystem uses the designed algorithm to detect damage of the collected images. The response subsystem reacts to the detection results in real time. If there is a tear, the conveyor belt will stop immediately. If there is a crack, the system issues a warning and does not stop. If the conveyor belt is normal or scratched, the system runs properly. Therefore, the image detection subsystem is the core component of belt damage detection. The rationality of algorithm of the subsystem affects the real-time performance and accuracy of belt tear detection, hence its design is most important.

In DCGAN, the generator model is a deconvolutional neural network whose pooling layers are replaced by fractional-strided convolution. The discriminator model is a CNN adopting strided convolution instead of pooling layers. When the traditional DCGAN is used for image detection, its batch normalization of DCGAN can help solve the problem of training fluctuations caused by poor initialization. In the process of generating images, the pixel space in the generator is not uniformly covered due to batch normalization during upsampling feature extraction, so artifacts are easily produced. These can lead to deviations in the characteristics learned by the generator, which affect the accurate detection of the type of conveyor belt damage. At the same time, when performing network training on large batches of image data, batch normalization can normalize the input of each layer to N(0,1), helping to speed up the training. We use small batches of seven images to train the network, but batch normalization is likely to use much calculation time and memory, so we remove it from the generator model. The output of the discriminator uses two classification functions. Using this model, only the torn and undamaged parts of the conveyor belt can be detected, but not potential hazards such as scratches and cracks, preventing timely maintenance of the conveyor belt. Given this problem, a multi-class softmax function is applied to the output of the discriminator to detect scratches, cracks, and tears. The generator and discriminator use the same learning rate. During training, the generator updates many times, while the discriminator updates only once. Hence the discriminator reaches the local optimal solution too early, causing the model to converge and then collapse. In response to this problem, we introduce a two-scale update rule. The generator and discriminator use different learning rates, update according to α:β , and define α:β as 2:1. It can maintain a balance between the generator and discriminator, preventing the discriminator from reaching the optimal solution too early and causing the model to not converge. The model is optimized through the update rule of the discriminator and generator to improve the accuracy of belt tear detection.

4  Conveyor Belt Detection Algorithm Design

4.1 Multi-Class DCGAN

In belt tear detection, the traditional generator model of DCGAN is a deconvolutional neural network. The generator inputs a random noise vector, extracts upsampling features on the belt image through the input and deconvolutional layers, and converts it to a fake image that is very close to the real image. The conventional discriminator model is an improved CNN. A sigmoid binary classification function is employed on the output layer, and the output value is in [0,1]. An output of 1 indicates that the input image is the detection result of real data. An output of 0 means that the generated input image is a fake. Due to these features of the sigmoid binary classification function, only torn and undamaged parts can be detected, while scratches cannot be identified. Inspired by Salimans et al. [49], we use the softmax function as the output function of the discriminator to identify scratches, cracks, and tears. We call this a multi-class deep convolution generative adversarial network.

Suppose the random vector z has a uniform noise distribution pz(z) , and the generator model G(z) maps it to the data space of a real image. The input x of the discriminator is a real or a fake image with label y , and its distribution is Pdata(x,y) . Its full connection layer output is a ( k+1 )-dimensional vector l={l1,l2,...,lk+1} , which is converted by the softmax function to a ( k+1 )-dimensional category probability p={p1,p2,...,pk+1} . The real image is judged as among the first k classes, and the fake image will be judged as the (k+1)th class. The softmax function is

pj=elj∑i=1keli,j∈{1,2,...,k+1}, (1)

where li is the input vector of the fully connected layer, lj is the class vector output by the fully connected layer, pj is the class probability of the output, and e is the base of the natural logarithm, approximately 2.71828.

We select the cross-entropy function as the loss function of the discriminator D(y|x) to determine the closeness between the actual and expected output. The smaller the loss value the better the model learns. Therefore, it is necessary to optimize the network model by minimizing the loss function. Define

D(y|x)=−∑jyj′log⁡(pj), (2)

where j is the category, y′ is the expected category, and pj is the probability of the category output. One-hot coding is adopted for y and y′ , i.e., if the discriminator outputs the jth class, the corresponding positions are coded as 1, and other positions are coded as 0.

According to Eq. (2), when the input is a real image, then D(y|x,y<k+1) can be expressed as

D(y|x,y<k+1)=−∑j=1ky′log⁡(pj), (3)

where y′ is the expected category and pj is the category probability of the output. When the input is a fake image, it can be simplified to

D(y|x,y=k+1)=−log⁡(pk+1), (4)

where pk+1 is the category probability of the fake image.

Fig. 1 shows the principle diagram of the multi-class damage detection of a conveyor belt based on the softmax function. The type of damage is identified by the softmax function, and the damage category is labeled as 1, 2, 3, or 4, corresponding to the characteristics of a tear, crack, scratch, or fake image, respectively.

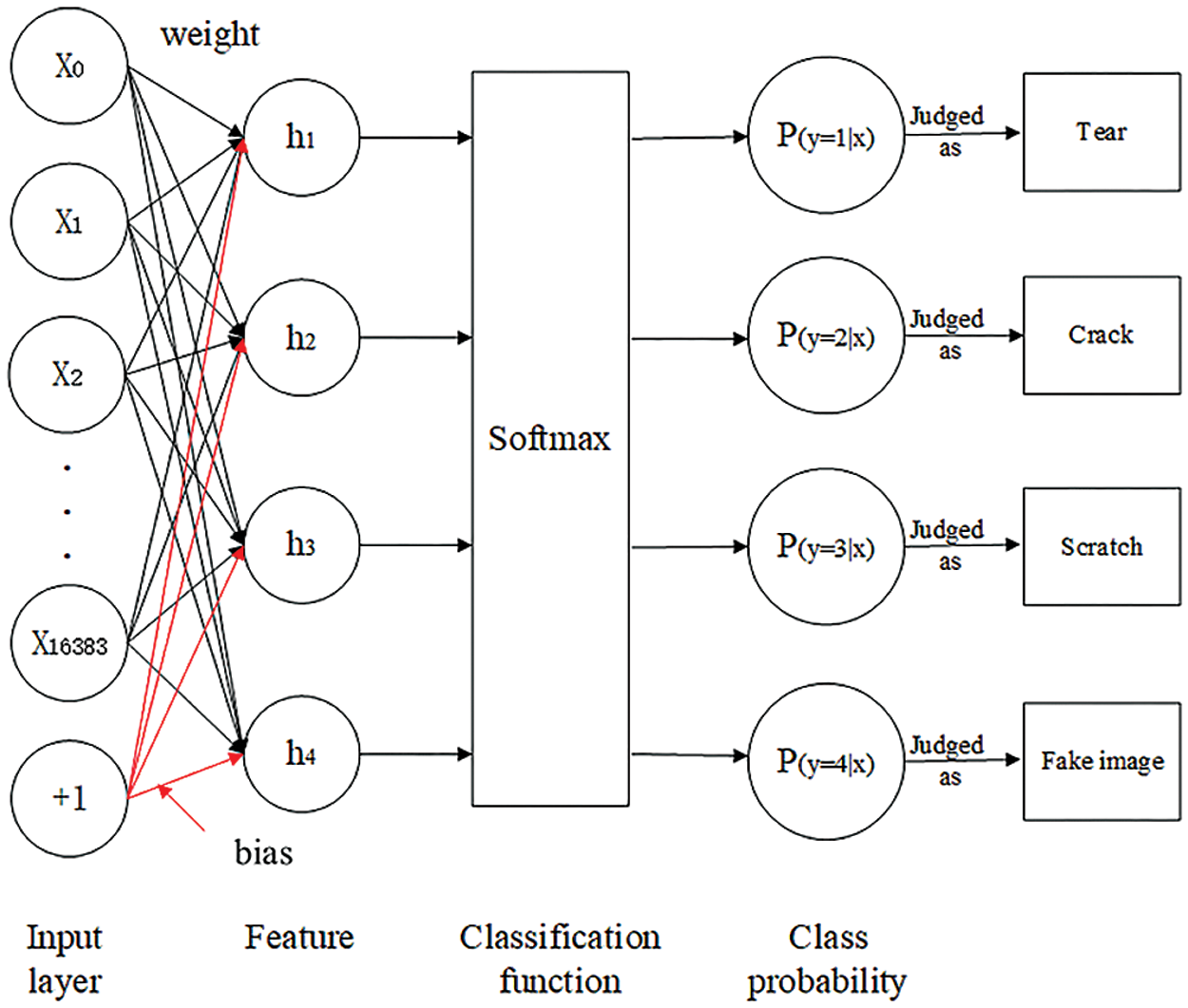
Figure 1: Principal diagram of multi-class damage detection for conveyor belts

4.2 Two-Scale Update Rule

The generator and discriminator of the traditional DCGAN use the same learning rate, so their updating rates must be balanced carefully to avoid collapse. Inspired by Heusel, we improve the two time-scale update rule to a two-scale update rule, where the generator and discriminator use different learning rates, update according to the ratio of α:β , and define α:β as 2:1.

We define the discriminator as D(y|x) with gradient h(d) , while the generator model is G(z) , with gradient h(g) . Suppose the discriminator and generator have m input image samples in each training iteration x(t) , where 1≤t≤m . The gradient of the discriminator model is defined as

h(d)=∇θd1m∑t=1m[D(y|x(t),y<k+1)+D(y|G(zt),y=k+1)], (5)

where y<k+1 is the first k classes, y=k+1 is the class of fake image, x(t) is the tth input image sample, G(zt) is the tth generated image sample, and θd is the parameter of the discriminator model.

The gradient of the generator model is defined as

h(g)=∇θg1m∑t=1mD(y|G(zt),y=k+1), (6)

where y=k+1 represents the fake image, m represents the input image sample, G(zt) is the ith image sample, and θg is the parameter of the generator model. If the discriminator is updated too quickly, the learning time of the generator is insufficient, and the extracted features are incomplete. If the generator is updated too quickly, then the discriminator prematurely reaches a local optimum, which results in a mode crash. Therefore, the updating rates of discriminator and generator should be balanced carefully in training. We adopt the two-scale update rule,

hn+1=βahn(d)+αbhn(g), (7)

where a and b are the learning rates of the discriminator and generator, respectively, and n is the number of iterations, where 1≤n≤m . The iterative update of the generator and discriminator models according to the ratio α:β enables steadier network training more steadily and better extraction of the image features of the conveyor belt.

4.3 Algorithm Description

We proposed a new belt-tear detection method, which used a multi-class deep convolution generative adversarial network based on the two time-scale update rule. The algorithm steps are shown below.

Step 1: The images with surface light source are collected by a CCD camera, and some are labeled with a damage type, forming a small number of labeled datasets and a large number of unlabeled datasets, as shown in Fig. 2. Belt damage is marked as follows: the red box represents tears, the blue box represents cracks, and the green box represents scratches.

Figure 2: Types of damage

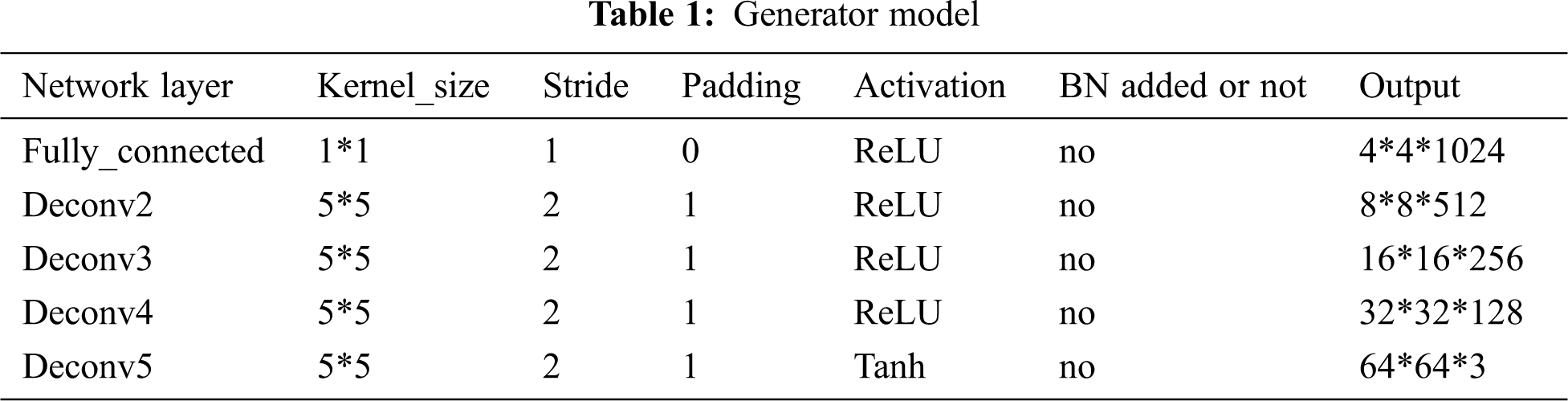
Step 2: Build the generator model: The input vector is 100-dimensional random noise, which is converted to a 16384-dimensional vector through a fully connected layer, and then to a 4 *4*1024 feature map by the reshape function. Through deconvolutional layers 1, 2, 3, and 4 for upsampling, a 64*64*3 belt image is generated. We do not adopt batch normalization in deconvolutional layers 1, 2, and 3. The model structure is shown in Tab. 1.

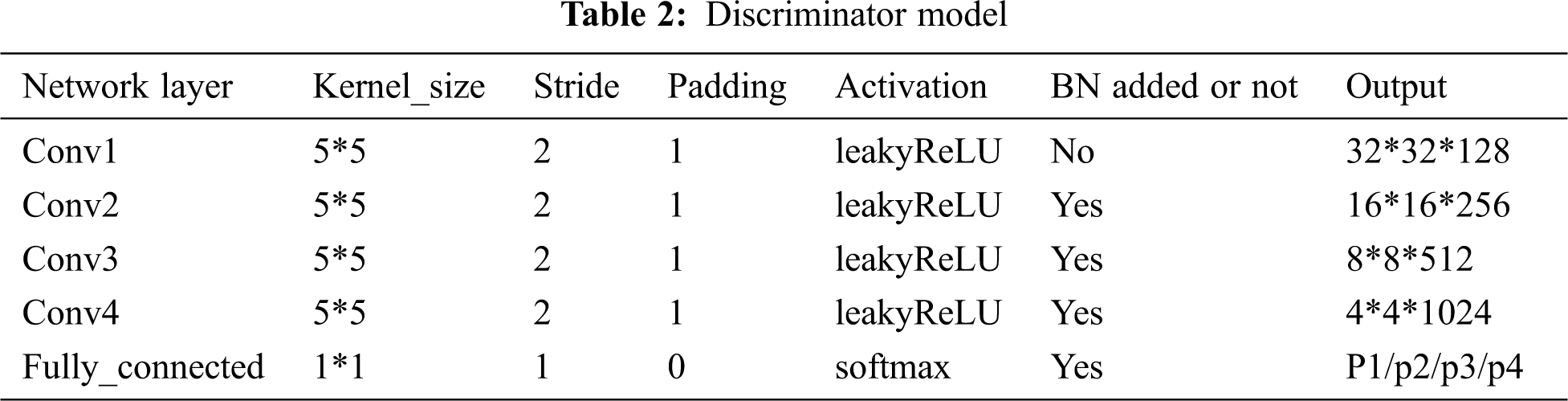
Step 3: Build the discriminator model: The input consists of 64*64*3 images. By downsampling in convolutional layers 1, 2, 3, and 4, the final output is a 4*4*1024 feature map. It is reshaped into a (4*4*1024)-dimensional vector. Through the full connection layer, the probability values of scratches, cracks, tears and fake images are output by the softmax function to judge the damage type. The model structure is shown in Tab. 2.

Step 4: Training network: Eq. (7) introduces the two-scale update rule, setting α:β to 2:1. If the loss value of the model in Eq. (2) drops to a certain value and tends to be stable, then the model has converged, the characteristics of scratches, cracks, and tears can be obtained, and the damage type of the image can be predicted.

Step 5: Based on the predicted results, the system responds in real time. If there is a tear, then the conveyor belt stops immediately. If there is a crack, the system issues a warning and does not stop. If the conveyor belt is detected as normal or if there are scratches, then the system operates normally.

The detection process of the belt image is shown in Fig. 3.

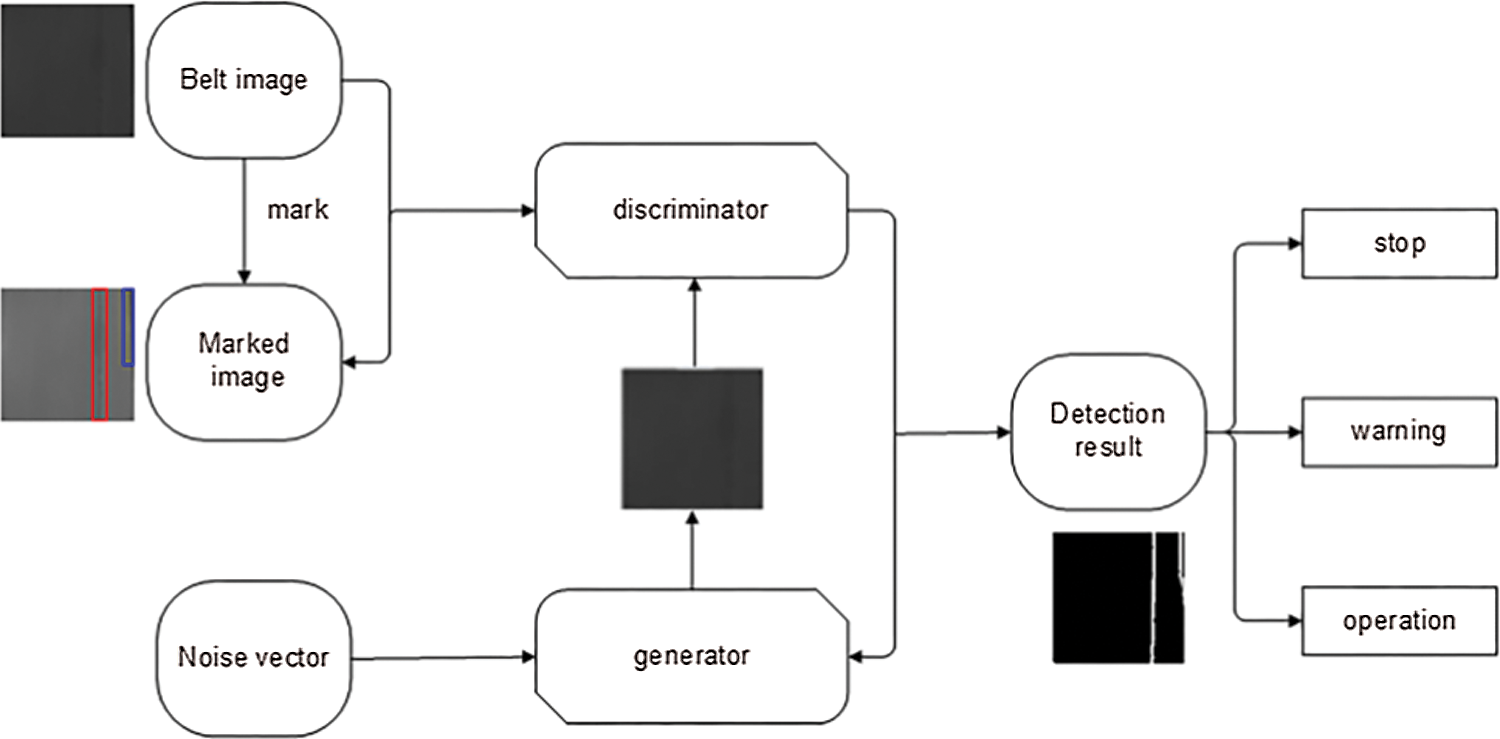
Figure 3: Detection process of the belt image by the improved DCGAN

5  Experiment and Analysis

5.1 Data Collection and Preprocessing

The conveyor belt was turned on and reached a constant rate, and a surface light source was added to make the collected data clearer. The CCD camera captured the image of the surface of the conveyor belt and transmitted it to the computer through the data transmission line. Accelerated by an Nvidia GPU, the processing module classified the damage, and the control module responded in real time according to the type of damage, either maintaining normal operation or stopping the conveyor belt immediately.

Image collection occurred under ideal conditions, i.e., without water, dust, or other environmental factors that could affect the test results. We acquired a total of 3200 images and divided them into four groups of 800 images. The experimental parameters are the height of the CCD camera and the speed of the conveyor belt. In the first group, the belt ran at a low speed (1 m/min). The height of the CCD camera was set to 0.4 m, and the resolution was 900*700. In the second group, the conveyor belt was still running at a low speed (1 m/min), the height of the CCD camera was set to 0.8 m, and the resolution was 1800*1400. In the third group, the conveyor belt ran at a high speed (2 m/min), while the CCD camera ran at a low setting (0.4 m) with a resolution of 900*700. In the fourth group, the belt ran at a high speed (2 m/min), and the CCD camera ran at a high setting (0.8 m) with a resolution of 1800*1400. We randomly selected 200 images from each group for labelling to obtain 800 labelled images and 2,400 unlabelled images.

5.2 Model Training and Results

The experiment ran on the PyCharm 2017 software platform. The Python library included TensorFlow, SciPy, and NumPy. A Windows 10 operating system ran on an Intel i5-9300HQ CPU at 2.40 GHz and an Nvidia GeForce GTX 1650 GPU. We used batch processing to load data. Each batch was loaded with seven images for training. We set the epoch size to 300, and uniformly adjusted the collected images to 64*64 pixels.

The update ratios of the generator and discriminator were set to 2:1 for 300 epochs, and the network was optimized by Adam with momentum of 0.5. Figs. 4 and 5 show the convergence of the generator and discriminator, respectively, during training.

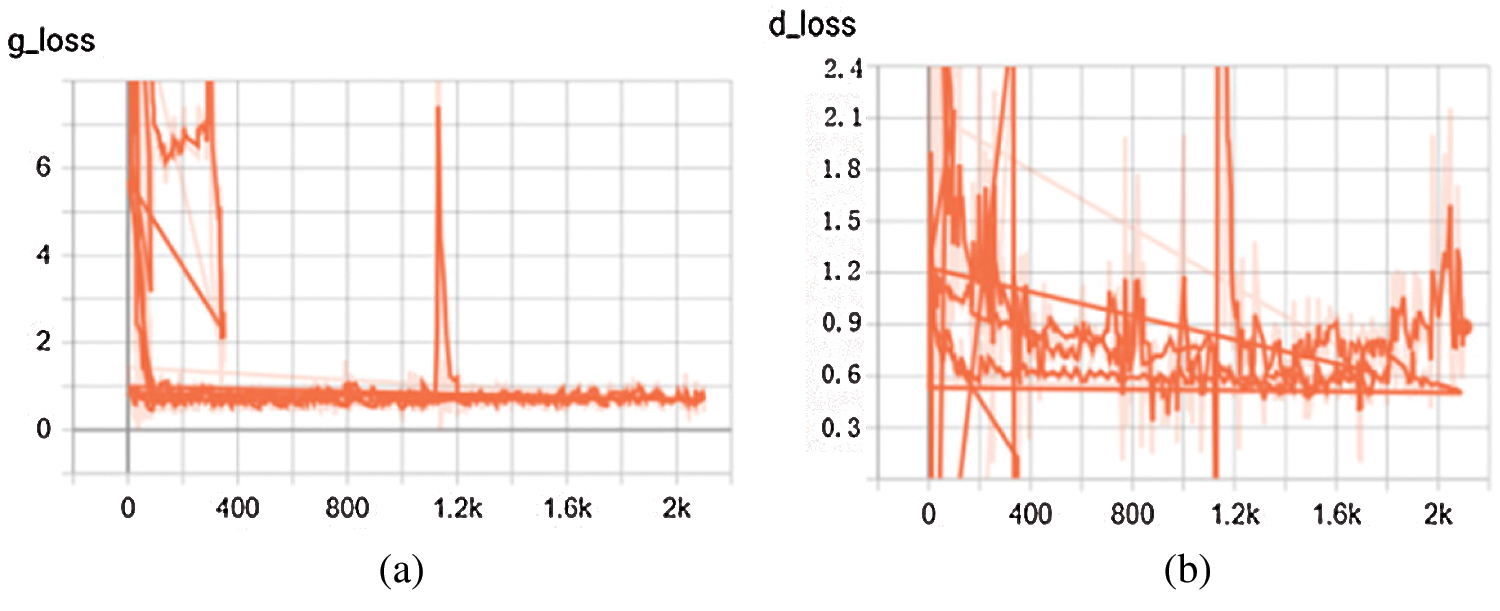
Figure 4: Generator and discriminator loss functions [48]. (a) Generator loss function, (b) Discriminator loss function

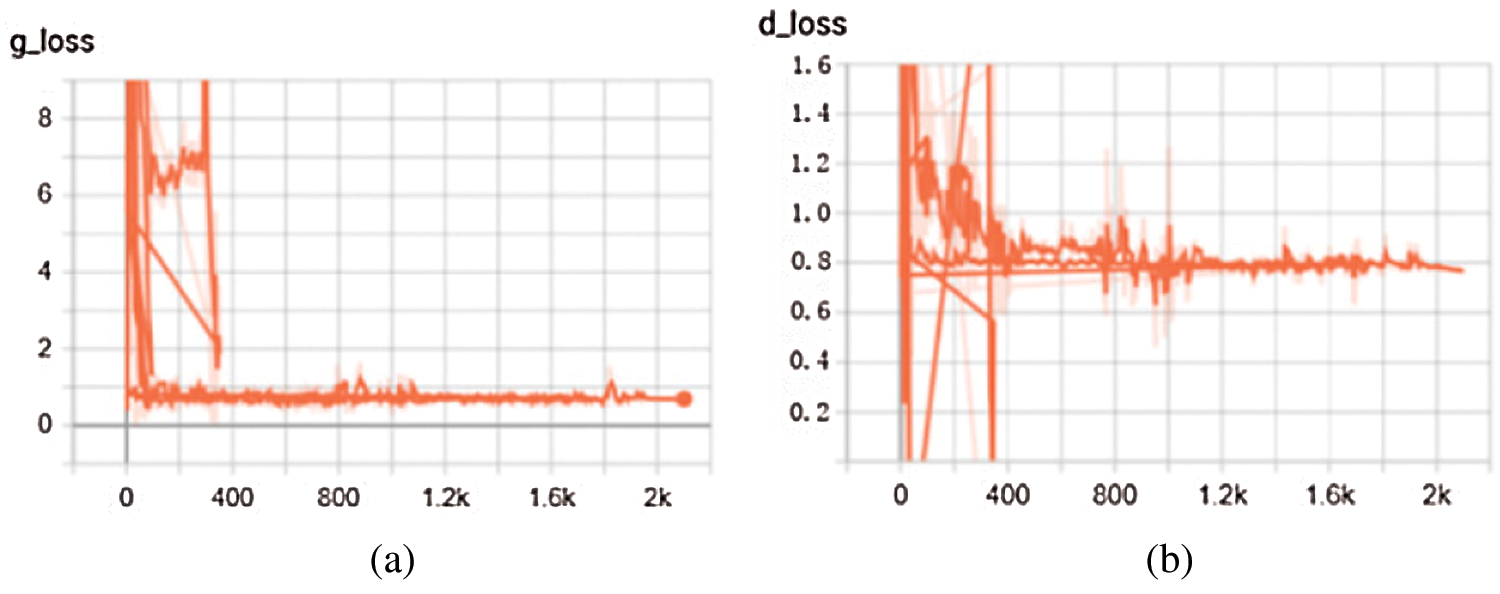
Figure 5: Generator and discriminator loss functions by proposed algorithm. (a) Generator loss function, (b) Discriminator loss function

In Figs. 4 and 5, the ordinate represents the loss function, and the abscissa represents the number of iterations, where g_loss and d_loss are the losses of the generator and discriminator, respectively. Fig. 4 is the change curve of the loss value by the method of Heusel et al. [48] proposed, where the generator learning rate is a=0.0002 , the discriminator learning rate is b=0.0004 , and the update ratio α:β=1:1 . In Fig. 4(a), the generator model fluctuates at 1200 iterations, and in Fig. 4(b), the larger fluctuations of the discriminator model at 1200 iterations become smaller at 2000 iterations. Hence it can be seen that the model in Heusel et al. [48] is unstable in the training process. In comparison, the change curve of the loss value by the method in this paper is shown in Fig. 5, where the learning rates of the generator and discriminator are a=0.0002 and b=0.0004 , respectively, and the update ratio. As shown in Fig. 5(a), the generator model tends to be stable, and the loss value drops to 0.8 after 380 iterations, and in Fig. 5(b), the discriminator model tends to be stable after 400 iterations, and the loss value drops to 0.8. In summary, we can conclude that the training stability of the method in this paper is superior to the training method in Heusel et al. [48].

Taking the 64*64 image and the fake image generated by the generator as the input of the discriminator, the downsampling features are extracted through convolutional layers 1–4 to output a 4*4*1024 feature map. The final detection result map is obtained via the fully connected layer. Fig. 6 is the collected belt damage image, unified it to 64*64 pixels. Fig. 7 shows the detection result corresponding to each image in Fig. 6. Panels (a) to (g) in both images represent scratches, cracks, tears, scratches + cracks, scratches + tears, tears + cracks, and scratches + cracks + tears, respectively.

Figure 6: 64*64 pixel belt image

Figure 7: Test result diagram

We evaluate this method by

Accuracy=TPTP+FP, (8)

where TP is the number of correctly judged pixels in the damaged region, and FP is the number of misjudged pixels. Thus the accuracy of the algorithm in this paper is obtained, as shown in Fig. 8.

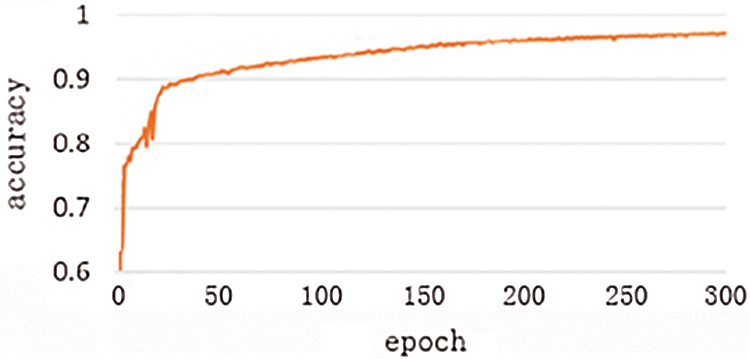
Figure 8: Average accuracy of the algorithm

It can be seen from Tab. 3 that the method in this paper has nearly the same accuracy as the method in Li et al. [29] at detecting scratches. However, only one type of damage can be detected by the latter, while our method can detect various types of damage, and the overall detection accuracy is improved. Our algorithm has better accuracy than [42] and [48]. The algorithm in Zhou et al. [42] requires a large number of manual annotations on acquired images, and it takes more time. Using Heusel et al. [48], as shown in Fig. 6, fluctuations may occur during iterative training of the generator and discriminator, thereby affecting the extraction of features and resulting in low detection accuracy.

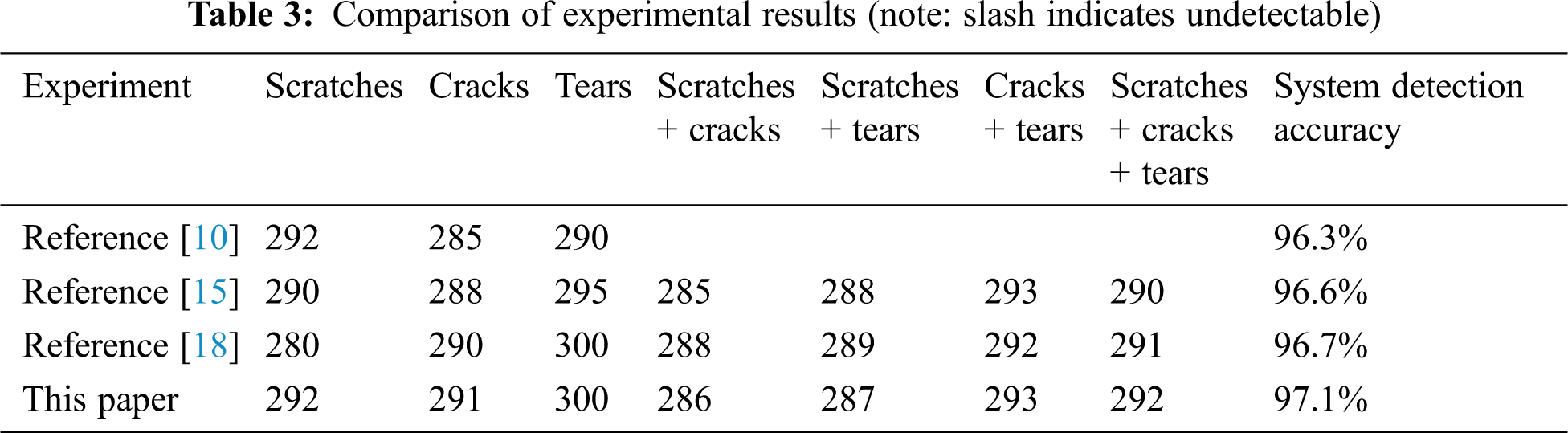
According to the response accuracy in Tab. 4, the detection accuracy of tears using our algorithm is as high as 100% and a stop can be made in time. From the perspective of reliability, we achieved accurate detection for the tears to ensure timely stopping of the conveyor belt, thereby effectively reducing the frequency of accidents. The average accuracy of this experiment is about 97.1%.

6  Conclusion

Based on multi-class DCGAN, we proposed a reliable and fast method to detect longitudinal tears in a conveyor belt, removing batch normalization of the generator and thus reducing artifacts in the generated images, so that features extracted from the generator model are more accurate. The two-scale update rule makes the model converge faster and prevents its collapse. The output of the discriminator is a multi-class softmax function, which can accurately detect and classify the types of damage. Experimental results showed that this method is suitable for detecting multiple types of damage in an image, with higher accuracy and reliability, in a shorter time than comparison algorithms.

Acknowledgement: The authors thank Shanxi Province of China for funding this research project.

Funding Statement: This work was supported by the Shanxi Province Applied Basic Research Project, China (Grant No. 201901D111100). Xiao-li Hao received the grant. The URL of the sponsor’s website is http://kjt.shanxi.gov.cn/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. J. He, Y. S. Pang and G. Lodewijks, “Green operations of belt conveyors by means of speed control,” Applied Energy, vol. 188, no. 12, pp. 330–341, 2017. [Google Scholar]

 2.  Y. Ren, J. Qi, Y. Cheng, J. Wang and O. Asama, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]

 3.  J. Wang, W. Chen, L. Wang, Y. Ren and R. S. Sherratt, “Blockchain-based data storage mechanism for industrial Internet of Things,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 1157–1172, 2020. [Google Scholar]

 4.  L. H. Zhao, “Typical failure analysis and processing of belt conveyor,” Procedia Engineering, vol. 26, no. 11, pp. 942–946, 2011. [Google Scholar]

 5.  C. Ge, Z. Liu, J. Xia and L. Fang, “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 8, pp. 1, 2019. [Google Scholar]

 6.  T. Li, Y. Ren and J. Xia, “Blockchain queuing model with non-preemptive limited-priority,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 1111–1122, 2020. [Google Scholar]

 7.  A. K. Błażej, L. Jurdziak, R. Burduk and R. Błażej, “Forecast of the remaining lifetime of steel cord conveyor belts based on regression methods in damage analysis identified by subsequent DiagBelt scans,” Engineering Failure Analysis, vol. 100, no. 2, pp. 119–126, 2019. [Google Scholar]

 8.  L. Xiang, W. Wu, X. Li and C. Yang, “A linguistic steganography based on word indexing compression and candidate selection,” Multimedia Tools and Applications, vol. 77, no. 5, pp. 28969–28989, 2018. [Google Scholar]

 9.  W. Zhao, J. Liu, H. Guo and T. Hara, “ETC-IoT: Edge-node-assisted transmitting for the cloud-centric internet of things,” IEEE Network, vol. 32, no. 3, pp. 101–107, 2018. [Google Scholar]

10. Q. Wang, “Adhesive tape tearing device based on infrared temperature sensor design,” Coal Mine Mach, vol. 36, no. 7, pp. 11–13, 2015. [Google Scholar]

11. L. Fang, C. Yin, L. Zhou, Y. Li, C. Su et al., “A physiological and behavioral feature authentication scheme for medical cloud based on fuzzy-rough core vector machine,” Information Sciences, vol. 507, pp. 143–160, 2020. [Google Scholar]

12. Y. Ren, Y. Leng, J. Qi, K. S. Pradip, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, pp. 304–313, 2021. [Google Scholar]

13. M. Andrejiova and A. Grincova, “Classification of impact damage on a rubber-textile conveyor belt using Naïve-Bayes methodology,” Wear, vol. 415, no. 8, pp. 59–67, 2018. [Google Scholar]

14. C. Ge, W. Susilo, Z. Liu, J. Xia, P. Szalachowski et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable and Secure Computing, vol. 20, no. 3, pp. 1, 2020. [Google Scholar]

15. Y. Mao, J. Zhang, H. Qi and L. Wang, “DNN-MVL: DNN-multi-view-learning-based recover block missing data in a dam safety monitoring system,” Sensors, vol. 19, no. 13, pp. 1–22, 2019. [Google Scholar]

16. R. Błażej, L. Jurdziak, T. Kozłowski and A. Kirjanów, “The use of magnetic sensors in monitoring the condition of the core in steel cord conveyor belts—Tests of the measuring probe and the design of the DiagBelt system,” Measurement, vol. 123, no. 3, pp. 48–53, 2018. [Google Scholar]

17. Y. Zhou, X. Zhao, S. Liu, X. Long and W. Luo, “A time-aware searchable encryption scheme for EHRs,” Digital Communications and Networks, vol. 5, no. 3, pp. 170–175, 2019. [Google Scholar]

18. X. Shao, C. Wang, C. Zhao and J. Gao, “Research on network coding aware energy efficient routing for wireless sensor networks,” EURASIP Journal on Wireless Communications and Networking, vol. 213, no. 5, pp. 1–31, 2018. [Google Scholar]

19. G. Fedorko, V. Molnar, P. Michalik, M. Dovica, T. Tóth et al., “Extension of inner structures of textile rubber conveyor belt—Failure analysis,” Engineering Failure Analysis, vol. 70, no. 7, pp. 22–30, 2016. [Google Scholar]

20. J. Xu, L. Wei, A. Wang, Y. Zhang, F. Zhou et al., “Dynamic fully homomorphic encryption-based Merkle tree for lightweight streaming authenticated data structures,” Journal of Network and Computer Applications, vol. 107, no. 8, pp. 113–124, 2018. [Google Scholar]

21. Y. Zhou, X. Long, L. Chen and Z. Yang, “Conditional privacy-preserving authentication and key agreement scheme for roaming services in VANETs,” Journal of Information Security and Applications, vol. 47, no. 8, pp. 295–301, 2019. [Google Scholar]

22. D. J. He, Y. S. Pang and G. Lodewijks, “Green operations of belt conveyors by means of speed control,” Applied Energy, vol. 188, no. 12, pp. 330–341, 2017. [Google Scholar]

23. J. Y. Ren, Y. Leng, Y. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]

24. S. Zeng, Y. Mu, M. He and Y. Chen, “New approach for privacy-aware location-based service communications,” Wireless Personal Communications, vol. 101, no. 2, pp. 1057–1073, 2018. [Google Scholar]

25. L. Fang, Y. Li, X. Yun, Z. Wen, S. Ji et al., “THP: A novel authentication scheme to prevent multiple attacks in SDN-based IoT network,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 5745–5759, 2020. [Google Scholar]

26. Y. Yang, C. C. Hou, T. Z. Qiao, H. T. Zhang and L. Ma, “Longitudinal tear early-warning method for conveyor belt based on infrared vision,” Measurement, vol. 147, no. 7, pp. 106817, 2019. [Google Scholar]

27. Y. Chang, S. Zhang, G. Wan, L. Yan, Y. Zhang et al., “Practical two-way QKD-based quantum private query with better performance in user privacy,” International Journal of Theoretical Physics, vol. 58, no. 7, pp. 2069–2080, 2019. [Google Scholar]

28. Y. Ren, F. Zhu, K. S. Pradip, J. Wang, T. Wang et al., “Data query mechanism based on hash computing power of blockchain in Internet of Things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]

29. J. Li and C. Y. Miao, “The conveyor belt longitudinal tear on-line detection based on improved SSR algorithm,” Optik, vol. 127, no. 5, pp. 8002–8010, 2016. [Google Scholar]

30. C. P. Ge, W. Susilo, J. Baek, Z. Liu, Xia J. et al., “Revocable attribute-based encryption with data integrity in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 2, pp. 1–12, 2021. [Google Scholar]

31. T. Z. Qiao, L. L. Chen, Y. S. Pang, G. W. Yan and C. Y. Miao, “Integrative binocular vision detection method based on infrared and visible light fusion for conveyor belts longitudinal tear,” Measurement, vol. 110, no. 6, pp. 192–201, 2017. [Google Scholar]

32. G. Xu, X. Li, L. Jiao, W. Wang, A. Liu et al., “BAGKD: A batch authentication and group key distribution protocol for VANETs,” IEEE Communications Magazine, vol. 58, no. 7, pp. 35–41, 2020. [Google Scholar]

33. G. Q. Xu, X. Xie, S. Huang, J. Zhang, L. Pan et al., “JSCSP: A novel policy-based XSS defense mechanism for browsers,” IEEE Transactions on Dependable and Secure Computing, vol. 20, no. 7, pp. 1–12, 2020. [Google Scholar]

34. X. L. Hao and H. Liang, “A multi-class support vector machine real-time detection system for surface damage of conveyor belts based on visual saliency,” Measurement, vol. 146, no. 6, pp. 125–132, 2019. [Google Scholar]

35. J. Y. Ren, Y. Liu, S. Ji, A. K. Sangaiah and J. Wang, “Incentive mechanism of data storage based on blockchain for wireless sensor networks,” Mobile Information Systems, vol. 2018, no. 8, pp. 1–10, 2018, 2018. [Google Scholar]

36. L. Gong, B. Yang, T. Xue, J. Chen and W. Wang, “Secure rational numbers equivalence test based on threshold cryptosystem with rational numbers,” Information Sciences, vol. 466, no. 10, pp. 44–54, 2018. [Google Scholar]

37. H. Li, C. W. Pan, Z. Chen, A. Wulamu and A. Yang, “Ore image segmentation method based on u-net and watershed,” Computers Materials & Continua, vol. 65, no. 1, pp. 563–578, 2020. [Google Scholar]

38. Y. Ren, J. Qi, Y. Cheng, J. Wang and O. Alfarraj, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]

39. B. Hu, F. Xiang, F. Wu, J. Liu, Z. Sun et al., “Research on time synchronization method under arbitrary network delay in wireless sensor networks,” Computers Materials & Continua, vol. 61, no. 3, pp. 1323–1344, 2019. [Google Scholar]

40. F. Bi, X. Ma, W. Chen and W. D. Fang, “Review on video object tracking based on deep learning,” Journal of New Media, vol. 1, no. 2, pp. 63–74, 2019. [Google Scholar]

41. J. Wang, Y. Gao, W. Liu, A. K. Sangaiah and H. Kim, “An intelligent data gathering schema with data fusion supported for mobile sink in wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 15, no. 3, pp. 1–9, 2019. [Google Scholar]

42. H. Zhou, Y. J. Chen and S. M. Zhang, “Ship trajectory prediction based on BP neural network,” Journal on Artificial Intelligence, vol. 1, no. 1, pp. 29–36, 2019. [Google Scholar]

43. J. Wang, Y. Q. Yang, T. Wang, R. S. Sherratt and J. Y. Zhang, “Big data service architecture: A survey,” Journal of Internet Technology, vol. 21, no. 2, pp. 393–405, 2020. [Google Scholar]

44. I. Goodfellow, J. Pougetabadie, M. Mirza, B. Xu, D. Wardefarley et al., “Generative adversarial nets,” in Proc. Neural Information Processing Systems, Montreal, QC, Canada, pp. 2672–2680, 2014. [Google Scholar]

45. K. Gu, X. Dong and W. Jia, “Malicious node detection scheme based on correlation of data and network topology in fog computing-based VANETs,” IEEE Transactions on Cloud Computing, vol. 16, pp. 1, 2020. [Google Scholar]

46. A. Radford, L. Metz and S. Chintala, “Unsupervised representation learning with deep convolutional generative adversarial networks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPRBoston, BST: America, 2015. [Google Scholar]

47. Y. Ren, J. Qi, Y. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM transactions on Internet Technology, vol. 21, no. 1, pp. 1–19, 2021. [Google Scholar]

48. M. Heusel, H. Ramsauer, T. Unterthiner, B. Nessler and S. Hochreiter, “GANs trained by a two time-scale update rule converge to a local nash equilibrium,” in Proc. Neural Information Processing Systems, California, CA, USA, pp. 6629–6640, 2017. [Google Scholar]

49. T. Salimans, I. Goodfellow, W. Zaremba and V. Cheung, “Improved techniques for training GANs,” in Proc. Neural Information Processing Systems, Barcelona, BCN, Spain, pp. 2234–2242, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.