Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.016761
Article

Image Denoising Using a Nonlinear Pixel-Likeness Weighted-Frame Technique

P. Vinayagam1,*, P. Anandan2 and N. Kumaratharan3

1Department of ECE, Velammal Engineering College, Chennai, Tamilnadu, India
2Department of ECE, C. Abdul Hakeem College of Engineering & Technology, Melvisharam, India
3Department of ECE, Sri Venkateswara College of Engineering, Sriperumbudur, India
*Corresponding Author: P. Vinayagam. Email: vinayagampece@gmail.com
Received: 11 January 2021; Accepted: 09 May 2021

Abstract: Recent advances in the development of image denoising applications for eliminating the various sources of noise in digital images have employed hardware platforms based on field programmable gate arrays for attaining speed and efficiency, which are essential factors in real-time applications. However, image denoising providing for maximum denoising performance, speed, and efficiency on these platforms is subject to constant innovation. To this end, the present work proposes a high-throughput fixed-point adaptive edge noise filter architecture to denoise digital images with additive white Gaussian noise in realtime using a nonlinear modified pixel-likeness weighted-frame technique. The proposed architecture works in two stages. The first stage involves normal and conditional sorting. The second stage is a decision-oriented output selection unit. Decision-oriented adaptive windowing is included for better impulse noise suppression and edge preservation. The denoising performance of the proposed denoising scheme is demonstrated to be superior to those currently available state-of-the-art approaches. Moreover, the power consumption is reduced by 25.01% compared to conventional algorithms.

Keywords: Adaptive edge noise; additive white Gaussian noise; image denoising; PLWF; peak signal-to-noise ratio

1  Introduction

The Discrete Wavelet Transform (DWT) of a noisy image includes a substantial number of factors with low SNRs, and shrinking the wavelet coefficients associated with these DWT factors with low Signal to Noise Ratio (SNRs) was demonstrated to be a useful procedure for denoising images, particularly those with additive white noise. In addition to digital images, the good performance of DWT-based denoising strategies has made these strategies useful for speech signals, electrocardiograms (ECGs), and encephalograms [1–4]. Like many recent implementations of image processing, DWT-based image denoising is executed on Field Programmable Gate Array (FPGA) platforms owing to their good computational performance and low resource consumption. In addition, these developments have focused mainly on the convolution method. The denoising method utilizing DWT consists of three stages: forward DWT (FDWT), adaptive thresholding, and inverse DWT (IDWT). While recent advances in the development of DWT-based image denoising employing hardware platforms based on FPGAs have attained high computational speed and efficiency [5–7].

To this end, the present work proposes continuous use of the forward/backward pixel likeness weighted frame (PLWF) technique for image denoising. The proposed method is planned and executed on an FPGA platform utilizing the Xilinx System Generator (XSG), MATLAB 2017a, and the XUP Vertex-II Pro improvement board. The Pixel Likeness Weighted Frame (PLWF) is employed in conjunction with a modified Adaptive Edge Noise (AEN) filter to minimize noise such as salt-and-pepper and Gaussian noise [8]. The algorithm employs two stages: separating the filtering windows into four orthogonal edge direction patterns and the identification of the ideal directions of the edges, which are those with highly indistinguishable pixels. Knowledge regarding the ideal directions of the edges enables the identification of more edge pixels, which helps to reduce edge degradation during the denoising process. To this end, the present work adopts the average deviation from the mean (i.e., the standard deviation) because it yields better outcomes than the difference or change in other methods for estimating the noise levels of pixels [9–13].

2  Materials and Methods

A block diagram of the proposed PLWF image denoising algorithm is presented in Fig. 1. Its architecture consists of five principal blocks, which include odd and even line buffers, register bank, threshold determination, and an AEN filter. These are presented in detail as follows.

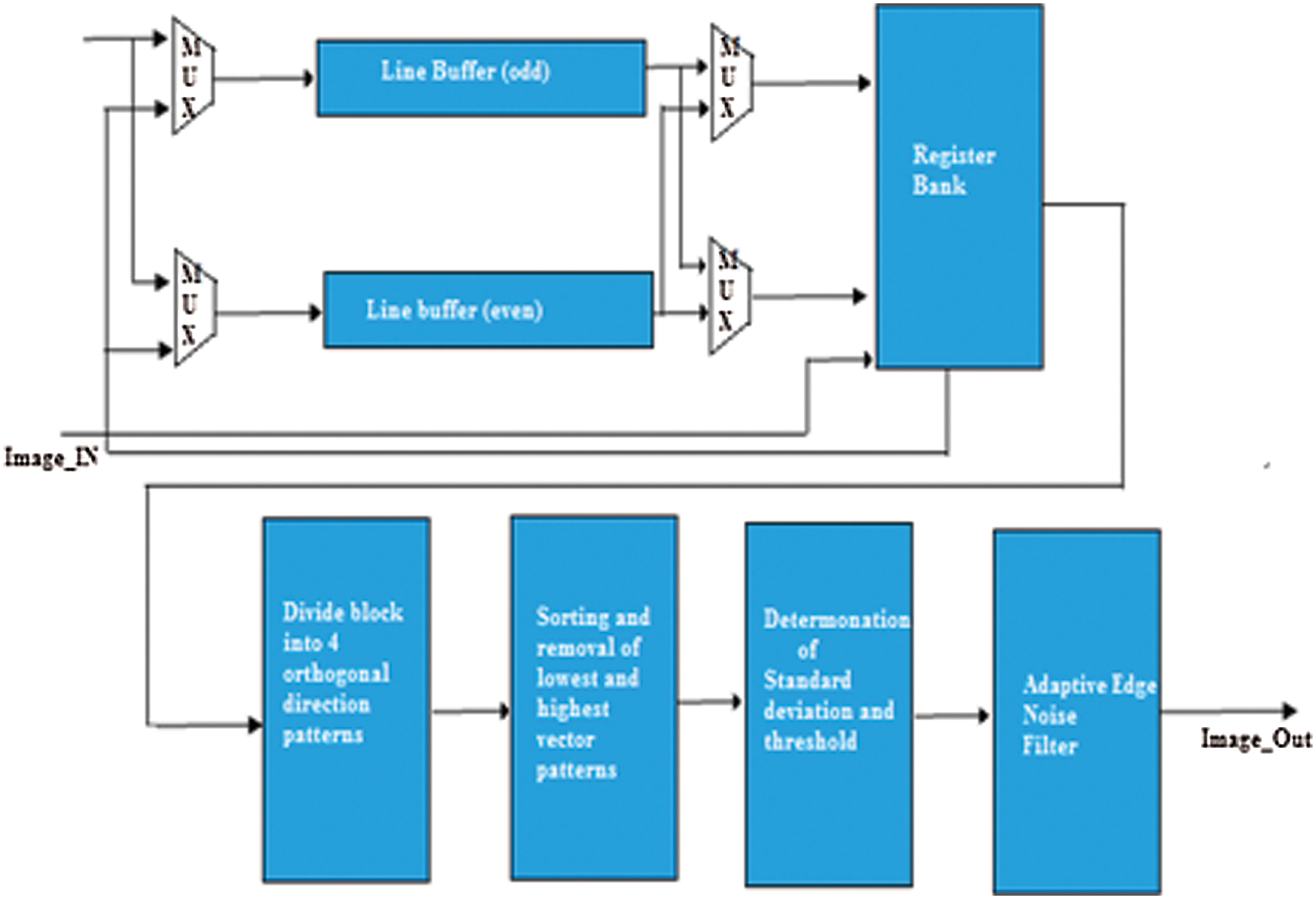
Figure 1: Block diagram of the PLWF image denoising scheme

A. Line buffers

The proposed algorithm employs a 3 × 3 convolution mask. Therefore, the computation is facilitated by four hybrid multiplexers and two line buffers, where the odd and even line buffers store pixels at odd and even column positions, respectively. The cost and power consumption of the implementation are reduced by adopting a double-port SRAM in the line buffers to conduct the computational activity [14–16].

B. Register bank

The register bank consists of 12 registers, Reg0 to Reg11, that accumulate the 3 × 3 pixel estimates of the present convolution masks. The architecture of the line buffers and register bank are illustrated in Fig. 2, where every three registers are associated sequentially to obtain evaluations of the three-pixel rows a mask [17–21].

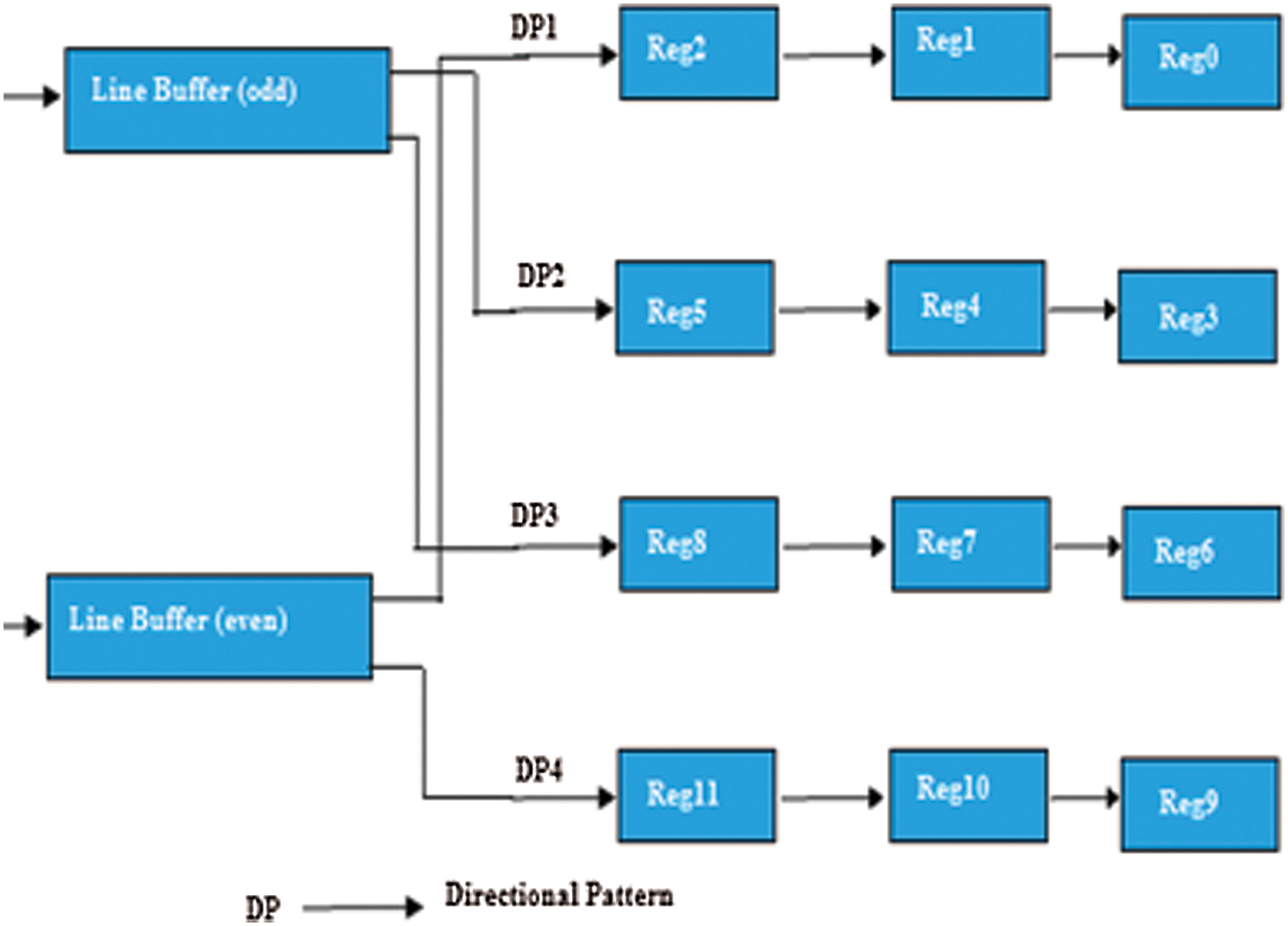
Figure 2: Architecture of the line buffers and register bank

C. Threshold block

The threshold block design is illustrated in Fig. 3. The evaluation of whether the input value is greater or lower than the threshold limit (Ts) is more important than the Ts itself. Accordingly, one clock cycle is enough for the line buffer, but two clock cycles are needed for the AEN filter during the noise removal process [22–24].

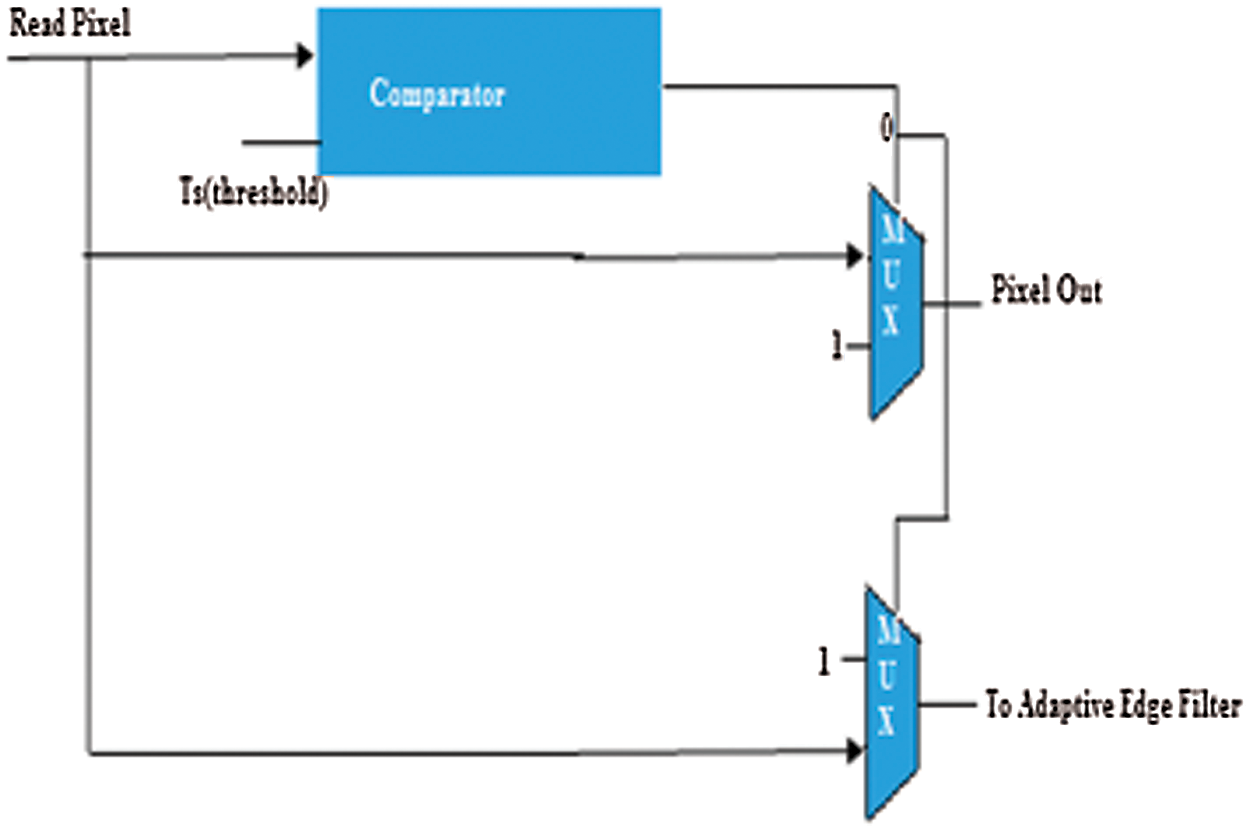
Figure 3: Architecture of the threshold block

D. Adaptive edge noise filter

The two-stage pipeline design of the AEN filter is illustrated in Fig. 4. Here, the adder (ADD) unit locates the two input sources and transfers the added value to the multiplexer. The ADD modules help in locating the four orthogonal edge direction patterns composed of highly indistinguishable pixels [25–28]. The directional contrasts for the four edge directions are determined by the ADD units. At this point, the smallest distinction is chosen by the DIV/9 unit. The final block provides the mean of the two-pixel values, i.e., the output after filtering [19–31].

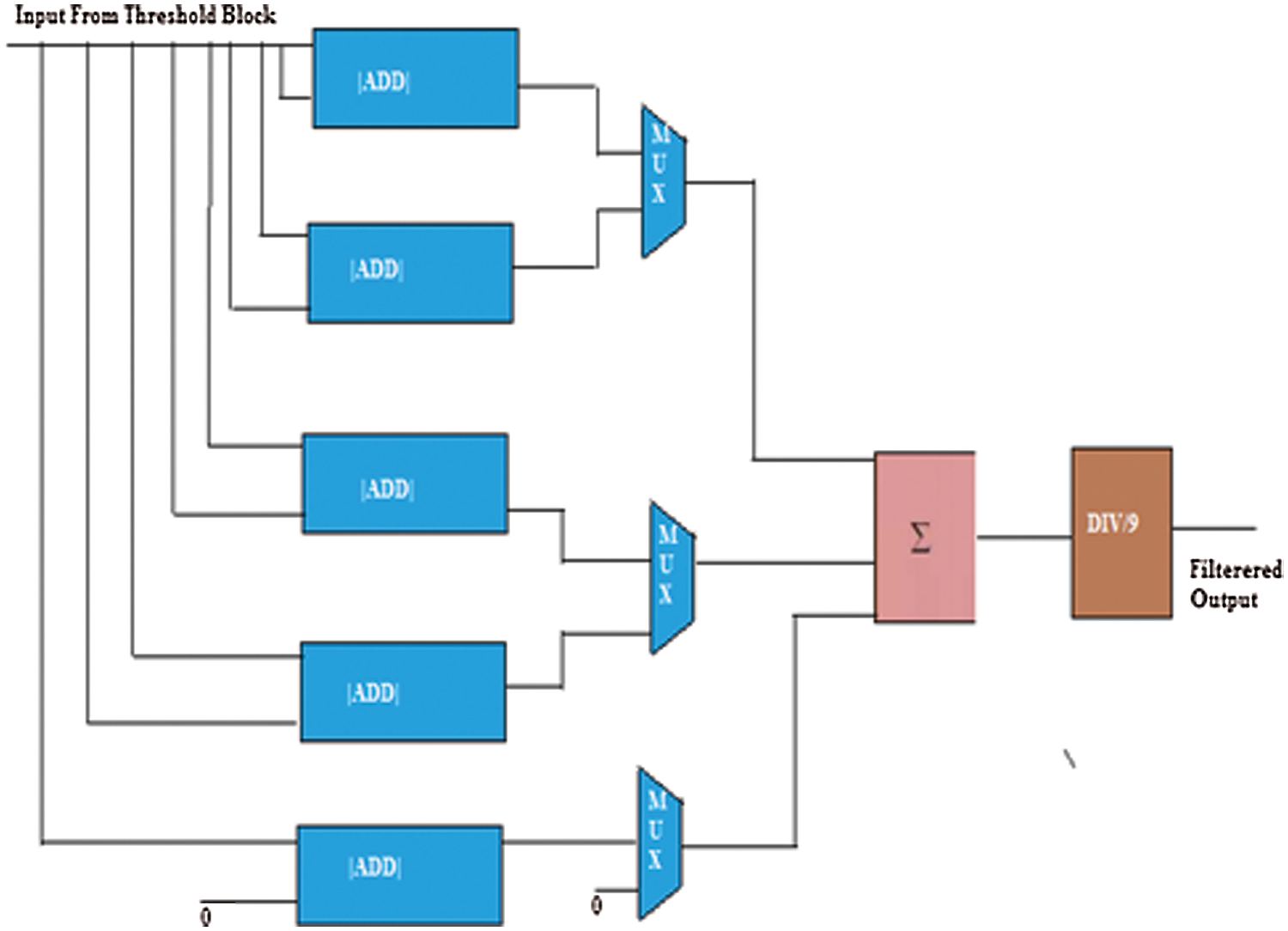
Figure 4: Architecture of the adaptive noise filter

3  Pixel Likeness Weighted Frame Algorithm

A flowchart of the proposed PLWF algorithm is presented in Fig. 5. These stages are presented in detail as follows.

Stage 1: Applya two-dimensional (2D) window of size 3 × 3 to a center pixel with an 8-bit grayscale value denoted as Pij .

Stage 2: If 0 < Pij < 255, the center pixel is considered to be uncorrupted; thus, no procedure is required and its value is left unaltered.

Stage 3: If Pij = zero or 255, then the center pixel is corrupted by salt-and-pepper noise. This yields two possible cases.

Case I: The window includes pixels with values that are not exclusively 0 or 255. Then, find the adaptive edge of the remaining pixels and replace Pij with its adaptive value.

Case II: The window includes pixels with values that are only 0, 255, or both. Then, the center pixel may be either zero or 255; again this is a small issue. Then, replace Pij with the mean deviation (Fig. 5).

Stage 4: Apply stages 1–3 to every pixel in the image.

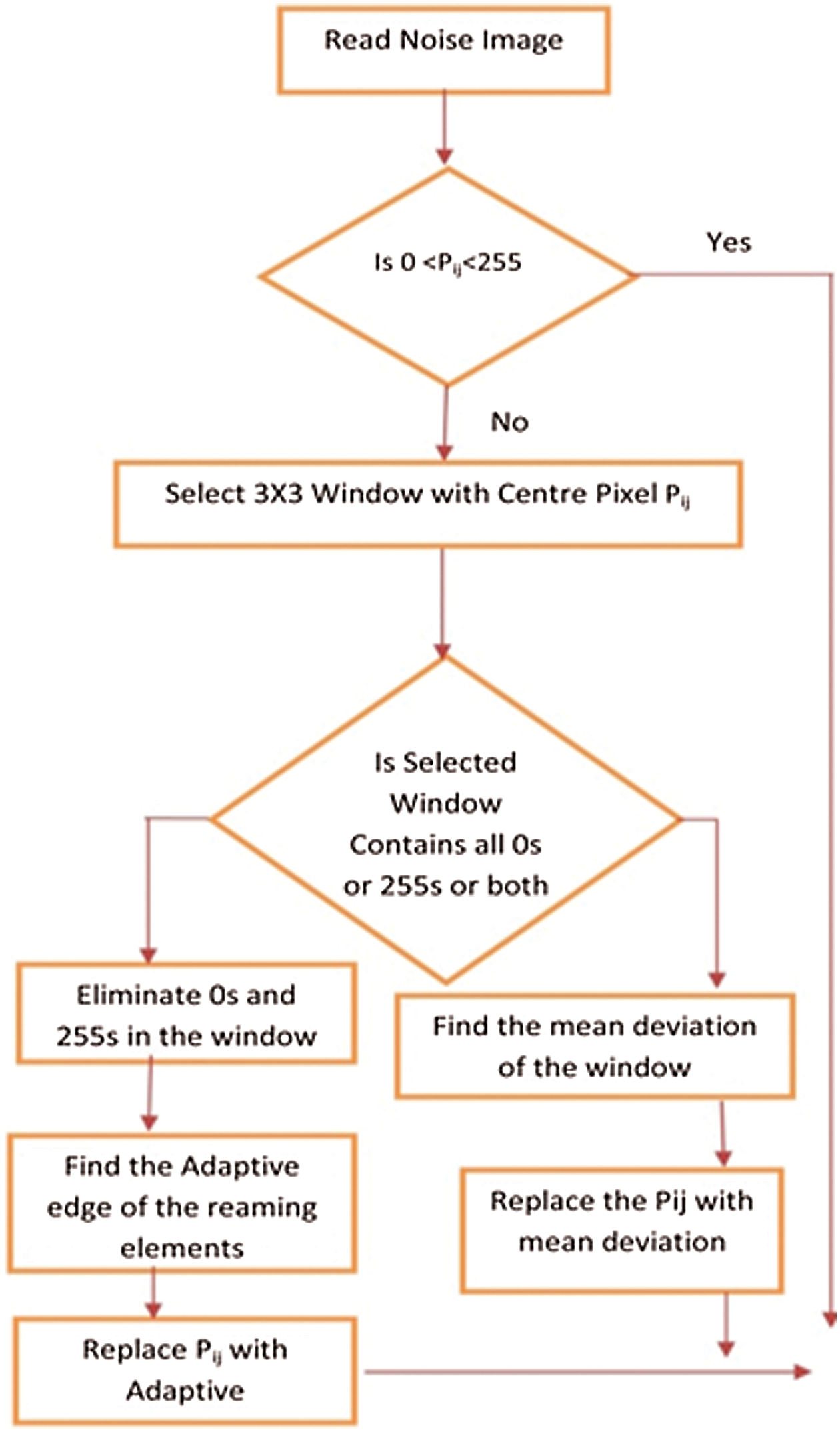
Figure 5: Flow chart of the proposed PLWF algorithm

4  Results and Discussion

The performance and operational characteristics of the proposed PLWF algorithm were compared to those of various other state-of-the-art noise-removal algorithms, including iterative pixel compression (IPC), and those based on the discrete cosine transform (DCT) and the DWT. To this end, the algorithms were applied to standard Lena and Cameraman8-bit grayscale images composed of 512 × 512 pixels. Salt and pepper noise having pixel values of 0 and 255 with equal probability was deliberately added to all images in proportions of 10% to 90% using MATLAB. For this, a window size of 9 × 9 was uniformly applied.

Tab. 1 shows the evaluation parameters used in the proposed system.

The results of applying the proposed PLWF algorithm to the Lena and cameraman images in MATLAB are presented in Figs. 6 and 7, respectively.

Figure 6: Results of applying the proposed PLWF algorithm to the Lena image. (a) Input image (b) Noisy image (c) Noise pixels detected (d) Denoised image (first level) (d) Denoised image (second level)

Figure 7: Results of applying the proposed PLWF algorithm to the cameraman image. (a) Input image (b) Noisy image (c) Noise pixels detected (d) Denoised image first level (d) Denoised image second level

The noise-reduction performances of the algorithms compared were evaluated according tothe peak signal-to-noise ratio (PSNR) and mean square error (MSE), which are defined as follows [5,19]:

MSE=∑M,N⁡[I1(m,n)−I2(m,n)]2M∗N, (1)

PSNR=10log10(R2MSE), (2)

where M and N are the respective numbers of rows and columns in the image, m and n are the indices of the rows and columns, respectively, I1and I2 represent the ground truth noise-free image and the denoised image, respectively, and R is the maximum possible pixel value in the input image (i.e., 255). Here, the noise reduction performance of an algorithm increases with decreasing MSE and with increasing Peak Signal to Noise Ration (PSNR).

The PSNR and MSE values obtained by the various noise reduction algorithms for the Lena and cameraman images under different salt and pepper noise levels are listed in Tab. 2. In addition, we plot the PSNR values listed here in Fig. 8 for a more intuitive comparison. These results indicate that the proposed PLWF algorithm provides better visual quality than the other methods considered.

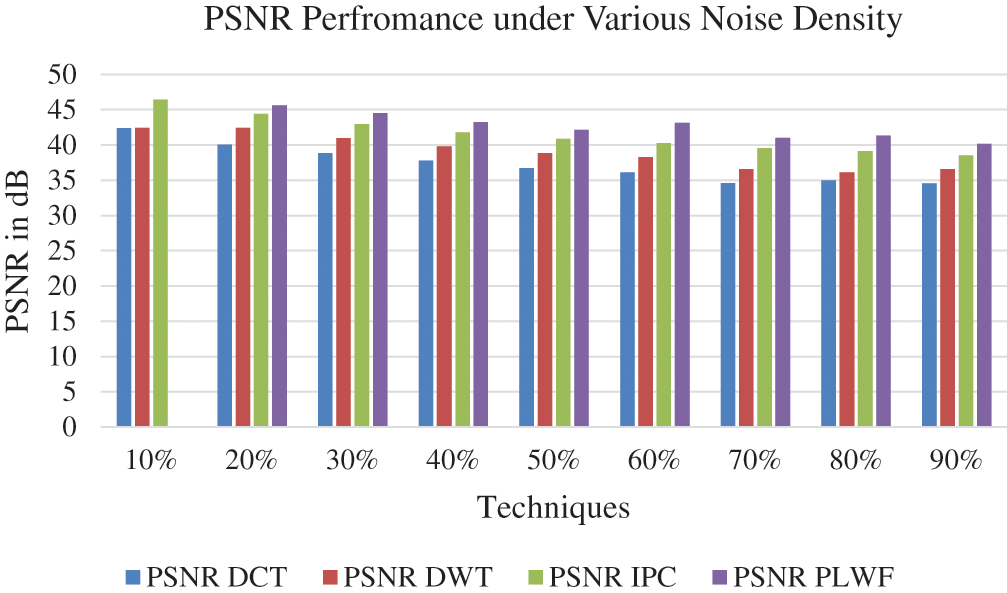
Figure 8: Comparison of PSNR performances obtained under different salt and pepper noise levels

Other factors, such as the complexity of the hardware implementation and the power consumption of denoising algorithms, are equally important as the denoising performance. Therefore, we compare the percentages of the total area employed to implement the denoising algorithm and the percentage of total power consumed by that implementation in Fig. 9. These results demonstrate that the proposed PLWF algorithm provides minimum area complexity and power consumption compared to the other methods considered. In addition, the complexity of logic utilization and the computational times required by the different algorithms are listed in Tab. 3. These results further demonstrate the superiority of the hardware implementation of the proposed PLWF algorithm.

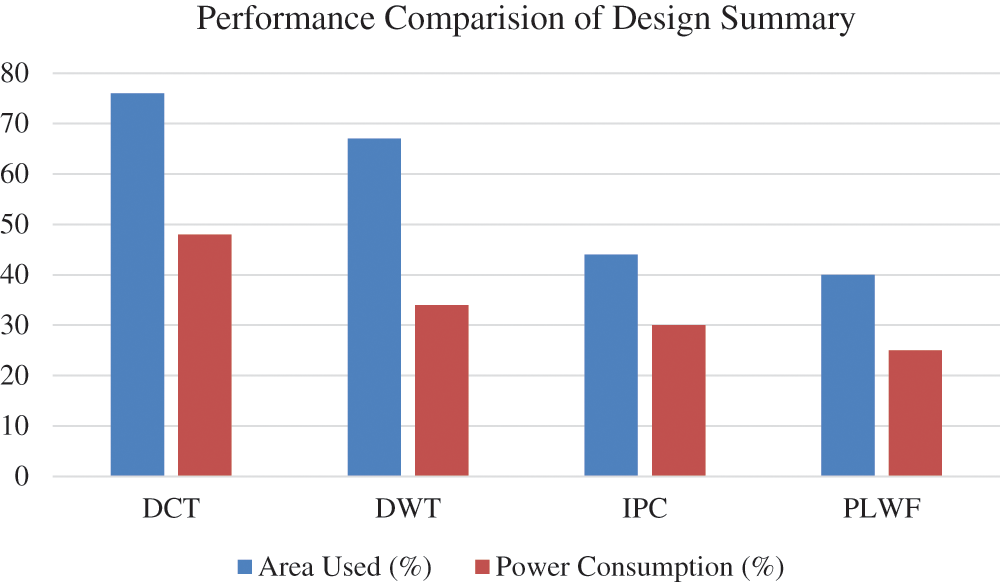
Figure 9: Comparison of area and power consumption

5  Conclusion

The present work addressed the need for developing image denoising algorithms with maximum denoising performance, speed, and efficiency on FPGA platforms by proposing a high-throughput fixed-point AEN filter architecture to denoise digital images in real time using a nonlinear modified PLWF technique. The denoising performance of the proposed denoising scheme was demonstrated to be superior to the denoising performances of IPC and those algorithms based on the DCT and DWT. Moreover, the hardware implementation of the proposed PLWF algorithm required less area and less power consumption than the other implementations considered, and the logic utilization and computational speed were both improved.

Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.

Funding Statement: The authors have received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Zhang, J. Zhang, C. Yang and X. Zhang, “Performance simulation and architecture optimization for CMOS image sensor pixels scaling down to 1.0 μm,” IEEE Transactions on Electron Devices, vol. 57, no. 4, pp. 788–794, 2010. [Google Scholar]

 2.  D. L. Marks, J. Hahn, R. Horisaki and D. J. Brady, “Computational photography and compressive holography,” in proc. IEEE Int. Conf. on Computational Photography (ICCPCambridge, MA, pp. 1–8, 2010. [Google Scholar]

 3.  H. C. Burger, B. Scholkopf and S. Harmeling, “Removing noise from astronomical images using a pixel-specific noise model,” in proc. IEEE Int. Conf. on Computational Photography (ICCPPittsburgh, PA, pp. 1–8, 2011. [Google Scholar]

 4.  H. E. Fortunato and M. M. Oliveira, “A gentle introduction to coded computational photography,” in proc. 24th SIBGRAPI Conf. on Graphics, Patterns, and Images Tutorials, Alagoas, pp. 39–55, 2011. [Google Scholar]

 5.  S. Deb, S. Chakraborty and T. Bhattacharjee, “A study on eigen faces for removing image blurredness through image fusion,” The International Journal of Multimedia & Its Applications (IJMA), vol. 4, no. 3, pp. 67–80, 2012. [Google Scholar]

 6.  R. Rithe, P. Raina, N. Ickes, S. V. Tenneti and A. P. Chandrakasan, “Reconfigurable processor for energy-efficient computational photography,” IEEE Journal of Solid-State Circuits, vol. 48, no. 11, pp. 2908–2919, 2013. [Google Scholar]

 7.  D. Stoker, J. V. D. Laan, E. Lavelle, C. Sakai and J. Wedd, “A computational photography shootout: Wavefront coding vs. lattice focal imaging,” in in proc. IEEE Int. Conf. on Image Processing (ICIPParis, pp. 31–35, 2014. [Google Scholar]

 8.  F. Larbi, S. Oussalah, N. Belkhelfa and A. Lounis, “Pixel sensor guard-ring geometry optimization by TCAD simulation,” in proc. 26th Int. Conf. on Microelectronics (ICMDoha, pp. 29–31, 2014. [Google Scholar]

 9.  S. Mann, R. Janzen, Tao Ai, S. N. Yasrebi, J. Kawwa et al. “Toposculpting: computational lightpainting and wearable computational photography for abakographic user interfaces,” in proc. IEEE 27th Canadian Conf. on Electrical and Computer Engineering (CCECEToronto, ON, pp. 1–10, 2014. [Google Scholar]

10. T. Y. Jung, D. L. Park, J. S. Park, J. H. Lee and S. Kim, “Pixel design optimization of fringe-field switching mode for applying negative liquid crystals in high-resolution mobile displays,” Journal of Display Technology, vol. 11, no. 3, pp. 229–235, 2015. [Google Scholar]

11. J. Gu, Z. Wu, Y. Li, Y. Chen, Z. Wei et al., “Parallel optimization of pixel purity index algorithm for hyperspectral unmixing based on spark,” in proc. Third Int. Conf. on Advanced Cloud and Big Data, Yangzhou, pp. 159–166, 2015. [Google Scholar]

12. J. Venter and S. Sinha, “Noise reduction by pixel circuit optimization in 4-T pixel structure detectors using integrated circuit technologies,” in in proc. IEEE Int. Conf. on Microwaves, Communications, Antennas and Electronic Systems (COMCASTel Aviv, pp. 1–6, 2015. [Google Scholar]

13. T. Sonoda, H. Nagahara, K. Endo, Y. Sugiyama and R. Taniguchi, “High-speed imaging using CMOS image sensor with quasi pixel-wise exposure,” in in proc. IEEE Int. Conf. on Computational Photography (ICCPEvanston, IL, pp. 1–11, 2016. [Google Scholar]

14. Y. Luo, N. Guo, S. Mirabbasi and D. Ho, “CMOS computational pixel for binary temporal optically encoded high-speed imaging,” in proc. IEEE Int. Conf. on Electron Devices and Solid-State Circuits (EDSSCHong Kong, pp. 44–47, 2016. [Google Scholar]

15. F. Calderon, C. Parra and C. Nino, “A modular robotic platform for visual perception and computational photography,” in in proc. IEEE Colombian Conf. on Robotics and Automation (CCRABogota, pp. 1–6, 2016. [Google Scholar]

16. A. Kumar, M. Sarkar and M. Suri, “Hybrid CMOS-OxRAMimage sensor for overexposure control,” in proc. IEEE 8th Int. Memory Workshop (IMWParis, pp. 1–4, 2016. [Google Scholar]

17. A. Boukhayma, A. Peizerat and C. Enz, “A sub-0.5 electron read noise VGA image sensor in a standard CMOS process,” IEEE Journal of Solid-State Circuits, vol. 51, no. 9, pp. 2180–2191, 2016. [Google Scholar]

18. M. Radpour and S. M. Sayedi, “A systemc model of energy harvesting CMOS digital pixel sensor,” in proc. 4th Int. Conf. on Robotics and Mechatronics (ICROMTehran, pp. 192–195, 2016. [Google Scholar]

19. Z. Xu, Q. Zhang, Z. Cao and C. Xiao, “Video background completion using motion-guided pixel assignment optimization,” in proc. IEEE Transactions on Circuits and Systems for Video Technology, vol. 26, no. 8, pp. 1393–1406, 2016. [Google Scholar]

20. S. Shen, Y. Sun, S. Song, D. P. Palomar and R. D. Murch, “Successive boolean optimization of planar pixel antennas,” in proc. IEEE Transactions on Antennas and Propagation, vol. 65, no. 2, pp. 920–925, 2017. [Google Scholar]

21. C. Aguerrebere, A. Almansa, J. Delon, Y. Gousseau and P. Muse, “A bayesian hyperprior approach for joint image denoising and interpolation, with an application to hdr imaging,” IEEE Transactions on Computational Imaging, vol. 99, pp. 1–20, 2017. [Google Scholar]

22. M. S. Asif, A. Ayremlou, A. Sankaranarayanan, A. Veeraraghavan and R. G. Baraniuk, “FlatCam: Thin, lensless cameras using coded aperture and computation,” in proc. IEEE Transactions on Computational Imaging, vol. 3, no. 3, pp. 384–397, 2017. [Google Scholar]

23. S. Marconi, T. Hemperek, P. Placidi, A. Scorzoni, E. Conti et al., “Low-power optimisation of a pixel array architecture for next generation High Energy Physics detectors,” in proc. 13th Conf. on Ph.D. Research in Microelectronics and Electronics (PRIMEGiardini Naxos, pp. 201–204, 2017. [Google Scholar]

24. M. R. Hamzescu, C. Polonschii, S. Oprea, D. Popescu, S. David et al., “High speed CMOS acquisition system based on FPGA embedded image processing for electro-optical measurements,” Review of Scientific Instruments, vol. 89, no. 065103, pp. 1–12,2018. [Google Scholar]

25. B. Ham, M. Cho and J. Ponce, “Robust guided image filtering using nonconvex potentials,” in proc. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 40, no. 1, pp. 192–207, 2018. [Google Scholar]

26. P. Keunyeol, M. Song and S. Y. Kim, “The design of a single-bit CMOS image sensor for iris recognition applications,” Sensors, vol. 18, no. 2, pp. 1–10, 2018. [Google Scholar]

27. F. Siddiqui, S. Amiri, U. I. Minhas, T. Deng, R. Woods et al., “FPGA-based processor acceleration for image processing applications,” Journal of Imaging, vol. 5, no. 16, pp. 1–22, 2019. [Google Scholar]

28. Y. Luo, J. Jiang, M. Cai and S. Mirabbasi, “CMOS computational camera with a two-tap coded exposure image sensor for single-shot spatial-temporal compressive sensing,” Optics Express, vol. 27, no. 22, pp. 31475–31489, 2019. [Google Scholar]

29. E. R. Fossum, “The invention of CMOS image sensors: A camera in every pocket,” in proc. Pan Pacific Microelectronics Sym. (Pan PacificHI, USA, pp. 1–6, 2020. [Google Scholar]

30. A. Suneetha and E. S. Reddy, “Robust gaussian noise detection and removal in color images using modified fuzzy set filter,” Journal of Intelligent Systems, vol. 30, no. 1, pp. 240–257, 2020. [Google Scholar]

31. K. Mahalakshmi and S. Jaya Prakash, “Implementation of pixel likeness weighted frame (PLWF) filter technique based digital image denoising for dsp applications,” International Journal of Recent Technology and Engineering (IJRTE), vol. 8, no. 3, pp. 6887– 6894, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.