Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.018242
Article

Decision Making Based on Fuzzy Soft Sets and Its Application in COVID-19

S. A. Alblowi1, M. El Sayed2 and M. A. El Safty3,*

1Department of Mathematics, College of Science, University of Jeddah, Jeddah, Saudi Arabia
2Department of Mathematics, College of Science and Arts, Najran University, Najran, 66445, Saudi Arabia
3Department of Mathematics and Statistics, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
*Corresponding Author: M. A. El Safty. Email: m.elsafty@tu.edu.sa
Received: 02 March 2021; Accepted: 08 April 2021

Abstract: Real-world applications are now dealing with a huge amount of data, especially in the area of high-dimensional features. Trait reduction is one of the major steps in decision making problems. It refers to the determination of a minimum subset of attributes which preserves the final decision based on the entire set of attributes. Unfortunately, most of the current features are irrelevant or redundant, which makes these systems unreliable and imprecise. This paper proposes a new paradigm based on fuzzy soft relationship and level fuzzy soft relationship, called Union - Intersection decision making method. Using these new principles, the decision-making strategy is structured to choose a fuzzy set of optimal elements from the alternatives on the basis of a fuzzy soft set. Finally, we used our proposed method in medical application to make the decision to diagnose COVID-19. Moreover, we used MATLAB programming to obtain the results; this has coincided with the announcement by the World Health Organization and an accurate proposal was examined, which competes with that of the method of Zhao.

Keywords: COVID-19; fuzzy set; rough set; rule generation; intelligence discovery; decision making

1  Introduction

The most recent Coronavirus (COVID-19) epidemic was an outbreak in China at the start of 2020. China increased its national public-health response to the highest level on January 23, 2020. A variety of initiatives have introduced public social distancing to reduce the rate of COVID-19 transmission as part of the emergency response [1]. The infection is transmitted through droplets when a person contacts a person with respiratory symptoms (such as coughing or sneezing) in close contact (within a distance of 1 meter), which puts this person at risk of exposing his mucous membranes (mouth and nose) or conjunctiva (eye) into potential respiratory droplets. Infection can also be spread through contaminated equipment found in the area around an infected person, making it an infection. As a result, many papers were published by several researchers to study and analyze this virus, such as ([1–13]).

In diverse research areas, the mathematical modeling of vagueness and ambiguity has become an increasingly important topic. For many decades, people when making and taking their own decisions usually depend on the results of analyzing the available data about their problems of interest [14,15]. The communications and information technology revolution are currently defined, but this means that the collected data could be incomplete, lacking, ambiguous and unclear [16]. There is another statistical instrument that has been used in many aspects of life [17–19].

The concepts of the core and the reduced are two central concepts of the rough set theory in the case of attributes and knowledge [20]. The development of artificial intelligence has been implemented worldwide in recent years and linked to data analysis. Recently, work on soft set theory is advancing rapidly, for instance, fuzzy set theory and intuitionistic fuzzy set theory [21,22]. The fuzzy topology is extended to the general topology’s fundamental principles, which is very helpful in solving many life problems [23]. One such application used with a soft fuzzy collection in the field of medical diagnostics is presented. In this technique, soft fuzzy set is developed as a prediction framework for COVID-19 with the aim of solving many issues that have been found by insufficient knowledge from intelligent systems.

Decision making plays a critical role in our everyday lives, and among multiple alternatives, this mechanism offers the best alternative. There exist several decision making applications, such as ([23–32]). Fuzzy soft applications have made great progress, especially in decision making, such as soft level sets applied by Feng et al. [25] to solve fuzzy soft set-based decision making. Several attempts have been made to further generalize the fuzzy soft set and their applications in various fields [26]. In this theory, the notions of the fuzzy soft lower (resp. upper) approximations used can be helpful in fixing the knowledge concealed in the information system and then articulated in the form of a problem of decision making [27]. Liu et al. [28] has proposed a decision model based on the optimal solution and the fuzzy soft set. Tang [31] proposed a novel fuzzy soft set approach in decision making focused on grey relational analysis.

The main contribution in the current work is to introduce a new concept based on fuzzy soft relation with level fuzzy soft relation called Union-Intersection decision making method and it enables us to determine the optimal traits or elements most affected by the disease.

The main contributions of this paper are as follows:

Step 1: Input the two fuzzy soft sets (F,A) and (G,B) .

Step 2: choose α -level fuzzy soft set

Step 3: we find (F,A)α and (G,B)α

Step 4: We find ∩a∈A⁡∪b∈B⁡((F,A)α∨(G,B)α) .

Step 5: We find ∩b∈B⁡∪a∈A⁡((F,A)α∨(G,B)α)

Step 6: We compute (∩a∈A⁡∪b∈B⁡((F,A)α∨(G,B)α)∩(∩b∈B⁡∪a∈A⁡((F,A)α∨(G,B)α) to find the optimal elements and the decision for this issue from the given data.

Step 7: We get high accuracy of classification data based on the Union-Intersection method and the important symptom coronavirus.

Finally, we illustrate the importance of the proposed method in medical science for application in decision making problems. In fact, a medical application in decision making for information system of medical diagnosis of COVID-19 disease is presented with algorithm. In general, we believe that this work provides a readable framework that will be useful for medical fields that rely on decision making according to a set of symptoms on a specific group of patients, such as the application of COVID-19. The relation between the attributes and the knowledge of any attribute of significance in the Coronavirus epidemic (COVID-19) was also explained. We would like to note that the sample was composed of 1000 patients from whom the information was gathered for this research on coronavirus. This was investigated using the various methods described in the analysis. Finally, we also used the algorithms to get the basic symptoms casing of the COVID-19 coating of a sample of patients. These results may help the physician in making the best decision.

The paper is structured as follows: The basic concepts of the rough set theory and fuzzy set were explored in section two. The implementation of COVID-19 for each subclass of attributes in the information systems and comparative analysis was presented in section three. Section four concludes and highlights future scope.

2  Fuzzy and Rough Sets

The incomplete technology of modern mathematical knowledge, i.e., ambiguity, is included in the fuzzy and rough sets. Fuzzy set works on the data features while rough set works on an attribute set of the data. Therefore, the approximation of fuzzy input in the crisp approximation space is the consequence of rough-fuzzy hybridization set.

2.1 Pawlak Rough Set Theory

In 1982, in order to deal with vagueness in knowledge-based systems, information systems and data dissection, Pawlak [20] presented the principle of rough set as a modern mathematical technique or basic tools. In many areas that are used for process management, economics, such as medical diagnosis, chemistry, psychology, finance, marketing, biochemistry, environmental science, smart agents, image analysis, genetics, conflict analysis, telecommunication, and other fields, this principle has many applications.

Definition 2.1 [20] Let (U, R) be a knowledge representation system, then

i) Information systems (IS) is a pair (U, R), in which the finite set is U and R.

ii) The equivalence class R-indiscernibility relation [Y]R of an element x∈Y consists of all objects y∈Y such that x R y.

iii) Let IS = (U, R), then with any C⊆R there is an associated equivalence relation:

INDIS(C)={(b,b′)∈U2:∀a∈C,a(b)=a(b′)}, where INDIS(C) is devoted to the C-indiscernibility relation.

2.2 Fuzzy Soft Set Theory

In this part, we focus on developing a Union - Intersection method based on fuzzy soft relationship.

Definition 2.2 [32] Let (I,C) and (J,D) be two fuzzy soft sets then the Cartesian product of (I,C) and (J,D) as (K,E) where E=CXD is defined as K:E→P(U)∼ and K(c,d)=I(c)XJ(d) where (c,d)∈CXD , c∈C,d∈D .

Definition 2.3 [32] Let (I,C) and (J,D) be two fuzzy soft sets then the Cartesian product or of (I,C) and (J,D) is denoted by (M,N)=(I,C)∨(J,D) is defined as where E=CXD is defined as M:CXD→P(U) and M(c,d)=I(c)XJ(d) where (c,d)∈CXD .

Definition 2.4 [32] Let (I,C) and (J,D) be two fuzzy soft sets then the a relation from (I,C) to (J,D) is a fuzzy soft subset of (I,C)X(J,D) is denoted by (L,O)=(I,C)∨(J,D) is defined as where E=CXD is defined as L:CXD→P(U)∼ and M(c,d)=I(c)XJ(d) where (c,d)∈CXD , c∈C,d∈D .

Definition 2.5 [32] Let (I,C) and (G,B) be two fuzzy soft sets, the α -level fuzzy soft set of a fuzzy soft set (I,C) is a crisp soft set defined by (I,C)α={x:U,I(x)(e)≥α},∀e∈C,α∈[0,1] such that (I,C)α is also a fuzzy soft set, and it is a fuzzy subset of (I,C) .

3  Application

We will introduce the fuzzy soft relationships and intersection functions of Union - Intersection operators below. Here, as an example, we choose the ∨− product, but it is comparable with ∧ - products. Throughout this section, ∨P(U) is denoted as a fuzzy set of all ∨− product of the fuzzy soft.

Definition 3.1 Let (F,A)∨(G,B) be a fuzzy soft set. Then the Union - Intersection operators for ∨− product of two fuzzy soft sets denoted by ∪a∈A⁡∩b∈B and ∪b∈B⁡∩a∈A respectively, are defined as follows: ∩a∈A⁡∪b∈B:∨U→P(U)∼,∩a∈A⁡∪b∈B⁡((F,A)∨(F,B))=∩a∈A⁡∪b∈B⁡(FA∨B(a,b)) and ∩b∈B⁡∪a∈A:∨U→P(U)∼,∩b∈B⁡∪a∈A⁡((F,A)∨(G,B))=∩b∈B⁡∪a∈A⁡(FA∨B(a,b))

where ∩a∈A⁡∪a∈B⁡((F,A)∨(G,B)) and ∩a∈B⁡∪a∈A⁡((F,A)∨(G,B)) are fuzzy soft subsets of (F,A)∨(G,B) Then, the intersection and union function for ∨− product of two fuzzy soft sets, denoted by ∩∪ is defined as by:

∩∪:∨U→P(U)∼∩∪((F,A)∨(G,B))=∩a∈A⁡∪b∈B⁡((F,A)∨(G,B))∩∩b∈B⁡∪a∈A⁡((F,A)∨(G,B)) where ∩∪((F,A)∨(G,B)) is also a fuzzy soft subset of P(U)∼ Now, based on the Union - Intersection fuzzy soft relationship and level fuzzy soft relationship, we concentrate on building a Union - Intersection decision making process.

3.1 Proposed Method

We implement the proposed method in this application [2], and it is possible to define the application of Coronavirus (COVID-19) as follows; we would like to note that the knowledge obtained in this Coronavirus study is from 1000 patients. This big sample of 1000 patients were reduced to 10 patients describing the most severe symptoms of the Coronavirus due to the similarity of the attributes in rows (objects). where objects were classified as; U = {P1, P2, …, P10} denotes 10 mentioned patients, the symptoms as S = {s1, s2, …, s6} = {breathing difficulty, chest pain, temperature, dry cough, headache, loss of taste or smell} and {d} is a decision, as follows in the data collected by the World Health Organization as well as by Coronavirus medical groups (COVID-19).

Taking the following knowledge system into account in Tab. 1, we get the following:

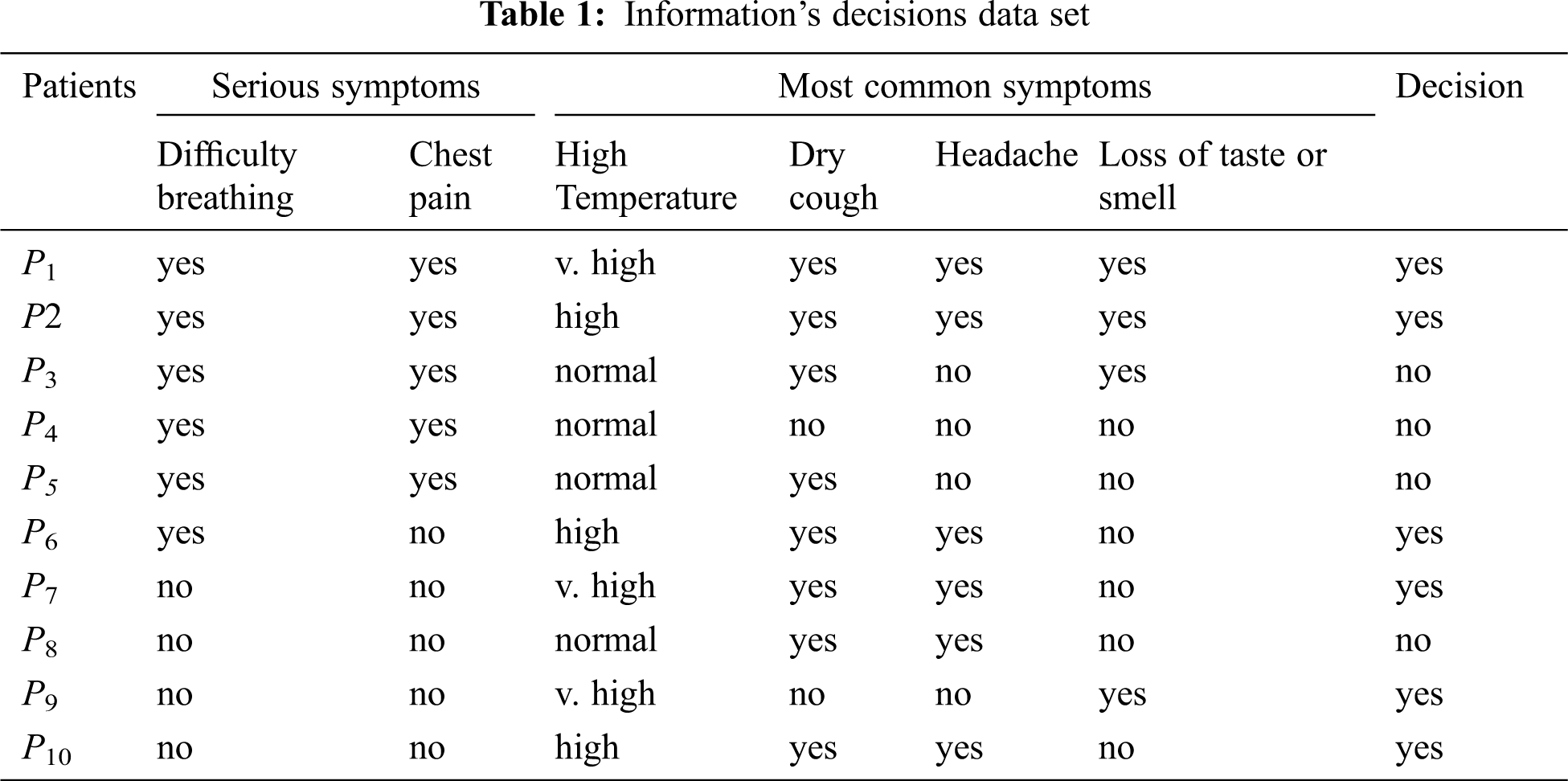
We rewrite Tab. 1 again in fuzzy as shown in Tab. 2,

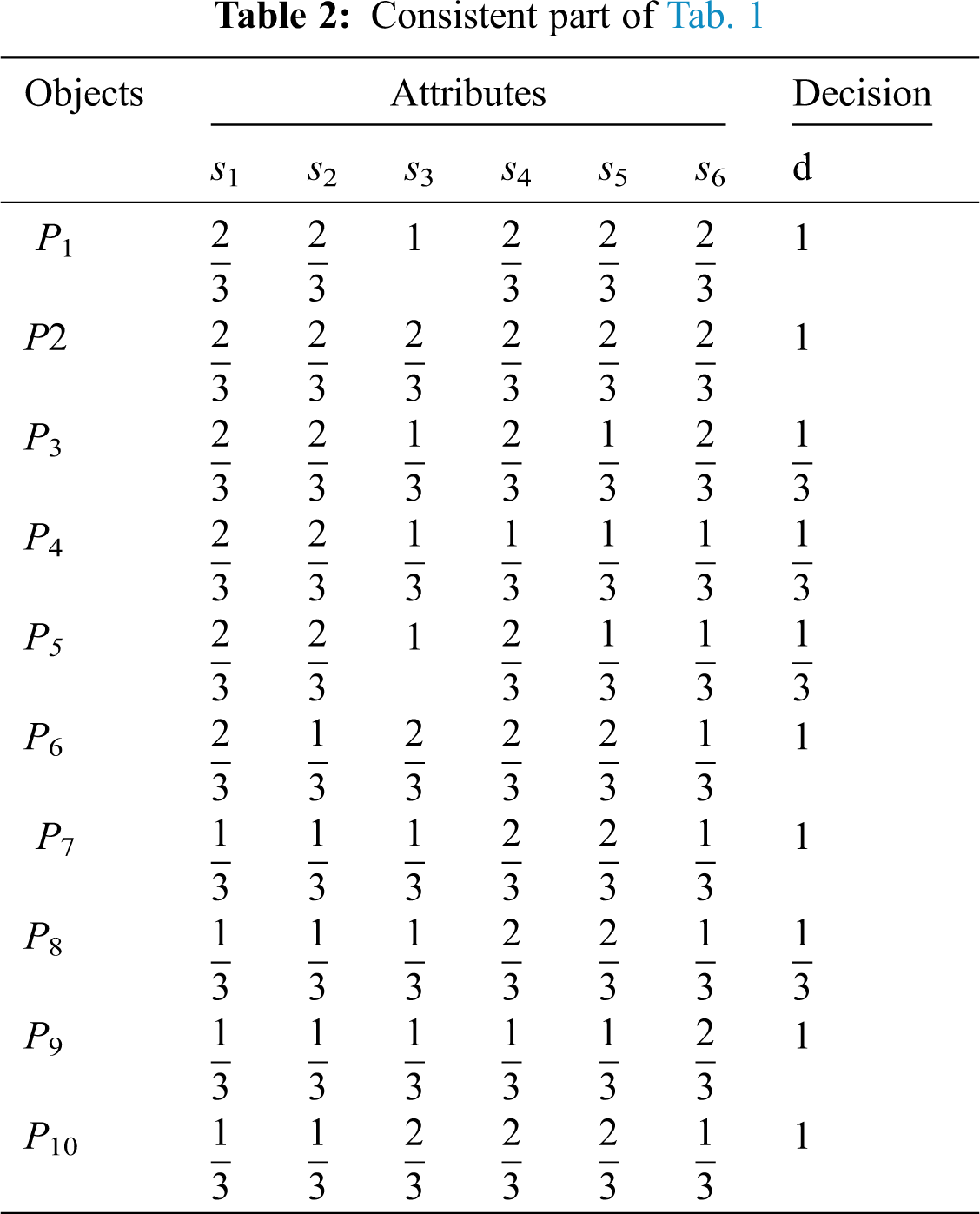
Next in Tab. 3, by using the relations [18], if IND (S) ≠ IND (S – {s1}), …etc. Then s1 is indispensable. Also, if IND (S) = IND (S – {s2}), then s2 is superfluous.

Leave s1 attribute as follows:

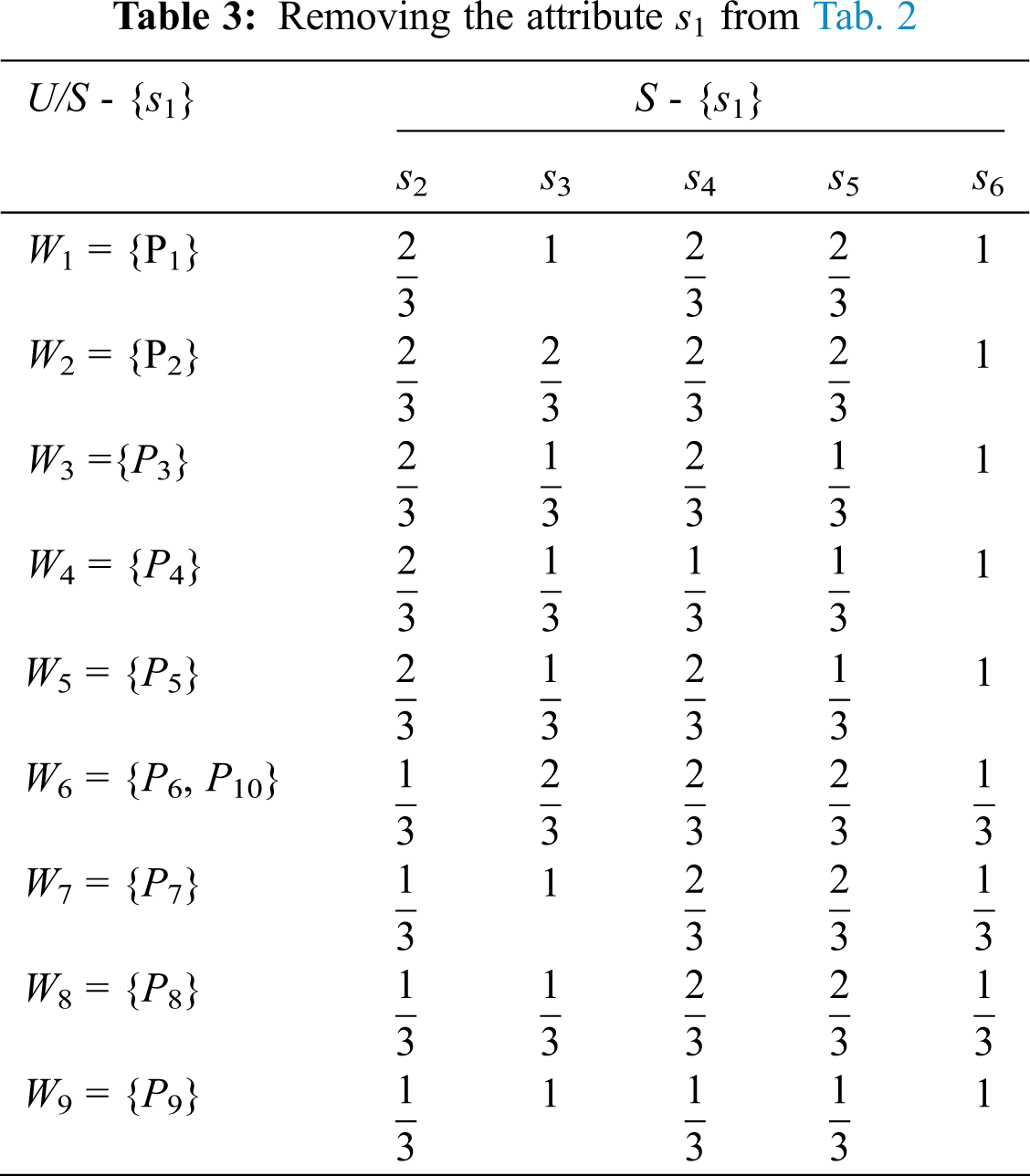
Using the Algorithm 1, and IND (S) ≠ IND (S – {s1}), …etc, then s1, s3, s4 and s6 are indispensable. We also get IND (S) = IND (S – {s2}), and then s2, and s5 are superfluous.

Then, we get the removal of attributes as in Tab. 4.

Tab. 5, therefore, presents a new information table based on this reduct.

3.2 Discussion

3.2.1 Discussion - s1

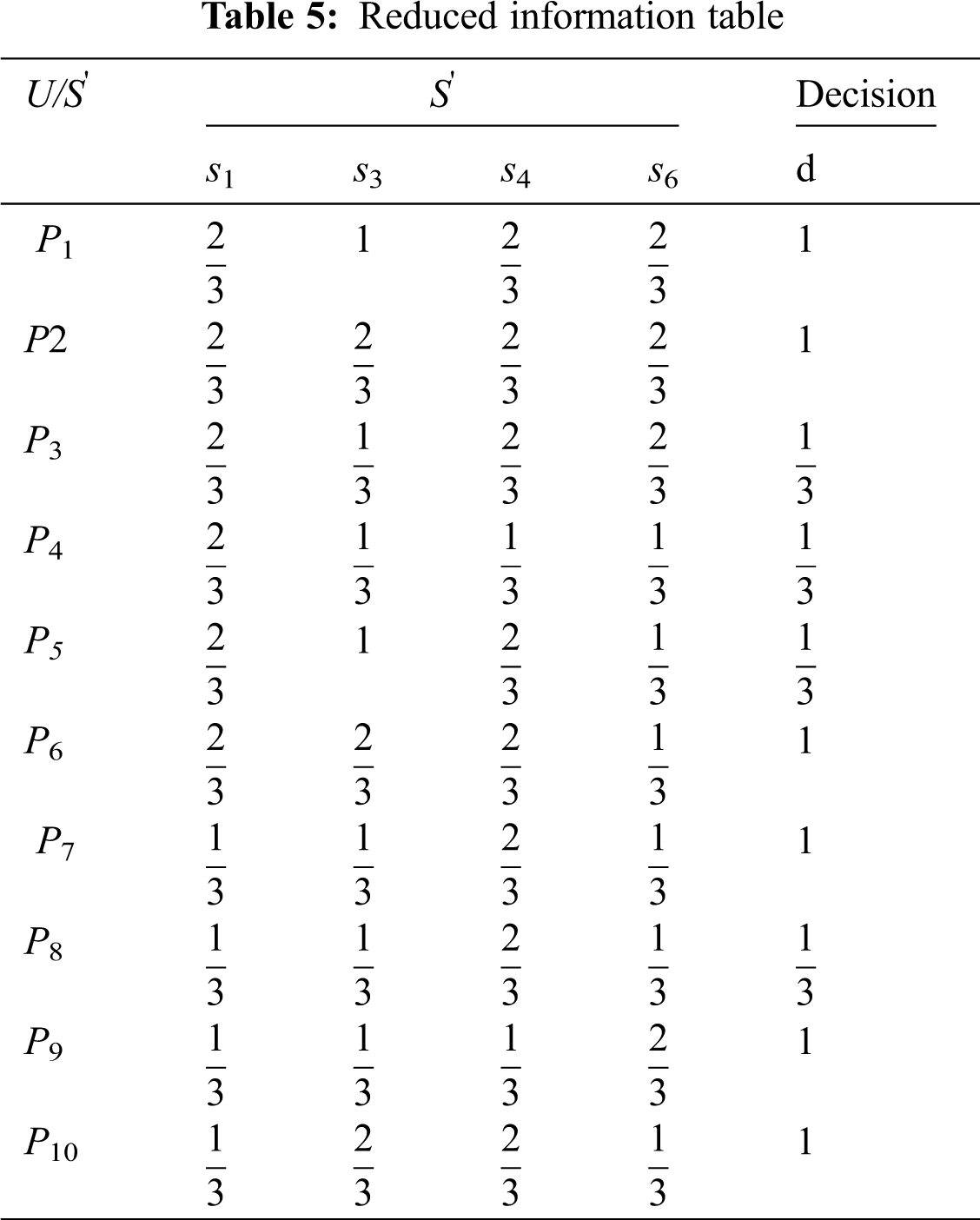
Removed attribute s1: we get the results

For s1 [(d= yes, XYes={p1,p2,p6,p7,p9,p10} ), (d = No, XNo={p3,p4,p5,p8} )]

X=XYes+XNo , we get the following Tab. 6.

When we remove the attribute s1 from the whole table, according to the above knowledge, we get two fuzzy soft sets from the Tab. 5. When α=23 , we get 23 - level fuzzy soft set from Tab. 5, we get (F,A)23 as in Tab. 6 and (G,B)23 as in Tab. 7 where S={s3,s4,s6} and B={s1,s4,s6} are the set of attributes of decision makers.

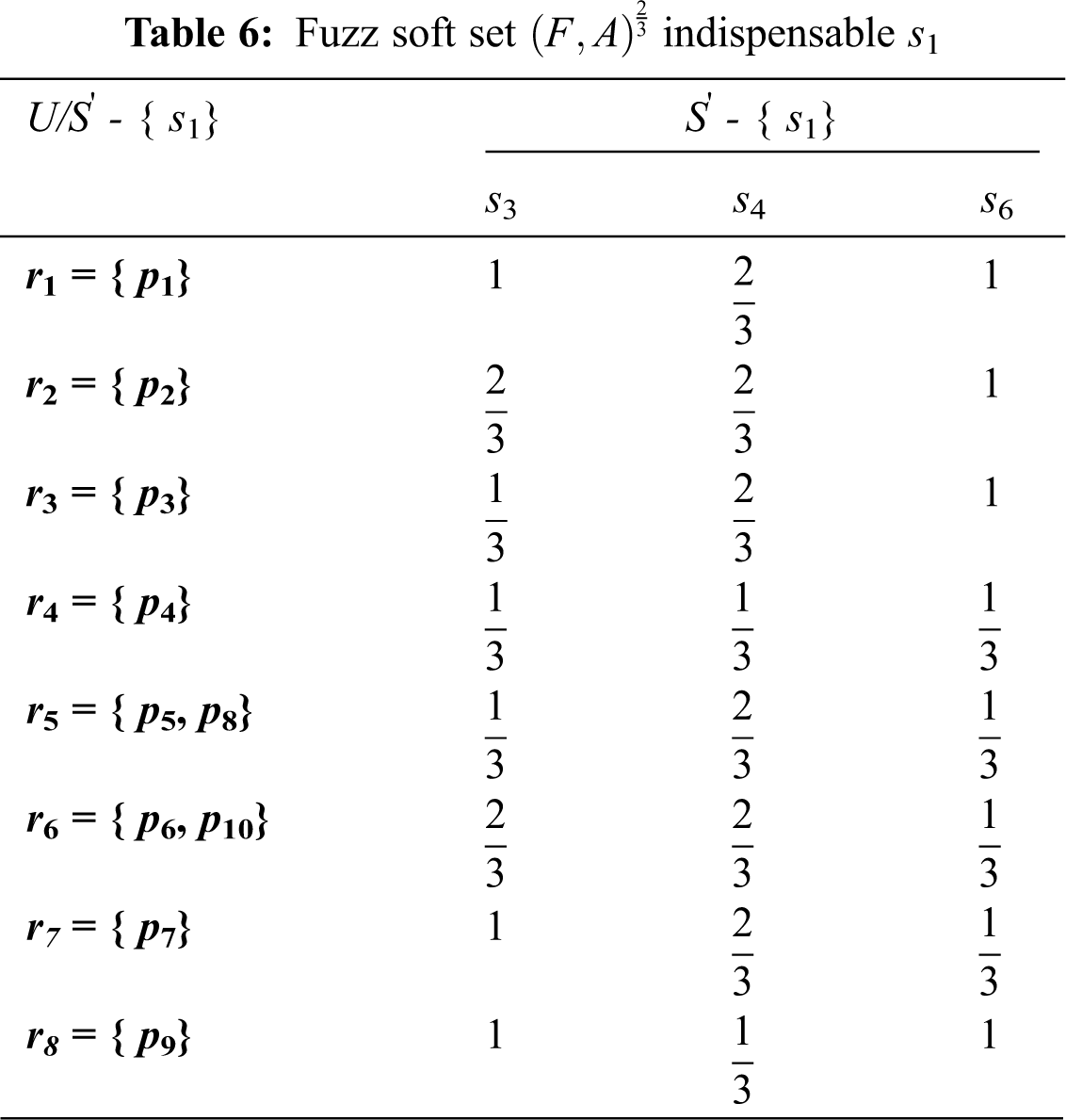
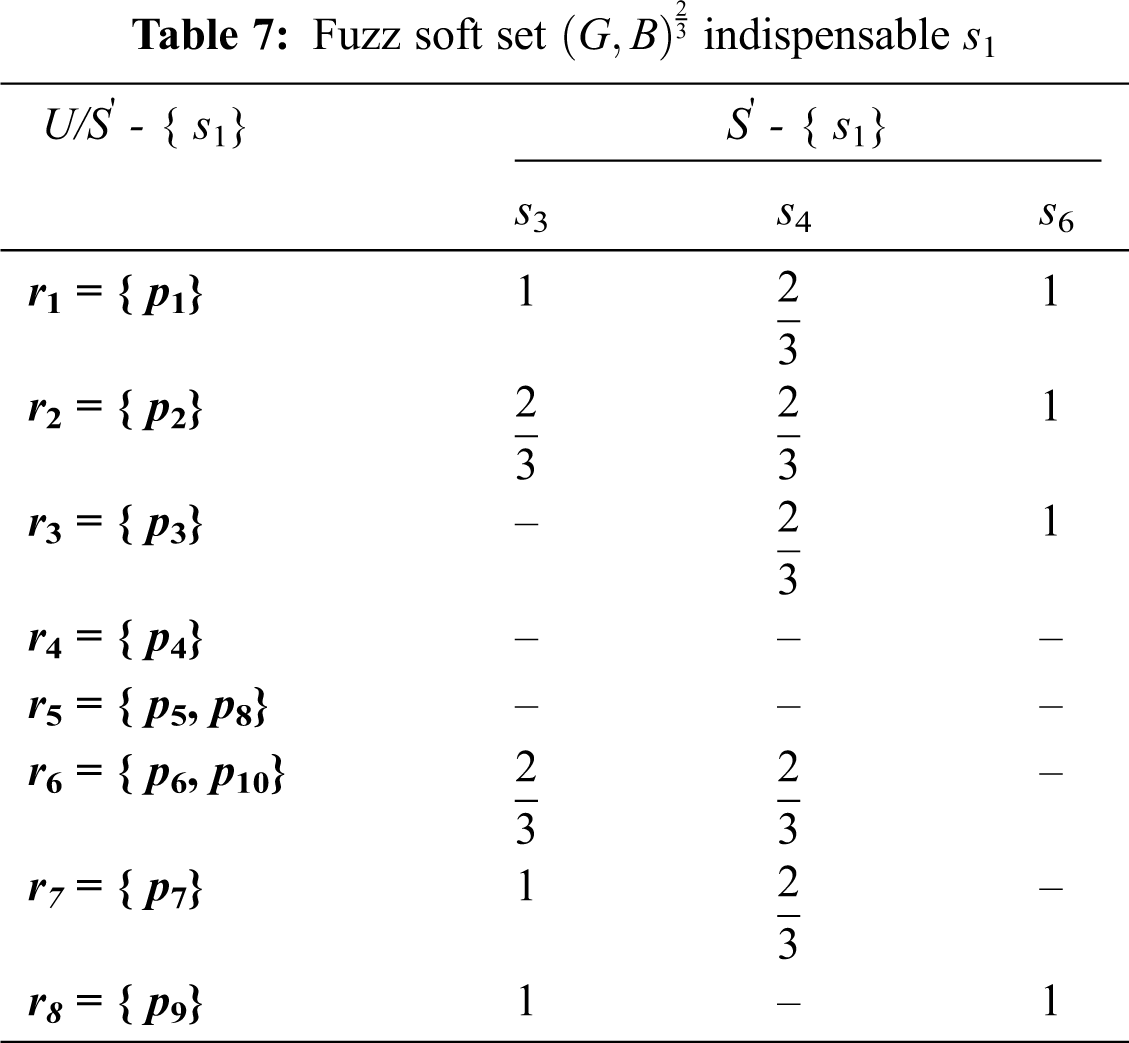
Also, we present Tab. 7 as follows:

3.2.2 Discussion – s3

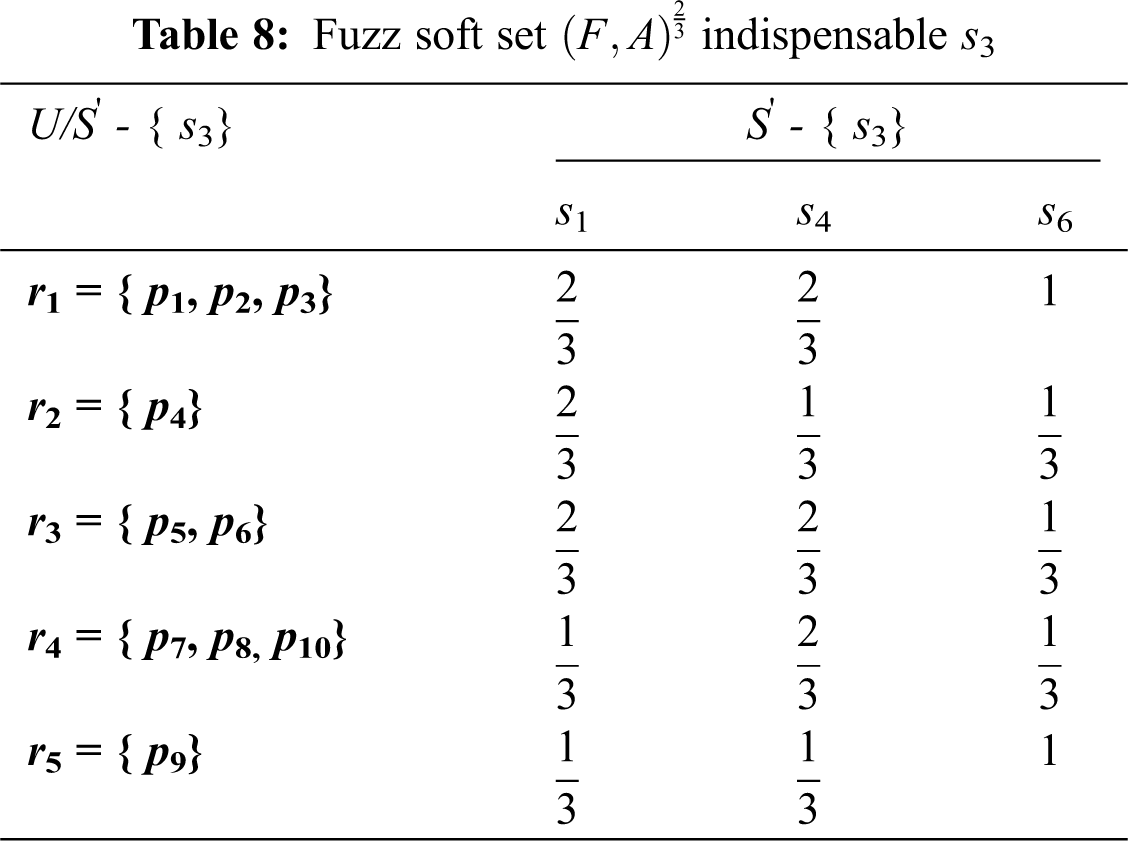
Removed attribute s3: We’ll get the results shown below:

When we remove the attribute s3 from Tab. 8, we get the (G,B)23 as in Tab. 9 where and B={s1,s4,s6} are the sets of attributes of decision maker.

The following Tab. 10 shows ∨− Product for two fuzzy sets (F,A)23∨(F,B)23

∩s∈S⁡∪b∈B⁡((F,A)23∨(F,B)23)=∩{∪{(s3,s1),(s3,s4),(s3,s6)}∪{(s4,s1),(s4,s4),(s4,s6)}∪{(s6,s1),(s6,s4),(s6,s6)}=∩{{r11,r232},{r11,r232,r233},{r11,r12,r13}}={r11,r232} ={p1}

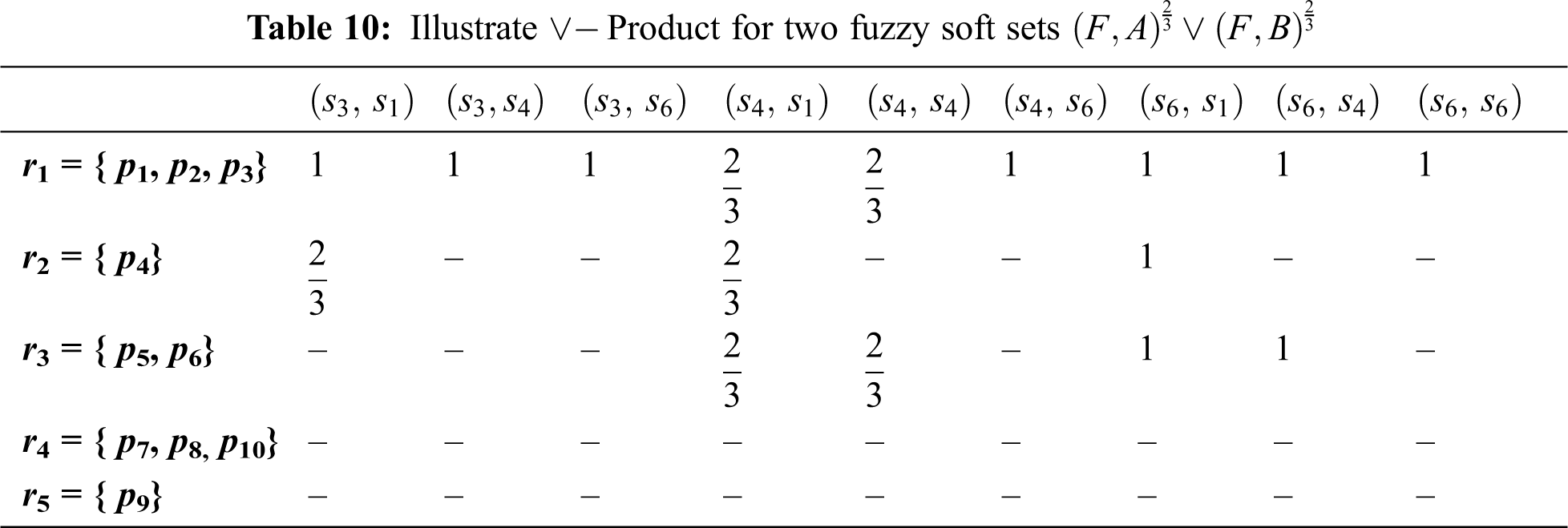
Also, we find the intersection and union function for ∨− Product of 23 - level fuzzy sets

∩b∈B⁡∪s∈S⁡((F,A)23∨(F,B)23)=∩{∪{(s3,s1),(s4,s1),(s6,s1)}∪{(s3,s4),(s4,s4),(s6,s4)}∪{(s3,s6),(s4,s6),(s6,s6)}=∩{{r11,r12,r13},{r11,r13},{r11}}={r11}={p1,p2,p3} ={T1,T2,T3} ,

Then, we find the result of the function Union - Intersection of (F,A)23∨(F,B)23=(∩s∈S⁡∪b∈B⁡((F,A)23∨(F,B)23)∩(∩b∈B⁡∪s∈S⁡((F,A)23∨(F,B)23))={r11}={p1,p2,p3}

It is clear that we have identified the main symptoms of COVID-19, which are {p1,p2,p3} according to this method applied in this paper. This is because the technique adopted helps us identify the group of individuals infected with COVID-19, On the other hand, when decision makers work to reduce data for any problem in life to get the right decision, we can use this process.

4  Conclusion

The present paper represents the Cartesian product of two fuzzy soft sets. We also have a description of the fuzzy soft relationship extending to the level of fuzzy soft relationship, and to the Union - Intersection fuzzy soft relationship. Union - Intersection making method based on a fuzzy soft set is constructed since this technique allows any expert to make a decision about any real problem. Additionally, our approach has provided a new insight into the problem of attribute reduction, and also suggested more semantic properties preserved by an attribute reduction. Consequently, our method provides more flexibility to the decision-maker to choose which is suitable for him. We also obtained a proposed level of accuracy that depends upon the fuzzy soft set, which was found to be better than that of Zhao accuracy [32]. Also, this method has proven effective in obtaining the basic symptoms that cause COVID-19. We plan to extend the suggested methodology in future work to cover the issue of multi-label classification.

Contributions of the Author: This paper is written with the efforts of all contributions. The individual contributions and roles of both authors can be summarized as follows: The concept of the entire article was developed by El- Sayed, and Alblowi, along with doing the paper preparations. El Safty examined the work of the current fuzzy soft set and reviewed the article.

Funding Statement: This work has been funded by the University of Jeddah, Saudi Arabia, under Grant No. (UJ-20-DR-131). The authors, therefore, acknowledge with thanks the University's technical and financial support.

Conflict of Interest: The authors declare no conflicts of interest in this paper. This article does not contain any studies with human or animals participants performed by any of the authors.

References

 1.  L. F. Carvalho, L. A. S. Galloway, R. Saoud, P. K. Agarwal and L. Stamatakis, “Considerations about Non-Metastatic Bladder Cancer Management during the COVID-19 Pandemic,” Bladder Cancer, vol. 6, no. 2, pp. 99–106, 2020. [Google Scholar]

 2.  M. A. El Safty and Samirah AlZahrani, “Topological modeling for symptom reduction of Coronavirus,” Punjab Uni. J. Math., vol. 53, no. 3, pp. 47–59, 2021. [Google Scholar]

 3.  L. X. Feng, J. Shuanglin, S. Hu, D. Wang and H. Huo, “Modelling the effects of media coverage and quarantine on the COVID-19 infections in the UK,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 3618–3636, 2020. [Google Scholar]

 4.  X. Feng, J. Chen, K. Wang, L. Wang, F. Zhang et al., “Phase-adjusted estimation of the COVID-19 outbreak in South Korea under multi-source data and adjustment measures: A modelling study,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 3637–3648, 2020. [Google Scholar]

 5.  M. R. Hashmi, M. Riaz and F. Smarandache, “m-polar neutrosophic generalized weighted and m-polar neutrosophic generalized einstein weighted aggregation operators to diagnose coronavirus (COVID-19),” Journal of Intelligent & Fuzzy Systems, vol. 39, no. 5, pp. 7381–7401, 2020. [Google Scholar]

 6.  S. Jha, M. K. Goyal, B. Gupta and A. K. Gupta, “A novel analysis of COVID-19 risk in India incorporating climatic and socioeconomic Factors,” Technological Forecasting and Social Change, vol. 167, pp. 1–11, 2021. [Google Scholar]

 7.  G. Kampf, D. Todt, S. Pfaender and E. Steinmann, “Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents,” J. Hospital Infect., vol. 104, no. 3, pp. 246–251, 2020. [Google Scholar]

 8.  A. M. Kozae, M. Shokry and M. Omran, “Intuitionistic fuzzy set and its application in Corona (COVID-19),” Applied and Computational Mathematics, vol. 9, no. 5, pp. 146–154, 2020. [Google Scholar]

 9.  M. Naveed, M. Rafiq, A. Raza, N. Ahmed and I. Khan, “Mathematical analysis of novel coronavirus (2019-ncov) delay pandemic model,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1401–1414, 2020. [Google Scholar]

10. J. Tian, J. Wu, Y. Bao, X. Weng, L. Shi et al., “Modeling analysis of COVID-19 based on morbidity data in Anhui, China,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 2842–2852, 2020. [Google Scholar]

11. L. Wang, J. Wang, H. Zhao, Y. Shi, K. Wang et al., “Modelling and assessing the effects of medical resources on transmission of novel coronavirus (COVID-19) in Wuhan, China,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 2936–2949, 2020. [Google Scholar]

12. J. Yang, G. Wang and S. Zhang, “Impact of household quarantine on SARS-Cov-2 infection in mainland China: A mean-field modelling approach,” Mathematical Biosciences and Engineering, vol. 17, no. 5, pp. 4500–4512, 2020. [Google Scholar]

13. C. C. Zhu and J. Zhu, “Spread trend of COVID-19 epidemic outbreak in China: Using exponential attractor method in a spatial heterogeneous SEIQR model,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 3062–3087, 2020. [Google Scholar]

14. S. AlZu’bi, M. Shehab, M. Al-Ayyoub, Y. Jararweh and B. Gupta, “Parallel implementation for 3D medical volume fuzzy segmentation,” Pattern Recognition Letters, vol. 130, pp. 312–318, 2020. [Google Scholar]

15. M. A. Elsafty and A. M. Alkhathami, “A Topological method for reduction of digital information uncertainty,” Soft Computing, vol. 24, no. 1, pp. 385–396, 2020. [Google Scholar]

16. M. A. Elsafty, “Topological method for a study of discriminating three categories of banks and its use in attributes reduction,” International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET), vol. 7, no. 5, pp. 221–233, 2020. [Google Scholar]

17. M. El Sayed, “Generating simply approximation spaces by using decision tables,” Journal of Computational and Theoretical Nanoscience, vol. 13, no. 10, pp. 7726–7730, 2016. [Google Scholar]

18. A. M. Kozae, M. Elsafty and M. Swealam, “Neighbourhood and reduction of knowledge,” Advances in information Sciences and Service Sciences (AISS), vol. 4, no. 1, pp. 247–253, 2012. [Google Scholar]

19. N. Kumar, V. Poonia, B. B. Gupta and M. K. Goyal, “A novel framework for risk assessment and resilience of critical infrastructure towards climate change,” Technological Forecasting and Social Change, vol. 165, pp. 1–12, 2021. [Google Scholar]

20. Z. Pawlak, “Rough sets,” Int J. of Information and Computer Sciences, vol. 11, no. 5, pp. 341– 356, 1982. [Google Scholar]

21. M. El Sayed, Kh Abd-Rabou and M. A. Elsafty, “New classes of soft open sets in soft generalized topological spaces,” Journal of Fuzzy Mathematics, vol. 28, pp. 721–732, 2020. [Google Scholar]

22. D. Molodtsov, “Soft set theory-Frst results,” Computers & Mathematics with Applications, vol. 37, no. 4–5, pp. 19–31, 1999. [Google Scholar]

23. M. A. El Safty, A. A. Mousa, S. A. Alblowi and M. El Sayed, “Topological approach on fuzzy soft β–Closure and fuzzy soft β–Interior and its application in decision making,” Nanoscience and Nanotechnology Letters, vol. 12, no. 11, pp. 1329–1336, 2020. [Google Scholar]

24. M. El Sayed, A. A. Q. Al Qubati and M. K. El-Bably, “Soft pre-rough sets and its applications in decision making,” Mathematical Biosciences and Engineering, vol. 17, no. 5, pp. 6045–6053, 2020. [Google Scholar]

25. F. Feng, Y. Li and V. Leoreanu-Fotea, “Application of level soft sets in decision making based on interval-valued fuzzy soft sets,” Computers & Mathematics with Applications, vol. 60, no. 6, pp. 1756–1767, 2010. [Google Scholar]

26. A. Z. Khameneh and A. Kilicman, “Parameter reduction of fuzzy soft sets: Adjustable approach based on the three-way decision,” International J. of fuzzy Systems, vol. 20, pp. 928–942, 2018. [Google Scholar]

27. Z. Li, G. Wen and N. Xie, “An approach to fuzzy soft sets in decision making based on grey relational analysis and Dempster-Shafer theory of evidence: An application in medical diagnosis,” Artificial Intelligence in Medicine, vol. 64, no. 3, pp. 161–171, 2015. [Google Scholar]

28. Z. Liu, K. Qin and Z. Pei, “A method for fuzzy soft sets in decision making based on an ideal solution,” Symmetry, vol. 9, no. 10, pp. 246–268, 2017. [Google Scholar]

29. A. S. Nawar, M. K. El-Bably and A. F. El-Atik, “Certain types of coverings based rough sets with application,” Journal of Intelligent and Fuzzy Systems, vol. 39, no. 3, pp. 3085–3098, 2020. [Google Scholar]

30. A. R. Roy and P. K. Maji, “A fuzzy soft set theoretic approach to decision making problems,” Journal of Computational and Applied Mathematics, vol. 203, no. 2, pp. 412–418, 2007. [Google Scholar]

31. H. X. Tang, “A novel fuzzy soft set approach in decision making based on grey relational analysis and Dempster-Shafer theory of evidence,” Applied Soft Computing, vol. 31, pp. 317–325, 2015. [Google Scholar]

32. H. Zhao and J. Jia, “Fuzzy soft relation and its application in decision making,” 7th International Conference on Modelling, Identification and Control (ICMIC 2015) Sousse, Tunisia - Dec., (2015), pp. 1–4, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.