DOI:10.32604/iasc.2021.019341

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.019341 |  |
| Article |
Lowest-Opportunities User First-Based Subcarrier Allocation Algorithm for Downlink NOMA Systems
Department of Computer Engineering, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif, 21944, Saudi Arabia
*Corresponding Author: Mohammed Abd-Elnaby. Email: maahmed@tu.edu.sa
Received: 10 April 2021; Accepted: 19 May 2021
Abstract: Non-orthogonal multiple access (NOMA) is one of the promising 5G technologies to improve spectral efficiency massive connectivity and cell-edge throughput. The performance of NOMA systems mainly depends on the efficiency of the subcarrier allocation algorithm. This paper aims to jointly optimize spectral efficiency (SE), outage probability, and fairness among users with respect to the subcarrier allocation for downlink NOMA systems. We propose a low-complexity greedy-based subcarrier allocation algorithm based on the lowest-opportunities user’s first precept. This precept is based on computing the number of opportunities for each user to select a subcarrier with good channel gain by counting the number of available subcarriers with channel gains higher than a particular threshold value. So, the proposed algorithm allows the users with low opportunities to select their desired subcarriers first and hence improves their achieved data rates. Simulation results demonstrate that compared to orthogonal multiple access (OMA), and traditional NOMA algorithms, the proposed subcarrier allocation algorithm attains significantly superior spectral efficiency, fairness performance, user data rate, and outage probability. In addition, the proposed algorithm’s performance metrics improve as the number of users in the system increases, contrary to traditional NOMA algorithms.
Keywords: 5G; NOMA; user pairing; spectral efficiency; outage probability
Due to the fast growth of demands of high data rate applications over the mobile networks, the fifth-generation (5G) is represented the expected solution [1,2]. Non-orthogonal multiple access (NOMA) is considered as the target technology for 5G wireless networks. NOMA provides high spectral efficiency, high cell-edge data rate, massive device connectivity, fairness, low transmission latency, and high energy efficiency [3–5]. NOMA enabling multiple users to share the same subcarrier in power domain. The power-domain NOMA (PD-NOMA is the focus of this paper.
In PD-NOMA, distinct power levels are assigned for various users according to their channel condition. A higher-power level is assigned to the user with low channel gain. Meanwhile, the Lower-power level is given to the user with high channel gain [6–9]. This technique enables the successive-interference-cancellation (SIC) to be used at the receiving end to detect the user’s signals. Besides, efficient resource allocation schemes are needed to improve the performance of NOMA, such as energy efficiency (EE), spectral efficiency (SE), outage probability, and fairness among users.
User pairing (UP) and power allocation (PA) are the main mechanisms of the NOMA systems’ resource allocation scheme and have been investigated since the last decade in many research studies [10–26]. Therefore, this paper focuses on the UP problem which deals with the subcarrier allocation mechanism and the selection of the paired users for each subcarrier. The main contributions of this paper are as follows:
• A novel lowest-opportunities user first principle is proposed for subcarrier allocation. This principle is based on determining the number of opportunities of each user to select a subcarrier with a good channel gain by counting the number of available subcarriers with channel gains higher than a certain threshold value.
• Optimizing the fairness among users by increasing the possibility of getting a subcarrier with good channel gain for each user which consequently increases the achieved data rate for each user.
• Minimizing the outage probability by enhancing the users’ data rate.
• Finally, enhancing the spectral efficiency by improving the total system sum-rate.
The rest of the paper is organized as follows. In Section 2, we present the related works. Then, the system model and problem formulation is presented in Section 3. In Section 4, the proposed algorithm is presented and elucidated with a numerical example. Section 5 shows the results and discussions. Finally, the conclusion is given in Section 7.
There has been a grown interest recently to enhance the NOMA performance in order to find the optimal resource allocation scheme using efficient UP and PA techniques. One simple way to solve the UP issue is to apply random pairing [10] where the base station (BS) randomly selects users for allocation to sub-channels. Despite its low-complexity, using such a scheme doesn’t consider the channel gains of users, resulting in sub-optimal throughput. In [11], two NOMA’s UP systems are studied where the first one is based on fixed power allocation (F-NOMA), and the second one is based on cognitive radio NOMA (CR-NOMA). In F-NOMA, the worst channel gain user is paired with sub-carrier with the largest gain. Therefore, F-NOMA outperforms the orthogonal multiple-access (OMA) in providing a larger sum rate. On the other hand, to guarantee the quality of service (QoS), the worst user channel gain user is paired with the second-best sub-carrier gain.
In [12], the authors investigated two UP algorithms to accommodate capacity gains to users and paring them to mitigate the problem of cell mid-users. The first algorithm is called uniform channel gain difference” (UCGD) pairing where mid-users are paired with large or low gain users while large gain users are paired with only the mid-users. The second algorithm is called hybrid UP which uses the conventional pairing and works when high channel gain difference with extreme end users. However, when the channel gain difference decreases, it turns to pair using UCGD pairing. A virtual-UP strategy is proposed in [13] to solve the issue when far users in a cell are more than the near cell users. Their proposed solution is to share the frequency band of close-user with two far-users that have similar gains. As a result, all the frequency band of the near un-paired users can be utilized to enhance the performance of NOMA system. The authors of [14] introduced the idea of NOMA clusters fairness by applying the so-called divide-and-next-largest-difference-based user pairing algorithm (D-NLUPA). Here the capacity gain is distributed to ensure fairness between different NOMA clusters.
In [15], the authors used mixed-integer programming to optimize both UP and PA, aiming to find the achievable-sum-rate (ASR) where each user is constrained by minimum rate. To solve this problem, they started with two users to find their optimal PA, and then a simplified solution is used to analyze the UP. Finally, a closed-form globally-optimal solution is resulted to solve both UP and PA problems in NOMA system. In [16], the paper proposed a low complexity optimization model to solve both user grouping and power allocation problems to maximize the capacity of NOMA systems. The authors broke down the optimization problem into two sub-problems: the user sub-carrier grouping problem and the PA problem. In the former, they utilized the greedy solution based on reducing the complexity of the exhaustive search. In PA problem, they used a fixed group of sub-carriers employing the linear water filling and the fraction transmit power allocation (FTPA). In [17], it proposed subcarrier and PA optimization of the NOMA downlink cellular network to maximize the worst user individual EE and ensure user fairness. The authors decoupled the problem to reduce problem complexity due to non-convexity. They introduced a greedy-based algorithm for the subcarrier assignment. The greedy solution is based on assigning subcarrier to the worst-case user first. Then, they used fractional programming for PA.
Many works have been extensively discussed matching theory in the NOMA cellular network to find optimal solution to the UP problem by considering the computation complexity [18–23]. In matching theory, the main goal is to maximize the total sum-rate by joining between users and subcarriers where they are considered two sets of players. The first set of players represents the users (proposers), where the second set represents the subcarriers (selectors). The matching depends on the selection of favorite subcarriers from the list considering channel status consistency.
In [24], several optimum and suboptimum resource allocation schemes are proposed to minimize the used bandwidth. Also, a hybrid orthogonal-non orthogonal scheme is used to increase the total system throughput. The article [25] proposed three-step RA technique to maximize the total sum-rate of NOMA system. They investigated both subcarrier and PA problems to reach acceptable performance compared to Lagrangian-duality and dynamic programming (LDDP). First, they relaxed the problem so that any user can use all subcarriers at the same time. Second, they used convex programming to solve the problem and obtain user’s power vector. They utilized a greedy heuristic scheme to allocate subcarriers to the users with the resulted power vectors. Finally, the optimized system performance is found by customizing the proposed power control technique. In [26], it presented generic multi-cell multiple inputs single output NOMA (MISO-NOMA) to solve the power consumption minimization problem. They defined the problem as a mixed integer non-convex programming problem where the problem solution is from different perspectives: user grouping, power control, and beamforming (BF).
3 System Model and Problem Formulation
This section presents the downlink NOMA model, followed by formulating the optimization problem that maximizes the sum-rate in the entire system.
Downlink NOMA system consists of two integrated parts, base station (BS), and users at receiving end as shown in Fig. 1. In base station, the available bandwidth, B, is divided equally into multiple subcarriers, S, each subcarrier has a bandwidth W = B/S. The subcarrier allocation algorithm at the base station allocates each user, k, to an appropriate subcarrier based on the channel state information to achieve a specific goal such as improving SE, fairness optimization, and reduction of outage probability. Therefore, multiple users
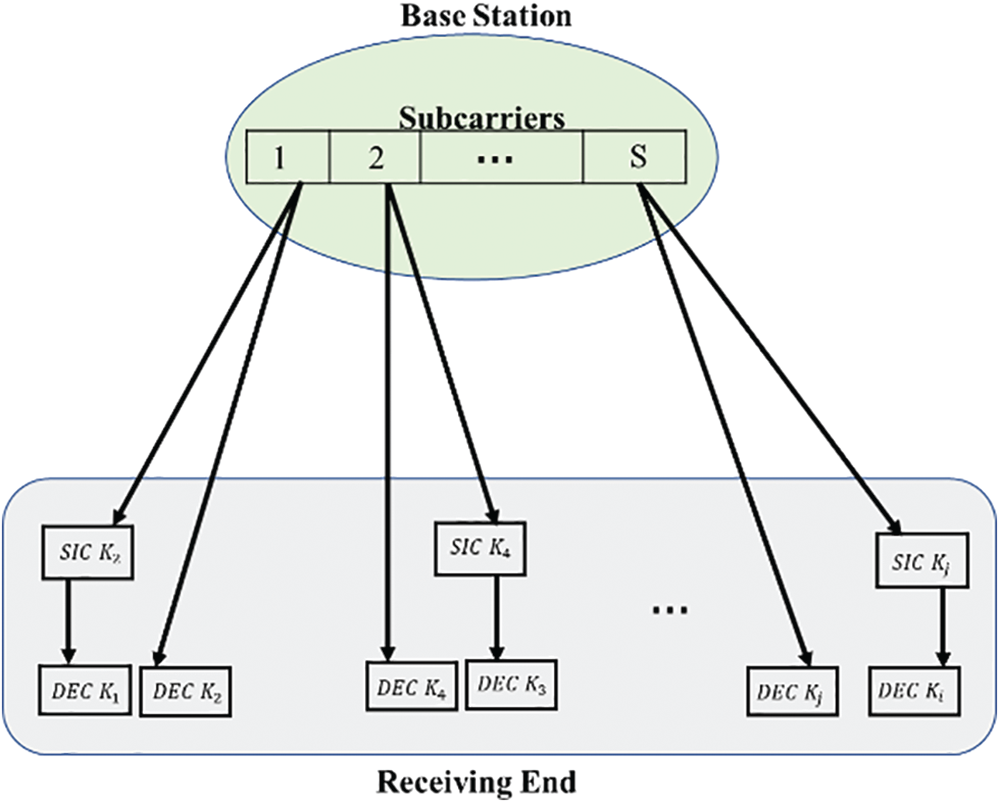
Figure 1: The downlink NOMA system model
The signal transmitted from the base station to the
where
The signal that received by the kth user,
To extract useful information from such signal it should be filtered from accompanying additive noise. Besides, it is necessary to be separated from other signals that are sent on the same subcarrier. Therefore, some interference cancellation techniques such as SIC algorithm can be used to cancel out possible interference. Particularly, the channel gains are normalized by the noise and vectored in descending order so that the last channel in the vector is with the lowest-gain and vice versa. Consequently, the user with the lowest channel gain on the subcarrier can directly decode its signal without performing the SIC technique and treats the other users’ signals as interference. In contrast, the user with the highest channel gain on the subcarrier requires decoding the messages of the other users using SIC technique and extracting them from the received signal to obtain its signal without any interference.
In the NOMA system, the base station compensates for low gain channels with more power allocation to achieve fairness and improve SIC efficiency. The received signal to interference plus noise ratio (SINR) of the kth user on subcarrier s is as follows:
Eventually, the data rate of the kth user on subcarrier, s is given by Eq. (4) under the assumption that the bandwidth for each subcarrier is normalized to 1 Hz with consistent noise power spectral density,
Then, the total system sum-rate is as follows:
where,
Pairing each use with its corresponding subcarrier is represented by the binary S × K matrix,
The complexity of SIC algorithm depends on the number of multiplexed users over a subcarrier. Conventionally, a single subcarrier can be allocated to a single user in OMA. However, the NOMA technique allows multiplexed users to be assigned to a single subcarrier. Therefore, the total number of users, K, is given as the number of multiplexed users in a subcarrier,
The objectives are maximizing the total system sum-rate, enhancing fairness, and improving outage probability with adherence to the following constraints:
1. The total power of all subcarriers- users must be less than or equal to the total base station power,
2. The power for each user in particular subcarrier must be non-negative.
3. Each subcarrier is allocated for limited number of users,
4. Each user gets its data only from its designated subcarrier
5. The indicator determines the possibility of subcarrier allocation,
4 The Proposed Lowest-Opportunities User First Subcarrier Allocation (LOUFSA) Algorithm
In this section, we propose a low complexity greedy-based subcarrier allocation algorithm. In the procedures of the proposed Lowest-Opportunities User First Subcarrier Allocation (LOUFSA) algorithm, we assume that
• optimizing the fairness among users.
• minimizing the outage probability by enhancing the data rate of users.
• maximizing the spectral efficiency by maximizing the total system sum-rate.
The LOUFSA achieves such objectives in five steps, as follows:
1. Given the subcarriers-users channel gain matrix, compute the channel gain threshold
2. Compute the number of opportunities of each user to select a subcarrier with a good channel gain
3. Order the users in ascending order according to their number of opportunities
4. If there is more than one user with the same number of opportunities
5. Each ordered user selects the available subcarrier with the highest channel gain (i.e., choose the largest value in each column in the subcarriers-users channel gain matrix). The subcarrier that gets its paired users becomes unavailable for the selection by any other users.
The following example utilizes the channel gain matrix to clarify the subcarrier allocation procedures of the LOUFSA in detail.
Step 1: Compute the channel gain threshold
Step 2: Detect the subcarriers with channel gains higher than
Step 3,4: Users sorted in ascending order according to
Step 5 is demonstrated in (M4). Each ordered user selects the available subcarrier with the largest channel gain. The subcarrier that gets its paired users becomes unavailable for the selection of any other users. Thus, user6 selects subcarrier2, user1 selects subcarrier3, user4 selects subcarrier3, and user3 selects subcarrier1. Since subcarrier3 gets its paired users (user1 and user4), it becomes unavailable for the selection by user5, which should use subcarrier2. Finally, user2 is lucky since it can be assigned on subcarrier1.
The subcarrier-user assignment matrix (

5 Validation and Simulation Results
Simulation results validate the proposed algorithm, and its performance is assessed based on a comparative study with the “conventional-user-pairing”, “random pairing”, and “orthogonal-multiple-access system” (OMA). A multipath frequency-selective-fading channel with a Rayleigh distributed fading parameter is considered for the downlink NOMA system.
For simplicity purposes, the total transmit power is uniformly distributed among subcarriers and a fixed power allocation is used to distribute the subcarrier power between its paired users, such that
• The Spectral efficiency (SE). It is assessed by (11), [24]:
• Jain’s fairness index. It is used to measure the fairness in distributing the system resources among the users. The fairness index (FI) is measured with respect to users’ data rate [27–28] as follows:
• The outage probability. It measures the likelihood that the achieved data rate of the user lower than a specific target data rate R0.
The proposed LOUFSA algorithm’s performance is evaluated versus “the signal-to-noise-ratio” (SNR) per subcarrier and the number of users. The first part of the simulation results is presented versus SNR for
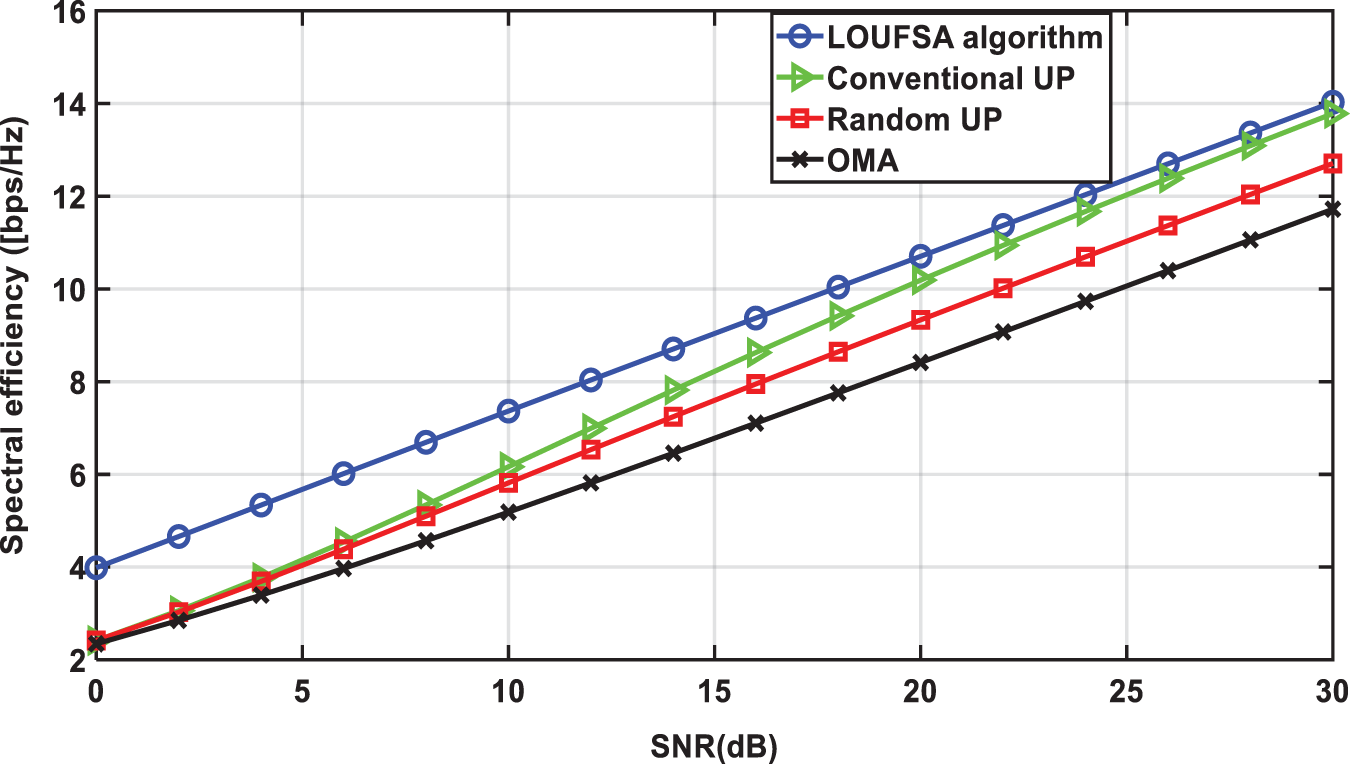
Figure 2: The spectral efficiency (SE) versus SNR
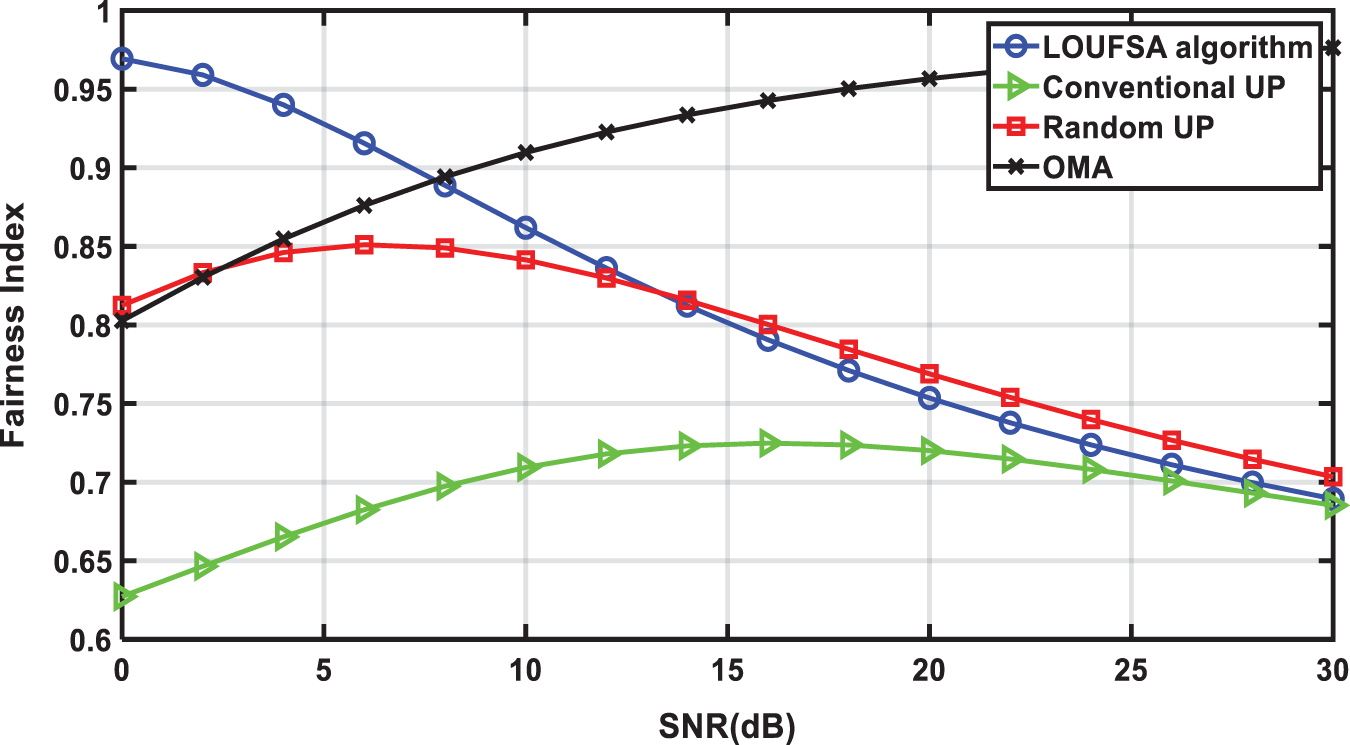
Figure 3: The fairness index versus SNR
The outage probability is presented for the whole users and the weak users as the latter suffer higher outage probability than strong users. Figs. 4 and 5 present the outage probability for the whole users at R0 equals 1 bps/Hz and 2 bps/Hz respectively. The figures show that the LOUFSA algorithm provides the noticeably lowest outage probability. As R0 increases, the achieved outage probability becomes more significantly superior than the other NOMA algorithms and OMA, as shown in Fig. 5. The outage probability for the weak users at R0 equals 1 bps/Hz, and 2 bps/Hz, respectively, as presented in Figs. 6 and 7. The figures show that the LOUFSA algorithm can provide a considerably lower outage probability for weak users, especially as R0 increases, as shown in Fig. 7.
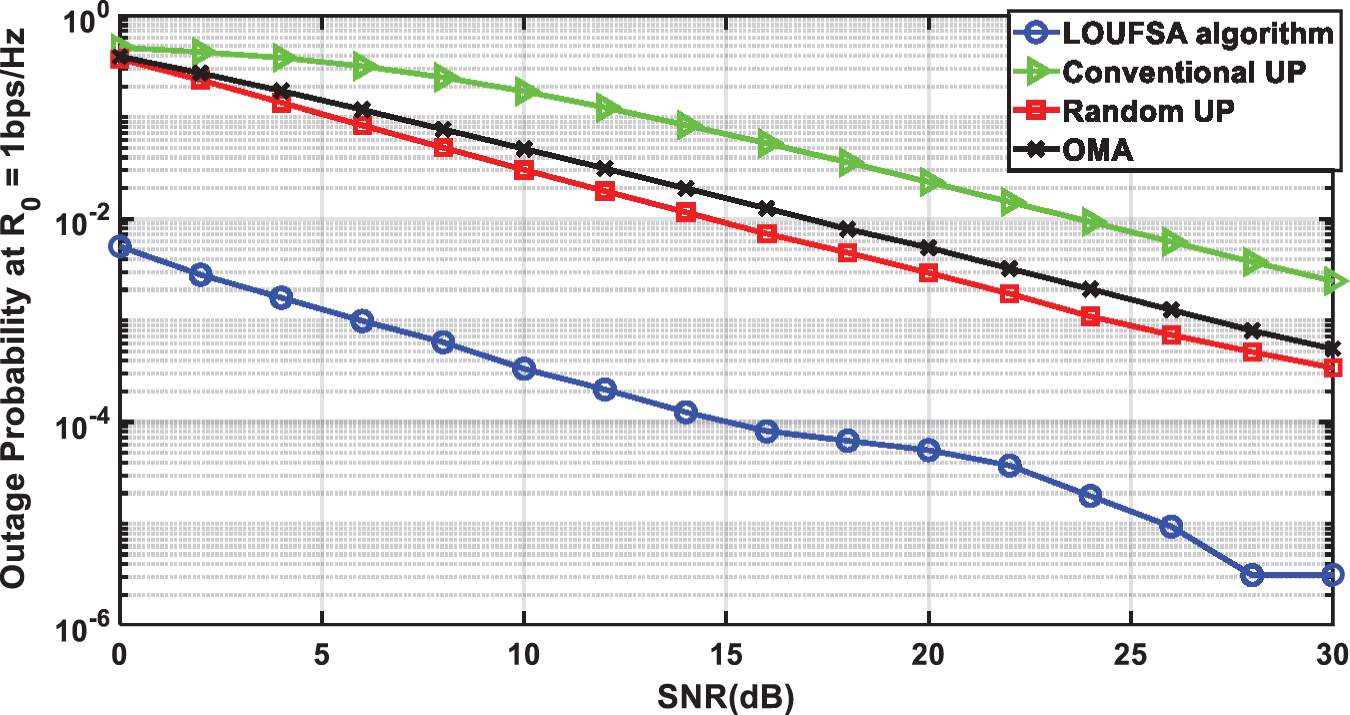
Figure 4: The outage probability versus SNR at R0 = 1 bps/Hz
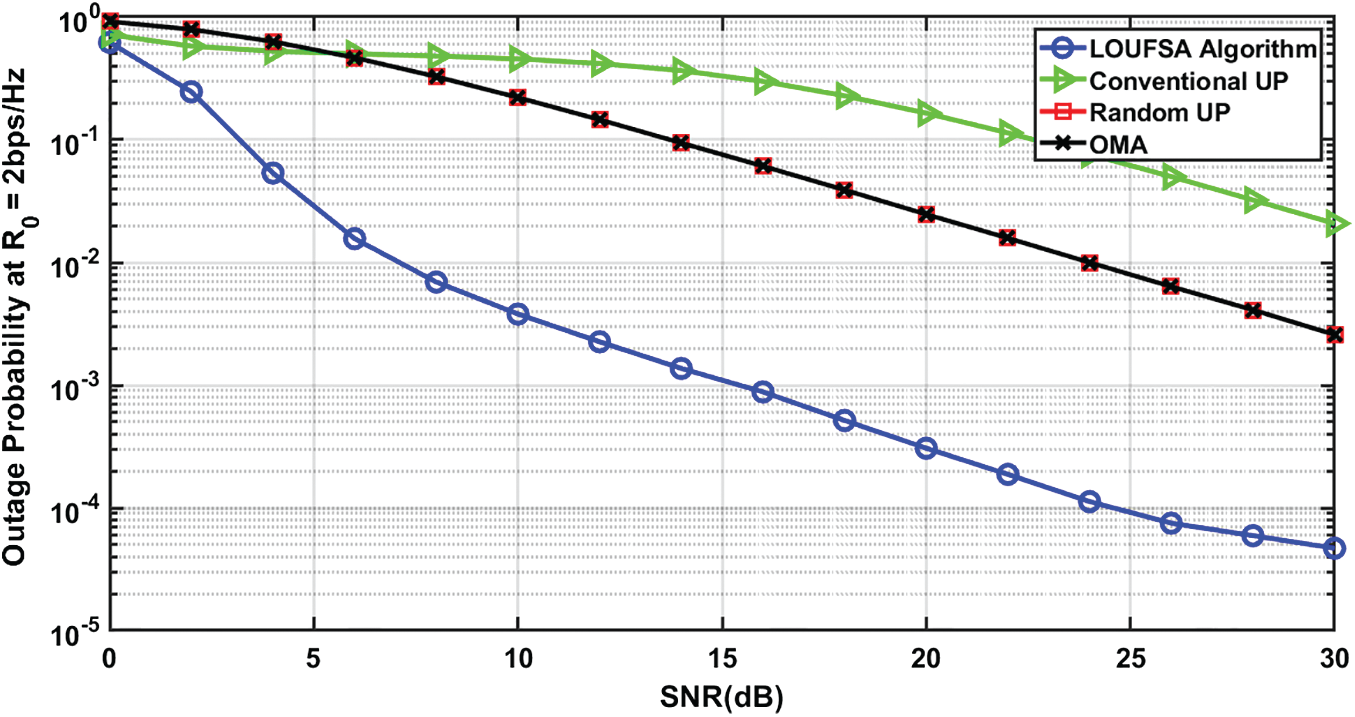
Figure 5: The outage probability versus SNR at R0 = 2 bps/Hz
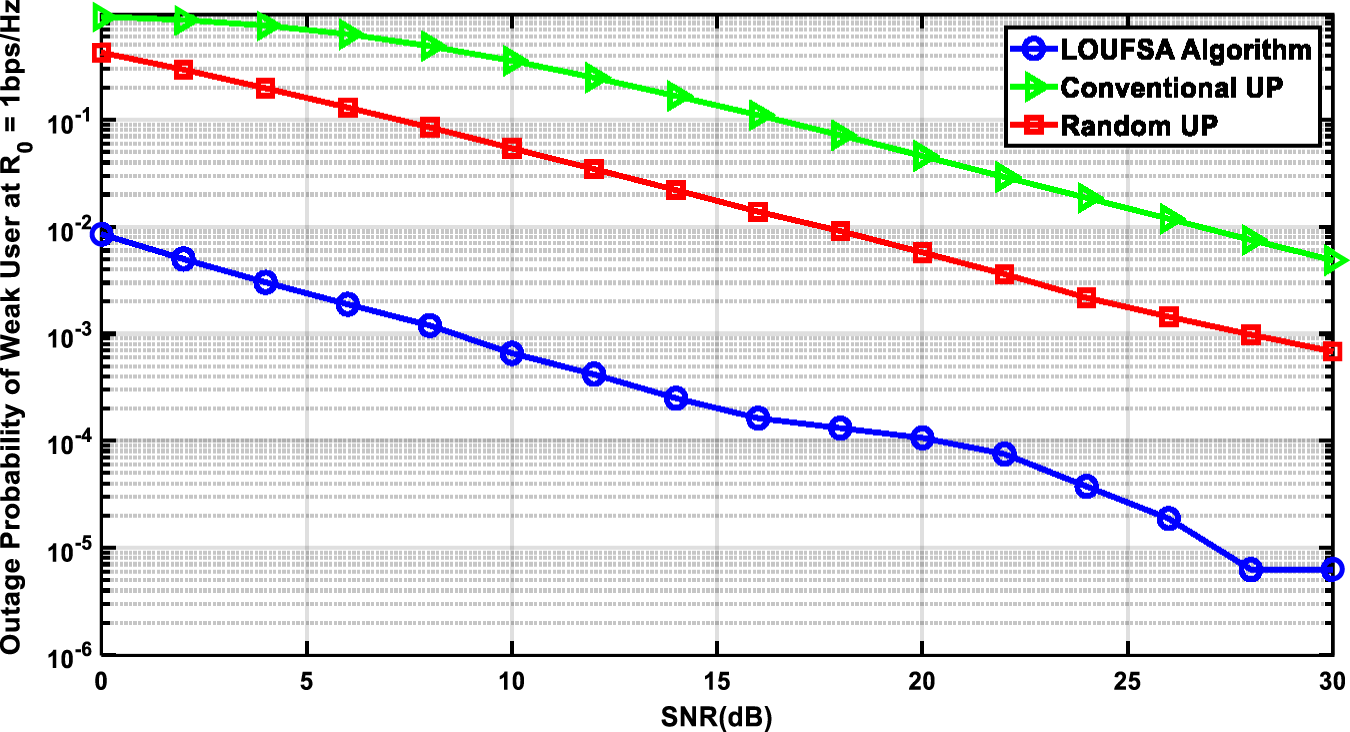
Figure 6: The outage probability of Weak Users versus SNR at R0 = 1 bps/Hz
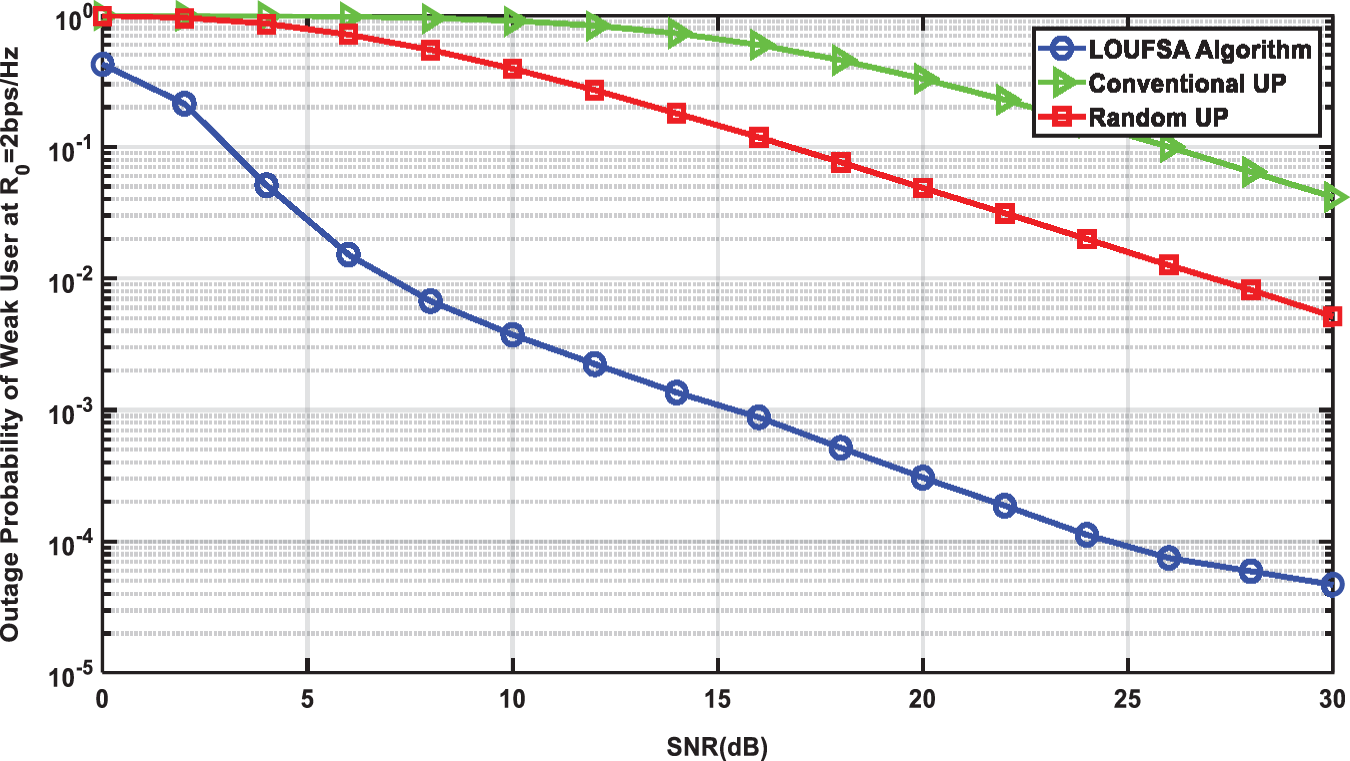
Figure 7: The outage probability of Weak Users versus SNR at R0 = 2 bps/Hz
Fig. 8 shows the achieved data rate of weak users versus SNR. It verifies that the LOUFSA algorithm guarantees the highest data rate for weak users over all SNR values. Also, it shows that the achieved data rate by the LOUFSA algorithm rapidly converges to the maximum value as SNR increases on the contrary of the other NOMA algorithms.
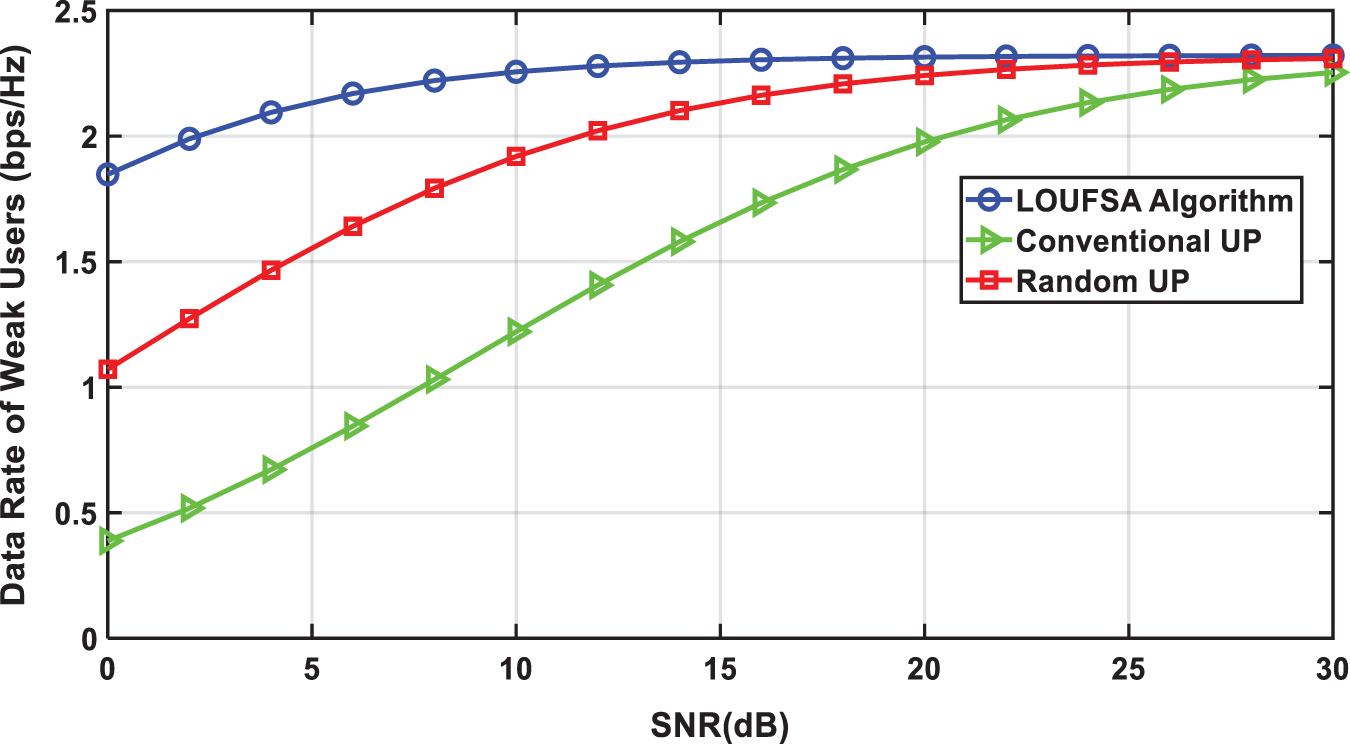
Figure 8: The data rate of weak users versus SNR
The second part of the simulation is to evaluate the proposed algorithm versus the number of users at SNR = 10 dB. Fig. 9 presents the SE and shows that the LOUFSA algorithm attains the highest SE and its achieved SE increases as the number of users increases. On the contrary, as the number of users becomes higher than 16 users, the achieved SE by conventional UP decreases while the SE of random UP and OMA remains constant. Fig. 10 shows that the fairness performance of both LOUFSA algorithm, and random UP algorithm is stable as the number of users increases while that of the conventional UP algorithm deteriorates as the number of users increases.
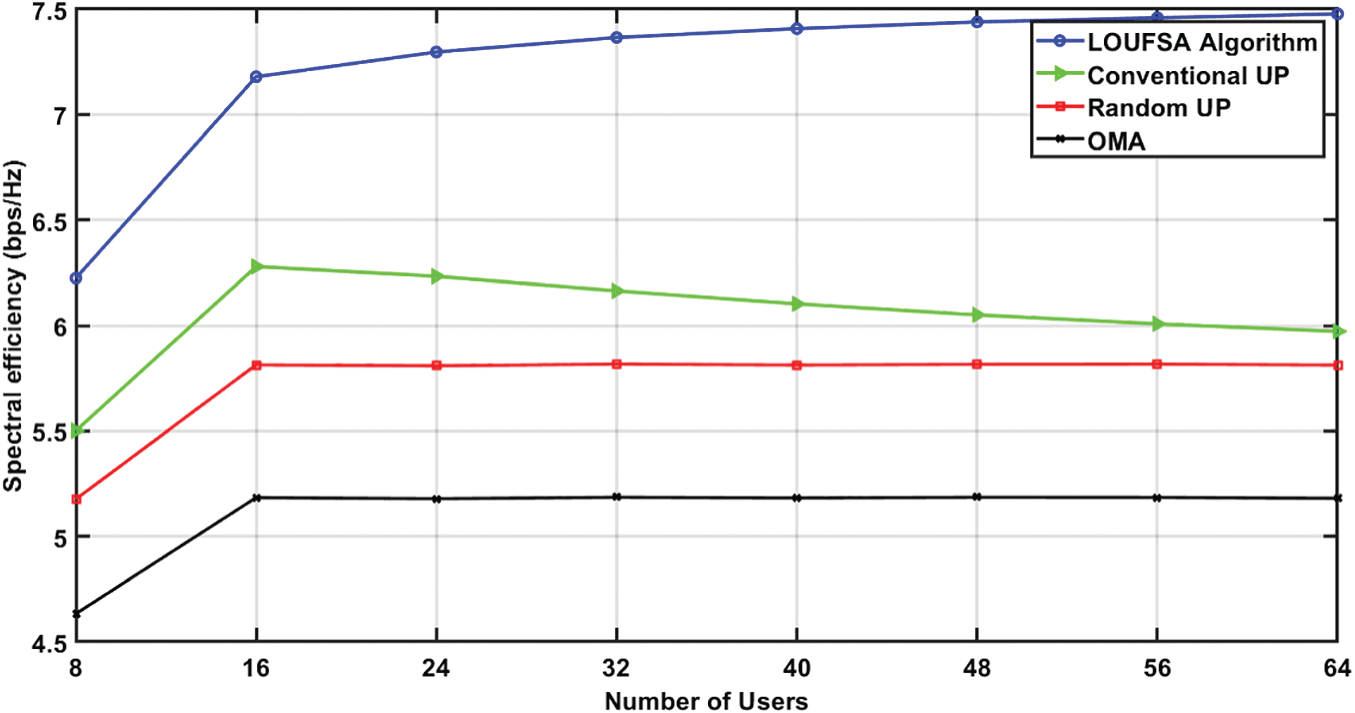
Figure 9: The spectral efficiency versus the number of users at SNR = 10 dB

Figure 10: The Fairness Index versus the number of users at SNR = 10 dB
The outage probability for the whole users at R0 equals 1 bps/Hz, and 2 bps/Hz, respectively. Figs. 11 and 12 demonstrate that only the LOUFSA algorithm can efficiently reduce the outage probability as the number of users increases in addition to its significant superior performance, especially as R0 increases. For the weak users, the outage probability at R0 equals 1 bps/Hz, and 2 bps/Hz, respectively is presented in Figs. 13 and 14. The figures show that the LOUFSA algorithm can significantly improve the outage probability as the number of users increases and its outage probability significantly outperforms the other algorithms as R0 increases. Finally, Fig. 15 shows that the LOUFSA algorithm achieves the highest data rate for weak users, and the achieved data rate by both the LOUFSA algorithm and random UP algorithm is constant as the number of users increases, while that of the conventional UP algorithm deteriorates as the number of users increases.
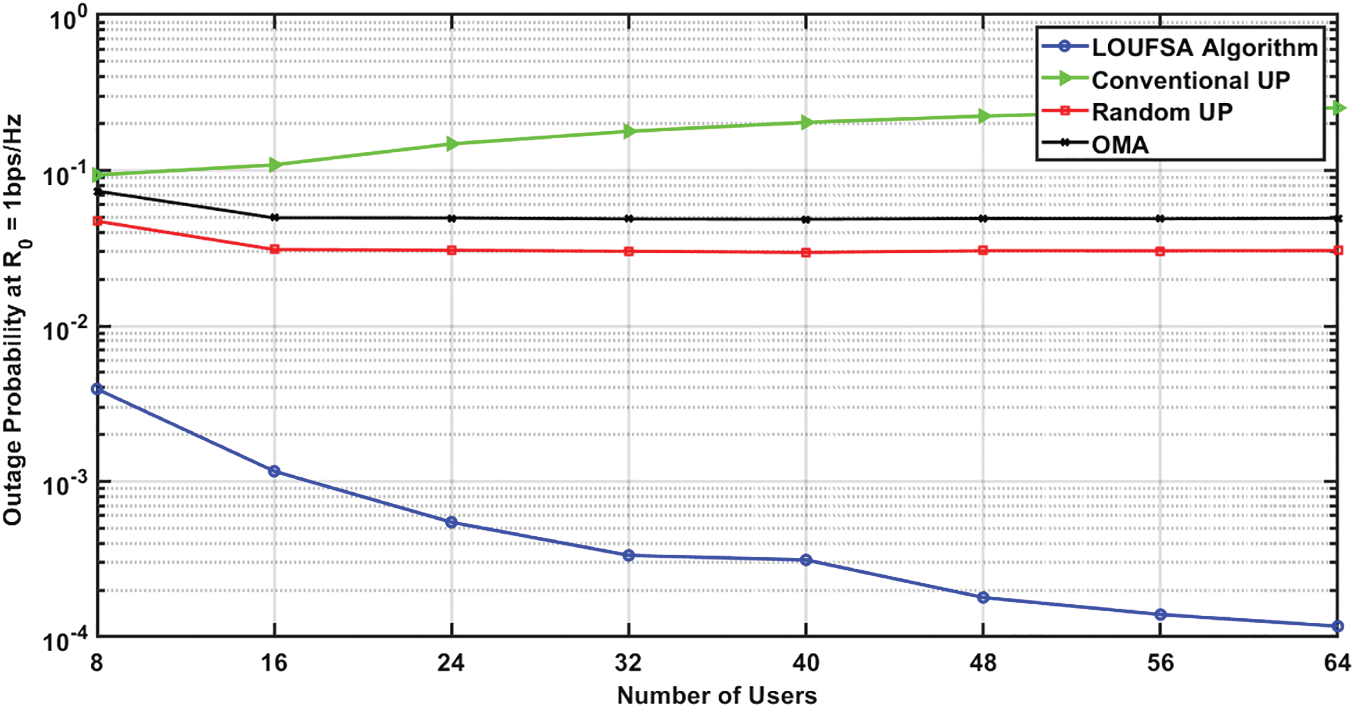
Figure 11: The outage probability at R0 = 1 bps/Hz versus the number of users at SNR = 10 dB

Figure 12: The outage probability at R0 = 2 bps/Hz versus the number of users at SNR = 10 dB
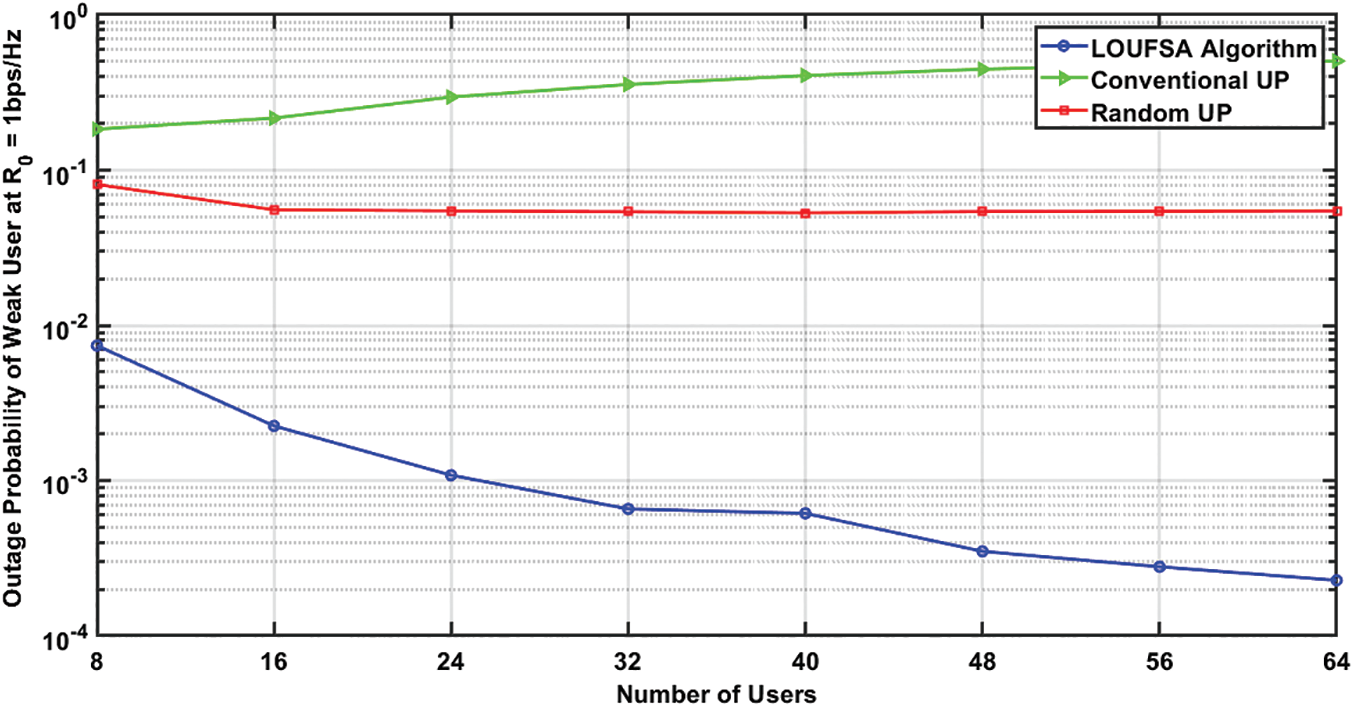
Figure 13: The outage probability of weak users at R0 = 1 bps/Hz versus the number of users at SNR = 10 dB

Figure 14: The outage probability of weak users at R0 = 2 bps/Hz versus the number of users at SNR = 10 dB
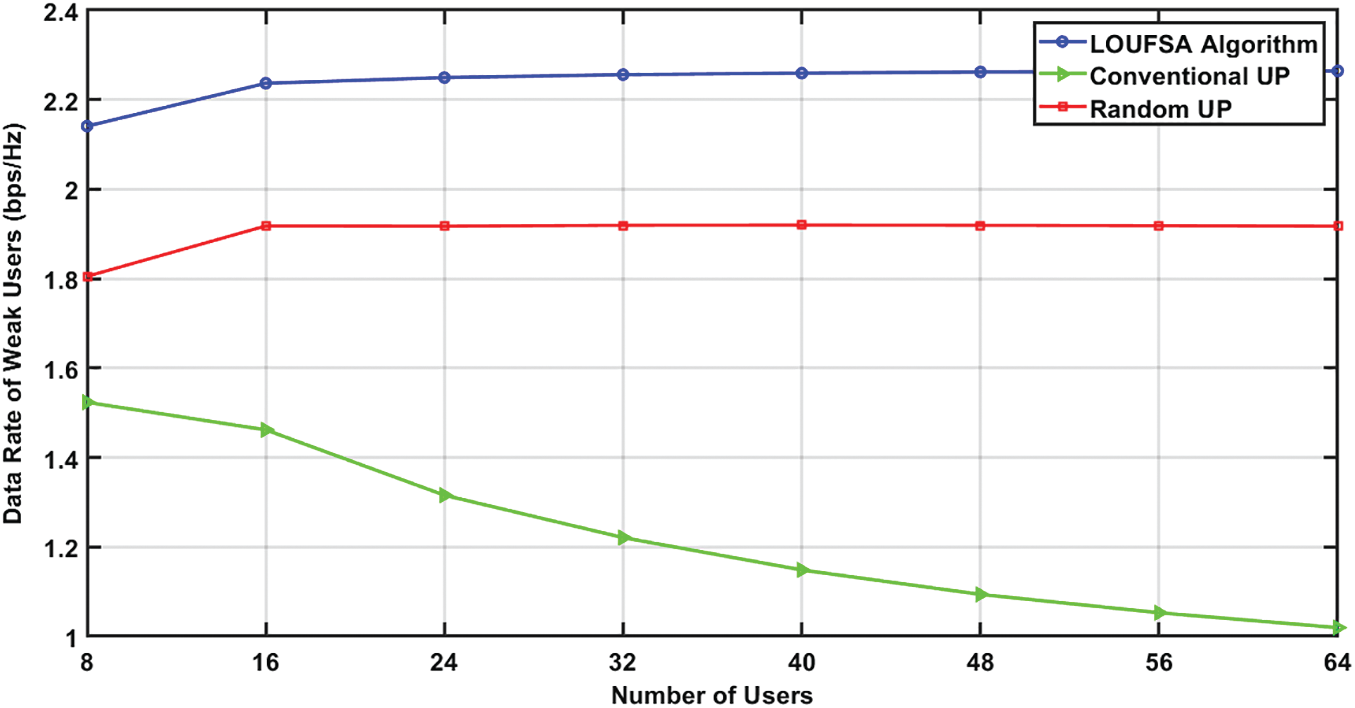
Figure 15: The Data rate of Weak Users versus the number of users at SNR = 10 dB
A new low complexity subcarrier allocation algorithm based on the lowest-opportunities user first precept is proposed to optimize spectral efficiency (SE), outage probability, and fairness among users. The new proposed lowest-opportunities user first principle is based on counting the number of available subcarriers with channel gains higher than a particular threshold value for each user. Simulation results demonstrate that the proposed algorithm considerably outperforms OMA, and traditional NOMA algorithms for all evaluated performance metrics such as spectral efficiency, fairness index, user data rate, and outage probability. The superiority of achieved outage probability by the proposed algorithm improves as the target data rate increases, especially for weak users. Besides, the proposed algorithm’s performance metrics improve as the number of users in the system increases contrary to traditional NOMA algorithms.
Acknowledgement: The authors would like to acknowledge the support received from Taif University Researchers Supporting Project Number (TURSP-2020/147), Taif University, Taif, Saudi Arabia.
Funding Statement: This research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/147), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
1. S. M. R. Islam, N. Avazov, O. A. Dobre and K. Kwak, “Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and Challenges,” IEEE Communications Surveys & Tutorials, vol. 19, no. 2, pp. 721–742, 2nd quarter 2017. [Google Scholar]
2. S. M. R. Islam, M. Zeng, O. A. Dobre and K. Kwak, “Non-orthogonal multiple access (NOMAHow it meets 5G and beyond,” Wiley 5G Ref, pp. 1–28, Dec. 2019. [Google Scholar]
3. L. Dai, B. Wang, Z. Ding, Z. Wang, S. Chen et al., “A survey of non-orthogonal multiple access for 5G,” IEEE Communications Surveys & Tutorials, vol. 20, no. 3, pp. 2294–2323, 3rd quarter 2018. [Google Scholar]
4. M. Aldababsa, M. Toka, S. Gokceli, G. K. Kurt and O. Kucur, “A tutorial on non-orthogonal multiple access for 5G and beyond,” Wireless Communications and Mobile Computing, vol. 2018, pp. 1–24, Jun. 2018. [Google Scholar]
5. L. Dai, B. Wang, Y. Yuan, S. Han, I. Chih-lin et al., “Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends,” IEEE Communications Magazine, vol. 53, no. 9, pp. 74–81, Sep. 2015. [Google Scholar]
6. Y. Saito, Y. Kishiyama, A. Benjebbour, T. Nakamura, A. Li et al., “Non-Orthogonal Multiple Access (NOMA) for future radio access,” in Proc. 2013 IEEE 77th Vehicular Technology Conference (VTC SpringDresden, Jun. 2013. [Google Scholar]
7. K. Higuchi and A. Benjebbour, “Non-orthogonal multiple access (NOMA) with successive interference cancellation for future radio access,” IEICE Transactions on Communications, vol. E98B, no. 3, pp. 403–414, Mar. 2015. [Google Scholar]
8. Z. Wei, J. Yuan, D. W. K. Ng, M. Elkashlan and Z. Ding, “A survey of downlink non-orthogonal multiple access for 5G wireless communication networks,” ZTE Communications, vol. 14, no. 4, pp. 17–26, Oct. 2016. [Google Scholar]
9. Z. Ding, X. Lei, G. K. Karagiannidis, R. Schober, J. Yuan et al., “A Survey on non-orthogonal multiple access for 5G networks: research challenges and future trends,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 10, pp. 2181–2195, Oct. 2017. [Google Scholar]
10. Z. Ding, P. Fan and H. V. Poor, “User pairing in non-orthogonal multiple access downlink transmissions,” in Proc. 2015 IEEE Global Communications Conference (GLOBECOMSan Diego, CA, pp. 1–5, 2015. [Google Scholar]
11. Z. Ding, P. Fan and H. V. Poor, “Impact of user pairing on 5G nonorthogonal multiple-access downlink transmissions,” IEEE Transactions on Vehicular Technology, vol. 65, no. 8, pp. 6010–6023, Aug. 2016. [Google Scholar]
12. M. B. Shahab, M. Irfan, M. F. Kader and S. Young Shin, “User pairing schemes for capacity maximization in non-orthogonal multiple access systems,” Wireless Communications and Mobile Computing, vol. 16, no. 17, pp. 2884–2894, Sep. 2016. [Google Scholar]
13. M. B. Shahab, M. F. Kader and S. Y. Shin, “A virtual user pairing scheme to optimally utilize the spectrum of unpaired users in non-orthogonal multiple access,” IEEE Signal Processing Letters, vol. 23, no. 12, pp. 1766–1770, Dec. 2016. [Google Scholar]
14. S. M. R. Islam, M. Zeng, O. A. Dobre and K. Kwak, “Resource allocation for downlink noma systems: key techniques and open issues,” IEEE Wireless Communications, vol. 25, no. 2, pp. 40–47, Apr. 2018. [Google Scholar]
15. L. Zhu, J. Zhang, Z. Xiao, X. Cao and D. O. Wu, “Optimal user pairing for downlink non-orthogonal multiple access (NOMA),” IEEE Wireless Communications Letters, vol. 8, no. 2, pp. 328–331, Apr. 2019. [Google Scholar]
16. O. A. Saraereh, A. Alsaraira, I. Khan and P. Uthansakul, “An efficient resource allocation algorithm for OFDM-based NOMA in 5G systems,” Electronics, vol. 8, no. 12, pp. p.–1399, Nov. 2019. [Google Scholar]
17. J. Muhammed, Z. Ma, P. D. Diamantoulakis, L. Li and G. K. Karagiannidis, “Energy-efficient resource allocation in multicarrier NOMA systems with fairness,” IEEE Transactions on Communications, vol. 67, no. 12, pp. 8639–8654, Dec. 2019. [Google Scholar]
18. Di, S. Bayat, L. Song and Y. Li, “Radio resource allocation for downlink non-orthogonal multiple access (NOMA) networks using matching theory,” in Proc. 2015 IEEE Global Communications Conference (GLOBECOMSan Diego, CA, pp. 1–6, 2015. [Google Scholar]
19. Di, L. Song and Y. Li, “Sub-channel assignment, power allocation, and user scheduling for non-orthogonal multiple access networks,” IEEE Transactions on Wireless Communications, vol. 15, no. 11, pp. 7686–7698, Nov. 2016. [Google Scholar]
20. F. Fang, H. Zhang, J. Cheng and V. C. M. Leung, “Energy-efficient resource allocation for downlink non-orthogonal multiple access network,” IEEE Transactions on Communications, vol. 64, no. 9, pp. 3722–3732, Sept. 2016. [Google Scholar]
21. W. Liang, Z. Ding, Y. Li and L. Song, “User pairing for downlink non-orthogonal multiple access networks using matching algorithm,” IEEE Transactions on Communications, vol. 65, no. 12, pp. 5319–5332, Dec. 2017. [Google Scholar]
22. J. Zhu, J. Wang, Y. Huang, S. He, X. You et al., “On optimal power allocation for downlink non-orthogonal multiple access systems,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 12, pp. 2744–2757, Dec. 2017. [Google Scholar]
23. D. Pliatsios and P. Sarigiannidis, “Resource allocation combining heuristic matching and particle swarm optimization approaches: the case of downlink non-orthogonal multiple access,” Information-an International Interdisciplinary Journal, vol. 10, no. 11, pp. 336, Oct. 2019. [Google Scholar]
24. M.-R. Hojeij, J. Farah, C. A. Nour and C. Douillard, “New optimal and suboptimal resource allocation techniques for downlink non-orthogonal multiple access,” Wireless Personal Communications, vol. 87, no. 3, pp. 837–867, 2016. [Google Scholar]
25. Y. Fu, L. Salaün, C. W. Sung and C. S. Chen, “Subcarrier and power allocation for the downlink of multicarrier NOMA systems,” IEEE Transactions on Vehicular Technology, vol. 67, no. 12, pp. 11833–11847, Dec. 2018. [Google Scholar]
26. Y. Fu, M. Zhang, L. Salaün, C. W. Sung and C. S. Chen, “Zero-forcing oriented power minimization for multi-cell MISO-NOMA systems: a joint user grouping, beamforming, and power control perspective,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 8, pp. 1925–1940, Aug. 2020. [Google Scholar]
27. R. Jain, D. Chiu and W. Hawe, “A quantitative measure of fairness and discrimination for resource allocation in shared computer systems,” Eastern Research Laboratory, Digital Equipment Corporation, Hudson, Mass, USA, 1998. [Google Scholar]
28. M. Elsherief, M. Elwekeil and M. Abd-Elnaby, “Resource and power allocation for achieving rate fairness in D2D communications overlaying cellular networks,” Wireless Networks, vol. 25, pp. 4049–4058, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |