Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.019486
Article

Cryptanalysis of an Online/Offline Certificateless Signature Scheme for Internet of Health Things

Saddam Hussain1, Syed Sajid Ullah2,*, Mohammad Shorfuzzaman3, Mueen Uddin4 and Mohammed Kaosar5

1Department of Information Technology, Hazara University, Mansehra, 21120, KPK, Pakistan
2Department of Electrical and Computer Engineering, Villanova University, PA, USA
3Department of Computer Science, College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
4Digital Science, Faculty of Science, Universiti Brunei Darussalam, Jln Tungku link, Gadong, BE1410, Brunei Darussalam
5Discipline of Information Technology, Media and Communications, College of Arts, Business, Law and Social Sciences (ABLSS), Murdoch University, 90 South Street, Murdoch, WA6150, Australia
*Corresponding Author: Syed Sajid Ullah. Email: sullah1@villanova.edu
Received: 15 April 2021; Accepted: 18 May 2021

Abstract: Recently, Khan et al. [An online-offline certificateless signature scheme for internet of health things,” Journal of Healthcare Engineering, vol. 2020] presented a new certificateless offline/online signature scheme for Internet of Health Things (IoHT) to fulfill the authenticity requirements of the resource-constrained environment of (IoHT) devices. The authors claimed that the newly proposed scheme is formally secured against Type-I adversary under the Random Oracle Model (ROM). Unfortunately, their scheme is insecure against adaptive chosen message attacks. It is demonstrated that an adversary can forge a valid signature on a message by replacing the public key. Furthermore, we performed a comparative analysis of the selective parameters including computation time, communication overhead, security, and formal proof by employing Evaluation based on Distance from Average Solution (EDAS). The analysis shows that the designed scheme of Khan et al. doesn’t have any sort of advantage over the previous schemes. Though, the authors utilized a lightweight hyperelliptic curve cryptosystem with a smaller key size of 80-bits. Finally, we give some suggestions on the construction of a concrete security scheme under ROM.

Keywords: Cryptanalysis; Internet of health things; online-offline signature

1  Introduction

The concept of an online/offline signature was first proposed in 1990 by Evan et al. [1]. The main idea is to divide the signature generation algorithm into two phases (i.e., online and offline phase). The signing algorithm performs the offline step to manage most of the heavy computations and stores without knowing the signed message. Once the signed message arrives, the signature algorithm runs the online step very fast and only light computations are required. Online offline signatures are more useful on some storage limited devices such as smart cards, wireless sensors, and RFID tags, as the offline step can be done with a background computation during the device manufacturing process or whenever the device power is connected. There are numerous offline/online signature schemes [2–5], designed for different applications.

In 2008, Yu and Tate [3], presents three effective online/offline signature approaches. The authors claim that the given is formally secure in the standard model under the assumptions of RSA. Unfortunately, the given scheme is affected by high-cost consumptions i.e., computation time and communication overhead. Besides, Ma et al. [4], found that the first scheme of Yu and Tate [3], is not secure.

In 2010, Wu et al. [5], suggest an identity-based online/offline signature scheme under ROM using the hardness of bilinear pairing. Unfortunately, the given scheme is affected by high-cost consumptions due to the use of heavy pairing operation which makes it inefficient.

In 2020, Addobea et al. [6], suggest a certificateless online/offline signature scheme for mobile health devices under ROM using the hardness of bilinear pairing. Nonetheless, the given scheme also suffers from high-cost consumptions due to the use of heavy pairing operation that shows the inefficiency of the designed scheme for the resource-constrained devices of mobile health.

1.1 Motivation and Contribution

To minimize the cost consumptions, Khan et al. [7], recently presented a new certificateless online/offline signature scheme for IoHT under the hardness of hyperelliptic curve discrete logarithm problem. The authors also claimed that the given scheme was proven secure “against adaptive chosen-message” in the ROM. In this paper, we analyzed the formal security of Khan et al.’s scheme and proving its insecurity against “adaptive chosen-message and identity attacks”. Furthermore, we suggest some comments on the formal security issues of the Khan et al. [7] scheme that should be considered while proposing a concrete security scheme. The following are some of our contributions.

•   First, we proved the insecurity of Khan et al. [7] scheme against adaptive chosen message attacks.

•   Then, we suggest a concrete construction of the given scheme.

•   We performed a comparative analysis of the selective parameters including computation time, communication overhead, security, and formal proof based on Evaluation based on Distance from Average Solution (EDAS). The analysis shows that the designed scheme of Khan et al. doesn’t have any sort of advantage over the previous schemes. For comparative analysis, we choose the same environment (hardware and software) and the same online-offline scheme with which the authors compared their scheme.

1.2 Organization of Paper

The rest of the paper is organized as; Section 2 presents the definition for HDLP, Section 3 reviews the construction of the Khan et al. scheme. Section 4, shows the insecurity and Section 5 presents formal correction. Section 6 shows the cost efficiency, while Section concludes our research work.

2  Definition 1: Hyperelliptic Curve Discrete Logarithm Problem (HDLP) Assumptions

•   Let ⍬, ℇ { 1,2,3,…n−1} and R=⍬.D , then finding ⍬ and R is known as HDLP.

3  Review of Khan et al. Scheme

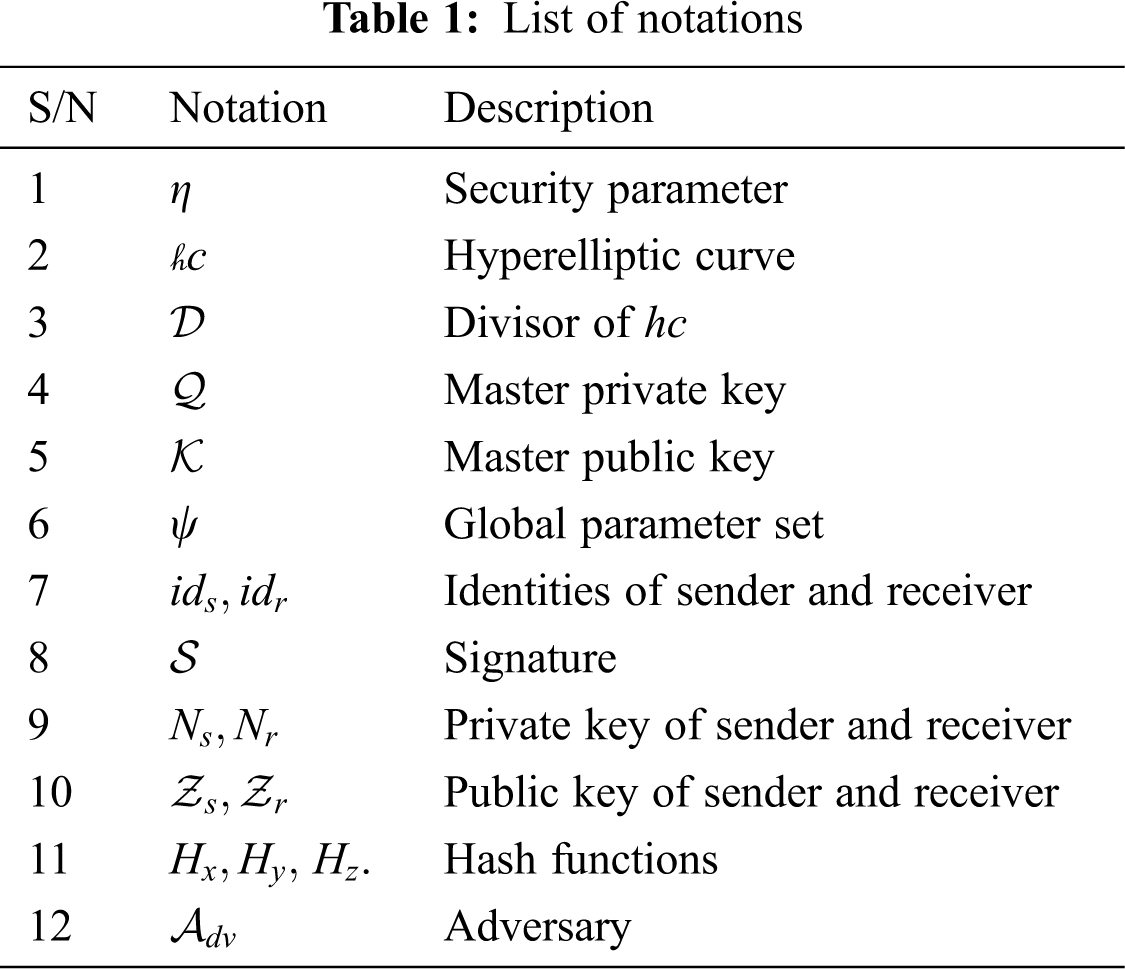
Here we present the constructions of the Khan et al. [7] scheme. Additionally, the notations used in the constructions are listed in Tab. 1.

Setup:

•   Given the security parameter η , the KGC select,

•   A hyperelliptic curve ( hc ) with field f ( n ), where the size of n≽280

•   Devisor ( D ) from hc

•   Hash functions Hx,Hy and Hz .

•   It also picks Q ∈ {1,2,3,……n−1} as a master key and computes the public key as K=Q.D .

•   Finally, produces a public parameter set ψ = {K,Hx,Hy,Hz,D,hc} n≽280 .

Set Secret value:

The participating entities with identity idi picks li ∈ {1,2,3,……n−1} as a secret value and computes Vi = li . D as a public key.

Set Partial private key:

For an entity with identities idi the KGC picks ϑi ∈ {1,2,3,……n−1} , computes μi=ϑi.D , calculates Wi=ϑi+QHx(idi,Vi,μi ), and send Γi=(Wi,μi) to the entities with idi using a secure channel.

Set Private key:

The entities, with identity idi sets Ni=(Γi,li) of its private key.

Set Public key:

The entities, with identity idi sets Zi=(Vi,μi) of its public key.

Signature Generation:

The computations of the sender are divided into two steps;

Offline Step:

Executed on the server equipped with high resources.

•   It picks d ∈ {1,2,3,……n−1} and computes t=d.Vs

•   Compute P=Hy(ids,μs,m,t) and X=Hz(ids,Vs,m,t)

•   Gives ( d , t , P , X ) to the sensor nodes

Online phase:

•   Compute S=ls.d−(ls.X+P.Ws)

•   Set ϕ=(t,S) as a signature and send it to the receiver

Verification:

Upon reception ϕ , the receiver can verify S as follows

•   Compute P=Hy(ids,μs,m,t) and X=Hz(ids,Vs,m,t)

•   checks if S.D=t.XVs−P(μs+Hx(ids,Vs,μs)K) hold.

4  Analysis of Khan et al. Scheme

An Adv can forge the valid signature on a message ( m ) by replacing a public key ( K ).

•   Subsequently after obtaining the ( ids,μs ), the Adv randomly choose WAdv , lAdv ∈ {1,2,3,……n−1} , computes VAdv=lAdvD , Hx(ids,μs,VAdv)K′=WAdvD−μs ) ,Hx−1 and replace the master public key ( K ) with K′ and idsVs with VAdv so that WAdvD=μs+Hx(ids,μs,VAdv)K′ holds.

•    Adv set ( ΓAdv,lAdv ) as their full private key of signer where ΓAdv=(WAdv,μs) , and sets ( VAdv,μs ) as their full public key.

•   For signing a message ( m ), the Adv select choose dAdv ∈ {1,2,3,……n−1} , compute tAdv=dAdvVAdv , PAdv=Hy(ids,μs,m,tAdv) and XAdv=Hz(ids,m,VAdv,tAdv) .

Finally, Adv computes SAdv=lAdvdAdv−(XAdvlAdv+PAdvWAdv) and generate the signature ( SAdv,tAdv ) on the given message m.

Because tAdv=dAdvVAdv=dAdvlAdv PAdv=Hy(ids,μs,m,tAdv) and XAdv=Hz(ids,m,VAdv,tAdv)

Thus, SAdvD=tAdv−XAdvVAdv−PAdv(μs+Hx(ids,VAdv,μs)K′) .

Therefore, we argue that the produced signature can pass through the verification successfully and the A can generate a signature.

5  Proof and Correction

While designing a signature protocol as designed by Khan et al. [7], the public key K needs to be hashed to eliminate the prospect of this type of forgery. The correction with formal proof is given below.

•   While executing partial private key extraction in Khan et al. [7], if the K is hashed in Hx , the private part Wi is computed as Wi=ϑi+QHx(idi,Vi,μi,K ), so a user can authenticate their tuple of the partial private key ( Wi,μi) , if Adv tries to forge the signature as described in Khan et al. scheme, it then randomly pick WAdv , lAdv ∈ {1,2,3,…n−1} , computes lAdvD,Hx(idi,μi,Vi,K),K′=(WAdvD−μs),Hx−1 and replace the master public key K with K′ and idsVs with VAdv .

•   On verification, one can prove the equation Wi=ϑi+QHx(idi,Vi,μi,K ) WAdvD = Vs + Hx(ids,μs,VAdv,K′),K′ , which cannot be held. Hence, we can claim that forgery is not possible.

6  Efficiency

In this section, we evaluate the performance of our cryptanalysis in comparison with Khan et al. [7]. For our comparative analysis, we adopt the running time of costly mathematical operations from [8] and [9]. Here, we only consider the operations that are used in the particular scheme of Khan et al. [6]. According to [8] and [9], the cost of a single pairing-based point multiplication ( PBML ) is 4.31 milliseconds, the cost of bilinear pairing ( BPairing ) is 14.90 milliseconds, the cost of exponentiation ( EPO ) is 1.25 milliseconds and the cost of a single HCDM is approximately 0.48 milliseconds [8,9]. The total computation cost of signing in the Khan et al. [7] scheme is 4 HCDM and the total computation cost of verification is 3 HCDM.

Note: Here we consider the same schemes with which Khan et al. [7] perform the comparative analysis in terms of computation time and communication overhead. Tab. 2, shows cost analysis of the selected schemes.

6.1 Computation Time

•   According to Khan et al. [7] the computation time of Yu and Tate [3], is; 1EPO+3PBML in the signing phase while 3EPO+4PBML in the Verifying phase.

•   The computation time of Yu and Tate [3] scheme 2 is; 2EPO+3PBML in the signing phase while 3EPO+3PBML in the Verifying phase.

•   The computation time of Wu et al. [5] scheme is; 3PBML in the signing phase while 2BPairing+2PBML in the Verifying phase.

•   The computation time of Addobea et al. [6] scheme is; 3PBML in the signing phase while 3BPairing+4PBML in the Verifying phase.

•   Similarly, the computation time of Khan et al. [7] scheme is; 4 HCDM in the signing phase while 3 HCDM in the Verifying phase.

6.2 Communication Overhead

•   According to Khan et al. [7], the communication overhead of Yu and Tate Scheme-I [3] is; 3|G|+|m| .

•   The communication overhead of Yu and Tate Scheme-II [3] scheme 2 is; 3|G|+|m| .

•   The communication overhead of Wu et al. [5] scheme is; 3|G|+|m| .

•   The communication overhead of Addobea et al. [6] scheme is; 3|G|+|m| .

•   Similarly, the communication overhead of Khan et al. [7] scheme is; 2|n|+|m|.

6.3 Comparison With Our Cryptanalysis

•   The total computation cost of our cryptanalysis is; 7(HCDM)=7(0.48)=3.36ms

•   The total computation cost of the Khan et al. [7] scheme is; 7(HCDM)=7(0.48)=3.36ms

Findings

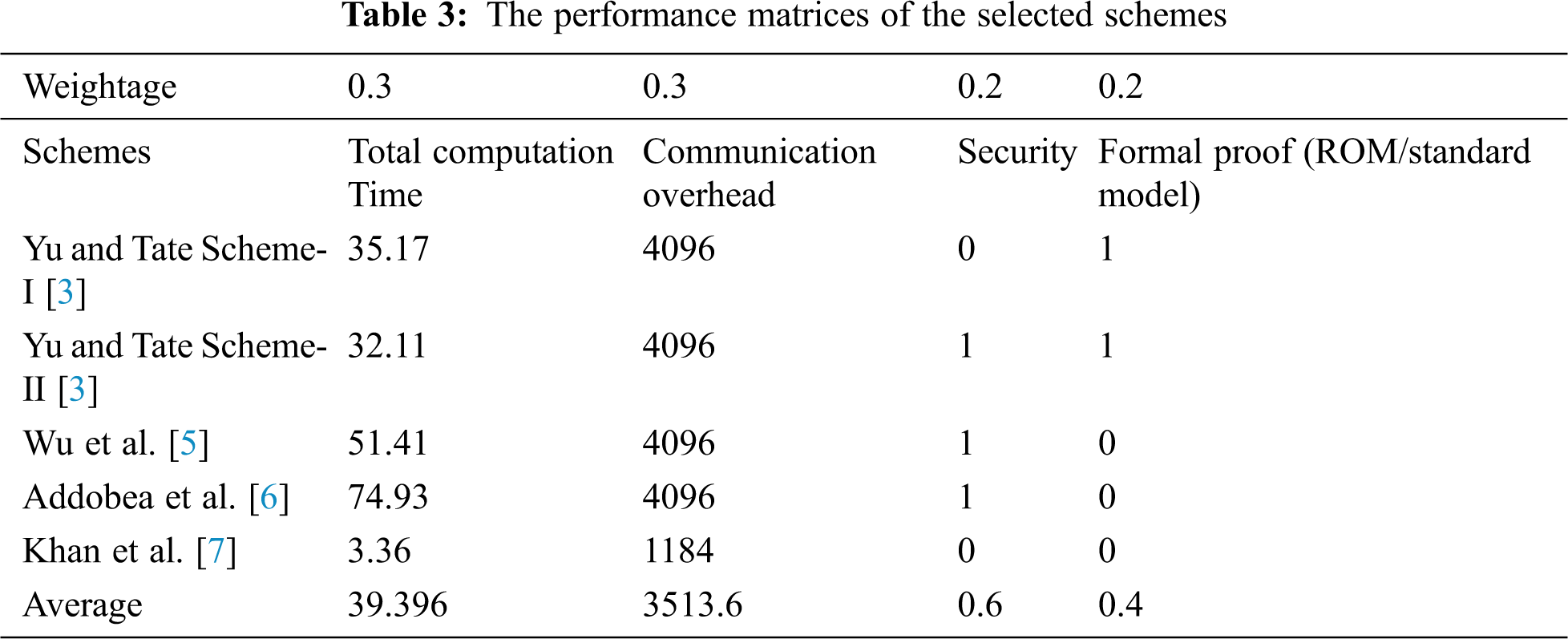
As we have seen from the aforementioned discussion, Khan et al. [7], perform an analysis of the respective scheme based on two parameters, i.e., computation time and communication overhead. However, these two parameters do not give us a clear advantage of Khan et al. [7], over the others. therefore, we consider four parameters for the performance analysis such as computation time, communication overhead, security, and formal proof respectively. Furthermore, we adopt the technique of EDAS for the performance analysis of the chosen parameters in Section 6.4 below.

6.4 Evaluation based on Distance from Average Solution (EDAS)

In this section, we adopt the multi-criteria decision-making method also known as Evaluation based on Distance from Average Solution (EDAS) [10–13]. The method is considered very useful when we have some conflicting criteria [14,15]. Different performance parameters are identified in the literature are considered for our comparative analysis including computation time, communications overhead, security, and formal proof as shown in Tab. 3. On the other hand, for evaluation, the cross EDAS method is used to extract the cross effective values among the selected schemes based on the chosen parameters. The assessment score ( α ) is used to obtain the ranking among the selected schemes and to calculate the positive distance from average ( Pd ) and negative distance from average ( Nd ) [16,17]. The performance matrices of the selected schemes are shown in Tab. 3.

Step-I:

Calculate the average solution ( ϕ ) according to the selected criteria shown below.

(ϕ)=[ϕb]1×β (1)

Where,

(ϕ)=∑i=1yXaby (2)

The aggregate calculation of the aforementioned Eqs. (1) and (2) can be obtained as an average solution ( ϕ ) as shown in Tab. 3.

Step-II:

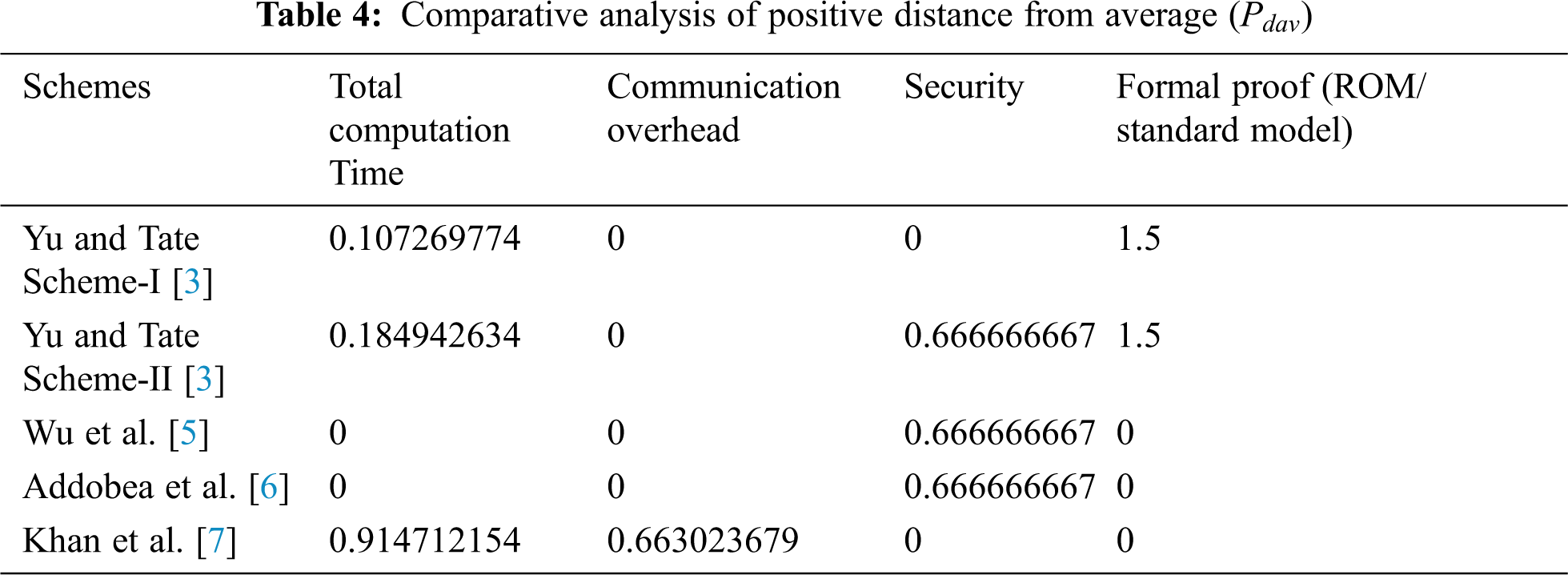
In this particular step, the positive distance from average is calculated using the following equations

Pdav=[(Pdav)ab]β×β (3)

If the bth scenario is favorable than

(Pdav)ab=MAX(0,(Aveb−Xab))Aveb (4)

If less favorable then

(Pdav)ab=MAX(0,(Xab−Aveb))Aveb (5)

In the above-mentioned equations Pdav denote the positive distance from the average solution. The results obtained are shown in Tab. 4.

Step-III

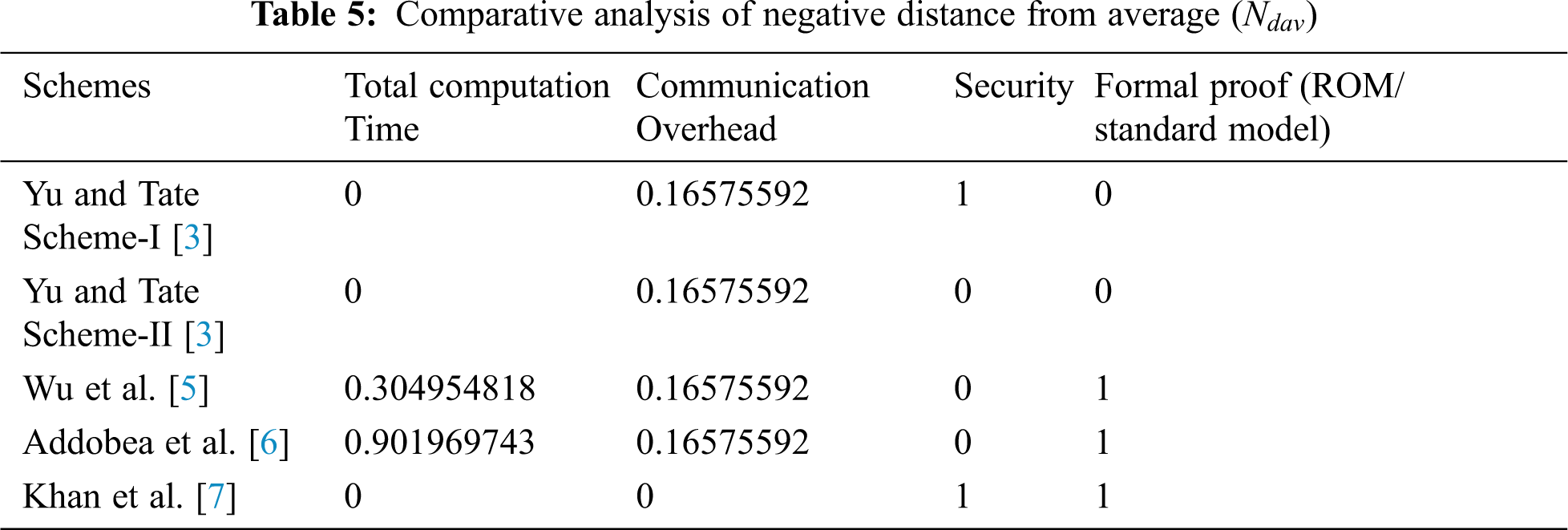
In this particular step, the negative distance from average ( Ndav ) is calculated using the following equations

(Ndav)=[(Ndav)ab]β×β (6)

If the bth scenario is favorable than

(Ndav)ab=MAX(0,(Aveb−Xab))Aveb (7)

If less favorable then

(Ndav)ab=MAX(0,(Xab−Aveb))Aveb (8)

In the above-mentioned equations (Ndav)ab denote the positive distance from the average solution. The results obtained are shown in Tab. 5.

Step-IV:

In this step, the weighted sum of the positive distance ( Pd ) is calculated using the following equation. The results obtained are shown in Tab. 6.

(WSPd)a=∑b=1yλb(Pd)ab (9)

Step-V:

In this step, the weighted sum of the negative distance ( Pd ) is calculated using the following equation. The results obtained are shown in Tab. 7.

(WSNd)a=∑b=1yλb(Nd)ab (10)

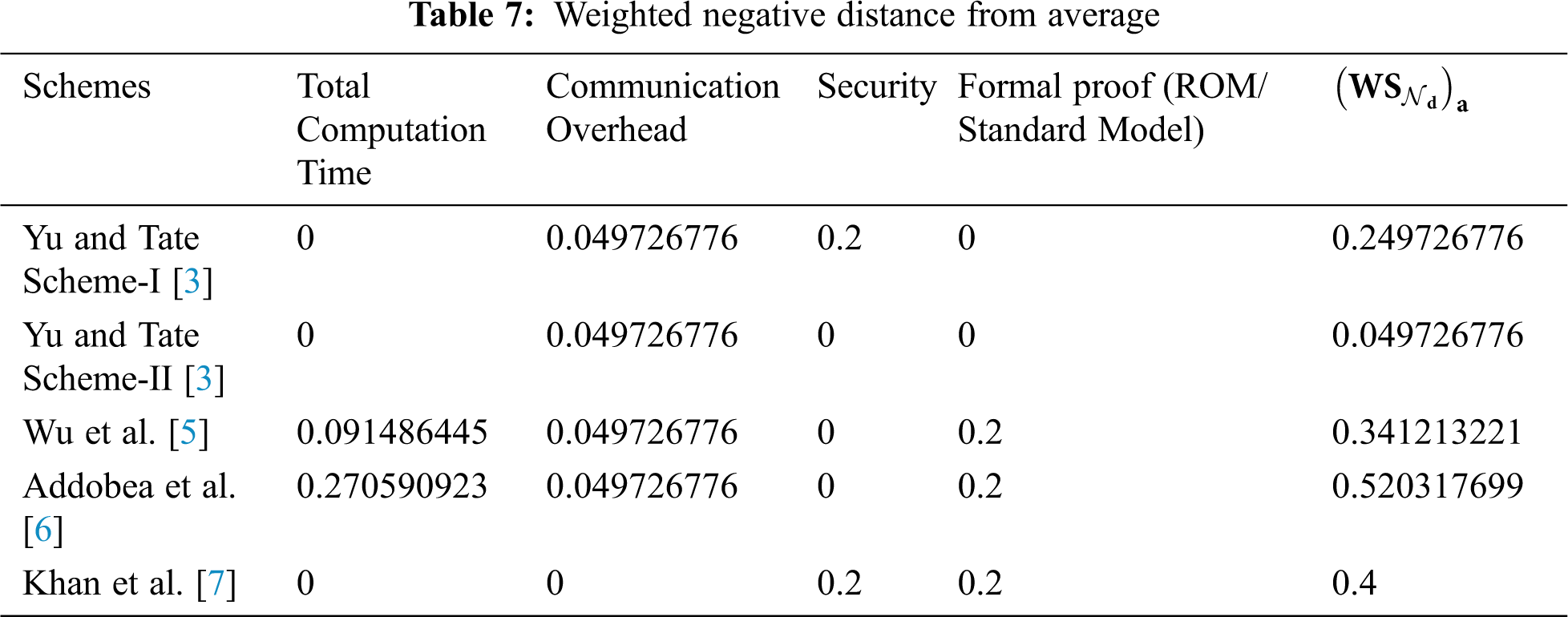
Step-VI:

In this step, the calculated scores obtained from (WSPd)a&(WSNd)a are normalized as follows,

N(WSPd)a=(WSPd)aMAXa((WSPd)a) (11)

N(WSNd)a=1−(WSNd)aMAXa((WSNd)a) (12)

Step-VII:

In this step, we calculate the appraisal score of all the selected schemes as follows,

ψa=12(N(WSPd)a−N(WSNd)a) (13)

Where 0⪯ψa⪰1 .

The result of ψa is determined using aggregate score values of the NWSPd& NWSNd .

Step-VII:

In this step, we calculate a sequence of activities to our measurement of evaluation scores (ψ) and determines the ranking of the selected schemes. The results suggest that the best ranking solution has a higher ψ compared to the other. Therefore, in the following Tab. 8, the scheme of Yu and Tate [3] Scheme 2 has the highest evaluation scores (ψ). So, the last calculated rank result is shown in Tab. 8.

6.5 Lesson Learned

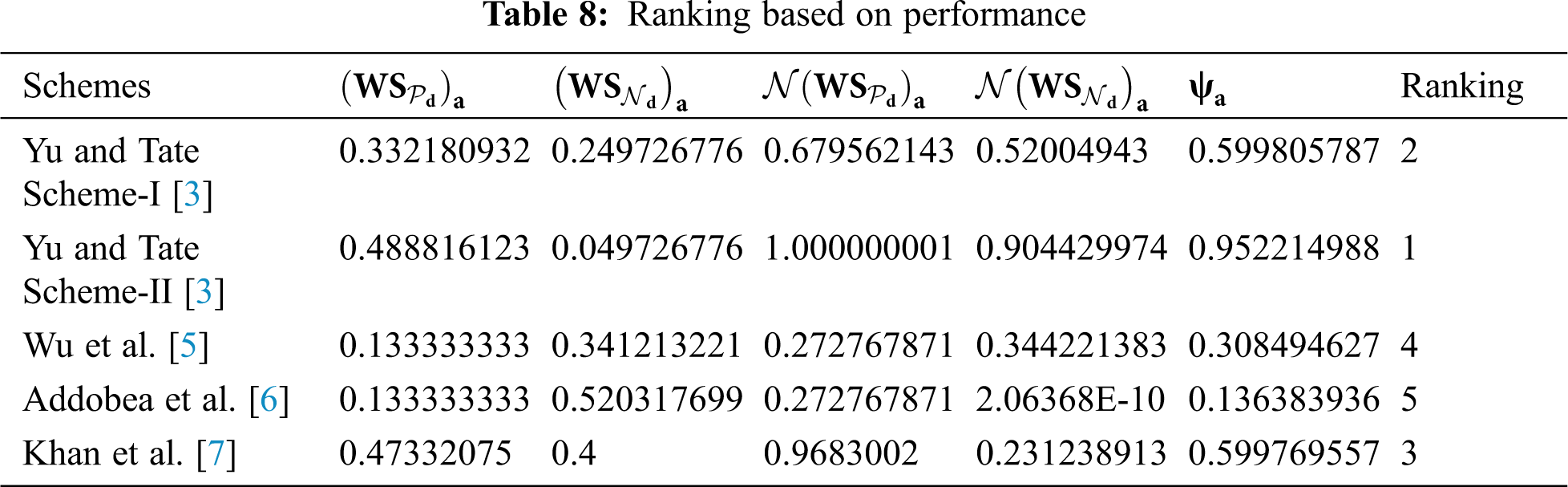
From the aforementioned evaluation, we conclude that the designed scheme of Khan et al. [7] is efficient in terms of computation time and communication overhead. However, the given is insecure against adaptive chosen message attacks. Further, the proposed scheme of Khan et al. [7] is claimed to be secure under ROM. On the other hand, the given scheme of Yu and Tate [3] Scheme 2 is formally secured under the standard model. Though the given scheme has some limitations in terms of cost efficiencies but secure and proved in the standard model.

7  Conclusion and Future Work

Recently, Khan et al. presented a new certificateless online/offline signature scheme for the Internet of Health Things (IoHT) to fulfill the authenticity requirement for the resource-constrained environment of (IoHT) devices. The authors claim that the newly proposed scheme is secure against Type-I adversary under the Random Oracle Model (ROM). Unfortunately, their scheme is insecure against adaptive chosen message attacks. It is demonstrated that an adversary can forge a valid signature on a message by replacing the public key. Furthermore, we performed a comparative analysis of the selective parameters including computation time, communication overhead, security, and formal proof by employing Evaluation based on Distance from Average Solution (EDAS). The analysis shows that the designed scheme of Khan et al. doesn’t have any sort of advantage over the previous schemes. Though, the authors utilized a lightweight hyperelliptic curve cryptosystem with a smaller key size of 80-bits. Finally, we give some suggestions on the construction of a concrete security scheme under ROM. Soon, we intend to improve the security of Khan et al. under the standard model.

Acknowledgement: The authors would like to thank Taif University Researchers Supporting Project number (TURSP-2020/79), Taif University, Taif, Saudi Arabia.

Funding Statement: Taif University Researchers Supporting Project number (TURSP-2020/79), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest.

References

 1.  S. Even, O. Goldreich and S. Micali, “On-line/off-line digital signatures,” Advances in Cryptology—CRYPTO’ 89 Proceedings, vol. 435, pp. 263–275, 2001. [Google Scholar]

 2.  A. Shamir and Y. Tauman, “Improved online/offline signature schemes,” Advances in Cryptology-CRYPTO, vol. 2139, pp. 355–367, 2001. [Google Scholar]

 3.  P. Yu and S. R. Tate, “Online/offline signature schemes for devices with limited computing capabilities,” in Cryptographers’ Track at the RSA Conference 2008 (CT-RSA 2008San Francisco, CA, USA, vol. 4964, pp. 301–317, 2008. [Google Scholar]

 4.  X. L. Ma, Z. W. Wang, L. Z. Gu and Y. Yang, “Remark on Yu et al.’s online/offline signature scheme in CT-RSA 2008,” in 2009 Fifth International Conference on Information Assurance and Security, Xi’an, China, vol. 2, pp. 719–720, 2009. [Google Scholar]

 5.  T. Wu, Y. Chen and K. Lin, “ID-based online/offline signature from pairings,” in Proc. of the International Computer Symposium (ICS2010Tainan City, Taiwan, pp. 198–203, 2010. [Google Scholar]

 6.  A. A. Addobea, J. Hou and Q. Li, “MHCOOS: an offline- online certificateless signature scheme for m-health devices,” Security and Communication Networks, vol. 2020, pp. 1–12, 2020. [Google Scholar]

 7.  M. A. Khan, S. U. Rehman, M. I. Uddin, S. Nisar, F. Noor et al., “An online-offline certificateless signature scheme for internet of health things,” Journal of Healthcare Engineering, vol. 2020, pp. 1–10, 2020. [Google Scholar]

 8.  S. Hussain, I. Ullah, H. Khattak, M. Adnan, S. Kumari et al., “A lightweight and formally secure certificate based signcryption with proxy re-encryption (cbsre) for internet of things enabled smart grid,” IEEE Access, vol. 8, pp. 93230–93248, 2020. [Google Scholar]

 9.  S. S. Ullah, I. Ullah, H. Khattak, M. A. Khan, M. Adnan et al., “A lightweight identity-based signature scheme for mitigation of content poisoning attack in named data networking with internet of things,” IEEE Access, vol. 8, pp. 98910–98928, 2020. [Google Scholar]

10. Y. Y. Li, J. Q. Wang and T. L. Wang, “A linguistic neutrosophic multi-criteria group decision-making approach with EDAS method,” Arabian Journal for Science and Engineering, vol. 44, no. 3, pp. 2737–2749, 2019. [Google Scholar]

11. A. Waheed, A. I. Umar, M. Zareei, N. Din, N. U. Amin et al., “Cryptanalysis and improvement of a proxy signcryption scheme in the standard computational model,” IEEE Access, vol. 8, pp. 131188–131201, 2020. [Google Scholar]

12. L. A. Zadeh, “Fuzzy logic,” Computer, vol. 21, no. 4, pp. 83–93, 1988. [Google Scholar]

13. K. Tanaka, An introduction to fuzzy logic for practical applications. Vol. 6. New York: Springer-Verlag, pp. 1–148, 1997. [Google Scholar]

14. N. A. Malik and M. Rai, “Enhanced secure and efficient key management algorithm and fuzzy with trust management for MANETs,” in Proc. of the Int. Conf. on Innovative Computing & Communications (ICICCSingapore, Malaysia, pp. 1–8, 2020. [Google Scholar]

15. G. Mehmood, M. Z. Khan, A. Waheed, M. Zareei and E. M. Mohamed, “A trust-based energy-efficient and reliable communication scheme (trust-based ERCS) for remote patient monitoring in wireless body area networks,” IEEE Access, vol. 8, pp. 131397–131413, 2020. [Google Scholar]

16. D. Zindani, S. R. Maity and S. Bhowmik, “Fuzzy-EDAS (evaluation based on distance from average solution) for material selection problems,” in Advances in Computational Methods in Manufacturing, pp. 755–771, 2019. [Google Scholar]

17. M. Yazdani, A. E. Torkayesh, E. D. S. Gonzalez and S. K. Otaghsara, “Evaluation of renewable energy resources using integrated shannon entropy-edas model,” Sustainable Operations and Computer, vol. 1, pp. 35–42, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.