DOI:10.32604/iasc.2022.015810

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.015810 |  |
| Article |
Particle Swarm Optimization with New Initializing Technique to Solve Global Optimization Problems
1Govt. College Women University Sialkot, Sialkot, 51310, Pakistan
2University of Jeddah, College of Computing and Information Technology at khulais, Dept. of information Technology, Jeddah, Saudi Arabia
3University of Gujrat, Gujrat, 50700, Pakistan
4University of Jeddah, College of Computer Science and Engineering, Dept. of Software Engineering, Jeddah, Saudi Arabia
*Corresponding Author: Waqas Haider Bangyal. Email: waqas_bangyal@hotmail.com
Received: 08 December 2020; Accepted: 24 May 2021
Abstract: Particle Swarm Optimization (PSO) is a well-known extensively utilized algorithm for a distinct type of optimization problem. In meta-heuristic algorithms, population initialization plays a vital role in solving the classical problems of optimization. The population’s initialization in meta-heuristic algorithms urges the convergence rate and diversity, besides this, it is remarkably beneficial for finding the efficient and effective optimal solution. In this study, we proposed an enhanced variation of the PSO algorithm by using a quasi-random sequence (QRS) for population initialization to improve the convergence rate and diversity. Furthermore, this study represents a new approach for population initialization by incorporating the torus sequence with PSO known as TO-PSO. The torus sequence belongs to the family of low discrepancy sequence and it is utilized in the proposed variant of PSO for the initialization of swarm. The proposed strategy of population’s initialization has been observed with the fifteen most famous unimodal and multimodal benchmark test problems. The outcomes of our proposed technique display outstanding performance as compared with the traditional PSO, PSO initialized with Sobol Sequence (SO-PSO) and Halton sequence (HO-PSO). The exhaustive experimental results conclude that the proposed algorithm remarkably superior to the other classical approaches. Additionally, the outcomes produced from our proposed work exhibits anticipation that how immensely the proposed approach highly influences the value of cost function, convergence rate, and diversity.
Keywords: Particle swarm optimization; swarm intelligence; TO-PSO; quasi-random sequence
Optimization is currently an effective paradigm of research and development. In this era, unbeatable optimization algorithms like PSO are needed to efficiently deal with complex real-world optimization problems [1]. A fundamental subdivision of artificial intelligence is Swarm intelligence (SI) that is responsible to process the multi-agent system and its morphological design; additionally, SI provides satisfactory results on complex optimization problems. SI is influenced by the community actions of social insects like wasps, termites, ants, bees, as well as, by other social animal colonies i.e., (bird flocking or fish schooling) [2]. The title SI was firstly defined by Beni et al. [3] during the process of the cellular robotic system. For several years, researchers have indicated their curiosity towards the colonies of social insects, however, their community activities and behavior have remained hidden. While a single citizen is perceived to be an un-cultured single citizen in such communities, although, they have a strong capacity to solve complicated problems on a community basis. The transfer of knowledge between each participant and their comparatively uncomplicated acts improves their quality to accomplish the complex undertaking. SI techniques have been utilized successively in the domain of optimization, which becomes a major fact for science and industry.
Particle swarm optimization (PSO) is accepted as the SI-based stochastic algorithm, introduced by Kenndy et al. [4], is undoubtedly acknowledged as a beneficial approach to solving global optimization problems. PSO has been recognized as the most famous technique to solve complex optimization problems due to robustness and non-complexity, which is illustrated in the heterogeneous fields of engineering and science. In PSO, the target solution population becomes the swarm and is used to investigate the new search space; social movements of “flocks, birds” during their search for the food will be recorded in this new search area. From the observations of the remaining swarm, the transmission of information between all entities is considered as particles, occurs and all singles are accommodated. Each individual has two rules to endure, first looking to return to its previous best point and the other pursuing its swarm’s sub sequential best position.
In the standard PSO, Velocity (vi) and Positions (xi), for i = 1 to n, are upgraded as given in Eqs. (1) and (2):
where r1 and r2 are two different function search that gives a vector of irregular values, which is uniformly generated in an interval of [0,1]. b1 and b2 are acceleration co-efficient. Inertia co-efficient
The EAs and PSO techniques are implemented with the generation of random numbers, so the generation of random numbers works very well on these techniques for the small area of problems i.e., (low dimensional search areas). High dimensional search regions, though, appear to decrease the performance due to the premature particle convergence, as this causes sub-optimal outcomes [5]. For multimodal problems, this pattern is more persevering and intolerable, since it includes many local and global optimums. The inadequate distribution of the population in the search region can be the most important factor for this deprived performance, i.e., to assume that if the initial population does not properly scan the entire search space, which makes it difficult to recognize the robust global solution [6]. By adding the most formal and coordinated random distribution for population initialization, this issue can be resolve. Sequences of random numbers differ in the essence of their morphological design i.e., (quasi-random sequences, pseudo-random sequences, and probability distribution).
In the study of EAs, genetic algorithms, and PSO, it is observed that not sufficient research was performed to consider the QRS when initializing the swarm population in the search space [7]. Due to this fact, we have proposed a new low discrepancy sequence called Torus sequence for initializing the particles in the search space at an early stage. The totus algorithm is used to engage the particles with determined prime iterations using the Torus sequence. In comparison with the nine real-time classification problems, the proposed algorithm TO-PSO has been observed with several uni-modal, multimodal, and rotated benchmark functions. The analogy with many other variants of PSO base on low discrepancy sequences has clarified that TO-PSO offers better performance, primarily for the complex optimization problems of higher dimensions. Comparison studies have also observed that TO-PSO outperforms in real-time classification problems than others.
The majority of the paper is organized as follows: Section II. Overviews the previous literature. The initialization methodologies and inertia weight strategies are discussed in Section III. Section IV addresses the implementation and comparison of initialization techniques using inertia weight on fifteen functions of benchmark measures, as well as the findings of our proposed TO-PSO in terms of the research accuracy. Finally, Section V will conclude the paper.
Researchers were interested to adopt the probability sequence and QRS to increase the reliability of population-based EAs [8], contrasting the generator of pseudo-random sequences with the generator of low discrepancy sequences showed that the generator of low discrepancy sequences performs best on the Halton sequence incorporated by EAs [9], which is one of the sets of low discrepancy sequences. The Halton sequence has been used to increase the efficiency of genetic algorithms.
For population initialization, the Sobol sequence and Faure sequence are incorporated in Brits et al. [10]. Furthermore, a comprehensive comparison of the sequences of Halton, Sobol, and Faure has been formed by [10].
Van der Corput sequence [11] is compatible with many of the associated low discrepancy sequences and can be initialized for the dimension and foundation.
In Krohling et al. [12], for the fine-tuning of PSO parameters, they utilize Exponential distribution. Comparative probability distribution analysis, including Gaussian, Beta, Gamma, and Exponential, was carried out in Thangaraj et al. [13].
The Non-linear simplex method (NSM) approach was implemented by Parsopoulos et al. [14]. The first particles of vertices (D + 1) are included in NSM, where D shows the dimensional search space. The first S(D + 1) particles are introduced to initiate them in a random position based on their initial vertices, wherein S is the size of the targeted population.
To initiate the initial point of the swarm population, Mark Richards and Dan Ventura conducted a centroidal Voronoi tessellations CVT generator [15].
Chengwei Yang [16] introduced a novel initialization approach QRS and time-varying inertia weight, titled LHNPSO, for non-linear high-order functions. The successful initialization of PSO using the Quasi-random Sobol and Halton sequences was validated by Shubham et al. [17].
A novel O-PSO algorithm belongs to the opposition-based particle learning implemented by the researchers [18], which increases the likelihood of capturing the global minimum at a very early stage. Three independent variants of the PSO algorithm focused on the following initialization techniques were contrasted by authors in Gutiérrez et al. [19]: the chaotic initialization, the orthogonal array initialization, and the opposition-based initialization.
In 2017 [20], researchers presented two modifications to the standard PSO as it is termed PSO-IM. These two modifications are, first, the heuristic inertia weight equation for accurate and rapid convergence of PSO, and two different types of mutations implemented on swarm particles, and selection of fuzzy controller. Large inertia weight is initially used to explore search space, but it continues to decrease with the growth in the number of iterations so local search in the final iteration will be essential. At the initial point, few randomly selected particles are used for each tournament, and particles with the best-fitted value are chosen. Repeat this process until the mutation is chosen for a given group of particles and then the uniform mutation and non-uniform mutation are applied, which improves the searchability of PSO particles and avoids premature convergence. Finally, relative to the standard PSO, the PSO-IM variant exhibits optimal performance.
Kessentini & Barchiesi in 2015 [21] highlighted the drawbacks of the standard PSO algorithm, which is not sufficient to solve engineering problems related to optimization because it slows down and converges to local optima in large dimensional scenarios. Numerous PSO variants that maintain an intact harmony between local and global discovery have been suggested to deal with these limitations. Initially, Y. Shi and R. Eberhart [22], intruded inertia weight in PSO, later on, many types of research were denoted on this and considered as an essential part of PSO to balance search ability at local and global levels. An adaptive inertia weight (w-PSO) technique was presented in this study. For dynamic inertia weight setting, the feedback response from the best-positioned particle in the swarm is used. In w-PSO, the dynamic environment ranges varies from 0.4 to 0.9, which drastically increases the searchability of PSO. Results of the significant improvement of w-PSO on the set of CEF 2014 benchmark functions compared to other variants of PSO [23].
In 2016, Taherkhani et al. [24] explored the key and critical parameter in EA’s algorithm (PSO) to limit particles in the search space, termed as inertia weight. This research presented an adaptive approach, based on the individual executions of particles and their distance from the best location,to remove inertia weight from all the dimensions and for all particles.
On the traditional PSO algorithm, four various population initialization methodologies have been implemented, which are Uniform Pseudo-Random initialization technique [8]: Halton sequence for initialization [25], Sobol sequence for initialization [26], and finally a proposed technique is based on Quasi-Random Sequences (QRS) termed as Torus Sequence (low discrepancy sequence) [27], opposed to pseudo-random sequence when applied on traditional benchmark functions, the Torus technique enhances the performance of standard PSO and achieve optimal results.
By following a uniform-distribution [8], the pseudo-random sequence produces random numbers and can be characterized by probability-density-function (PDF) of const. Uniform-distribution. As is given in Eq. (4) as:
whereas, the maximum likelihood parameters are variables
An improved version of the Van Dar Corput [11] sequence is presented by J. Halton [25] is known as the Halton sequence. Halton sequence emphasizes on co-prime base to generate the random sequence pattern. The pseudo-code for the Haltom sequence generation is given as follows:

Ilya M. Sobol, who was a Russian mathematician, primarily proposed Sobol [26] sequence. Sobol sequence works by re-constructing the coordinates. For each dimension, all of these co-ordinates possess linear recurrence relations. Let, a non-negative instance s contains an expression in binary form, where s is as follows in (6):
Then, the ith instance for dimension D is generated using the (7) as follows:
However,
Torus is a geometric term introduced in 1987 [27], primarily focused on the development of geometric co-ordinate structure Torus-mesh. The foundation of game development is also concentrated on the mesh structure that can be achieved with torus sequence. With torus-mesh, the coordinated structure of the left and right hands can be easily accomplished. Torus has various shapes at different dimensions. For example, for 1D-shapes is the line, 2D-shapes are circle, rectangle and 3D shapes is a donut, mainly 3D shape is generated by the given set of Eqs. (9)–(11) given as:
whereas,
Here,
Inertia weight was firstly presented by Y. shi and R. Eberhart [22] and recently, the most important PSO parameter is inertia weight. High velocity in the standard PSO allows particles to exist from the search space limits. To deal with this limitation, the velocity-clamping or maximum velocity limit is set. The introduction of a new inertia weight parameter increases the standard PSO performance because particles do not diverge and the inertia weight range is set from 0.4 to 0.9. These inertia weight values are an integral part of balancing local and global search. Furthermore, two inertia weight strategies are applied in this research work [28] on standard PSO, which are Linearly Decreasing inertia-weight and the Chaotic inertia-weight (with and without Torus initialization) to enhance the standard PSO efficiency.
3.2.1 Linear Decreasing Inertia-Weight
Linearly-decreasing inertia-weight has also been implemented on standard PSO [29]. Using linear-decreasing inertia weight, the speed of the exploration process increases inside the search space, which took more time to complete with the standard PSO. Therefore for each repetition, iterative evaluation of inertia weight is conducted using (13) as:
Here, wmax = 0.9, wmin = 0.4, k = current iteration and itermax = max. iterations. The initialization of this strategy will linearly decrease inertia-weight from 0.9 to 0.4.
Chaotic inertia-weight (
Then in an iterative process, the value of inertia weight is also measured from the (15) as:
Whereas,
4.1 Experimental Settings of Particle Swarm Optimization
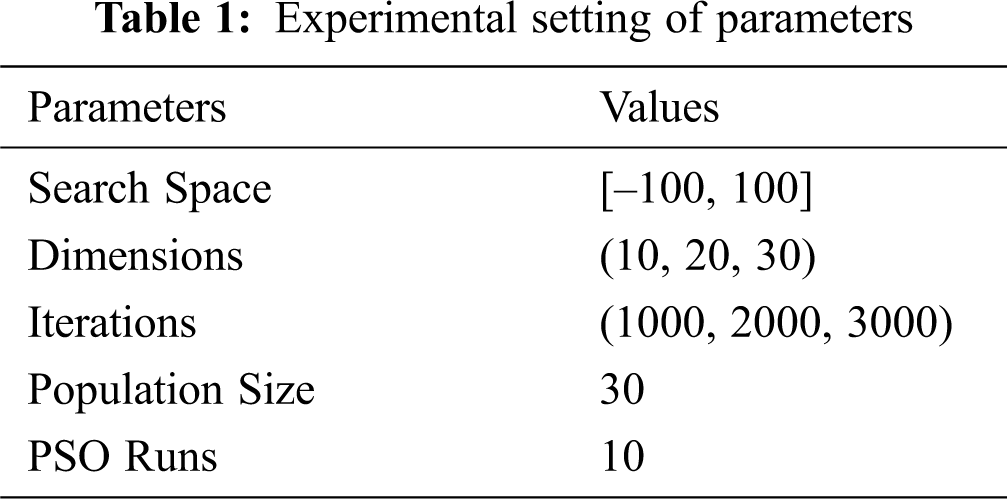
Upper and lower boundary of the search space is set according to the applied function, population size will be 30, three dimensional levels will be used for PSO that are 10, 20 and 30 for three sets of iterations 1000, 2000 and 3000 used for each size represented in Tab. 1. PSO was run 10 times and the average value was calculated.
Standard benchmark functions [31] are given in Tab. 2 over the continues range of values available in the literature (used by different researchers) used to implement the evolutionary computing algorithm/s.

4.2 Implementation Results of Initialization Techniques
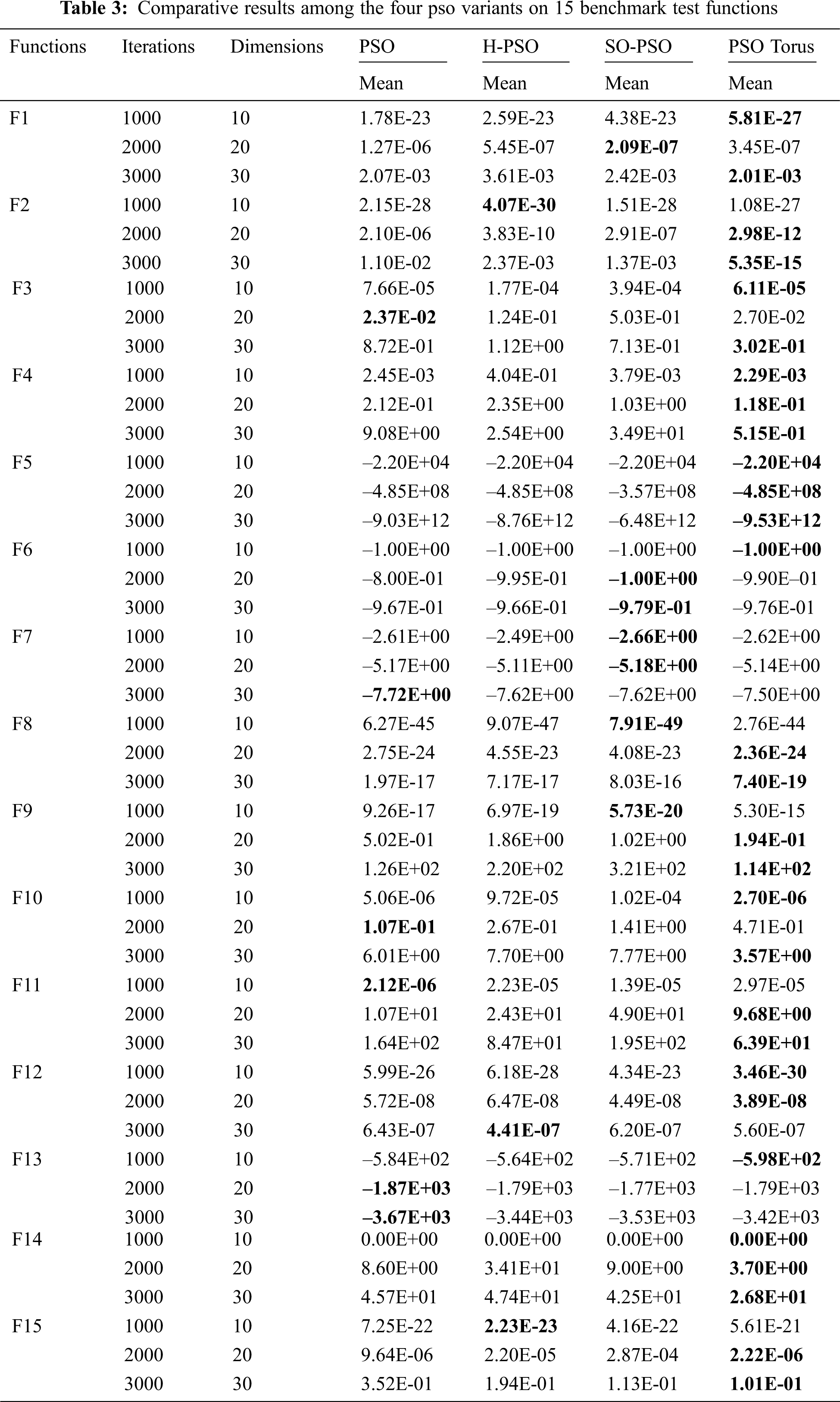
The comparative results of four PSO initialization techniques on 23 benchmark test functions are given in Tab. 3, where the column ‘‘Mean’’ shows the calculated mean value. Bold values are describing the winner function among the four PSO algorithms.
The comparative results of four different population initialization techniques are generated by using the standard PSO. All these four PSO initialization variants are implemented on fifteen benchmark test functions, where ‘‘Mean’’ shows mean value. The best results are presented in bold among the four PSO algorithms. In contrast with the traditional PSO, SO-PSO, and H-PSO, TO-PSO technique performs remarkably well. In terms of improved convergence, speed, consistency and durability, the TO-PSO sequence based on QRS showed better performance on implemented benchmark functions for minimization optimization than other initialization techniques.
4.3 Graphs of PSO Initialization Techniques
All the graphs shown in Fig. 1 are generated as per the results of Tab. 3 with 10 dimensions and 1000 iterations, 20 dimensions and 2000 iteration similarly 30 dimensions and 3000 iterations.
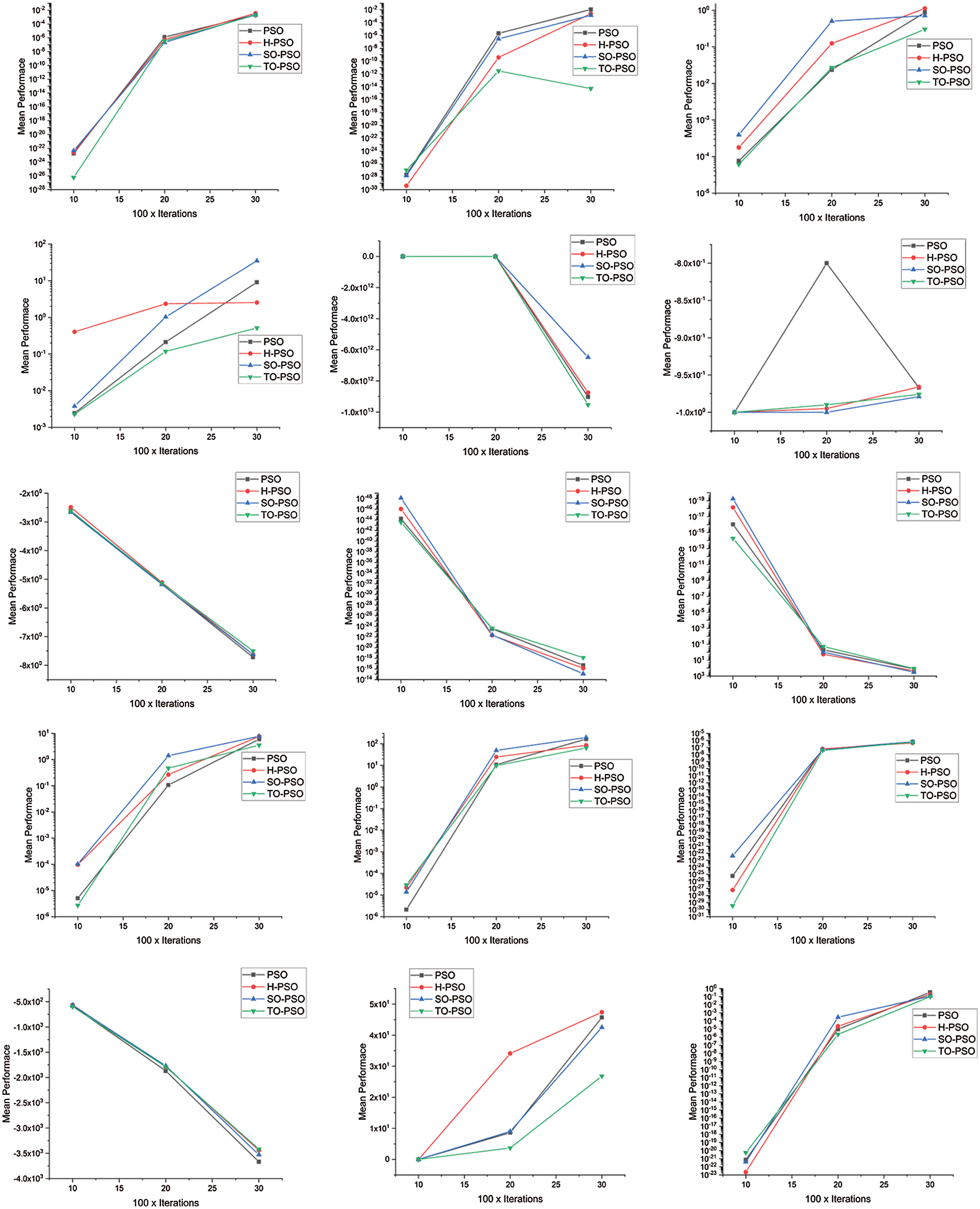
Figure 1: Graphs of PSO initialization techniques
4.4 Implementation Results of Initialization Techniques using Linear Decreasing and Chaotic Inertia Weights
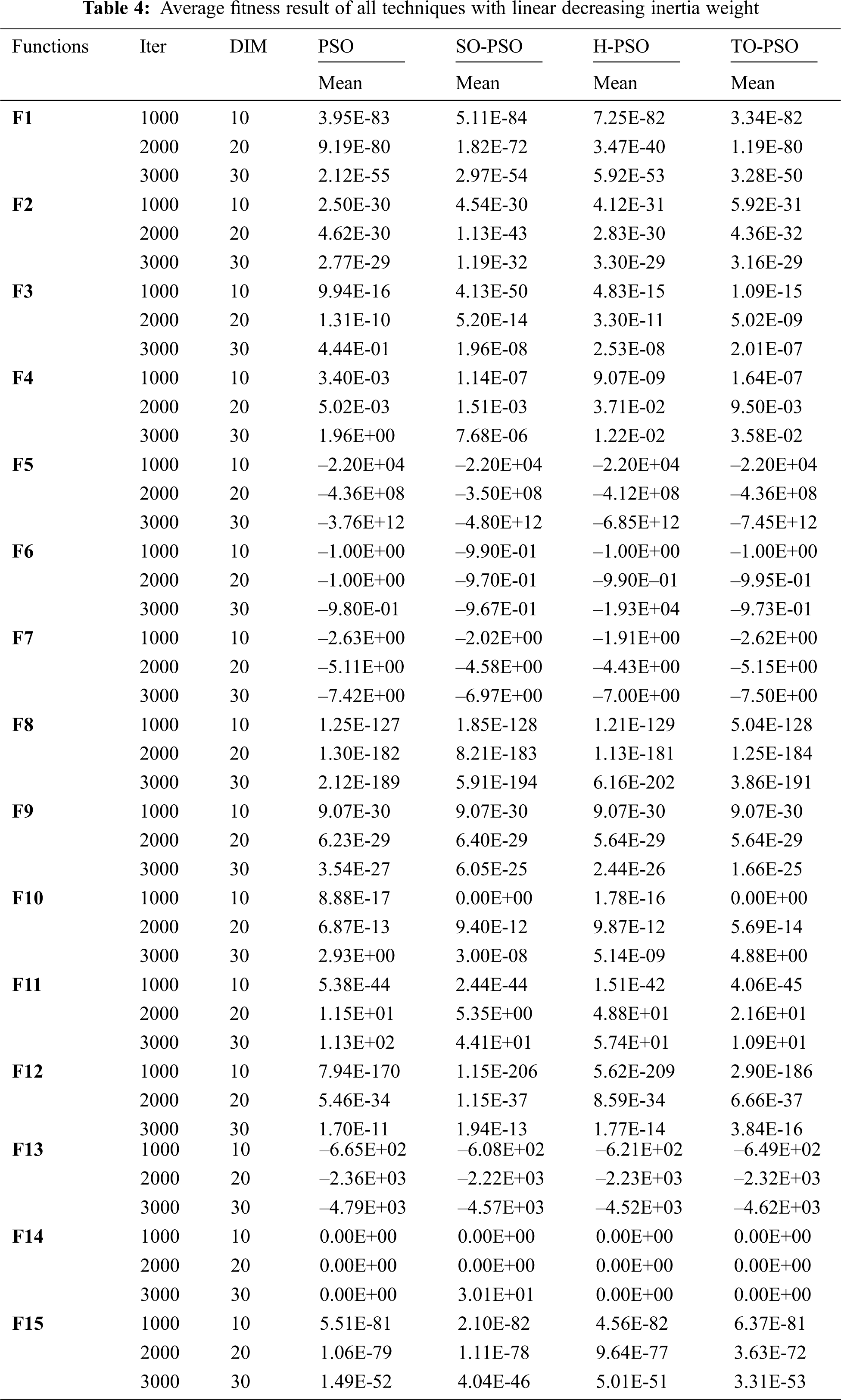
Inertia weight is an essential parameter of the PSO algorithm, which plays a vital role to balance the global exploration and local exploitation of the search space. Due to the importance of inertia weight, we have used the linear decreasing inertia weight (LDIW) with PSO, SO-PSO, and H-PSO and proposed initialization approach TO-PSO. The impact of linear decreasing inertia weight is remarkably good on the performance of all variants that can observe from the aforementioned Tab. 4. Our proposed technique beats the other three PSO initialization approaches on fifteen benchmark functions. The winner results among all the four PSO approaches are differentiated as bold.
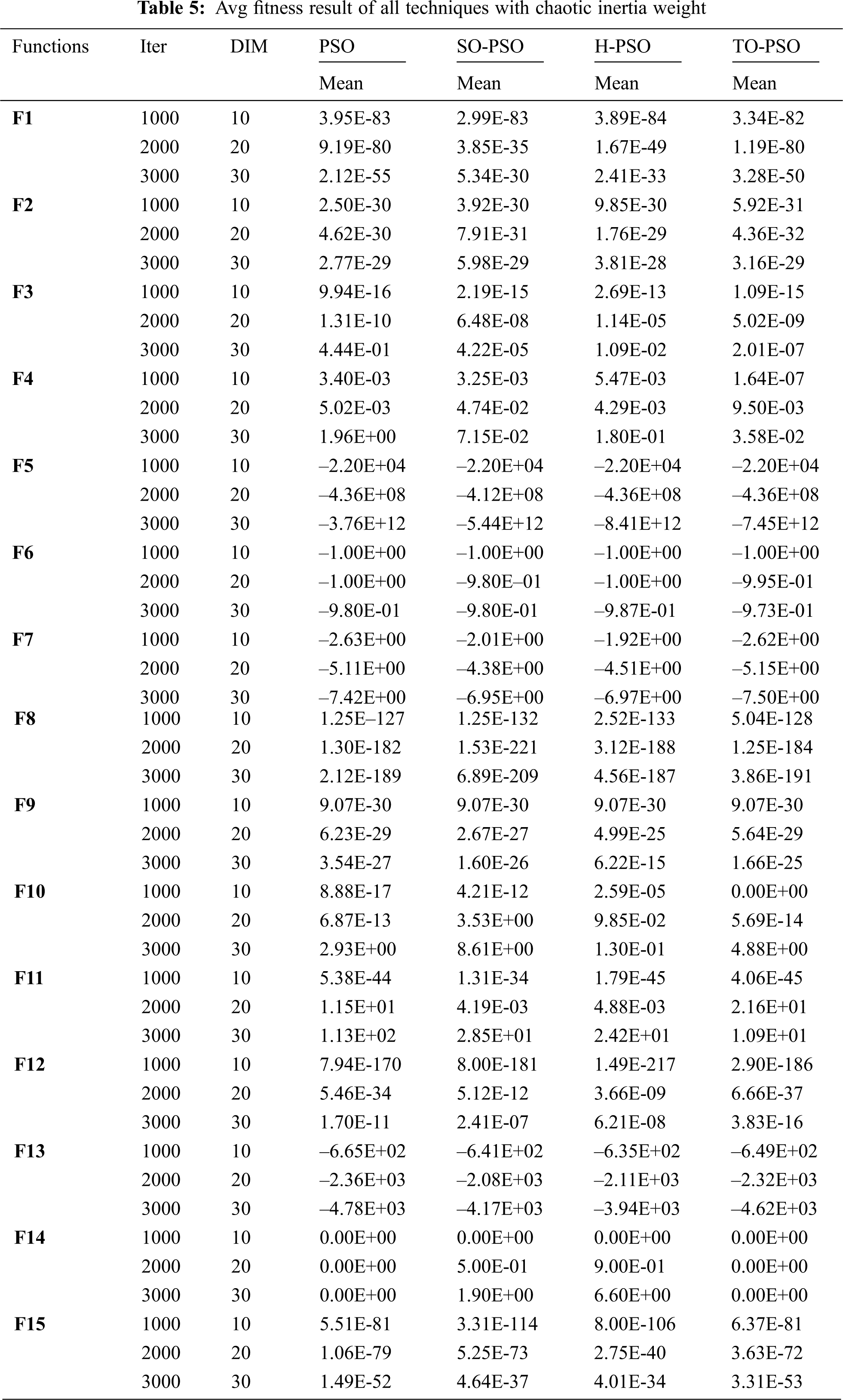
The use of chaotic mapping to adjust the coefficient is the fundamental concept of chaotic inertia weight. In this work logistic mapping is being used. The logistic mapping is:
z = µ × z × (1-z)
when 3.57 < µ ≤ 4, chaotic phenomena arise during logistic mapping.
Result from Tab. 5, of chaotic inertia weight with PSO strategies has a positive effect on the optimization of functions relative to the fixed inertia weight of PSO. PSO initialization strategies with chaotic inertia weight initially perform search covering a wide range called “rough search”, while the search obtains a relatively small range called “minute search” during the optimization process.
In this study, a novel initialization technique is proposed for the population’s initialization of PSO. For experimental validation, a set of twenty-three unimodal and multi-modal benchmark test functions are utilized. The analysis of experimental results shows that the proposed technique enhances the convergence speed and improves the search ability to find a better region for the swarm, as well as, maintains the diversity of the swarm. The presented technique also emphasizes that if there is no information on the existence of candidate solutions, then it is possible to proceed with the most suitable candidate solution first. Additionally, the evaluation of results illustrates that the proposed TO-PSO initialization technique outperforms the standard PSO, and other variants such as PSO with Sobol and Halton sequences as well. To measure the performance efficiency of PSO, the inertia weight factor in PSO is also embedded using TO-PSO initialization, similarly, it is compared with the other inertia weights presented in the literature. The primary objective of this research work is generic but applicable to other stochastic based metaheuristic algorithms that develops the future direction of our work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors have no conflicts of interest to report regarding the present study.
1. V. Bhaskar, S. K. Gupta and A. K. Ray, “Applications of multiobjective optimization in chemical engineering,” Vol. 16, no. 1, pp. 1–54, 2000. [Google Scholar]
2. C. Blum and X. Li, “Swarm intelligence in optimization,” in Swarm intelligence: Springer, pp. 43–85, 2008. [Google Scholar]
3. G. Beni and J. Wang, “Swarm intelligence in cellular robotic systems,” in Robots and biological systems: Towards a new bionics?: Springer, pp. 703–712, 1993. [Google Scholar]
4. R. Eberhart and J. Kennedy, “Particle swarm optimization,” in Proc. of the IEEE int. conf. on neural networks: Citeseer, vol. 4, pp. 1942–1948, 1995. [Google Scholar]
5. H. Liu and A. Abraham, “Fuzzy adaptive turbulent particle swarm optimization,” in Fifth Int. Conf. on Hybrid Intelligent Systems (HIS’05IEEE, pp. 6, 2005. [Google Scholar]
6. Crina Grosan, A. Abraham and M. Nicoara, “Search optimization using hybrid particle sub-swarms and evolutionary algorithms,” in International Journal of Simulation Systems, Science & Technology, vol. 6, no. 10, pp. 60–79, 2005. [Google Scholar]
7. M. Pant, R. Thangaraj, C. Grosan and A. Abraham, “Improved particle swarm optimization with low-discrepancy sequences,” in 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational IntelligenceIEEE, pp. 3011–3018, 2008. [Google Scholar]
8. N. Q. Uy, N. X. Hoai, R. I. McKay and P. M. Tuan, “Initialising PSO with randomised low-discrepancy sequences: the comparative results,” in 2007 IEEE Congress on Evolutionary Computation: IEEE, pp. 1985–1992, 2007. [Google Scholar]
9. S. Kimura and K. Matsumura, “Genetic algorithms using low-discrepancy sequences,” in Proc. of the 7th annual conf. on Genetic and evolutionary computation: ACM, pp. 1341–1346, 2005. [Google Scholar]
10. R. Brits, A. P. Engelbrecht and F. Van den Bergh, “A niching particle swarm optimizer,” Proc. of the 4th Asia-Pacific conf. on simulated evolution and learning: Singapore: Orchid Country Club, vol. 2, pp. 692–696, 2002. [Google Scholar]
11. J. Van der Corput, Verteilungsfunktionen: Mitteilg 7. NV Noord-Hollandsche Uitgevers Maatschappij, 1936. [Google Scholar]
12. R. A. Krohling and L. dos Santos Coelho, “PSO-E: Particle swarm with exponential distribution,” in 2006 IEEE Int. Conf. on Evolutionary Computation: IEEE, pp. 1428–1433, 2006. [Google Scholar]
13. R. Thangaraj, M. Pant and K. Deep, “Initializing PSO with probability distributions and low-discrepancy sequences: The comparative results,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBICIEEE, pp. 1121–1126, 2009. [Google Scholar]
14. K. E. Parsopoulos and M. N. Vrahatis, “Initializing the particle swarm optimizer using the nonlinear simplex method,” in Advances in intelligent systems, fuzzy systems, evolutionary computation, vol. 216, pp. 1–6, 2002. [Google Scholar]
15. M. Richards and D. Ventura, “Choosing a starting configuration for particle swarm optimization,” IEEE Int. Joint. Conf. Neural, vol. 3, pp. 2309–2312, 2004. [Google Scholar]
16. C. Yang, W. Gao, N. Liu and C. Song, “Low-discrepancy sequence initialized particle swarm optimization algorithm with high-order nonlinear time-varying inertia weight,” vol. 29, pp. 386–394, 2015. [Google Scholar]
17. S. K. Gupta, H. Gupta, S. Arora, P. Nayak and T. Shrivastava, “Efficient Initialization of Particle Swarm Optimization Using Low Discrepancy Sequence,” in Int. Conf. on Soft Computing and Pattern Recognition: Springer, pp. 440–449, 2016. [Google Scholar]
18. H. Jabeen, Z. Jalil and A. R. Baig, “Opposition based initialization in particle swarm optimization (O-PSO),” in Proc. of the 11th Annual Conf. Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers: ACM, pp. 2047–2052, 2009. [Google Scholar]
19. A. L. Gutiérrez, M. Lanza, I. Barriuso, L. Valle, M. Domingo et al., “Comparison of different pso initialization techniques for high dimensional search space problems: A test with fss and antenna arrays,” in Proc. of the 5th European Conf. on Antennas and Propagation (EUCAPIEEE, pp. 965–969, 2011. [Google Scholar]
20. S. Sheikhpour and A. Mahani, “Particle swarm optimization with intelligent mutation for nonlinear mixed-integer reliability-redundancy allocation,” vol. 16, no. 01, pp. 1750003, 2017. [Google Scholar]
21. S. Kessentini and D. Barchiesi, “Particle swarm optimization with adaptive inertia weight,” vol. 5, no. 5, pp. 368, 2015. [Google Scholar]
22. Y. Shi and R. Eberhart, “A modified particle swarm optimizer,” in 1998 IEEE int. conf. on evolutionary computation proceedings. IEEE world congress on computational intelligence (Cat. No. 98TH8360IEEE, pp. 69–73, 1998. [Google Scholar]
23. A. R. Lynn, “Instrumentation Set Points,” Los Alamos National Lab.(LANLLos Alamos, NM (United States), vol. 11, no. 61, pp. 723A–734A, 2015. [Google Scholar]
24. M. Taherkhani and R. Safabakhsh, “A novel stability-based adaptive inertia weight for particle swarm optimization,” vol. 38, pp. 281–295, 2016. [Google Scholar]
25. X. Wang and F. J. Hickernell, “Randomized halton sequences,” vol. 32, no. 7-8, pp. 887–899, 2000. [Google Scholar]
26. M. Pant, R. Thangaraj, V. P. Singh and A. Abraham, “Particle swarm optimization using Sobol mutation,” in 2008 First Int. Conf. on Emerging Trends in Engineering and Technology: IEEE, pp. 367–372, 2008. [Google Scholar]
27. V. V. Nikulin and I. R. Shafarevich, Geometries and groups. Springer Science & Business Media, 2012. [Google Scholar]
28. J. C. Bansal, P. Singh, M. Saraswat, A. Verma, S. S. Jadon et al., “Inertia weight strategies in particle swarm optimization,” in 2011 Third world congress on nature and biologically inspired computing, IEEE, pp. 633–640, 2011. [Google Scholar]
29. M. Pluhacek, R. Senkerik, D. Davendra, Z. K. Oplatkova, I. J. C. Zelinka et al., “On the behavior and performance of chaos driven PSO algorithm with inertia weight,” vol. 66, no. 2, pp. 122–134, 2013. [Google Scholar]
30. Y. Feng, G. F. Teng, A. X. Wang and Y. M. Yao, “Chaotic inertia weight in particle swarm optimization,” in Second Int. Conf. on Innovative Computing, Information and Control (ICICIC 2007IEEE, pp. 475, 2007. [Google Scholar]
31. M. Jamil and X. S. Yang, “A literature survey of benchmark functions for global optimization problems,” International Journal of Mathematical Modelling and Numerical Optimisation, vol. 4, no. 2, pp. 150–194, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |