Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.017705
Article

Estimation of Locational Marginal Pricing Using Hybrid Optimization Algorithms

M. Bhoopathi1,* and P. Palanivel2

1Department of EEE, Jayaram College of Engineering and Technology, Trichirappalli, 621014, India
2Department of EEE, EGS Pillay Engineering College, Nagappattinam, 611002, India
*Corresponding Author: M. Bhoopathi. Email: mbasugapri1@gmail.com
Received: 08 February 2021; Accepted: 10 May 2021

Abstract: At present, the restructured electricity market has been a prominent research area and attracted attention. The motivation of the restructuring in the power system is to introduce the competition at various levels and to generate a correct economic signal to reduce the generation cost. As a result, it is required to have an effective price scheme to deliver useful information about the power. The pricing mechanism is dependent on the demand at the load level, the generator bids, and the limits of the transmission network. To address the congestion charges, Locational Marginal Pricing (LMP) is utilized in restructured electricity markets. To improve the system efficiency, in this paper, a Hybrid Backtracking Search Optimization Algorithm with Grey Wolf Optimization (GWO-HBOA) is proposed, based on the Security Constrained Economic Dispatch (SCED). The objective of the proposed scheme is to minimize fuel cost in the transmission system under the loss and lossless conditions, considering both the normal and congestion conditions. BOA is conducted first, and Grasshopper Optimization Algorithm (GOA) is subsequently combined with the BOA, which results in the GWO-HBOA. To predict the demand for generator power, the demand response is estimated exactly. Moreover, the load LMP can be segregated at service security levels with respect to various load entities. In this way, the overcharging and underpayment issues can be solved under the security constrained market optimization. Furthermore, to determine the LMP loss, DC optimal power flow is analyzed. The proposed GWO with constrained security is estimated on IEEE 30-bus test system. Compared with the existing techniques, the proposed algorithm achieves better performance, in terms of fuel cost, voltage stability, voltage deviations, real power loss, and reactive power loss.

Keywords: Locational marginal pricing; grey wolf optimization; security constrained economic dispatch

1  Introduction

Power is essential for economic growth and national development. Emerging electrical power system requires the operation plans to handle the economic and security problems. Optimal Power Flow (OPF) is one of the best research sub-field to investigate the optimal operation of the power system. The OPF problem is a non-linear and non-convex optimization problem which is solved by various classical and natural-inspired methods [1]. However, the state-of-the-art methods are sensitive to the control variables, as well as having poor convergence and long computation delay. Furthermore, the previous work problem has high complexity and fails to solve the OPF problems with multiple control parameters as well as multiple objectives [2].

To tackle the above-mentioned problems, a newly designed algorithm, i.e., Hybrid Backtracking Search Optimization Algorithm with Grey Wolf Optimization (GWO-HBOA), is proposed in this work. Based on the IEEE 30-bus test system, the performance of the proposed GWO-HBOA is evaluated. The 30-bus test system, as shown in Fig. 1, is operated with 6 Distributed Generators (DGs) which distribute the power equally across the system. The objective of the proposed algorithm is to minimize the fuel cost which is essential for the generator. To this end, the power loss of the generators is reduced and the voltage stability of the DGs is enhanced. The proposed method can achieve low fuel costs under loss and lossless conditions. It outperforms the existing works in terms of voltage stability, voltage deviation, real power loss, and reactive power loss. Furthermore, the stable results can be obtained by the proposed algorithm in the IEEE 30-bus test system, even though the congestion occurs.

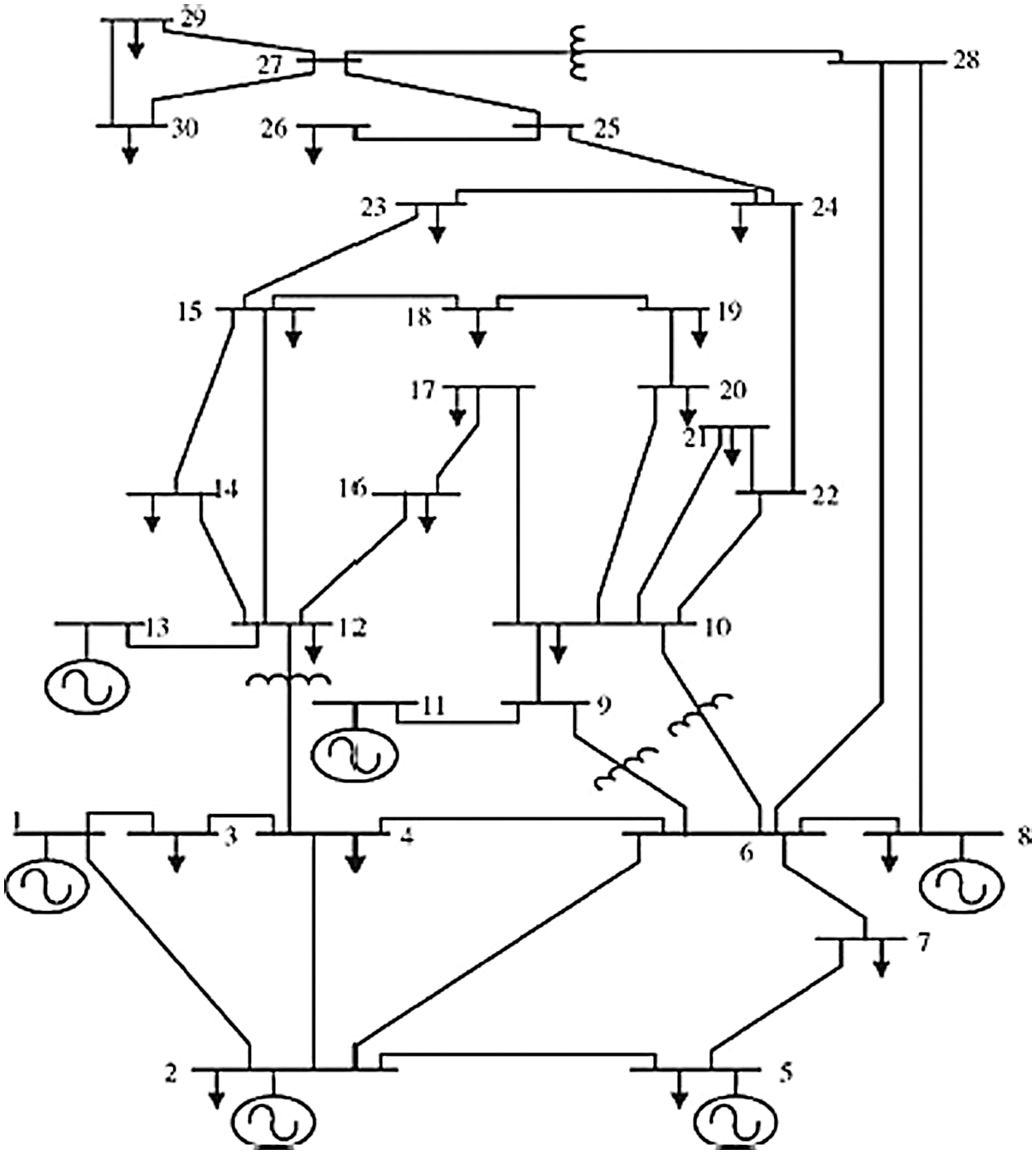
Figure 1: The representation of the IEEE 30-bus test system

2  Related Work

2.1 Various Techniques of Optimization Algorithms

To solve the OPF problem, a variety of classical methods are investigated in literature [3,4], including Gradient Methods (GM), Interior Point Method (IPM), Newton Method (NM), Linear Programming (LP), Decomposition Algorithm (DA), and Quadratic Programming (QP). Based on the formulation of the OPF problems, different control variables, e.g., real and reactive power of generators, phase shifter, tap changing of regulating transformers, real power outputs, switched capacitors and reactors, etc. [5,6], are manipulated to achieve an optimal setting in the power system. However, these methods are sensitive to the initial searching points, handling integers, and discrete variables. As a result, they are not applicable to solve the non-differentiable and non-convex objective functions.

In recent years, due to the advance of computer performance, it is possible to utilize the heuristic optimization methods (HOMs) to solve the OPF problem, including Particle Swarm Optimization (PSO), Biographically Based Optimization (BBO), Genetic Algorithm (GA), Artificial Bee Colony (ABC), Gravitational Search Algorithm (GSA), and so on. In particular, the ABC algorithm is proposed to optimize the ED problem in power dependent systems, taking into account the valve-point effect [7]. It is implemented in several test systems with the incremental fuel cost function. However, the HOM is prone to premature convergence and slow convergence, and thus failsto obtain the optimum solution.

2.2 Backtracking Optimization Methodology

Backtracking Search Algorithm (BSA) is a population-based evolutionary algorithm for numerical optimization problems, which is studied by researchers for solving the OPF problem [8]. To assign the DGs along with the radial distribution networks, El-Fergany [9] proposes the Backtracking Search Optimization Algorithm (BSOA). The algorithm has a unique control parameter as one of its key features. With the BSOA, the network real power loss is reduced and the voltage function is enhanced to improve the operational performance. Moreover, reduction in the network reactive power loss is determined, as well as the combined power factor. The initial DG locations are identified by the bus voltages and a set of fuzzy expert rules using loss sensitivity factors. Chaib et al. design a BSOA to solve the OPF problem. The proposed algorithm is tested in 16 different cases on several IEEE bus test systems, i.e., IEEE 118-bus system, IEEE 30-bus system, and IEEE 57-bus system. Besides the generating fuel cost, other factors, like the multi-fuel options and the valve-point effect, are measured. Moreover, the work considers various objectives, like voltage stability enhancement, voltage profile improvement, and emission reduction. The results show that BSOA outperforms the previous optimization algorithm for solving the OPF problems. Abd Ali et al. [10] utilize the Backtracking Search Algorithm (BSA) for maintaining the induction motor drive speed along with adaptive Fuzzy Logic Controller (FLC) design. The Mean Absolute Error (MAE) of the rotor speed response is used as a fitness function for a three-phase induction motor. Deploying the BSA-based FLC (BSAF) fitness function, the MAE is minimized and tuned for optimizing the induction motor performance, considering the changes in torque and speed. The real parameters of the induction motor are measured with three different practical examinations. To validate the developed controller, the BSAF is compared with the Gravitational Search Algorithm (GSA) and the Particle Swarm Optimization (PSO), respectively. Zhang et al. [11] propose a novel hybrid model for predicting the short-term wind speed. The predictor of the model is a compound structure of the Extreme learning machine (ELM) which selects features and optimizes parameters utilizing the hybrid backtracking search algorithm (HBSA). To improve the convergence speed of BSA. Wang et al. [12] design a modified BSA inspired by simulated annealing (BSAISA). Based on the Metropolis criterion in simulated annealing, the control factor (F) of the amplitude can be modified in the proposed BSAISA. The F will be decreased with the number of iterations increasing. The strict constraints are handled by a self-adaptive ɛ-constrained approach. The performance of the proposed BSAISA is compared with the normal BSA and other classical algorithms. Five problems of engineering design, as well as 13 constrained benchmarks, are solved during the simulation. The results show that the BSAISA is more efficient than the normal BSA and presents a higher convergence speed than other compared classical algorithms.

2.3 Optimal Power Flow

Anese et al. [13] study the distribution networks featuring the inverter-interfaced distributed energy resources. The distributed feedback controllers are developed to continuously drive the inverter output powers to solve the AC OPF problems. The power set points are updated by controllers according to the voltage measurements and the OPF targets. The basic and fundamental procedures are implemented on the microcontrollers at low cost, which accompanies the power-electronics interfaces of gateways and inverters. In recent years, the convex relaxations for the power flow equations, e.g., Semi-Definite Programming (SDP) and Second Order Cone relaxations (SOC), have attracted attention from researchers. Constraints are imposed to preserving strong connections among voltage variables with the convex envelops of polar representation l. Carleton et al. [14] analyze the value of Quadratic Convex (QC) relaxation for AC OPF subject to the realistic side restrictions. The theoretical results present that the QC relaxation outperforms the SOC relaxation. The QC relaxation does not dominate or is dominated by the SDP relaxation. Shao et al. [15] determine the OPF in a multi-carrier energy system via a novel Mixed Integer Linear Programming (MILP) technique. Instead of introducing the conventional dispatch factor variables, a state variable based linear energy hub model is investigated. The approximation error is analyzed in the non-convex natural gas transmission constraints which are represented by the multi-dimensional piecewise linear approximation approach. Hence, the OPF is transferred into a MILP problem. Compared with the non-linear models, it is available to utilize the easy-implemented method in literature to solve the proposed model in the optimal power system scheduling problem. The proposed algorithm is evaluated in the modified 6-bus and IEEE-118-bussystems. The results show that the proposed method improves the speed of solving the OPF problem while meeting the requirement of accuracy, which is applicable to large-scale hub systems. Bouchekara et al. [16] propose an Improved Colliding Bodies Optimization (ICBO) method for solving the OPF problem efficiently. The optimization problem is modeled by objectives, constraints, and formulations at both ordinary and preventive processing circumstances. The validity and feasibility of the proposed algorithm are evaluated on three IEEE standard test systems with 16 scenarios. Mohamed et al. [17] propose a moth swarm algorithm for solving the OPF problem, which is inspired by the orientation of moths towards the moonlight. To improve the process of Lévy-mutation, they introduce the associative learning mechanism with population variety crossover and instant storage. The proposed algorithm is compared with the other four heuristic algorithms on the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus power system. Fourteen cases with several parameters are studied to evaluate the performance of the proposed algorithm. Viola et al. [18] investigate the Optimal Reactive Power Dispatch (ORPD) for improving voltage stability. A Chaotic Krill Herd algorithm is proposed to achieve ORPD in the power system. The proposed algorithm is analyzed on the standard IEEE 30-bussystem, which aims at optimizing the total voltage deviation, the voltage stability index, and the power loss. Anbarasan et al. [19] introduce a novel method, i.e., Moth Flame optimization algorithm, to solve the ORPD problem. The aim of the algorithm is to reduce the energy loss and control the bus voltage in the power system. The optimal settings of the parameters are obtained using the standard IEEE 30-bus and 57-bus systems. The proposed algorithm can outperform other state-of-the-art work with efficient test results. Mohagheghi et al. [20] develop a framework for the OPF to improve both the feasibility and optimality in the process of power distribution under intermittent wind energy penetration. They minimize the Mixed-Integer Nonlinear Programming (MINLP) problem with two phases, i.e., the forecast phase and the realization phase. Here, the proposed algorithm is demonstrated in a 41-bus distributed network.

In summary, the state-of-the-art algorithms have low exploration capability, of which performance is thus limited. Moreover, considering the assembling of the distributed resource, the interaction among aggregators should be clarified further at the high-level transformation in the existing systems. Furthermore, the systems are facing various inbuilt computational challenges, due to the enormous distributed resources.

3  Proposed Algorithms for OPF Problem

To handle these problems, it is required to design a reliable optimization algorithm. In this research work, Hybrid Backtracking Search Optimization Algorithm with Grey Wolf Optimization (GWO-HBOA) is proposed to tackle various OPF problems, such as the high total fuel cost of the generation units, power losses, and unstable voltages during unintended variations. The performance of the proposed algorithm will be demonstrated on the IEEE 30-bus system in two specific cases: (i) with the optimal placement of Distributed Generators (DG) and (ii) without the placement of this DG at all.

3.1 Backtracking Search Optimization Algorithm

The BSOA [21] mainly consists of five phases as follows. At each iteration, the population P and the historical population Old P are triggered randomly, as indicated in the following basic steps. Random symbols are temporarily allocated to discriminate different variables, whenever the mathematical relations are introduced for the implementation of a typical BSA phenomenon. For instance, the population will be allocated as I, the uniform will be denoted as R, and the mutation will be allocated as D

Phase 1: Initialization

Initialization phase in BOA can be represented as

Iij∼R(lessj,highj)oldIij∼R(lessj,highj) (1)

where i represents the i-th individual in the population, and i is smaller than N, i.e., the number of the individuals in the population j denotes the Dimensions D.lessj and highj are the minimum and the maximum of the parameters, respectively.

The overall process flow of the proposed GWO-HBOA algorithm is shown in Fig. 2, which is based on the IEEE 30-bus system.

Phase 2: Preference 1

Preference 1 phase can be given by

{I,if(x<y|x,y∼R(0,1))oldI,otherwise (2)

oldI: = permuting(oldI)

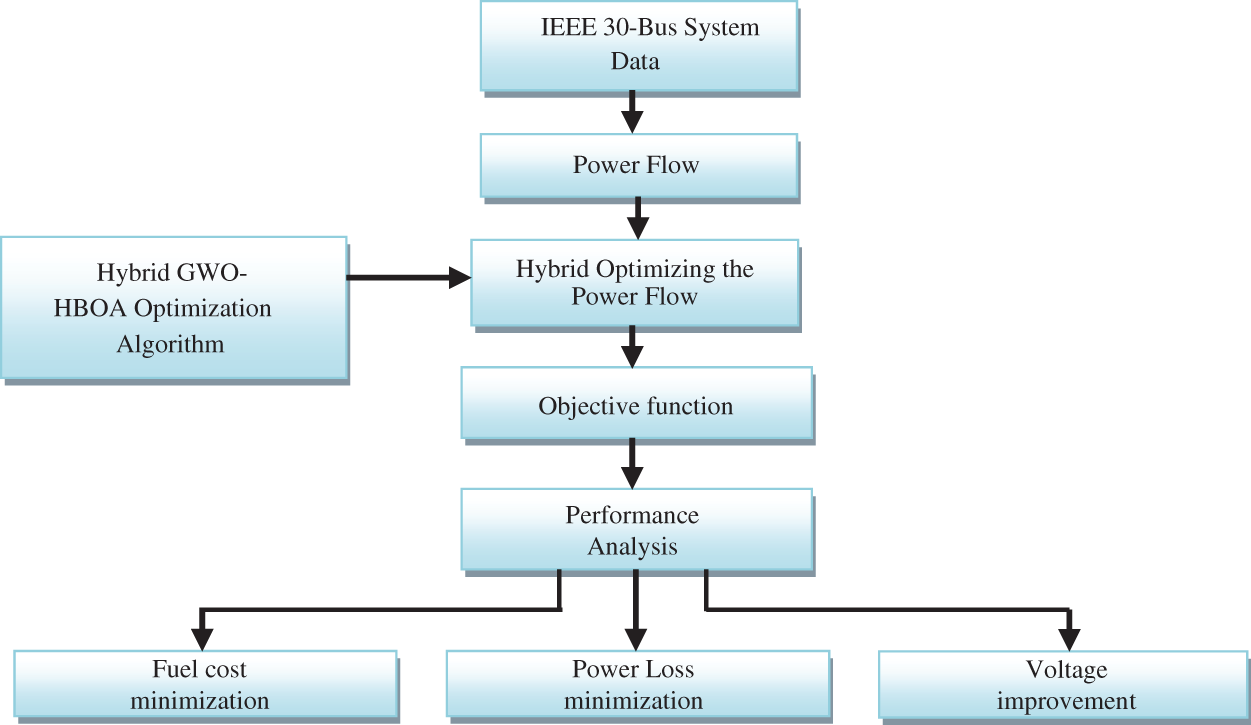
Figure 2: The proposed flow diagram

where the operation “:=” shows if the attributes on the two sides are equal, x and y are two randomized numbers, and the operating permuting( ) outputs a value ranging from 1 to n.

Phase 3: Mutation

Mutation phase is expressed by

Dij=Iij+K∗(oldIij−Iij) (3)

where Iij and old Iij represent the corresponding gene locus of the individual i and j, respectively.

Phase 4: Crossover

Crossover phase is given by

Wi,j={Ii,jifmapi,j=1Di,j,otherwise (4)

where Ii,j and Di,j represent the corresponding gene locus of the individual i and j, respectively.

Phase 5: Preference 2

Preference 2 phase is given by

Ii={Wi,iff(Wi)≤f(Ii)Ii,otherwise (5)

where Wi representsweights of ith vector. Subsequently, GWO will be modified and implemented by computing the LMP, which is discussed in the following subsection.

3.2 LMP Calculation

When calculating the LMP, the DCOPF problem is solved with GWO, considering the fixed and linear bids with concentrated loss and without concentrated loss, respectively. To optimize the problem, the active power generation of the generators is regarded as the variable, where the slack generation is excluded. The achieved power generation is used during the LMP calculation for the congested transmission system. The transmission line flows can be calculated by the Generation Shift Factor (GSF) and include the marginal losses price on nodal price; a Delivery Factor (DF) at buses is used. After the computation, the demand response of the proposed system is estimated in terms of the OPF problem.

3.3 Generation Shift Factor (GSF)

The GSF is defined as the proportion of the variation in power discharge in the line, i.e., k, to the variation injecting the power on the bus, i.e., i. The factor for GSF is calculated as,

GeneratorShiftFactor,GSFk−i=(B(a,i)−1−B(b,i)−1)Xk (6)

where a is the transmitting bus, B−1 is the imaginary of the bus matrix Y, b is the receiving bus of line k, and Xk is the reactance of line k.

3.4 Delivery Factor

The DF on the ith bus denotes the strong power supplied to the user for serving the load at the same bus. Based on the marginal loss factor, the marginal loss price will be considered, as well as the ordinary LF, the marginal DF, and the ordinary DF. The following equation represents the mathematical formation of the delivery factor.

DF=1−LFi=1−∂Ploss∂Pi (7)

where LFi, L is loss factor at bus i.

Ploss=∑k=1M⁡Fk2×Rk (8)

Fk=∑k=1M⁡GSFk−i×Pi (9)

where Rk is the resistance of line k and Fk is the Line Flow of k.

The Ploss could can be calculated by the summation of line flow and the resistance of the line. The line flow is found by the generator shift factor of the ith bus and the power of the ith bus.

Pi=PGi−PDi=injectionatbus′i′ (10)

We use GSFk−i to denote the GSF from the ith bus to line k . The LF of the ith bus can be observed by the variation of the total system loss regarding the power injection increasing in the same bus.

3.5 LMP Calculation without Concentrated Loss

In this process, the key purpose is to reduce the overall marginal production cost affecting the restrictions of line flow and demand balance. These issues are solved with the proposed GWO technique. Based on the generator power outputs, the LMPs are calculated. The total fuel cost can be analyzed with the existing GA and LP approaches. This calculation depends on the payments from ISO to generators, the generator profit, payments from load to ISO, and the ISO profit. As a result, the objective function is defined as

MinimizeJ=∑i=1N⁡Ci(s) (11)

s.t∑i=1N⁡PGi=∑i=1N⁡PDi (12)

Fk≤limitk (13)

k=1,2,…MPGimin≤PGi≤PGimaxi=1,2,…N (14)

where N denotes the number of buses, M is the number of lines, PGi denotes the output power of the generator on ith bus, Fk is the line flow of line k , PDi represents the power demand at bus i, and limitk is the thermal limit of line k.

Under the lossless condition, the cost function of the generator is calculated. In this way, two output powers of the generator at the ith bus are considered. The unit of the generation cost is in dollars per hour.

Ci(s)=biPGi+ciPGi2in$/hr (15)

where Ci(s) is the cost function of the generator.

3.6 LMP Calculation with Concentrated Loss

In this subsection, the total marginal production cost, related to the line flow constraints and the energy balance, is required to be minimized. However, in the electricity markets, the LMP-based system marginal loss has a huge effect on the economy of the power system operation. Therefore, the system marginal loss ought to be considered for obtaining highly accurate prices. In this model, we consider that the slack bus generator supplies the total system loss.

The problem is formulated as

MinimizeJ=∑i=1N⁡Ci(s) (16)

s.t∑i=1N⁡(DFi×Pi)+Ploss=0 (17)

Fk≤limitk (18)

k=1,2,…MPGimin≤PGi≤PGimaxi=1,2,…N (19)

where Ploss is the total system loss, and it is utilized for offsetting the doubled average system loss produced by the marginal LF and the marginal DF. Then the output power of the generator is obtained on the dispatch, and the slack bus power will be deliberated. The price of the slack bus is calculated by changing the slack bus with fixed or linear bids. The congestion and loss price will be zero in the reference bus. Moreover, the energy component price will be equal to the reference bus price.

3.7 Decomposition of LMP

LMPBcong=−∑k=1M⁡GSFk−B×μk (20)

where μk is the restricted cost of line k and is defined as:

μk=changeintotalcostchangeinconstraint′sflow (21)

LMPBloss=λ×(DFB−1) (22)

(LMPBloss=0forlosslesspowersystem) (23)

LMP=LMPenergy+LMPBcong+LMPBloss (24)

The total LMP at each bus is obtained by calculating the individual components of the LMP. It is beneficial to determinate the demand response of the generated power in the developed circuit.

3.8 LMP computation for optimizing with Hybrid GWO-HBOA

First of all, BSO is proceeded with some variations. Then GWO is implemented and combined with BSO, namely the novel Hybrid GWO-HBOA method. The algorithm is described by the pseudo code as follows.

Algorithm for LMP computation using Hybrid GWO and HBOA

Step-1: Gather the data of the respective IEEE 30-Bus analysing system along with the concerned data of generators

Step-2: Load the count of Searching Agents, Maximum iteration value for Hybrid GWO and HBOA

Step-3: Calculate the Power Generation and Power Demand using the information obtained from Step-1

Step-4: Track the search agents in a random manner

Step-5: Compute the Factor of Generation Shift

Step-6: Compute the line flows

Step-7: Compute the loss of the system, i.e., Ploss in each line for a loss condition

Step-8: Estimate the delivery factor (DF) at each bus

Step-9: Let to initialize the α, β, ϑ positions

Step-10: αp = zeros(1, di )

4  Experiment Results

In this section, four existing methods, i.e., Refs. [22–25], are compared with the proposed algorithm. Tab. 1 shows that the proposed method has a better performance than the other two previous algorithms, since the GWO-HBOA can achieve less fuel cost values than the others by generating the appropriate power.

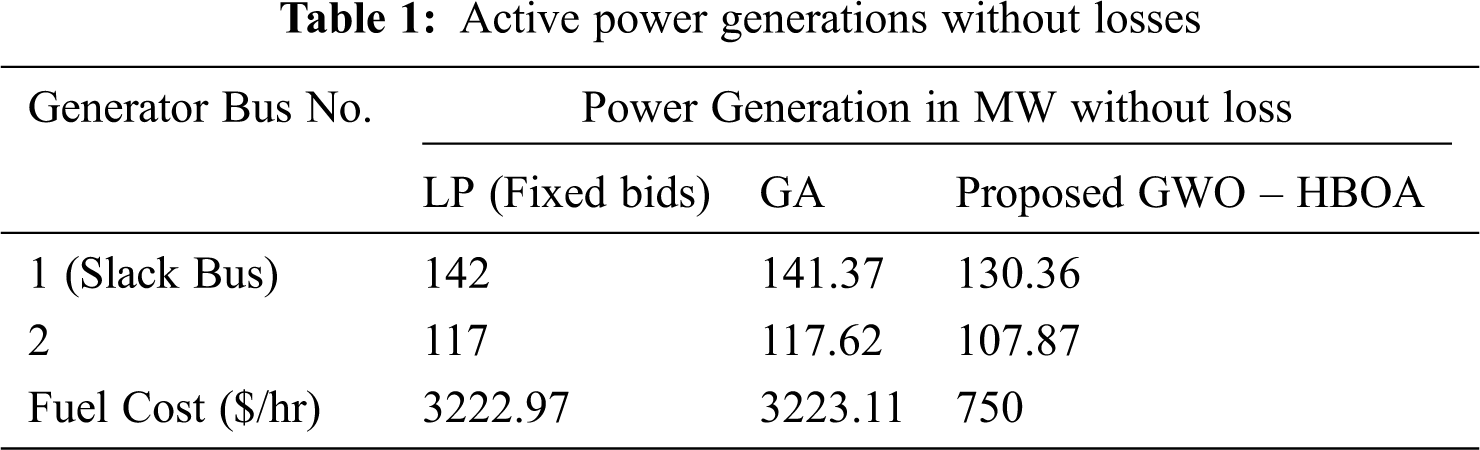
From Fig. 3, we can observe that the proposed method has less fuel cost than the GA and the LP with fixed bids, regardless of the losses in the circuit.

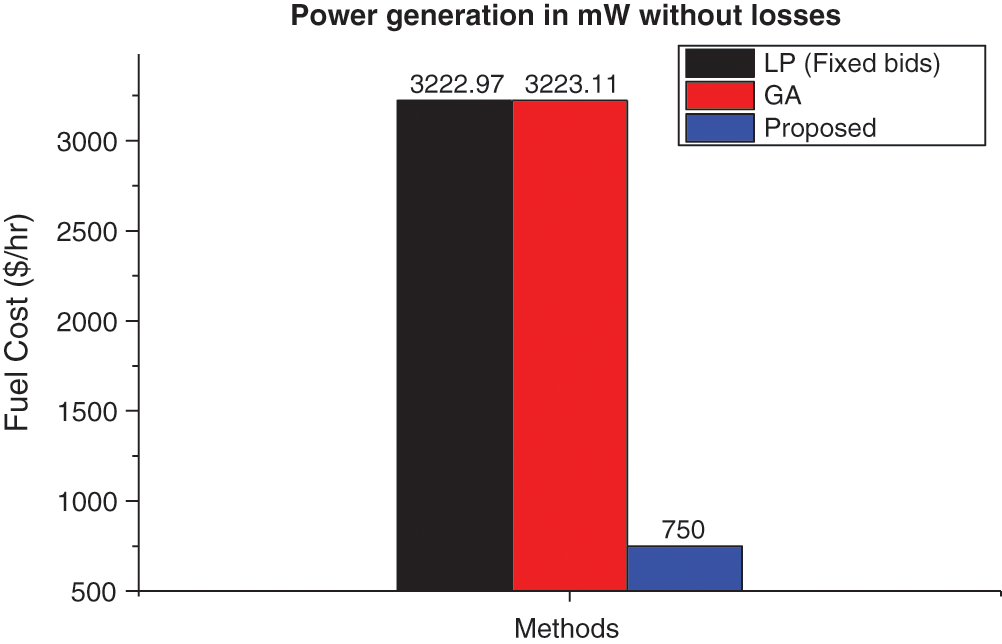
Figure 3: The fuel cost performance of GWO-HBOA without losses

Similarly, Tab. 2 and Fig. 4 present that our method obtains less fuel cost than the other two algorithms, even when the losses are considered. Moreover, from Tab. 3, we can see that the proposed algorithm outperforms the existing method QP, since it is efficient enough to reduce the cost.

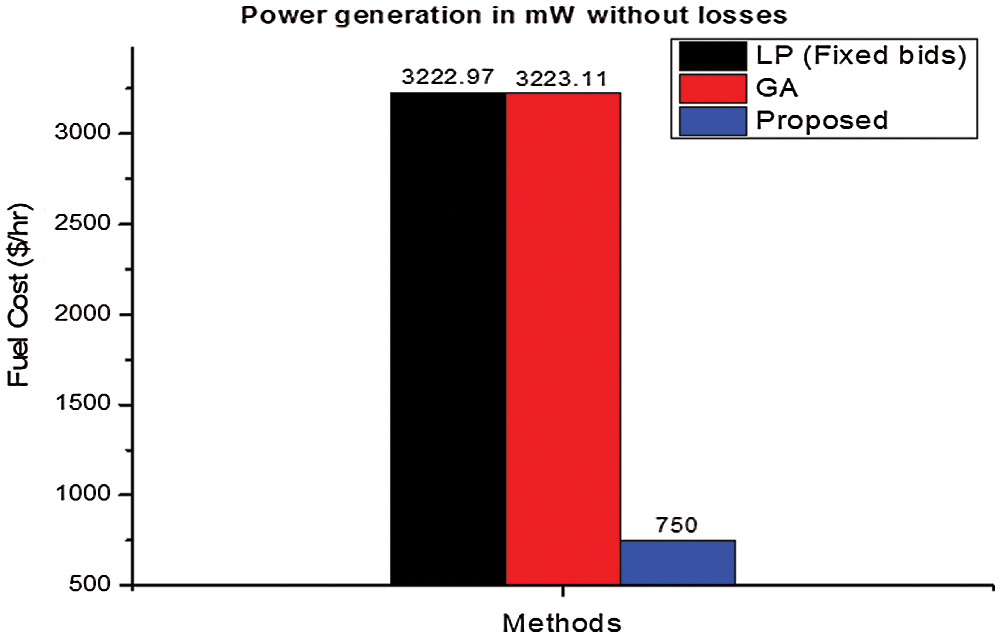
Figure 4: The fuel cost performance of GWO-HBOA with losses

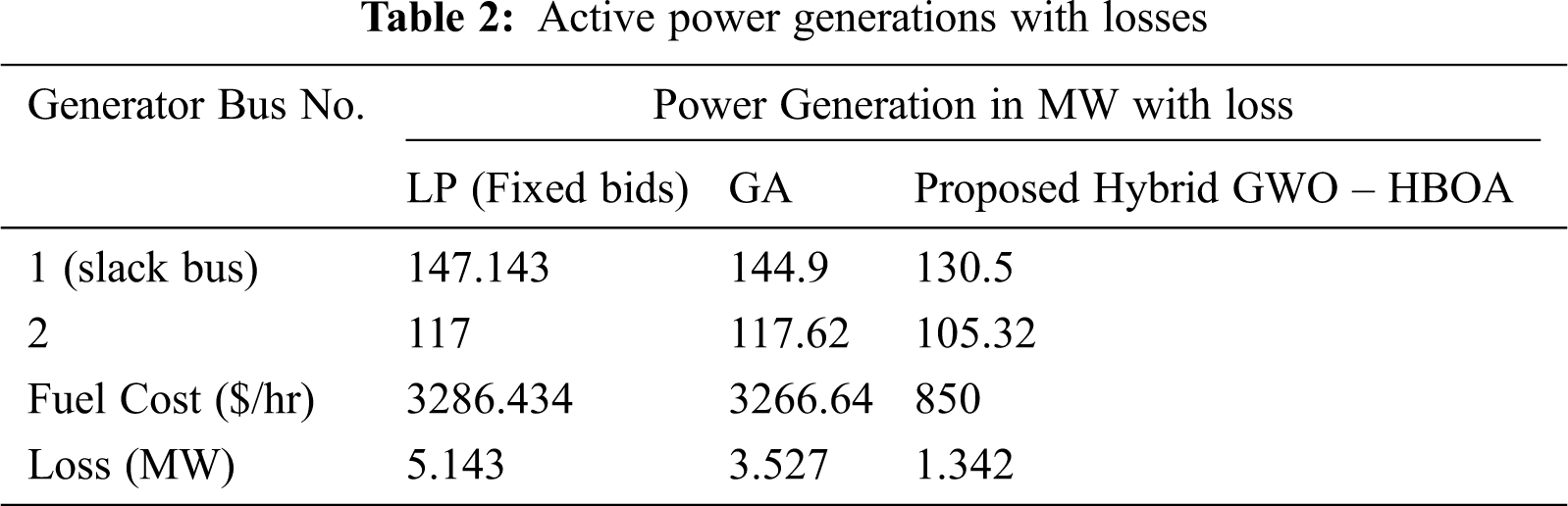
Fig. 5 illustrates the performance of the proposed method when the normal condition is considered. We can observe that our method has stable and similar results with the LMP, and it has smaller augmented LMP values than QP. In addition, Tab. 4 shows that the proposed methodology is better than the existing method QP, as it is efficient enough to have lower LMP values.

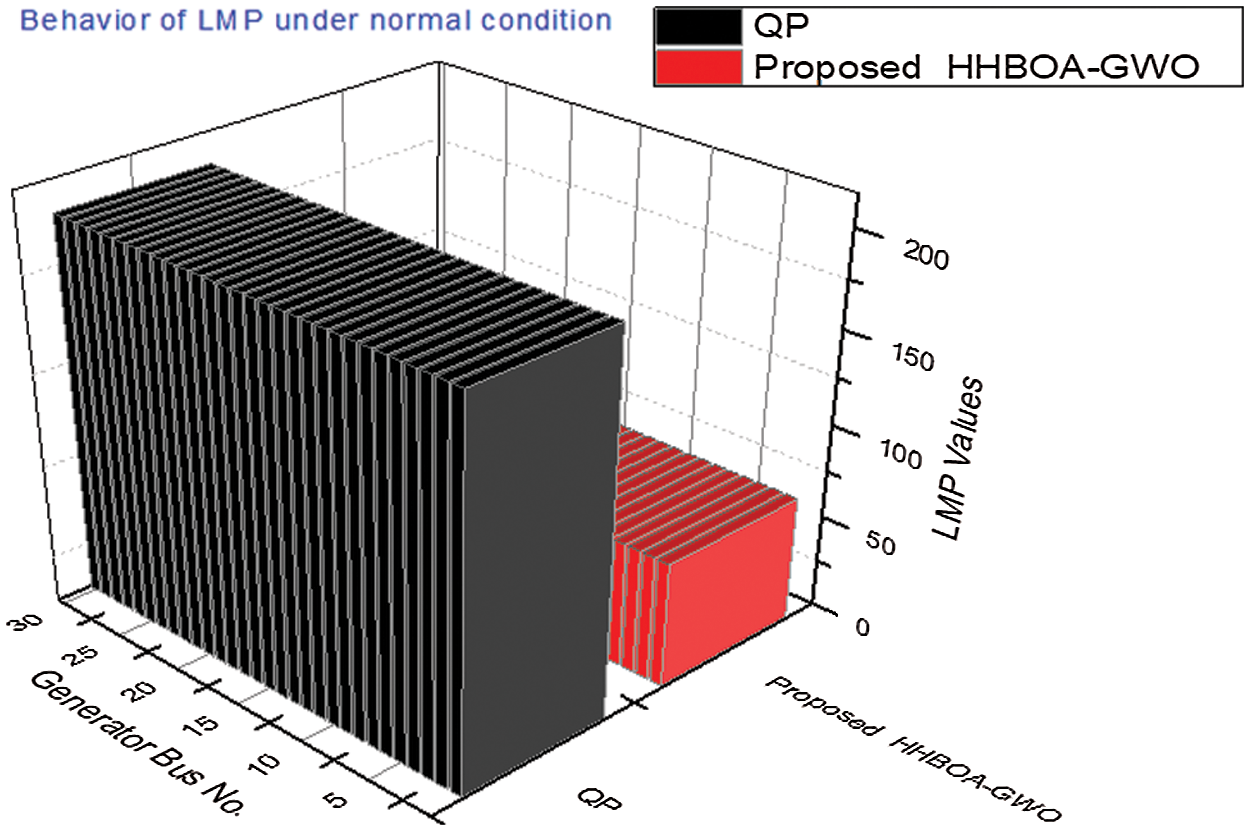
Figure 5: The behavioral investigation of LMP under normal conditions

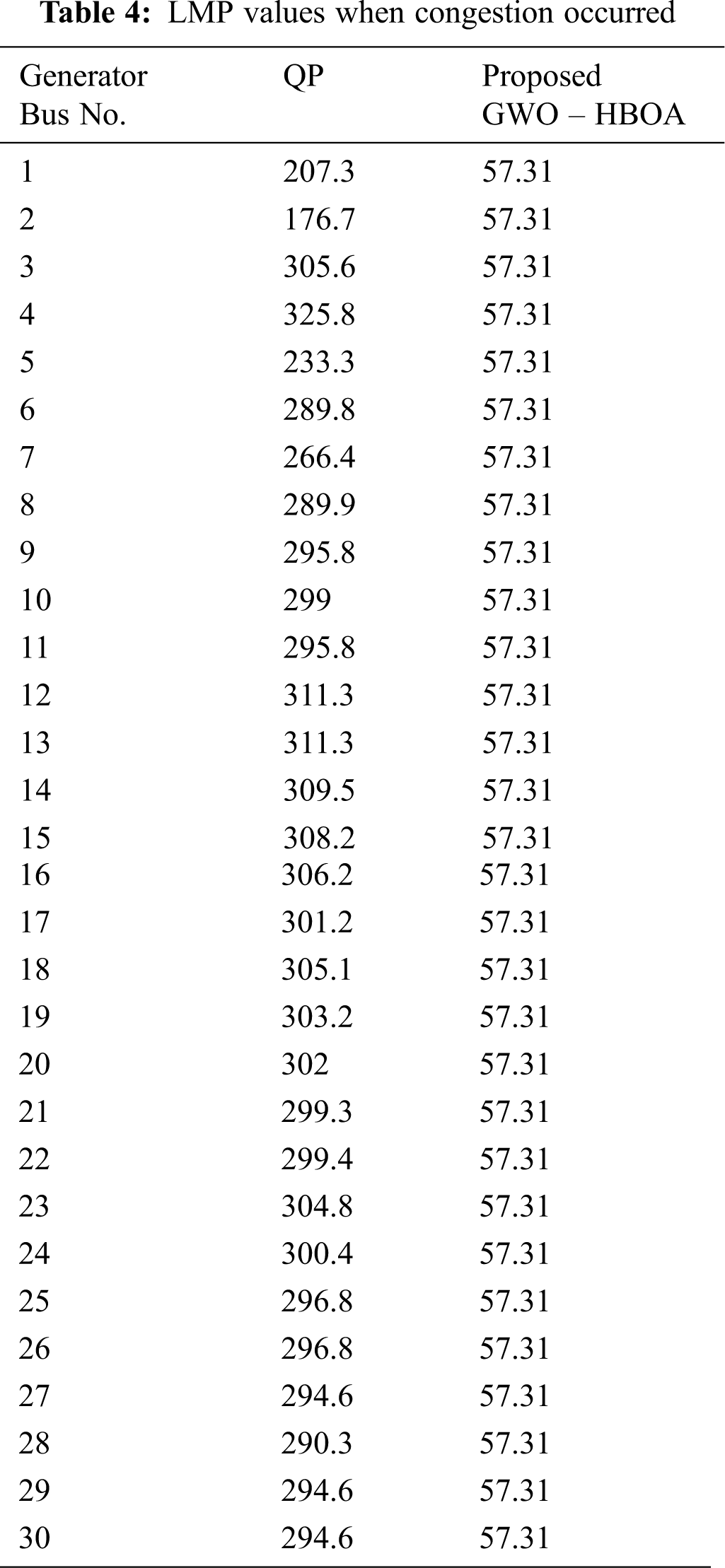
Fig. 6 depicts the nature of the proposed method, subjected to congestion conditions. We can observe that our method obtains stable LMP even under the congestion condition. Compared with that, the LMP of the existing method QP is higher and varies dramatically.

The following will compare the simulation results of the GWO-HBOA at Matlab with the conventional GWO and BSA, in terms of fuel cost, voltage stability, voltage deviation, as well as real and reactive power losses.

Figure 6: The behavioral investigation of LMP under congestion conditions

In Fig. 7, the fuel cost is represented as the current cost during the Matlab simulations. Five hundred iterations are implemented at each simulation. From the figure, we can see that the GWO-HBOA has a lower fuel cost than both the GWO and BSA.

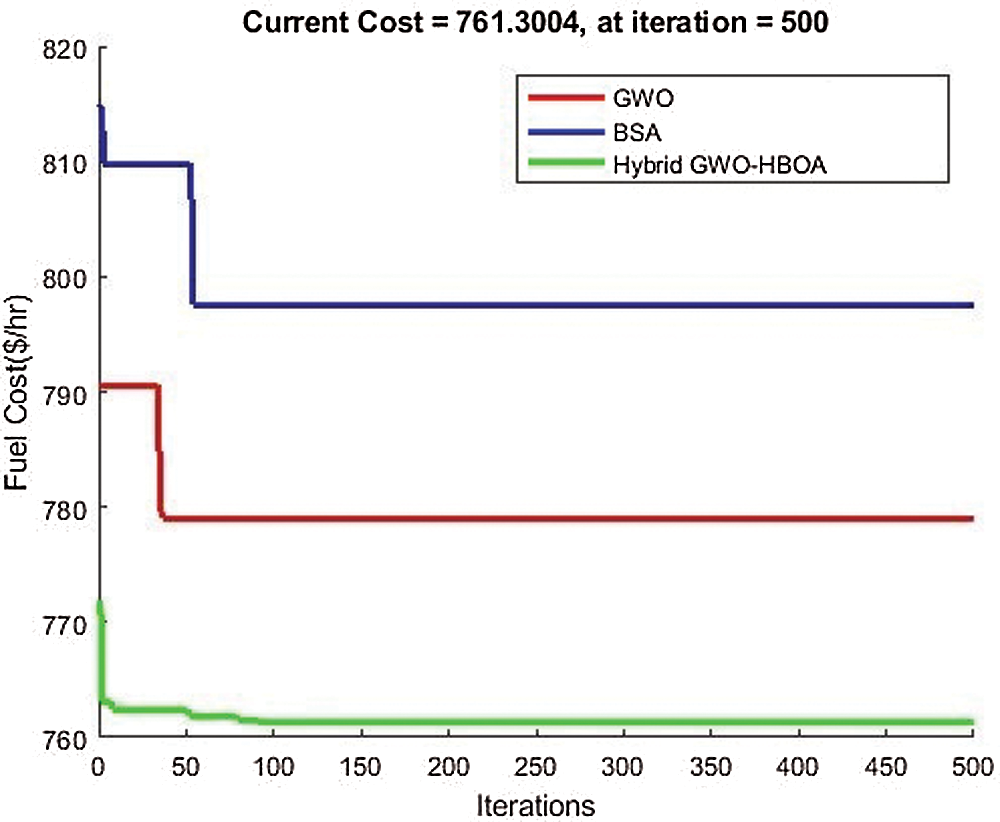
Figure 7: Minimized fuel cost against the existing GWO and BSA

The comparison of the voltage stability among different algorithms is indicated in Fig. 8. The figure shows that the proposed GWO-HBOA obtains better voltage stability than the existing methods.

In Fig. 9, the voltage deviation is analyzed among different algorithms. Compared with the GWO and BSA, the proposed algorithm has lower voltage deviations and smaller fuel costs. Furthermore, in terms of the real and reactive power losses, the proposed method outperforms the other two algorithms in Figs. 10 and 11, respectively, during the 500 simulation iterations.

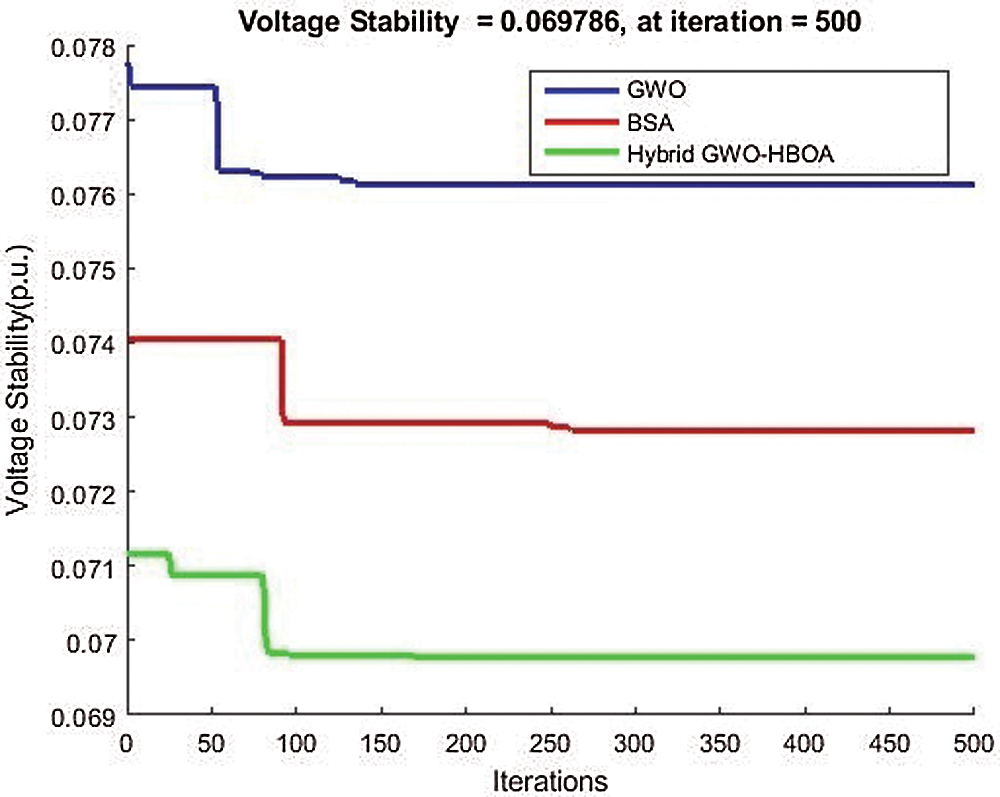
Figure 8: Minimized voltage stability against the existing methods of GWO and BSA

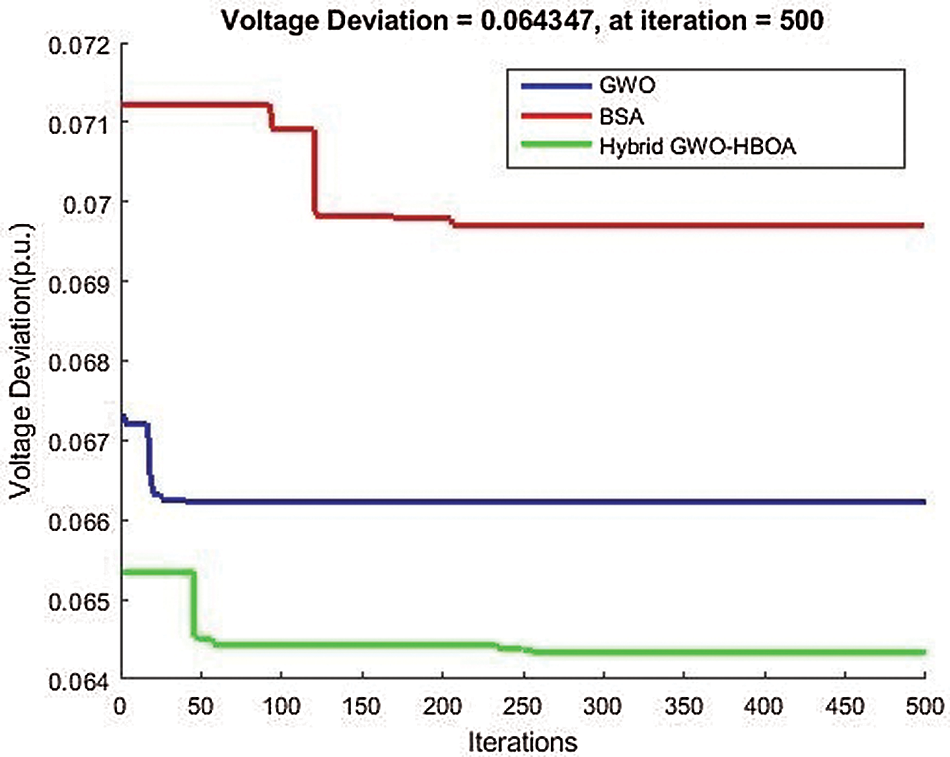
Figure 9: Minimized voltage deviation against the existing GWO and BSA

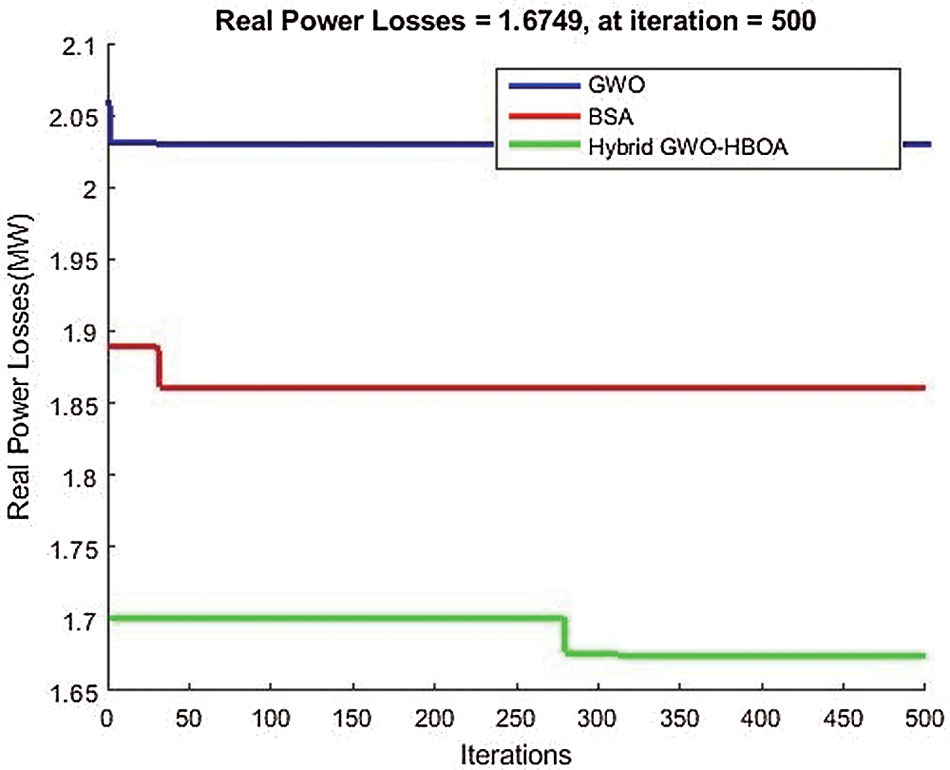
Figure 10: Minimized real power loss against the existing methods of GWO and BSA

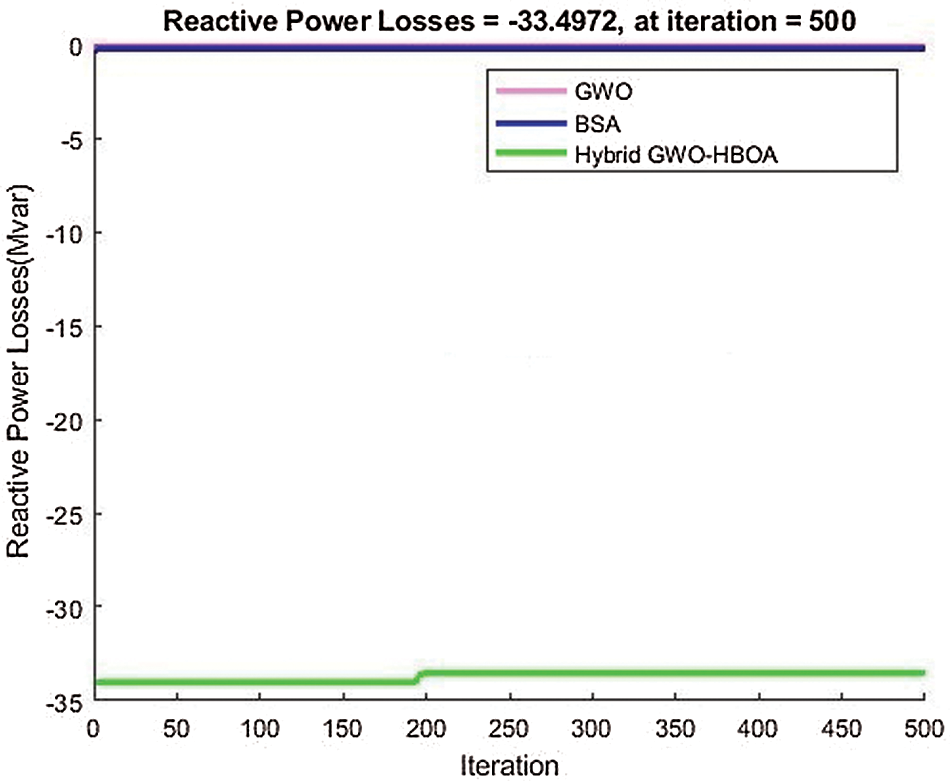
Figure 11: Minimized reactive power loss against the existing methods of GWO and BSA

5  Conclusion

As the LMP plays an important role in restructured energy markets, a simple transmission pricing scheme, i.e., GWO-HBOA, is proposed to obtain the optimal power. Firstly, the LMP is calculated under the loss and lossless conditions for both fixed bids and linear bids. Then, to determine the LMP loss, DC optimal power flow is investigated, and the DCOPF problem under each loss case is analyzed as well. The proposed algorithm is evaluated on the IEEE 30-bus test system. Based on the power generation analysis, the proposed method can consume less fuel cost than the existing algorithm, under both the loss and lossless conditions. Moreover, the proposed GWO-BSOA can improve voltage stability, voltage deviation, real power loss, and reactive power loss in the system. The simulation results are stable even though the congestion occurs. And the same results are obtained when the normal congestion is considered. Furthermore, by estimating the demand response of the generated power, the proposed scheme can solve the overloading problem which is the major issue of LMP.

Acknowledgement: We appreciate the linguistic assistance provided by TopEdit (www.topeditsci.com) during the preparation of this manuscript.

Funding Statement: The authors received no specific funding for this research work.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that may have appeared to influence the work reported in this paper.

References

 1.  M. Abdo, S. Kamel, M. Ebeed, J. Yu and F. Jurado, “Solving non-smooth optimal power flow problems using a developed grey wolf optimizer,” Energies, vol. 11, pp. 1692, 2018. [Google Scholar]

 2.  E. Mohagheghi, M. Alramlawi, A. Gabash and P. Li, “A survey of real-time optimal power flow,” Energies, vol. 11, pp. 3142, 2018. [Google Scholar]

 3.  V. Yadav and S. P. Ghoshal, “Optimal power flow for IEEE 30 and 118-bus systems using Monarch Butterfly optimization,” in Technologies for Smart-City Energy Security and Power (ICSESP), pp. 1–6, 2018. [Google Scholar]

 4.  S. Elsaiah, N. Cai, M. Benidris and J. Mitra, “Fast economic power dispatch method for power system planning studies,” IET Generation, Transmission & Distribution, vol. 9, pp. 417–426, 2015. [Google Scholar]

 5.  J. Zhu, Optimization of Power System Operation. Hoboken, NJ: John Wiley & Sons, 2015. [Google Scholar]

 6.  J. C. Bansal, S. S. Jadon, R. Tiwari, D. Kiran and B. K. Panigrahi, “Optimal power flow using artificial bee colony algorithm with global and local neighborhoods,” International Journal of System Assurance Engineering and Management, vol. 8, pp. 2158–2169, 2017. [Google Scholar]

 7.  Y. Labbi, D. B. Attous and B. Mahdad, “Artificial bee colony optimization for economic dispatch with valve point effect,” Frontiers in Energy, vol. 8, pp. 449–458, 2014. [Google Scholar]

 8.  A. Chaib, H. Bouchekara, R. Mehasni and M. Abido, “Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm,” International Journal of Electrical Power & Energy Systems, vol. 81, pp. 64–77, 2016. [Google Scholar]

 9.  A. El-Fergany, “Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm,” International Journal of Electrical Power & Energy Systems, vol. 64, pp. 1197–1205, 2015. [Google Scholar]

10. J. Abd Ali, M. Hannan, A. Mohamed and M. G. Abdolrasol, “Fuzzy logic speed controller optimization approach for induction motor drive using backtracking search algorithm,” Measurement, vol. 78, pp. 49–62, 2016. [Google Scholar]

11. C. Zhang, J. Zhou, C. Li, W. Fu and T. Peng, “A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting,” Energy Conversion and Management, vol. 143, pp. 360–376, 2017. [Google Scholar]

12. H. Wang, Z. Hu, Y. Sun, Q. Su and X. Xia, “Modified backtracking search optimization algorithm inspired by simulated annealing for constrained engineering optimization problems,” Computational intelligence and neuroscience, vol. 2018, no. Article ID 9167414, pp. 1–28, 2018. [Google Scholar]

13. D. Anese and A. Simonetto, “Optimal power flow pursuit,” IEEE Transactions on Smart Grid, vol. 9, no. 2, pp. 942–952, 2016. [Google Scholar]

14. C. Carleton, H. L. Hijazi and P. V. Hentenryck, “The QC relaxation: Theoretical and computational results on optimal power flow. arXiv preprint arXiv:1502.07847, 2015. [Google Scholar]

15. C. Shao, X. Wang, M. Shahidehpour, X. Wang and B. Wang, “An MILP-based optimal power flow in multicarrier energy systems,” IEEE Transactions on Sustainable Energy, vol. 8, pp. 239–248, 2016. [Google Scholar]

16. H. R. Bouchekara, A. Chaib, M. A. Abido and R. A. El-Sehiemy, “Optimal power flow using an improved colliding bodies optimization algorithm,” Applied Soft Computing, vol. 42, pp. 119–131, 2016. [Google Scholar]

17. A. A. A. Mohamed, Y. S. Mohamed, A. A. El-Gaafary and A. M. Hemeida, “Optimal power flow using moth swarm algorithm,” Electric Power Systems Research, vol. 142, pp. 190–206, 2017. [Google Scholar]

18. R. Viola and A. Subramanian, “Optimal reactive power dispatch using chaotic krill herd algorithm,” Asian Journal of Applied Science and Technology (AJAST), vol. 1, pp. 283–287, 2017. [Google Scholar]

19. P. Anbarasan and T. Jayabarathi, “Optimal reactive power dispatch using Moth-flame optimization algorithm,” International Journal of Applied Engineering Research, vol. 12, pp. 3690–3701, 2017. [Google Scholar]

20. E. Mohagheghi, A. Gabash and P. Li, “A framework for real-time optimal power flow under wind energy penetration,” Energies, vol. 10, pp. 535, 2017. [Google Scholar]

21. P. Civicioglu, “Backtracking search optimization algorithm for numerical optimization problems,” Applied Mathematics and Computation, vol. 219, pp. 8121–8144, 2013. [Google Scholar]

22. M. Murali, M. S. Kumari and M. Sydulu, “LMP based electricity market simulation using genetic algorithm,” in 2012 7th IEEE Conf. on Industrial Electronics and Applications (ICIEApp. 1285–1290, 2012. [Google Scholar]

23. N. Rezaei, M. N. Uddin, I. K. Amin, M. L. Othman and I. Z. Abidin, “Grey wolf optimization based improved protection of wind power generation systems,” in 2018 IEEE Industry Applications Society Annual Meeting (IASpp. 1–8, 2018. [Google Scholar]

24. F. Zou, D. Chen and R. Lu, “Hybrid hierarchical backtracking search optimization algorithm and its application,” Arabian Journal for Science and Engineering, vol. 43, pp. 993–1014, 2018. [Google Scholar]

25. A. Abirami and T. Manikanda, “Locational M"locational marginal pricing approach for a deregulated electricity market,” International Research Journal of Engineering and Technology, vol. 2, pp. 348–354, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.