DOI:10.32604/iasc.2022.019525

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.019525 |  |
| Article |
H-infinity Controller Based Disturbance Rejection in Continuous Stirred-Tank Reactor
1Department of Electrical and Instrumentation Engineering, Thapar Institute of Engineering and Technology, Patiala, 147004, India
2Department of Electrical and Instrumentation Engineering, Thapar Institute of Engineering and Technology, Patiala, 147004, India
*Corresponding Author: Smarajit Ghosh. Email: sghosh@thapar.edu
Received: 16 April 2021; Accepted: 18 May 2021
Abstract: This paper offers an H-infinity (H∞) controller-based disturbance rejection along with the utilization of the water wave optimization (WWO) algorithm. H∞ controller is used to synthesize the guaranteed performance of certain applications as well as it provides maximum gain at any situation. The proposed work focuses on the conflicts of continuous stirred-tank reactor (CSTR) such as variation in temperature and product concentration. The elimination of these issues is performed with the help of the WWO algorithm along with the controller operation. In general, the algorithmic framework of WWO algorithm is simple, and easy to implement with a small-size population and only a few control parameters. The planned work gives the enhanced performance by means of disturbance rejection when compared with the PID, ADRC and ANN controllers. Additionally, the proposed work improves the lifespan of the offered application through the elimination disorders. The overall process is implemented in the MATLAB working platform and the results are compared with the preceding methods to show the expected performance.
Keywords: Artificial neural networks; soft computing; h-infinity controller; continuous stirred-tank reactor; temperature; water wave optimization
Generally, H∞ methods are the type of control theory used to stabilize the performance of controllers through synthesizing the corresponding compensator. In this method, issues related to the controller can be considered as the mathematical optimization problems and solved by selecting precise controller. These methods give direct solution to all kinds of problems than other approaches like optimization methods, non-linear programming and theoretical method. But it requires mathematical understanding to provide better outcomes for controlling purpose [1,2]. Actually, the conversion of electrical energy into mechanical energy is the main principle of DC motor. The current flow can be changed with the help of internal mechanism such as electromechanical mechanisms [3]. The supply voltage or current flow can be altered to change the motor speed. In general, DC brushless motor is more beneficial than the brushed types [4,5].
Armature, commutator segments and brushes are the main parts of the DC motor. Control strategies are normally utilized to eliminate the non-linearity present in the DC motors. Through these control techniques, optimization of motor position or rotor speed is possible under the variable load torque [6,7]. Commonly, issues related to tracking problem can be solved through the architecture design known system parameters [8]. Input–output linearization techniques are well suitable to generate the common controlling mechanisms. It is possible when the system has better knowledge about the plant non-linearity [9,10]. The H∞ control theory contains two inputs and two outputs and among them the input includes the reference signal and disturbances [11].
It is a special type of methodology in order to enable the controller design. Because, each and every tuning parameter has clear effectiveness of this method [12]. Similarly, the evaluation of feedback quality can be performed with the help of a certain set of analysis tools. But the feed forward type provides better performance than the other one. In general, control objective reformulation can be played as the important factor in the controller design [13,14]. If the H∞ criterion is smaller, the corresponding objective satisfaction is more when compared with the existing methods [15–17]. The continuous stirred-tank reactor is a common term used in the field of chemical engineering. The robust H-infinity control strategy has been proposed for a tractor trailer system in kinematic and dynamic framework [18]. A robust H-infinity control output feedback control is designed using μ synthesis for the H infinity disturbance rejection controller, aiming at robustness.
The proposed system can run at steady state with the non-stop flow of products and reactants, which contains uniform feed composition as that of the exit tank system [19]. It requires a 65% time for the conversion of body from one form to steady state. The classification includes tubular, semi-batch, flow and batch reactors. All industrial chemicals contain chemical kinetics and reactor design as the important information. The selection of reactor system must be clear to avoid the failure of the chemical plant [20]. In Hurtado et al. [21], fluid dynamic behavior is represented in CSTR by means of numerical analysis. Actually, mixing is one of the vital steps in compensator system. Gas injection and mechanical agitation, are the main processes commonly performed during the mixing procedure.
The H∞ filters used in the electric vehicle was clearly explained by Chen et al. [22]. It accurately estimated the efficiency and state of charge operation of the batteries used in the electric vehicles. It was very apt for both fast and slow varying parameters in the battery state. But the offline experimental data were verified and compared with the help of single/multi-scale dual Kalman filters. Gil et al. [23] had proposed a modular multilevel converter, which was based on the direct current method. In their paper, controlling robustness had been provided using H∞ controller. The reduction of harmonics due to the utilization of switching function was also possible in the grid side switch spacing.
Brahim et al. [24] had designed a type of position controllers for travelling wave ultra-sonic motor along with the provision of robust motion of the entire system. The detail description of motor resonance behavior could be varied in the presence of signal analysis. There was no need of an additional compensator system for the adjustment of the load system due to the usage of compensator controller. State time-varying delay for a singular system had been studied by Long et al. [25]. The time varying delay was also compared with the invariant time systems based on the Lyapunov–Krasovskii functional method. Boudjellal et al. [26] had developed a super twisting sliding mod-based error estimator with robust and high gain observation by using CSTR.
A fuzzy controller based back stepping technique for the CSTR control had been proposed by Salehi et al. [27]. Here, stability was enhanced for the closed loop system as well as external disturbances had also been reduced in the estimation procedure along with the arbitrary attenuation of error values. Li [28] had designed an efficient CSTR system, which relied on the adaptive control strategy with the presence of unknown dead zone input. CSTR design on the basis of TSMC approaches had been explained by Li [29]. The shortcomings of [29] had been overcome by the method presented by Zhao et al. [30] with the suitable consideration of lay and a safe operation.
Wallam et al. [31] had introduced parametric uncertainties centered control scheme without changing the set point of the disturbance parameters and that was not eligible for providing high stability in case of desired performance attainment. STA-SMC and IISMC bargained the easy implementation of nonlinear control technique. IISMC suddenly settle with the minor overshoot. Finally, those methods were compared with the CISMC and STA-SMC. However, it enabled the local stability with the STA-SMC and had no overshoot. However, most of the existing papers did not deal with the use of H∞ controller for CSTR in an effective way. Thus, we planned to deal with the design of WWO optimization-based H∞ controller in this work for the design of CSTR. In this work, disturbance of CSTR will be eliminated with the help of WWO optimization-based H∞ controller. The tuning of H∞ controller with WWO algorithm reduces the computational complexity and time consumption of proposed work design. This performance is better when compared with other comparative existing works.
This paper is organized as follows, some of the working related to the research paper is discussed in the Section 1. After that, part 2 & 3 give the detail description about proposed method and water wave optimization algorithm respectively. The result and comparative analysis are shown in the section 4. Finally, the overall methodology is concluded in the last part.
The main objective of the proposed method was the development of optimization based on H∞ controller feedback design method with disturbance as the constraint. Then this control is applied to the continuous stirred-tank reactor analysis. In the proposed work, initially the set point is calculated from the temperature. Then the temperature variations are measured as the disturbance parameter for the different time duration. Overall procedures for the planned work are described in the following sections.
2.1 H-infinity Controller Design [32]
To extract the standard H-infinity control design problem from the feedback structure, the connections shown in Fig. 1 can be simplified and equivalently converted to a lower linear fractional transformation (LFT) form as depicted in Fig. 2.
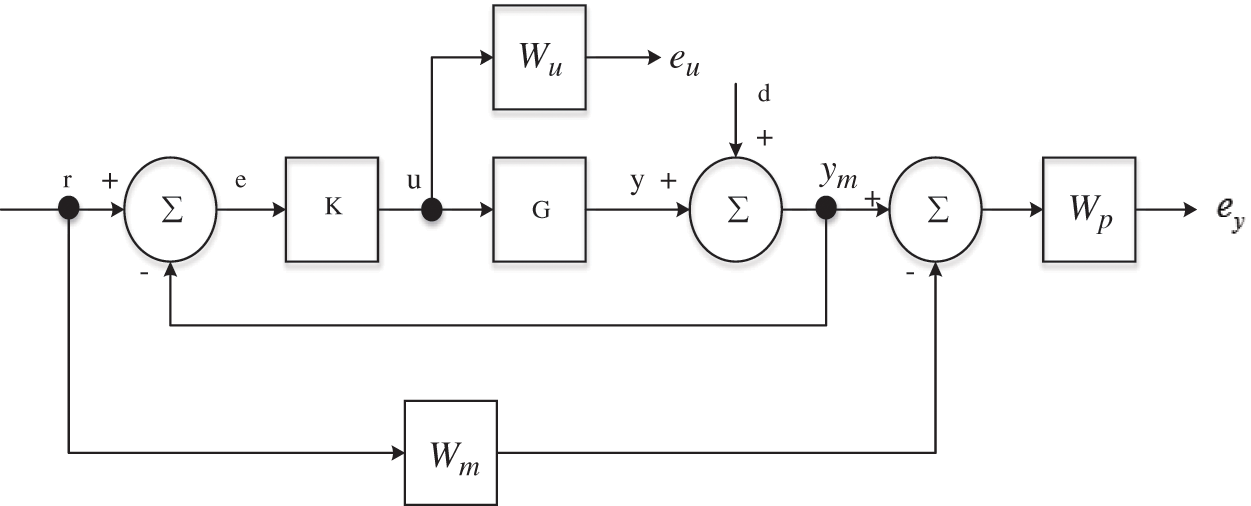
Figure 1: Feedback structure of H-infinity controller
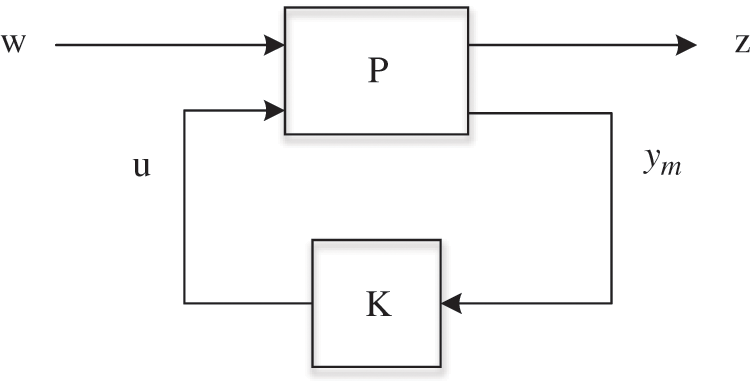
Figure 2: LFT form of the closed-loop system
According to input and output array represented as
The transfer function matrix of the design structure is denoted as
where So and To are sensitivity function and complementary sensitivity function respectively, which are defined by Eqs. (3) and (4) respectively.
Elements in Tzw stand for four robust performance specifications:
According to Eq. (5), controller K could be obtained by using γ-iteration, which involves an internal optimization process that is capable of minimizing the H-infinity norm of Tzw.
2.2 Continuous Stirred-Tank Reactor (CSTR)
CSTR is one type of reactor in chemical engineering field in which temperature control can be considered as a major issue. This kind of difficulty is eliminated through the utilization of optimization-based H∞ controller with feedback design method. The graphical representation of CSTR is shown in the Fig. 3. The system consists of a cylindrical vessel with DC motor, which provides support for agitation with the need of heavy input.
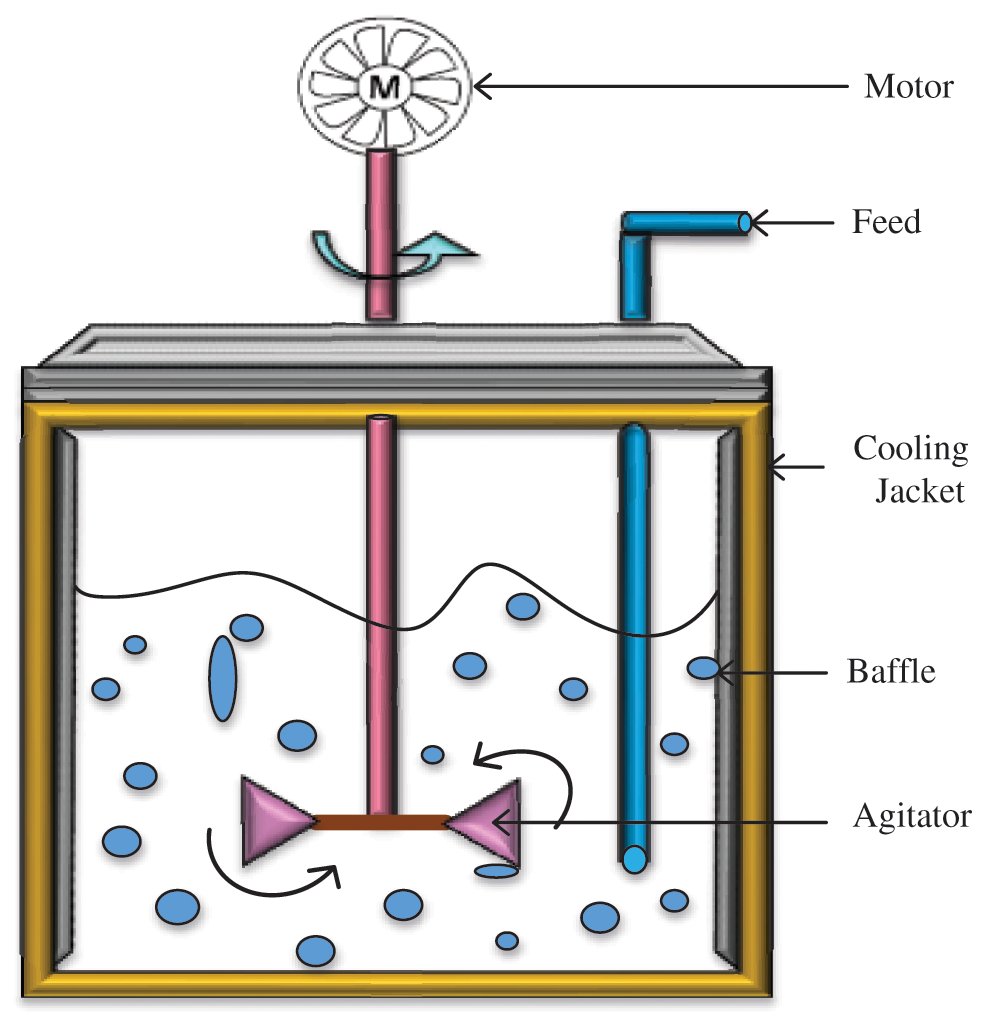
Figure 3: Continuous stirred-tank reactor
The reaction took place inside the reactor is represented by Eq. (6), and the temperature of the system can control with the help of proposed feedback controller. It is measured at the outlet side of the reactor.
The addition of the H∞ controller to CSTR will eliminate the unwanted disturbances, which may upset the functioning of compensator. The controller is used to regulate the output variables such as temperature or flow rate by comparing it with the set point called as desired value. The difference between the measured value and the desired value is called as error signal. It is given in Eq. (7).
The formula for calculating set point is given as follows,
The temperature variation (
Where,
The time varying strategies are indicated as t1 and t2 in the above Eq. (10). The concentration of liquid inside the CSTR can be computed by using the following Eq. (11).
In the above formula,
The set point of the CSTR system is considered as

Figure 4: Control of CSTR
In Fig. 4, tsp and t represent desired and measured temperature respectively. The main objective of the proposed method is the reduction of external disturbances. The transfer function of the plant can be represented by Eq. (12).
From the above equation, the error and measured signals can be computed by using the Eqs. (13) and (14).
Where, t and
The final formula for the error calculation is given by Eq. (16)
The function
• Good disturbance rejection at low frequency regions can be done by making the term
• The minimization of closed loop transfer function can be achieved with the help of functional value
• Protection units for parameter variations can be achieved by reducing
Finally, the minimization function can be expressed by Eq. (17).
where, W1 and W3 are the frequency dependent matrices [33].
3 Water Wave Optimization (WWO) Algorithm
It is one of the nature inspired optimization methods mainly enthused by the shallow water wave model with the solution space equivalent to the seabed area. Here, each solution is similar to the wave with the height (H) and the wavelength (
a) Propagation
To find the best solution in each iteration is the main operation of this step. The related equation is given by Eq. (18).
where, uniform distribution of special function at particular range is denoted as rand. L denotes the length of the search space. The formula for wavelength calculation is represented in the Eq. (19).
In Eq. (14),
b) Breaking
Actually, this step is optional for the proposed method. The algorithm divides high wavelength into many smaller wavelengths to reach the best solution.
In Eq. (20)
c) Refraction
This operation makes the height reduction to zero value of the best solution. Position of the new solution is measured as a random number placed halfway between the original and the new position of the best solution.
The exploration of larger areas performs local search around best solution for the sake of improving accuracy. The pseudocode for WWO algorithm is explained as below.
Initialize disturbance parameter for population of P
for each temperature value in the population
propagate t to new t’ based on Eq. (18)
If f(t’) < f(t) then
If f(t’) < f(t*) then
Break t based on Eq. (21)
Update t* with t’
End
Replace t* with t’
Else
Decrease t by 1 until it reaches set point
End
Refract t to t’ based on Eqs. (21) and (22)
End
The working flow of WWO optimization-based H∞ controller is diagrammatically represented in the Fig. 5 along with the appropriate explanation.

Figure 5: Block diagram of WWO optimization-based H∞ controller
The objective function to minimize the error value
The parameters such as temperature and product concentration are taken as the disturbances from the CSTR. Initially, set point for the proposed system is calculated by using appropriate equations. The measured values are 244°C and 0.0836 mol/liter for temperature and product concentration respectively. The parameter description and their corresponding constant values are listed in the Tab. 1.

The disturbance can be caused due to the rapid change of temperature and concentration, both are indicated in Figs. 6a and 6b respectively. These may damage the system lifetime and hence the proposed method keeps target on the removal of such issues with the help of H∞ controller.

Figure 6: CSTR with disturbance (a) Temperature (b) Concentration
The error reduction using the proposed controller is shown in the Fig. 7. For the purpose of error reduction, water wave optimization technique is used. As the number of iterations increases, the error in both parameters has been reduced gradually. Nearer to the fourth iteration a greater number of faults are eliminated to the desired value. After the fault clearance, the CSTR produces the output as displayed in the Fig. 8.

Figure 7: Error Reduction using WWO algorithm (a) Temperature (b) Concentration

Figure 8: CSTR after disturbance Rejection (a) Temperature (b) Concentration
Fig. 8 shows the resultant output after error rejection. It represents the graph with less amount of error. For both parameters, the red color line (disturbed value) becomes closer to the set point value.
The comparison of the proposed method with the existing methods is signified in the Fig. 9 for temperature value. It shows the better performance of proposed controller that is more or less similar to the set point value. Commonly, there is a bigger deviation from the required value in case of existing methods. Among the existing techniques, PID controller shows the worst performance than the active disturbance rejection control (ADRC).

Figure 9: Temperature comparison with existing methods
Fig. 10 represents the comparison graph for the liquid concentration. Here, PID and artificial neural network-based controller are taken as the existing methods for the performance evaluation. As well as, the time at which set point attainment for the existing methods are longer than the planned work.

Figure 10: Comparison of concentration with existing methods

Proposed method reaches the desired value within 2.5 sec after the rejection of instabilities due to the usage of H∞ controller. It is clearly represented in the Tab. 2 along with the comparison of previous practices. Among the prevailing systems, PID, ADRC and ANN take 7.5, 7 and 5.5 Sec to reach the preferred value respectively. Furthermore, the H∞ controller performs the disturbance rejection through the utilization of WWO. Hence it provides better performance than other methods.
An H∞ controller was offered for effective disturbance rejection through the utilization of the water wave optimization algorithm. H∞ controllers are widely used to provide high gain at any kind of complex situations. The application taken for the development of the proposed work is continuous stirred-tank reactor in which non-linear complex reactions are very common. Variation in temperature and product concentration have been taken as the disturbances in CSTR. So that, an algorithm was proposed along with the controller action for eliminating these issues. The implementation results were compared with the existing controllers and performance enhancement has also been shown.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. Carlos, D. M. Prett and M. Morari, “Model predictive control: Theory and practice—A survey,” Automatica, vol. 25, no. 3, pp. 335–348, 1989. [Google Scholar]
2. E. Davison and I. Ferguson, “The design of controllers for the multivariable robust servomechanism problem using parameter optimization methods,” IEEE Transactions on Automatic Control, vol. 26, no. 1, pp. 93–110, 1981. [Google Scholar]
3. Y. Zhang, C. M. Akujuobi, W. H. Ali, C. L. Tolliver and L. S. Shieh, “Load disturbance resistance speed controller design for PMSM,” IEEE Transactions on Industrial Electronics, vol. 53, no. 4, pp. 1198–1208, 2006. [Google Scholar]
4. R. A. DeCarlo, S. H. Zak and G. P. Matthews, “Variable structure control of nonlinear multivariable systems: a tutorial,” Proceedings of the IEEE, vol. 76, no. 3, pp. 212–232, 1988. [Google Scholar]
5. H. Z. Akpolat, G. M. Asher and J. C. Clare, “A practical approach to the design of robust speed controllers for machine drives,” IEEE Transactions on Industrial Electronics, vol. 47, no. 2, pp. 315–324, 2000. [Google Scholar]
6. J. H. Horng, “Adaptive tracking control of a DC motor,” in Proc. The First IEEE Regional Conf. on Aerospace Control Systems, Westlake Village, CA, USA, pp. 231–235, 1999. [Google Scholar]
7. G. C. Sincero, J. Cros and P. Viarouge, “Efficient simulation method for comparison of brush and brushless DC motors for light traction application,” in 13th European Conf. on Power Electronics and Applications, Barcelona, Spain, pp. 1–10, 2009. [Google Scholar]
8. R. Hirschorn, “Invertibility of multivariable nonlinear control systems,” IEEE Transactions on Automatic Control, vol. 24, no. 6, pp. 855–865, 1979. [Google Scholar]
9. A. Teel, R. Kadiyala, P. Kokotovic and S. Sastry, “Indirect techniques for adaptive input-output linearization of non-linear systems,” International Journal of Control, vol. 53, no. 1, pp. 193–222, 1991. [Google Scholar]
10. T. Das and I. N. Kar, “Design and implementation of an adaptive fuzzy logic-based controller for wheeled mobile robots,” IEEE Transactions on Control Systems Technology, vol. 14, no. 3, pp. 501–510, 2006. [Google Scholar]
11. A. Isidori and A. Astolfi, “Disturbance attenuation and H/sub infinity/-control via measurement feedback in nonlinear systems,” IEEE Transactions on Automatic Control, vol. 37, no. 9, pp. 1283–1293, 1992. [Google Scholar]
12. B. Chaudhuri, B. C. Pal, A. C. Zolotas, I. M. Jaimoukha and T. C. Green, “Mixed-sensitivity approach to H/sub/spl infin//control of power system oscillations employing multiple FACTS devices,” IEEE Transactions on Power Systems, vol. 18, no. 3, pp. 1149–1156, 2003. [Google Scholar]
13. G. Rigatos, P. Siano, A. Melkikh and N. Zervos, “A nonlinear H-infinity control approach to stabilization of distributed synchronous generators,” IEEE Systems Journal, vol. 12, no. 3, pp. 2654–2663, 2017. [Google Scholar]
14. G. Rigatos, P. Siano and G. Raffo, “A nonlinear H-infinity control method for multi-DOF robotic manipulators,” Nonlinear Dynamics, vol. 88, no. 1, pp. 329–348, 2017. [Google Scholar]
15. M. Hirata, S. Ishizuki and M. Suzuki, “Two-degree-of-freedom H-infinity control of combustion in diesel engine using a discrete dynamics model,” Control Theory and Technology, vol. 15, no. 2, pp. 109–116, 2017. [Google Scholar]
16. G. Rigatos, O. Siano, P. Wira, K. Busawon and R. Binns, “A nonlinear H-infinity control approach for three-phase voltage inverters,” Intelligent Industrial Systems, vol. 3, no. 2, pp. 129–142, 2017. [Google Scholar]
17. J. Qin, Q. Ma, W. X. Zheng, H. Gao and Y. Kang, “Robust H-infinity group consensus for interacting clusters of integrator agents,” IEEE Transactions on Automatic Control, vol. 62, no. 7, pp. 3559–3566, 2007. [Google Scholar]
18. A. D. Mary, A. T. Mathew and J. Jacob, “A robust h- infinity control approach of uncertain tractor trailer system,” IETE Journal of Research, vol. 59, no. 1, pp. 38–47, 2013. [Google Scholar]
19. P. Gray and S. K. Scott, “Autocatalytic reactions in the isothermal, continuous stirred tank reactor: isolas and other forms of multi-stability,” Chemical Engineering Science, vol. 38, no. 1, pp. 29–43, 1983. [Google Scholar]
20. A. Uppal, W. H. Ray and A. B. Poore, “On the dynamic behaviour of continuous stirred tank reactors,” Chemical Engineering Science, vol. 29, no. 4, pp. 967–985, 1974. [Google Scholar]
21. F. J. Hurtado, A. S. Kaiser and B. Zamora, “Fluid dynamic analysis of a continuous stirred tank reactor for technical optimization of wastewater digestion,” Water Research, vol. 71, no. 1, pp. 282–293, 2015. [Google Scholar]
22. C. Chen, R. Xiong and W. Shen, “A lithium-ion battery-in-the-loop approach to test and validate multi-scale dual H infinity filters for state of charge and capacity estimation,” IEEE Transactions on Power Electronics, vol. 33, no. 1, pp. 332–342, 2017. [Google Scholar]
23. E. Gil, H. Song and K. Chun, “H∞ controller design for robust control in MMC-HVDC system,” International Journal of Mechanical Engineering and Robotics Research, vol. 6, no. 2, pp. 82–87, 2017. [Google Scholar]
24. M. Brahim, I. Bahri and Y. Bernard, “Real time implementation of H-infinity and RST motion control of rotary traveling wave ultrasonic motor,” Mechatronics, vol. 44, no. 1, pp. 14–23, 2017. [Google Scholar]
25. S. Long and S. Zhong, “H∞ control for a class of singular systems with state time-varying delay,” ISA Transactions, vol. 66, pp. 10–21, 2017. [Google Scholar]
26. M. Boudjellal and R. Illoul, “High-order sliding mode and high-gain observers for state estimation and fault reconstruction for a nonlinear CSTR,” in 6th Int. Conf. on Systems and Control, Batna, Algeria, pp. 231–236, 2017. [Google Scholar]
27. S. Salehi and M. Shahrokhi, “Adaptive fuzzy backstepping approach for temperature control of continuous stirred tank reactors,” Fuzzy Sets and Systems, vol. 160, no. 12, pp. 1804–1818, 2009. [Google Scholar]
28. D. J. Li, “Neural network control for a class of continuous stirred tank reactor process with dead-zone input,” Neurocomputing, vol. 131, no. 1, pp. 453–459, 2014. [Google Scholar]
29. D. Li, “Adaptive neural network control for a class of continuous stirred tank reactor systems,” Science China Information Sciences, vol. 57, no. 10, pp. 1–8, 2014. [Google Scholar]
30. D. Zhao, Q. Zhu and J. Dubbeldam, “Terminal sliding mode control for continuous stirred tank reactor,” Chemical engineering Research and design, vol. 94, pp. 266–274, 2015. [Google Scholar]
31. F. Wallam and A. Y. Memon, “A robust control scheme for nonlinear non-isothermal uncertain jacketed continuous stirred tank reactor,” Journal of Process Control, vol. 51, pp. 55–67, 2017. [Google Scholar]
32. G. Willmann, D. F. Coutinho, L. F. A. Pereira and F. B. Líbano, “Multiple-loop H-infinity control design for uninterruptible power supplies,” IEEE Transactions on Industrial Electronics, vol. 54, no. 3, pp. 1591–1602, 2007. [Google Scholar]
33. Z. Chen, Q. Zheng and Z. Gao, “Active disturbance rejection control of chemical processes,” in IEEE Int. Conf. on Control Applications, Singapore, pp. 855–861, 2007. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |