DOI:10.32604/iasc.2022.021778

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.021778 |  |
| Article |
A Fuzzy MCDM Model of Supplier Selection in Supply Chain Management
1Institute of Marine Affairs and Business Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
3Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Chia-Nan Wang. Email: cn.wang@nkust.edu.tw
Received: 14 July 2021; Accepted: 16 August 2021
Abstract: According to a new study by the International Labor Organization (ILO), the COVID-19 pandemic has had a strong impact on the garment industry in the Asia-Pacific region. A sharp drop in retail sales in key export markets has affected workers and businesses across supply chains. To ensure the effectiveness and efficiency of garment supply chain, choosing a sustainable supplier should be a main concern of all businesses. The supplier selection problem in garment industry involves multiple quantitative and qualitative criteria. There have been many research and literatures about the development and application of Multicriteria Decision Making (MCDM) models in solving decision-making problems in different industry sectors such as supplier selection or investment assessment. Many different MCDM models have been introduced over the years, and each model is uniquely dedicated into solving a particular problem. There is very little MCDM models incorporated with fuzzy set theory to support decision makers with decision-making problem in uncertain environments. This paper introduces a Fuzzy MCDM-based approach to the problem by utilizing Fuzzy-Analytic Hierarchical Process (FAHP) and Weighted Aggregated Sum Product Assessment (WASPAS) methods to support the decision makers. The aim of the paper is developing a decision-making tool that supports the decision maker in deciding the suitable supplier in garment industry under fuzzy environment. The proposed MCDM model is applied to a real-world case study to demonstrate the application steps of the model as well as its feasibility. The model assisted in successfully its proposed goals that resulted in an optimal supplier in garment industry.
Keywords: Fuzzy theory; multi-criteria decision making model; garment industry; sustainability
The garment industry has been a growing industry due to the increase of demand for garment products. From the unpredictability of the demand for garment products since some may considered it as a commodity, it is very important that the supply chains of garment products remain at a strong consistency. There are many factors that could affect the demand of garment products such as the color of the apparel [1], the type of fabric (rib and single knit fabric) [2], competition amongst other garment companies, social media marketing, and, importantly, supplier issues [3]. As popular garment companies such as Zara and H&M have been studied globally for their supply chains and how they are able to meet such high demand satisfaction, it is undeniable that the supplier selection process for the garment industry it crucial for its survival [4].

Figure 1: Supplier selection process [5]
The supplier selection can happen at any stage of the supply chain. Some garment businesses seek an overseas supplier of raw materials that ensures the global quality standard. On the other hand, garment companies seek outsource or third parties in order to subcontract the production process of their products. The supplier selection process for subcontracting can be referred to in Fig. 1 (RFQ being the Request for Quote in order for suppliers can bargain and compete of the suitable pricing for the contractors) [5].
With such a huge pool of suppliers available globally, there are many factors that helps businesses determine the best choice of suppliers such as geographical, pricing, competition, quality, and many more as referenced by Karami et al. [6]. Therefore, Multi-criteria Decision Making (MCDM) methods have been continuously studied as these factors turn into criteria for businesses as a decision maker role when deciding the best supplier for their companies. Popular MCDM methods such as Technique for Order Preference Similarity to Ideal Solution (TOPSIS), Fuzzy TOPSIS, Analytical Hierarchy Process (AHP), Fuzzy AHP, Data Envelopment Analysis (DEA), and Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) [7–10], have continued to show their strengths and weaknesses into solving the supplier selection problem for decision makers depending on the nature of the criteria based on qualitative or quantitative behaviors. The paper applies a real case study that requires solving a similar supplier selection problem that utilized the FAHP and Weighted Aggregated Sum Product Assessment (WASPAS) processes in order to determine the most suitable supplier.
In the past decades, many researchers have studied the application of MCDM methods in solving decision-making problems in various industries [11–18]. In many cases, MCDM models utilized fuzzy sets theory to solve decision making problems that involved qualitative criteria and information [19–23].
There have been many literatures regarding the application of MCDM techniques in solving location and supplier selection problems for multiple industries. Rao et al. [24] approached the City Logistics Center location selection with a fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) based MCDM model. The proposed model used in the aforementioned paper considered the problem under a sustainability perspective and included economic, environmental, and social criteria. Guneri et al. [25] developed an MCDM model based on fuzzy Analytical Network Process (ANP) method to solve a shipyard location selection problem. The approach combined fuzzy set theory in order to help the model deal with the uncertainty of the decision-making environment. Choudhury et al. [26] introduced a novel MCDM based approach to solve a surface water treatment plant location selection problem. The model utilized Sinusoidal Analytic Hierarchy Process (SAHP) to calculate the weighting of relevant selection criteria and stepwise forward regression method to determine the ranking of the potential alternatives regarding sustainability. Tadić et al. [27] developed a hybrid grey MCDM model to support the dry port terminal location evaluation process. The proposed model is based on Analytical Hierarchy Process (AHP) and Combinative Distance-based Assessment (CODAS) methods in a grey environment. Karaşan et al. [28] extended classical MCDM methods (DEMATEL, AHP and TOPSIS) with Intuitionistic Fuzzy Sets (IFSs) to solve the vehicles charging stations location selection problem. The proposed model was verified by applying into a real-world case study in Turkey.
MCDM methods are also frequently applied to solve decision-making problems specifically renewable energy development projects. Solangi et al. [29] developed a hybrid MCDM model, based on AHP and Fuzzy TOPSIS methods, in order to solve a wind power plant location selection. The proposed model is applied to determine an optimal wind plant location in the Southeastern region of Pakistan. Villacreses et al. [30] applied the Ordered Weighted Averaging (OWA) method in combination with Geographic Information Systems (GIS) to create a decision support system for the sustainable wind energy plant location selection. The model was applied to solve a wind farm location selection problem in Ecuador. Mostafaeipour et al. [31] combined the Stepwise Weight Assessment Ratio Analysis (SWARA) and the Additive Ratio Assessment (ARAS) methods to solve the geothermal project location selection problem in Afghanistan. The proposed model also compared other MCDM methods such as TOPSIS, VIKOR, and WASPAS. Erdin [32] proposed a MCDM model based on Entropy and TOPSIS methods under Interval Valued Pythagorean Fuzzy sets to solve a hydrogen production facility location selection problem. The model is applied to the cities in the Black Sea region of Turkey. Nie et al. [33] incorporated Interval neutrosophic sets into the WASPAS technique to create a fuzzy MCDM model to solve a solar-wind power plant location selection problem. Sensitivity analysis and comparative analysis are performed to verify the performance of the proposed model.
In this research, the aim is to develop an MCDM model to determine the optimal supplier evaluation and selection process under fuzzy decision-making environment in Vietnam. Fuzzy AHP and WASPAS methods are utilized to calculate the criteria weights and the ranking of the potential suppliers.
A Fuzzy Multi-Critieria Decision Model (F-MCDM) model by using FAHP and WASPAS in order to decide suitable supplier in garment industry. Three main steps are involved shown in Fig. 2.
Step 1: From the literature review and experts’ opinions, all of the criteria and sub-crtieria which are used to determine the supplier selection process are identified and listed.
Step 2: FAHP is then applied in order to determine the ranking of importance for each identified criteria and sub-criteria based on literature review and experts’ opinions.
Step 3: WASPAS is then applied to determine the final ranking of all alternatives based on the weights of each criteria and the scoring of each alternative. The ranking is used as evidence to support the decision-maker finalize the optimal supplier.

Figure 2: Research process
In order to approach the uncertainty and unclearness of human thinking and opinions in hoping to numerize such behavior, Zadeh [34] first introduced the fuzzy set theory. The theory since then has been utilized widely mainly assisting in analyzing ambiguous data, like opinionated answers, with an addition of allowing mathematical operators to be applied. Since then, the theory was able to give decision-maker a powerful tool into analyzing qualitative data. A fuzzy set is defined as a set of numeric values incorporated with a membership function where each value is assigned with a grade of membership from 0 to 1. A Triangular Fuzzy Number (TFN) denoted as
The membership function of

Figure 3: A Triangular fuzzy number
A fuzzy number can be defined by its corresponding left and right-side representation:
With
where
3.3 Fuzzy Analytical Hierarchy Process (FAHP) Model
Fuzzy Analytical Hierarchy Process (FAHP) is an extension of the Analytical Hierarchy Process (AHP) that applies with the fuzzy set in order to minimize the uncertainty in a decision-making environment. We denote
where
Fuzzy synthetic extent value of the
The possibility that
where the pair
Since
and
where
With
In order to do a
The possibility for a convex fuzzy number to be greater than
and,
Under the assumption that:
for
where
The Normalized weight vectors calculated as follows:
With
The consistency of the pair-wise comparison matrices are tested using a classical consistency test utilized in all AHP processes where:
where:
– Consistency Ratio (CR);
– Consistency Index (CI);
– Random Index (RI).
3.4 Weighted Aggregated Sum Product Assessment (WASPAS)
The Weighted Sum Model (WSM) is one of the most common and efficient multicriteria decision models used to assess multiple alternatives. First,
where the linear normalization for each initial criteria value are calculated as follows:
if
if
The Weight Product Model (WPM) is another model that is commonly utilized for assessing multiple options using the total relative significance of option
The weights of total relative importance are then equally divided between the WSM and WPM results for a total score in order to combine both models in evaluating further the significance of options:
The results shown from the WSM and WPM models can further be examined in order to adapt suitably by looking at the environment that is required based on the research above and the improvement of the accuracy and effectiveness in decision making. The modification of such results is called the Weighted Aggregate Sum Product Assessment model and this model is used to rank the alternatives in this research. If the decision maker has no preference,
In the first months of 2021, Vietnamese garment enterprises received optimistic signals when many orders increased. However, in the context of the complicated and unpredictable COVID-19 epidemic worldwide, Vietnamese enterprises are also facing internal challenges. Standing in the top 3 of the world’s leading textile and garment exporting countries, the value brought by Vietnam’s Textile and Garment Industry is very low, with a profit margin of about 5% to 10%. The existence mentioned above is because Vietnam have not been able to proactively source raw materials and auxiliary materials in the country and depend on foreign imports. Therefore, when there is a supply problem, the production and business activities of enterprises are negatively affected. For sustainable development, forcing textile and garment units to invest and actively seek alternative sources of supply.
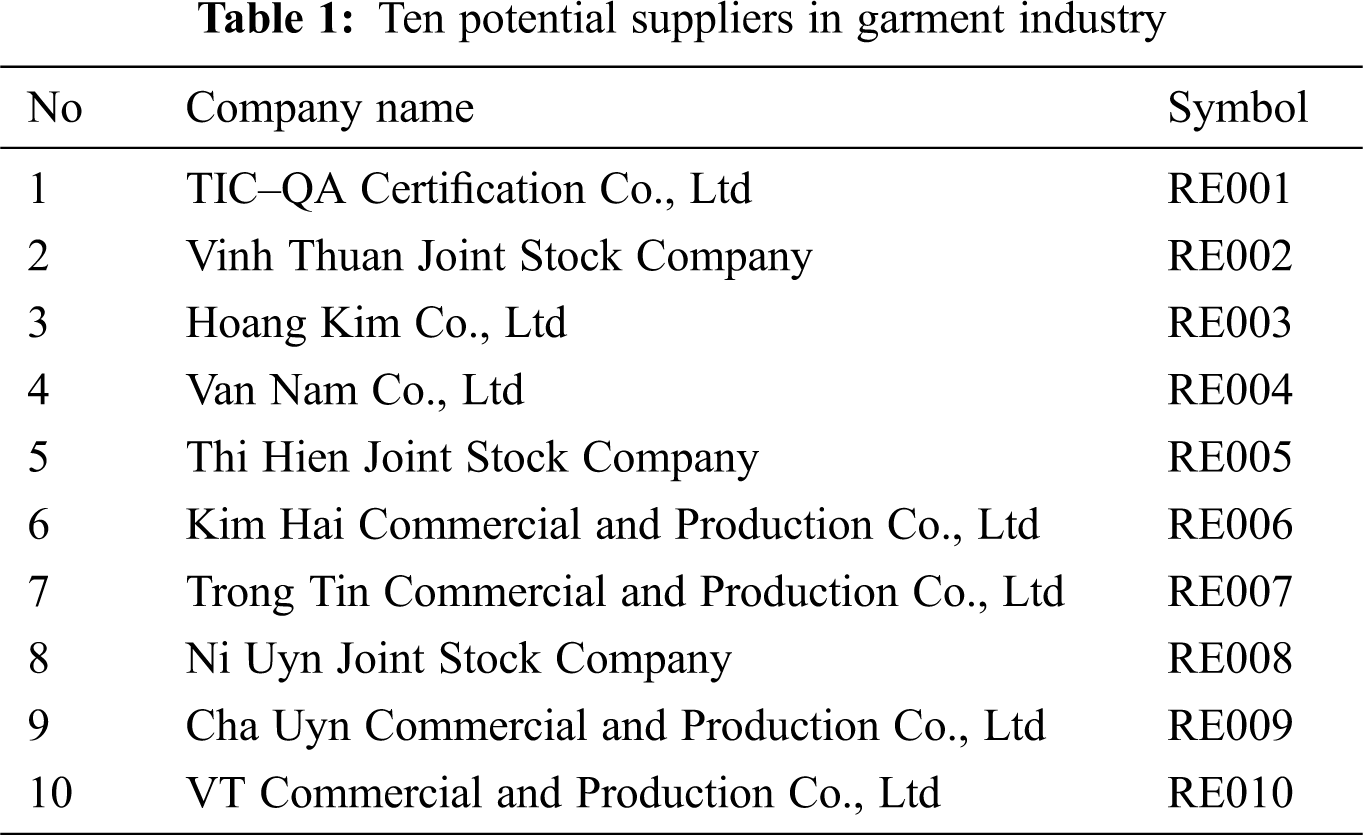
Therefore, the research evaluates the potential of suppliers through a Multi-Criteria Decision Making (MCDM) process that determines the potential suppliers in garment industry. The process used the FAHP and WASPAS as mentioned. To apply the proposed models, 10 supplier are taken into consideration (Tab. 1).
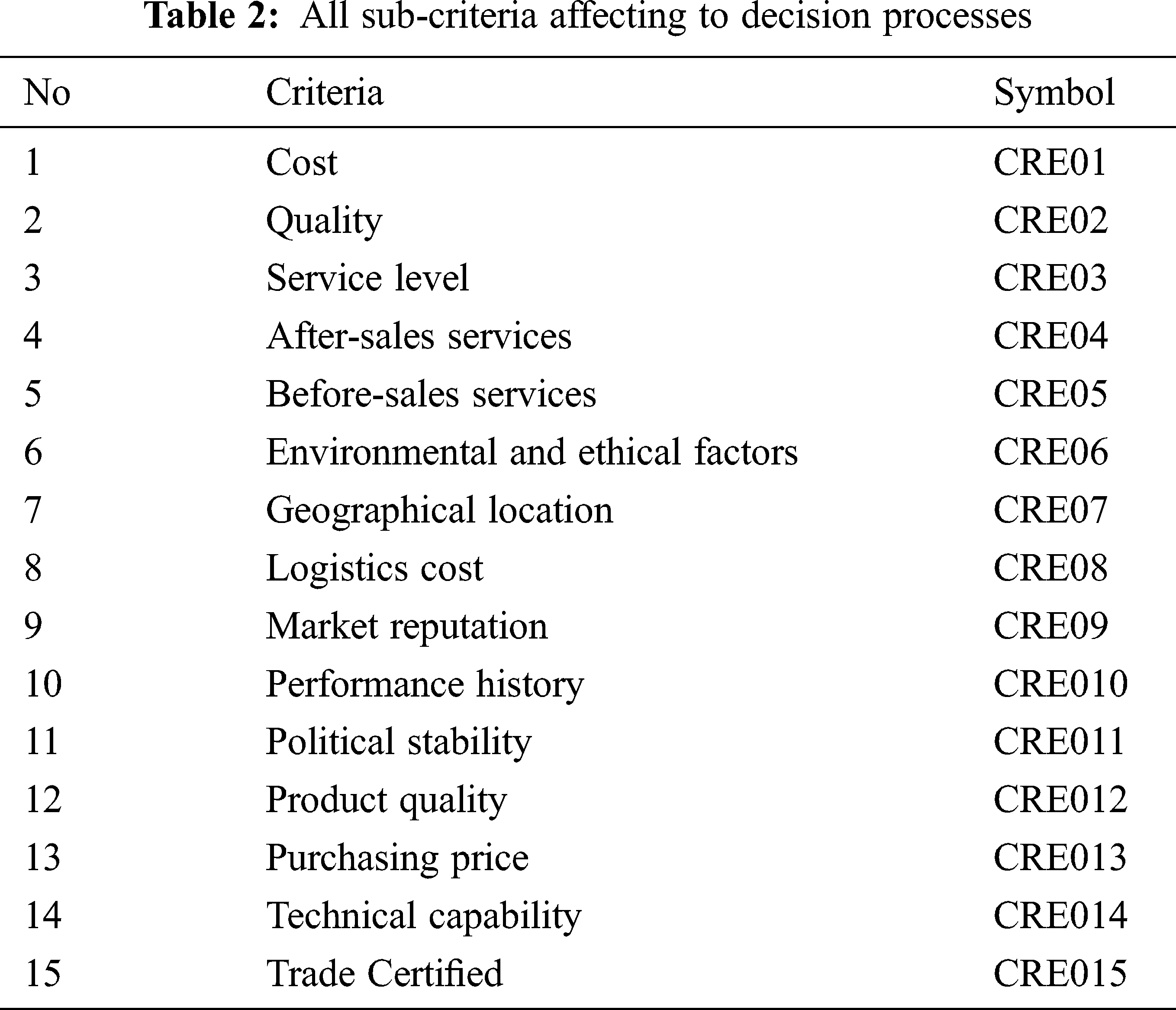
To determine the possible evaluation in choosing the best supplier, 15 standards are chosen. (Tab. 2)
All standards and criteria were determined by 12 experts. The decision-making procedure is then initiated in order to analyze the given data.
Firstly, a fuzzy comparison matrix for all criteria from FAHP model are shown in Tab. 3:
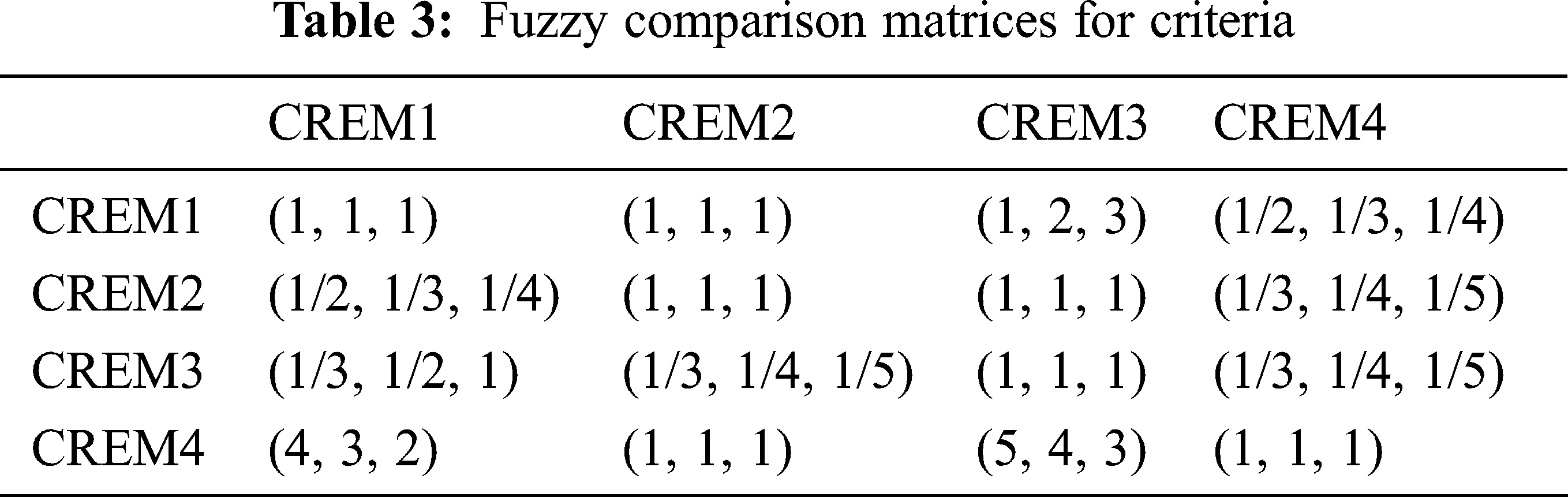
During the defuzzification process, the coefficients values are selected with α = 0.5 and β = 0.5. In it, α represents the uncertain environment, β represents the attitude of the evaluator is fair and unbiased [37].
g0.5, 0.5
f0.5(L CREM1, CREM2) = (3.25 – 3)
f0.5(U CREM1, CREM2) = 5 – (5 – 3.25)
g0.5, 0.5
The remaining calculation are similar to the above, as well as the fuzzy number priority point, the real number priority when comparing the main criteria pairs presented in Tab. 4.

To calculate the maximum individual value as following:
YZ1 = (1
YZ2 = (1/3
YZ3 = (1/2
YZ4 = (3
Since the number of criteria is 4, we get n = 4, λmax and CI are calculated as follows:
For CR, with n = 4 we get RI = 0.9 as pre-determined from an AHP study.
We have CR = 0.0101 ≤ 0.1, so the pairwise comparison data is consistent and does not need to be re-evaluated.
The calculated weight of each sub criteria using FAHP is shown in Tab. 5.

WASPAS model is applied for ranking all potential suppliers in final stages. The normalized matrix and normalized weighted matrix are show in Tabs. 6 and 7 below.

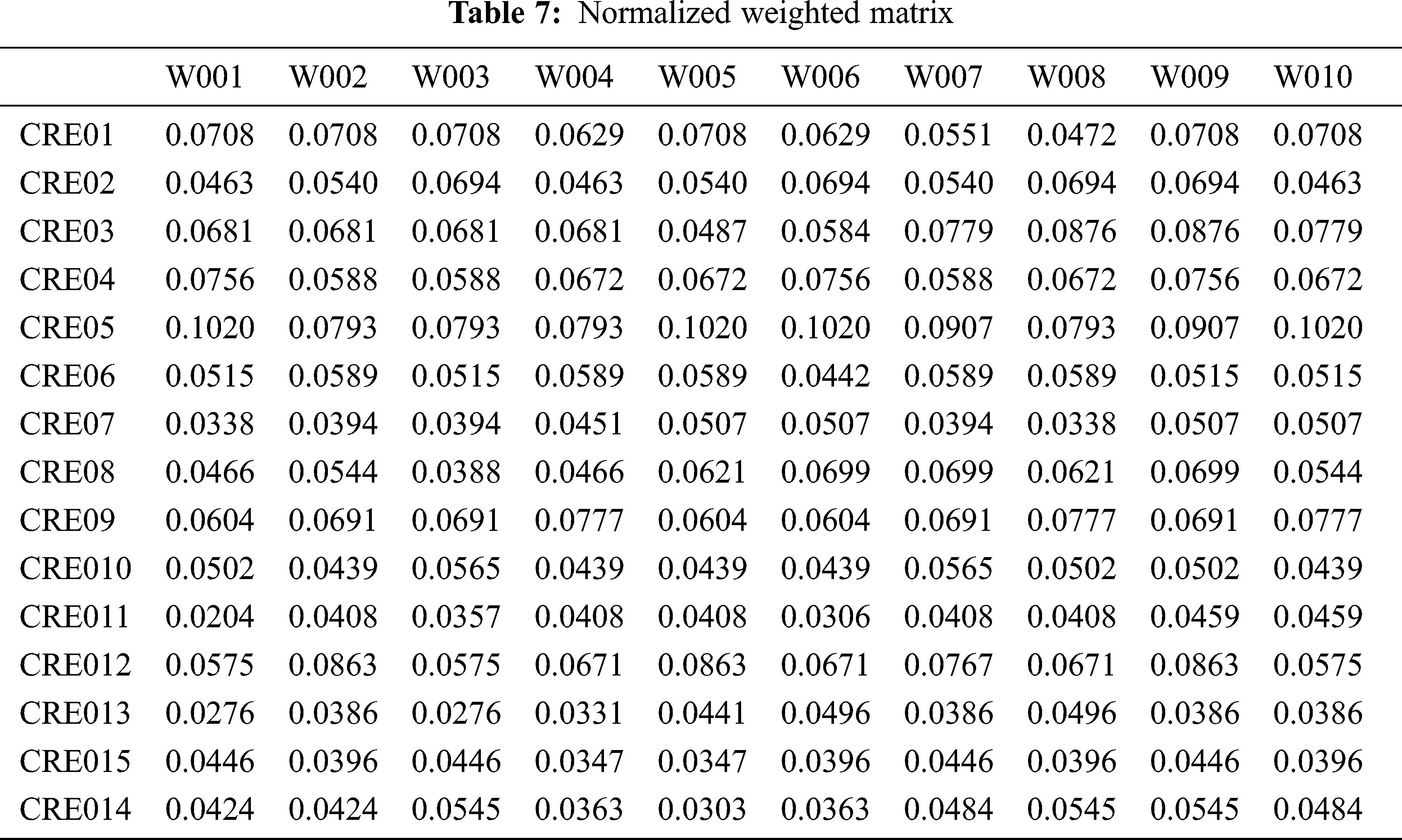


Exponentially weighted matrix is shown in Tab. 8. After applying the suitable models and evaluating all of the criteria from each experts’ opinions regarding the suitable supplier in garment industry using quantitative and qualitative factors, a ranking of alternatives have been produced using MCDM tools suitable being the FAHP and WASPAS models. Tab. 9 and Fig. 4 displays the final ranking after the calculation in ascending order, which are, RE009, RE010, RE008, RE006, RE007, RE005, RE002, RE003, RE001, RE004. Therefore, Da Nang (RE009) appears to be the optimal supplier.

Figure 4: Final ranking from WASPAS
The complexity of the result for the model is examined using sensitivity analysis. In this case, the results of the model were re-examined in the case of the social criteria (CRE011, CRE012, CRE013, CRE014) were not considered. The results of the analyzed model using the case mentioned is shown in Fig. 5.
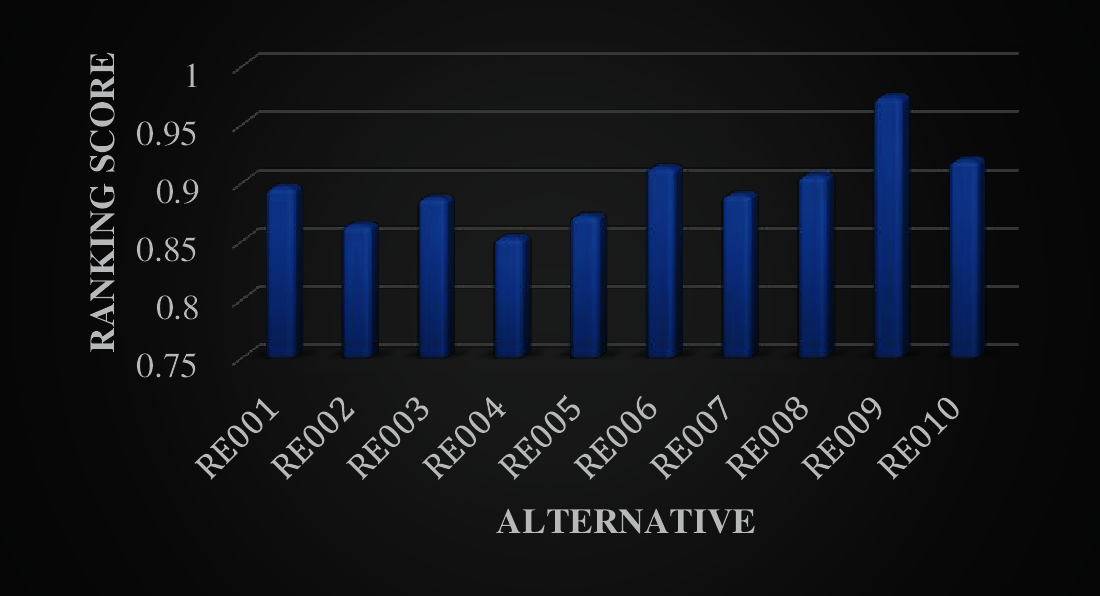
Figure 5: Ranking from WASPAS without social criteria
Although there were changes for lower ranking alternatives, the results of the sensitivity analysis concluded that RE009 as the optimal supplier followed by RE010 even when the social criteria were removed from the model. This suggested that the social criteria have small impact compared to the original result of the model, which is explained since RE009 and RE010 both have higher performance in other criteria that allowed them to be prioritized even when the social criteria are not considered. Therefore, the proposed model’s result can be considered complex.
An application process applied decision making problems is the main activity that is proposed in this research regarding determining an optimal supplier in garment industry. The MCDM models are taken into consideration after a data collection phase has been conducted to analyze the data. This paper utilized the application of Fuzzy-MCDM due to the nature of the data being uncertain amongst the experts consulted. From the nature of the data, the proposed FAHP and WASPAS models are then applied to process and successfully determined the optimal supplier using 10 alternatives over a set of 4 criteria and 15 sub-criteria. The research successfully developed the highest accuracy of estimation in determining supplier in a multi-criteria framework.
A real problem of supplier ‘s assessment in garment industry is handled to examine the performance of the proposed model. By some comparative analysis and through the evidence, the stability of the Fuzzy MCDM model is also approved. The proposed model can be applied to supplier selection problems in other industries. However, as the proposed model is based on the fuzzy AHP method, the interdependency of the criteria has not been fully considered. A comparative study between the proposed model and a similar ANP-based model should also be performed in the future to further understand the interdependency of the criteria. Further studies regarding this topic can be further expanded across multiple MCDM tools that helps in determining the best alternative such as data envelopment analysis (DEA) or the decision-making trial and evaluation laboratory (DEMATEL).
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. İ. Güven and F. Şimşir, “Demand forecasting with color parameter in retail apparel industry using artificial neural networks and support vector machines methods,” Computers & Industrial Engineering, vol. 147, no. 8, pp. 106678, 2020. [Google Scholar]
2. L. Gozali, I. A. Marie, S. Hoswari, A. J. Christifan, P. A. Gunawan et al., “Forecasting using artificial neural networks and aggregate production planning and dynamic model of inventory control for rib and single knit fabric,” IOP Conference Series: Materials Science and Engineering, vol. 1007, pp. 012023, 2020. [Google Scholar]
3. F. Katemauswa and M. Naude, “Factors influencing demand forecasting and planning in the South African apparel industry: A case study,” The Retail and Marketing Review, vol. 16, no. 2, pp. 1–17, 2020. [Google Scholar]
4. S. Chopra, Supply Chain Management. Harlow, United Kingdom: Pearson Education Canada, 2019. [Google Scholar]
5. Sigmoidal, “ML & predictive analytics for supplier selection–sigmoidal,” 2021. [Online]. Available: https://sigmoidal.io/case-studies/machine-learning-supplier-selection/. [Google Scholar]
6. S. Karami, R. Ghasemy Yaghin and F. Mousazadegan, “Supplier selection and evaluation in the garment supply chain: An integrated DEA–PCA–VIKOR approach,” The Journal of The Textile Institute, vol. 112, no. 4, pp. 578–595, 2020. [Google Scholar]
7. T. Azad, “Implementation of TOPSIS method for multi criteria decision making of supplier selection,” European Journal of Advances in Engineering and Technology, vol. 6, no. 11, pp. 22–27, 2019. [Google Scholar]
8. F. Alam and K. Shahed, “Multicriteria decision making models for performance evaluation and selection of suppliers applying fuzzy TOPSIS and DEA,” International Journal of Applications of Fuzzy Sets and Artificial Intelligence, vol. 10, pp. 227–250, 2020. [Google Scholar]
9. I. Badi and D. Pamucar, “Supplier selection for steelmaking company by using combined Grey-Marcos methods,” Decision Making: Applications in Management and Engineering, vol. 3, no. 2, pp. 37–48, 2020. [Google Scholar]
10. M. Rahman and K. Ahsan, “Supplier selection and evaluation by fuzzy AHP extent analysis: A case study RMG sector of Bangladesh,” SSRN Electronic Journal, vol. 9, no. 1, pp. 41–47, 2019. [Google Scholar]
11. C. Wang, V. Thanh, J. Chyou, T. Lin and T. Nguyen, “Fuzzy multicriteria decision-making model for raw materials supplier selection in plastics industry,” Mathematics, vol. 7, no. 10, pp. 981, 2019. [Google Scholar]
12. M. Alizadeh, M. Hashim, E. Alizadeh, H. Shahabi, M. R. Karami et al., “Multicriteria decision making model for seismic vulnerability assessment of urban residential buildings,” ISPRS International Journal of Geo-Information, vol. 7, no. 11, pp. 444, 2018. [Google Scholar]
13. K. P., U. Govindarajan, V. K. Ramachandaramurthy and T. S., “Multiple criteria decision making based economic analysis of solar PV system with respect to performance investigation for Indian market,” Sustainability, vol. 9, no. 5, pp. 820, 2017. [Google Scholar]
14. G. Tzeng, C. Chiang and C. Li, “Evaluating intertwined effects in e-learning programs: A novel hybrid MCDM model based on factor analysis and DEMATEL,” Expert Systems with Applications, vol. 32, no. 4, pp. 1028–1044, 2007. [Google Scholar]
15. S. Mousavi, A. Danehkar, M. Shokri, H. Poorbagher and D. Azhdari, “Site selection for artificial reefs using a new combine multicriteria decision-making tools for coral reefs in the Kish Island,” Persian Gulf, vol. 111, no. 1, pp. 92–102, 2015. [Google Scholar]
16. S. Aydin and C. Kahraman, “Evaluation of e-commerce website quality using fuzzy multi-criteria decision-making approach,” IAENG International Journal of Computer Science, vol. 39, no. 1, pp. 64–70, 2012. [Google Scholar]
17. D. Xu, X. Cui, H. Xian, Y. Hong and D. Hu, “A novel TOPSIS-MABAC method for multi-attribute decision making with interval neutrosophic set,” IAENG International Journal of Applied Mathematics, vol. 50, no. 2, pp. 273–278, 2020. [Google Scholar]
18. H. Yano and R. Zhang, “Interactive decision making for multiobjective fuzzy random programming problems with simple recourse through a fractile model,” IAENG International Journal of Applied Mathematics, vol. 46, no. 3, pp. 379–387, 2016. [Google Scholar]
19. D. Ighravwe and S. Oke, “A fuzzy-grey-weighted aggregate sum product assessment methodical approach for multi-criteria analysis of maintenance performance systems,” International Journal of System Assurance Engineering and Management, vol. 8, no. 2, pp. 961–973, 2016. [Google Scholar]
20. M. Hanine, O. Boutkhoum, A. Maknissi, A. Tikniouine and T. Agouti, “Decision making under uncertainty using PEES-fuzzy AHP-fuzzy TOPSIS methodology for landfill location selection,” Environment Systems and Decisions, vol. 36, no. 4, pp. 351–367, 2016. [Google Scholar]
21. M. Kuo, “A novel interval-valued fuzzy MCDM method for improving airlines’ service quality in Chinese cross-strait airlines,” Transportation Research Part E: Logistics and Transportation Review, vol. 47, no. 6, pp. 1177–1193, 2011. [Google Scholar]
22. P. Wanke, M. Kalam Azad, C. Barros and A. Hadi-Vencheh, “Predicting performance in ASEAN banks: An integrated fuzzy MCDM-neural network approach,” Expert Systems, vol. 33, no. 3, pp. 213–229, 2015. [Google Scholar]
23. M. Deveci, N. Demirel and E. Ahmetoğlu, “Airline new route selection based on interval type-2 fuzzy MCDM: A case study of new route between Turkey-North American region destinations,” Journal of Air Transport Management, vol. 59, no. 2, pp. 83–99, 2017. [Google Scholar]
24. C. Rao, M. Goh, Y. Zhao and J. Zheng, “Location selection of city logistics centers under sustainability,” Transportation Research Part D: Transport and Environment, vol. 36, no. 6, pp. 29–44, 2015. [Google Scholar]
25. A. Guneri, M. Cengiz and S. Seker, “A fuzzy ANP approach to shipyard location selection,” Expert Systems with Applications, vol. 36, no. 4, pp. 7992–7999, 2009. [Google Scholar]
26. S. Choudhury, P. Howladar, M. Majumder and A. Saha, “Application of novel MCDM for location selection of surface water treatment plant,” IEEE Transactions on Engineering Management, pp. 1–13, 2019. [Google Scholar]
27. S. Tadić, M. Krstić, V. Roso and N. Brnjac, “Dry port terminal location selection by applying the hybrid grey MCDM model,” Sustainability, vol. 12, no. 17, pp. 6983, 2020. [Google Scholar]
28. A. Karaşan, İ. Kaya and M. Erdoğan, “Location selection of electric vehicles charging stations by using a fuzzy MCDM method: A case study in Turkey,” Neural Computing and Applications, vol. 32, no. 9, pp. 4553–4574, 2018. [Google Scholar]
29. Y. Solangi, Q. Tan, M. Khan, N. Mirjat and I. Ahmed, “The selection of wind power project location in the southeastern corridor of Pakistan: A factor analysis, AHP, and fuzzy-TOPSIS application,” Energies, vol. 11, no. 8, pp. 1940, 2018. [Google Scholar]
30. G. Villacreses, G. Gaona, J. Martínez-Gómez and D. Jijón, “Wind farms suitability location using geographical information system, based on multi-criteria decision making methods: The case of continental Ecuador,” Renewable Energy, vol. 109, no. 8, pp. 275–286, 2017. [Google Scholar]
31. A. Mostafaeipour, S. Hosseini Dehshiri, S. Hosseini Dehshiri, M. Jahangiri and K. Techato, “A thorough analysis of potential geothermal project locations in Afghanistan,” Sustainability, vol. 12, no. 20, pp. 8397, 2020. [Google Scholar]
32. C. Erdin and G. Ozkaya, “Turkey’s 2023 energy strategies and investment opportunities for renewable energy sources: Site selection based on ELECTRE,” Sustainability, vol. 11, no. 7, pp. 2136, 2019. [Google Scholar]
33. R. Nie, J. Wang and H. Zhang, “Solving solar-wind power station location problem using an extended weighted aggregated sum product assessment technique with interval neutrosophic sets,” Symmetry, vol. 9, no. 7, pp. 106, 2017. [Google Scholar]
34. L. Zadeh, “Fuzzy sets,” Information Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]
35. D. Chang, “Applications of the extent analysis method on fuzzy AHP,” European Journal of Operational Research, vol. 95, no. 3, pp. 649–655, 1996. [Google Scholar]
36. E. Triantaphyllou and S. Mann, “An examination of the effectiveness of multi-dimensional decision-making methods: A decision-making paradox,” Decision Support Systems, vol. 5, no. 3, pp. 303–312, 1989. [Google Scholar]
37. Y. Tang and M. Beynon, “Application and development of a fuzzy analytic hierarchy process within a capital investment study,” Journal of Economics and Management, vol. 1, no. 2, pp. 207–230, 2005. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |