DOI:10.32604/iasc.2022.020235

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020235 |  |
| Article |
A Modelling and Scheduling Tool for Crowd Movement in Complex Network
1College of Computing and Information Systems, Umm Al-Qura University, Makkah, Saudi Arabia
2Institute of Consulting Research and Studies, Umm Al-Qura University, Makkah, Saudi Arabia
3Computer Engineering Department, King Fahad University of Petroleum and Minerals, Saudi Arabia
*Corresponding Author: Faizan Ur Rehman. Email: fsrehman@uqu.edu.sa
Received: 16 May 2021; Accepted: 03 July 2021
Abstract: Managing events pose a unique challenge to the stakeholders and authorities to control the crowd in all three phases of the event (pre, during and post), ensuring crowd safety. One of the fundamental keys to provide crowd safety is to consider the mobility infrastructure hosting the crowd, i.e., routes, areas, entrances and exits. During Hajj, where millions of pilgrims worldwide fulfil the annual event’s rites, mina encampment incorporates pilgrims performing recurring stoning ritual conducted over multi-level Jamarat bridge. Pilgrims mobility through the available complex road network, to and back from the Jamarat bridge, forces upon authorities in charge to set out mobility plans which may require off and on modification as per attendees’ preferences and organizational needs. This paper presents a basis for mathematical modelling of pilgrims’ mobility pattern in Mina by considering available corridors’ capacity, limited times, group size restrictions, and road segment connectivity. The developed mathematical model can generate an efficient schedule to control the flow through these corridors, assess crowd management risks when corridors’ capacity is affected by any emergency, and scientifically estimate each corridor’s maximum allowable occupants
Keywords: Crowd management; scheduling; mathematical modelling; simulation; decision-making
Increasingly affordable travelling facilities have mobilized a significant percentage of the world population for sports events, leisure trips, education, adventure, medical treatments and pilgrimage [1]. Mostly in sports or religion-related activities, people count reaches millions or even more. A few of the large gatherings1 are Kumbh Mela (2013), gathering at the shrine of Husayn Ibn Ali (2013), the funeral of C. N. Annadurai (1969), the concert was given by Rod Stewart (1994), Hajj2 the annual pilgrimage to Makkah, Dubai Exposition, protest in Circus Maximus, Rome against the government of Silvio Berlusconi (2002), to name a few. For all such gatherings, pedestrian movement is mainly coupled with certain spatial and temporal constraints. Nevertheless, participants have common interests and try their best to symmetrize their social interactions with other fellow participants [2].
Hajj is an annual gathering, pilgrimage to Makkah. More than 2 million pilgrims from all over the world, of different ethnic and cultural backgrounds, get together for a concise duration to perform a series of Hajj rituals [3]. The arrival and departure of pilgrims from all over the world span over about four–five weeks in time, centred with the second week (8th–12th) days of the month. In the last two decades3, the number of pilgrims increased from 1.8 to 3.2 million over the previous two decades. The majority of pilgrims are old aged and performing Hajj first time in their life, adding wariness to the level of satisfaction of their Hajj rituals. Among the Spatio-temporal rituals, one is the Mina encampment, where pilgrims board themselves for five days in the Mina area (Fig. 1a.), which is about 5 km2. To interdigitate themselves with other rituals, pilgrims visit the other holy places Al-Haram Mosque, Arafat, Muzdalifah and Jamarat, with the compulsion to return to their tents over and above temporal constraints [4]. Unlike other rituals, stoning at the Jamarat (Ramy al Jamarat) (Jamarat is a multi-level pedestrian bridge in the Mina area) is a recurring ritual, whereby pilgrims have to leave their tents and walk for a distance (ranging from a few 100 meters to a few kilometres) and gather at the Jamarat bridge to perform the stoning ritual, for three consecutive days (10th –12th day of Dhul-Hijjah). Fig. 1b. below shows a multi-level Jamarat bridge, where pilgrims can throw stones at the three Jamarah pillars4 (Al-Jamarah Al-Sughra; Al-Jamarah Al-Wusta; and Al-Jamarah Al-Kubra or Jamarat Al-Aqaba) from either the ground level or any other pre-allotted floor. Due to the topographical nature of the Makkah city, pilgrims are bound to move through different types of transfer corridors (uphill, downhill, zigzag, Y, L, T, and U-shape) (Fig. 1.) while they move to other places for performing Hajj rituals, which antes up possibilities of stampedes across the corridors crossings.

Figure 1: (a) Mina area–pilgrims tents, (b) Multilevel Jamarat bridge-for stoning the three Jamarah pillars (Jamarah Al Sugrah (small), Wusta (medium) and Kubra (big)), (c) Road-Ramps towards Jamarat bridge, (d) Different types (uphill, downhill, zigzag, Y, L, T, and U-shape), of transfer corridors, (e) The stampede location (the red circle) during the Hajj 2015 event
The temporal implication is one of the solemn challenges for organizing authorities to make necessary arrangement to mobilize a massive Hajj crowd till the pilgrims safely reach back to their places after they had performed the rituals. It requires hosting authorities to integrate pedestrian movement and crowd safety with available resources and thoroughly analyze crowd’s behaviour and utilize their mobility parameters like average speed/crowd density at the different hours of the day to set out efficient mobility plans, which can be deployed and be modified on demand to avoid any possible crowd shockwaves [5], disasters [6] and massive causalities such as Mina stampede in 2015 [7]. Pilgrims’ sacerdotal interest keeps them cooperative with other pilgrims, which provides sustained parameters like their speed and crowd density when they pass through different transfer corridors and adapt precautionary behaviour during their mobility. This helps us consider speed and crowd density as starting parameters along with road capacity, temporal restrictions, groups size and threshold safety measures to model crowds’ mobility across multiple transfer corridors in order to generate an efficient schedule to control and any possibility of stampedes due to possible crossflows at junctions.
In this paper, we detail the development of our mathematical model, which considers crowds safety parameters (road capacity and density, average walking speed etc.) set by the hosting authorities, the number of pilgrims in different tents which were allotted certain roads to go and come back to their place, after performing rituals, and possibly crossflows across the junctions. The model generates an efficient time schedule to control crowd flow, helping to manage risks in emergencies when there is the possibility of crossing the road capacity and density limits. We used this model for multiple scenarios, including understanding the corridor connectivity, generate mobility time schedules according to numerous criteria, find the maximum number of pilgrims that can occupy a particular area, find the minimum time to schedule all occupants, and test the impact on crowd mobility with dynamic changing of the corridors capacity, the number of pilgrims, group sizes and forbidden times.
To validate the model, we added a sample scenario by considering a small mina area with ten tents and seven connecting road segments and the Jamarat bridge as the pilgrims’ final destination during the stoning ritual. The simulation was carried out, and the model was tested with two features, the impact of changing road capacity and forbidden time slots set by the organizing authorities and or pilgrims’ preferences. Implementation details and related statistics are presented in the paper.
The rest of the paper is organized as: After the introduction section, we have added state-of-the-art by the past researchers, followed by modelling in Section 3. Next, we presented a use case describing pilgrims’ movement within the Mina area under spatio-temporal and safety constraints in Section 4. Later in Section 5, we show the implementation details and finally added Section 6 for more information on the results and discussion.
Mina is most important for its role during the entire Hajj event, where the complex nature of pedestrian walkways and possible crossflows of pilgrims need continued efforts to integrate crowd behaviour in terms of speed/density with analysis of interconnectivity of the Mina roads. This section includes past researchers’ contribution in this area and different models to analyze pedestrian movement and proposed mobility plans for large gatherings.
Templeton et al. [8] presented pedestrian behaviour while they were walking through the crossflow. By comparing the individuals and the groups based on pedestrians’ speed and the distance travelled towards the junctions, the study showed that the crowd self organizes to reduce the impact of possible stampede over the junctions.
Li et al. [9] conducted a qualitative study to understand both unidirectional and bidirectional pedestrian movement on a zigzag corridor located in a business district in Yiyuan, China. To study the movement patterns, videos were captured by the surveillance cameras installed in the study area of the corridor that was divided into three right-angled corners and two straight corridors. Image processing techniques were used to manually extract each pedestrian’s spatial coordinate during both Uni and bidirectional flow. Thus, their trajectories were obtained to analyze the crowd density, velocity, and other related movement characteristics. Their findings supported the unidirectional movement and emphasized focusing more on straight corridor boundaries to avoid clustering.
Dridi [10] developed a microscopic model that uses PedFlow simulation [2] to discuss the high-density crowd behaviour in autonomous and controlled scenarios. To validate the model, the simulation was carried out to study the high-density pilgrims crowd cramming the Jamarat bridge during the Hajj event. Analyzing mobility patterns at different speeds and under different circumstances provided different evacuation control strategies to ensure pedestrian safety.
The centrifugal force model describes the pedestrian movement in terms of their acceleration towards their desired velocities, the attraction or repulsion between them. At the same time, they are in motion and their interaction with walls and other rigid objects in their way [11]. Charaibi et al. [12,13] presented a modified spatially continuous forced-based model that described the pedestrian movement quantitative in one and two dimensions (on several geometrical paths). The oscillations and overlapping of an elliptical volume exclusion were introduced compared to the standard circular one for narrow and wide corridors. Simulating the model with experimental data deduced that the model could be improved by considering a density-dependent repulsive force.
Wang et al. [5], Helbing et al. [14] presented the social force model, explained crowd shockwave (Fig. 2.) as one of the causes of crowd destabilization and stampede accidents. They utilized social force theory and presented a crowd shockwave simulation model to understand the crowd shockwave transmission mechanism. Its amplitude was defined in terms of crowd density, propagation speed, and duration.

Figure 2: A crowd shockwave, the pedestrian moving at relatively high speed at the bottleneck [5]
They carried out an experiment where pedestrians were asked to move through a high fences flank channel along with a waiting area on its right side in a college building in Nanjing Technology University. Two cameras and a UAV (unnamed aerial vehicle (drone)) were used to capture mobility videos of volunteers wearing white shirts and red hats and were asked to move under multiple constraints. The resulting crowd shockwaves were analyzed, and control strategies helped reduce the crowd shockwaves and prevent stampedes were proposed in similar scenarios.
Chen et al. [15] presented extended LGM (Lattice Gas Model) for simulating pedestrian movements using statistical methods. They introduced the concept of local density in their two-dimensional pedestrian movement study, which described the spatial occupancy of a small area around a pedestrian, leading them to derive the relationship between the local density and the pedestrian movement. The proposed model successfully demonstrated fair numerical results when applied to an open dataset comprising a series of unidirectional pedestrian flow experiments and clarified pedestrian movements’ statistical characteristics.
Helbing et al. [14] presented the social force model, and later Helbing explained the Fluid Dynamic Model [16] to describe pedestrian motion. The forces are considered as the internal motivations of the individuals during their activity. Considering the pedestrians’ behaviour in terms of pedestrians’ acceleration towards their desired velocities, distances between themselves and from the borders, and modelling attractive effects, the modelled resulted in nonlinearly coupled Langevin equations. The model was validated by simulating with pedestrians’ crowd and successfully described the self-organizing pedestrian behavior.
Still et al. [17] presented an implementation report of a crowd safety management tool for the places where there is public assembly and a significant event. This tool provides insight into strategic planning to reduce the potential threats to crowd safety. Continuing their research in the same area, later Still [18] presented their article addressing the importance of crowd counting that is the core objective before planning for the safety crowd plans.
Dietrich et al. [19] set of Force Based Model, Georgoudas et al. [20] used a simulation tool for modelling pedestrian dynamics during large areas’ evacuation. Kang et al. [21] showcased a realistic and straightforward Pedestrian Model for Crowd Simulation and Application, and Blue and Adler used “Cellular automata microsimulation for modelling bi-directional pedestrian walkways [22].
Hajj crowd is different in terms of participants’ ethnic and cultural background, various age groups and language diversity, which in addition to available multi-shaped transfer corridors, gathering for a long duration of about a week, and personal and managerial preferences are challenging for hosting authorities to ensure crowd safety from arrival till the safe departure of all pilgrims back to their homes. In the past, researchers work limit us to utilize their models over the Hajj crowd partially. However, several constraints’ dynamic nature requires designing an intelligent system that can accommodate all and modify demand. In this context, we modelled crowds’ mobility during the Hajj and presented the implementation details and related statistics.
In this section, we present our model for groups scheduling. Let
We denote the assignment of groups to road segment by
Note the
where
Now, we introduce the formulation of an optimization problem pertaining to scheduling group dispatching over
Fig. 3. depicts an example setup for road segments (

Figure 3: Example setup
For example,
Solving the optimization problem (Equation xx), we obtain the optimal scheduling with a cost of 7950 by dispatching the first, second, and third groups at k1, k2, and k4, respectively. Fig. 4. illustrates the dispatch schedule over time.
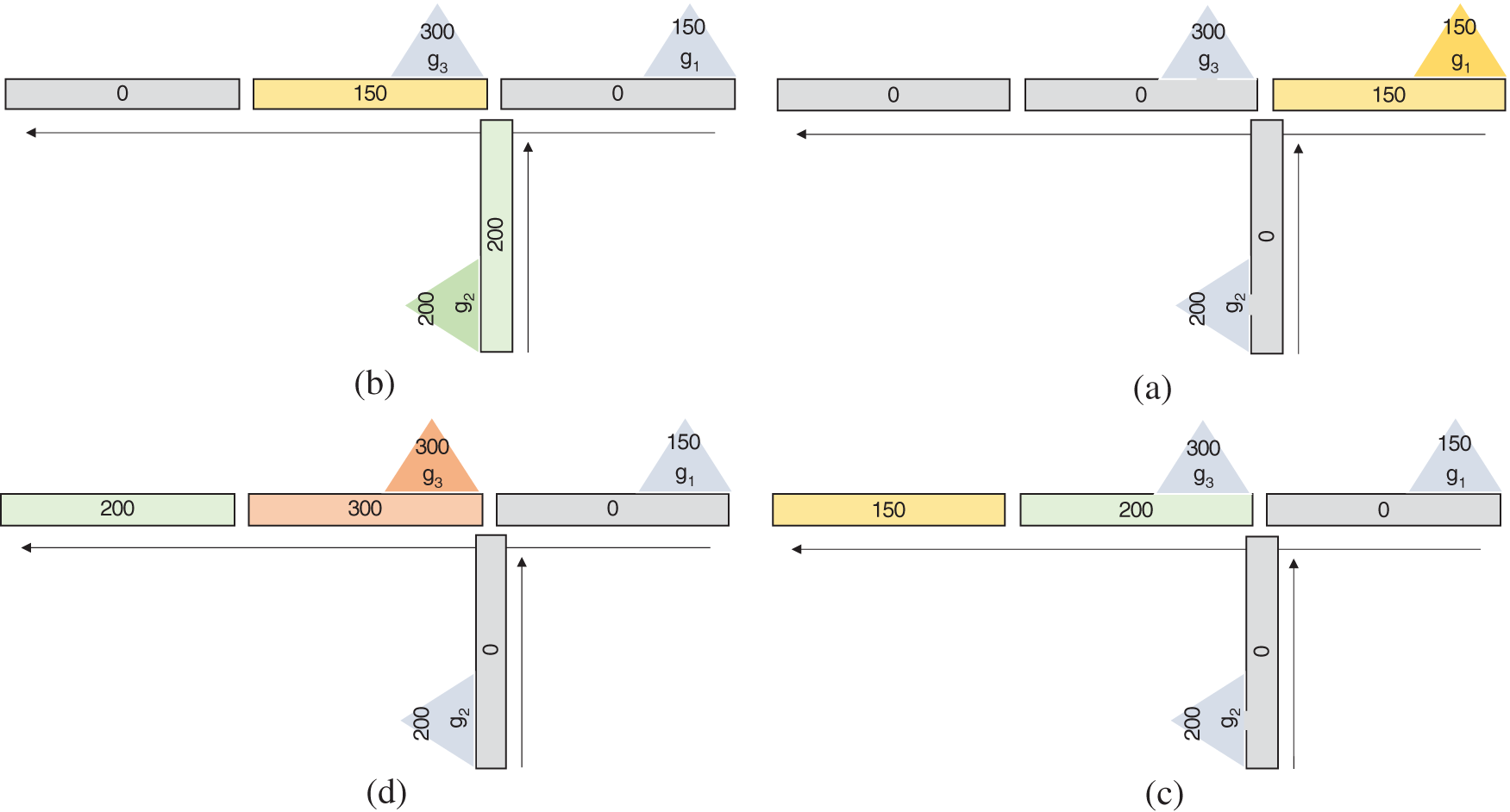
Figure 4: Dispatch schedule over time (a) Group ‘g1’ dispatched at time ‘t0’ from segment ‘S1’, (b) Group ‘g1’ dispatched at time ‘t1’ from segment ‘S3’, (c) Group ‘g1’ dispatched at time ‘t2’ from segment ‘S4’, (d) Group ‘g1’ reached its destination at time ‘t3’ from segment ‘S1’
4 Mina Area-A Use Case of Hajj
Mina is most important for its role during the entire Hajj event, where the complex nature of pedestrians’ walkways and possible crossflows of pilgrims need continuum efforts to integrate crowd behaviour in terms of speed/density with analysis of interconnectivity of the Mina roads. In the Mina area’s topographical nature, pilgrims are bound to move through different types of transfer corridors (uphill, downhill, zigzag, Y, L, T, and U-shape). Mina, also known as the largest city of tents globally, is a valley near Makkah covering roughly 20 km2 (7.7 sq mi) of area. In this area, 2 million pilgrim stays in thousands of camps to perform stoning rituals. There are 16 main roads to access Jamarat and five returns roads towards Mina camps.
Unlike other rituals, stoning at Jamarat (Ramy al Jamarat) (Jamarat is a multi-level pedestrian bridge in the Mina area) is a recurring ritual, whereby pilgrims have to leave their tents and walk for a distance (ranging from a few 100 m to 4.5 km) and gather at the Jamarat bridge to perform the stoning ritual, for three consecutive days (10th–12th day of Dhul–Hijjah). Fig. 1b shows a multi-level Jamarat bridge, where pilgrims can throw stones at the three Jamarah pillars5 (Al-Jamarah Al-Sughra; Al-Jamarah Al-Wusta; and Al-Jamarah Al-Kubra or Jamarat Al-Aqaba) from either the ground level or any other pre-allotted floor. The Jamarat is a five-storey building with a capacity of 100,000 of each level. The facility includes multiple stairs, elevators, and ramps. The top floor of the Jamarat floor is connected with Mina 3 Train station. Fig. 5. shows part of the Mina area and the highlighted camps allotted to south Asian pilgrims (209 tents and 693027 pilgrims) during the Hajj 2019 event. As a part of safe crowd management, these pilgrims were bound only to use the third floor of the Jamarat bridge for stoning the devil ritual. For this purpose, routes G (shown in green) and the pilgrims of tent T1 used r (shown in red). Other than the large section of route G (route R on return) that all the pilgrims of this section commonly used, several sub-routes (used by pilgrims of other tents) merged into this route, agitating the movement of pilgrims of tent T1. A similar can be imagined about pilgrims’ movement of other tents using different paths integrating into route G.
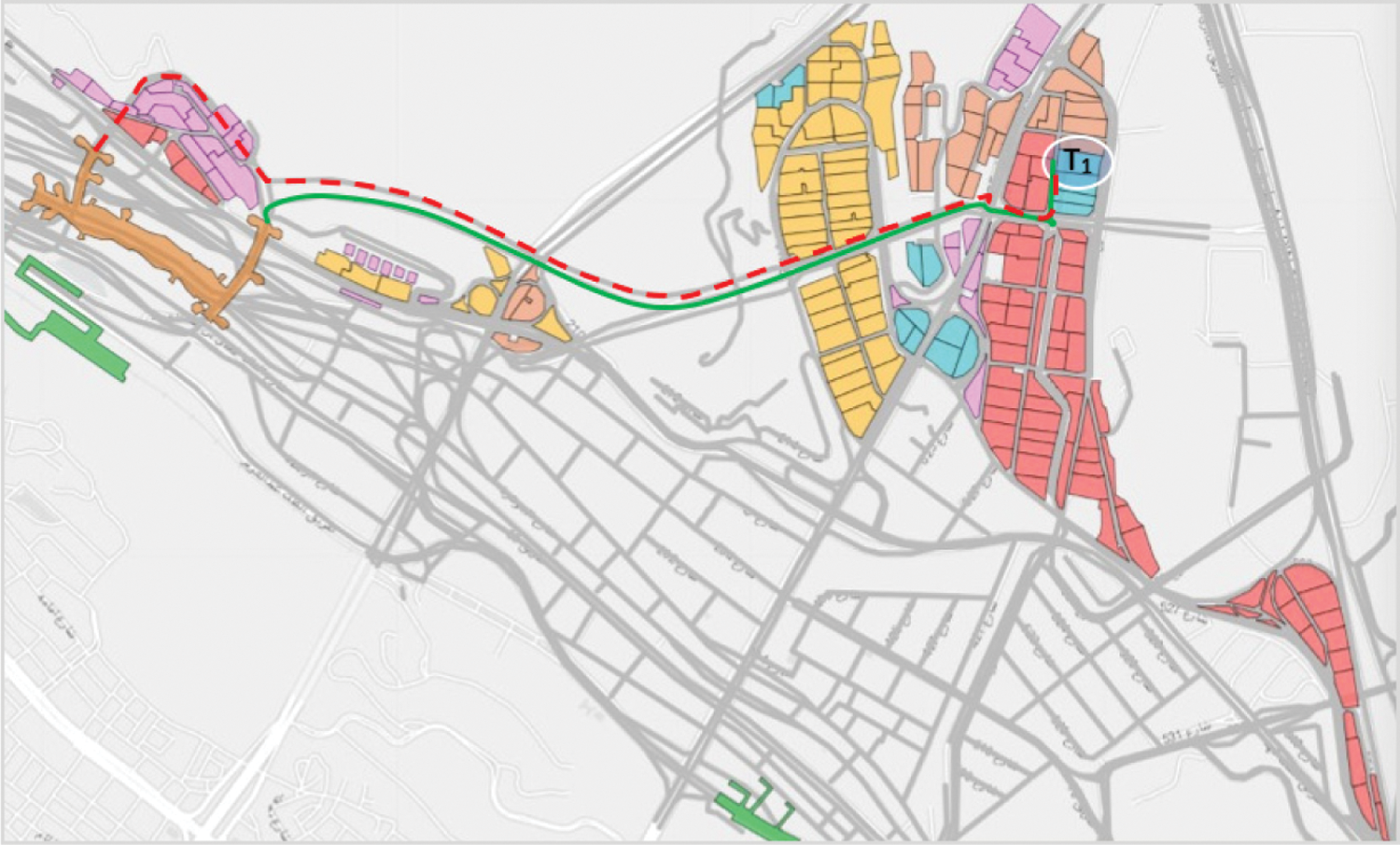
Figure 5: Aerial view of path allotted to a group of pilgrims to go (green) to the Jamarat bridge and return (red)
MATLAB (an abbreviation of “matrix laboratory”) has been used to implement the model. We used the R2020b version on i7 processor, 1.6 GHz speed and with 8 GB RAM. MATLAB leverages the mathematical operation and various operation on the matrix. The full implementation of the model is configurable, connecting as many road segments, tents, and pilgrims in each tent. The model also allows the user to update the road’s capacity and set the maximum allowed threshold.
The implementation has been divided into two parts. The first part is building up the model with all the configuration and the second part is to select the output with minimum cost. The code also considers special conditions such as partial closing any segment or stopping scheduling for a given period.
To validate our model, we run the simulation and analyses the same using a density heat map. The simulation was carried out using a desktop computer, ensuring no other task was being processed by the machine. The software details are provided in Tab. 1 below.
We digitize the small area of Mina with the factual information of pilgrims to prove our proposed model, as shown in Fig. 6. We modelled this area with ten camps and seven segments, where each segment’s length is 300 m. A total of 34,575 pilgrims are distributed in 10 different tents, as shown in Tab. 2. We assume that the pilgrims’ destination, i.e., the Jamarat building, is at the end of segment seven.
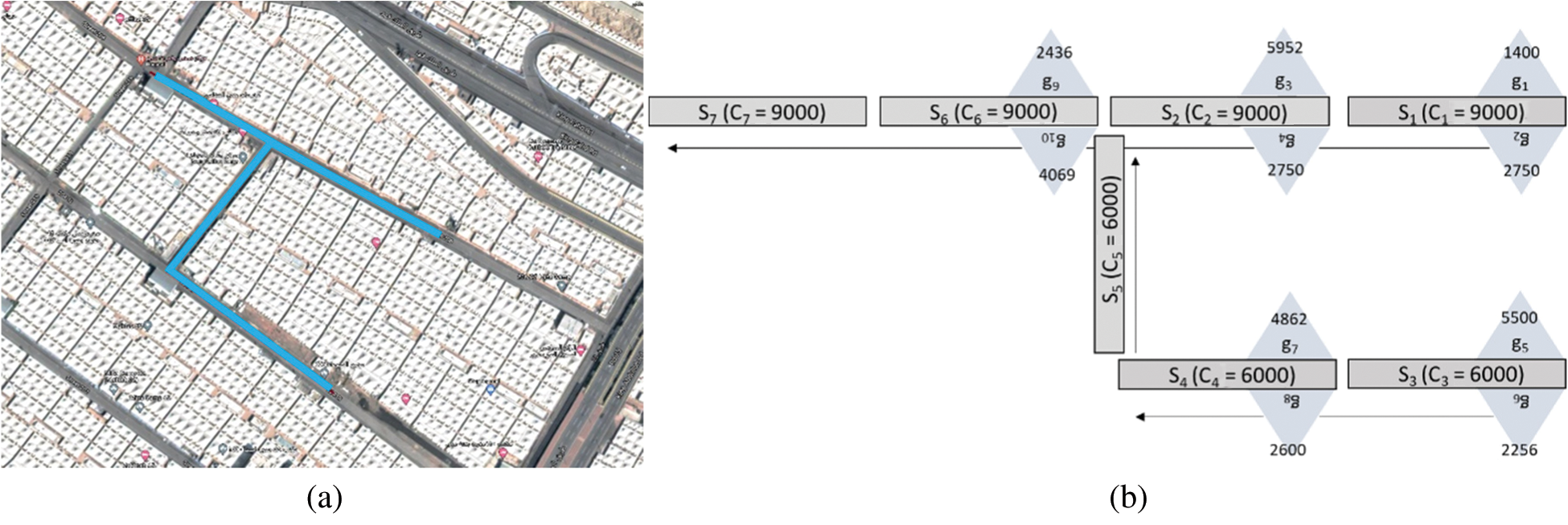
Figure 6: Actual Mina area and our modelled part (a) Mina Roads and area that we modelled (b) Our modelled part of Mina
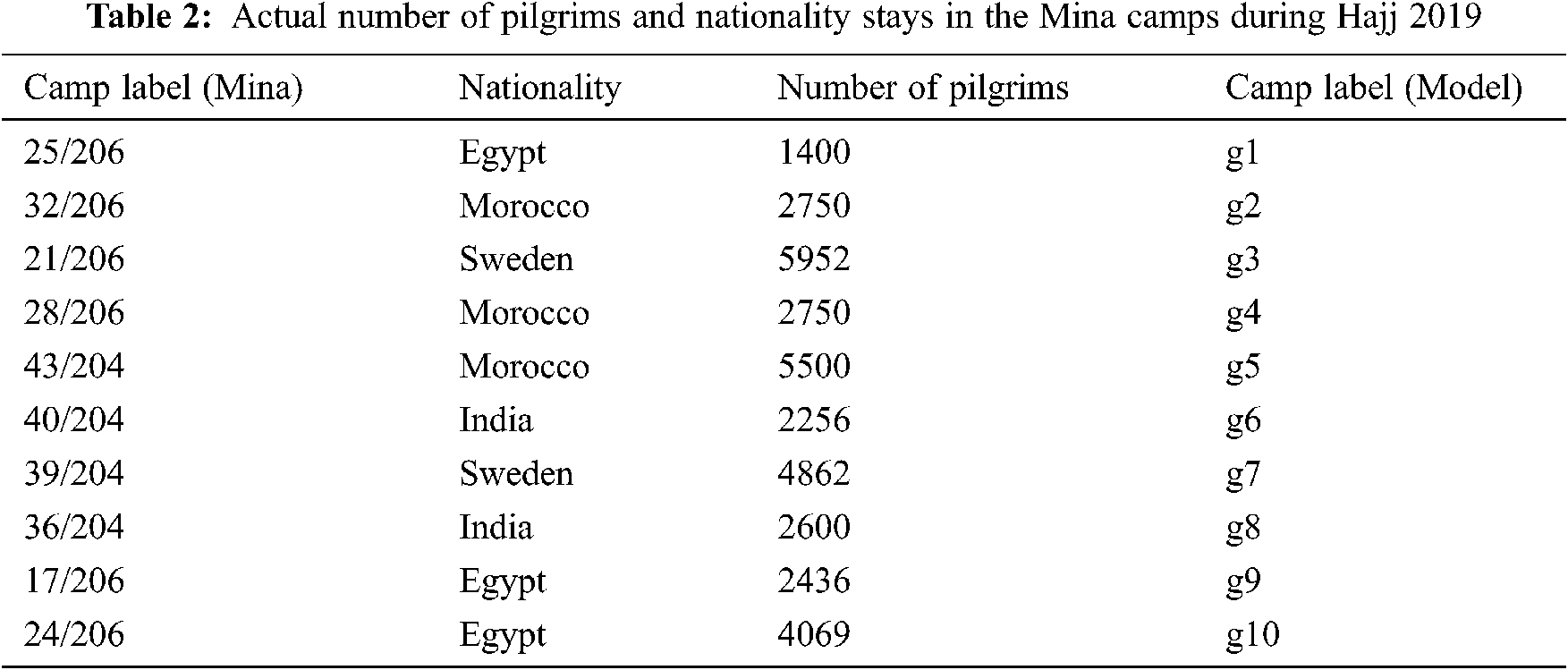
Fig. 6b. depicts a model setup for road segments
The groups size is
6.1 Understand the Digitize Infrastructure (How to Model the Infrastructure/Corridors)
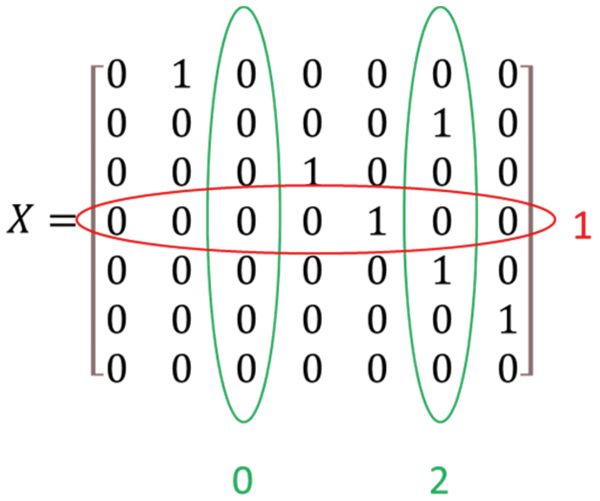
The road segment matrix helps stakeholders and decision-makers to identify all the multi-connected and unconnected segments quickly. For example, matrix ‘X’ rows and columns submission provides deep insights. The following matrix shows the sum of columns and rows of ‘X’. If the column sum is more than one, then it means that the segment has multiple inputs, as segment six sum is two, so it implies that segment 6 has two input segments. Similarly, we can find the split segment into more than one parts from the sum of rows.
6.2 Schedule the Movement of Pilgrims
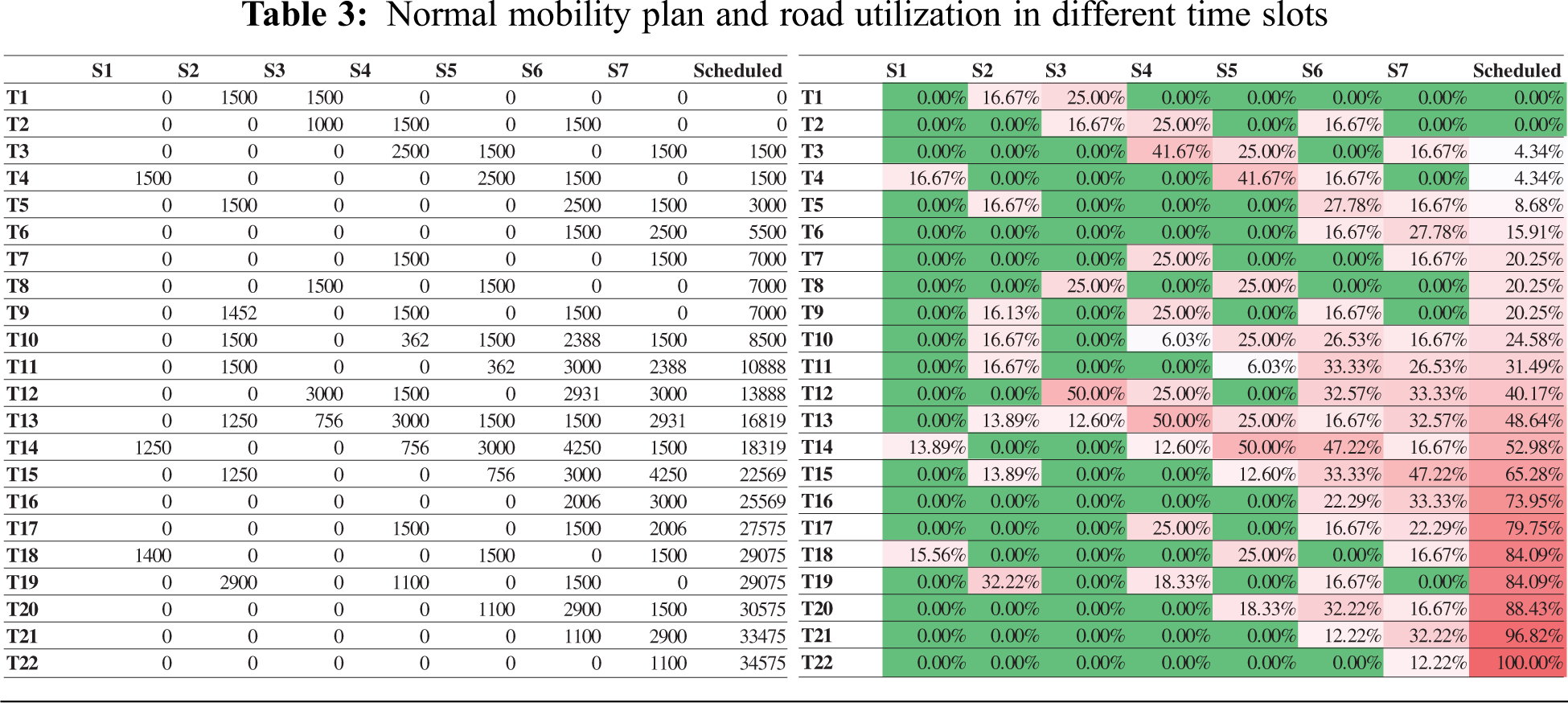
To move mobility safe and efficient, the Ministry of Hajj and Umrah need to schedule pilgrims from their camps to the Jamarat with constraints such as road capacity cannot be more than 50%, dispatching pilgrims cannot be done in the meantime forbidden hours etc. Our proposed model schedules pilgrims’ mobility plan from different segments and time slots, as shown in Tab. 3. The table also shows the percentage of road utilization during all time slots. The time slots T1, T2 … Tn values can be updated as per requirements, such as the length of the segment and crowd flow speed. Each time slot is with a difference of 5 min in our scenario, assuming the segment’s size is 300 m long and the crowd speed is 1 m/s. Therefore, the total time to schedule 34575 pilgrims is 110 min without violating 50% road capacity constraint.
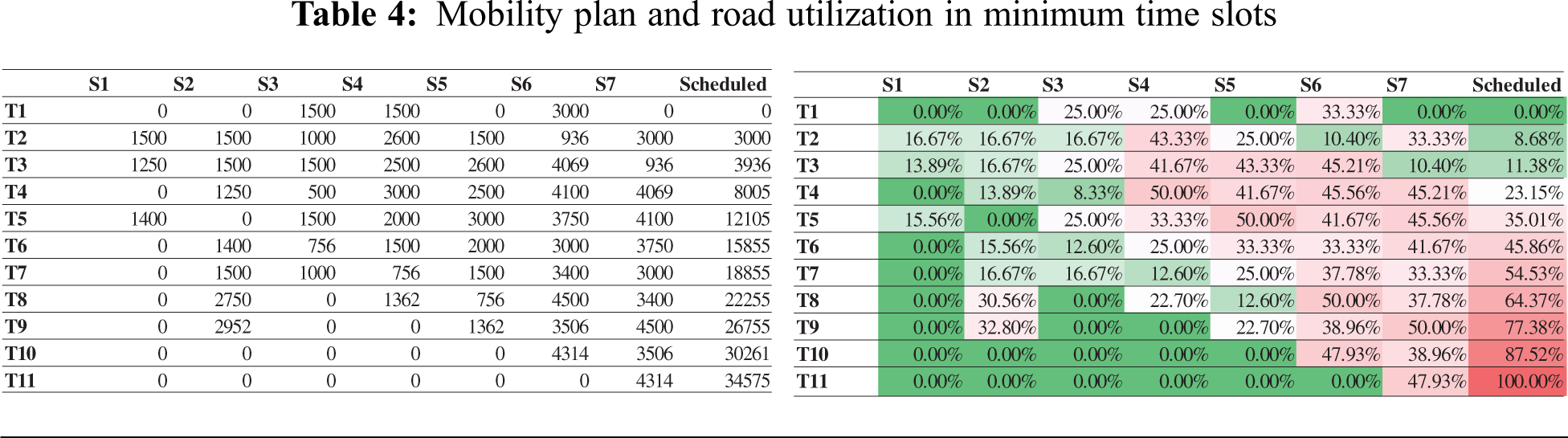
6.3 Recommend Minimum Time Frame to Schedule the Given Number of Pilgrims
Operating parties are always interested in minimizing their service time to provide crowd management support. The model takes the infrastructure, i.e., matrix
6.4 Recommend Maximum Number of Pilgrims
As per vision 2030, authorities are planning to increase the number of pilgrims. Our proposed model will recommend the maximum number of pilgrims who can safely schedule the current infrastructure and provide a time frame. First, the model takes the infrastructure, i.e., matrix
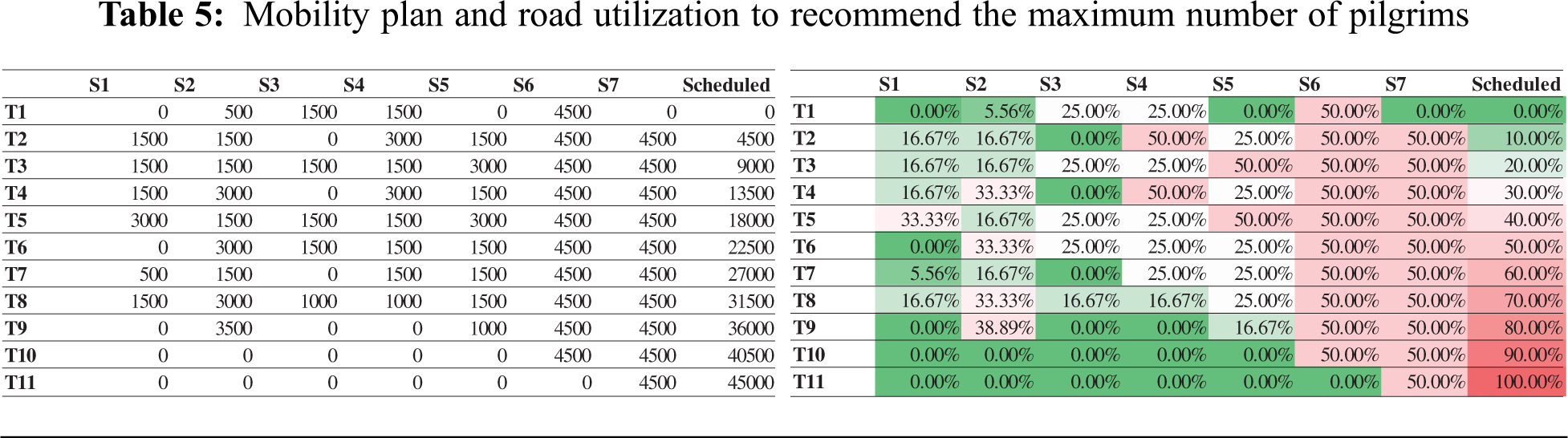
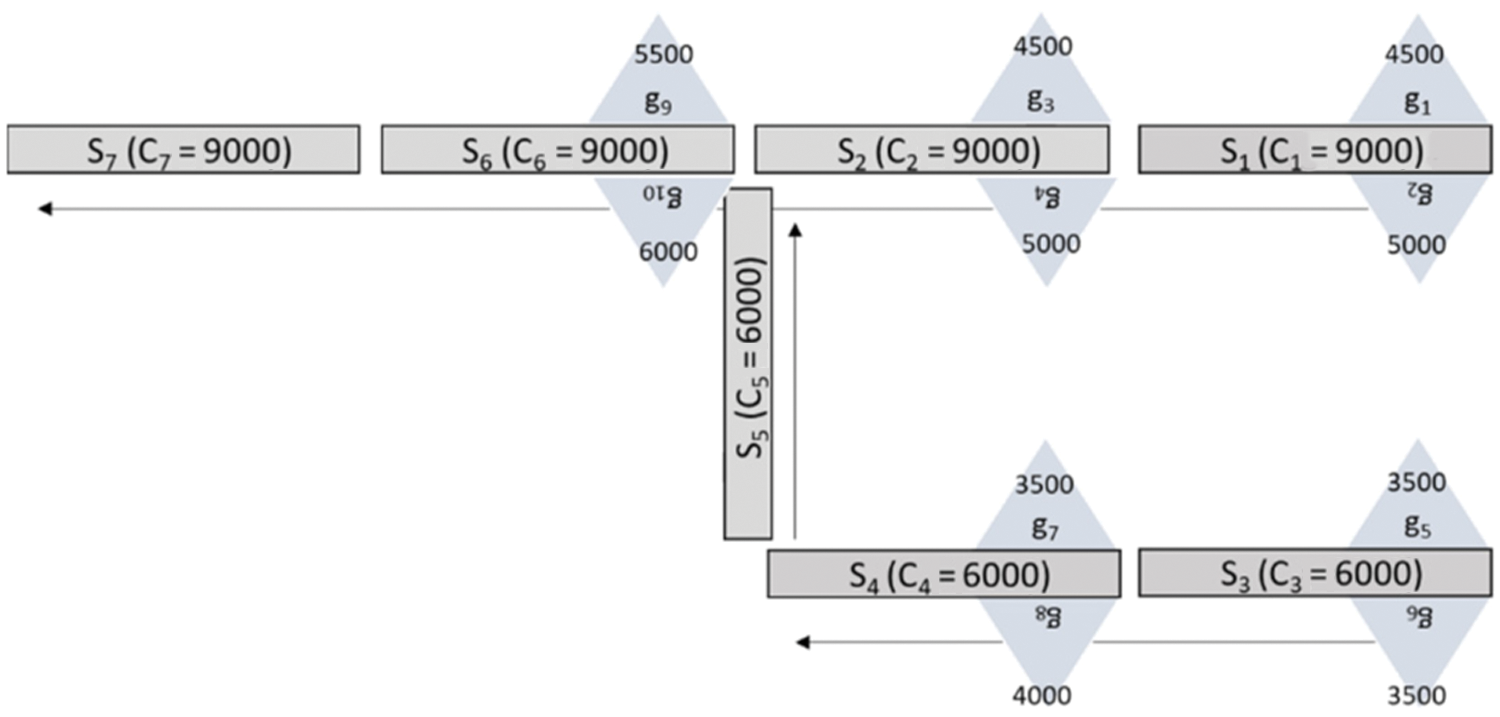
Figure 7: Distribution of pilgrims in tents and segments after increasing the number of pilgrims to 45,000
6.5 Test the Impact of Forbidden Hours
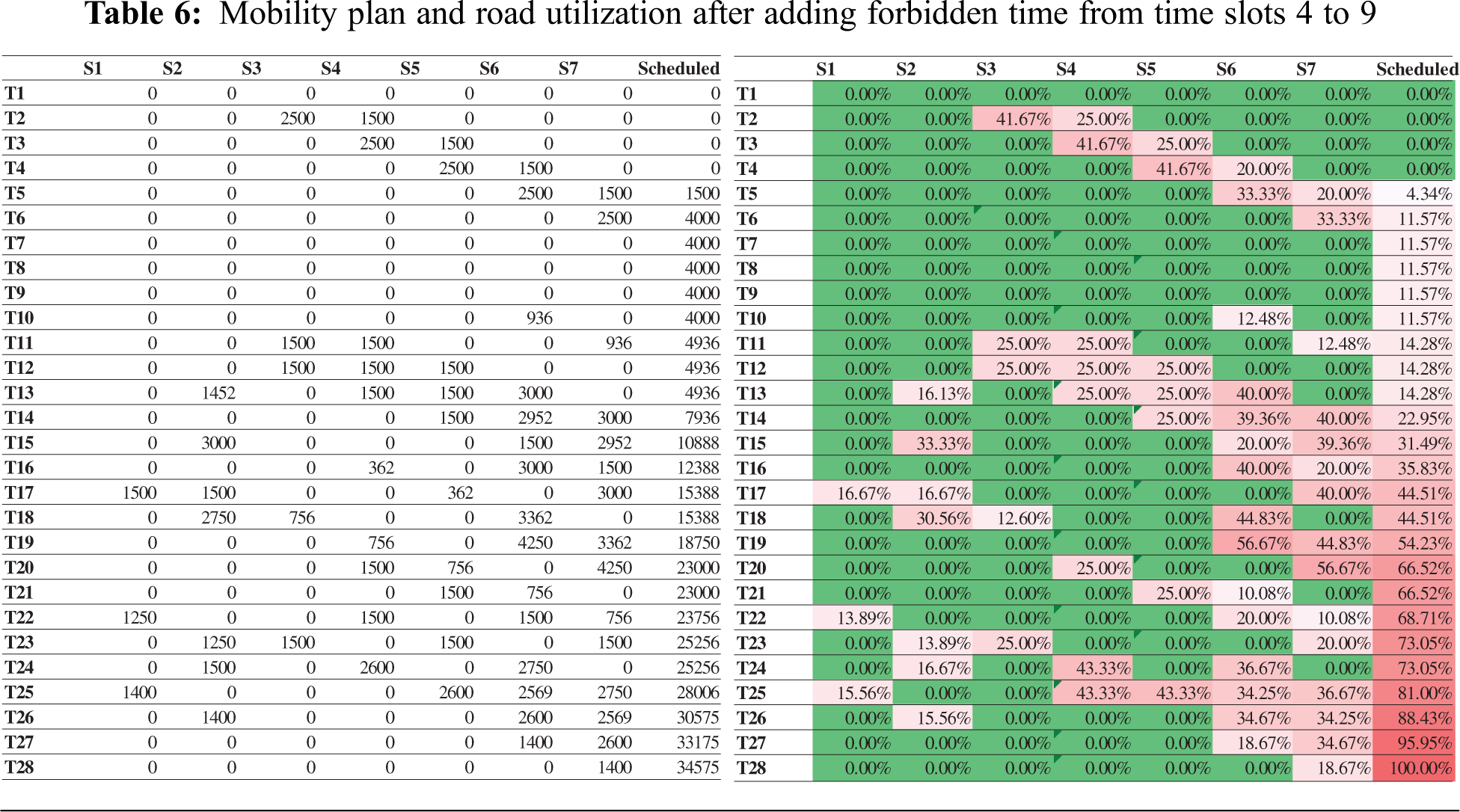
The Ministry of Hajj and Umrah pause the mobility operation during each day of Hajj for a particular period to minimize congestion. For example, Day 10th Dhul Hijjah, 6–10 am, is forbidden for Jamarat rituals. At that time, pilgrims were not allowed to leave their camps for stoning ritual. Our model provides the flexibility to add forbidden hours and generate the schedule plan. Tab. 6 shows that we can schedule 34,575 pilgrims in 28 times slots by adding forbidden time to time slots (4, 5, 6, 7, 8, and 9). The table shows the schedule plan and road utilization.
6.6 Test the Impact of Increasing or Decreasing the Capacity of a Particular Segment/Segments
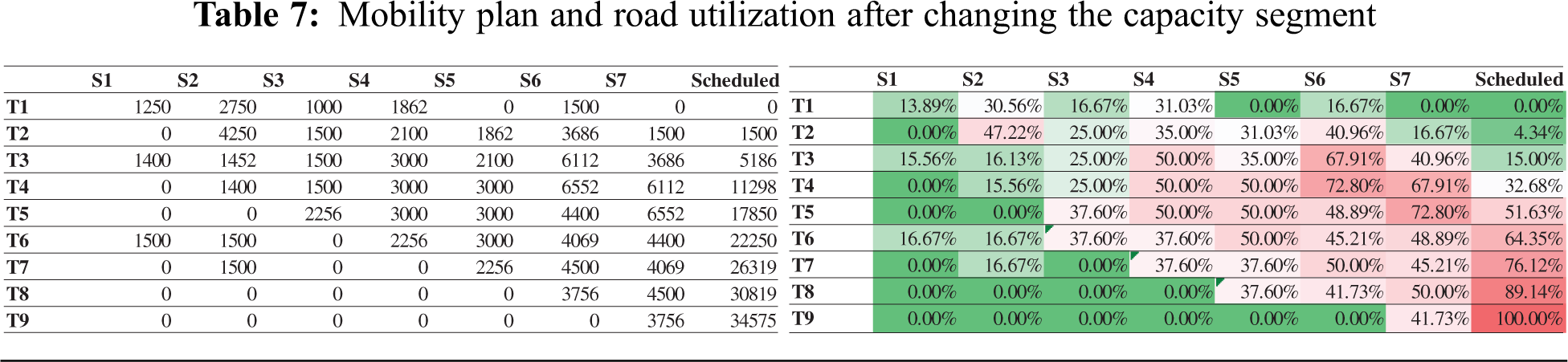
During the season’s operation, the corridors’ capacity is dynamically changing due to many reasons such as service care blocking the road, accumulation of waste on the passage, or partially closed due to any incident or construction. The model allows the stakeholders to see the impact by increasing or decreasing a specific segment or multiple segments’ capacity. The model will also help in decision-making in case authorities plans to enhance the infrastructure. Tab. 7 shows the mobility plan and road utilization after increasing the capacity of segments S6 and S7 by 25%, i.e., 13500. After expanding the capacity, the minimum time slot reduced by two as compared to Tab. 4. On the other side, if we decrease the segment’s capacity by 25%, i.e., 6750, the number of time slots will increase by 5.
6.7 Validation of the Model using Simulation
The visualization helps the stakeholders identify the bottleneck areas and be in the state of preparedness during the operation phase, as shown in Fig. 8. The model and its results can be easily visualized using any simulation tool. We envisioned the result in the Mass motion 10.5.9 crowd simulation tool on Windows 10. Fig. 8a. demonstrates crowd movement on the intersection of segment S2, S5 and S6, whereas Fig. 8b. shows the movement’s analysis with the help of a density heat map.

Figure 8: Simulation of the crowd movement using mass motion tool (a) Simulation of crowd movement on the intersection of segment S2, S5 and S6 (b) Average density map analysis of the simulation
This paper presented a model to schedule the pilgrims’ movement in the Mina area safely and efficiently. The model is generic, and all the inputs are configurable that allows stakeholders to run multiple queries.
In this project, we developed a basis for mathematical modelling to model the mobility pattern of the Pilgrims in Mina, considering all of the critical details that govern this action, such as available corridor capacity, limited times, group size restrictions and road segment connectivity. We developed the model based on more information such as group sizes, basic corridor connectivity and dynamic capacity. The model has been used to generate mobility scheduling for the Pilgrims to control their flow on those corridors. We used this model to
• Understand the corridor connectivity,
• Generate mobility time schedules according to multiple criteria
• Find the maximum number of Pilgrims that can occupy a particular area
• Find the minimum time to schedule all occupants
• Test the impact on crowd mobility with dynamic changing of corridors capacity, number of pilgrims, group sizes and forbidden times.
We believe that this work can be further developed to mathematically describe the mobility of the crowd in Mina during Hajj seasons in more details and by including more complex parameters to enhance its accuracy. Furthermore, the utilization of this model can be advantageous to related planning and operating authorities such as the Royal Commission of Makkah and the Mashaer, Makkah Region Development Authority, Ministry of Hajj and Umrah and crowd management, security forces to achieve the goal of Vision 2030 of hosting more than 30 Million Umrah and Hajj visitors.
Acknowledgement: The authors gratefully acknowledge technical and financial support from the Emirate of Makkah Province and King Abdulaziz University, Jeddah, Saudi Arabia. This research work was funded by Makkah Digital Gate Initiative under Grant Number MDP-IRI-9-2020.
1https://en.wikipedia.org/wiki/List_of_largest_peaceful_gatherings
2Fifth pillar of Islam
3Central Department of Statistics and Information, KSA
4https://hajjumrahplanner.com/rami-al-jamarat/
Funding Statement: This research work was funded by Makkah Digital Gate Initiative under Grant Number MDP-IRI-9-2020.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
5https://hajjumrahplanner.com/rami-al-jamarat/
1. A. Ahmad, “Complex network modelling and analysis of Hajj crowd and MERS-CoV outbreak,” Ph.D. dissertation. International Islamic University, Malaysia, 2017. [Google Scholar]
2. R. Löhner, “On the modeling of pedestrian motion,” Applied Mathematical Modeling, vol. 34, no. 2, pp. 366–382, 2010. [Google Scholar]
3. A. Ahmad, M. A. Rahman, F. U. Rehman, A. Lbath, A. Imad et al., “A framework for crowd-sourced data collection and context-aware services in Hajj and Umrah,” in Proc. IEEE/ACS, Doha, Qatar, pp. 405–412, 2014. [Google Scholar]
4. A. Ahmad, M. A. Rahman, M. R. Wahiddin, F. U. Rehman, A. Khelil et al., “Context-aware services based on spatio-temporal zoning and crowdsourcing,” Behaviour & Information Technology, vol. 37, no. 7, pp. 736–760, 2018. [Google Scholar]
5. J. Wang, M. Chen, B. Jin, J. Li and Z. Wang, “Propagation characteristics of the pedestrian shockwave in dense crowd: Experiment and simulation,” International Journal of Disaster Risk Reduction, vol. 40, no. 2, pp. 101287, 2019. [Google Scholar]
6. K. Haase, M. Kasper, M. Koch and S. Müller, “A pilgrim scheduling approach to increase safety during the Hajj,” Operational Research, vol. 67, no. 2, pp. 376–406, 2019. [Google Scholar]
7. M. Ganjeh and B. Einollahi, “Editorial: Mass fatalities in Hajj in 2015,” Trauma Monthly, vol. 21, no. 5, pp. 1–3, 2016. [Google Scholar]
8. A. Templeton, J. Drury and A. Philippides, “Placing large group relations into pedestrian dynamics: Psychological crowds in counterflow,” Collective Dynamics, vol. 24, no. 2, pp. 1–22, 2020. [Google Scholar]
9. X. Li, R. Ye, Z. Fang, Y. Xu, B. Cong et al., “Uni-and bidirectional pedestrian flows through zigzag corridor in a tourism area: A field study,” Adaptive Behaviour, vol. 29, no. 3, pp. 281–296, 2021. [Google Scholar]
10. M. H. Dridi, “Simulation of high density Pedestrian flow: Microscopic model,” Open Journal of Modelling and Simulation, vol. 3, no. 3, pp. 81–95, 2015. [Google Scholar]
11. R. Lubaś, J. Miller, M. Mycek, J. Porzycki and J. Wąs, “Three different approaches in pedestrian dynamics modeling–a case study,” in Proc. Advances in Intelligent Systems and Computing, vol. 224, no. 2014, pp. 285–294, 2013. [Google Scholar]
12. M. Chraibi, A. Seyfried and A. Schadschneider, “Generalized centrifugal-force model for pedestrian dynamics,” Physical Review E, vol. 82, no. 4, pp. 46111, 2010. [Google Scholar]
13. M. Chraibi, “Validated force-based modeling of pedestrian dynamics validated force-based modeling of pedestrian dynamics inaugural,” Ph.D. dissertation, Institute for Advanced Simulation (IASJülich Supercomputing Centre (JSC2018. [Google Scholar]
14. D. Helbing and P. Molnár, “Social force model for pedestrian dynamics,” Physical Review E, vol. 51, no. 5, pp. 4282–4286, 1995. [Google Scholar]
15. T. Chen, W. Wang, Y. Tu and X. Hua, “Modelling unidirectional crowd motion in a corridor with statistical characteristics of pedestrian movements,” Mathematical Problems in Engineering, vol. 2020, pp. 1–11, 2020. [Google Scholar]
16. D. Helbing, “A fluid dynamic model for the movement of pedestrians,” Complex Systems, vol. 6, no. 5, pp. 1–23, 1998. [Google Scholar]
17. K. Still, M. Papalexi, Y. Fan and D. Bamford, “Place crowd safety, crowd science? Case studies and application,” Journal of Place Management and Development, vol. 13, no. 4, pp. 385–407, 2020. [Google Scholar]
18. G. K. Still, “Crowd science and crowd counting,” Impact, vol. 2019, no. 1, pp. 19–23, 2019. [Google Scholar]
19. F. Dietrich and G. Köster, “Gradient navigation model for pedestrian dynamics,” Physical Review E, vol. 89, no. 6, pp. 62801, 2014. [Google Scholar]
20. I. G. Georgoudas, G. C. Sirakoulis and I. T. Andreadis, “A simulation tool for modelling pedestrian dynamics during evacuation of large areas,” in Proc. IFIP Int. Conf. on Artificial Intelligence Applications and Innovations, Athens, Greece, pp. 618–626, 2006. [Google Scholar]
21. W. Kang and Y. Han, “A simple and realistic pedestrian model for crowd simulation and application,” arXiv preprint, vol. abs/1708.03080, pp. 1–6, 2017. [Google Scholar]
22. V. J. Blue and J. L. Adler, “Cellular automata microsimulation for modeling bi-directional pedestrian walkways,” Transportation Research Part B Methodological, vol. 35, no. 3, pp. 293–312, 2001. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |