DOI:10.32604/iasc.2022.021206

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.021206 |  |
| Article |
Optimized U-Net Segmentation and Hybrid Res-Net for Brain Tumor MRI Images Classification
1Department of Information and Communication Engineering, Anna University, Chennai, 600025, India
2Department of Electronics and Communication Engineering, M. Kumarasamy College of Engineering, Thalavapalayam, Karur, 639113, India
*Corresponding Author: R. Rajaragavi. Email: raja_ragavi30@yahoo.co.in
Received: 26 June 2021; Accepted: 27 July 2021
Abstract: A brain tumor is a portion of uneven cells, need to be detected earlier for treatment. Magnetic Resonance Imaging (MRI) is a routinely utilized procedure to take brain tumor images. Manual segmentation of tumor is a crucial task and laborious. There is a need for an automated system for segmentation and classification for tumor surgery and medical treatments. This work suggests an efficient brain tumor segmentation and classification based on deep learning techniques. Initially, Squirrel search optimized bidirectional ConvLSTM U-net with attention gate proposed for brain tumour segmentation. Then, the Hybrid Deep ResNet and Inception Model used for classification. Squirrel search optimizer mimics the searching behavior of southern flying squirrels and their well-organized way of movement. Here, the squirrel optimizer is utilized to tune the hyperparameters of the U-net model. In addition, bidirectional attention modules of position and channel modules were added in U-Net to extract more characteristic features. Implementation results on BraTS 2018 datasets show that proposed segmentation and classification outperforms in terms of accuracy, dice score, precision rate, recall rate, and Hausdorff Distance.
Keywords: MRI; convlstm; hausdorff distance; squirrel search
Automatic separation or segmentation of affected tissue from the healthy region is a difficult task due to the complicated structure and appearance of the tumor [1]. The tumor region may spread into the entire region of the brain. Early diagnosis of a tumor may recover the patient’s life. The manual segmentation of tumors is a difficult task and may lead to misclassification. So, an automated computer-aided model is needed to segment a brain tumor exactly [2].
Many types of segmentation work use the clustering model for segmentation. The previous segmentation works on the basis of Otsu thresholding, k means clustering and adaptive clustering. The main objective of the segmentation is to identify the tumor area very accurately. Recently, machine learning and deep learning model gives more attention to the researcher by their accuracy. Convolutional Neural Networks (CNN) is a category of deep learning algorithm used by many researchers for segmentation and classification [3]. It can learn the image by extracting features. It encouraged a proposal of a new segmentation and classification model with an optimized U-Net and hybrid classifier. In the segmentation stage, a modified U net model was proposed for segmentation. It combines a bi-directional ConvLSTM layer and attention gate in order to increase accuracy. In addition, SSA optimization is used for hyperparameter tuning. In the classification stage, the concept of hybrid architecture was utilized. It combines Residual Network (ResNet) architecture with the inception model to improve classification accuracy.
Today, most of the segmentation and classification algorithms use deep learning algorithms. This section reviews various research works related to deep learning models for segmentation and classification. Hamamci et al. [4] have presented a cellular automata (CA) based seeded tumor segmentation for radiosurgery planning and assessment. Initially, the graph-theoretic principle was applied to handle shortest path difficulties. Then, the state transition is estimated to identify the correct shortest path. Finally, the tumor portions are segmented by line drawing. Results show that the proposed approach less sensitive to seed initialization and better in terms of computation time.
Islam et al. [5] have proposed a technique to extract multi-fractal features by developing multi-fractional Brownian motion (mBm) model. In addition, a patient-independent tumor segmentation method was introduced by altering the conventional AdaBoost technique. Ma et al. [6] have presented a gliomas segmentation method for MR images by combining random forests with an active contour model. Various level of structure features linked in the forest model to increase the segmentation accuracy. The active contour model is utilized for feature extraction by utilizing the features of sparse representation. Alves et al. [7] have proposed a CNN based approach for automatic brain tumor segmentation. The difficulty of overfitting is eliminated by exploring a small 3*3 kernal and a minimum number of weights in a network. Implementation results on BRATS data set indicate that technique achieves a Dice Similarity Coefficient of about 0.75 for enhancing regions. Zhou et al. [8] have developed a novel high-resolution multi-scale encoder-decoder network (HMEDN) model for blurry medical image segmentation. In the proposed architecture, high-resolution pathways are combined to gather high-resolution semantic information in order to localize boundary values exactly. Wang et al. [9] have proposed a hybrid approach for brain tumor segmentation by combining CNNs into a bounding box and scribble-based segmentation pipeline. Implementation results show that the proposed fine-tuning increases the segmentation performance and decreases the efforts needed for training.
Some of the works proposed are based on optimizing hyperparameters of the learning model by metaheuristic algorithms. Huo et al. [10] have a semi-supervised automatic segmentation algorithm using particle swarm optimization (PSO). The hyperparameters of the learning model are optimized based on the PSO fitness function. By the use of maximum data extracted from unlabeled data. Wang et al. [11] have proposed a particle swarm and genetic algorithm combined CNN for segmentation. Both PSO and genetic developed to search optimal CNN parameters in order to provide a better learning rate. Shrestha et al. [12] have introduced a genetically optimized hyperparameter tuning in DNN architecture. Monte Carlo method based training is used for variance reduction. Zhang et al. [13] have proposed population-based optimization for tuning DNN. Evolutionary Stochastic Gradient Descent (ESGD) optimization integrated to vary the step size with fitness function for achieving higher accuracy. Bibaeva et al. [14] have designed DNN architecture with automating hyperparameter tuning. Memetic algorithm incorporated to increase the efficiency of DNN architecture. Memetic is a combination of both metaheuristic algorithms of evolutionary computation and local search motivated by natural evolution. Lee et al. [15] have presented a parameter-setting-free harmony search (PSF-HS) algorithm-based DNN architecture. PDF-HS is utilized to tune the hyperparameters in the stage of feature extraction. The fitness or weight of PSF-HS is changed based on the loss of DNN.
The rest of the paper is structured as follows; Modified U-Net architecture is described in Section 2. Section 3 consists of the optimization procedure of the U-Net. Section 4 describes the proposed hybrid classification. The implementation results explained in Section 5. Finally, Section 6 concludes our results.
2 Bidirectional u-NET Based Segmentation
U net is introduced by Ronneberger et al, especially for medical image segmentation. Compared to other networks, it has the advantage of utilizing both context data and global location with minimum training samples. This work proposes a bidirectional ConvLSTM U-Net with an attention gate for segmentation. The hybrid model is used for classification. The overall workflow is shown in Fig. 1.
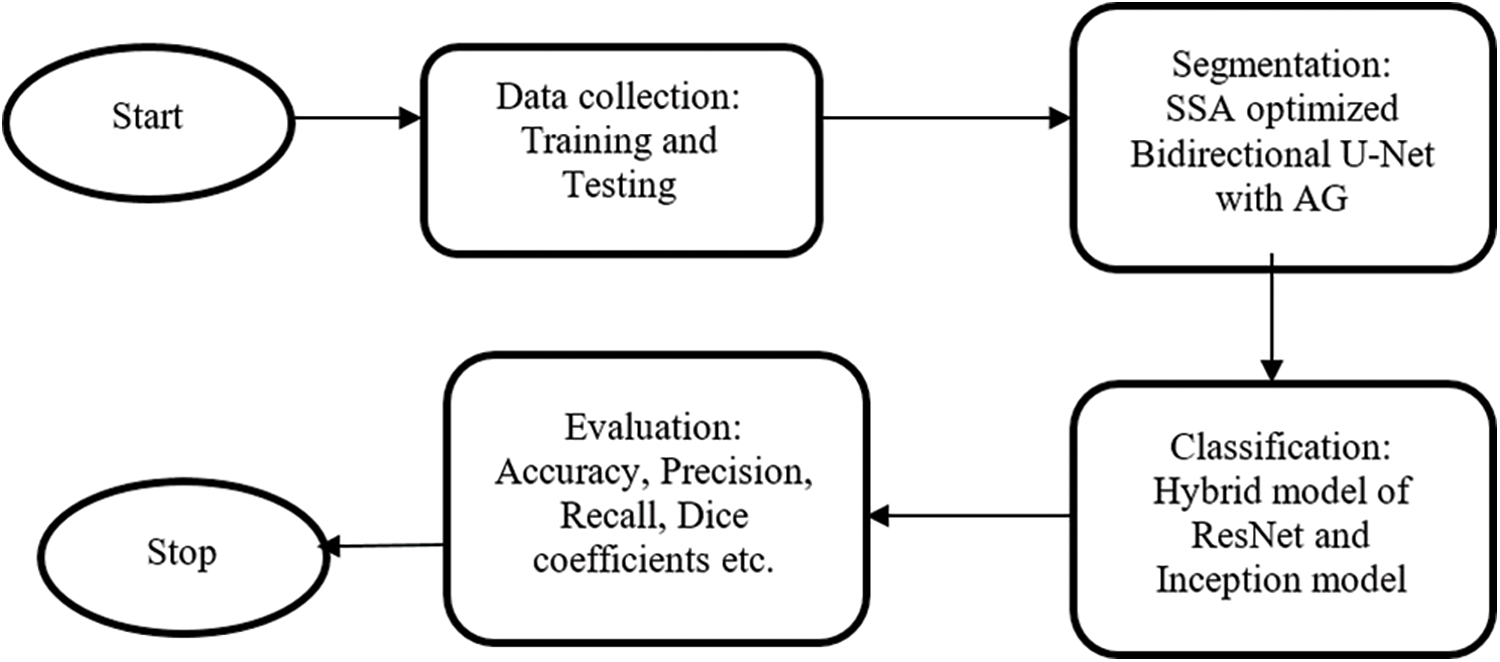
Figure 1: The overall workflow
The proposed model consists of four major stages: Encoding Path, Decoding Path, Bi-Directional ConvLSTM, and Attention gate as shown in Fig. 2. In the contraction path, two 3*3 convolutional filter operations followed by 2*2 max-pooling and ReLU performed in each step. It is used to extract image representation and for their dimension improvement.
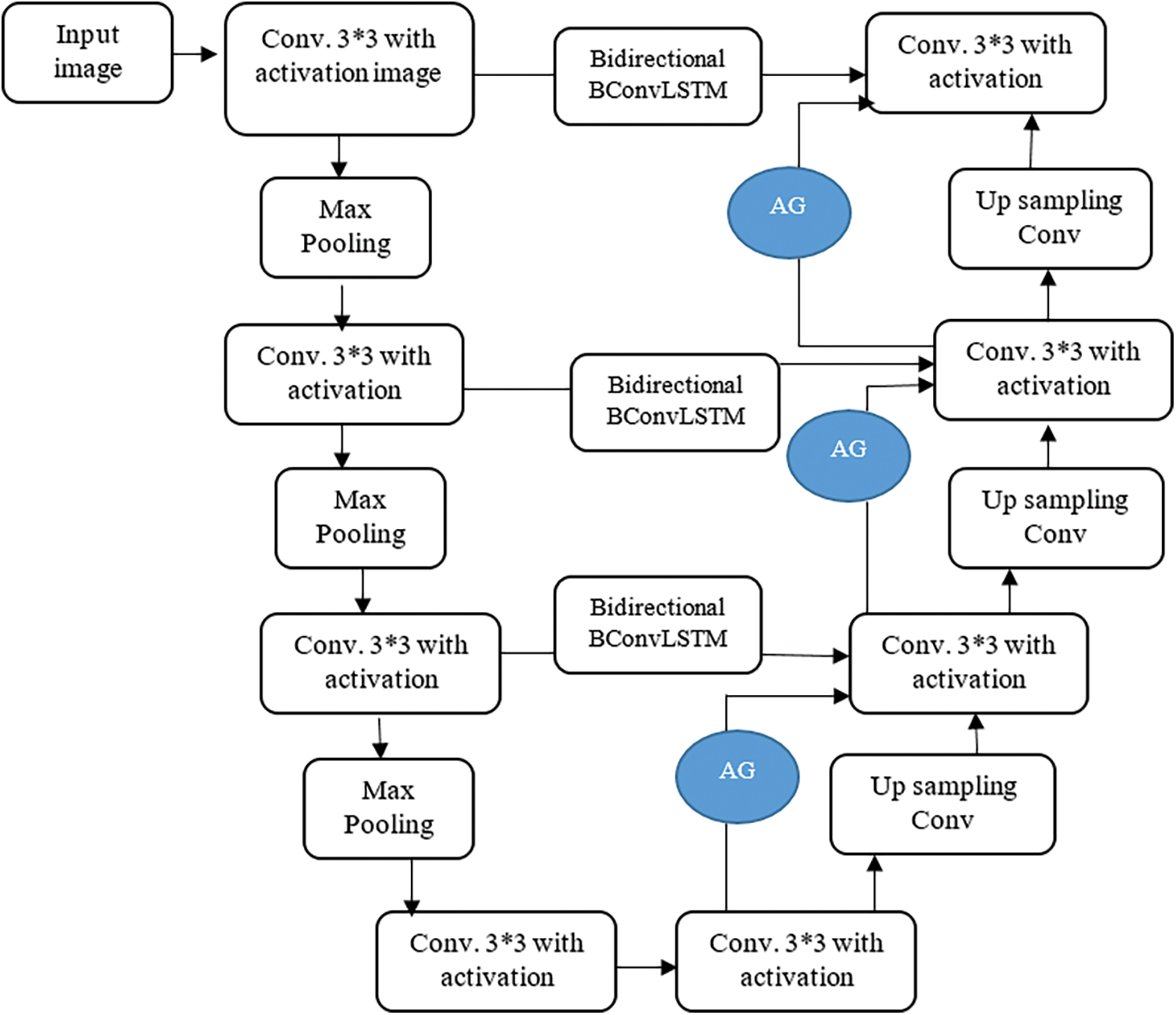
Figure 2: Proposed U-Net model
The upsampling operation of the previous layer is carried out in the decoding path. The feature maps from the encoding path are directly copied and connected to the decoding path in conventional U-Net. To strengthen the features and reusing purpose, the features from encoding path connected to decoding path by Bi-Directional ConvLSTM. The features from both encoding path and previous layer combined to perform upsampling 2*2 convolution operation. The size of the image increased layer by layer to get the original image size in the final layer.
Bi-Directional ConvLSTM consists of two ConvLSTMs to process the data in both forward and backward directions. ConvLSTMs were proposed by Yan et al. [16] to perform convolution in a state to state and input to a state conversion. The bidirectional operation between encoding and decoding path used to handle the data dependencies in both directions and all data fully considered as shown in Fig. 3.
where b is a bias term. Fwd and Bwd denote both forward and backward states. the purpose of using tanh activation function is to combine both states in a non-linear manner.
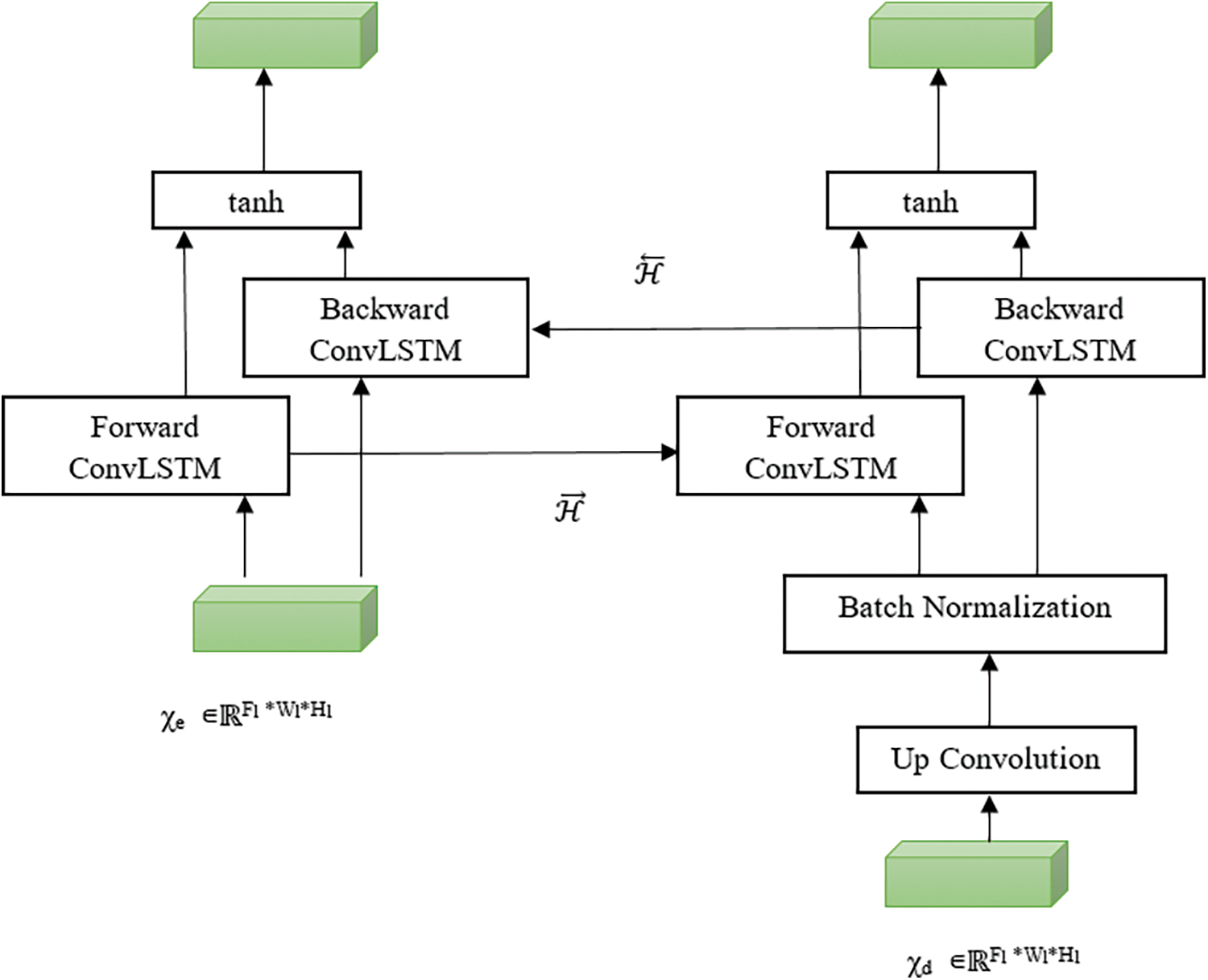
Figure 3: Bi-directional convLSTM
Attention gate or AGs are inserted in the decoding path to highlight salient features in skip connections. AGs are used to suppress feature responses in unrelated background portions without the process of localization. The schematic of AG is shown in Fig. 4. The gating signal (g) is used to produce activations and contextual information for selecting spatial regions. Input features (xl) are scaled by attention coefficients (α). Trilinear interpolation was used to resample the attention coefficients. AG gate expressed as follows:
where
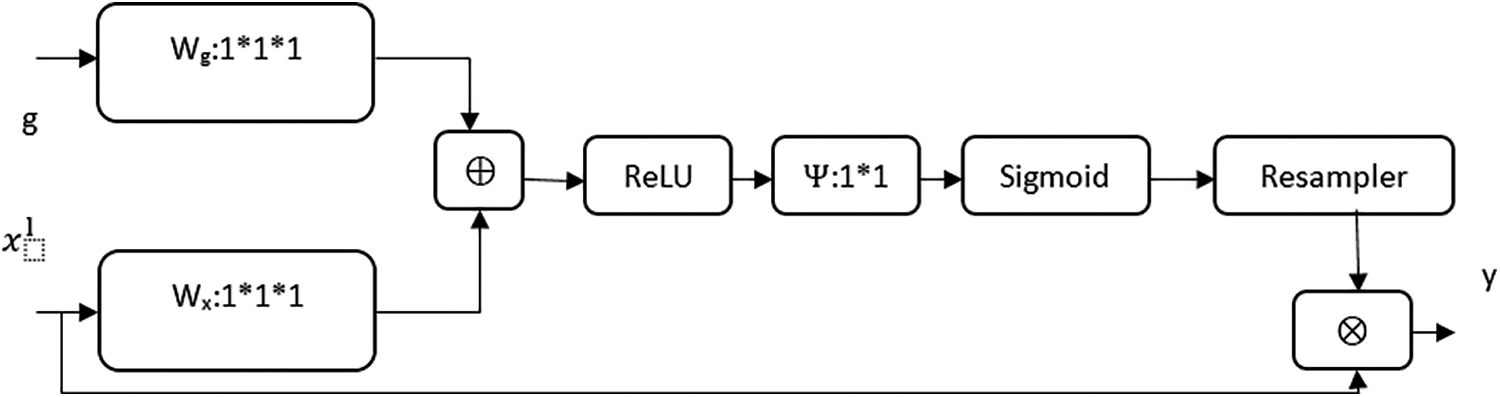
Figure 4: Attention gate
2.5 Squirrel Search Algorithm (SSA)
The flying squirrels begin their exploration and thereby the searching process starts [17]. To find food resources, the squirrels slither from one tree to another, during autumn season. In the intervening time, they alter their whereabouts and discover various regions of forest. These squirrels gain their daily energy requirements easily and swiftly by feeding on the acorns available abundantly, during the hot climatic conditions. After finding their acorns they devour them straightaway without any delay. Once they are satisfied with their daily energy requirement, they begin their search for hickory nuts, a prime food source of winter. It can maintain its energy requirements in severe weather conditions by storing the collected hickory nuts intelligently, thereby reducing the cost of foraging outings. Meanwhile, it also enhances the possibility of their existence. Throughout winter deciduous forests shed their leaves and it forms a leaf cover, which made the predators to hunt for their prey easily. This makes the squirrels to become less active, yet they don't lie dormant. This process repeats continuously and it forms the base of SSA and remains till the flying squirrel’s lifespan.
Each Squirrel starts with a random location which is a uniform Distribution that are specified by a vector for optimization. Three types of movement happening in the food searching process of Squirrel with the absence of predator. The random walk forced to nearby walloping place whereas the presence of a predator. Three types of moves correspond to Acorn Nut trees (AT), Hickory nut Tree(HT) and Normal tree (NT) expressed as follows:
Hovering squirrels move from AT trees to HT termed as:
where
acorn nut trees (HSat)
dg → random gliding distance
t→ the current iteration
Gc → gliding constant
R1→ Random number between 0 to 1
Move from NT to AT to accomplish their regular energy needs termed as:
R2→ Random number between 0 to 1
NT to towards HT in order to stock their hickory nuts termed as:
R3→ Random number between 0 to 1
Towards the end of the winter period, squirrels will change to alternate ways that are utilized to find a good food source. The repositioning of such movement is expressed as:
Levyn → Levy distribution increases effectual search space exploration
For seasonal monitoring condition, the rate of the seasonal constant calculated as:
A = tm/2.5
t → current iteration
tm → maximum iteration
For the stopping criterion, a maximum number of iterations is considered.
3 SSA Based Hyperparameter Tuning
The set of variables related to model structure and network training is called hyperparameters. The proposer selection hyperparameters lead to higher accuracy. It is divided into two types. Related to a structure are s: Kernel size , Kernel Type, Stride, Hidden layer–layers between input and output layers and Activation functions. Related to a structure are Learning rate, Momentum–regulate, number of epochs and batch size. The proposed combination of the above variables increases the performance of the model. In this work, SSA optimization is used to search optimum hyperparameters of our U-Net model.

4 Hybrid Net-Based Classification
This work combines ResNet with the Inception net model for classification. ResNet is a unique deep convolutional architecture with layers of 152. The problem of vanishing gradients is eliminated by the concept of skip connections. Inception net was introduced to overcome the drawback of GoogleNet. It consists of a pooling layer, network layer and convolution layer. All the layers are processed sequentially in a classical model. This model all the layer works in parallel to reduce the number of parameters and operations. Due to parallel operation, the memory and processing cost are also reduced.
Compared to other models, the ResNet and Inception Net combined hybrid model takes the benefits of both and has confirmed their capability to scale up thousands of layers. The residual networks contain number residual blocks for identity mapping. The Inception network consists of many convolutional networks. The operation of convolution and input data conversion the rectified linear unit (ReLU) function is performed in convolutional layers. This hybrid model contains of three convolutional layers as shown in Fig. 5. Each layer contains 9 filters to extract 9 feature maps. The process of each filter expressed as:
where * denotes the convolution operation
Fi denotes the filter
Di-1 denotes the input data
β denotes the bias
Di denotes output feature map
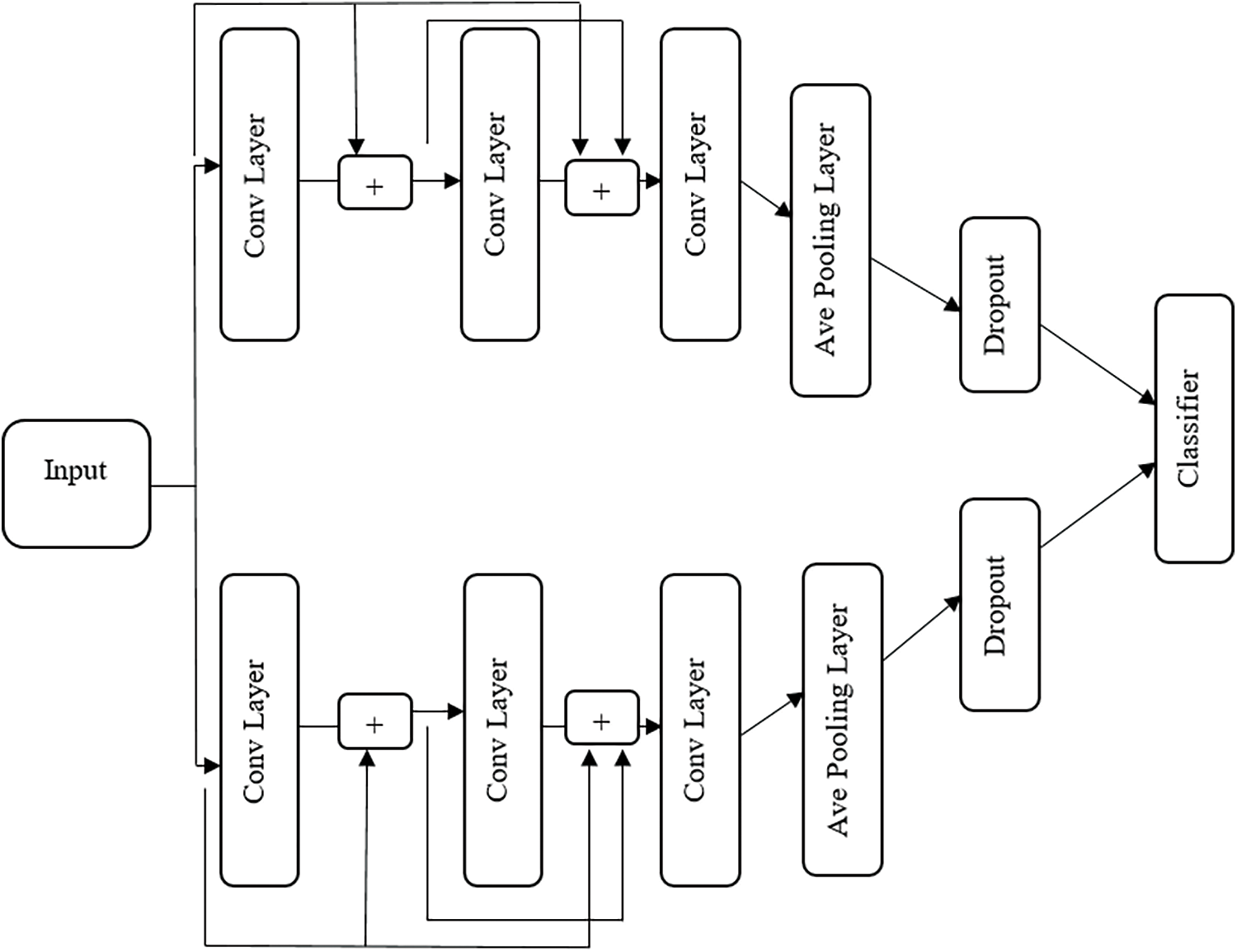
Figure 5: Hybrid classification model
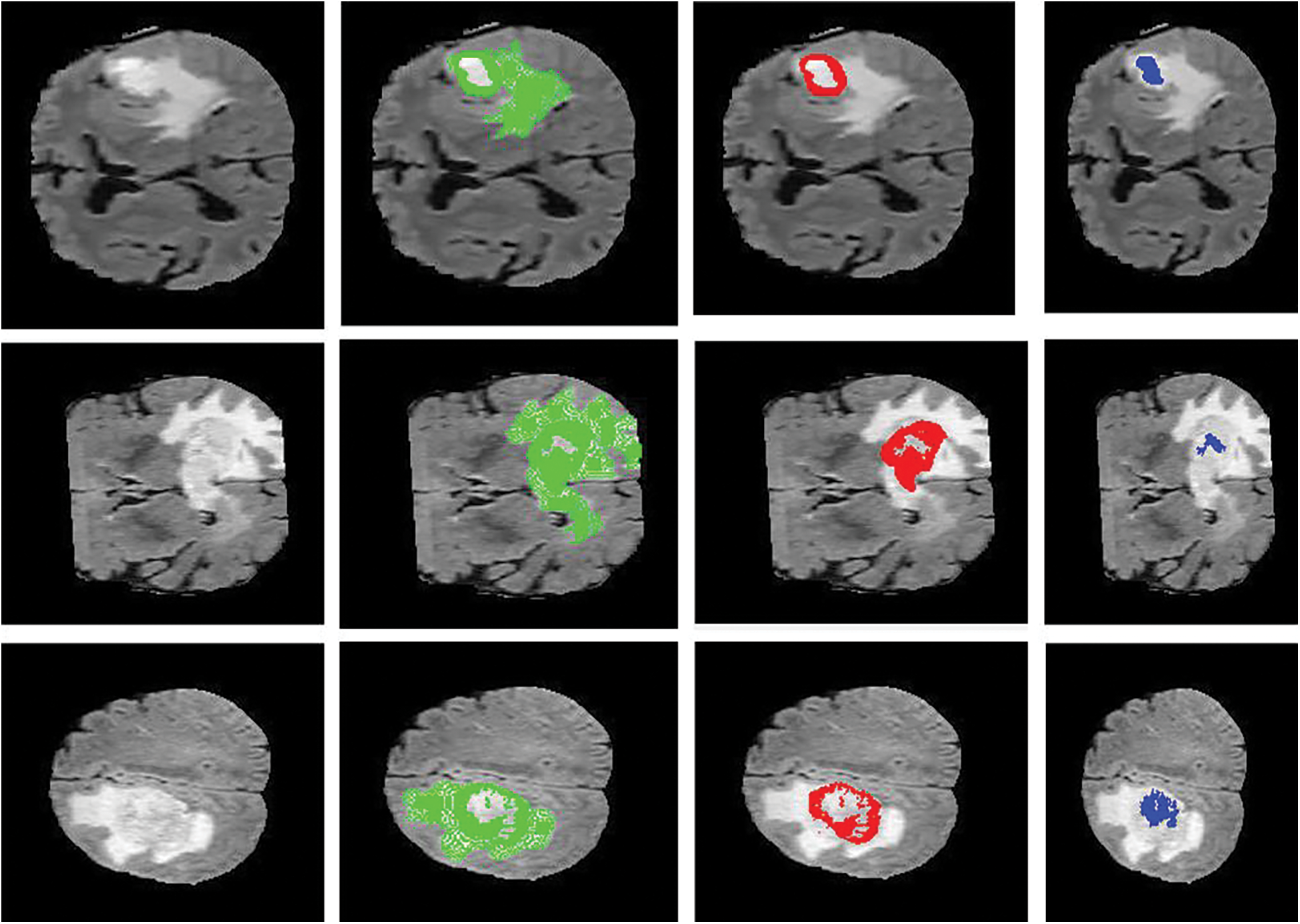
Figure 6: Sample visualization resutls (The first column shows the input image, second column represnets the Edema region, thrid column denotes the Enhancing region, and fourth column represets the Necrotic region)
The process of upper residual block expressed as
The process of lower residual block expressed as
By the motivation of the inception net, both upper and lower blocks are computed parallelly. In the above equation, the last two lines indicate pooling and drop out of the operation. The pooling layer computes the average pooling operation with a filter size of 2.
In this section, the efficiency of the proposed bidirectional U-Net on BraTS 2018 database are evaluated using MATLAB. It BraTS 2018 uses multi-institutional pre-operative MRI scans to segment gliomas-based brain tumors. Gliomas are heterogeneous in their appearance and shape. BraTS 2018 includes 66 unlabeled patient themes for the validation dataset. The training dataset includes 335 glioma patients with a high-grade glioma cases count of 259 cases and a low-grade glioma cases count of 76.
The intratumor structures of edema, necrotic, enhancing tumor and nonenhancing tumor core have been clustered into regions of: The enhancing tumor region (ET) which contains entire tissues of tumor. (b) The tumor core region (TC) is used to enhance tumor, non-enhancing tumor core and necrotic. (c) The whole tumor region (WT). Sample visualization of the results attained are demonstrated in Figs. 6 and 7.
The performance parameters of Sensitivity, Specificity, Accuracy, F1Score, Dice Score and Hausdorff Distance (HD) are used to appraise the performance of suggested algorithm against existing segmentation and classification algorithms. First, we calculated True Negative (TN), True Positive (TP), False Negative (FN) and False Positive (FP) to compare with a ground truth image (GT) and predicted image (PI) to find sensitivity, specificity, and Accuracy and F1Score values.
Tab. 1 shows the measured values of the proposed method and compared against other optimization likes particle swarm optimization (PSO), glow swarm optimization (GSO), whale swarm optimization, Brain-Storm Optimization (BSO), and Fuzzy Brain-Storm Optimization (FBSO). The computation of sensitivity, specificity and accuracy values of the proposed method is 96.6102, 92.4242 and 94.4 respectively.

As shown in Tabs. 2 and 3, for all the types of tumor areas, the proposed method attains the best results Compared to other methods [18–22], the Dice score of the proposed algorithm higher than other techniques. We can note that the proposed method enhanced the segmentation outputs in terms of on average Dice Score and Hausdroff Distance for whole, core and enhancing tumor, correspondingly.
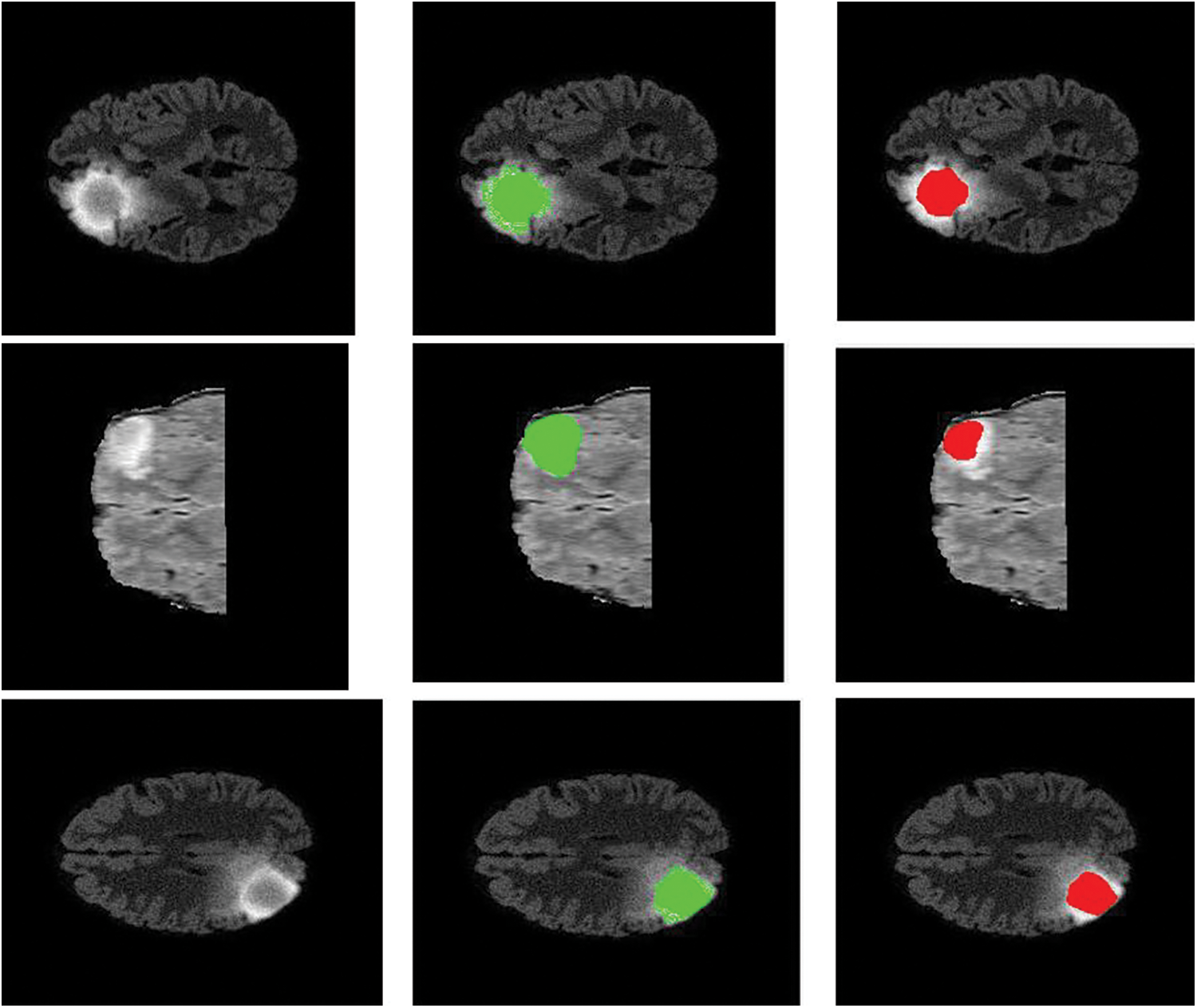
Figure 7: Sample visualization resutls (The first column shows the input image, second column represnets the Edema region, and thrid column denotes the Enhancing region)


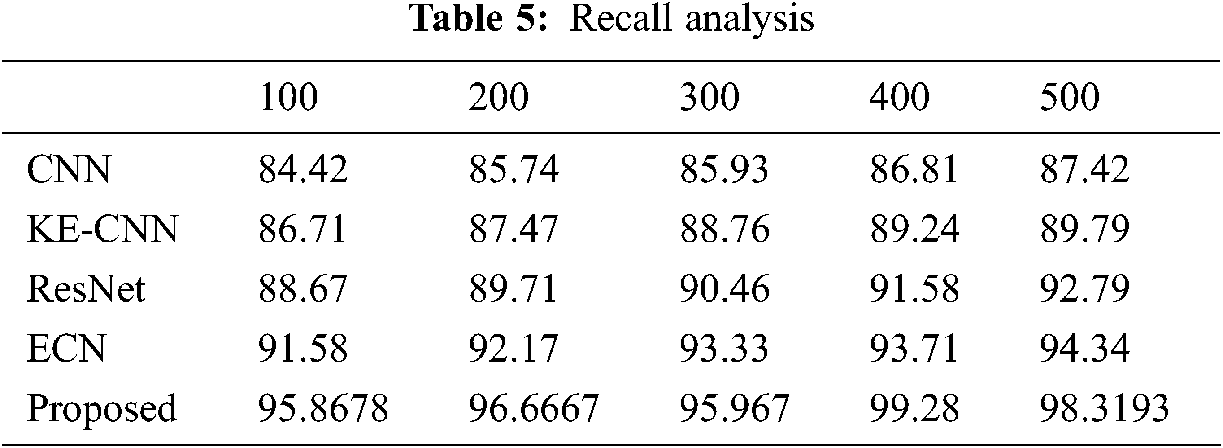
The classification results of the proposed method tabulated in Tabs. 4–7. The proposed method compared against Convolutional Neural Network (CNN), Residual Network (ResNet), Enhanced Capsule Networks (ECN), Kernel Extreme Learning Machine (KE-CNN). The results plotted for every method have varied below 500 no of epochs with step sizes of 100 epochs. The suggested hybrid classifier gives optimum precision, recall and accuracy rate than other classifiers.



This work proposes a deep learning technique based on segmentation and classification model for brain tumor. To achieve higher accuracy, a squirrel search optimizer was used to tune the hyperparameters of the U net. We also combine bidirectional and attention modules to the U net model to extract more specific features. The hybridization of ResNet and Inception net was used to classify the tumor type. The proposed models implemented on BraTS 2018 database. Results show that proposed segmentation and classification outperforms in terms of accuracy, dice score, precision rate, recall rate, and Hausdorff Distance.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Z. Tang, S. Ahmad and P. T. Yap, “Multi-atlas segmentation of mr tumor brain images using low-rank based image recovery,” IEEE Transactions on Medical Imaging, vol. 1, no. 1, pp. 32–41, 2018. [Google Scholar]
2. M. Huang, W. Yang, Y. Wu, J. Jiang, W. Chen et al., “Brain tumor segmentation based on local independent projection-based classification,” IEEE Transactions on Biomedical Engineering, vol. 61, no. 10, pp. 2633–2645, 2014. [Google Scholar]
3. S. Pereira, A. Pinto, J. Amorim, A. Ribeiro, V. Alves et al., “Adaptive feature recombination and recalibration for semantic segmentation with fully convolutional networks,” IEEE Transactions on Medical Imaging, vol. 1, no. 1, pp. 25–32, 2019. [Google Scholar]
4. A. Hamamci, N. Kucuk, K. Karaman and G. Unal, “Tumor-cut: Segmentation of brain tumors on contrast enhanced mr images for radiosurgery applications,” IEEE Transactions on Medical Imaging, vol. 31, no. 3, pp. 790–804, 2012. [Google Scholar]
5. A. Islam, S. M. Reza and K. M. Iftekharuddin, “Multifractal texture estimation for detection and segmentation of brain tumors,” IEEE Transactions on Biomedical Engineering, vol. 60, no. 11, pp. 3204–3215, 2013. [Google Scholar]
6. C. Ma, G. Luo and K. Wang, “Concatenated and connected random forests with multiscale patch driven active contour model for automated brain tumor segmentation of mr images,” IEEE Transactions on Medical Imaging, vol. 37, no. 68, pp. 1012–1021, 2018. [Google Scholar]
7. A. Alves, V. Pereira, S. Pinto and C. A. Silva, “Brain tumor segmentation using convolutional neural networks in mri images,” IEEE Transactions on Medical Imaging, vol. 35, no. 5, pp. 1240–1251, 2016. [Google Scholar]
8. S. Zhou, D. Nie, E. Adeli, J. Yin, J. Lian et al., “High-resolution encoder-decoder networks for low-contrast medical image segmentation,” IEEE Transactions on Image Processing, vol. 1, no. 1, pp. 512–522, 2019. [Google Scholar]
9. G. Wang, W. Li, M. A. Zuluaga, R. Pratt, P. A. Patel et al., “Interactive medical image segmentation using deep learning with image-specific fine tuning,” IEEE Transactions on Medical Imaging, vol. 37, no. 7, pp. 715–723, 2018. [Google Scholar]
10. Q. Huo, G. Tang and F. Zhang, “Particle swarm optimization for great enhancement in semi-supervised retinal vessel segmentation with generative adversarial networks,” Machine Learning and Medical Engineering for Cardiovascular Health and Intravascular Imaging and Computer Assisted Stenting, vol. 5, no. 6, pp. 117–132, 2019. [Google Scholar]
11. B. Wang, Y. Sun and B. Xue, “A Hybrid GA-PSO Method for Evolving Architecture and Short Connections of Deep Convolutional Neural Networks,” Lecture Notes in Computer Science, vol. 11672. New York, Springer, Cham, 2019. [Google Scholar]
12. A. Shrestha and A. Mahmood, “Optimizing deep neural network architecture with enhanced genetic algorithm,” in 2019 18th IEEE Int. Conf. on Machine Learning and Applications (ICMLABoca Raton, FL, USA, pp. 1365–1370, 2019. [Google Scholar]
13. W. Zhang and Z. Tüske, “Evolutionary stochastic gradient descent for optimization of deep neural networks,” in NIPS'18: Proc. of the 32nd Int. Conf. on Neural Information Processing Systems, Montréal Canada, pp. 6051–6061, 2018. [Google Scholar]
14. V. Bibaeva, “Using metaheuristics for hyper-parameter optimization of convolutional neural networks,” in 2018 in IEEE 28th Int. Workshop on Machine Learning for Signal Processing (MLSPAalborg, pp. 1–6, 2018. [Google Scholar]
15. W. Y. Lee, S. M. Park and K. B. Sim, “Optimal hyperparameter tuning of convolutional neural networks based on the parameter-setting-free harmony search algorithm,” Optik, vol. 172, pp. 359–367, 2018. [Google Scholar]
16. Q. Yan, F. Ji, K. Miao, Q. Wu, Y. Xia et al., “Convolutional residual-attention: A deep learning approach for precipitation nowcasting,” Advances in Meteorology, vol. 2020, pp. 1–12, 2020. [Google Scholar]
17. M. Jain, V. Singh and A. Rani, “A novel nature-inspired algorithm for optimization: Squirrel search algorithm,” Swarm and Evolutionary Computation, vol. 44, pp. 148–175, 2019. [Google Scholar]
18. O. Ronneberger, P. Fischer and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, pp. 234–241, 2015. [Google Scholar]
19. G. Shen, Y. Ding, T. Lan, H. Chen and Z. Qin, “Brain tumor segmentation using concurrent fully convolutional networks and conditional random fields,” in Proc. of the 3rd Int. Conf. on Multimedia and Image Processing - ICMIP 2018, Guiyang, China, pp. 24–30, 2018. [Google Scholar]
20. Y. Hu, X. Liu, X. Wen, C. Niu and Y. Xia, “Brain tumor segmentation on multimodal mr imaging using multi-level upsampling in decoder,” in Int. MICCAI Brainlesion Workshop, Springer, pp. 168–177, 2018. [Google Scholar]
21. A. Myronenko, “3d mri brain tumor segmentation using autoencoder regularization,” in Int. MICCAI Brainlesion Workshop, Springer, pp. 311–320, 2018. [Google Scholar]
22. T. Zhou, S. Canu, P. Vera and S. Ruan, “Latent correlation representation learning for brain tumor segmentation with missing mri modalities,” IEEE Transactions on Image Processing, vol. 30, pp. 4263–4274, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |