DOI:10.32604/iasc.2022.021581

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.021581 |  |
| Article |
Coronavirus Decision-Making Based on a Locally
1Department of Mathematics and Statistics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Mathematics, College of Science, University of Jeddah, Jeddah, Saudi Arabia
3Department of Mathematics, College of Science, King Khalid University, Abha, Saudi Arabia
4Department of Mathematics, College of Science and Arts, Najran University, Najran, 66445, Saudi Arabia
*Corresponding Author: M. A. El Safty. Email: m.elsafty@tu.edu.sa
Received: 06 July 2021; Accepted: 07 August 2021
Abstract: Real-world applications now deal with a massive amount of data, and information about the world is inaccurate, incomplete, or uncertain. Therefore, we present in our paper a proposed model for solving problems. This model is based on the class of locally generalized closed sets, namely, locally simply* alpha generalized closed* sets and locally simply* alpha generalized closed** sets (briefly,
Keywords: Corona virus; simply* alpha open sets; locally simply* alpha generalized closed*sets; decision making
The most recent Coronavirus epidemic was an outbreak in China at the start of 2019. China increased its national public-health response to the highest level on January 23, 2020. A variety of public social distancing initiatives to minimize the transmission rate of Corona virus have been introduced as part of the emergency response [1]. As a result, many papers were published by several researchers to study and analyze this virus, such as [1–7].
In diverse research areas, the mathematical modeling of vagueness and ambiguity has become an increasingly important topic. There exists another statistical instrument that has been utilized in many aspects of life [8,9]. Topology is an important branch of mathematics which contains several subfields such as soft topology, algebraic topology, and differential topology [10,11]. These subfields increase the limit of the topology applications [12]. The field of topology has many results and concepts, which can help us to discover the hidden information of data, composed of real-life applications [13]. The topological methods are thus compatible with the processing static methods and geometric representation the concept of a locally closed set-in topological space, introduced by Balachandran et al. [14]. Ganster et al. [15–17] continued to study of locally closed sets.
Our aim in this paper is to introduce three new classes of sets called
Finally, we explain the importance of the proposed method in the medical sciences for application in decision making problems. In fact, a medical application has been introduced in the decision making process of COVID-19 Medical Diagnostic Information System with the algorithm. This application may help the world to reduce the spread of Coronavirus.
The paper is structured as follows: The basic concepts of the locally generalized closed set and locally simply* α -generalized closed sets are introduced in Section Two and Three. The implementation of COVID-19 for each subclass of attributes in the information systems and comparative analysis is presented in Section Four. Section Five concludes and highlights future scope.
In this section, the present study is inspired by pointing out locally generalized closed set blind spots.
Definition 2.1 [17] A subset
Definition 2.2 A subset
i. Locally-closed [15] if
ii. Generalized locally closed [14] (briefly
iii.
iv.
Definition 2.3 [14] A topological space
3 Locally Simply*α-Generalized Closed Sets
In this section, we shall introduce a new class of generalization say
Definition 3.1 A subset
Definition 3.2 A subset
i. Simply alpha interior (shortly,
ii. Simply alpha closure (briefly,
Definition 3.3 A subset
Remark 3.1 The following Fig. 1 shows the relation between a new class of generalization and the other types of generalization of sets such that the implication in this diagram cannot be reversible as indicated in Example 3.1.
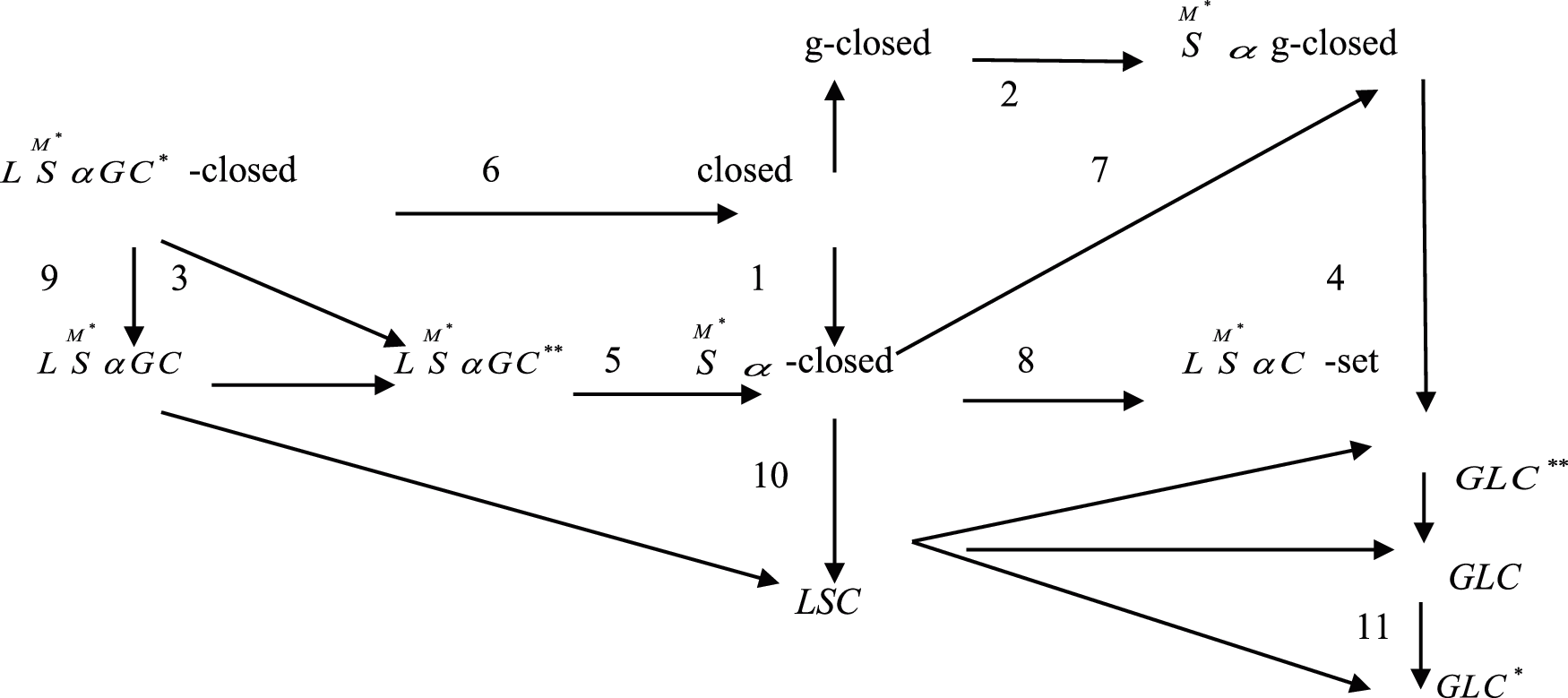
Figure 1: Shows the relation between a new class of generalized closed-sets
Definition 3.4 A subset
i. Simply
ii. Simply
iii. Locally
iv. Locally simply
v. Locally simply
vi. Locally simply*α -closed set (shortly,
The collection of all locally simply* alpha generalized closed set (resp. locally simply* alpha generalized closed* set, and locally simply* alpha generalized closed** set) of a universe set
Example 3.1 Let
(implication 3) A set
(implications 6, 7) A set
(implication 5, 1)
(implication 6, 2, 4)
(implication 8, 9, 10, 11) A set
Remark 3.2 For any topological space
i.
ii.
iii. α g-closed sets and
iv.
v. g-closed sets and
vi.
vii. LSC and
viii.
ix.
x.
Example 3.2 From example 3.1 we have.
i. There exist a set
ii. There exists a set
iii. There exist a set
iv. There exists a set
v.
vi. There exists a set
vii. There exists a set
viii. There exists a set
ix. There exists a set
x. There exists a set
Definition 3.5 A subset
Theorem 3.1 The collection of all
The following example indicates this theorem;
i. From Example 2.1 we get that there exists a set
ii. Let
Remark 3.3 From the above result, the classes of
Theorem 3.2 For a subset
i.
ii.
iii.
iv.
Proof : i) → ii) and
ii ) → i ) Since
ii ) → iii) Since
iii ) → ii ) Let
iii ) → iv) Let
iv ) → iii ) Let
Remark 3.4 It is not true that
Example 3.3 Let
Definition 3.6 A topological space
Proposition 3.1 A topological space
Proof. Let
i.e., U is
Proposition 3.2 For a subset
Proof. Let
4 Application via Simply Alpha Open Set-in Decision Making of Coronavirus
In this section, we provide an application of our approaches for decision making for information systems on Coronavirus infections. Indeed, our approach identifies the critical factors for Coronavirus infection in humans. We find gatherings, contacting with injured people, and working in hospitals is the only factor determining the transmission of infection. We conclude that staying home and not having contact with humans protect against viral infection with the Coronavirus. According [2], (Human-to-Human transmissions have been described with incubation times between 2–10 days, facilitating its spread via droplets, contaminated hands or surfaces). We present a method for data reduction using the class of simply alpha star open sets, where in this method the topology is calculated from the right neighborhood, then we form the class of simply alpha star open sets for the whole table. Then, we delete one of the symptoms and repeat the previous step and make a comparison process between the class of simply alpha star open sets and the resulting sets from the whole table, if they are equal, then it is reduct otherwise core.
We would like to recall that the information obtained in this analysis of the Coronavirus is from 1000 patient. Because the attributes in rows (objects) were identical, it has been reduced to 10 patients. The application can be described as follows, where the objects as; U = {s1, s2, ….., s10} denotes 10 listed patients, the features as A = {a1, a2, ……, a10}={Difficulty breathing, Chest pain, Temperature, Dry coughs Headache, Loss of taste or smell} and Decision Coronavirus {d}, as information was collected by the World Health Organization as well as through medical groups specializing in Coronavirus. The following information system is illustrated in Tab. 1 and Tab. 2,

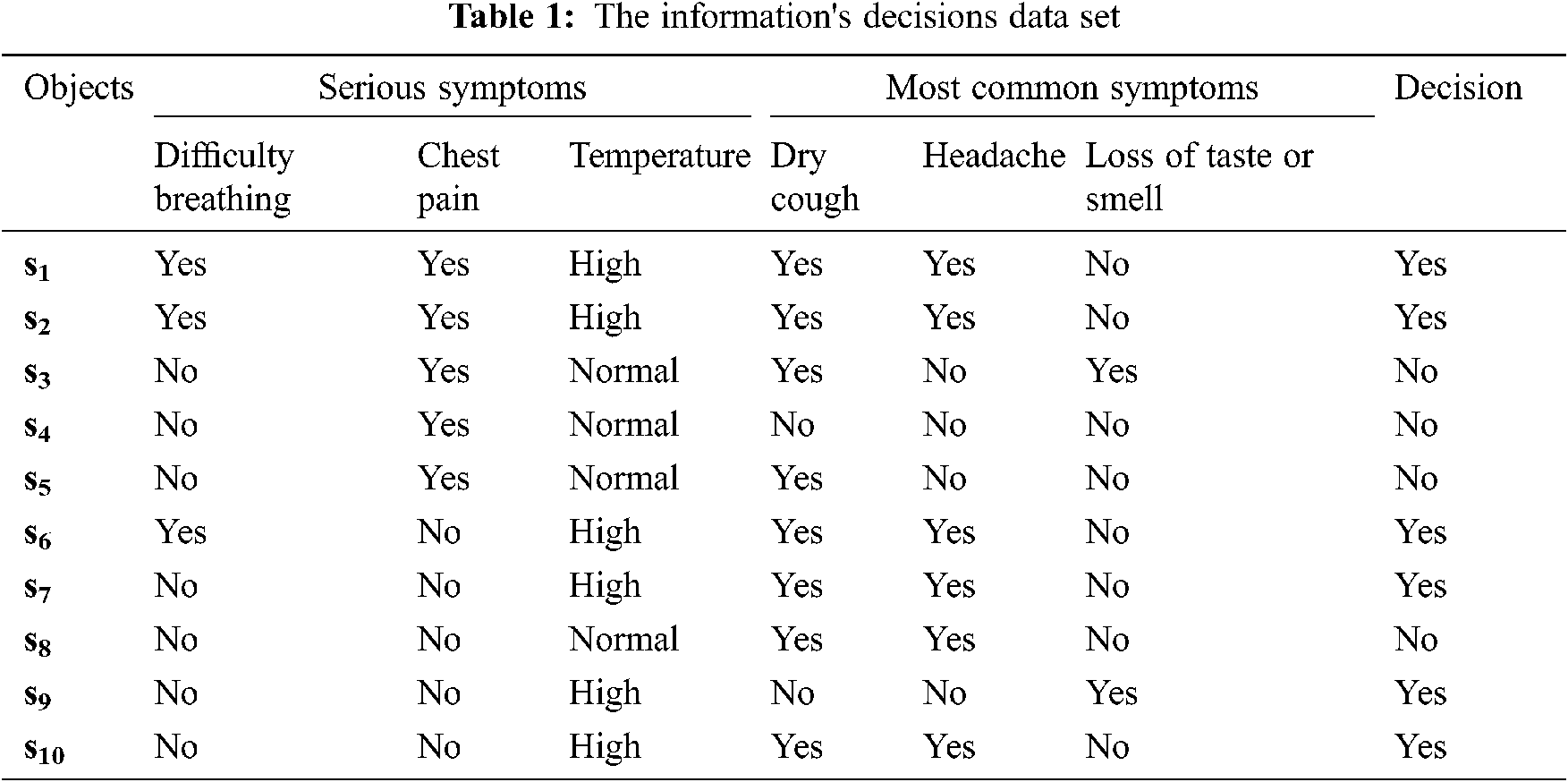
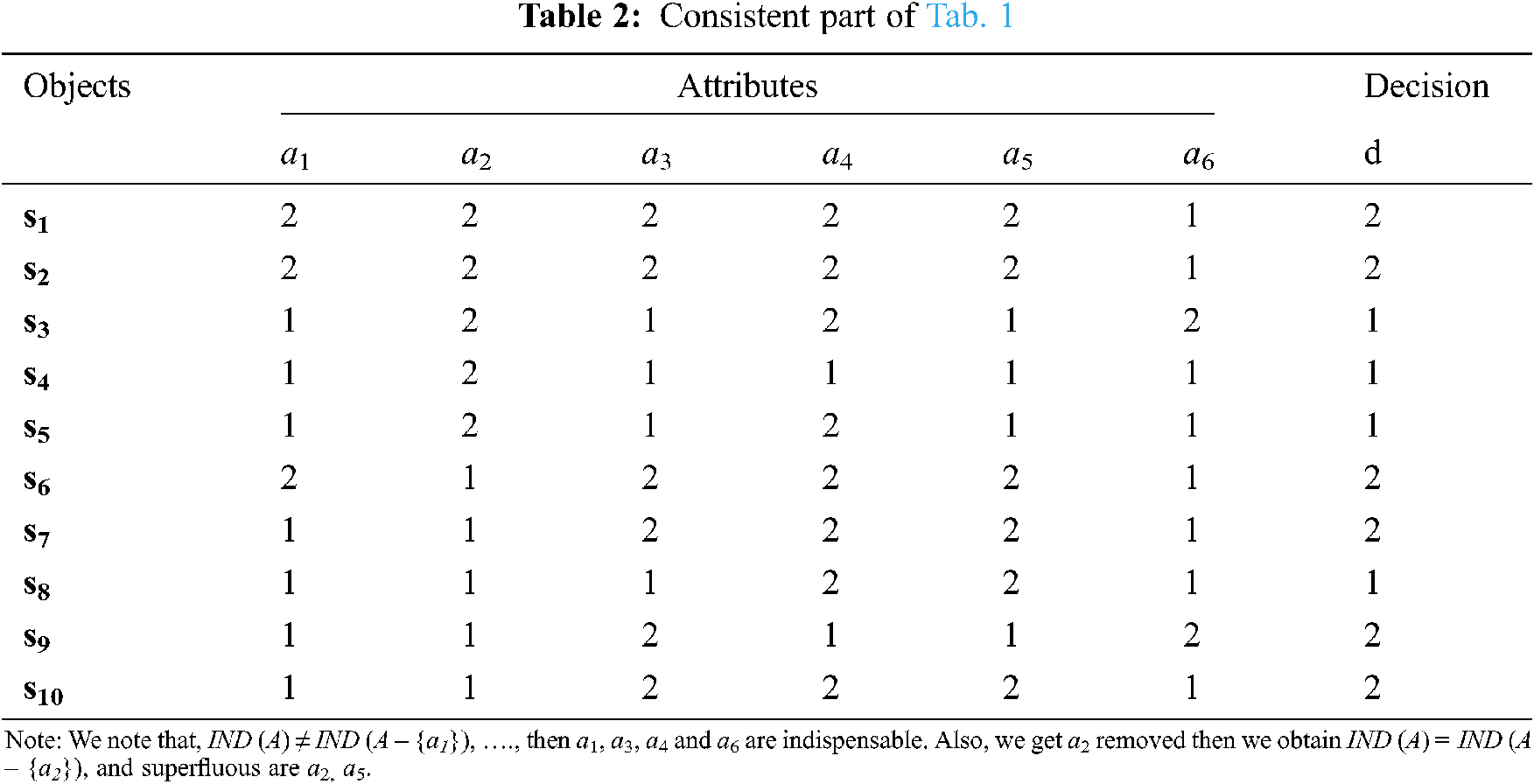
Then, we get the removal of attributes as the next Tab. 3,
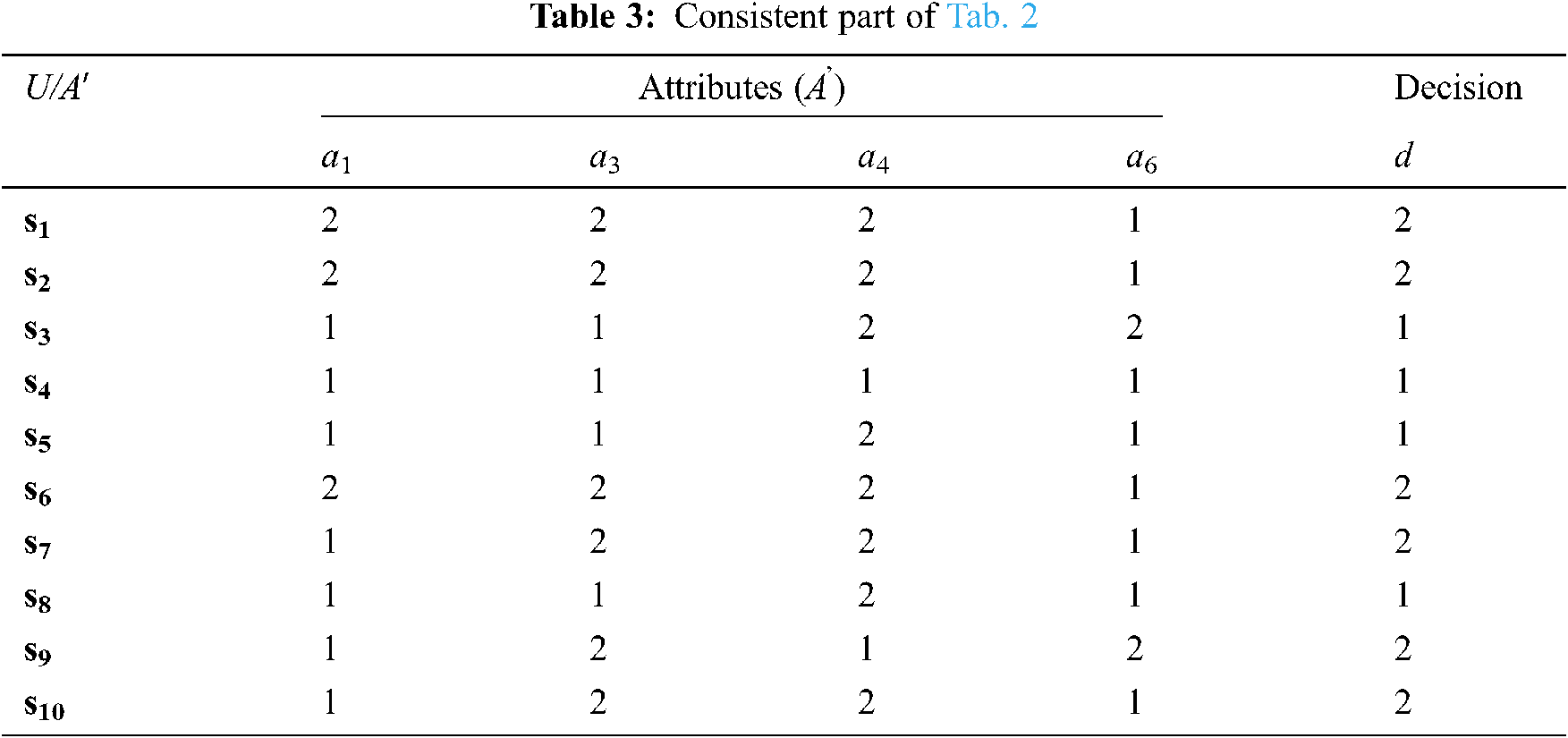
From Tab. 3 we obtain the symptoms of every patient as follows:
V(s1) = {a1, a3, a4}, V(s2) = {a1, a3, a4}, V(s3) = {a4, a6}, V(s4) =
We apply this relation for all features in the table to induce the neighborhoods as follows.
R = {(s1, s1), (s1, s2), (s2, s2), (s2, s1), (s3, s3), (s4, s4), (s4, s1), (s4, s2), (s4, s3), (s4, s5), (s5, s5), (s5, s1), (s5, s2)}. Thus, the right neighborhoods of each element in U of this relation are Rr s1 = {s1, s2}, Rr s2 = {s1, s2},
Rr s3 = {s3}, Rr s4 = U, Rr s5 = { s1, s2, s3, s5}. Then the topology deduced from this relation is T = {U, , {s1, s2}, {s3}, {s1, s2. s3}, {s1, s2, s3, s5}}, Tc = {U, , {s4, s5}, {s4}, {s5, s4. s3}, {s1, s2, s4, s5}}.
Then, we construct the following Tab. 4 to obtain the class of simply* alpha open set,
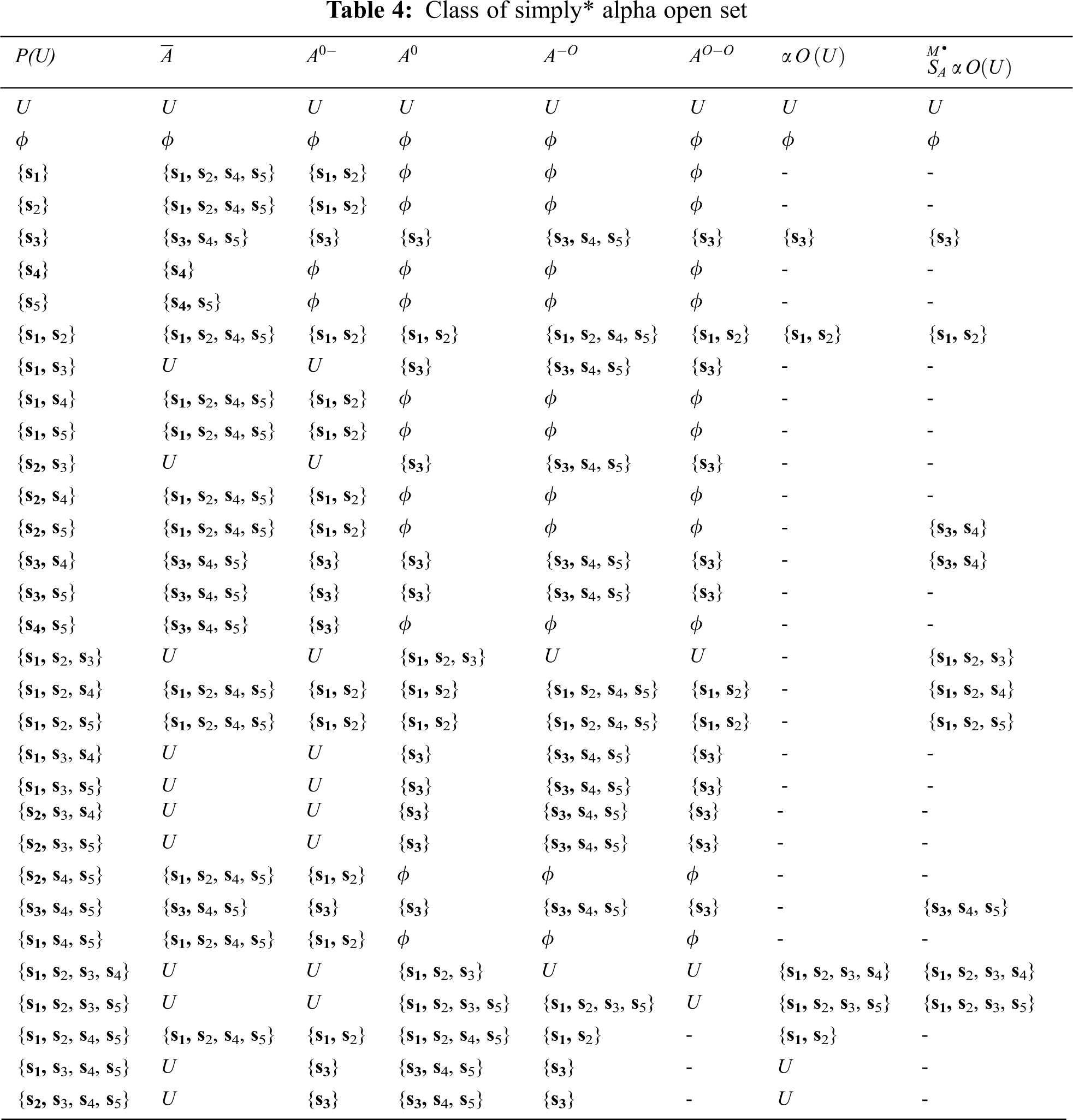
Then the class of simply* alpha open set is
Step 1: When the feature a1-Difficulty breathing is removed, the symptoms of every patient are: V(s1) = {a3, a4}, V(s2) = {a3, a4}, V(s3) = {a4, a6}, V(s4) = , and V(s5) = {a4}.
Thus, the right neighborhoods of each element in U of this relation are.
Then the topology deduced from this relation is
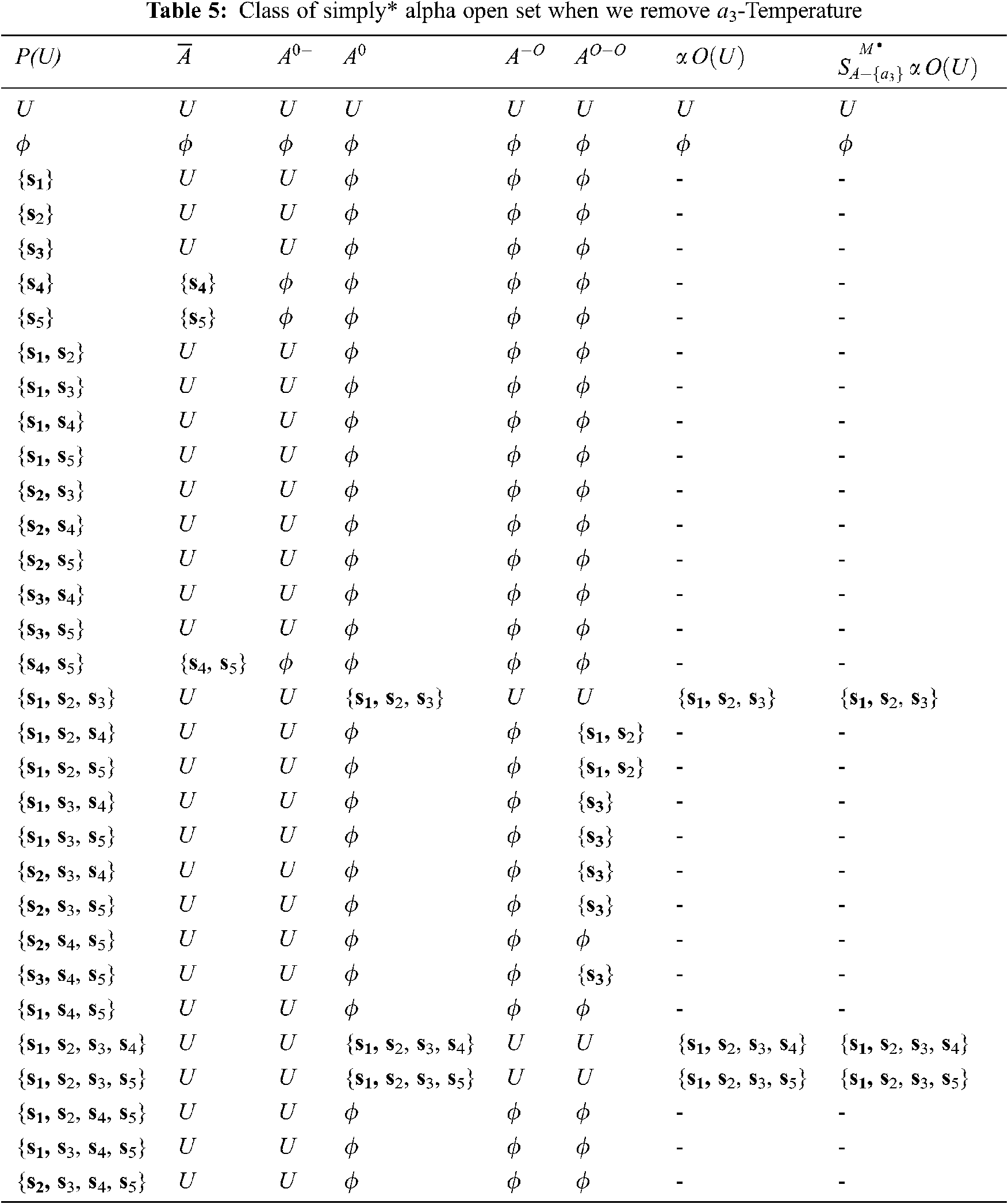
Step 2: When the feature a3-Temperature is removed, the symptoms of every patient are: V(s1) = {a1, a4}, V(s2) = {a1, a4}, V(s3) = {a1, a4, a6}, V(s4) = {a1}, and V(s5) = {a1, a4}.
Thus, the right neighborhoods of each element in U of this relation are.
Rr(s1) = {s1, s2, s3}, Rr(s2) = {s1, s2, s3}, Rr(s3) = {s3}, Rr(s4) = {s1, s2, s3, s4}, and Rr(s5) = {s1, s2, s3, s5}. Then, the topology deduced from this relation is T = {U, , {s1, s2, s3}, {s1, s2, s3, s4}, {s1, s2, s3, s5}}, Tc = {U, , {s4, s5}, {s5}, {s4} }, and hence the class of simply* alpha open set of the whole is not identical with the class of simply* alpha open set without the symptom a3, if
Step 3: When the feature a4-Dry cough is removed, the symptoms of every patient are:
Thus, the right neighborhoods of each element in U of this relation are Rr(s1) = {s1, s2}, Rr(s2) = {s1, s2}, Rr(s3) = {s3}, Rr(s4) = U, and Rr(s5) = U.
Then the topology deduced from this relation is T = {U, , {s1, s2}, {s3}, {s1, s2, s3}}, Tc = {U, , {s3, s4, s5}, {s1, s2, s4, s5}, {s4, s5}}, and hence the class of simply* alpha open set of the whole is identical with the class of simply* alpha open set without the symptom a4, this means that

Step 3: When the feature a6-Loss of taste or smell is removed, the symptoms of every patient are: V(s1) = {a1, a3}, V(s2) = {a1, a3}, V(s3) = {a1, a6}, V(s4) = {a1}, and V(s5) = {a1}.
Thus, the right neighborhoods of each element in U of this relation are Rr(s1) = {s1, s2}, Rr(s2) = {s1, s2}, Rr(s3) = {s3}, Rr(s4) = U, and Rr(s5) = U.
Then the topology deduced from this relation is T = {U, , {s1, s2}, {s3}, {s1, s2, s3}}, Tc = {U, , {s3, s4, s5}, {s1, s2, s4, s5}, {s4, s5}}, and hence the class of simply* alpha open set of the whole is not identical with the class of simply* alpha open set without the symptom a6-Loss of taste or smell this means that
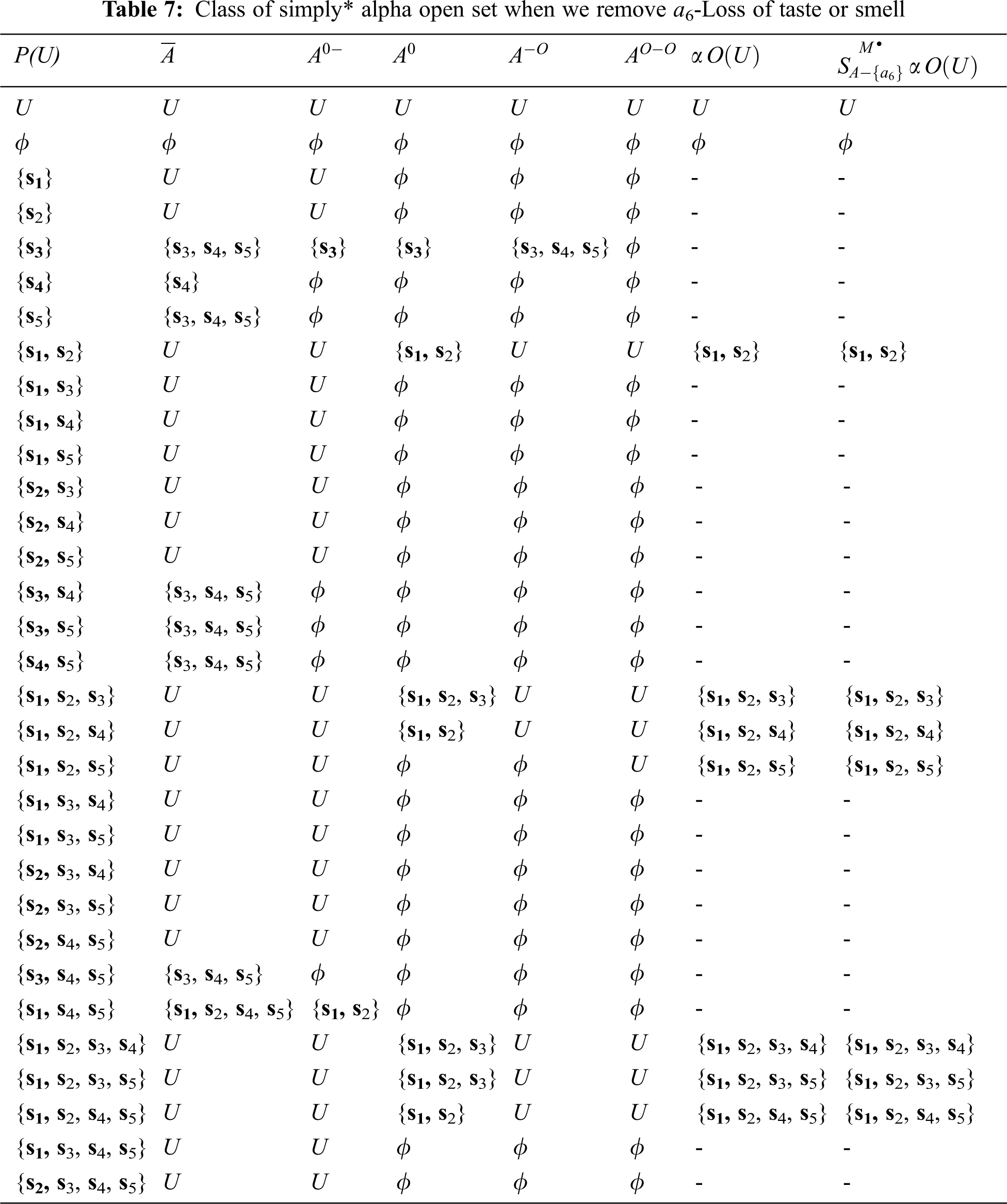
Hence, from Steps (1–3), we observe that: the CORE is {a3, a6}, that is the impact factors to determine Coronavirus infection are High Temperature and Loss of taste or smell.

Our study in this article aims for defining a new type of simply* alpha generalized namely Simply*α -generalized closed, locally simply*α-generalized closed, and locally simply*α-generalized closed** sets. We show the relation between this type of set and the other of generalized open sets. We concluded that the generalized simple closed set contains most of the generalized closed sets and also, we defined new kinds of locally generalized simply closed sets based on simply* alpha open set. Furthermore, we studied the relation between these collections and other. We presented an application to a group of patients, where we presented a method using topological concepts to determine one of the main symptoms causing Coronavirus. Finally, using the class of simply alpha* open set, we identified the impact factors of Coronavirus infection and then we helped the physician to make an accurate decision making about patients. At the end of paper, this method has also proven effective in acquiring the basic symptoms that cause COVID-19. We plan to extend the proposed methodology in future work to include a multi-label classification issue.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant Number R.G.P. 1/206/42.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. G. Kampf, D. Todt, S. Pfaender and E. Steinmann, “Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents,” J. Hospital Infection, vol. 104, pp. 246–251, 2020. [Google Scholar]
2. S. A. Alblowi, M. El Sayed and M. A. El Safty, “Decision making based on fuzzy soft sets and its application in COVID-19,” Intelligent Automation & Soft Computing, vol. 30, no. 3, pp. 961–972, 2021. [Google Scholar]
3. M. A. El Safty and S. AlZahrani, “Topological modeling for symptom reduction of coronavirus,” Punjab University Journal Mathematics, vol. 53, no. 3, pp. 47–59, 2021. [Google Scholar]
4. L. X. Feng, S. L. Jing, S. K. Hu, D. F. Wang and H. F. Huo, “Modelling the effects of media coverage and quarantine on the COVID-19 infections in the UK,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 3618–3636, 2020. [Google Scholar]
5. M. A. El Safty, M. El Sayed and S. A. Alblowi, “Accuracy based on simply* alpha open set in rough set and topological space,” Soft Computing, vol. 25, no. 16, pp. 10609–10615, 2021. [Google Scholar]
6. M. A. El Safty, S. A. L. Zahrani, M. K. El-Bably and M. El Sayed, “Soft exai -rough set and its applications in decision making of coronavirus,” Computers, Materials & Continua, 2021. [Google Scholar]
7. M. El Sayed, M. A. El Safty and M. K. El-Bably, “Topological approach for decision-making of COVID-19 infection via a nano topology model,” AIMS Mathematics, vol. 6, no. 7, pp. 7872–7894, 2021. [Google Scholar]
8. M. A. El Safty, “Modeling uncertainty knowledge of the topological methods,” Poincare Journal of Analysis & Applications, vol. 8, no. 1, pp. 89–102, 2021. [Google Scholar]
9. M. A. Elsafty and A. M. Alkhathami, “A topological method for reduction of digital information uncertainty,” Soft Computing, vol. 24, no. 1, pp. 385–396, 2020. [Google Scholar]
10. M. E. Abd Monsef and R. A. Mahmoud, “On generalized continuous mappings,” Delta J. Science., vol. 8, no. 2, pp. 407–420, 1984. [Google Scholar]
11. T. N. Alharthi and M. A. El Safty, “Attribute topologies based similarity,” Cogent Mathematics, vol. 3, no. 1, pp. 1–11, 2016. [Google Scholar]
12. M. A. El Safty, A. A. Mousa, S. A. Alblowi and M. El Sayed, “Topological approach on fuzzy soft β-closure and β-interior and its application in decision making,” Nanoscience and Nanotechnology Letters, vol.12, no. 11, pp. 1323–1328, 2020. [Google Scholar]
13. M. A. El Safty, “Topological method for a study of discriminating three categories of banks and its use in attributes reduction,” International Journal of Scientific Research in Science, Engineering and Technology, vol. 7, no. 5, pp. 221–233, 2020. [Google Scholar]
14. K. Balachandran, P. Sundaram and H. Maki, “Generalized locally closed sets and GLC-continuous function,” Indian J. Pure & Applied Mathematics, vol. 27, no. 3, pp. 235–244, 1996. [Google Scholar]
15. M. Ganster and I. Reilly, “Locally closed sets and LC-continuous function,” International Journal of Mathematics and Mathematical Sciences, vol. 12, no. 3, pp. 417–424, 1989. [Google Scholar]
16. M. Ganster, I. Reilly and M. K. Vamanamurthy, “Remarks on locally closed sets,” Mathematics Pannonica, vol. 3, no. 2, pp. 107–113, 1992. [Google Scholar]
17. J. Cao, M. Ganster and I. Reilly, “On generalized closed sets,” Topology and its Applications, vol. 123, no. 1, pp. 37–46, 2002. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |