Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.021779
Article

Massive MIMO Codebook Design Using Gaussian Mixture Model Based Clustering

S. Markkandan1,*, S. Sivasubramanian2, Jaison Mulerikkal3, Nazeer Shaik4, Beulah Jackson5 and Lakshmi Naryanan6

1Department of ECE, SRM TRP Engineering College, Tamil Nadu, 621105, India
2Dhanalakshmi College of Engineering, Chennai, 601301, Tamil Nadu, India
3Department of Information Technology, Rajagiri School of Engineering and Technology, Kerala, India
4Department of CSE, Bapatla Engineering College, Bapatla, 522102, India
5Department of ECE, Saveetha Engineering College, Tamil Nadu, India
6Gojan School of Business and Technology, Tamil Nadu, India
*Corresponding Author: S. Markkandan. Email: markkandan@gmail.com
Received: 14 July 2021; Accepted: 26 August 2021

Abstract: The codebook design is the most essential core technique in constrained feedback massive multi-input multi-output (MIMO) system communications. MIMO vectors have been generally isotropic or evenly distributed in traditional codebook designs. In this paper, Gaussian mixture model (GMM) based clustering codebook design is proposed, which is inspired by the strong classification and analytical abilities of clustering techniques. Huge quantities of channel state information (CSI) are initially saved as entry data of the clustering process. Further, split into N number of clusters based on the shortest distance. The centroids part of clustering has been utilized for constructing a codebook with statistic channel information, with an average distance that is the shortest towards the true channel data. The enhanced GMM based clustering codebook design outperforms traditional methods, particularly in the situations of non-uniform distribution of channels as demonstrated via simulation results which match theoretical analyses concerning achievable rate. The proposed GMM based clustering codebook design is compared with DFT-based clustering codebook design and k-means based clustering codebook design.

Keywords: Gaussian Mixture Model (GMM) based clustering; Massive MIMO; Codebook design; DFT

1  Introduction

Massive multiple-input multiple-output (MIMO) is becoming the major driver for 5th generation wireless communication as well as transmission systems to enhance data speeds [1]. The precision of channel state information (CSI) has been important for beam development and spatial multiplexing improvements in transceivers with a huge number of antenna components [2]. The most popular approach for acquiring CSI is restricted feedback dependent on codebook, in which the receiver exclusively transmits return to the transmission index of the optimal weight vector of MIMO from a predefined codebook.

A significant study has been dedicated to the construction of a codebook in recent decades. To optimize the lowest gap between the codebook of MIMO vectors, a codebook namely the Grassmannian quantization codebook is developed. The independent channel is considered and involved in performing an identical distribution that its dominating acute singular vectors are uniformly distributed in space [3,4]. The alternative method namely random vector quantization (RVQ) produced the codebook randomly using MIMO vectors as isotropic assumption [5,6]. Furthermore, the DFT codebook technique evenly split the whole angular domain further into two B accelerated portions as well as created the codebook solely depending on the acceleration of the angle of arrival or departure [7,8], wherein the amount of feedback bits is denoted as B. The Multi-input multi-output (MIMO) channel is isotropic or distributed uniformly, which is a frequent assumption. This assumption is mostly not met in the real-world wireless environment. Thus, the MIMO channel being limited in the angular zone [9], and its multiple directions are focused on a specific angle limit. This prompted [10] to investigate a non-uniform codebook model that surpassed the uniform codebook approach. The propagation atmosphere is either uniform or not, it must be adopted by the codebook design.

By employing a machine learning approach, it is possible to design a wireless physical layer [11–13], feedback method of CSI depending on deep learning technique for massive MIMO has been implemented, where convolutional neural networks convert the indices of the channels to receiver's compressed expressions and then inverse transformation is performed on transmitter side [14,15]. Comparable to mentioned techniques, the channel is considered sparse, which isn't a universal assumption; for example, it's not appropriate for a dynamic dispersed ecosystem. The K-means algorithmic approach is well-known as it is often utilized as a clustering technique. It is utilized in MIMO identification [16,17], and NOMA client clustering [18] due to its capacity to classify and analyze huge volumes of data. It's essential mentioning that channel data may be divided into several groups, where each can be defined using clustering centroids.

A Gaussian mixture is a multiple distributions probability of a convex combination, often termed as mixture components [19]. Since finite mixture methods have been more popular in recent times are utilized as a combination of two distinct normal distributions to evaluate measurements of a large dataset containing 1000 crab. In diverse fields including medicine [20], sociology [21], physics [22], and several others application fields, Gaussian finite mixture models having proved effective for modeling complicated data.

Cluster analysis is a method of classifying information flows into various groups or clusters, and hence, the group containing the data points is comparable with one another rather than data points available in other clusters. The various types of clustering process can be categorized into divisive algorithms or hierarchical agglomerative with distinct linkages, partition optimization methods including model-based clustering [23], K-mean, Kmedoids, and density-based clustering. The connection among clustering and Gaussian mixture models is used in the latter. It is assumed that every mixture component oversees simulating a certain data set. Whereas this assumption is broken and requires a specific treatment, including combining mixture components [24–26], may be necessary, and concentrate mainly on the one-to-one connection among clusters as well as mixture components.

In this paper, Section 2 includes the literature review related to massive MIMO codebook design. Section 3 includes the proposed Gaussian mixture model (GMM) based clustering for designing a massive MIMO codebook. Section 4 compares the performance of the proposed system model with DFT, and k-means based clustering method concerning achievable rate and Section 5 includes the conclusion.

2  Literature Survey

Depending on the MIMO channel properties, certain codebook designs for large MIMO systems have been studied. The codebooks for massive MIMO systems are generated by the compression of channel matrices to a smaller dimension through sparsity leveraging of channel descriptions in the domain of angle [27–30]. The construct the MIMO channel description into overfitted dictionaries because the departure angle, as well as the arrival angle, are non-uniform inside the angle-domain. With the premise that the departure angle information stays invariant in a departure angle coherence period, the departure angle adaptive subspace codebook formulated the channel profits very accurately [31]. An adaptive codebook depending on instantaneous CSI is proposed with the codebook scaling size only proportionally with the channel correlation matrix's ranking [32]. Thus, the statistical property is heavily reliant on these traditional codebook designs.

The antenna arrays have been customizable, as well as the transmission methods are more adaptable, according to developing wireless transmission systems. The azimuth codebook of Kronecker-product as well as the elevation codebook derived from 2 unique feedback mechanisms produces a codebook for 2D antenna arrays [33]. A novel double codebook is presented for the rectangular array construction in a uniform co-polarized. The correlation matrices of the 2 orthogonal directions based on Kronecker-product [34] represent the entire long-term characteristics. To summarize, the codebook design must account for a wide range of wireless situations as well as antenna array topologies in large MIMO systems.

Deep learning (DL) methods are preferred mainly for prediction for successfully tackle the CSI feedback issue [35–39]. In [40], a deep neural network (DNN) understands the characteristics of the wireless communication channel as well as the geographical features in the angle zone using training to provide channel estimate and departure angle estimation. At the receiver site, Conventional neural networks (CNNs) understand the structural channel sparsity acquired from training sampling data then converted CSI into a relatively optimum amount of codewords in [41–43].

3  System Model

The massive MIMO system communication is provided with one downlink cell is considered wherein base station (BS) is linked with both Nt antennas as well as K antenna users at the same time. A pre-coding matrix w is selected appropriately from the codebook based on the current Pre-coding Matrix Indicator (PMI) to pre-process the transferring information. Therefore, the k-th user xk a sent signal is computed as xk=wsk , wherein sk is the representation of signal meant for k users.

The signal power generally assumed to be normalized is given as E [skskH] , wherein E[⋅] represents the expectation operator as well as I identity matrix. The k-th number of users with received signal may be represented as

yk=hkwsk+nk (1)

Here, Nt1 channel sequence acquired from a base station (BS) is transmitted to k-th users is denoted as hk and nk∼CN(0,σ) is a Gaussian mixture white noise vector having identical and independent distribution to the k-th mobile user acquired from BS. We use ‖w‖2=1 to account for the transmitter's power constraints.

As illustrated in Fig. 1, the codebook with C=c1,c2,c3,….,c2B is shared among the transmitter as well as the receiver. The CSI measurement including reference signals are forwarded by the transmitter, whereas the receiver chooses a pre-coding vector w from N=2B codewords depending on the relevant selection criterion.

Figure 1: Massive MIMO system

w=argci∈Cmax⁡(|Hkci|2),∀i (2)

The receiver returns the matching codeword index to the transmitting side using a limited feedback method. The transmitting side selects pre-coding matrix w acquired from the codebook C depending on the index followed by the transmitted signals using the chosen w is produced. Unlike conventional codebook design approaches, Gaussian mixture model-based clustering codebook design will use the GMM based clustering processing unit to evaluate CSI statistical characteristics and create a codebook depending on representation values of the statistical characteristics.

3.1 Channel Model

At the BS, the antennas including a uniform rectangular array (URA) as well as uniform linear array (ULA) configurations have been considered. ULA offers better performance in terms of capacity than URA due to azimuthal orientation of the array. The traditional channel model depending on narrowband ray is used. The antennas with ULA consist of downlink channel sequence may be written as

hk=Nt∑i=1Pkgk,ia(θk,i)H (3)

Here, Pk represents the amount of dominating pathways to the k-th users obtained from BS, gk,i represents the complex profit of k-th users in i-th path, assuming it to be autonomous and identical distribution with no mean as well as 1 variance, and Angle of Departure (AoD) of the k-th users in i-th path is represented using θk,i . The antenna array response a(θk,i) may be computed using the following formula:

a(θk,i)=1Nt[1,ej2πdλsin⁡θk,i,…,ej2π(Nt−1)dλsin⁡θk,i]T (4)

Here, BS’s antenna spacing is denoted as d, and the carrier with wave-length is denoted as λ. Angle of Departure (AoD) of the k-th users in i-th path is represented using θ(k,i). The number of users simulated is from 1 to 100 for antenna size of 10 to 100.

The channel matrix of downlink for a URA of antennas comprising horizontal antennas is denoted as Nt1 as well as vertical antennas is denoted as Nt2 may be written as

hk=Nt∑i=1Pkgk,ia(φk,i,θk,i)H (5)

Here, Nt=Nt1×Nt2 . The response array a(φk,i,θk,i) is written as follows:

a(φk,i,θk,i)=1Nt[1,ej2πdλsin⁡θk,i,…,ej2π(Nt−1)dλsin⁡θk,i]T⊗1Nt[1,ej2πdλcos⁡θk,isin⁡φk,i,…,ej2π(Nt−1)dλcos⁡θk,isin⁡φk,i]T (6)

The AoD’s elevation as well as the azimuth of the k-th users in i-th route are θk,i as well as φk,i . The combination of channel vectors across all K users is denoted by

H=[h1,h2,……..,hk] (7)

3.2 Problem Formulation

Assuming, overhead to remain constant is N=2B¯ , the goal of this study is to create a suitable Gaussian mixture model based clustering codebook for a massive MIMO system communication. Using the constrained feedback method, k-th user with the achievable rate Rk is expressed as

Rk=log2(1+SINRk)=log2(1+γK|hkHwk|2γK∑i=1,i≠kK|hkHwi|2) (8)

Here, the precoding matrix chosen from codebook C is denoted as w, and the transmitting power is denoted as γ . As a result, matric wk may also be represented as ck . Eq. (8) may be rewritten in the following way:

Rk=log2(1+γK|hkHck|2γK∑i=1,i≠kK|hkHci|2) (9)

The function achievable rate is given as ck∈C . As a result, a quantizer may be built to optimize the mean of the achievable rate. The decent codebook construction inappropriate scenario setting might improve the achievable rate of every client, in distinct locations at distinct time moments. Thus, by resolving the constraint optimization issue as follows, the greatest mean achievable rate may be attained.

maxE[Rk]c=maxEc[log2(1+γK|hkHck|2γK∑i=1,i≠kK|hkHci|2)]s.t.ck∈C,∀k‖ck‖2=1 (10)

The above equation is rewritten and expressed as,

ck=arg⁡maxEc[log2(1+γK|hkHck|2γK∑i=1,i≠kK|hkHci|2)]s.t.ck∈C,∀k‖ck‖2=1 (11)

The difference among statistics channel information is denoted as H. and actual channel information is represented as d(H,H.)=|H−H.| . For lower d(H,H.) , the codebook design technique is observed to yield a greater sum rate. Increasing the mean rate may accomplish via the reduction of mean distance as much as possible.

maxE[Rk]c=maxEck∈C[d2(H,H.)] (12)

As a result, the proposed efficient codebook design reduces the sum distance between actual as well as statistics channel information.

3.3 Key Propagation Characteristics

The DNN is particularly designed to determine critical propagation properties including delay, elevation angle, channel gains, and azimuth angle. A formula A^=fs(H,Θ) governs the prediction process, with A^ denoting undetermined propagation properties, H denoting acquired channel sequences, Θ denoting DNN weights, as well as fs(⋅) denoting the sigmoid function.

The fully connected ‘L’ layers in DNN, comprising a single input layer, L-2 hidden layers followed by a single output layer, are chosen Fig. 2. The channel sequence H with the nonlinear cascaded transformation is the output A^ acquired from the DNN model. A^ maybe computed in this way:

Figure 2: The proposed codebook design

A^=fs(H,Θ)=fss(l−1)(fss(l−2)(…fss(1)(H))) (13)

The q-th characteristic a^q as an instance is utilized to show how the GMM based clustering process works, which is identical for all other qualities. To take advantage of the channel information as well as to speed up the convergence process in GMM based clustering method, with q-th characteristic of N uniform centroids a^q={a^q,1,…,a^q,i,….,a^q,I} , I have been selected as the early centroids tq={tq,1,tq,2,…..,tq,N} , in which a^q,i is representing the q-th characteristic in i-th data samples, the number of sample data is denoted as I, the q-th characteristic’s l-th centroid is denoted as tq,l , and the no. of clusters is denoted as N.

Every data object is linked with the nearby centroid as per the nearest neighbor principle. The data item a^q,i is allocated to l-th GMM based clustering, with the shortest length between i-th component a^q,i and l-th GMM based centroid cluster tq,l . It may be stated as follows:

l∗=argmin−0.7pcl∈N{d(a^q,i,tq,1)} (14)

Here, d(a^q,i,tq,1)=‖(a^q,i,tq,1)‖2 , then combine a^q,i with GMM based cluster clusterq,l∗ which denotes the a^q term’s l∗th cluster.

Following the assignment of all data items, the centroids are upgraded using the centroid criterion, which selects the things with the smallest mean distance of each cluster as the fresh centroid. The q-th characteristic’s l-th cluster a^q , is shown as follows,

tq,l=argmin−0.7pctq,1∈clusterq,l∑a^q,i∈clusterq,id(a^q,i,tq,1),∀i,j (15)

Here, a^q l-th cluster is denoted as clusterq,l .

Continue GMM based clustering procedure still items, as well as centroids of every cluster, remain the same. Lastly, the a^q q-th features of N centroids tq is obtained. The centroids set may then be generated by repeating this procedure for all propagation features and expressing it as T=[t1,….,tq]T . The following method summarizes the GMM based clustering process.

3.4 Codebook Construction

In the massive MIMO, we examine several codebook designs approaches to enhance the resilience of the proposed model designing. The codebook construction technique will be shown using a variety of important propagation properties.

Both in correlated and uncorrelated channel environments, the angle features are critical for codebook design. The structural codebook only requires angle features in the event of substantial channel correlation. Therefore, we use the angle features to understand a unique propagation feature’s codebook design. The method of codebook building will be illustrated in detail using DFT codebook design depending on centroids.

The angle characteristic with centroid generates every individual codeword cl,i . The proposed codebook may be represented as C1=[c1,1,c1,2,…,c1,N] , wherein C1 is the first entry.

c(l,i)=1Nt[1e−j2πdλcos⁡θi……….e−j2πdλ(Nt−1)cos⁡θi]T (16)

Angle-based codebooks are expressed as follows as per the centroids:

C1(:,i)=1Nt∗e−j2πdλ(Nt−1)cos⁡(phase(t1,i)) (17)

=1Nt∗A(t1,i) (18)

In codebook design, the gain, as well as angular features, is employed once the channel is uncorrelated. Each codeword is formed using the x-axis component as well as the y-axis component depending on the valid space v¯={v¯1,v¯2,…..,v¯N} .

C2(:,i)=1Nt∗e−j2πdλ(Nt−1)cos⁡(phase(t1,i))∗t2,i (19)

=1Nt∗A(t1,i)∗t2,i (20)

The double-polarized channel codebook construction is done initially utilizing horizontal as well as elevation angles; later k-means clustering is used to get the final codebook.

C3(:,i)=1Nt∗e−j2πdλ(Nt−1)cos⁡(phase(t1,i))⊗1Nt∗e−j2πdλ(Nt−1)cos⁡(phase(t1,j)) (21)

=1Nt∗[A(t1,i)⊗A(t1,j)] (22)

Here, the horizontal angles are represented as t1,i and elevation angles are represented as t1,j .

3.5 Algorithm of the Proposed Codebook Design

STEP 1: As the beginning centroids provide N sample data of the q-th propagation feature, expressed as a tq={tq,1,tq,2,…..,tq,N} .

STEP 2: The ‘d’ distance is estimated using d(a^q,i,tq,1)=‖(a^q,i,tq,1)‖2 , in which a^q,i∈a^q .

STEP 3: a^q,i combined with GMM based cluster clusterq,l∗ as per the closest neighbor principle.

STEP 4: Depending on the centroid criterion, every individual cluster are upgraded with the centroid tq,l=arg⁡mintq,1∈clusterq,l∑a^q,i∈clusterq,id(a^q,i,tq,1),∀i,j .

STEP 5: If the q-th characteristic’s centroid is constant, then step 3 as well as step 4 as to be recurrently used still acquiring the final centroid output tq={tq,1,tq,2,…,tq,N} .

STEP 6: The propagation characteristics of every centroid have to be recurrently performed still acquiring T=[t1,…,tq]T .

STEP 7: The valid space is obtained using v¯={v¯1,v¯2,…,v¯N} .

STEP 8: For various circumstances, generate the codeword that corresponds to v¯ .

The proposed Gaussian mixture model (GMM) based clustering codebook design approach performs in massive MIMO systems. The difference rate is estimated among the perfect CSI as well as enhanced codebook-based feedback method. In an ideal world, the optimal pre-coding vector is represented as cideal , and the associated achievable rate Rideal maybe obtained through the following expression.

Rideal=E[log2(1+|hkHcideal|2)] (23)

The rate difference, which is determined by ΔR=Rideal−R , may be represented as

E[log2(|hkHcideal|2−|hkHci|2)] (24)

Eq. (20), can be recast as for the 2nd codebook design technique discussed in the previous subsection.

ΔR=E[log2(|hkHcideal|2−|hkHA(t1,i)t2,i)|2)] (25)

The reduction in minimizing rate interest as,

minΔR=max|hkHA(t1,i)t2,i)|2 (26)

Using the above-mentioned expression because of the channel model,

=sin2(AkH,A(t1,i))sin2(gkH,t2,i) (27)

4  Result and Discussion

The aggregate rate of the GMM-based clustering codebook technique has been provided in this section under a variety of situations and with distinct antenna array configurations. The aggregate rate of proposed GMM-based clustering models is also compared to the traditional DFT method and K-means for Nt=16 and Nt=128 is shown in Figs. 3 and 4. The CSI matrices are randomly constructed depending on the channel system include both pieces of training as well as a testing (3). The mean angles of AoD are fixed to φ=φ0+Δφ , in which φ0 is a constant selected randomly from the range [0,φBW] , as well as the angle dispersion, are fixed to Δφ . Δφ is selected randomly from the range [0,φBW] . The angle dispersion φBW is the parameter that distinguishes between the various channel distributions. The codebook construction of the conventional DFT angel range is analyzed in this experiment. If φBW=π6orπ , non-uniform as well as uniform channel scenarios are indicated. The conventional DFT codebook is created in the simulations using the AoD evenly generated within π .

Fig. 5 shows the achievable rates for the corresponding SNR for k-means based clustering codebook method for various numbers of antennas Nt=16,32,64,128 . As the k-means clustering codebook is better compared to DFT-based clustering, it is mainly used for the analysis in comparison with the proposed GMM based clustering codebook model. Fig. 6 shows that the proposed GMM based clustering codebook performs efficiently and acquires achievable rates for various antenna values Nt=16,32,64,12 . The performance of the system in a situation with larger antennas surpasses rather than other scenarios consisting of minimum antennas implying that using massive antennas in GMM based clustering codebook method efficiently improves the system performance of massive MIMO.

Figure 3: Comparison of proposed GMM based clustering with k-means and DFT based clustering methods for Nt=16

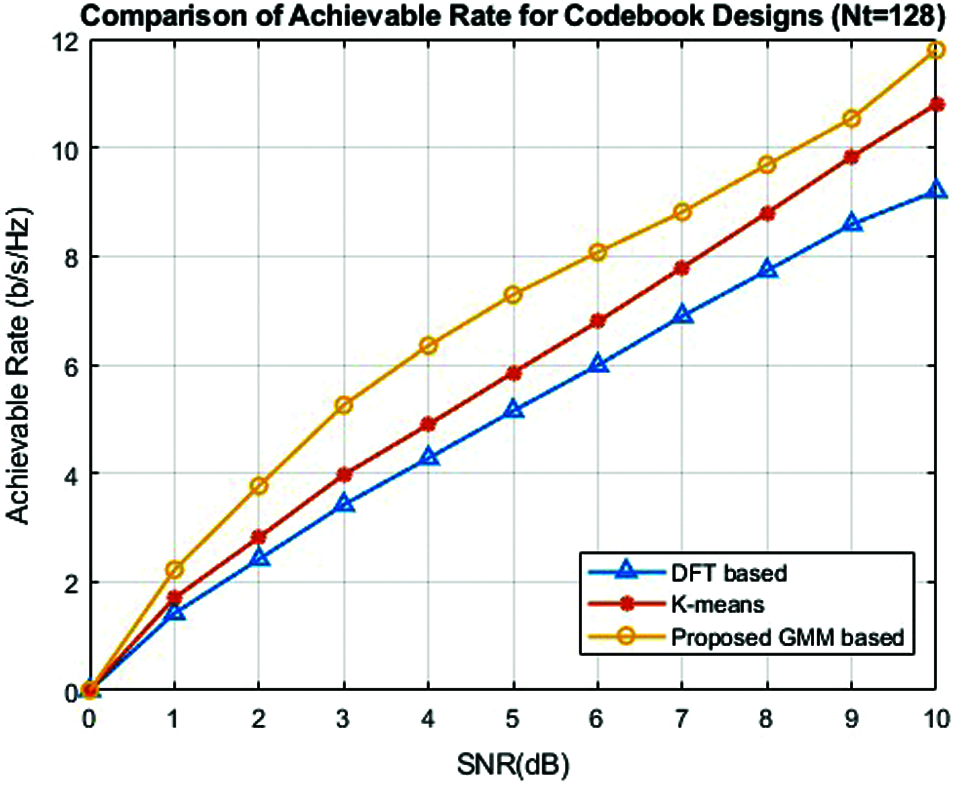
Figure 4: Comparison of proposed GMM based clustering with k-means and DFT based clustering methods for Nt=128

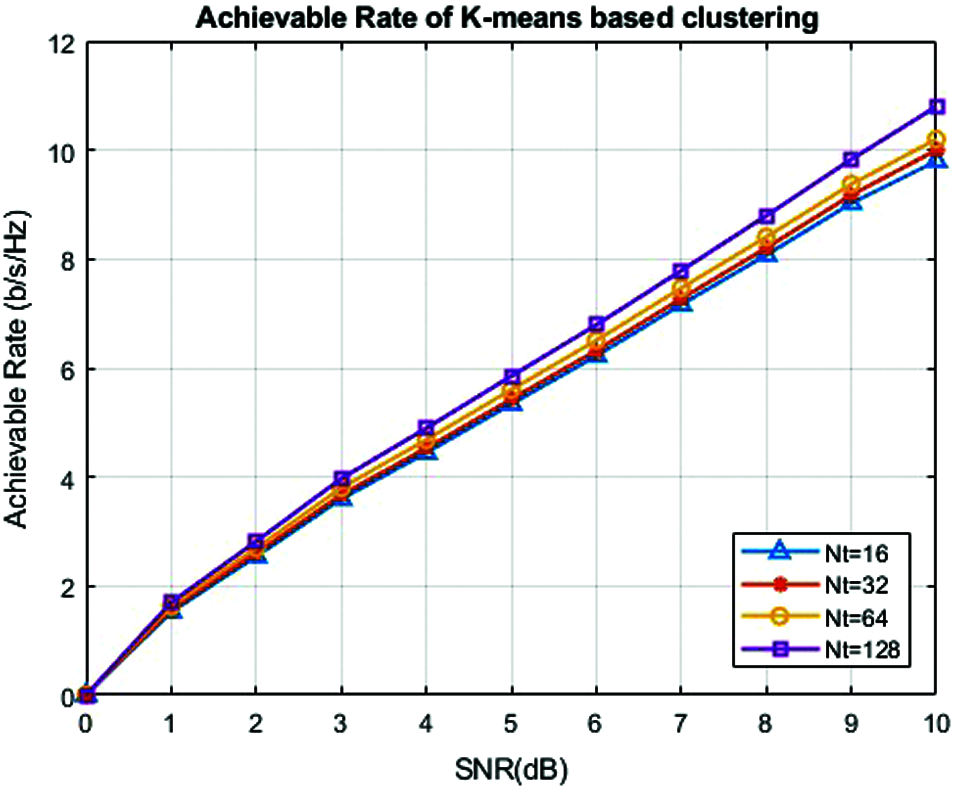
Figure 5: Achievable rate of k-means based clustering codebook model

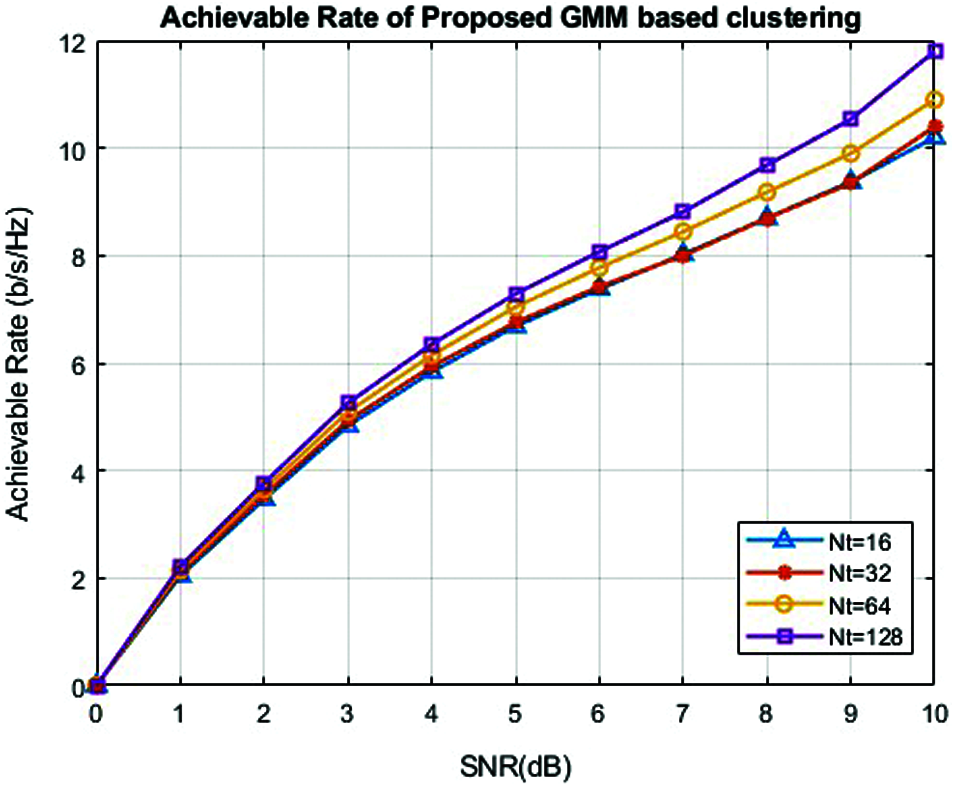
Figure 6: Achievable rate of GMM based clustering codebook model

The Symbol-error-rate (SER) of proposed GMM based clustering with DFT and k-means based clustering is plotted in Fig. 7. The SER is defined using Nt=128 as the fixed antenna value. The Symbol-error-rate (SER) performance approaches towards a channel with complete information. Although the GMM-based clustering receiver has an error rate of, higher Signal-to-noise ratio (SNR) regime, reduction in the error rate is achieved by using additional receive nodes in case of both perfect and approximated channel knowledge scenarios. The performance of the suggested GMM-based clustering codebook design for Nt=16,32,64,128 is shown in Fig. 8 shows that massive MIMO has a lower symbol error rate and there is no noticeable difference between the two massive MIMO codebooks in the lower SNR situation, but the proposed codebook design outperforms effectively in the higher SNR scenario. As a result, the proposed GMM-based clustering is suitable for large MIMO codebook construction.

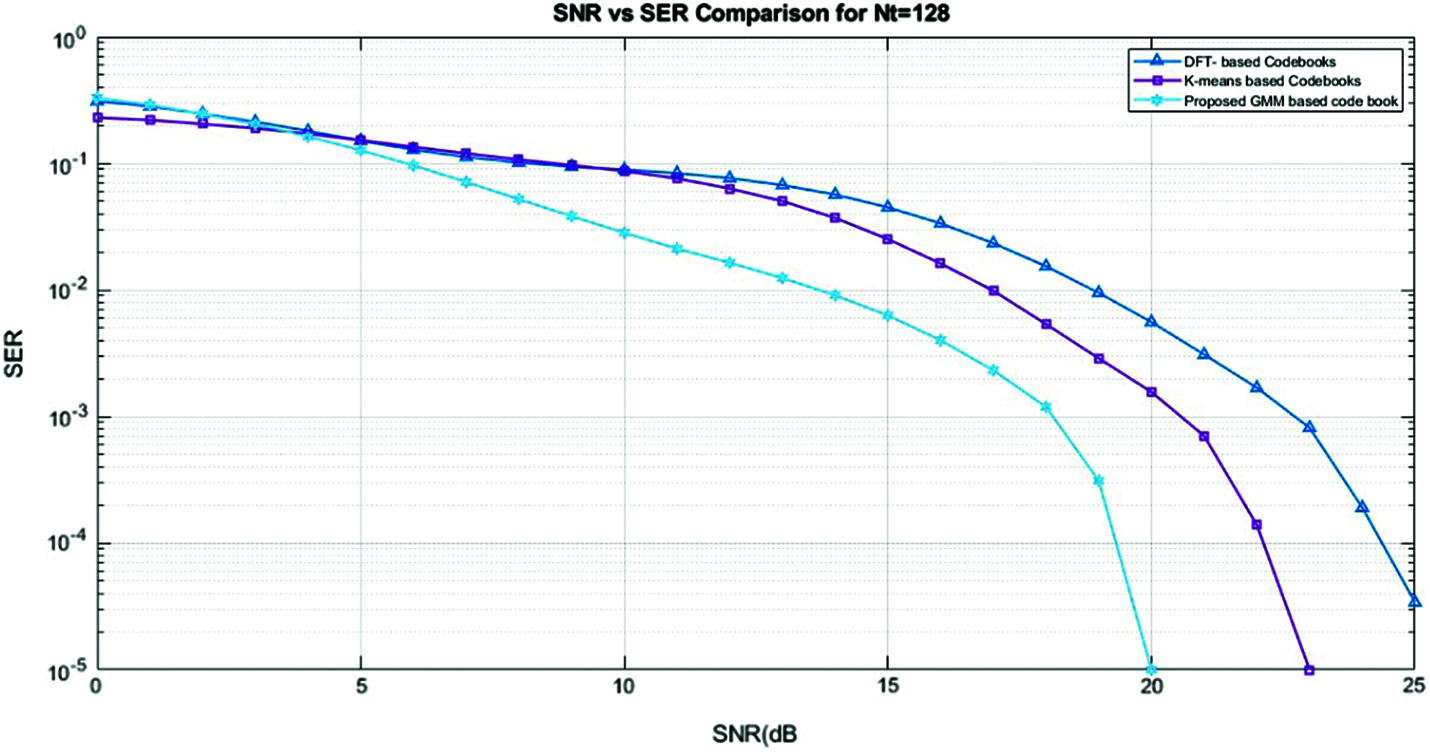
Figure 7: SNR vs. SER comparison for Nt=128

Figure 8: SNR vs. SER of the proposed GMM based clustering model

5  Conclusion

We presented a Gaussian mixture model (GMM) based codebook approach for massive MIMO in this paper. It combines GMM with clustering methods that were used to create the codebook. The DNN learns the important CSI characteristics whereas the GMM based clustering algorithms obtain the statistic information for the associated characteristics. By utilizing DNN frameworks, the proposed GMM based clustering codebook approach can reduce channel parameters. Furthermore, because the clustering algorithmic approach can understand characteristics of the wireless channel, it ensures CSI feedback's performance in a variety of changing wireless settings. The proposed GMM based clustering codebook design outperforms existing methods, as demonstrated by simulation results as well as theoretical analysis concerning achievable rate. Fortunately, by upgrading the clustering processes regularly, the suggested codebook architecture may understand and adapts to the real world.

Funding Statement: The authors received no specific funding for this research.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present research.

References

 1.  X. Su, J. Zeng, J. Li, L. Rong, L. Liu et al., “Limited feedback precoding for massive MIMO,” International Journal of Antennas and Propagation, vol. 2013, no. 1–2, pp. 1–9, 2013. [Google Scholar]

 2.  L. Lu, G. Y. Li, A. L. Swindlehurst, A. Ashikhmin and R. Zhang, “An overview of massive MIMO: Benefits and challenges,” IEEE Journal of Selected Topics in Signal Processing, vol. 8, no. 5, pp. 742–758, 2014. [Google Scholar]

 3.  D. J. Love, R. W. Heath and T. Strohmer, “Grassmannian beamforming for multiple-input multiple-output wireless systems,” IEEE Transactions on Information Theory, vol. 49, no. 10, pp. 2735–2747, 2003. [Google Scholar]

 4.  D. J. Love and R. W. Heath, “Grassmannian beamforming on correlated MIMO channels,” in IEEE Global Telecommunications Conference, GLOBECOM 04, Dallas, TX, 1, pp. 106–110, 2004. [Google Scholar]

 5.  V. Raghavan and V. V. Veeravalli, “Ensemble properties of RVQ-based limited-feedback beamforming codebooks,” IEEE Transactions on Information Theory, vol. 59, no. 12, pp. 8224–8249, 2013. [Google Scholar]

 6.  V. Raghavan, M. L. Honig and V. V. Veeravalli, “Performance analysis of RVQ-based limited feedback beamforming codebooks,” in 2009 IEEE Int. Symp. on Information Theory, Seoul, pp. 2437–2441, 2009. [Google Scholar]

 7.  D. J. Love and R. W. Heath, “Equal gain transmission in multiple-input multiple-output wireless systems,” IEEE Transactions on Communications, vol. 51, no. 7, pp. 1102–1110, 2003. [Google Scholar]

 8.  A. Alkhateeb, G. Leus and R. W. Heath, “Limited feedback hybrid precoding for multi-user millimeter wave systems,” IEEE Transactions on Wireless Communications, vol. 14, no. 11, pp. 6481–6494, 2015. [Google Scholar]

 9.  Y. Chen, D. Chen and T. Jiang, “Non-uniform quantization codebook-based hybrid precoding to reduce feedback overhead in millimeter wave MIMO systems,” IEEE Transactions on Communications, vol. 67, no. 4, pp. 2779–2791, 2019. [Google Scholar]

10. B. Wang, F. Gao, S. Jin, H. Lin and G. Y. Li, “Spatial- and frequency-wideband effects in millimeter-wave massive MIMO systems,” IEEE Transactions on Signal Processing, vol. 66, no. 13, pp. 3393–3406, 2018. [Google Scholar]

11. K. Sharma and R. Nandal, “A literature study on machine learning fusion with IOT,” in 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEIIndia, pp. 1440–1445, 2019. [Google Scholar]

12. C. Jiang, H. Zhang, Y. Ren, Z. Han, K. C. Chen et al., “Machine learning paradigms for next-generation wireless networks,” IEEE Wireless Communications, vol. 24, no. 2, pp. 98–105, 2017. [Google Scholar]

13. H. Huang, S. Guo, G. Gui, Z. Yang, J. Zhang et al., “Deep learning for physical-layer 5G wireless techniques: Opportunities, challenges and solutions,” IEEE Wireless Communications, vol. 27, no. 1, pp. 214–222, 2020. [Google Scholar]

14. M. Gao, T. Liao and Y. Lu, “Fully connected feedforward neural networks-based CSI feedback algorithm,” China Communications, vol. 18, no. 1, pp. 43–48, 2021. [Google Scholar]

15. T. Wang, C. Wen, S. Jin and G. Y. Li, “Deep learning-based CSI feedback approach for time-varying massive MIMO channels,” IEEE Wireless Communications Letters, vol. 8, no. 2, pp. 416–419, 2019. [Google Scholar]

16. Y. Huang, P. P. Liang, Q. Zhang and Y. Liang, “A machine learning approach to MIMO communications,” in 2018 IEEE Int. Conf. on Communications (ICCKansas City, MO, pp. 1–6, 2018. [Google Scholar]

17. H. Liang, W. Chung and S. Kuo, “Coding-aided K-Means clustering blind transceiver for space shift keying MIMO systems,” IEEE Transactions on Wireless Communications, vol. 15, no. 1, pp. 103–115, 2016. [Google Scholar]

18. J. Cui, Z. Ding, P. Fan and N. Al-Dhahir, “Unsupervised machine learning-based user clustering in millimeter-wave-NOMA systems,” IEEE Transactions on Wireless Communications, vol. 17, no. 11, pp. 7425–7440, 2018. [Google Scholar]

19. W. Wang, J. Xi and J. K. Hedrick, “A learning-based personalized driver model using bounded generalized Gaussian mixture models,” IEEE Transactions on Vehicular Technology, vol. 68, no. 12, pp. 11679–11690, 2019. [Google Scholar]

20. Y. Wang and T. Lei, “A new look at finite mixture models in medical image analysis,” Proceedings of ICSIPNN '94. Int. Conf. on Speech, Image Processing and Neural Networks, vol. 1, pp. 33–36, 1994. [Google Scholar]

21. M. Yue, Y. Li, H. Yang, R. Ahuja, Y. Chiang et al., “DETECT: Deep trajectory clustering for mobility-behavior analysis,” in 2019 IEEE International Conference on Big Data (Big DataLos Angeles, CA, USA, pp. 988–997, 2019. [Google Scholar]

22. M. Marczyk, G. Drazek, M. Pietrowska, P. Widlak, J. Polanska et al., “Modeling of imaging mass spectrometry data and testing by permutation for biomarkers discovery in tissues,” Procedia Computer Science, vol. 51, no. 23, pp. 693–702, 2015. [Google Scholar]

23. S. Agarwal, “Data mining: Data mining concepts and techniques,” in Int. Conf. on Machine Intelligence and Research Advancement, Katra, India, pp. 203–207, 2013. [Google Scholar]

24. J. P. Baudry, A. E. Raftery, G. Celeux, K. Lo and R. Gottardo, “Combining mixture components for clustering,” Journal of Computational and Graphical Statistics, vol. 19, no. 2, pp. 332–353, 2010. [Google Scholar]

25. C. Hennig, “Methods for merging Gaussian mixture components,” Advances in Data Analysis and Classification, vol. 4, no. 1, pp. 3–34, 2010. [Google Scholar]

26. V. Melnykov, “Merging mixture components for clustering through pairwise overlap,” Journal of Computational and Graphical Statistics, vol. 25, no. 1, pp. 66–90, 2016. [Google Scholar]

27. A. Hyadi, Z. Rezki and M. Alouini, “An overview of physical layer security in wireless communication systems with CSIT uncertainty,” IEEE Access, vol. 4, pp. 6121–6132, 2016. [Google Scholar]

28. P. Kuo, H. T. Kung and P. Ting, “Compressive sensing-based channel feedback protocols for spatially-correlated massive antenna arrays,” in 2012 IEEE Wireless Communications and Networking Conference (WCNCParis, France, pp. 492–497, 2012. [Google Scholar]

29. J. Shen, J. Zhang, E. Alsusa and K. B. Letaief, “Compressed CSI acquisition in FDD massive MIMO: How much training is needed?,” IEEE Transactions on Wireless Communications, vol. 15, no. 6, pp. 4145–4156, 2016. [Google Scholar]

30. P. N. Alevizos, X. Fu, N. D. Sidiropoulos, Y. Yang and A. Bletsas, “Limited feedback channel estimation in massive MIMO with non-uniform directional dictionaries,” IEEE Transactions on Signal Processing, vol. 66, no. 19, pp. 5127–5141, 2018. [Google Scholar]

31. W. Shen, L. Dai, B. Shim, Z. Wang and R. W. Heath, “Channel feedback based on AoD-adaptive subspace codebook in FDD massive MIMO systems,” IEEE Transactions on Communications, vol. 66, no. 11, pp. 5235–5248, 2018. [Google Scholar]

32. W. Shen, L. Dai, Y. Zhang, J. Li and Z. Wang, “On the performance of channel-statistics-based codebook for massive MIMO channel feedback,” IEEE Transactions on Vehicular Technology, vol. 66, no. 8, pp. 7553–7557, 2017. [Google Scholar]

33. D. Ying, F. W. Vook, T. A. Thomas, D. J. Love and A. Ghosh, “Kronecker product correlation model and limited feedback codebook design in a 3D channel model,” in 2014 IEEE International Conference on Communications (ICCSydney, NSW, Australia, pp. 5865–5870, 2014. [Google Scholar]

34. S. Bazzi and W. Xu, “On the amount of downlink training in correlated massive MIMO channels,” IEEE Transactions on Signal Processing, vol. 66, no. 9, pp. 2286–2299, 2018. [Google Scholar]

35. G. Gui, Y. Wang and H. Huang, “Deep learning based physical layer wireless communication techniques: Opportunities and challenges,” Journal of Communication, vol. 40, no. 2, pp. 19–23, 2020. [Google Scholar]

36. H. Huang, Y. Song, J. Yang, G. Gui and F. Adachi, “Deep-learning-based millimeter-wave massive MIMO for hybrid precoding,” IEEE Transactions on Vehicular Technology, vol. 68, no. 3, pp. 3027–3032, 2019. [Google Scholar]

37. Y. Wang, M. Liu, J. Yang and G. Gui, “Data-driven deep learning for automatic modulation recognition in cognitive radios,” IEEE Transactions on Vehicular Technology, vol. 68, no. 4, pp. 4074–4077, 2019. [Google Scholar]

38. H. Huang, W. Xia, J. Xiong, J. Yang, G. Zheng et al., “Unsupervised learning-based fast beamforming design for downlink MIMO,” IEEE Access, vol. 7, pp. 7599–7605, 2018. [Google Scholar]

39. G. Gui, H. Huang, Y. Song and H. Sari, “Deep learning for an effective nonorthogonal multiple access scheme,” IEEE Transactions on Vehicular Technology, vol. 67, no. 9, pp. 8440–8450, 2018. [Google Scholar]

40. T. Wang, C. K. Wen, H. Wang, F. Gao, T. Jiang et al., “Deep learning for wireless physical layer: Opportunities and challenges,” China Communication, vol. 14, no. 11, pp. 92–111, 2017. [Google Scholar]

41. H. Huang, J. Yang, H. Huang, Y. Song and G. Gui, “Deep learning for super-resolution channel estimation and DOA estimation based massive MIMO system,” IEEE Transactions on Vehicular Technology, vol. 67, no. 9, pp. 8549–8560, 2018. [Google Scholar]

42. C. K. Wen, W. T. Shih and S. Jin, “Deep learning for massive MIMO CSI feedback,” IEEE Wireless Communication Letter, vol. 7, no. 5, pp. 748–751, 2018. [Google Scholar]

43. T. Wang, C. K. Wen, S. Jin and G. Y. Li, “Deep learning-based CSI feedback approach for time-varying massive MIMO channels,” IEEE Wireless Communication Letter, vol. 8, no. 2, pp. 416–419, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.