Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.021788
Article

A Multi-Simplex Imperialist Competitive Paradigm for Solving Nonlinear Physical Systems

Javaid Ali1, Shaukat Iqbal2 and Salem Alkhalaf3,*

1Department of Mathematics, Govt. Graduate College Township, Lahore, Pakistan
2School of Systems and Technology, University of Management and Technology, Lahore, 54000, Pakistan
3Department of Computer, College of Science and Arts in Ar Rass, Qassim University, Ar Rass, Saudi Arabia
*Corresponding Author: Salem Alkhalaf. Email: s.alkhalaf@qu.edu.sa
Received: 14 July 2021; Accepted: 16 August 2021

Abstract: This paper proposes a novel gradient free multi-simplex topology fabric aided imperialist competitive algorithm (ICA) for solving nonlinear systems of algebraic equations by transforming them to equivalent global optimization problems. The high dependence of traditional gradient based solvers of such systems on initial guesses and the Jacobeans resulting in false convergence is the main motivation behind the present work. The present work provides a mechanism for enhancing exploitation powers of imperialist search phase of the algorithm and hence improves the convergence speed. The variants emerging from the proposed approach are applied to diverse nonlinear systems arising in different scientific areas and the results so obtained are analyzed in details. Based on the analysis of empirical results on complex benchmark models, it is observed that the proposed enhancement of ICA has not only boosted the problem solving power of the imperialist system when applied multidimensional nonlinear physical systems but also emerged as an efficient gradient/initial guess free alternative solver with high accuracy for nonlinear systems.

Keywords: Imperialist competitive system; simplex topology; nonlinear physical models; optimization

1  Introduction

Nonlinear systems of algebraic equations often arise in diverse scientific areas such as computational mechanics, economics, chemical engineering, weather forecasting, robotics, and electrical engineering. Nonlinear systems of equations are one of the non-deterministic polynomial-time (NP)-hard problems and resemble multi-objective optimization problems [1] and nondeterministic. For any n ∈ ℕ, let Ej:Ω ⊂ ℝn → ℝ be a nonlinear function for at least one j ∈ {1, 2, 3, …, n}. With these notations, the general nonlinear system of equations can be described as follows.

{E1(x1,x2,x3,…,xn)=0,E2(x1,x2,x3,…,xn)=0,⋮En(x1,x2,x3,…,xn)=0. (1)

Subject to the following bounds on variables:

xjL≤xj≤xjU:xjL,xjU∈R  ∀ 1≤j≤n. (2)

To develop new reliable techniques for solving nonlinear systems is a critical issue. Newton–Raphson method [2,3] is the most common method but it is very sensitive to starting solution and hence requires additional efforts for determining suitable initial guess. Moreover, traditional gradient based methods are applicable to the system (1) only when the availability of a suitable initial guess, the differentiability of each Ej and non-singularity of the associated Jacobean are guaranteed. However, gradient based methods may produce favorable results in a very limited number of iterations if the Taylor’s approximation is employed at the current initial guess occurring sufficiently close to the root of the system. Such kind of efficiency is beyond expectations when the initial guess is far from the exact solution [4]. The limitations of Newton type methods were highlighted when Powell [5] provided an interesting counter example showing divergence of Newton’s method to two different non-stationary points under absolute and squared residual merit functions when started with the same initial guess. Similarly, Byrd et al. [6] presented another counter example which caused singularity of the Jacobean at many points making the choice of initial guess to be difficult. Bader [7] highlighted the impracticality of Newton’s method to high dimensional problems and proposed a new Krylov subspace based tensor method that also requires first order continuously differentiability condition [8]. Recently, Vahidi et al. [9] and Sharma et al. [10] proposed new effective solvers for solution of nonlinear systems. Massive amount of existing literature [11–18] is dedicated to improve the convergence order of the classical deterministic recursive or iterative methods. The most recent trend for solving system of nonlinear equations is to transform it into an equivalent global optimization problem of the following form.

Minimizef(x)=∑j=1n⁡{Ej(x)}2+M×max{0,xjL−xj,xj−xjU:1≤j≤n} (3)

Here M is a large positive number.

Over the recent years, modern stochastic solvers have been employed to solve the global optimization problems associated with nonlinear systems. For examples, Luo et al. [19] proposed a combination of chaos search with a Newton type method, Sihwail et al. [20] proposed a hybrid of Haris Hawks Optimization with Newton’s method, Mo et al. [21] used a combination of the conjugate direction method (CD), particle swarm optimization (PSO) algorithm and its hybrid were used by Jaberipour et al. [22] and Ouyang et al. [23] respectively. Abdollahi et al. [24] used the standard imperialist competitive algorithm (ICA), Oliveira et al. [25] proposed a variant of simulated annealing algorithm with fuzzy rules adaptations, Wu et al. [26] used a new variant of the Social emotional optimization for solving nonlinear systems of equations. Other applications of metaheuristics for nonlinear systems include invasive weed optimization algorithm [27], polarization technique [28], cuckoo optimization algorithm [29], genetic algorithm [30–32], artificial bee colony algorithm [33] and multi-population parallel ICA [34] their successful applications, there also exist two main challenges for metaheuristics that are (i) maintaining balance between exploration and exploitation (ii) avoiding large computational cost. Abdollahi et al. [35] highlighted that in most of the previous applications [1,21–26,29,30,33,36,37] of metaheuristics to nonlinear systems large population sizes were used which resulted in high computation costs and slow convergence. To cope with these drawbacks, it is needed to construct an effective and reliable combination of local and global search algorithms for solving nonlinear systems of equations.

This work proposes a multi-simplex imperialist competitive algorithm (MS-ICA) for solving physical models described by the system of Eq. (1). The basic element of the proposed MS-ICA is to equip each imperialist with additional socio-political elements connected with it through a simplex topology. The operations on the associated simplex try to enhance the problem-solving abilities of the imperialist. Rest of the paper is ordered as follows: in Section 2, we describe the imperialist competitive algorithm (ICA), in Section 3, some well-known systems are presented to demonstrate the effectiveness and robustness of the proposed ICA and Section 4 presents statistical results of the proposed methods on some nonlinear systems. Finally, some concluding remarks are presented in the end.

2  Basic Concepts of the Imperialist Competitive Algorithm

Imperialist competitive algorithm (ICA) was developed by Atashpaz et al. [38] as a tool for modeling learning and imperialist evolution. The ICA belongs to a class of cultural/social algorithms [39]. Along with the essential population module of evolutionary algorithms, the ICA is equipped with a peer component of empires comprised of countries that are further classified as colonies and imperialists. Each of the empires stocks and deploys information that sequentially impacts the progress of the population component. The competition mechanism among the empires is identified through the imperialists’ policies to extend their empire’s powers and rules beyond their boundaries, which models the optimum search procedure of the ICA. The decision-making knowledge of the ICA resides in the elimination of weak empires and expansion of strong empires so that the strongest empire eventually takes possession of the other empires. Colonies and imperialists of the empires continuously interact while being governed by three basic operators called assimilation, revolution, and competition. Repeated interaction between the strategic action phases of members of the colonial space in the imperialist competitive environment leads to the genesis of “imperialist swarms” of individuals roving within the problem search space. The meta-level swarming of imperialist dominance evolves an algorithmic process in the problem domain with the aim of exploring the search space and exploiting promising areas, thus correctly locating the optimum. The standard pseudo code of the ICA is presented in Algorithm 1. The respective components of the ICA are described in the following subsections.

2.1 Initialization

Let Npop, Nimp and Ncol be positive integers. ICA is initiated by randomly generated population {xj ∈ Ω ⊂ ℝn:1 ≤ j ≤ Npop} of Npop solutions called countries each with cost cj = f(xj). For each k = 1, 2, 3, …, Nimp the kth imperialist state is denoted by xk,imp = arg((min({cj:1 ≤ j ≤ Npop} − {ci:1 ≤ i < k}))) with cost ck,imp. The remaining Ncol (= Npop − Nimp) countries are called colonial states. The kth imperialist state heads an empire and acquires NCk colonial states based on its normalized fitness pk defined below.

pk=|max1≤i≤Nimp⁡{ci,imp}−ck,imp∑i=1Nimp⁡ci,imp|;1≤k≤Nimp. (4)

NCk=round(pk×Ncol). (5)

2.2 Assimilation Phase

In the assimilation phase, an imperialist builds infrastructure and attempts to alter the position of its colonies within the space of its socio-political elements [40]. The colonial movement towards an imperialist (see Fig. 1a) is modeled by the following relation.

Newposition=oldposition+β×r⊗(imperialist−oldposition) (6)

Here, r is a 1 × n dimensional vector of random numbers drawn from the interval (0, 1), β is a real number having a default value of 1.5, and ⊗ denotes the Minkowski product of two vectors.

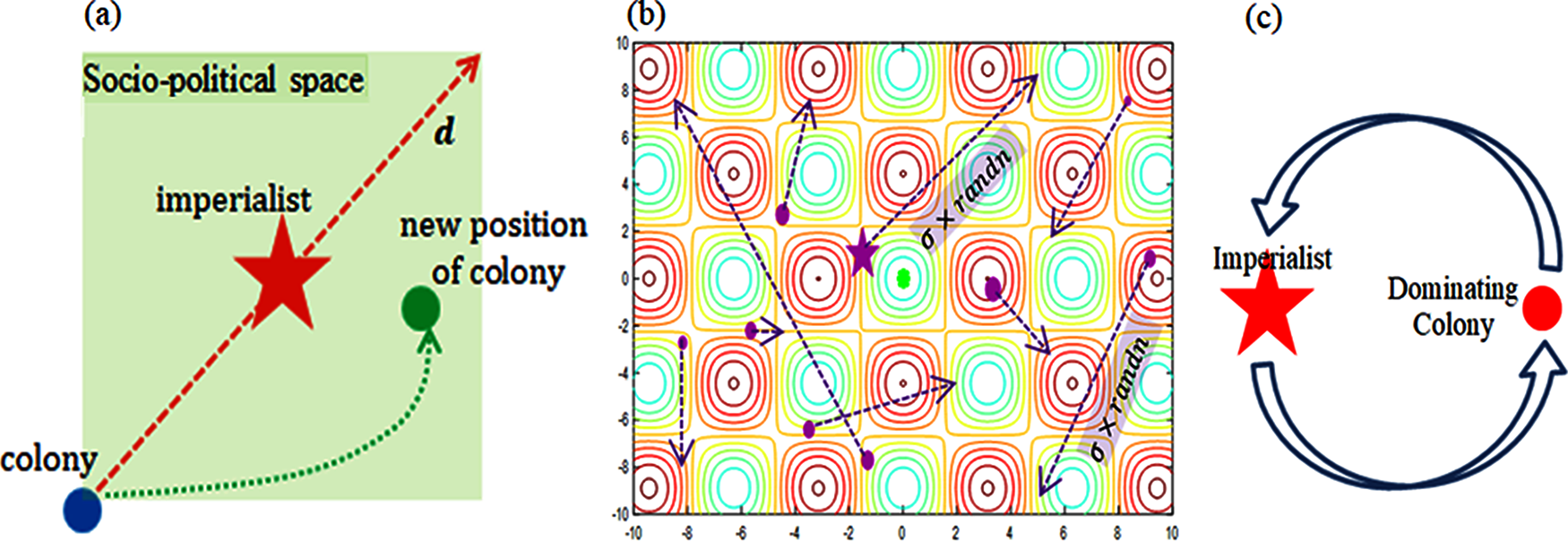
Figure 1: (a) Assimilation; (b) Revolution; and (c) Intra-empire competition

2.3 Revolutionary Phase

The revolutionary phase models the concept of resistive reforms of colonies to repel complete socio-political absorption into an empire [40,41] In this modeled phenomenon, colonies try to independently explore the search space by probabilistically undoing the influence of imperialists. The revolutionary explorative steps are carried out by the following two equations:

Newposition={oldposition+σ×randnifprobability≤PR,oldpositionotherwise (7)

oldposition(element #i)=newposition(element #i);1≤i≤ciel(n×μ). (8)

In Eq. (7), PR is the revolution probability, σ is an appositive real number, and randn is a 1 × n dimensional vector of pseudorandom numbers drawn from a standard normal distribution. In Eq. (8), the parameter μ ∈ [0, 1] is the revolution acceptance rate, and the function ciel denotes the smallest integer greater than or equal to a given real number. Fig. 1b shows the revolutionary phase of an empire.

2.4 Intra-Empire Competition

As a result of the assimilation and revolutionary phases, a colony may dominate an imperialist by acquiring a superior position in the empire. In such a case, an exchange of positions between an imperialist and dominating colony takes place [38]. The rest of the colonies preserve their current locations. Such a type of exchange of positions in an empire is the result of what is termed intra-empire competition [40,41]. Fig. 1c depicts the intra-empire competition process.

2.5 Inter-Empire Competition

In this phase, the stronger empires have likelihood-based tendency of taking possession of the weakest colony of the weakest empire. As a result of this process, an empire becomes the weakest by gradually losing its colonies to other empires until it ultimately collapses and is eliminated when all of its colonies are gone. The strength Pk of the kth empire is calculated as under.

Pk=|TCk^∑i=1Nimp⁡TCi^|. (9)

TCk=costofimperialist+ζ×meancostofitsallcolonies (10)

TCk^=max1≤i≤Nimp⁡{TCi}−TCk (11)

The parameter ζ is a real number in the interval (0, 1).

2.6 Termination

With the course of the imperialist evolutionary process, some empires will be weaker and collapse, and only one will eventually control all of the colonies in the population and be deemed the most powerful. As the algorithmic iterations proceed, the colonies will get closer to and help create a uniquely existing most powerful empire; at the end, all the colonies will capture the same position as that of the imperialist [38]. The algorithm is terminated at such a stage.

3  Proposed Multi-Simplex Imperialist Competitive Algorithm (MS-ICA)

The basic motivation behind the current work involves the related innovative ideas of social fabric implemented in [42,43]. Social fabric is defined as a living informational membrane woven by tissue fibers produced by the engineered emergence of mediators that illustrate the connectivity strain between a member and the community [42]. The tissue fiber is the basic unit of the fabric that defines and controls the topology and type of connectivity in the sense of interactions among its agents.

Several types of topologies exist in the PSO literature [44] to visualize interactions within the population. These include ring (lBest), fully connected (gBest), tree, star, hexagon, square, and octagon topologies. Figs. 2a–2b and 2d show the (lBest), (gBest) and tree topologies [42] respectively, whereas Fig. 2c provides a picture of the star topology [45].

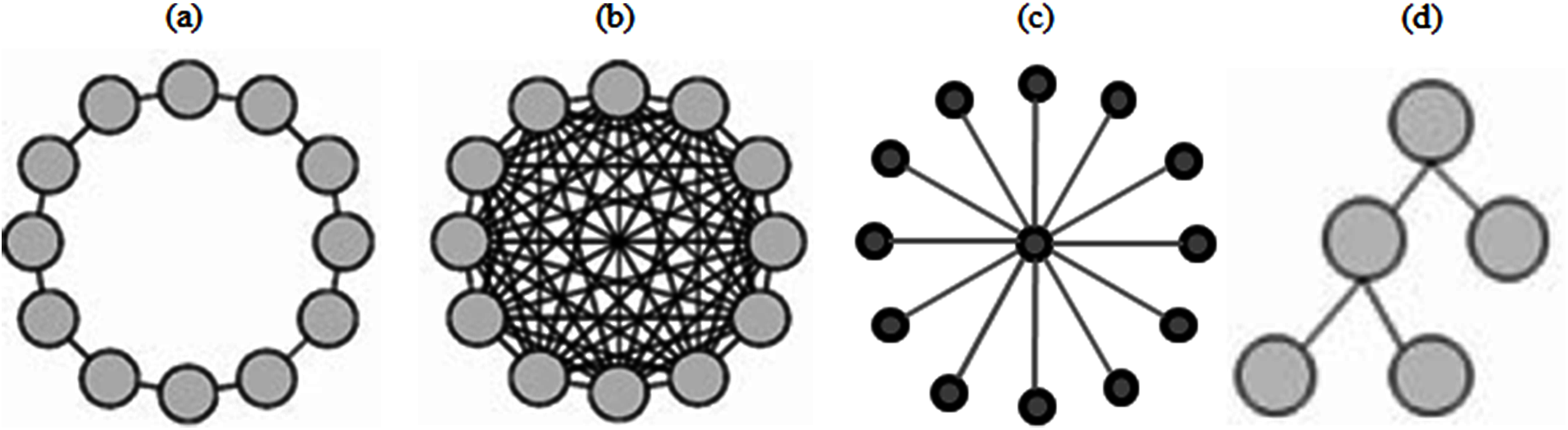
Figure 2: (a) Ring topology; (b) fully connected topology; (c) star topology; and (d) tree topology

The social fabric paradigm can be extended to economic, religious, military, geographical and political information connectivity among the countries in an imperialist competitive system. The topologies shown in Fig. 2 are often used for entire populations, but the actual focus of an imperial system is on improving and maintaining the efficiency of the imperialist. Many approaches, such as the subpopulations of countries, organizations, firms or NGOs can be incorporated through the social fabric to boost the supremacy of the imperialist. However, the present study considers the association of topological simplexes with imperialists. A simplex is a convex hull of n + 1 affine independent points in an n-dimensional search space. Fig. 3 presents two-, three-, and four-dimensional simplexes.

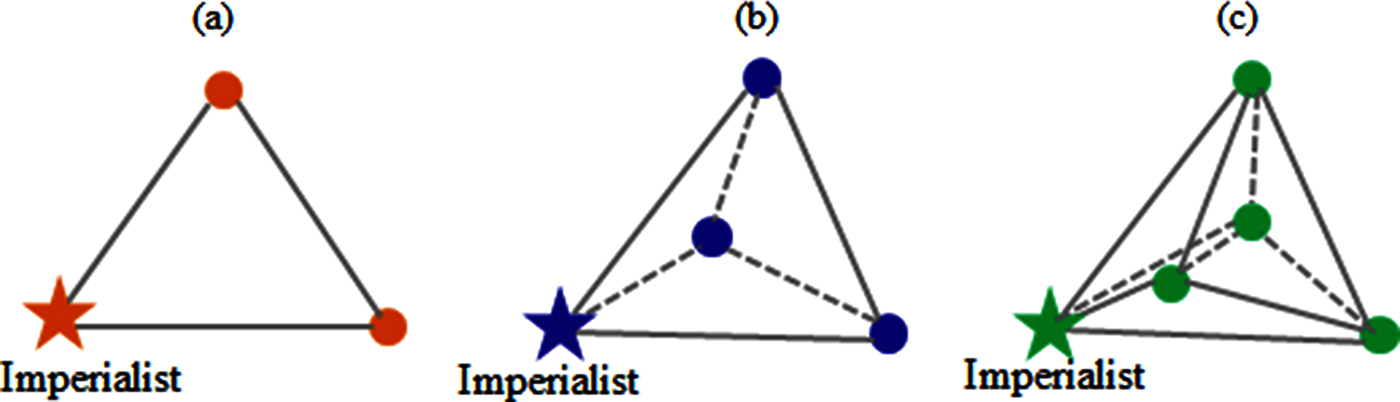
Figure 3: (a) Two-dimensional simplex; (b) three-dimensional simplex; and (c) four-dimensional simplex

The connectivity of members of a simplex can be established similar to that of [42]. Let C be a set of n + 1 individuals that involve an imperialist. The interactions among the members of C are defined by a simplex S=Vi:1≤i≤n+1 , where each Vi = (vi1, vi2, vi3, …, vin) ∈ ℝn is a vertex and has an invertible mapping of C onto S . The degree of each vertex/node of the simplex is n. The vertices are ranked from the best to the worst as to satisfy the following ordering condition:

f(V1)≤f(V2)≤f(V3)≤…≤f(Vn+1). (12)

The imperialist is always maintained as the best vertex V1 of S . Each imperialist is supported with a simplex in a similar fashion.

In the optimization process, the operations of reflection/rotation, expansion, contraction, and shrink are used to try to improve the vertices of the simplex. The nature of learning among associated individuals depends on the way in which a simplex is utilized in the dynamic behavior of a population. In the Nelder-Mead simplex (NMS) method [46], the operations of reflection, rotation, expansion, and contraction about the centroid of the face opposite to the best vertex are used to improve the worst vertex, whereas the shrink step is executed toward the best vertex. Fig. 4a shows the NMS operations of reflection, rotation, expansion, and contraction, whereas Fig. 4b shows its shrink operation.

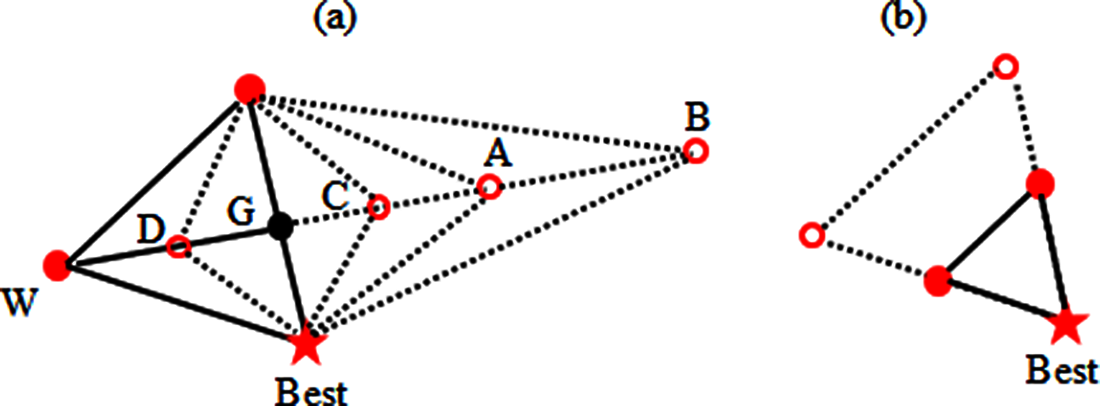
Figure 4: Operations on a simplex

Points A, B, C and D are the results of reflection, expansion, outside contraction and inside contraction respectively whereas G is the centroid of the face opposite of the worst vertex (W). The standard NMS method evaluates these points accordingly, as follows:

G=1n∑i=1n⁡Vi, (13)

y=Vn+1+ρ(G−Vn+1). (14)

The generated y is A, B, C or D according as ρ is set equal to 2, 3, 1.5 or 0.5. In the shrink step, the non-best vertices are replaced accordingly, as follows:

Vi←Vi+0.5(V1+Vi);2≤i≤n+1 (15)

Algorithm 2 is an extension of the standard NMS method extracted from the studies in [46–48]. The complete framework of the proposed MS-ICA is presented in Fig. 5.

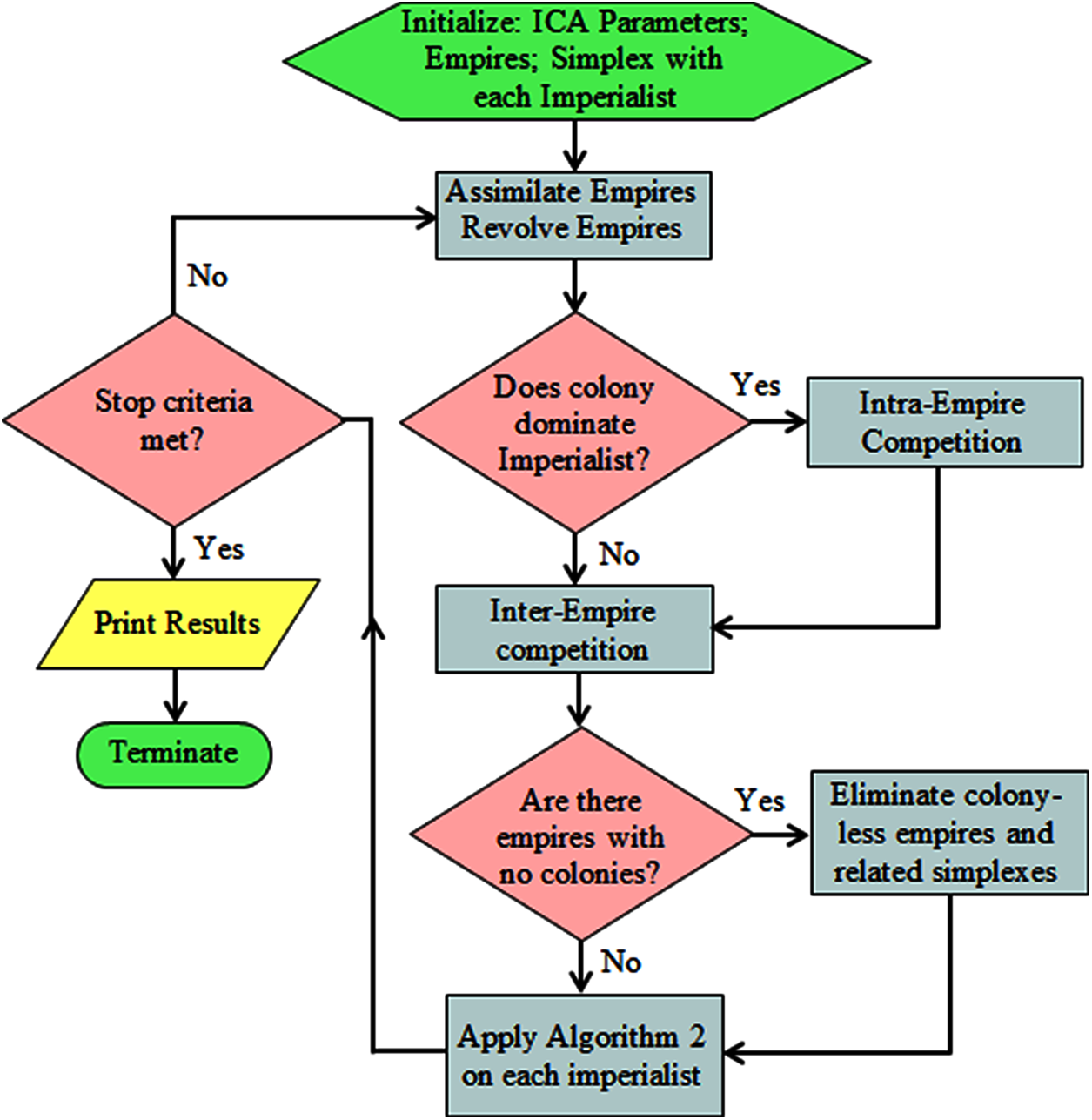
Figure 5: Flowchart of proposed MS-ICA

4  Experimental Framework and Benchmark Physical Models

A comprehensive analysis of different variants of the ICA and MS-ICA regarding different parametric settings was conducted. The parameters of the population size (nPop), selection pressure (α), revolution probability (p) and colony mean cost coefficient (θ) were fixed at 50, 1, 0.05 and 0.2, respectively. The variants of the ICA and the proposed MS-ICA were based on combinations of a number of parameters: the number of empires (nEmp1 = 5, nEmp2 = 10, nEmp3 =  20); assimilation coefficient (β1 = 1.5, β2 =  2); and revolution rate (μ1 = 0.1, μ2 =  0.5). For simplicity, a triplet (βi, μj, Empk): i = 1, 2; j = 1, 2; k = 1, 2, 3 of parameter settings is denoted by Pijk . The experimental design used the following seven benchmark systems of nonlinear equations to describe complex physical models. For numerical simulations have been implemented in MATLAB programming environment on a Core (TM) i3 machine with 2.00 GB RAM.

4.1 Kinematic Synthesis Problem (KS) [25]

where

ψ1=1.3954170041747090114,φ1=1.7461756494150842271,ψ2=1.7444828545735749268,φ2=2.0364691127919609051,ψ3=2.0656234369405315689,φ3=2.2390977868265978920,ψ4=2.4600678478912500533,φ4=2.4600678409809344550;−10≤xi≤10.

4.2 Chemical Equilibrium Problem (CE) [25]

E3(x)=2x2x32+2r5x32−8x5+r6x3+r7x2x3=0,E4(x)=r9x2x4+2x42−4rx5=0,

where r0=40 , r = 10, r5 = 0.193, r6 = 0.002597/r0, r7 = 0.003448/r0, r8 = 0.00001799/r0, r9 = 0.0002155/r0, r10 = 0.00003446/r0, xi > 0 for all i.

4.3 Combustion Problem (CP) [25,33]

4.4 Neurophysiology Problem (NP) [1,24,25,33,35]

4.5 Thin Wall Girder Section Problem (GS) [21,22,24,27]

where x1, x2, and x3 are the height, width, and thickness of the sections, respectively. The physical constraints on the system are:

4.6 Thin Wall Girder Section Problem (GS) [1,25]

4.7 Economic Modeling Problem (EM) [21,49]

A 5-dimensional economic modeling problem can be described as under:

5  Analyses of Results

According to the experimental framework, there were twelve variants of each of the proposed MS-ICAs and the original ICAs whose performances were to be assessed by the generated empirical data. Tab. 1 presents the best (B), mean (M) and standard deviation (SD) results for the objective function values of the MS-ICA for seven benchmarks after 50,000 function evaluations (FES) over 30 independent runs. Similarly, the statistical results of the ICA variants are shown in Tab. 2.

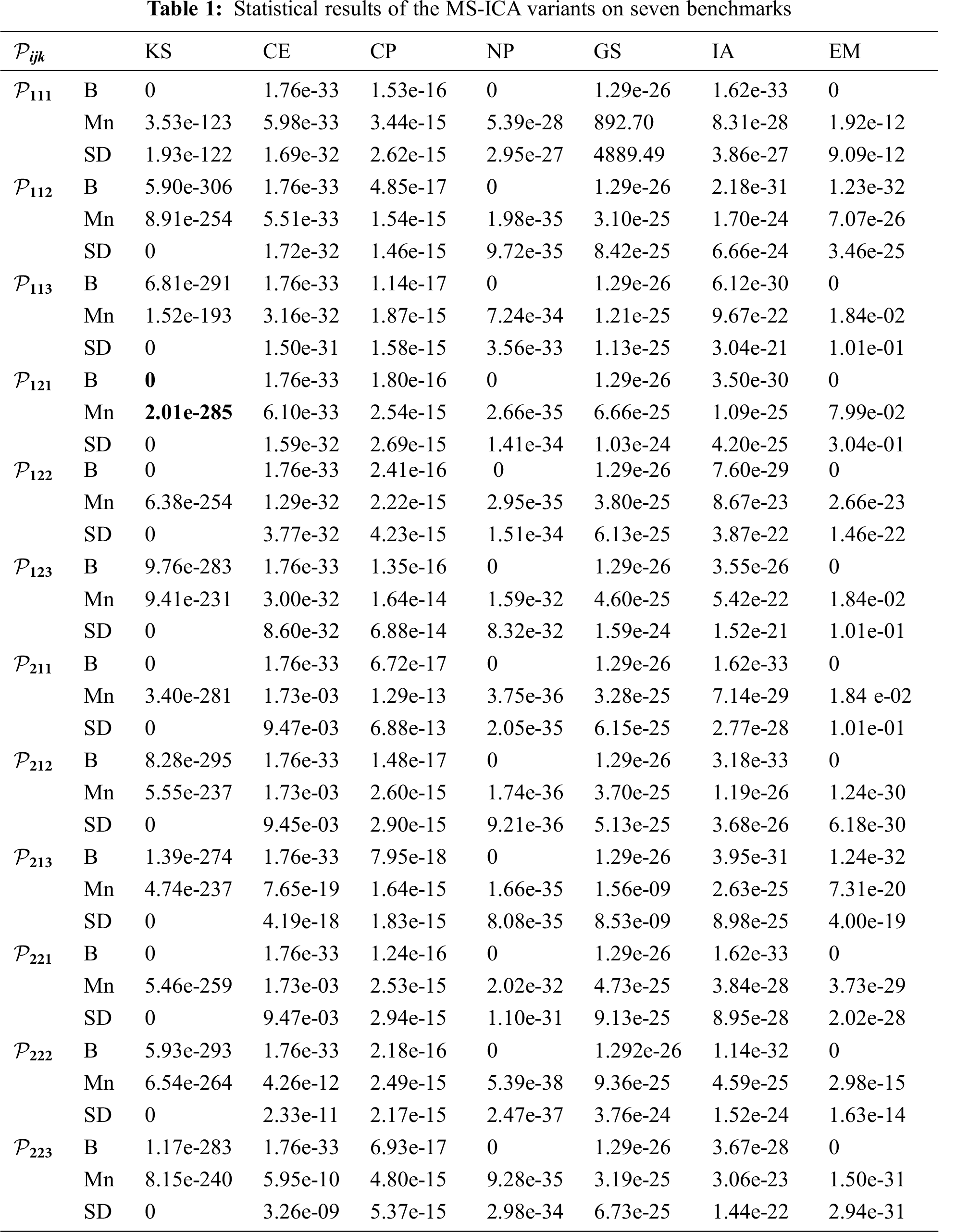
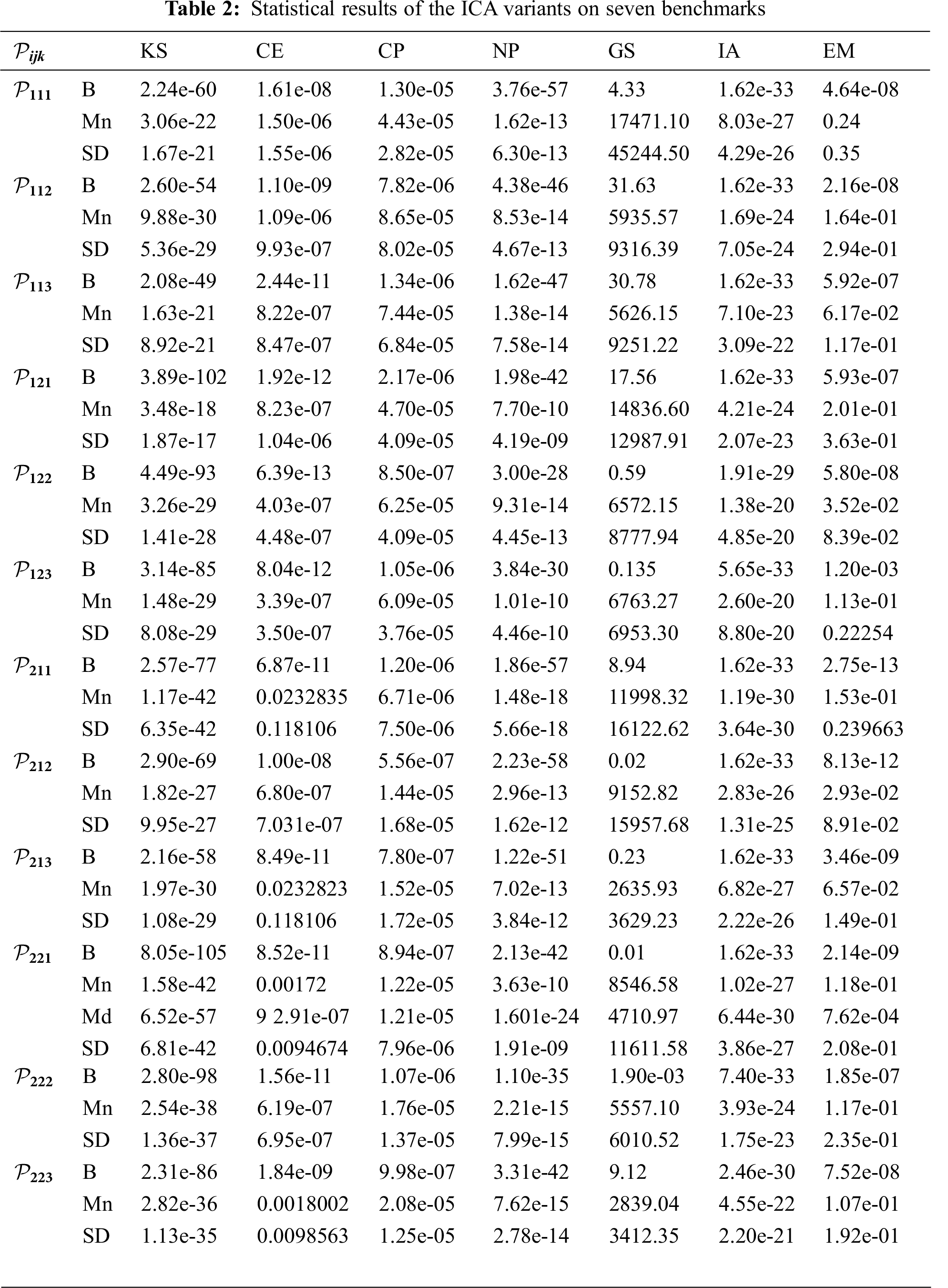
It can be seen from Tabs. 1–2 that all the variants of the MS-ICA were able to find better optimal solutions for every benchmark function. Regarding the KS benchmark, the variants P111,P121,P122 and P211 of the MS-ICA found exact roots, whereas the rest of the variants found the root with negligible error. The best optimum value found by any variant of the ICA was 8.05e-105 of P221, which was worse than the worst value of the MS-ICA variants. The smallest mean function value among all the MS-ICA variants was found by P121 and was better than the best value of any of the ICA variants.

For the CE benchmark, all the MS-ICA variants found the root with an accuracy of 1.76e-33 and P112 produced 5.51e-33 as the best mean value. In contrast, the best value of the ICA variants was 6.39e-13 as found by P122 and it was inferior to the mean value of the MS-ICA variants. The best approximate root of the combustion problem (CP) was found by the P213 variant of the MS-ICA, which also yielded 1.54e-15 as the smallest mean value. The respective best and smallest mean values of the associated objective function determined by the ICA variants were 5.56e-07 and 6.71e-06, which were related to P212 and P211 respectively. All the variants of the MS-ICA were able to find the exact root of the neurophysiology problem, and the smallest mean objective function value (5.39e-38) was returned by P222 . In contrast, no variant of the ICA was able to find the exact root of the problem. The best value (2.23e-58) among all the ICA variants was returned by P212 .

The MS-ICA variants found the root of the GS problem with the same accuracy of 1.29e-26, whereas the best value among all the ICA variants was 0.01 found by P221 . Clearly superior performances of the proposed MS-ICA variants on the GS benchmark regarding the best, mean and standard deviation results can be witnessed from Tabs. 1–2.

On the interval arithmetic benchmark, the variants  P111 ,   P211 and P221 of the MS-ICA found the same best value (1.62e-33) of the problem, which was also found by seven variants of ICA, namely, P111 , P112 , P113 , P121 , P211 , P221 and P213 . The overall performance of the ICA variants was better than the modified approaches. On the last benchmark, all the variants of the MS-ICA (except P112 and P213 ) found the exact root of the problem, whereas none of the ICA variants were able to find the exact root of the problem.

The statistical results presented in Tabs. 1–2 show that a variant of the MS-ICA or ICA that outperforms others on a specific problem may not show similar results on another problem. Therefore, to draw a clear conclusion about the performance of the proposed solvers, a collective non-parametric analysis of all the variants of MS-ICA and ICA was conducted.

Tab. 3 presents the Wilcoxon ranks of all the algorithms. It can be observed from Tab. 3 that the MS-ICA variant P112 ranked first by outperforming the rest of the variants. Each of the variants of the proposed MS-ICA acquired higher ranks as compared to those of the standard ICA. The mutual comparison of the variants shows that the variants P211 and P222 of the ICA achieved similar top ranks among all of the ICA variants.

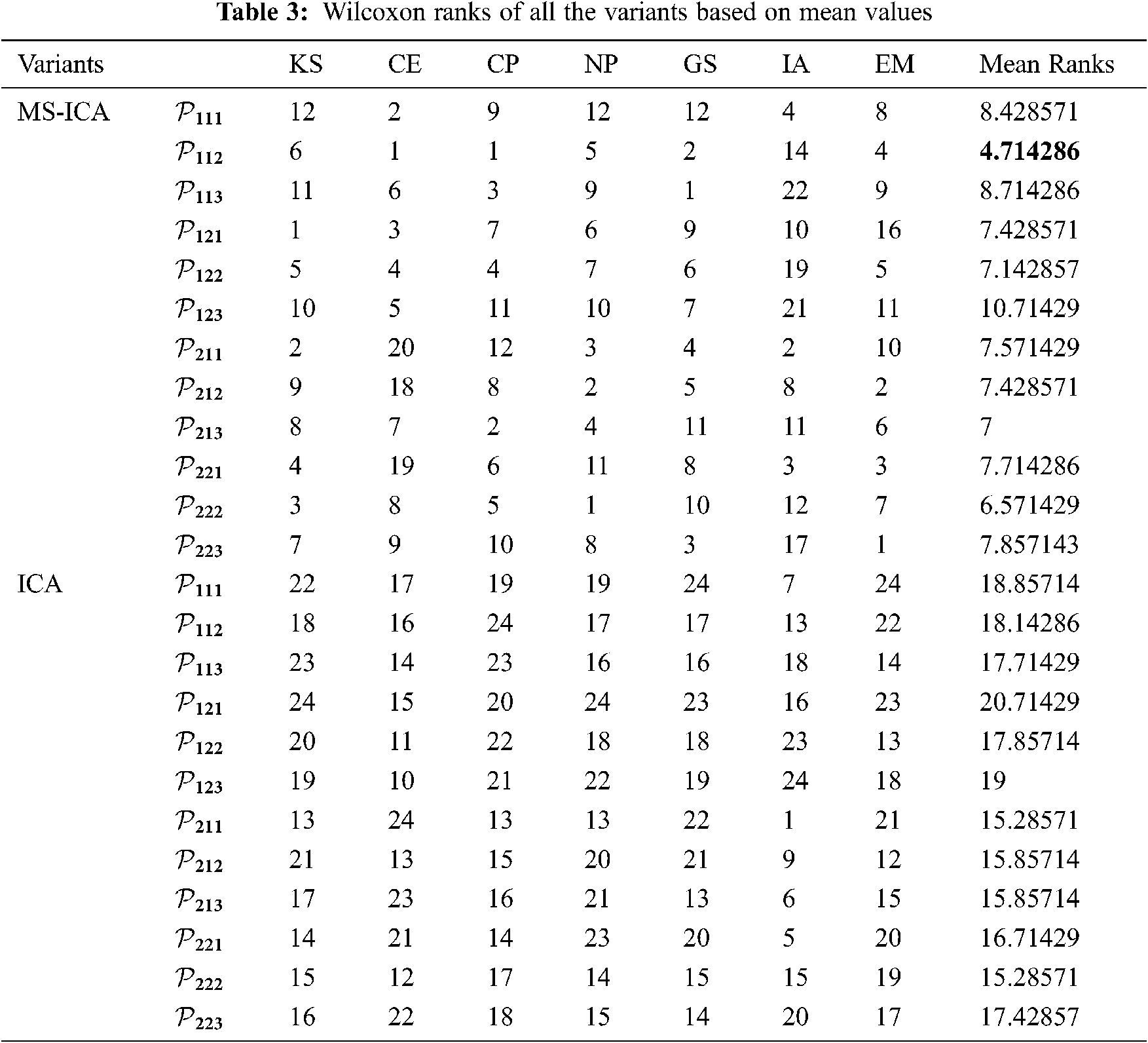
The subplots in Fig. 6 exhibit the convergence curves of the best and mean of 30 runs of the winner variants of the MS-ICA and ICA on the first six benchmark models. The number of function evaluations in hundreds is presented along the horizontal axis, whereas the logs of the best and mean fitness function values are presented along the vertical axis. It can be observed from Fig. 6 that the MS-ICA variant acquired average accuracies of 10−100 within 20,000 function evaluations on the KS problem, 10−20 within 30,000 function evaluations on the CE benchmark, 10−10 within 30,000 function evaluations on the test case CP, 10−20 within 20,000 function evaluations on the neurophysiology problem 5.4, 10−15 within 30,000 function evaluations for the GS problem and 10−15 within 30,000 function evaluations on test case IA. The respective mean function values of the ICA variant with similar function evaluations were 10−10, 10−02, 10−04, 10−06, 1004 and 10−18 on the first six benchmark models.

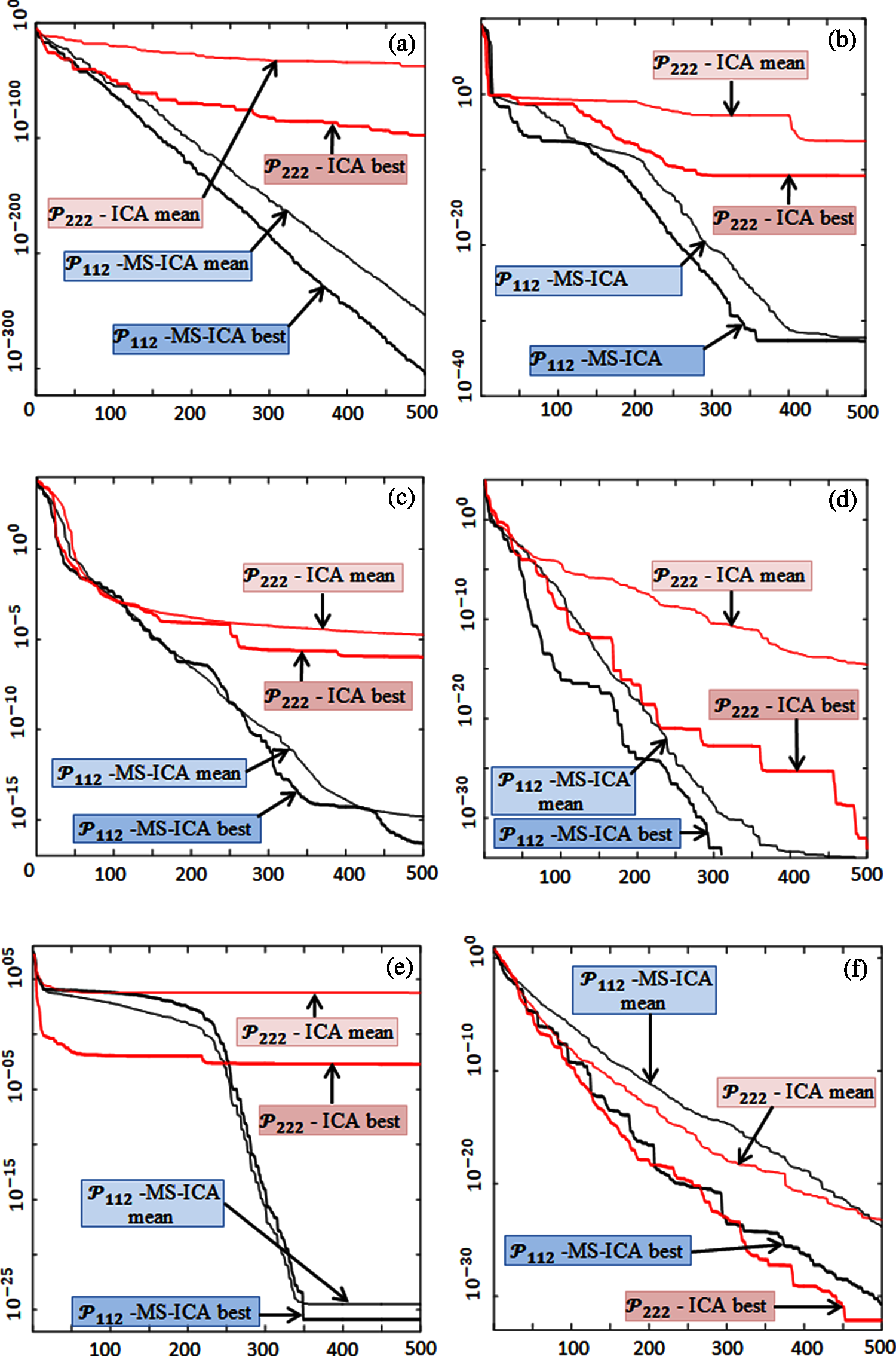
Figure 6: Best and mean curves for (a) KS; (b) CE; (c) CP; (d) NP; (e) GS; and (f) IA benchmarks

Fig. 7 presents the convergence curves of all the runs of the P112 variant of the MS-ICA and P222 variant of the ICA on the EM benchmark model. It can be observed that each run of the P112 -MS-ICA was able to find a solution of the EM problem with accuracy higher than 10−20, whereas the best ICA variant could find the best optimal value greater than 10−07. The best value found by the P222 -ICA variant was highly inferior to the mean value found by the P112 -MS-ICA.

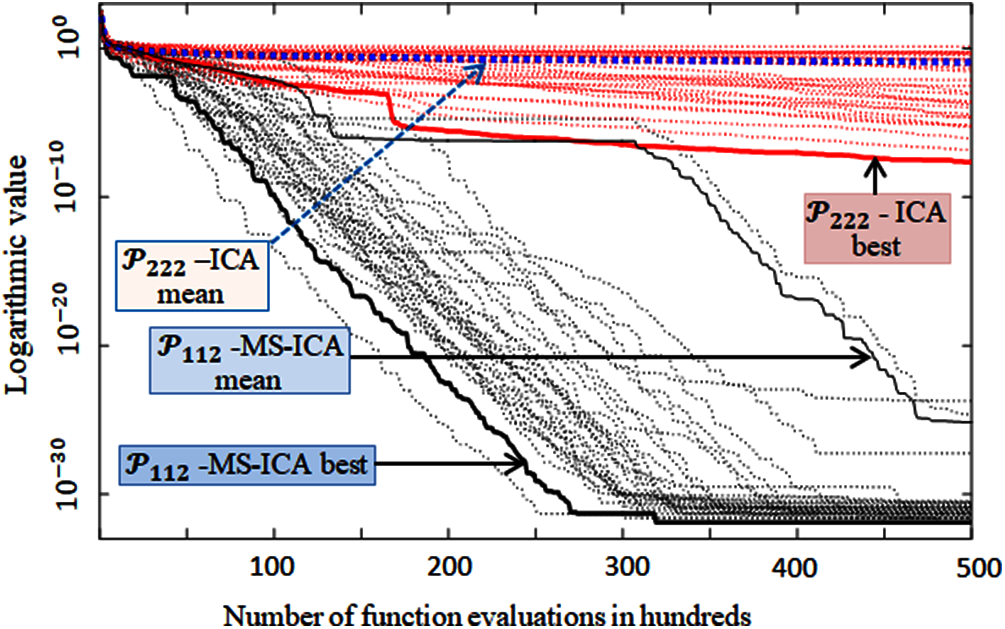
Figure 7: Convergence of 30 runs of P112 -MS-ICA and P222 -ICA on the EM benchmark model

6  Conclusion

In this work, a multi-simplex supported imperialist competitive algorithm has been proposed. Several variants of the proposed method were designed and investigated to explore the impact of the addition of simplex operations on the problem-solving ability of the imperialist system. An analysis of the empirical results revealed that operations on the associated simplexes accelerated the exploitation process of the imperialists. Through the Wilcoxon rankings, it was witnessed that the enhanced simplex operations used in the ICA were able to produce fast convergence and consistent performance while solving real-world physical models. The variants of the MS-ICA significantly outperformed those of the standard ICA. As future work, it is intended that the proposed MS-ICA will be investigated for its application to continuous as well as discrete engineering design problems.

Acknowledgement: Authors are highly thankful to all the reviewers for their valuable comments.

Funding Statement: The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. Gorsan and A. Abraham, “A new approach for solving nonlinear equations systems,” in Proc. IEEE Transactions on Systems, Man and Cybernetics-Part A: Systems and Humans, vol. 38, no. 3, pp. 698–714, 2008. [Google Scholar]

 2.  J. M. Ortega and W. C. Rheinboldt, In Iterative Solution of Nonlinear Equations in Several Variables, Philadelphia, USA: SIAM, 1970. [Online]. Available at: https://epubs.siam.org/doi/pdf/10.1137/1.9780898719468.fm. [Google Scholar]

 3.  C. T. Kelley, In Solving Nonlinear Equations with Newton’s Method,” Philadelphia, USA: SIAM, 2003. [Google Scholar]

 4.  B. S. Goh and D. B. McDonald, “Newton methods to solve a system of nonlinear algebraic equations,” Journal of Optimization Theory and Applications, vol. 164, pp. 261–276, 2015. [Google Scholar]

 5.  M. J. D. Powell, “A Hybrid Method for Nonlinear Equations,” in Numerical Methods for Nonlinear Algebraic Equations, P. Rabinowitz ed., Gordon and Breach, London, pp. 87–114, 1970. [Google Scholar]

 6.  R. H. Byrd, M. Marazzi and J. Nocedal, “On the convergence of newton iterations to non-stationary points,” Mathematical Programming, vol. 99, pp. 127–148, 2004. [Google Scholar]

 7.  B. W. Bader, “Tensor–Krylov methods for solving large-scale systems of nonlinear equations,” SIAM Journal of Numerical Analysis, vol. 43, no. 3, pp. 1321–1347, 2005. [Google Scholar]

 8.  B. Salimbahrami and B. Lohmann, “Order reduction of large scale second-order systems using krylov subspace methods,” Linear Algebra and its Applications, vol. 415, no. 2–3, pp. 385–405, 2006. [Google Scholar]

 9.  A. R. Vahidi, S. Javadi and S. M. Khorasani, “Solving system of nonlinear equations by restarted adomain’s method,” Applied Mathematical Sciences, vol. 6, no. 11, pp. 509–516, 2012. [Google Scholar]

10. J. R. Sharma and P. Gupta, “On some efficient techniques for solving systems of nonlinear equations,” Advances in Numerical Analysis, vol. 2013, ID: 252798, 2013. [Google Scholar]

11. O. S. Solaiman and I. Hashim, “An iterative scheme of arbitrary odd order and its basins of attraction for nonlinear systems,” Computers, Materials & Continua, vol. 66, no. 2, pp. 1427–1444, 2021. [Google Scholar]

12. M. J. D. Powell, “How bad are the BFGS methods when the objective function is quadratic,” Mathematical Programming, vol. 34, pp. 34–47, 1986. [Google Scholar]

13. J. R. Sharma, R. K. Guha and P. Gupta, “Improved king’s methods with optimal order of convergence based on rational approximations,” Applied Mathematics Letters, vol. 26, no. 4, pp. 473–480, 2013. [Google Scholar]

14. O. S. Solaiman and I. Hashim, “Efficacy of optimal methods for nonlinear equations with chemical engineering applications,” Mathematical Problems in Engineering, vol. 2019, pp. 11, 2019. [Google Scholar]

15. L. Min, “A polak–Ribie`re–Polyak method for solving large scale nonlinear systems of equations and its global convergence,” Applied Mathematics and Computation, vol. 248, no. C, pp. 314–322, 2014. [Google Scholar]

16. S. Amat, M. A. Hernández-Verón and M. J. Rubio, “Improving the applicability of the secant method to solve nonlinear systems of equations,” Applied Mathematics and Computation, vol. 247, pp. 741–752, 2014. [Google Scholar]

17. J. R. Sharma, H. Arora and M. S. Petkovic, “An efficient derivative free family of fourth order methods for solving systems of nonlinear equations,” Applied Mathematics and Computation, vol. 235, pp. 383–393, 2014. [Google Scholar]

18. O. S. Solaiman and I. Hashim, “Optimal eighth-order solver for nonlinear equations with applications in chemical engineering,” Intelligent Automation & Soft Computing, vol. 27, no. 2, pp. 379–390, 2021. [Google Scholar]

19. Y. Z. Luo, G. J. Tang and L. N. Zhou, “Hybrid approach for solving systems of nonlinear equations using chaos optimization and quasi-newton method,” Applied Soft Computing, vol. 8, no. 2, pp. 1068–1073, 2008. [Google Scholar]

20. R. Sihwail, O. S. Solaiman, K. Omar, K. A. Z. Ariffin, M. Alswaitti et al., “A hybrid approach for solving systems of nonlinear equations using harris hawks optimization and newton’s method,” IEEE Access, vol. 9, pp. 95791–95807, 2021. [Google Scholar]

21. Y. Mo, H. Liu and Q. Wang, “Conjugate direction particle swarm optimization solving systems of nonlinear equations,” Computers & Mathematics with Applications, vol. 57, no. 11–12, pp. 1877–1882, 2009. [Google Scholar]

22. M. Jaberipour, E. Khorram and B. Karimi, “Particle swarm algorithm for solving systems of nonlinear equations,” Computers & Mathematics with Applications, vol. 62, no. 2, pp. 566–576, 2011. [Google Scholar]

23. A. Ouyang, Y. Zhou and Q. Luo, “Hybrid particle swarm optimization algorithm for solving systems of nonlinear equations,” in IEEE International Conference on Granular Computing, GRC09, pp. 460–465, 2009. [Google Scholar]

24. M. Abdollahi, A. Isazadeh and D. Abdollahi, “Imperialist competitive algorithm for solving systems of nonlinear equations,” Computers & Mathematics with Applications, vol. 65, no. 12, pp. 1894–1908, 2013. [Google Scholar]

25. H. A. Oliveira Jr. and A. Petraglia, “Solving nonlinear systems of functional equations with fuzzy adaptive simulated annealing,” Applied Soft Computing, vol.13, no. 11, pp. 4349–4357, 2013. [Google Scholar]

26. J. Wu, Z. Cui and J. Liu, “Using hybrid social emotional optimization algorithm with metropolis rule to solve nonlinear equations,” in 10th IEEE International Conference on Cognitive Informatics and Cognitive Computing, vol. 10, pp. 405–411, 2011. [Google Scholar]

27. E. Pourjafari and H. Mojallali, “Solving nonlinear equations systems with a new approach based on invasive weed optimization algorithm and clustering,” Swarm and Evolutionary Computation, vol. 4, pp. 33–43, 2012. [Google Scholar]

28. N. Henderson, W. F. Sacco and G. M. Platt, “Finding more than one root of nonlinear equations via a polarization technique: An application to double retrograde vaporization,” Chemical Engineering Research and Design, vol. 88, no. 5–6, pp. 551–561, 2010. [Google Scholar]

29. R. Rajabioun, “Cuckoo optimization algorithm,” Applied Soft Computing, vol. 11, pp. 5508–5518, 2011. [Google Scholar]

30. N. E. Mastorakis, “Solving non-linear equations via genetic algorithms,” in Proc. of the 6th WSEAS International Conference on Evolutionary Computing, Lisbon Portugal, pp. 24–28, 2005. [Google Scholar]

31. I. M. M. El-Emary and M. M. Abd-El-Kareem, “Toward using genetic algorithm for solving nonlinear equation systems,” World Applied Science Journal, vol. 5, no. 3, pp. 282–289, 2008. [Google Scholar]

32. M. A. Z. Raja, Z. Sabir, N. Mahmood, S. A. Eman and J. A. Khan, “Stochastic solvers based on variants of genetic algorithms for solving nonlinear equations,” Neural Computing and Applications, vol. 26, pp. 1–23, 2015. [Google Scholar]

33. R. Jia and D. He, “Hybrid artificial bee colony algorithm for solving nonlinear system of equations,” in 8th Int. Conf. on Computational Intelligence and Security, pp. 56–60, 2012. [Google Scholar]

34. A. Majd, M. Abdollahi, G. Sahebi, D. Abdollahi, M. Daneshtalab et al., “Multi-population parallel imperialist competitive algorithm for solving systems of nonlinear equations,” in The Int. Conf. on High Performance Computing & Simulation (HPCS 20162016. [Google Scholar]

35. M. Abdollahi, A. Bouyer and D. Abdollahi, “Improved cuckoo optimization algorithm for solving systems of nonlinear equations,” The Journal of Supercomputing, vol. 72, pp. 1246–1269, 2016. [Google Scholar]

36. W. Zhijian and L. Kang, “A fast and elitist parallel evolutionary algorithm for solving systems of non-linear equations,” in The Congress on Evolutionary Computing, vol. 2, pp. 1026–1028, 2003. [Google Scholar]

37. G. Huan-Tong, S. Yi-jie, W. Qing-Xi and W. Ting-Ting, “Research of ranking method in evolution strategy for solving nonlinear system of equations,” in 1st Int. Conf. on Information Science and Engineering, pp. 348–351, 2009. [Google Scholar]

38. E. Atashpaz-Gargari and C. Lucas, “Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition,” in 2007 IEEE Congress on Evolutionary Computation, Singapore, pp. 4661–4667, 2007. [Google Scholar]

39. R. Reynolds and B. Peng, “Cultural algorithms: Computational modelling of how cultures learn to solve problems: An engineering example,” Cybernetics and Systems, vol. 36, no. 8, pp. 753–771, 2005. [Google Scholar]

40. S. Hosseini and A. Al-Khaled, “A survey on the imperialist competitive algorithm metaheuristic: Implementation in engineering domain and directions for future research,” Applied Soft Computation, vol. 24, pp. 1078–1094, 2014. [Google Scholar]

41. S. Nazari-Shirkouhi, H. Eivazy, R. Ghodsi, K. Rezaie and E. Atashpaz-Gargari, “Solving the integrated product mix-outsourcing problem by a novel meta-heuristic algorithm: Imperialist competitive algorithm,” Expert Systems with Applications, vol. 37, no. 12, pp. 7615–7626, 2010. [Google Scholar]

42. M. Z. Ali, A. Salhieh, R. T. Abu-Snanieh and R. G. Reynolds, “Boosting cultural algorithms with a heterogeneous layered social fabric influence function,” Computational and Mathematical Organization Theory, vol. 18, pp. 193–210, 2012. [Google Scholar]

43. R. G. Reynolds and M. Z. Ali, “The social fabric approach for a better knowledge integration in cultural algorithms,” in The IEEE World Congress on Computational Intelligence, 2008. [Google Scholar]

44. J. Kennedy, “Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance,” in Proc. of the 1999 Congress on Evolutionary Computation—CEC99, vol. 3, pp. 1031–1938, 1999. [Google Scholar]

45. Q. Ni and J. Deng, “A new logistic dynamic particle swarm optimization algorithm based on random topology,” Scientific World Journal, vol. 2013, ID: 409167, 2013. [Google Scholar]

46. J. Nelder and R. Mead, “A simplex method for function minimization,” The Computer Journal, vol. 7, no. 4, pp. 308–313, 1965. [Google Scholar]

47. C. J. Price, I. D. Coope and D. Byatt, “A convergent variant of the nelder-mead algorithm,” Journal of Optimization Theory and Applications, vol. 113, no. 1, pp. 5–19, 2002. [Google Scholar]

48. J. Ali, M. Saeed, N. A. Chaudhry, M. F. Tabassum and M. Luqman, “Low cost efficient remedial strategy for stagnated nelder-mead simplex method,” Pakistan Journal of Science, vol. 69, no. 1, pp. 119–126, 2017. [Google Scholar]

49. A. P. Morgan, In Solving Polynomial System Using Continuation for Scientific and Engineering Problems, Englewood Cliffs, NJ: Prentice-Hall, 1987. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.