Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020218
Article

MSM: A Method of Multi-Neighborhood Sampling Matching for Entity Alignment

Donglei Lu1, Yundong Sun2, Qinrui Dai2, Xiaofang Li3,*, Dongjie Zhu4, Haiwen Du2, Yansong Wang4, Rongning Qu3, Ning Cao1 and Gregory M. P. O’Hare5

1School of Artificial Intelligence, Wuxi Vocational College of Science and Technology, Wuxi, 214028, China
2School of Astronautics, Harbin Institute of Technology, Harbin, 150001, China
3Department of Mathematics, Harbin Institute of Technology, Weihai, 264209, China
4School of Computer Science and Technology, Harbin Institute of Technology, Weihai, 264209, China
5School of Computer Science, University College Dublin, Dublin, Dublin4, Ireland
*Corresponding Author: Xiaofang Li. Email: lixiaofang@hit.edu.cn
Received: 14 May 2021; Accepted: 15 June 2021

Abstract: The heterogeneity of knowledge graphs brings great challenges to entity alignment. In particular, the attributes of network entities in the real world are complex and changeable. The key to solving this problem is to expand the neighborhoods in different ranges and extract the neighborhood information efficiently. Based on this idea, we propose Multi-neighborhood Sampling Matching Network (MSM), a new KG alignment network, aiming at the structural heterogeneity challenge. MSM constructs a multi-neighborhood network representation learning method to learn the KG structure embedding. It then adopts a unique sampling and cosine cross-matching method to solve different sizes of neighborhoods and distinct topological structures in two entities. To choose the right neighbors, we apply a down-sampling process to select the most informative entities towards the central target entity from its one-hop and two-hop neighbors. To verify the effectiveness of matching this neighborhood with any neighborhood in the corresponding node, we give a cosine cross-graph neighborhood matching method and conduct detailed research and analysis on three entity matching datasets, which proves the effectiveness of MSM.

Keywords: Entity alignment; representation learning; heterogeneous network

1  Introduction

Entity alignment is designed to determine whether two or more entities with different knowledge graphs point to the same object in the real world. It not only contributes to the construction and expansion of knowledge base, but also plays an important role in solving cross-network crimes. For example, entity alignment is now widely used in graph networks and social networks [1,2]. The most advanced entity alignment solutions mainly rely on the structure information of knowledge map to judge the equivalence of entities, but in the real-world knowledge map, most entities only have low node degree and little structure information. In addition, the lack of annotated data greatly limits the effectiveness of the entity alignment model. Unfortunately, entity alignment is not trivial, because real-life knowledge graphs are often incomplete and different knowledge graphs typically have heterogeneous schemas and the equivalent entities in different graphs often have different neighborhood structures.

The aim of network entity alignment technique is to find the same entity in different networks. At present, increasing attention has been paid to the embedding-based methods [3–7]. Its core idea is to transform the nodes in the network into low-dimensional vectors by certain methods, whose vector dimensions are much lower than the number of nodes and contain the attributes of the nodes themselves and the semantic relationship information between the nodes. Unfortunately, these methods can only deal with homogeneous networks or multilingual knowledge graphs. The types of nodes and the relationships between nodes are same [8,9]. However, most of the network data in reality are heterogeneous networks. There are many kinds of node types or multiple node relationships. For example, in Fig. 1, United States of America is among the one-hop (direct) neighbors of Barack Obama in Wikidata. However, in Dbpedia, it is a two-hop neighbors.

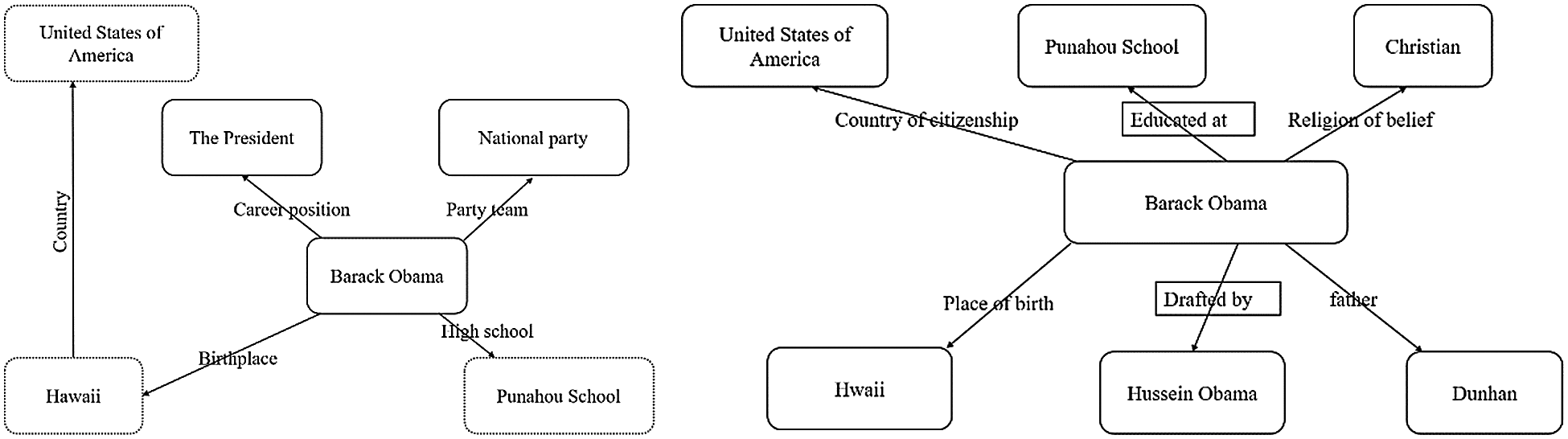
Figure 1: Non-isomorphic relational neighborhood of Barack Obama in DBpedia (left) and Wikidata (right), respectively

At the same time, the information contributed by the same order neighbor of the central entity is nonequivalent [8,9]. To elaborate on this point, let’s move on to Fig. 1. There are many city entities for USA which also have the entity United States of America. Consequently, the contribution of United States of America to the central entity is significantly less than that of Christian. Because existing embedding-based method are unable to choose the right neighbors, we need a better approach.

The challenge of resolving this issue lies in the difficulty of fully mitigating the non-isomorphism in the neighborhood structures of counterpart entities from different KGs. We present the Multi-neighborhood Sampling Matching Network (MSM), a novel Network embedded and Sampling-based framework. The goal of MSM is to obtain the neighborhood with the most valuable information and accurately estimate the similarity of neighborhood among entities in different knowledge graphs. To learn the embedding of knowledge graph structure, MSM utilizes multi-neighborhood network representation learning method to aggregate higher degree neighboring structural information for entities. We evaluate MSM by applying it to benchmark datasets DBP15K [10–16].

2  Multi-Neighborhood Sampling Matching

2.1 KG Structure Embedding

In addition to the one-hop neighborhood information, the non-directly related high-order neighborhood information is also very important for the representation of the central entity [16]. Therefore, MSM first constructed a multi-neighborhood network representation learning method (MNE), using this representation method learns the structure embedding of KG to gather the high-order neighborhood structure information of the entity. The overall architecture and processing pipeline of MNE is shown in Fig. 2. MSM uses pre-trained word vectors to initialize MNE.

We use G=(E,R,T) to represent a knowledge graph, in which E,R,T represents entities, relationships, and sets of triples. Without loss of generality, we consider the entity alignment task between two knowledge graphs G1 and G2 based on a set of pre-aligned equivalent entities. Our goal is to find an equivalent entity pair between G1 and G2 . We put G1 and G2 as a large input graph into MSM, each MNE layer consists of two layers of GCN aggregated entities of one-hop neighborhood information, a layer of attention-network (ATT-Net) aggregated entities two-hop neighborhood information and each GNN updates the node representation as:

hi,1(l)=ReLU(∑j∈N1(i)∪{i}1εiW1lhj(l−1)) (1)

where hi,1(l) is the output node features of l -th GCN layer. εi is the normalization constant. Ni is the set of neighbor indices of entity i . W1(l)∈Rd(l)×d(l−1) is the attention weight of l layer neighborhood of node i obtained by GNN training. To aggregate the two-hop neighborhood information of entity i , we have adopted ATT-Net. The hidden representation of entity i , denoted as hi,2l , is computed as follows:

hi,2(l)=ReLU(∑j∈N2(i)∪{i}αij(l)W2lhj,2(l−1)) (2)

where hi,2(l) is the output node features of l -th ATT-Net layer. αij(l) is a learnable attention weight for entities i and its neighbor j . W2(l)∈Rd(l)×d(l−1) is the wight matrix. Finally, for entity i , we use the gating mechanism to combine its one-hop and two-hop neighborhood information. The node representations are given as below:

hi(l)=g(hi,1(l))(g(hi,2(l))⋅hi,1(l)+(1−g(hi,2(l)))⋅hi,2(l)+(1−g(hi,1(l)))⋅hi,1(l) (3)

where g(hi,1(l))=σ(M1hi,1(l)+b1) , g(hi,2(l))=σ(M2hi,2(l)+b2) and M1 , M2 and b1 , b2 are the weight matrix and bias vector, respectively. In order to control the accumulated noise, we also introduce the highway network [15] into the MNE layer, which can effectively control the propagation of noise in the MNE layer.

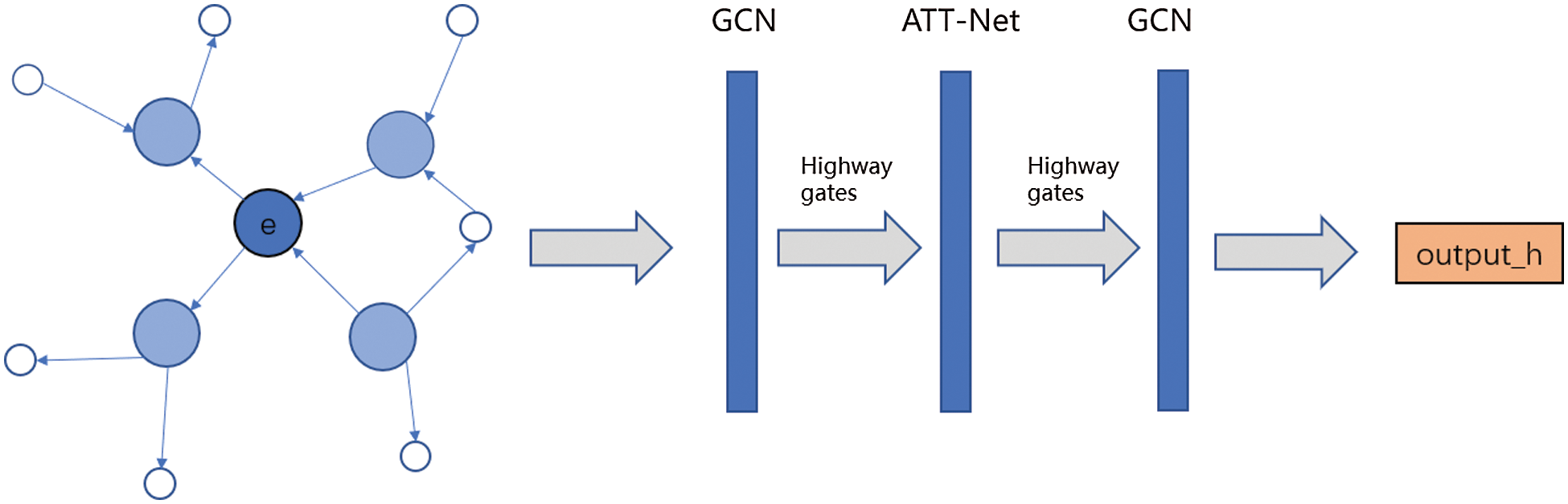
Figure 2: Overall architecture and processing pipeline of MNE

2.2 Neighborhood Sampling

The first-order and second-order neighborhoods of an entity are the key to determining whether the entity should be aligned with other entities. However, as we discussed before, not all first-order and second-order neighborhoods make a positive contribution to entity alignment. In order to select the correct neighbor, we use a down-sampling process to select the entity that provides the most information to the central target entity from its first-order and second-order neighborhoods. Previously, many random sampling methods were used, but the method have some randomness. The neighbor nodes sampled may not necessarily contribute the most. Therefore, we give a sampling method based on probability. Formally, given an entity ei , the calculation formula for sampling its first-hop domain ei−j and second-hop domain ei−j′ are [16]:

p(hi−j|hi)=softmax(hiW1hi−jT)=exp⁡(hiW1hi−jT)∑k∈Ni1exp⁡(hiW1hi−kT)p(hi−j′|hi)=softmax(hiW2hi−j′T)=exp⁡(hiW2hi−jT)∑k∈Ni2exp⁡(hiW2hi−kT) (4)

where Ni1 and Ni2 are the first-hop and second-hop neighborhood index set of the central entity ei , respectively. hi , hi−j and hi−j′ are the entity representation vectors of the entities ei , ei−j and ei−j′ respectively, and W1 , W2 are shared weight matrix.

By selectively sampling first-hop and second-hop neighborhoods, MSM gets the most valuable neighborhood information of each entity. In the end, MSM achieves the alignment of G1 and G2 through neighborhood matching and neighborhood aggregation.

2.3 Neighborhood Matching

In order to judge whether the two entities should be aligned, we need a similarity calculation to its neighbor nodes. MSM builds hence a neighborhood subgraph generated by the sampling process for each entity. Then MSM will only operate neighbors within the subgraph, achieving the neighborhood matching.

Inspired by the graph matching method [5], our specific matching method is as follows.

We need to compare the subgraphs of each candidate entity in its sampling neighborhood subgraph E2 to select the best aligned entity of the entity ei in E1 . But if each entity neighborhood in E2 is compared and calculated with ei , this requires too much calculation. Therefore, MSM adopts an approximate alternative method. Inspired by the candidate selection method [16], MSM samples an entity alignment set Ci={ci1,ci2,...,cit|cit∈E2} of ei , and then calculates the subgraph similarity between ei and these candidate entities. Therefore, for the entity ej in E2 , the calculation formula for it to be a candidate entity for ei is:

p(hj|hi)=exp⁡(hi⋅hj)∑k∈E2exp⁡(hi⋅hk) (5)

where hi and hj are the node vector representations of ei and ej output by MNE.

We propose the following graph matching network, which changes the node update module in each propagation layer. It not only considers the aggregated messages on the edge of each graph as before, but also considers a cross-graph matching vector, which measures the degree of matching between a node in one graph and one or more nodes in another graph. Define (ei,ej) as the entity pair to be measured, where ei∈E1 , ej∈E2 . The cross-matching vector of ei is calculated as follows:

aj→i=cos⁡ine(hi,hj)

hi−1=∑j=1Niaj→i⋅hj∑j=1Niaj−>i

mi=hi−hi−1 (6)

Here aj→i is the cosine similarities of entity ei in E1 with the entity ej in E2 , mi is the matching vector of node ei , Ni is the sampled neighbor set of ei , hi and hj are the node vector representations of ei and ej output by MNE, respectively. hi−1 is an attentive vector for the entire graph E2 . Then, we combine hi and mi to get the sampled neighbor representation of ei :

h⌢i=hi⊕β*mi (7)

where ⊕ indicates vector concatenation.

2.4 Entity Alignment

We give the loss function of MNE:

L=∑(i,j)∈X∑(i′,j′)∈X′max{0,d(i,j)−d(i′−j′)+γ} (8)

where d(i,j)=‖hi−hj‖L1 , ‖⋅‖L2 means L2−norm ; γ>0 is a margin hyper-parameter; X is the alignment seeds and X′ is the set of negative aligned entity pairs generated by nearest neighbor sampling [15].

The loss function of MSM after the pre-training phase, defined as:

L=∑(i,j)∈T∑(i′,j′)∈T′max{0, f(i,j)−f(i′−j′)+γ} (9)

where f(i,j)=‖h^i−h⌢j‖L1; T is the positive alignments set and T′ the negative alignments set.

3  Experiment

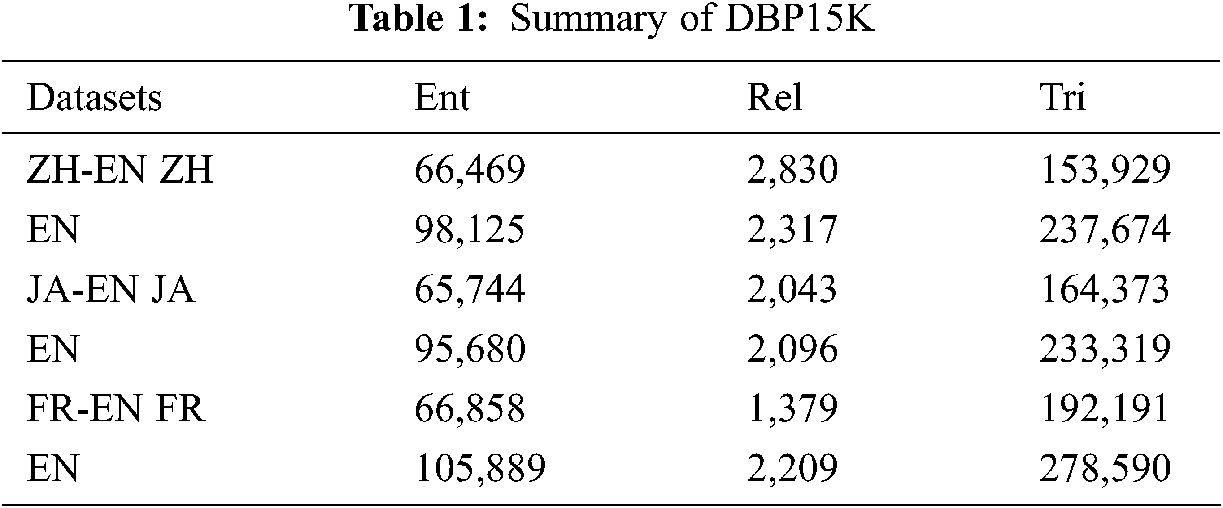
In this section, we evaluated the multi-neighborhood sampling matching model (MSM) on three data subsets of the open-source data set DBP15k by comparing with other methods. Tab. 1 gives detailed descriptions of the DBP15k datasets. We use the same split with previous work, 30% for training and 70% for testing.

The configuration we use in the DBP15K datasets is: β=0.1 , γ=1.0 , and we sample 5 neighbors for each entity in the neighborhood sampling stage.

The comparison method we use is as follows:

(1) JAPE [17]: A model for preserving attribute embedding for cross-language entity alignment. It embeds the structure of the two networks into a unified vector space, and further optimizes it by using the attribute correlation in the network. This model is a supervised learning model. In the experiment, 30% of the nodes in the data set are used as training data and 70% of the nodes are used as test data. The model parameters adopt the original default best parameter combination. In the experiment, 10 negative samples are drawn for each pre-aligned entity pair.

(2) AliNet [18]: In order to solve a new KG alignment network in which the replica entity has a non-isomorphic neighbor structure, it aims to alleviate the non-isomorphism problem of the neighbor structure in an end-to-end manner. Due to the heterogeneity of the schema, the direct neighbors of the replica entity are usually not similar. AliNet introduces distant neighbors to extend the overlapping part of the neighbor structure. The attention mechanism is also used to emphasize helpful distant neighbors and reduce noise. Then it uses the gate mechanism to aggregate the information of direct neighbors and distant neighbors.

(3) BoostEA [16]: The entity alignment based on the embedded usually depends on the alignment of the existing entities as training data. But the first alignment can be usually accounted for a small part. BoostEA proposes a bootstrapping method to solve the above challenges.

(4) GMNN [5]: Since the previous cross-language knowledge graph alignment research relies on the idea of entity embedding, it cannot be applied to the two knowledge graphs. GMNN combines the two kinds of map matching problems with entity context information into a map matching problem and proposes a matching model of a graph neural network, which includes map matching and pixel matching information.

(5) MSM: Firstly, the low-dimensional vector representation of nodes in the network is obtained by using the multi-neighborhood network representation learning method (MNE) proposed in Section 2 of this paper. Then, entity alignment is carried out by using the information entropy sampling and cross-graph neighborhood matching entity alignment method proposed in this paper.

3.1 Evaluation Index

To compares the various methods more objectively and comprehensively, in the experiment, the commonly used model evaluation indicators Hit@k in the field of entity alignment are used, and the calculation formula is as follows:

Hits@k=nrkN (11)

where nrk represents the number of times the target node appears in the k closest candidate target nodes, and N is the number of tests. We select Hits@1 and Hits@10 indicators according to the commonly used experimental methods.

3.2 Analysis of Results

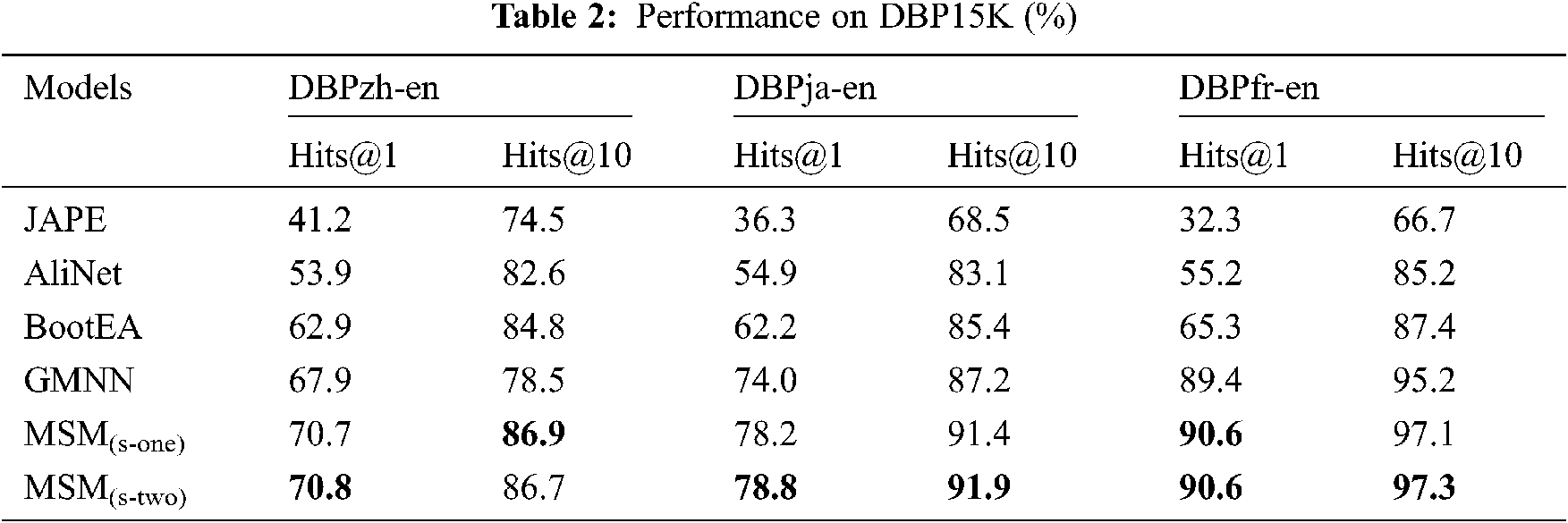
(1) The experimental results of each method on different data subsets of the data set DBP15k are shown in Tab. 2. From Tab. 2, we can see that under the evaluation index of Hits@1 , MSM has an improvement of 3% to 5% relative to GMNN, and also has an improvement of about 3% under the evaluation index of Hits@10 . The result meets 8% improvement on zh-en data subset. Compared with JAPE, AliNet and BoostEA, MSM has a greater improvement.

To evaluate the sampling method on the accuracy of the model, we implement a model variant (referred as MSM (s-two)) that samples two-hop neighbors. From Tab. 2, we find that the sampling two-hop neighbors leads MSM a gain of 0.4%~0.8% by Hits@1 and 0.1%~0.3% by Hits@10 relative to the sampling one-hop neighbors (referred as MSM (s-one)) on DBP15K. The result confirms the importance of the two-hop neighborhoods in KG structure embedding and neighborhood sampling.

(2) To explore the impact of using the pre-trained word embeddings to initialize the MSM. We remove the initialization part of the MNE, choosing the different sampling size for comparative analysis. From Fig. 3, for DBP15KZH-EN, we observe that the initialization of MNE is very important of MSM. More exactly, removing the initialization from MSM, leads to around a 43% drop in Hits@1 and a 40% drop in Hits@10 on average. On the other hand, MSM is sensitive to the size of sampling and the model works better when the size of sampling is 5.

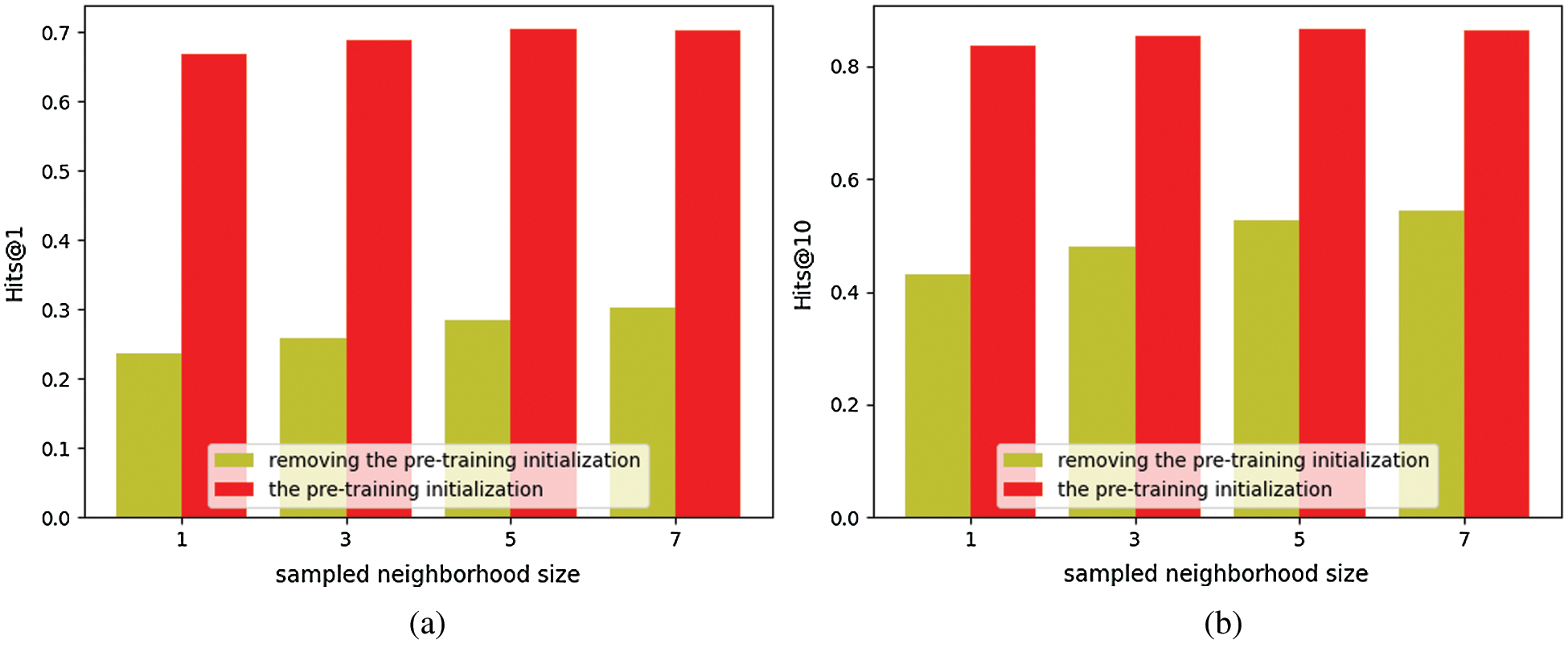
Figure 3: Comparison the pre-training with removing pre-training. a) The evaluation index of Hits@1 b) The evaluation index of Hits@10

(3) To verify the superiority of our cross-graph neighborhood matching method, we compare it with the common direct aggregate matching method. As shown in Fig. 4, when we choose different candidate set sizes, the cosine cross-neighborhood matching method performs better. It increases 0.5%~1% relative to the overall the cross-neighborhood matching method under the evaluation index of Hits@10 and about 0.2% under the evaluation index of Hits@1 . At the same time, the different matching candidate size also has some influence on MSM performance. When the size of candidate selection is 18, the performance of the MSM is better on DBP15KZH-EN.

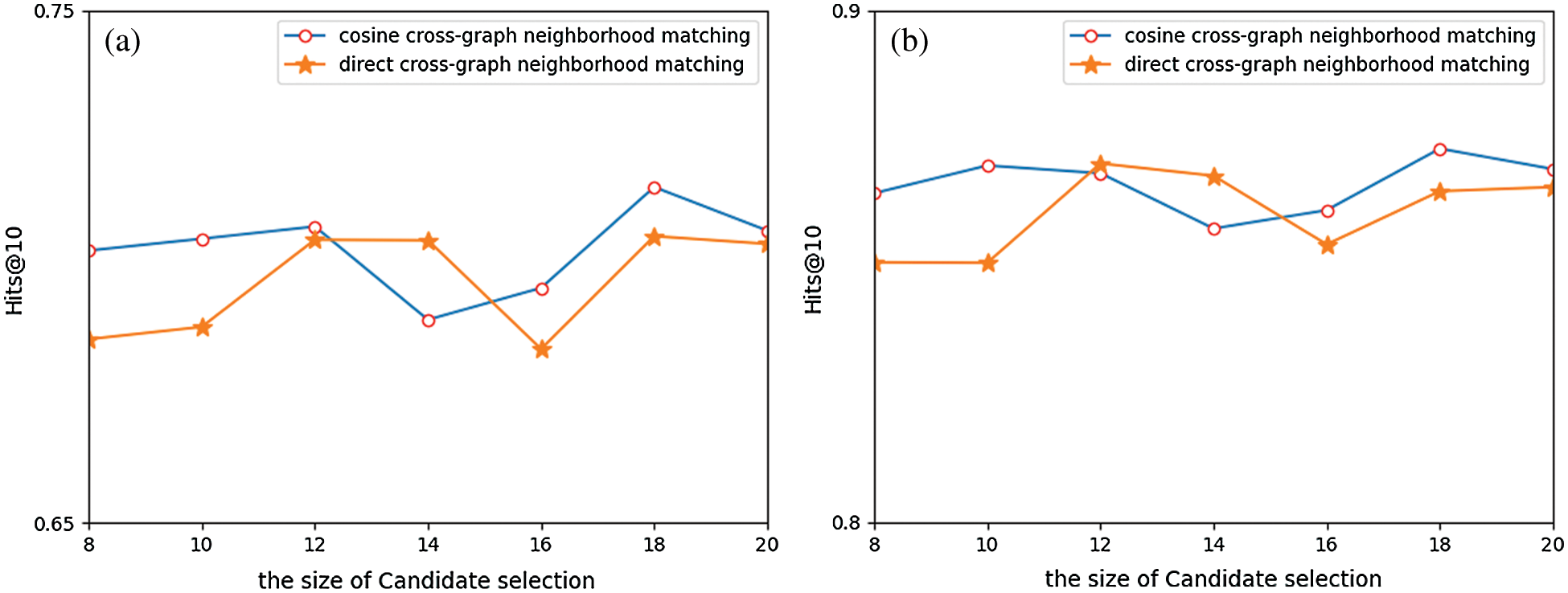
Figure 4: Comparison different matching methods. a) The evaluation index of Hits@1 b) The evaluation index of Hits@10

(4) To show the effect of entity alignment more intuitively, this part visually shows the node distribution consistency before and after entity alignment. We reduce the 300-dimensional vector to two-dimensional space through t-sne. Fig. 5 show the visualization of 4000 pairs of nodes randomly selected from two KG on DBP15KJA-EN.

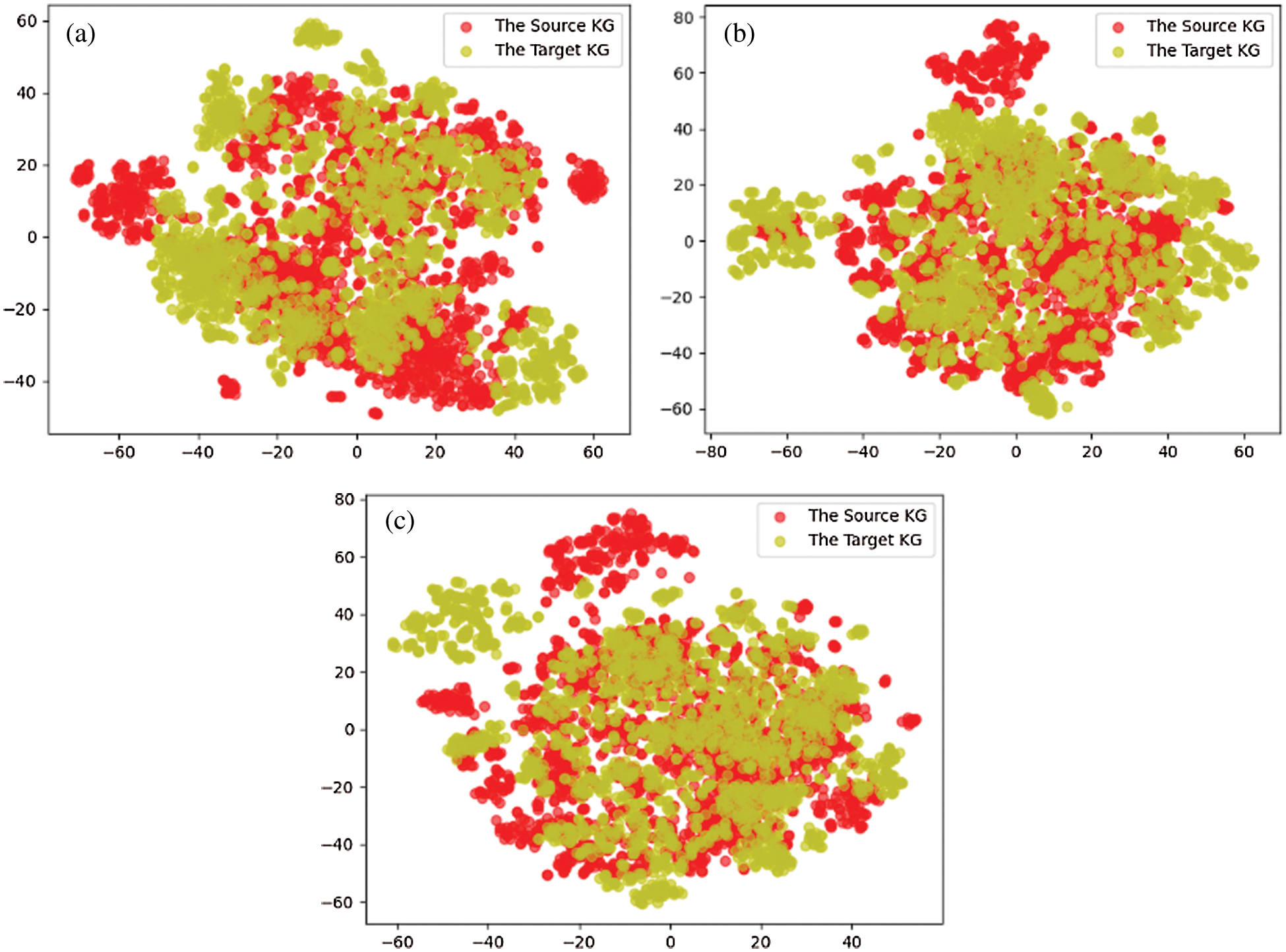
Figure 5: Visualization of spatial distribution of entity alignment nodes in DBP15KJA-EN dataset. a) Initial state b) After 200 rounds of training c) After 400 rounds of training

These result show that our pre-trained vectors, sampling and matching modules are particularly important, when the neighborhood sizes of equivalent entities greatly differ and especially there may be few common neighbors in their neighborhoods.

4  Conclusion

This paper proposes a multi-neighborhood sampling matching entity alignment method, which aims to solve the problem of different neighborhood sizes and topological structures in heterogeneous networks. We build a multi-neighborhood network representation learning method to achieve effective aggregation of entity neighborhood information and use a new sampling-based method to select the most informative neighbor for each entity, using the method of cosine cross-graph neighborhood matching to achieve rapid alignment of different network entities. We conducted extensive experiments on real-world data sets and compared MSM with four embedded-based entity alignment methods. Experimental results show that MSM obtains the best and more robust performance, and consistently outperforms competing methods in data sets and evaluation metrics. For future work, we plan to incorporate the multi-neighbor information of entities in other modes into our model structure. At the same time, since some alterative sampling techniques based on ranks information may lead more efficient procedure [19,20], this will be our follow-up work.

Acknowledgement: The authors are grateful to the anonymous referees for having carefully read earlier versions of the manuscript. Their valuable suggestions substantially improved the quality of exposition, shape, and content of the article.

Funding Statement: This work is supported by State Grid Shandong Electric Power Company Science and Technology Project Funding under Grant Nos. 520613200001, 520613180002, 62061318C002, Weihai Scientific Research and Innovation Fund (2020) and the Grant 19YG02, Sanming University.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. Zhu, Y. Wang and C. You, “MMLUP: Multi-source & multi-task learning for user profiles in social network,” Computers, Materials & Continua, vol. 61, no. 3, pp. 1105–1115, 2019. [Google Scholar]

 2.  C. You, D. Zhu and Y. Sun, “SNES: Social-network-oriented public opinion monitoring platform based on ElasticSearch,” Computers, Materials & Continua, vol. 61, no. 3, pp. 1271–1283, 2019. [Google Scholar]

 3.  N. Jia, X. Tian and Y. Y. Zhang, “Semi-supervised node classification with discriminable squeeze excitation graph convolutional networks,” IEEE Access, vol. 8, pp. 148226–148236, 2020. [Google Scholar]

 4.  D. Zhu, Y. Sun, H. Du, N. Cao, T. Baker et al., “HUNA: A method of hierarchical unsupervised network alignment for IoT,” IEEE Internet of Things Journal, vol. 8, no. 5, pp. 3201–3210, 2021. [Google Scholar]

 5.  K. Xu, L. Wang and M. Yu, “Cross-lingual knowledge graph alignment via graph matching neural network,” in 57th Annual Meeting of the Association-for-Computational-Linguistics, Florence, ITALY, pp. 3156–3161, 2019. [Google Scholar]

 6.  H. Zhu, R. Xie and Z. Liu, “Iterative entity alignment via joint knowledge embeddings,” in 26th Int. Joint Conf. on Artificial Intelligence, Melbourne, Australia, vol. 17, pp. 4258–4264, 2017. [Google Scholar]

 7.  D. Zhu, Y. Sun and X. Li, “MINE: A method of multi-Interaction heterogeneous information network embedding,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1343–1356, 2020. [Google Scholar]

 8.  Y. Cao, Z. Liu and C. Li, “Multi-channel graph neural network for entity alignment,” in 57th Annual Meeting of the Association-for-Computational-Linguistics, Florence, Italy, pp. 1452–1461, 2019. [Google Scholar]

 9.  Q. Zhu, X. Zhou and J. Wu, “Neighborhood-aware attentional representation for multilingual knowledge graphs,” in 28th Int. Joint Conf. on Artificial Intelligence, Macau, China, pp. 1943–1949, 2019. [Google Scholar]

10. S. Guan, X. Jin and Y. Wang, “Self-learning and embedding based entity alignment,” Knowledge and Information Systems, vol. 59, no. 2, pp. 316–386, 2019. [Google Scholar]

11. Z. Yan, R. Peng and Y. Wang, “CTEA: Context and topic enhanced entity alignment for knowledge graphs,” Neurocomputing, vol. 410, pp. 419–431, 2020. [Google Scholar]

12. C. Li, Y. Cao and L. Hou, “Semi-supervised entity alignment via joint knowledge embedding model and cross-graph model,” in 2019 Conf. on Empirical Methods in Natural Language Processing and 9th Int. Joint Conf. on Natural Language Processing, Hong Kong, China, vol. 1, pp. 2723–2732, 2019. [Google Scholar]

13. Y. Yan, L. Liu and Y. Ban, “Dynamic Knowledge Graph Alignment,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 35, no. 5, pp. 4564–4572, 2021. [Google Scholar]

14. S. Pei, L. Yu and X. Zhang, “Improving cross-lingual entity alignment via optimal transport,” in Int. Joint Conf. on Artificial Intelligence Organization, Macao, China, vol. 1, pp. 3231–3237, 2019. [Google Scholar]

15. Y. Wu, X. Liu and Y. Feng, “Neighborhood matching network for entity alignment,” in 58th Annual Meeting of the Association for Computational Linguistics, Washington, USA, vol. 1, pp. 6477–6487, 2020. [Google Scholar]

16. Z. Sun, W. Hu, Q. Zhang and Y. Qu, “Bootstrapping entity alignment with knowledge graph embedding,” in 27th Int. Joint Conf. on Artificial Intelligence, Macau, China, vol. 18, pp. 4396–4402, 2018. [Google Scholar]

17. Z. Sun, W. Hu and C. Li, “Cross-lingual entity alignment via joint attribute-preserving embedding,” in Int. Semantic Web Conf., Cham, Springer, 2017. [Google Scholar]

18. Z. Sun, C. Wang and W. Hu, “Knowledge graph alignment network with gated multi-hop neighborhood aggregation,” in 34th AAAI Conf. on Artificial Intelligence, New York, USA, vol. 34, pp. 222–229, 2020. [Google Scholar]

19. M. Mahdizadeh and E. Zamanzade, “Kernel-based estimation of P (X > Y) in ranked set sampling,” SORT-Statistics and Operations Research Transactions, vol. 1, no. 2, pp. 243–266, 2016. [Google Scholar]

20. M. Mahdizadeh and E. Zamanzade, “Smooth estimation of a reliability function in ranked set sampling,” Statistics, vol. 52, no. 4, pp. 750–768, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.