DOI:10.32604/iasc.2022.022743

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.022743 |  |
| Article |
Construction of Key-dependent S-box for Secure Cloud Storage
Department of Information Technology, Sri Venkateswara College of Engineering, Sriperumbudur, 602117, India
*Corresponding Author: A. Indumathi Email: aindumathi@svce.ac.in
Received: 17 August 2021; Accepted: 28 September 2021
Abstract: As cloud storage systems have developed and been applied in complex environments, their data security has become more prevalent in recent years. The issue has been approached through many models. Data is encrypted and stored in these models. One of the most widely used encryption methods is the Advanced Encryption Standard (AES). In AES, the Substitution box(S-box) is playing a significant part in imparting the job of confusion. The security of the entire cryptosystem depends on its nonlinearity. In this work, a robust and secure S-box is constructed using a novel method, i.e., fingerprint features-based permutation function. Two stages are considered to construct a strong S-box. Firstly, random numbers are generated from the fingerprint features such as bifurcation and ridge endings of the user transmitting data. Subsequently, the permutation function is adapted on the random numbers (developed in the first stage) to augment the strength of the S-box. National Institute of Standards and Technology (NIST) STS 800-22 test suite is considered to evaluate the randomness of the enhanced fingerprint-based S-box. Also, the robustness of the constructed S-box is tested using cryptographical properties, namely Strict Avalanche Criterion (SAC), Nonlinearity (NL), Differential Approximation (DA) probability and output Bits Independence Criterion (BIC). Later, the cryptographical properties of the proposed S-box are compared with several existing S-boxes. After analyzing the characteristics of the proposed scheme, it is revealed that the newly constructed S-box is powerful, robust, and safe against linear and differential assaults.
Keywords: Information Security; Cryptography; fingerprint; minutiae points; permutation function; substitution box (S-box)
A new trend in the computer field is cloud computing, which is used as a method of storing data. The physical storage device makes it impossible to store huge amounts of confidential or sensitive information. Therefore, cloud computing comes into play for storing the data in accordance with their needs. As long as the data is stored in the cloud, it is easily accessible to all, and maintaining its confidentiality is not possible. To protect the data from unauthorized user, encrypted data can be stored into the cloud. Encryption is the process which converts the plain text into an unreadable form. It has two significant types of encryption techniques which are symmetric cryptosystem, asymmetric cryptosystem. Symmetric cryptosystem uses a single key for both encryption and decryption. Stream cipher and Block cipher are the two categories of the Symmetric cryptosystem. Block cipher encrypts a block of plaintext at a time and uses confusion, diffusion process. It is hard for reverse encryption. On the other hand, stream cipher encrypts a plaintext byte-by-byte or bit-by-bit. It is dependent only on confusion, and also reversing the encrypted text is easy. Merely, a block cipher is more efficient than a stream cipher encryption algorithm. Substitution-Permutation and Feistel cipher are the two categories of block cipher encryption.
Many new cryptographic techniques are evolving recently, notably quantum computing and post-quantum cryptography. Post-quantum cryptography is a method to establish a new cryptosystem that offers better security against classical and quantum computers. NIST has recommended the AES 256 block cipher encryption algorithm as quantum-resistant, and it is one of the widely used block cipher encryption algorithms. AES converts the plaintext into ciphertext with a different number of round of operations. The number of rounds depends on the key length. Each round consists of set of operations that use a different key which includes Substitution and permutation operations. These are the essential function in AES which provides confusion and diffusion by using S-box and P-box respectively. Diffusion is the property that conceals the bond between the plaintext and ciphertext, accomplished through transposition function. P-Box (Permutation box) is responsible for diffusion operation. Confusion is the sole nonlinear component of S-box. It hides the relationship between the ciphertext and the key. S-box provides confusion by replacing one set of bits with another set of bits. Therefore, it is cumbersome for the attacker to find the key from the ciphertext. The complexity of the confusion process depends upon the robustness of an S-box. As the AES uses a static S-box in each round, it allows the attacker to cryptanalyze the ciphertext that is produced by the block cipher. In order to overcome this limitations, various methods have been suggested by the researchers for constructing S-box. Namely, Chaotic systems, affine transformation, Algebraic operations, Heuristic methods and etc. In this paper, A novel method is presented to get the robust S-box using fingerprint features. The robustness and the strength of the S-box is examined by the standard cryptographical properties needs to be examined to define the strength and robustness of an S-box. An intense literature study is carried out and described in the below section considering these needs.
Several authors have demonstrated numerous works to construct a robust S-box for effective operation. An intense literature study is carried out and portrayed below.
Jamal S.S [1] proposed the Mobius transformation method and chaotic Tent Sine system and proved that the generated S-box was strong. Wang et al. constructed dynamic S-boxes by using logistic map and Kent map [2]. Authors in [3] made use of Liu J S-boxes [4] as initial seed to construct 40320 S-boxes by utilizing S8 permutation operation on the elements of Liu J S-boxes. In [5], authors suggested Quantum Walk (QW) based S-box and used for designing a different steganography technique. Cryptographic QW S-box guaranteed high security, good visual quality, and high embedding capacity. But it requires seed values to generate the S-box.
Malik et al. [6] proposed chaos-based affine transformation generation and rotational matrices to generate dynamic AES S-boxes. It also entailed closer to optimal cryptographic properties, and therefore the proposed S-boxes are equal to AES S-box. Tian et al. [7] constructed an S-box by combining the Artificial Bee Colony Algorithm and six-dimensional hyperchaotic map (CSABC). It yielded a cryptographically strong S-box. In Reference [8], S-box was constructed based on the linear group action of a finite local ring. Authors in [9] utilized a Spatiotemporal nonlinear chaotic system and permutation function to construct the S-box. It had an improved output bit independence criterion and capacity to resist linear password attacks. Siddiqui et al. [10] constructed 8*8 robust S-box by adapting adjacency matrixes on the Galois field. Authors in [11] used the composition of transposition for constructing bijective S-boxes. They claimed that the proposed method has better cryptographic properties. Hussain et al. Constructed nonlinear S-boxes using Symmetric group, Mobius transformation, and Chaotic logistic map [12]. It had the potential to generate a high resistant S-box. In [13], authors used Cascaded quantum-inspired quantum walks and chaos inducement for generating S-box. Özkaynak et al. [14] constructed an S-box by employing FO chaotic Chen system and predictor-corrector scheme. But it failed to satisfy the bijectivity property. Khan et al. [15] proposed Gingerbreadman chaotic map and S8 permutation to build an efficient S-box. It was efficient for secure communications. Khan et al. [16] constructed an S-box from the binary chaotic sequences. They considered algebraic degree, Balancedness, Algebraic immunity, Correlation immunity to find the strength of the S-box. They didn’t evaluate some of the S-box properties like nonlinearity, differential uniformity, and SAC. Random numbers were generated from the fingerprint [17]. Dwivedi et al. [18] used the fingerprint of the sender and receiver to generate a symmetric key along with the Diffie-Hellman algorithm
1.2 Research Gap and Motivation
As discussed above, Researchers have proposed numerous methods to construct the strong S-box, notably the Pseudo-random number generator algorithm, inversion mapping, heuristic method, power polynomial, linear fractional transformation, algebraic method, and chaos-based system to generate the initial S-box due to its high randomness, nonlinearity, and simplicity. Followed by complex mathematical operations, and permutations were applied to improve the strength of the S-box. However, it adapted the initial seed values to produce the random number sequence. The attacker could easily predict these seed values that may reduce the reliability of the design. Therefore, it is essential to construct an S-box with unpredictable random sequences.
Here, we propose a method of constructing S-boxes using the fingerprint features of the sender [19] and Zigzag transformation-based permutation [20] for improving the performance of the S-box. The key reason for using fingerprint feature are as follows; fingerprint is unique for a human being, unpredictable in nature, and non-transferrable. It produces unique and random values that have better resistant to cryptanalysis attacks. The constructed S-box is utilized for at least ten rounds to encrypt the data in the AES algorithm. The S-box provides confusion by performing substitution operations among data while encrypting it. Then, the Permutation operation is employed to perform the transposition. Hence it is more difficult for the attackers to reach the original plaintext. In this way, the proposed S-box provides a higher level of security. Our proposed system is simple when compared with the existing approaches and constructs a highly secure, unpredictable S-box. We verified the numerical results of the standard cryptographical properties (SAC, NL, BIC-SAC, BIC-NL, DU), and the results show that the S-box proposed is strong.
Based on the perceived research gaps, this work targets the following objectives:
• To construct the initial S-box using biometric features of the user like ridges and bifurcations
• To adapt Zigzag transformation-based permutation function on initial S-box for optimal S-box design.
• To investigate the randomness of the fingerprint-based S-box using NIST SP 800-22 data.
• To analyze the cryptographical properties of the proposed scheme using the online tool ‘S-box analyzer’ [21].
• To design a robust S-box for effective security systems compared with existing methods.
The rest of the article is structured as follows: Section 2 represents the proposed method and its design factors such as image acquisition, preprocessing, and permutation; Section 3 describes the analysis features of constructed S-box using various characteristics; Section 4 demonstrates a detailed comparative study considering the previous works; Section 5 concludes the article based on the observed outcome from the proposed scheme.
2 Proposed Method and its Design
The elements of the S-box ought to be random, highly nonlinear. And, it needs to satisfy the basic cryptographical properties to use for encryption and decryption. Therefore, random numbers are generated from the adapted fingerprint patterns of the user transmitting the information. It has many special features, including spur, ridge endings, core points, ridge dots, bifurcations, delta points, ridge islands, ponds, and bridges. These are also known as minutiae points that can determine uniqueness, and the most frequently used features are ridges and bifurcations. In this work, we have constructed the S-box in two stages. Initially, we have built an S-box using the ridge and bifurcation features and explained in Section 2.1. And then, Zigzag transformation-based permutation is applied over the initial S-box to enhance the strength of the S-box. The user who wants to store their information in the cloud can encrypt the data using the enhanced fingerprint-based S-box. This allows the right person to decrypt the ciphertext.
2.1 Construction of Fingerprint-based S-box
Fingerprint-based S-box construction consists of four phases. It includes fingerprint image acquisition, preprocessing, feature extraction, and mathematical operations on the feature coordinates to fill the S-box. In order to prove that any fingerprint can provide a strong S-box, we have taken fingerprints of two users for our experiment.
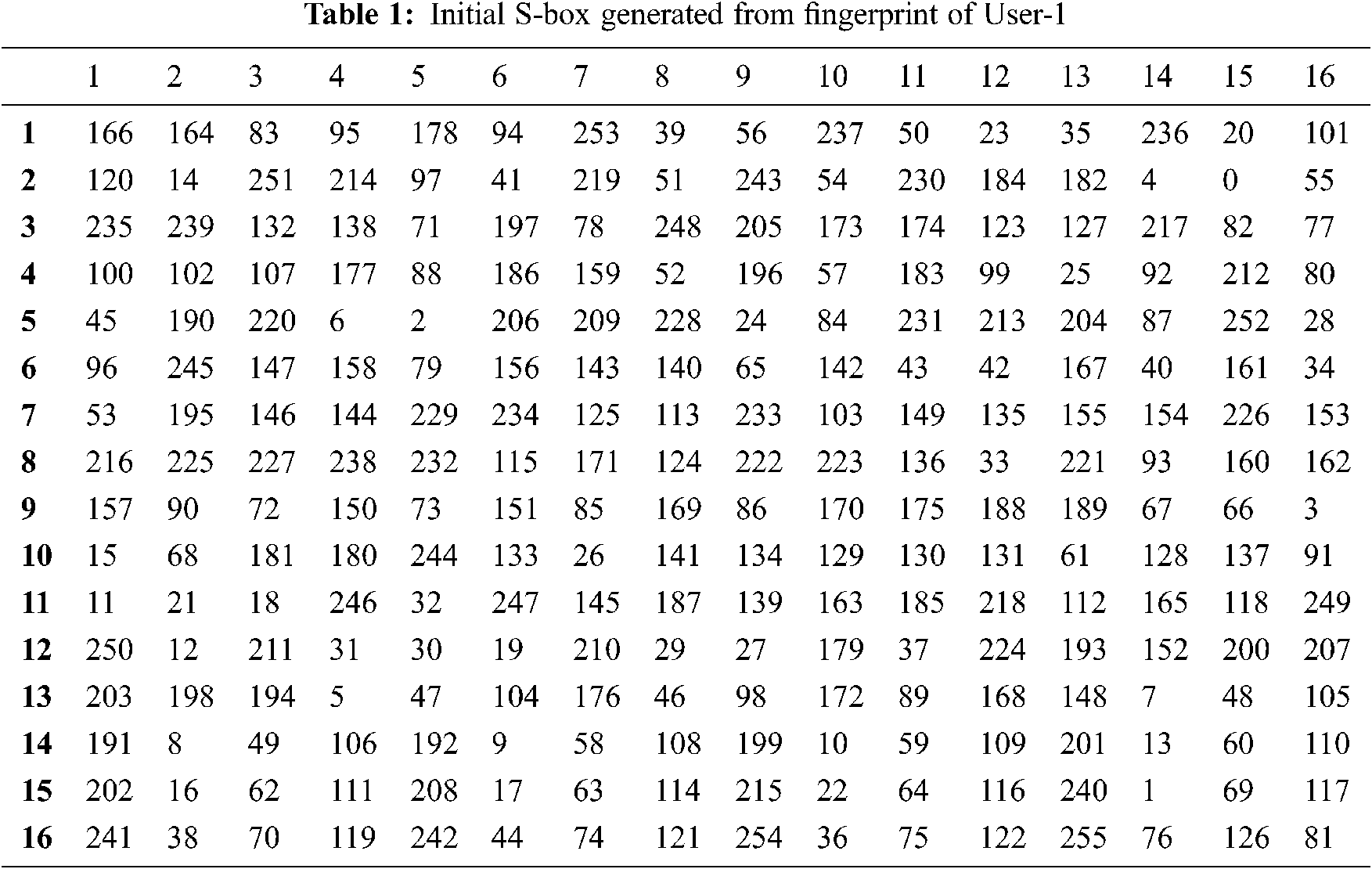
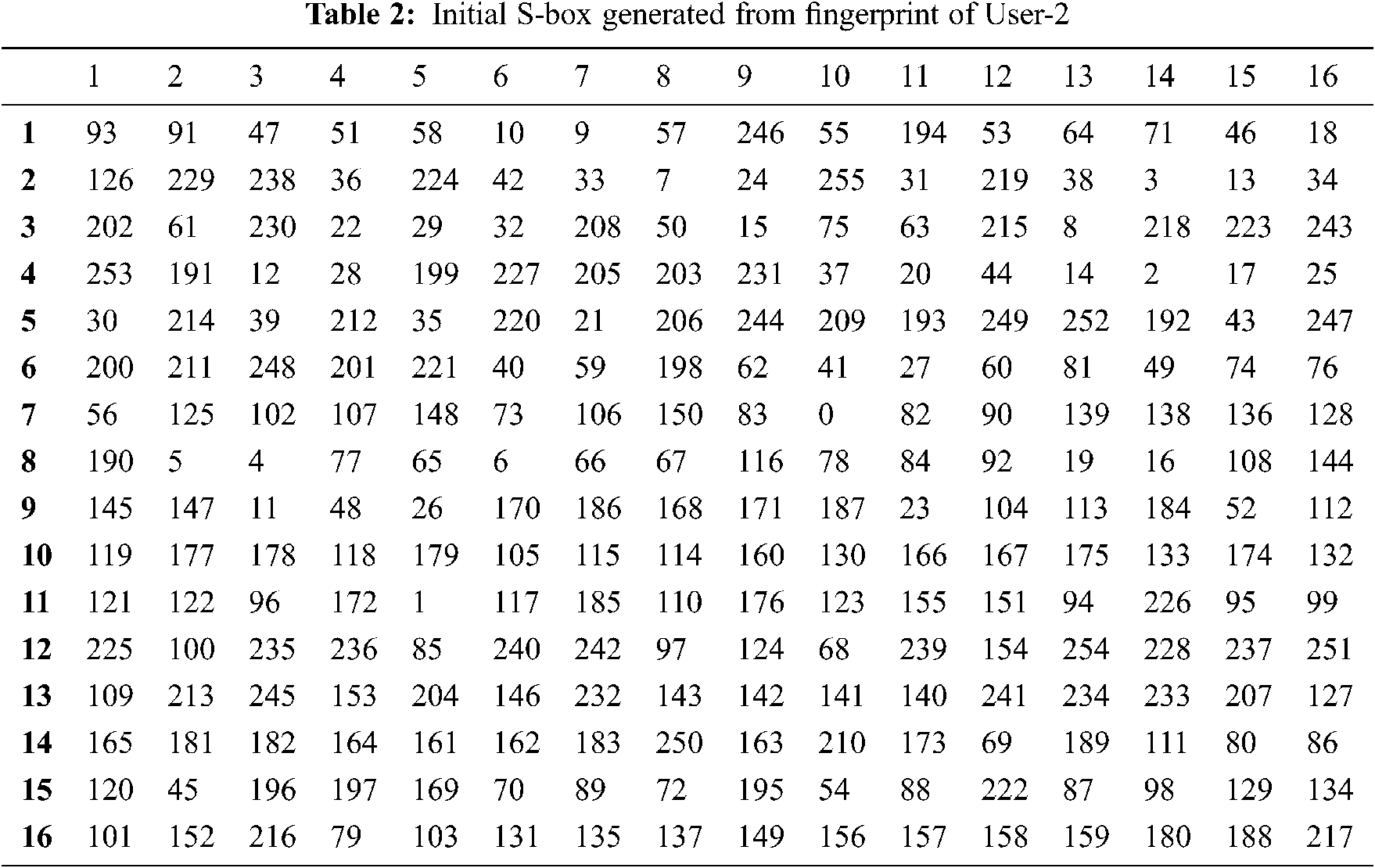
In this stage, the biometric scanner scans the user’s fingerprint. Notably, the fingerprint image’s quality depends on the scanner‘s quality and the finger’s position during the scanning process. It is not easy to extract accurate minutiae points from the poor-quality image. The researchers state that a good quality scanner can acquire 25 to 100 minutiae points. The observed source image of User1 and User2 from the scanner is shown in Fig. 1a.

Figure 1: (a) Original Image from Scanner (b) Binarized Image (c) Thinned Image (d) Minutiae Extraction
It plays a principal role in enhancing the quality of the acquired image. It helps to extract required features with high accuracy from the fingerprint image using the defined functions such as binarization and thinning.
i. Binarization: It is the process of transforming the acquired image into black and white (0’s and 1’s) through thresholding, as illustrated in Fig. 1b. The term thresholding is a technique of image segmentation that extracts the foreground image from the background image by comparing every pixel value of an image
ii. Thinning: It is a morphological operation and is performed number of times until the image no longer changes, intending to remove imperfections from the binary image. As an outcome, the skeleton of the image with a single-pixel wide is obtained and given in Fig. 1c.
iii. Feature Extraction (FE): The last step of preprocessing is called feature extraction (FE). There are two types of FE, namely local and global features. In this work, local features are considered ridge endings and ridge bifurcations. It reduces the dimension of an image to extract precise and essential components from an image. Minutiae points (Mp) are extracted from the thinned image (Fig. 1d) as denoted in Eq. (2). Blue color specifies ridge ending, and red color indicates ridge bifurcations. This minutiae point is the most distinguishing feature among the people.
where
We constructed the initial S-box from two different fingerprints by performing an XOR operation between coordinates of the fingerprint features, and the respective consequence is illustrated in Tabs. 1 and 2. To use the S-box for encryption and decryption, it should satisfy the NIST randomness test and cryptographic properties. We use the NIST randomness assessment to evaluate the randomness of S-box values that endorse this process. The observed results show that the elements of the initial S-box are highly random. “S-box analyzer tool” [21] is used to evaluate the performance of the initial S-box. As a result, the initial S-box had 106 as maximum nonlinearity and 16 as differential uniformity. Although the range of attained nonlinearity value is optimal, differential uniformity needs to be reduced to improve the S-box strength. Therefore, the Zigzag transformation-based permutation function is applied to the initial S-box to enrich the S-box nonlinearity and decrease the differential uniformity.
2.2 Zigzag Transformation-based Permutation
It is a process of rearranging the elements of the matrix in the shape of ‘Z’ letter. It can improve the diffusion level and enhances the strength of the S-box further. Three types of Zigzag transformation are in use to change the position of a matrix. Namely, the Standard Zigzag Transformation process (SZT), Modified Zigzag Transformation process (MZT), and Parallel way of the Zigzag Transformation process (PZT). In SZT, the matrix elements are scanned from the top left corner, and ending with the bottom right corner (Fig. 2a). Whereas MZT (Figs. 2b–2i), scans the matrix elements from the top right corner with the direction from the right to the left or top to the bottom and ending with the bottom left corner as represented in Figs. 2b and 2d. Similarly, the top left corner matrix elements are scanned downwards and ending with the bottom right corner (Fig. 2c). The parallel– Zigzag transformation process scans the matrix elements horizontally or vertically as depicted in Figs. 2j–2l. A Blue circle and a red circle denote the starting position and the ending position respectively. The authors of [22,23] used the MZT approach for image encryption. We use the recursive SZT permutation operation to improve the nonlinearity of the initial S-box.
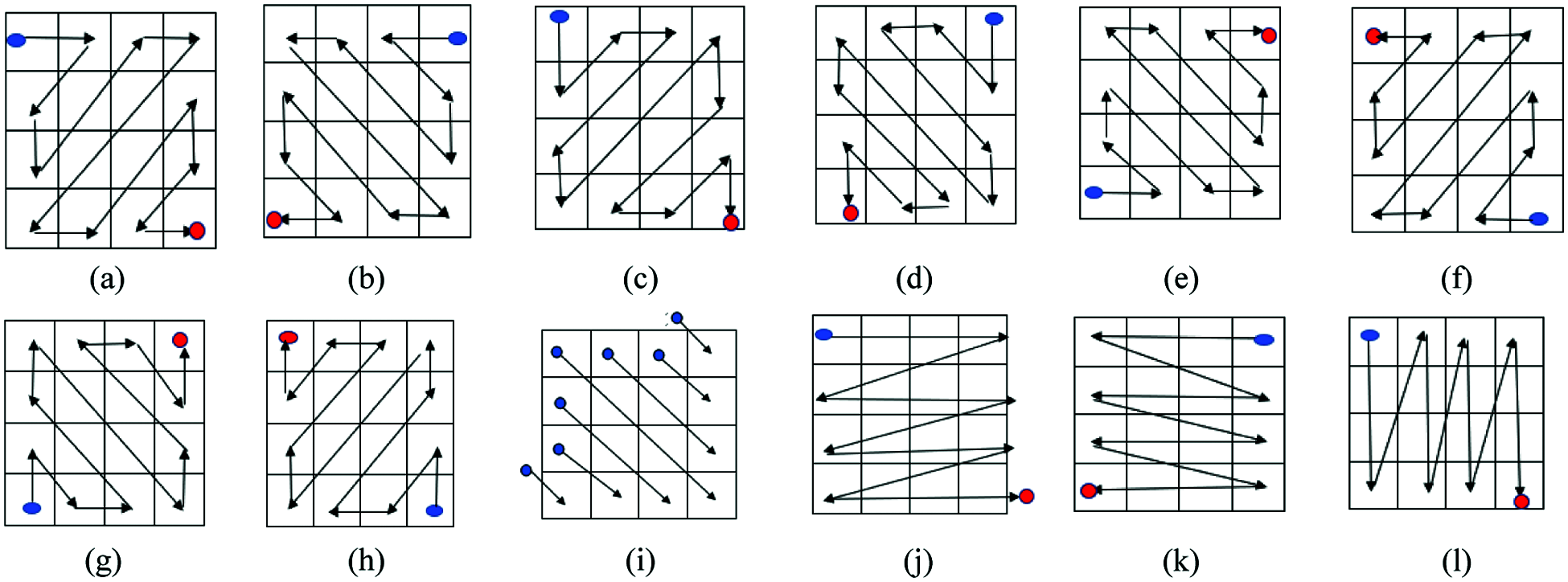
Figure 2: (a) – SZT, 2 (b) – 2 (i) – MZT, 2 (j) – 2 (l) – PZT
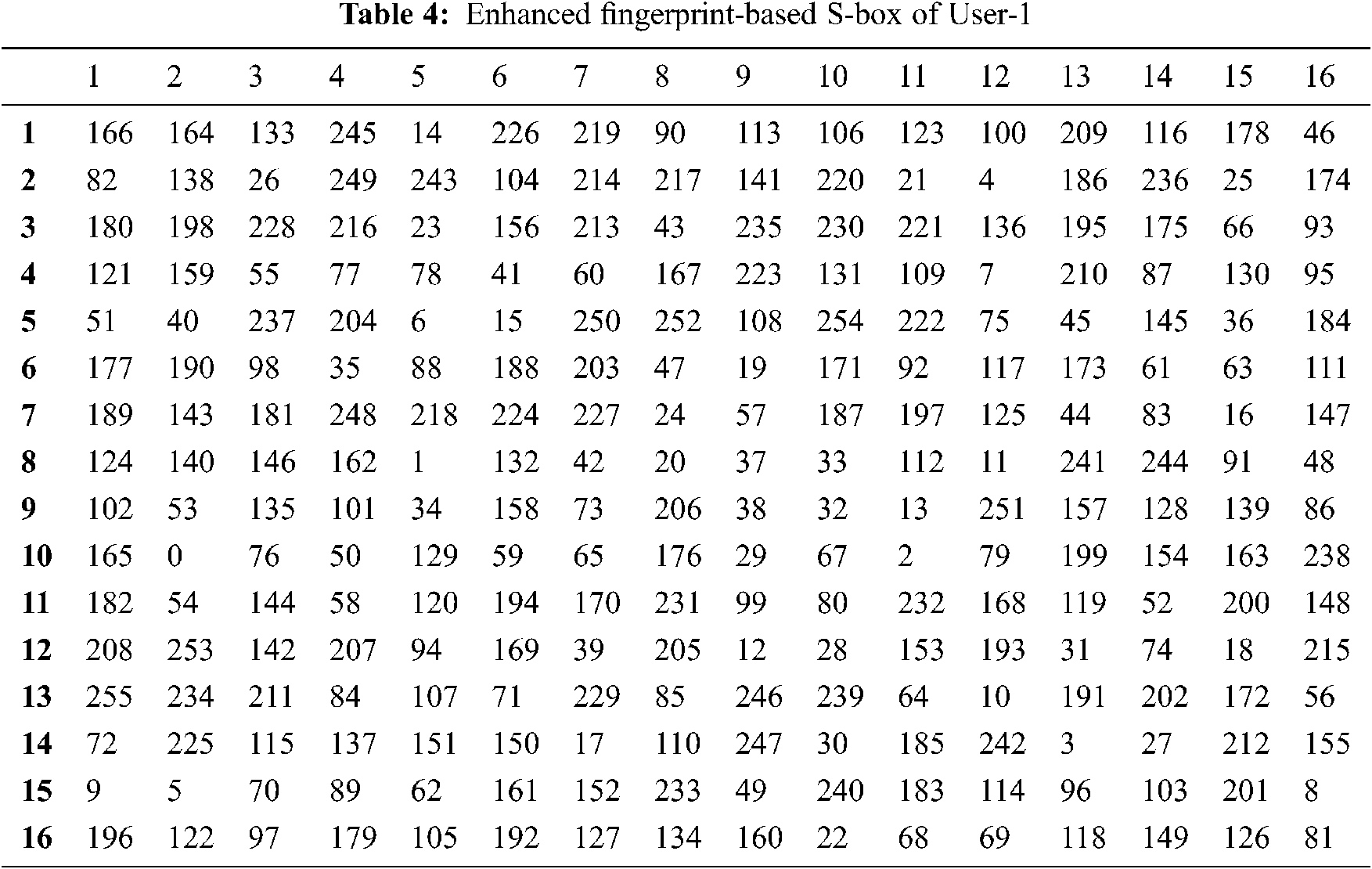
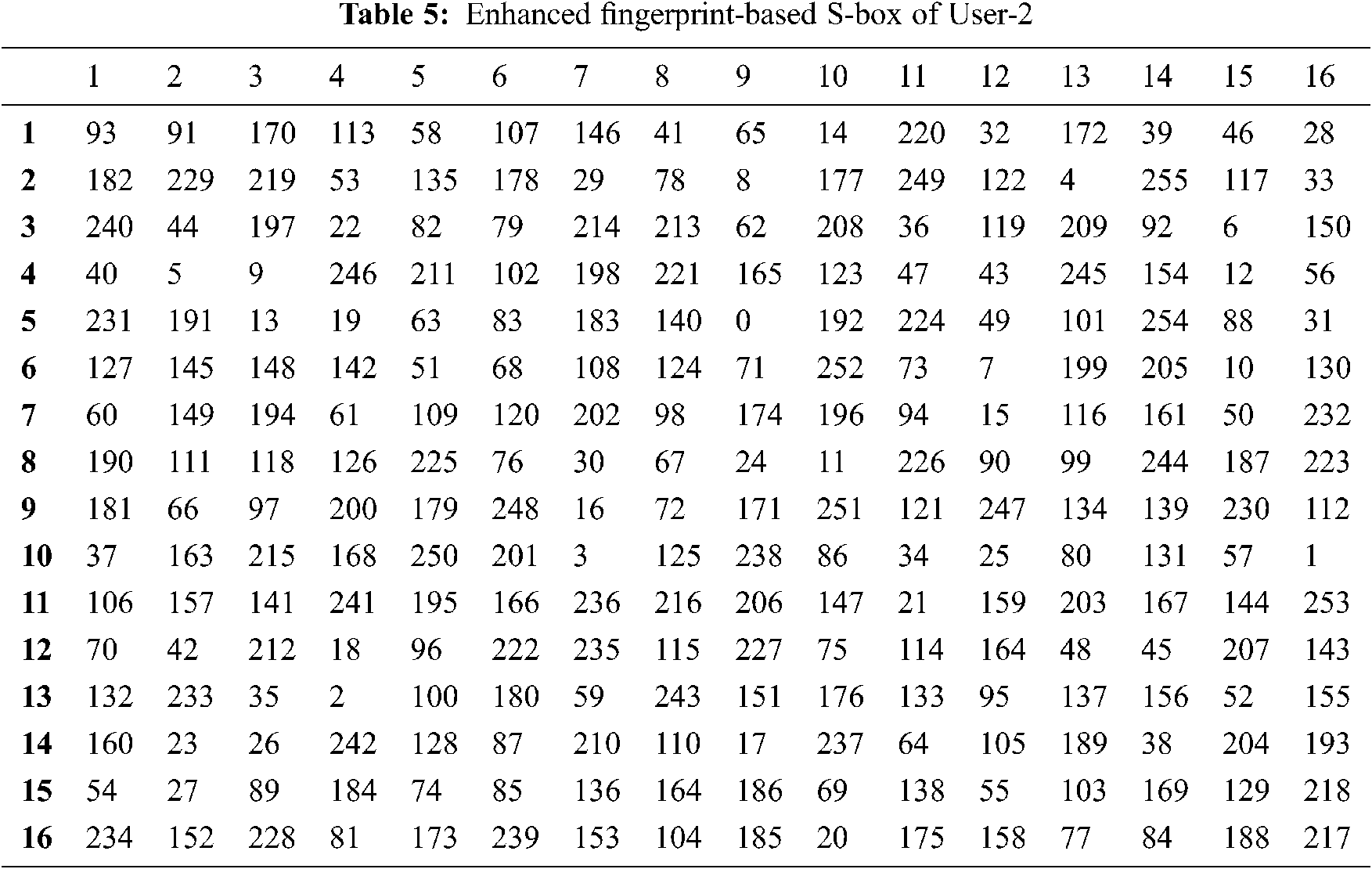
The flowchart of the complete process is given in Fig. 3 and the pseudocode is presented in Tab. 3. The enhanced fingerprint-based S-box (FSB) is illustrated in Tabs. 4 and 5.

3 Performance Analysis of Constructed S-box
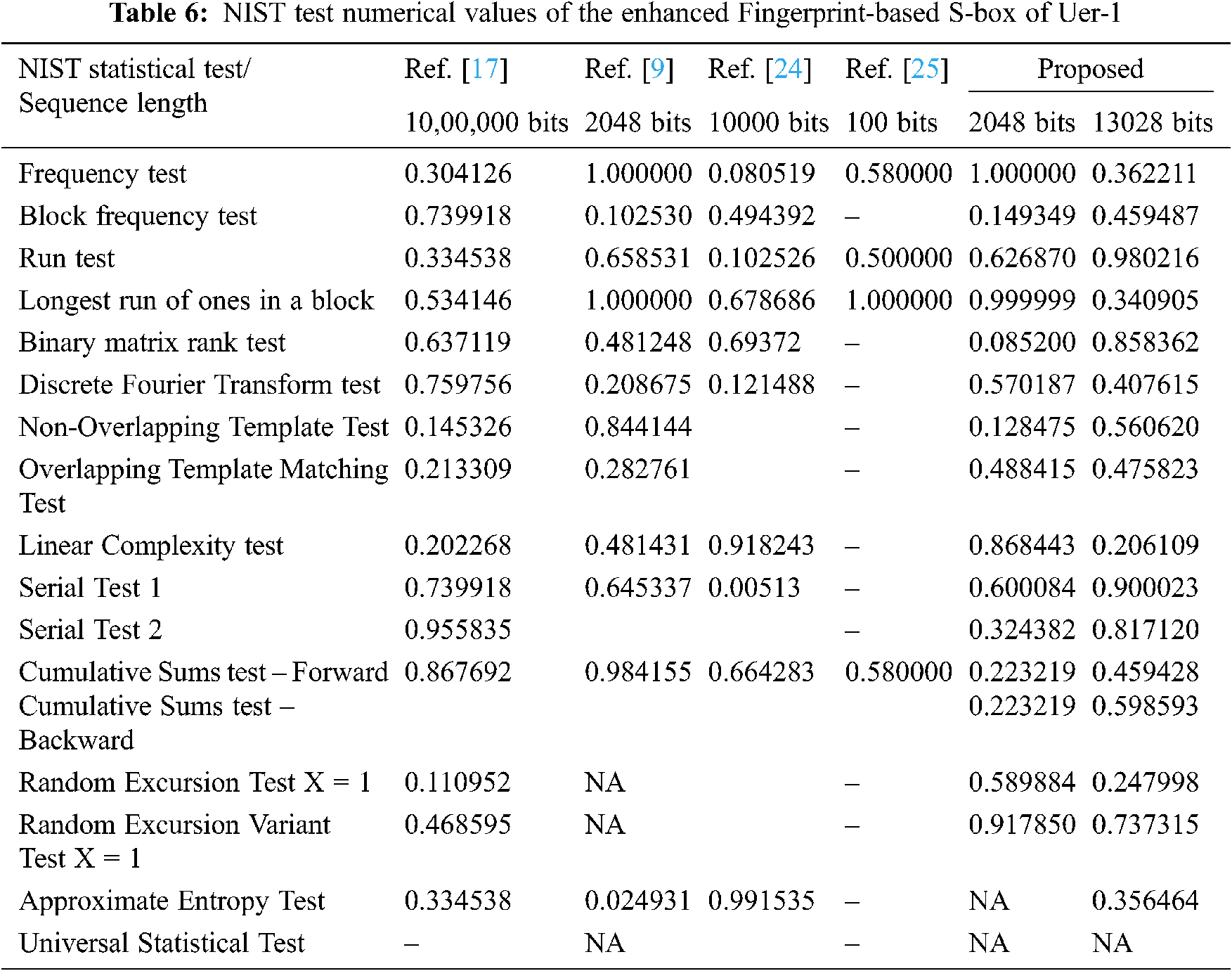
It is known that the S-box elements are random and nonlinear and it is necessary to maintain these elements as unpredictable. NIST STS, Dieharder Test are commonly used for randomness testing. Among these, NIST STS is the popular and faster random analysis method. The NIST randomness test considered fifteen statistical assessments to prove the randomness. These assessments determine the power of randomness, and the significant value (ρ) utilized for examination is 0.01, as expressed by NIST. Every assessment result is compared with the significant value (ρ). If ρ is greater than or equal to 0.01, then the sequence is random or irregular. If ρ < 0.01, then it is regular sequence. Moreover, if the significant value is 0, then the sequence is completely non-random. Also, if the ρ is 1, then the sequence is said to be perfectly random. The frequency test is the basic test to evaluate the randomness of the data. If the significant value (ρ) of the frequency test is less than 0.01, then there is the possibility of failing all other tests. The minimum sequence length to perform all the NIST STS test is 10,00,000 bits with minimum of 100 sequences. Each sequence should have 10,00,000 bits. Certain types of the test cannot be executed when the length of the sequences is less than the required limit. For example, the approximate entropy test and universal statistical test which requires 106 bits. In [24], the authors were used minimum of 1000 bits and maximum of 10000 bits for testing the randomness. In our case, 256 random elements are filled in the S-box proposed. To use this S-box in AES for encryption and decryption, its randomness has to be examined. We tested the randomness of the S-box elements using NIST STS-2.1.2, in two different methods.
1. The S-box elements are converted into binary sequences and concatenated together to form 2048 bits and its randomness is verified. It is perceived that the enhanced fingerprint-based S-box satisfies thirteen tests out of 15 tests. It fails to satisfy the approximate entropy test and universal statistical test because it requires a long sequence.
2. We have analyzed the randomness of Enhanced fingerprint-based S-box of User-1 from the obtained ciphertext by employing the proposed S-box in AES encryption [25]. We have generated Ciphertext of length 13028 bits and used it for randomness analysis. The numerical values of NIST tests are presented in Tab. 6 and compared with the related works. It reveals a success status for thirteen tests by considering 2048 bits as a sequence and fourteen tests for 13028 bits.
3.2 Performance Evaluation Test
Performance Evaluation Test is used to evaluate the strength of the S-box. To ensure an efficient S-box, it should satisfy the cryptographic criteria: Bijective, Nonlinearity, Bit Independence Criterion, Strict avalanche, and Linear approximation probability. In this section, the proposed S-box’s cryptographical capability is analyzed with the properties mentioned above using the S-box analyzer tool.
Commonly, the S-box is bijective when the observed output values of the proposed S-box fall between the defined interval. Also, a Boolean function
The term ‘hw’ represents a hamming weight; ai
Pieprzyk and Finkelstein introduced the nonlinearity model. It is the first and foremost requirement of the S-box. To realize the higher nonlinearity, the elements of the S-box should be highly random. The optimal value of nonlinearity of the Boolean function is defined as follows:
Further, Boolean function nonlinearity is described using the below equation.
Notably, the Walsh spectrum is used to compute the nonlinearity of the Boolean expression as described below.
For symmetric Boolean functions, the nonlinearity of S-box should lie between 100 and 120. If the experimental values violate the said band, it is susceptible to cryptanalysis. However, the proposed scheme offers the best value of about 108 as maximum nonlinearity and average nonlinearity of 106 (Tab. 7), which ensures the robustness of the newly constructed S-box.

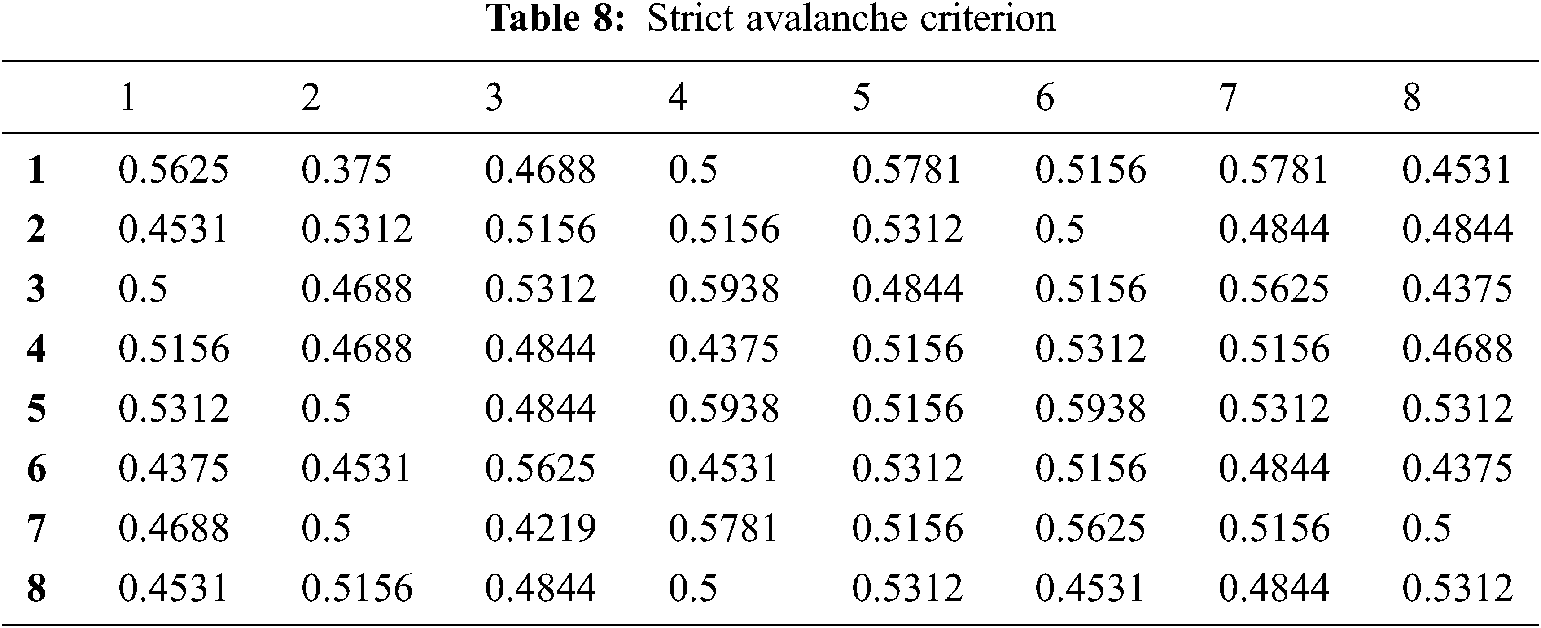
3.2.3 Strict Avalanche Criteria (SAC)
Tavares and Webster introduced SAC in 1986 to investigate the strength of the cryptosystem. Its scale should satisfy by changing a single input bit that reflects the change of about 50% of the output bits, i.e., the SAC value should be close to 0.5. The proposed scheme produces the SAC value of about 0.5039 which satisfies the SAC (Tab. 8). A dependence matrix is evaluated to test the SAC effectiveness using the following expressions.
3.2.4 Bit Independence Criterion (BIC)
BIC is a cryptosystem parameter introduced by Webster and Tavares. This analysis required maintaining the output bits that should not correlate with each other. Also, an adjustment in any single input bit and respective output bits should change independently for avalanche vectors. It is essential to satisfy the BIC with maximum nonlinearity and SAC, as shown in Tabs. 9 and 10.
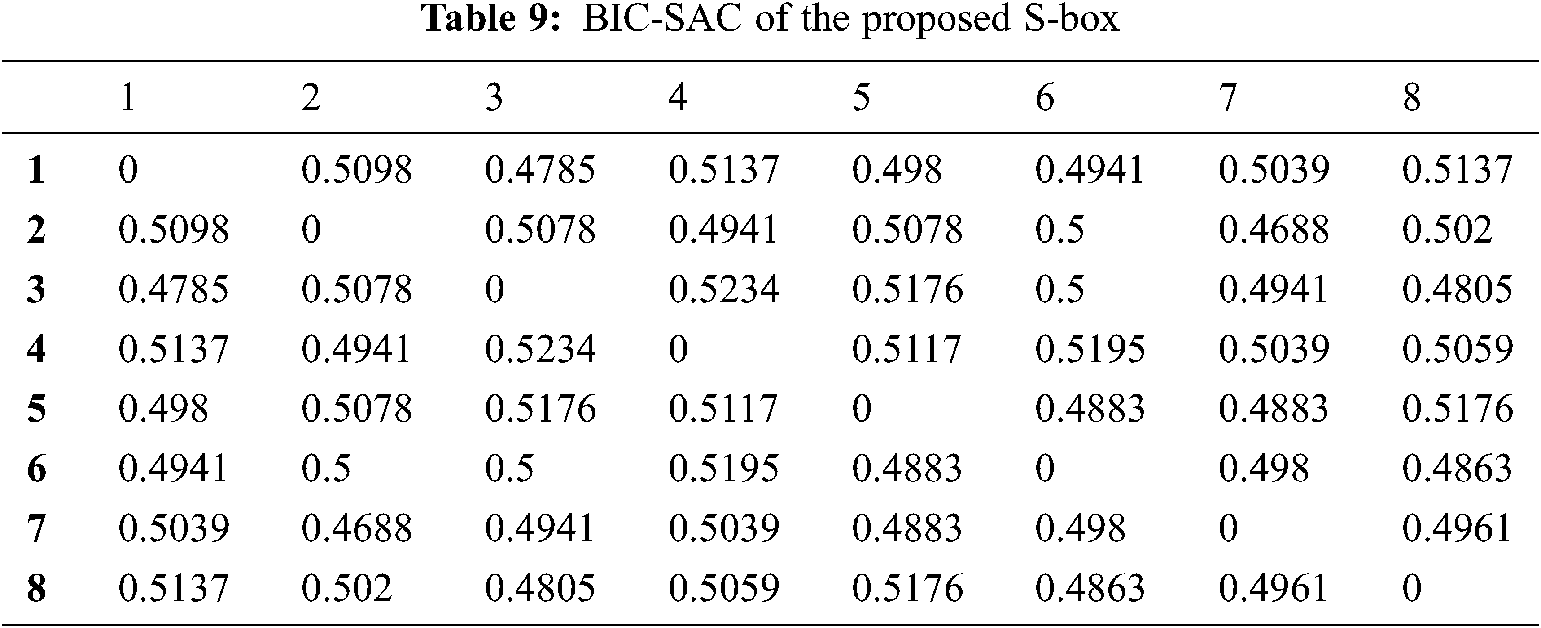
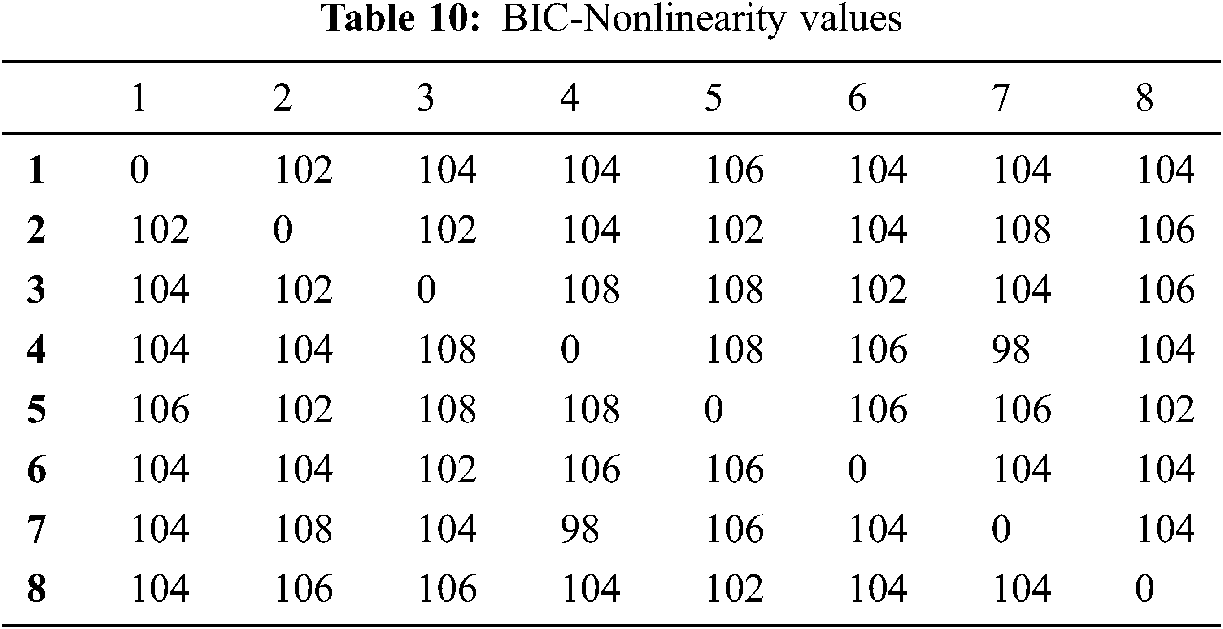
The above tables show that the value of BIC-nonlinearity and BIC-SAC are within the acceptable range. It ensures the robustness of the proposed S-box further.
It evaluates the resistance power against differential attacks. The lower range of Differential Uniformity value represent a high resistance during differential cryptanalysis attack and computed using the following equation.
where Z is a collection of all possible input values;
4 Comparative Analysis with Existing Works
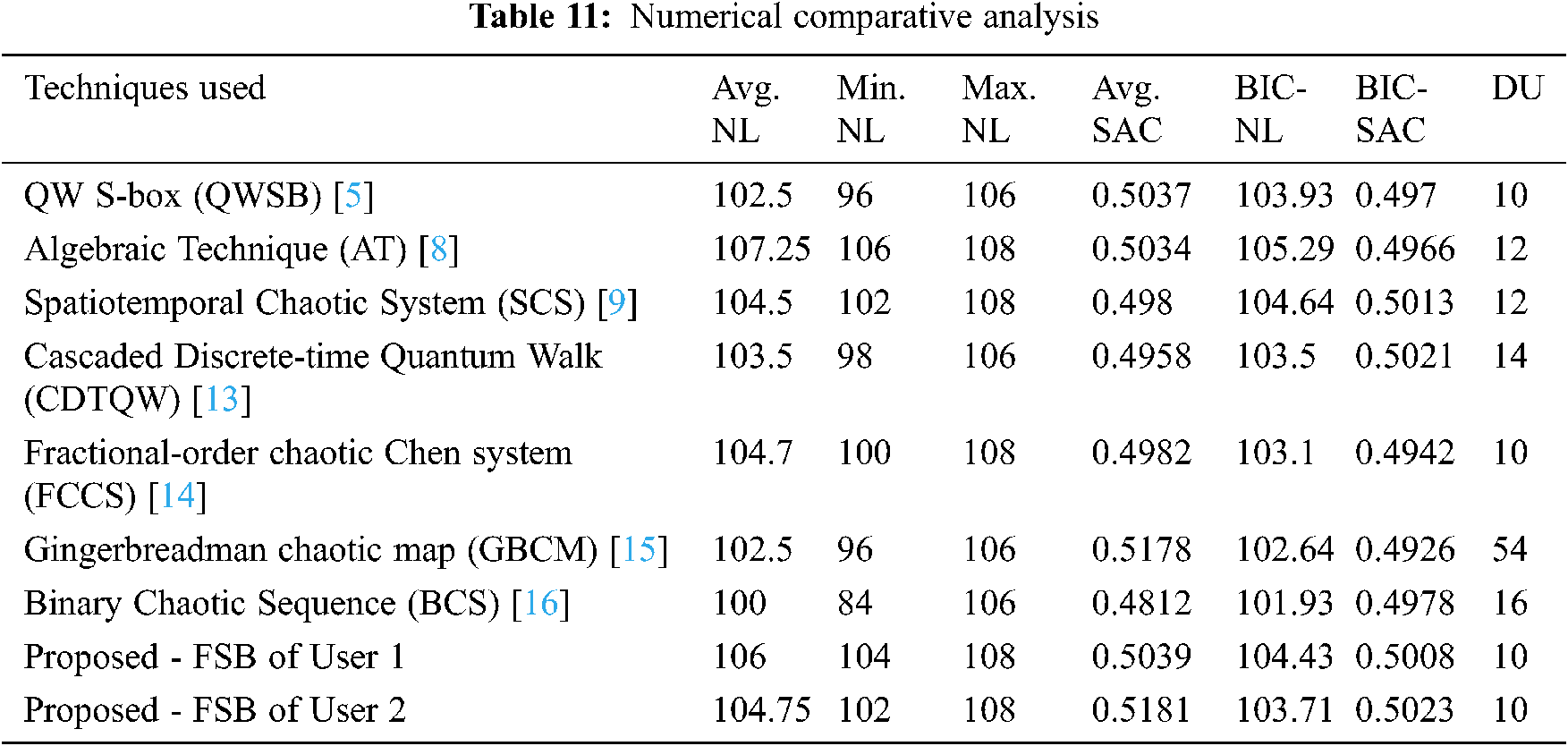
The observed results are compared with recently published works using different strategies to validate the effectiveness of the proposed S-box notably, QW S-box (QWSB) [5], Algebraic Technique (AT) [8], Spatiotemporal Chaotic System (SCS) [9], Cascaded Discrete-time Quantum Walk (CDTQW) [13], Fractional-order Chaotic Chen System (FCCS) [14], Gingerbreadman Chaotic Map (GBCM) [15], and Binary Chaotic Sequence (BCS). The figurative demonstration of the comparative study illustrated in Fig. 3 and the numerical reports are presented in Tab. 11.
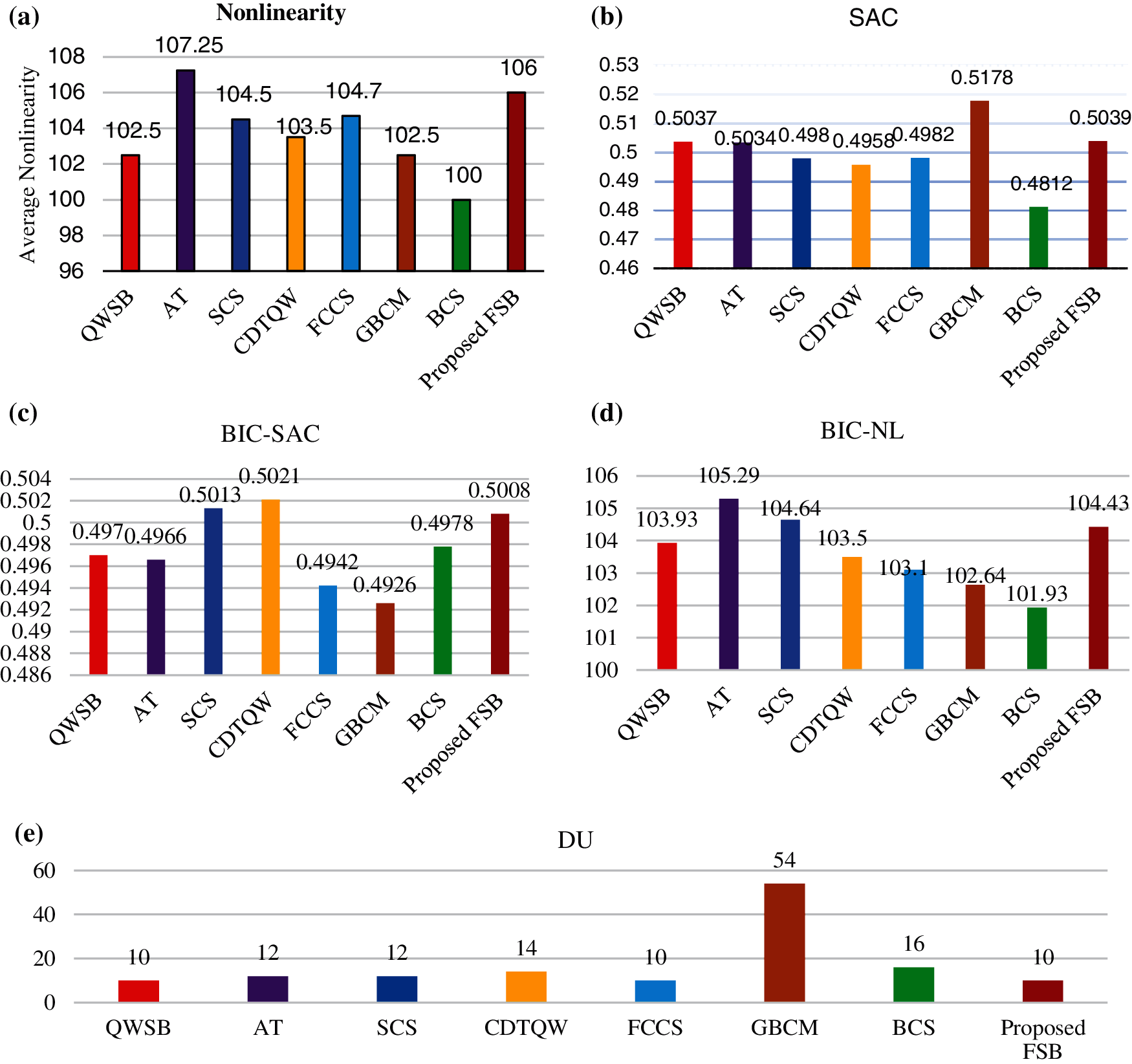
Figure 3: (a) Nonlinearity (b) SAC (c) BIC-SAC (d) BIC-NL (e) Differential Uniformity
It is perceived that the maximum nonlinearity of Fingerprint-based initial S-box-1 of user-1 was 106 initially, and then it is improved to 108 after permutation. Further, the average value of SAC value of the proposed scheme offered the best deal, about 0.5039. It shows that the proposed system satisfies the strict avalanche criterion. S-box quality is depending on the smaller value of differential uniformity. The differential uniformity of the enhanced FSB is 10, which is lesser than the other methodologies. The cryptographic criterions of S-box (NL, SAC, DU, BIC-SAC, BIC-NL) is compared with other S-boxes and illustrated in Tab. 11.
An effective S-box is constructed using fingerprint pattern and permutation function in this work. Initially, S-box is built from X-Y coordinates of the user’s extracted fingerprint features (ridges, bifurcation). Subsequently, Recursive Zigzag transformation-based permutation function is carried out on the initial S-box to boost the overall characteristics. Further, a randomness test and cryptographic efficiency are performed to check S-box’s strength. From the observed results, the following conclusions are made:
• The maximum range of nonlinearity is obtained from the proposed S-box of about 108 and the 106 as average nonlinearity.
• SAC shows a significant scale of about 0.5039, closer to the required band (0.5).
• BIC-NL and BIC-SAC offer the best value, about 104.43 and 0.5008, respectively.
• The rate of DU also superior for the proposed scheme compared with existing methods.
The statistical results reveal that the proposed scheme satisfies all the cryptographic properties, and therefore the proposed S-box is strong enough against linear and differential attacks. An optimization model can be incorporated with this scheme for further enhancement in the future.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding this study.
1. S. S. Jamal, A. Anees, M. Ahmad, M. F. Khan and I. Hussain, “Construction of cryptographic S-boxes based on Mobius transformation and Chaotic Tent-Sine System,” IEEE Access, vol. 7, pp. 173273–173285, 2019. [Google Scholar]
2. X. Wang and Q. Wang, “A novel image encryption algorithm based on dynamic S-boxes constructed by chaos,” Nonlinear Dynamics, vol. 75, no. 3, pp. 567–576, 2014. [Google Scholar]
3. I. Hussain, T. Shah, H. Mahmood and M. A. Gondal, “Construction of S8 Liu J S-boxes and their applications,” Computers & Mathematics with Applications, vol. 64, no. 8, pp. 2450–2458, 2012. [Google Scholar]
4. J. Liu, B. Wei, W. Cheng and X. Wang, “An AES S-box to increase complexity and cryptographic analysis,” in 19th Int. Conf. on Advanced Information Networking and Applications (AINA’05Taipei, Taiwan, vol. 1, pp. 724–728, 2005. [Google Scholar]
5. A. Ahmed, A. EL-Latif, B. Abd-El-Atty and S. E. Venegas-Andraca, “A novel image steganography technique based on quantum substitution boxes,” Optics & Laser Technology, vol. 116, no. 3, pp. 92–102, 2019. [Google Scholar]
6. M. S. M. Malik, M. A. Ali, M. A. Khan, M. Ehatisham-ul-haq, S. N. M. Shah et al., “Generation of highly nonlinear and dynamic AES Substitution-Boxes (S-boxes) using Chaos-based rotational matrices,” IEEE Access, vol. 8, pp. 35682–35695, 2020. [Google Scholar]
7. Y. Tian and Z. Lu, “S-box: Six-dimensional compound hyperchaotic map and artificial bee colony algorithm,” Journal of Systems Engineering and Electronics, vol. 27, no. 1, pp. 232–241, 2016. [Google Scholar]
8. Attaullah, S. S. Jamal and T. Shah, “A novel algebraic technique for the construction of strong substitution box,” Wireless Personal Communications, vol. 99, no. 1, pp. 213–226, 2018. [Google Scholar]
9. L. Liu, Y. Zhang and X. Wang, “A novel method for constructing the S-box based on Spatiotemporal Chaotic Dynamics,” Applied Sciences, vol. 8, no. 12, pp. 2650, 2018. [Google Scholar]
10. N. Siddiqui, F. Yousaf, F. Murtaza, M. Ehatisham-ul-Haq, M. U. Ashraf et al., “A highly nonlinear substitution-box (S-box) design using action of modular group on a projective line over a finite field,” PLOS ONE, vol. 15, no. 11, pp. e0241890, 2020. [Google Scholar]
11. L. Shuai, L. Wang and L. Miao, “Constructing Chaos based substitution boxes using the composition of transpositions,” Wireless Personal Communications, vol. 115, no. 3, pp. 1881–1897, 2020. [Google Scholar]
12. I. Hussain, A. Anees, T. A. Al-Maadeed and M. T. Mustafa, “Construction of S-box based on Chaotic map and algebraic structures,” Symmetry, vol. 11, no. 3, pp. 351, 2019. [Google Scholar]
13. A. A. Abd El-Latif, B. Abd-El-Atty, M. Amin and A. M. Iliyasu, “Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications,” Scientific Reports, vol. 10, no. 1, pp. 2322, 2020. [Google Scholar]
14. F. Özkaynak, V. Çelik and A. B. Özer, “A new S-box construction method based on the fractional-order chaotic Chen system,” Signal, Image and Video Processing, vol. 11, no. 4, pp. 659–664, 2017. [Google Scholar]
15. M. Khan and Z. Asghar, “A novel construction of substitution box for image encryption applications with Gingerbreadman chaotic map and S8 permutation,” Neural Computing and Applications, vol. 29, no. 4, pp. 993–999, 2018. [Google Scholar]
16. M. Khan, T. Shah and S. I. Batool, “Construction of S-box based on chaotic Boolean functions and its application in image encryption,” Neural Computing and Applications, vol. 27, no. 3, pp. 677–685, 2016. [Google Scholar]
17. L. Ying, W. Shu, Y. Jing and L. Xiao, “Design of a random number generator from fingerprint,” in Int. Conf. on Computational and Information Sciences, Chengdu, China, pp. 278–280, 2010. [Google Scholar]
18. R. Dwivedi, S. Dey and M. A. Sharma, “A fingerprint based crypto-biometric system for secure communication,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, no. 4, pp. 1495–1509, 2020. [Google Scholar]
19. O. Şengel, M. A. Aydın and A. Sertbaş, “An efficient generation and security analysis of substitution box using Fingerprint patterns,” IEEE Access, vol. 8, pp. 160158–160176, 2020. [Google Scholar]
20. F. Artuğer and F. Özkaynak, “A novel method for performance improvement of Chaos-based substitution boxes,” Symmetry, vol. 12, no. 4, pp. 571, 2020. [Google Scholar]
21. A. Özkaynak, “An analysis and generation toolbox for chaotic substitution boxes: A case study based on Chaotic Labyrinth Rene Thomas System,” Iranian Journal of Science and Technology, Transactions of Electrical Engineering, vol. 44, no. 1, pp. 89–98, 2020. [Google Scholar]
22. P. Ramasamy, V. Ranganathan, S. Kadry, R. Damaševičius and T. Blažauskas, “An image encryption scheme based on block scrambling, modified Zigzag transformation and Key generation using enhanced Logistic—Tent Map,” Entropy, vol. 21, no. 7, pp. 656, 2019. [Google Scholar]
23. X. Wang and H. Sun, “A chaotic image encryption algorithm based on zigzag-like transform and DNA-like coding,” Multimedia Tools and Applications, vol. 78, no. 24, pp. 34981–34997, 2019. [Google Scholar]
24. Z. Jiang and Q. Ding, “Construction of an S-box based on chaotic and bent functions,” Symmetry, vol. 13, no. 4, pp. 671, 2021. [Google Scholar]
25. D. G. Brosas, A. M. Sison, A. A. Hernandez and R. P. Medina, “Analysis of the randomness performance of the proposed stream cipher based cryptographic algorithm,” in 11th IEEE Control and System Graduate Research Colloquium (ICSGRCShah Alam, Malaysia, pp. 76–81, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |