DOI:10.32604/iasc.2022.023350

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023350 |  |
| Article |
Fuzzy Logic for Underground Mining Method Selection
1Department of Information Technology, Dr. NGP Institute of Technology, Coimbatore, 641048, Tamilnadu, India
2Department of Information Technology, Dr. Akhilesh Das Gupta Institute of Technology & Management, New Delhi 110053, Delhi, India
3School of Computer Science and Engineering, Vellore Institute of Technology, Chennai, India
4Department of Electronics and Communication Engineering, K. Ramakrishnan College of Engineering, Tiruchirapalli, 621112, Tamilnadu, India
5Department of Computer Science and Engineering, J. K. K. Munirajah College of Technology, Erode, 638506, Tamilnadu, India
6Institute of Biomedical Engineering, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, 602105, Tamilnadu, India
*Corresponding Author: S. Venkatraman. Email: venkats23@gmail.com
Received: 04 September 2021; Accepted: 13 October 2021
Abstract: The Selection of the mining method for underground minerals extraction is the crucial task for the mining engineers. Underground minerals extraction is a multi-criteria decision making problem due to many criteria to be considered in the selection process. There are many studies on selection of underground mining method using Multi Criteria Decision Making (MCDM) techniques or approaches. Extracting minerals from the underground involves many geological characteristics also called as input parameters. The geological characteristics of any mineral deposit vary from one location to another location. Thus only one mineral extraction method is not suitable for different deposit characteristics. There are many mineral extraction methods available for different characteristics of the ore deposit. As of now only MCDM approach or Hybrid MCDM approaches or MCDM approaches with fuzzy logic were used for selecting a mining method for underground metal mine. In this study, only fuzzy logic approach is used for selecting a mining method for different deposit characteristics. The proposed model considers five deposit characteristics as input parameters and seven underground mining methods output parameters The developed fuzzy logic based approach is also validated by the deposit characteristics of two Indian mines. The model produced the suitable mining method for extraction of the minerals at the specified Indian mines and the same mining methods are used by the mine authorities.
Keywords: Fuzzy logic; underground mining; mining methods; MCDM
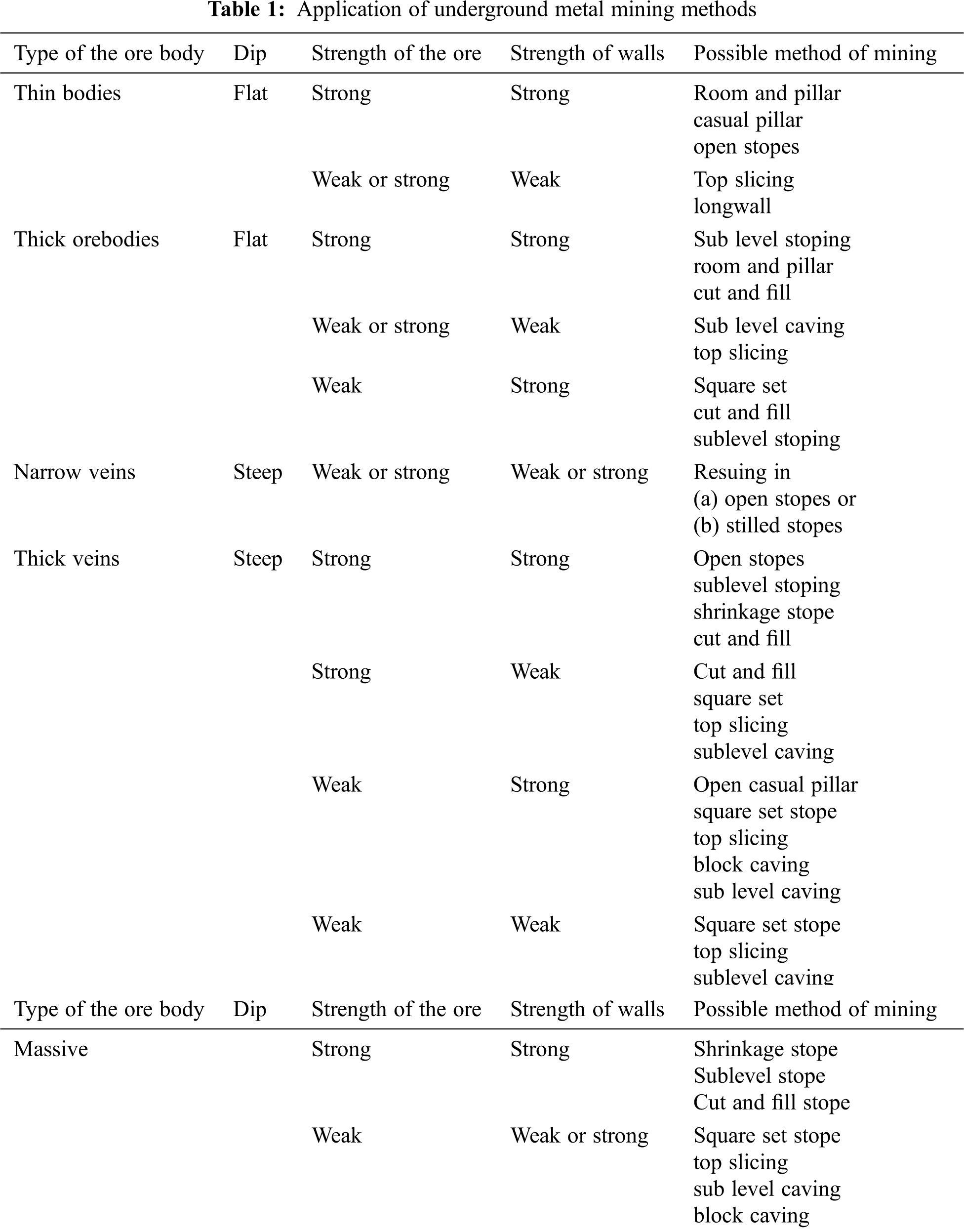
Mineral extraction process involves different characteristics of an ore deposit. These characteristics are ore body dip at which angle the ore exists, shape of the ore body, thickness of the ore body, ore body depth at which the minerals exist from the surface, grade distribution of the minerals in the ore body, and many other parameters. For various geological conditions, there are different mining methods for underground excavation. These methods include block caving, sub level stoping, sub level caving, room and pillar mining, shrinkage stoping, cut and fill stoping and square set stoping. These mining methods can be used for minerals extraction from the underground based on various geological conditions. The following Tab. 1 describes preferable mining method for different geological characteristics [1].
The task of selecting an underground mining method is multi-criteria decision-making process. There are many MCDM methods available to accomplish the best mining method when multiple geological characteristics are given. These MCDM methods are Analytic Hierarchy Process (AHP), Simple Additive Weighted method (SAW), Technique of Order Preference Similarity to the Ideal Solution (TOPSIS), The Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE), VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), ELimination Et Choice Translating Reality (ELECTRE), etc. There are many studies on underground metal mining method selection using these MCDM methods [2–6]. Some of these studies are not considered the uncertainty of the parameters. This uncertainty can be overcome by using fuzzy logic. In the present study, only fuzzy logic has been used to implement a preferable mining method for an ore deposit based on various geological characteristics.
The geological characteristics involve in the mining method selection process are uncertain in nature. Thus, fuzzy logic gives the preferable mining method for underground mineral extraction. This approach was not used in the area of mining method selection, but used in other research areas and some are mentioned here. Thakre et al. [7] proposed a fuzzy logic approach for evaluation of teacher performance. In this paper, fuzzification of crisp data is introduced to evaluate the performance of a teacher. Altrock et al. [8] suggested fuzzy logic based multi-criteria decision making in German automotive industry using fuzzy logic. This research work used fuzzy logic to evaluate the maturity of a component development to optimize the design process of a truck components. Paterson et al. [9] developed a fuzzy logic tool for multi-criteria decision making in fisheries. This study used a fuzzy logic-based electronic decision support tool for the eco system approach to fisheries. It is found that many other studies are used fuzzy logic for multiple criteria decision making.
The selection of specific alternative is the objective of any multi-criteria decision making model. The procedure of finding specific alternative using the fuzzy logic approach is as follows:
2.1 Selection of Input Parameters
The first thing in a decision-making process is we must consider the influencing parameters on the problem domain. These influencing parameters can be called as input parameters. Each input parameter specifies a range of values depending on the problem considered to solve. Most of the input parameters are uncertain in general.
2.2 Selection of Output Parameters
In multi-criteria decision-making, alternatives specify the output parameters. The preferable alternative for a specific problem depends on the various influencing or input parameters considered. The output parameter is the one that is the solution for a given set of input parameters. For given set of input parameters there can be many solutions. Thus, we rank the output parameters from highest to least based on the evaluated value.
In 1965, Zadeh et al. [10] introduced fuzzy logic to handle incomplete or ambiguous information. The objective of a fuzzy set is intuitive and natural because it does not specify strict boundaries as like ordinary sets. The following sub-sections explain the concept of fuzzy logic in detail.
Fuzzy logic allows the intermediate values to be defined between conventional evaluations such as true/false or high/low etc. Fuzzy logic can be called multi valued logic, which allows all the intermediate values in the set [11].
A fuzzy set consists of boundaries. Defining a fuzzy set to each input variable allows all the intermediate values in the set. The degree of belonging intermediate values in the set are called membership functions usually ranging from 0 to 1. But this can be any range of values depends on the application about to solve. Assuming X is a universe of discourse and elements are denoted as x, in contrast with crisp set, then the fuzzy set A of X has the characteristics function associated to it. Based on fuzzy set theory, fuzzy set A of X is defined by its membership function μA(x) using Eqs. (1) and (2) as shown below.
where
After identifying input and output parameters for the given problem, membership functions for each input parameter and output parameter should be defined. A membership function is defined as how the range of given input values can be mapped to membership value. There are various types of membership functions in the fuzzy logic. These membership functions include the triangular membership function, trapezoidal membership function, and Gaussian membership function. In this paper, the commonly used membership functions such as triangular membership function and trapezoidal membership function are explained in the following sub-sections.
2.3.4 Triangular Membership Function
In fuzzy logic, triangular membership function can be represented as T = (l, m, u), where ‘l’ denotes the lower limit of the original number, ‘m’ specifies the original value, and ‘u’ represents the upper limit of the actual number. Eq. (1) represents the membership function for the positive triangular fuzzy value.
2.3.5 Trapezoidal Membership Function
Trapezoidal membership function in fuzzy logic can be represented as T= (l, m, n, u), where ‘l’ represents the lower limit of the original number, ‘[m, n]’ denotes the range for original number, and ‘u’ specifies the upper limit of the actual number. Eq. (2) represents the membership function for the positive Trapezoidal fuzzy value
Once membership functions are ready for the input and output parameters, fuzzy rules can be framed using “IF-THEN” rules. In general fuzzy rule-based system is a rule-based system, where fuzzy logic and fuzzy sets are used as tools to represent various forms of knowledge about the problem given. Fig. 1 shows the general structure of a fuzzy rule-based system.
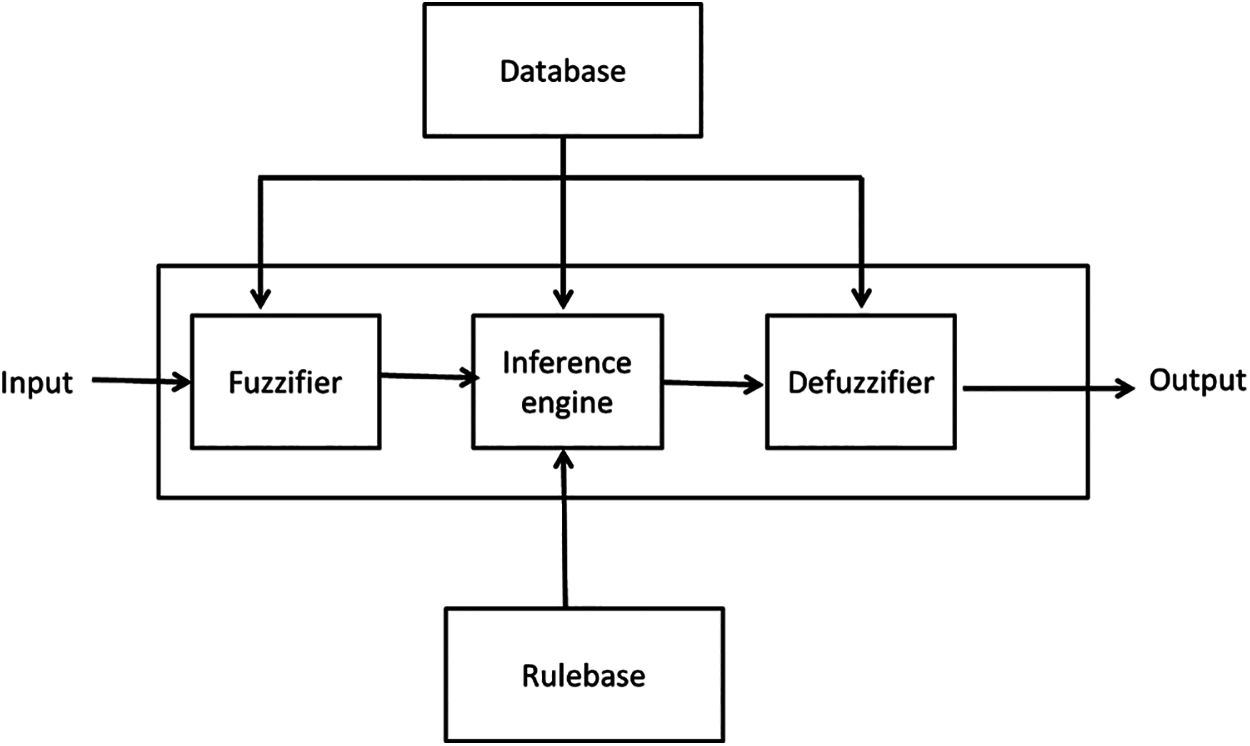
Figure 1: Fuzzy rule-based system structure
3 Fuzzy Logic Application for Mining Method Selection
In this section, various input parameters and output parameters for underground metal mining method selection have been identified. This section also addresses how the fuzzy logic is implemented for mining method selection based on input parameters and output parameters. The following sub-sections explain mining method selection using fuzzy logic.
3.1 Input Parameters Influencing Mining Method Selection
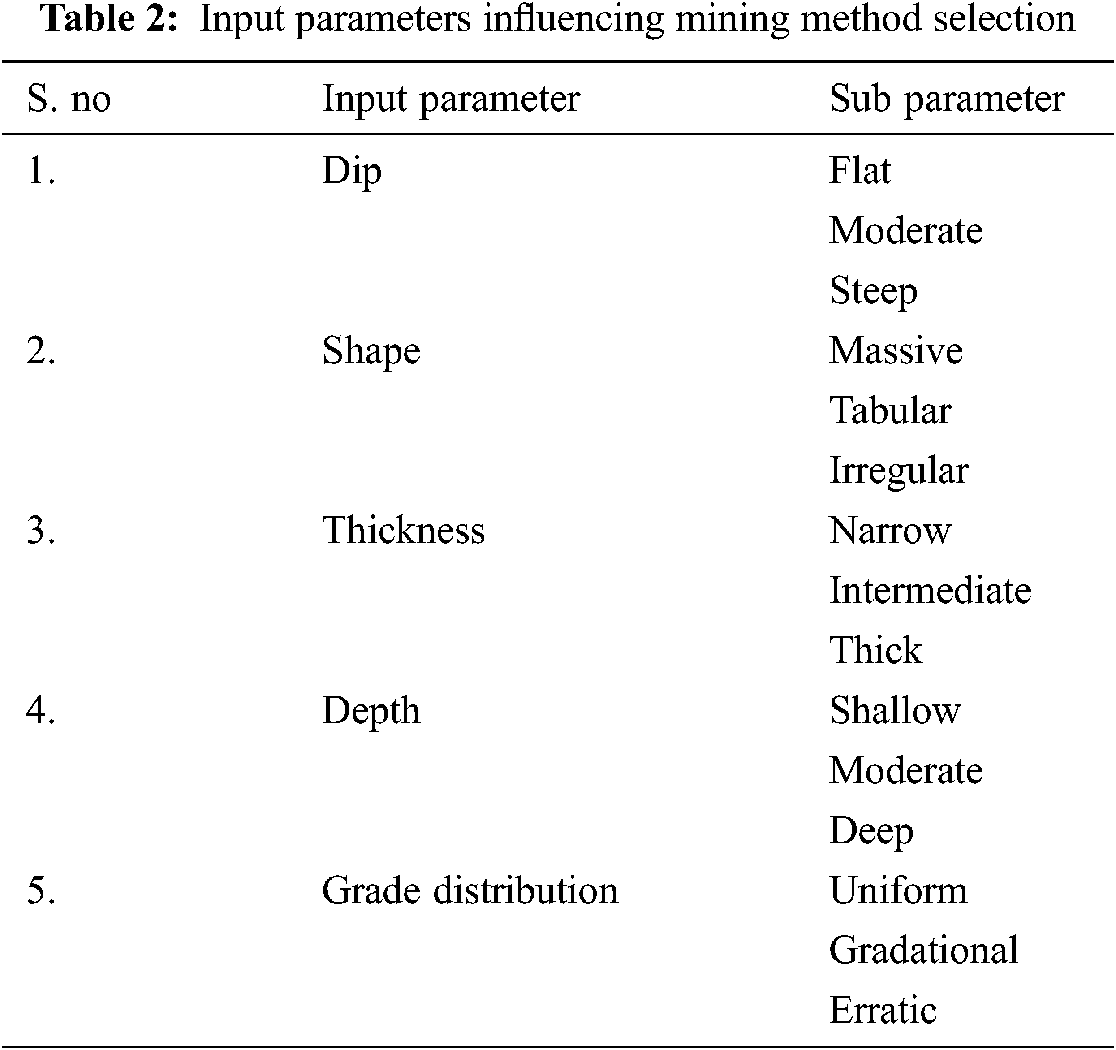
The selection of a preferable underground metal mining method depends on various influencing parameters. These parameters define the geological conditions of the ore deposits. The geological parameters that influence the mining method selection process are dip, shape, thickness, depth, grade distribution, RMR, RSS, and many other parameters [12–15]. In the present study, the more influencing parameters are considered for the selection of the mining method. These are dip, shape, thickness, depth, and grade distribution. Each input parameter is categorized into different sub-parameters. These sub-parameters specify the range of values to that specific category. Tab. 2 gives the five parameters, and its sub parameters.
3.2 Mining Methods as Output Parameters in Mining Method Selection
For various geological conditions, a single mining method is not sufficient for mining the minerals from underground. The mining methods considered in this study are block caving, sublevel stoping, sublevel caving, room and pillar, shrinkage stoping, cut and fill stoping, and square set stoping.
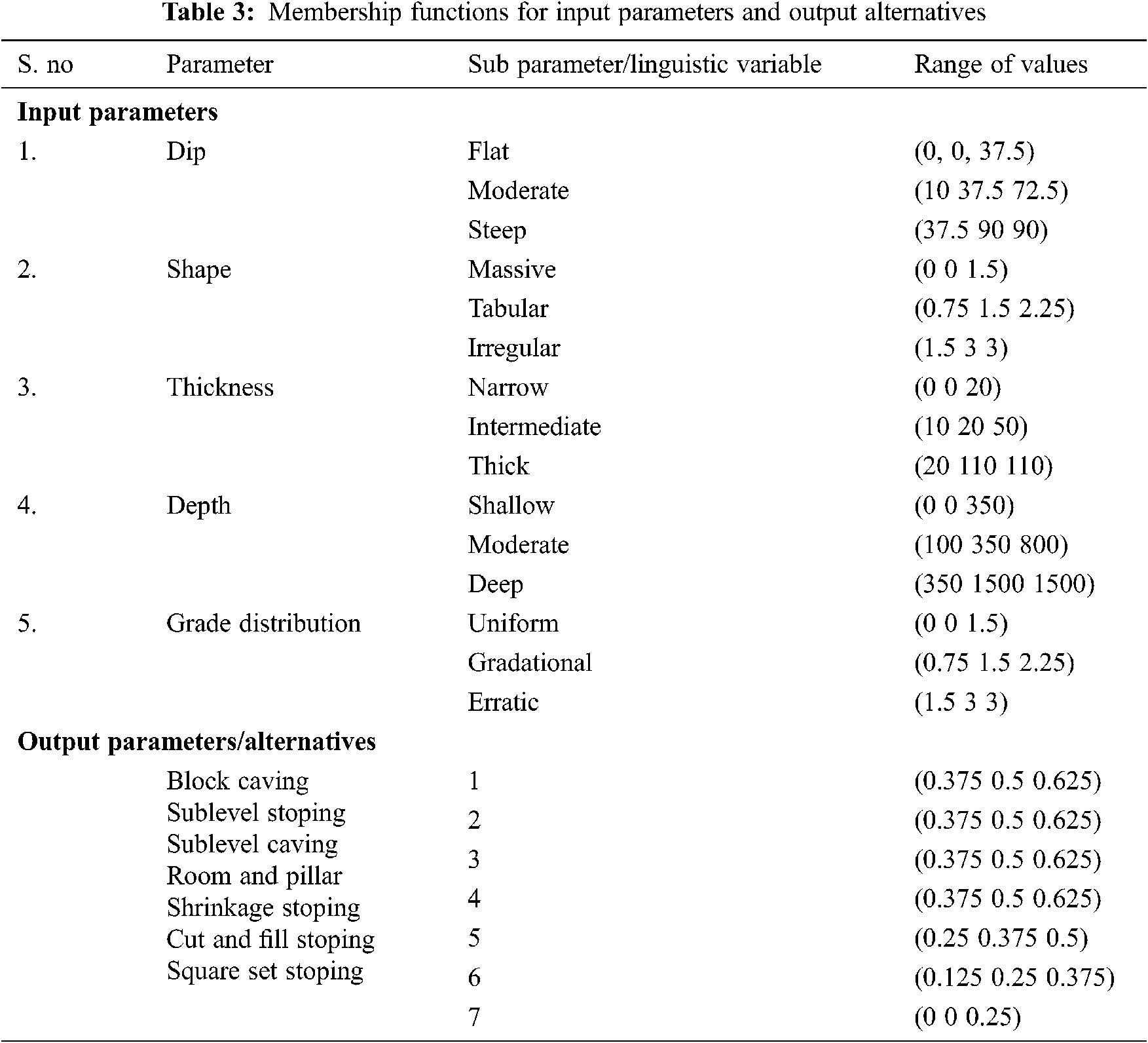
3.3 Membership Functions for Input Parameters and Output Alternatives
Tab. 3 shows the membership functions for the five input parameters and output parameters. For five different geological conditions, seven alternatives are to be ranked from higher to lower. The linguistic variables are the sub-parameters the input parameters. Thus the linguistic variable for these seven alternatives are named from 1 to 7. These linguistic variable ranges are common for all the alternatives or output parameters.
The following Figs. 2 and 3 show the membership functions for input parameters and output alternatives.
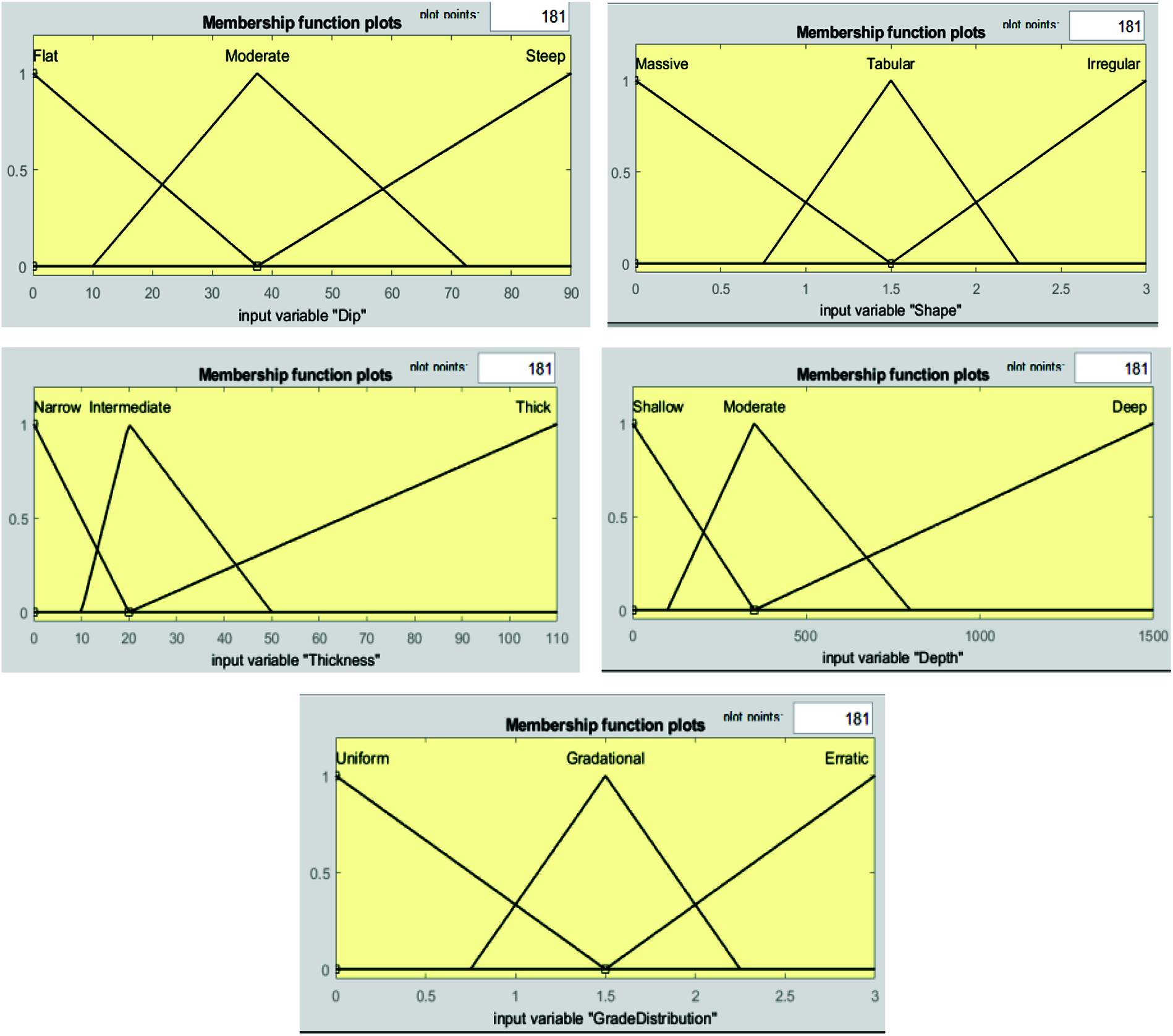
Figure 2: Membership functions of Dip, shape, thickness, depth, and grade distribution
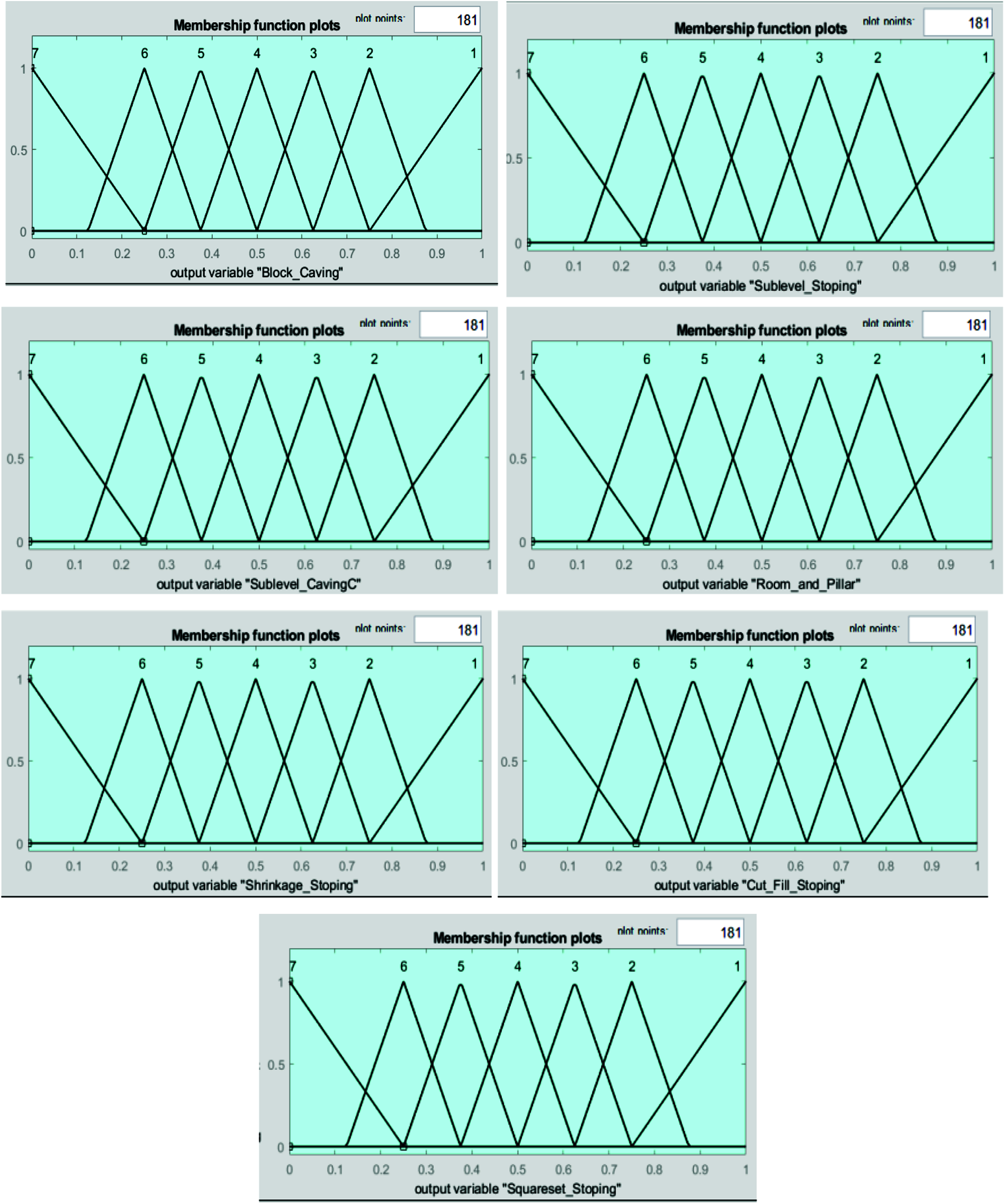
Figure 3: Membership functions of alternatives block caving, sublevel stoping, sublevel caving, room and pillar, shrinkage stoping, cut and fill stoping, and squareset stoping
3.4 Rule Based System for Mining Method Selection
The five input parameters dip, shape, thickness, depth, and grade distribution, are used to frame the rules in the rule-based system. The rules have been framed based on the previous study proposed by Miller et al. [16]. A total of 243 rules are framed using the five input parameters. These rules are framed using “IF-THEN” logic. For a specific rule, the seven mining methods are ranked from 1 to 7. Digit 1 indicates the highest priority, and 7 specifies the least priority [17]. The following is a sample rule which is framed in the rule-based system.
Ex:
IF Dip is Flat and Shape is Massive, and Thickness is Narrow, and Depth is Shallow, and Grade Distribution is Uniform
THEN Block caving is 2 and Sublevel stoping is 3, and Sublevel caving is 4 and Room and pillar is 1 and Shrinkage stoping is 5 and Cut and Fill is 7, and Squareset stoping is 6.
4 Model Validation Using Case Study
The developed fuzzy logic-based mining method selection is validated with the geological data of two Indian mines, namely Tummalapalle mine and Turamdih mine of Uranium Corporation of India Limited (UCIL). The geological conditions of these two mines are shown in Tab. 4.

The following are the results for the two specified mines based on the developed fuzzy logic rule-based model. Fig. 4 shows the data for the Tummalapalle mine, and it is identified that Room and Pillar (RP) mining method has the highest value of 0.871. The same mining method known as Room and Pillar method is adopted by the specified mine.
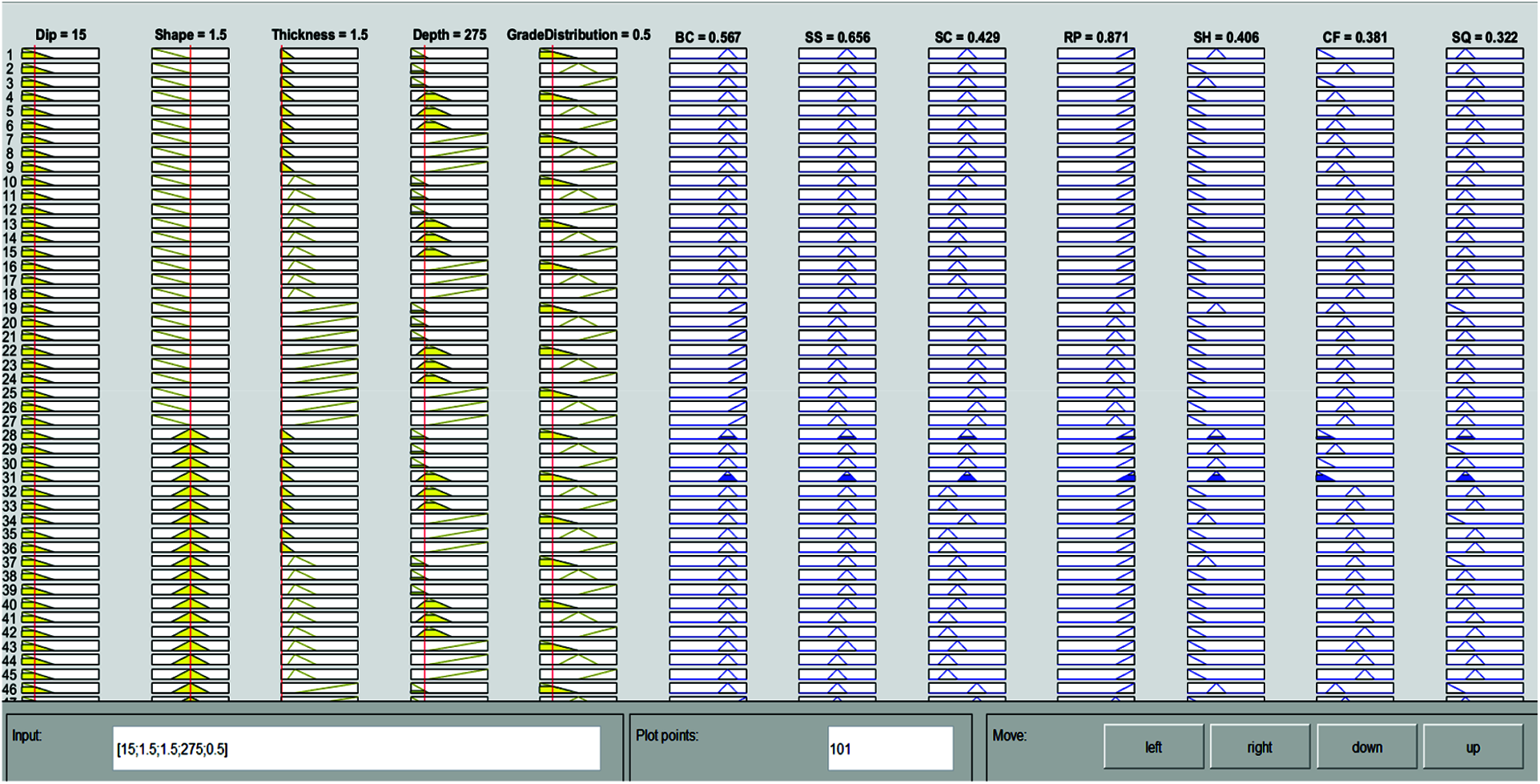
Figure 4: Scores of seven mining methods for tummalapalle mine
Similarly, geological data of the Turamdih mine is given to the developed fuzzy logic model. Fig. 5 shows the results for the Turamdih mine, and it is clear that Cut and Fill mining has the highest value of 0.904. The same cut and fill mining method is adopted by the specified mine.
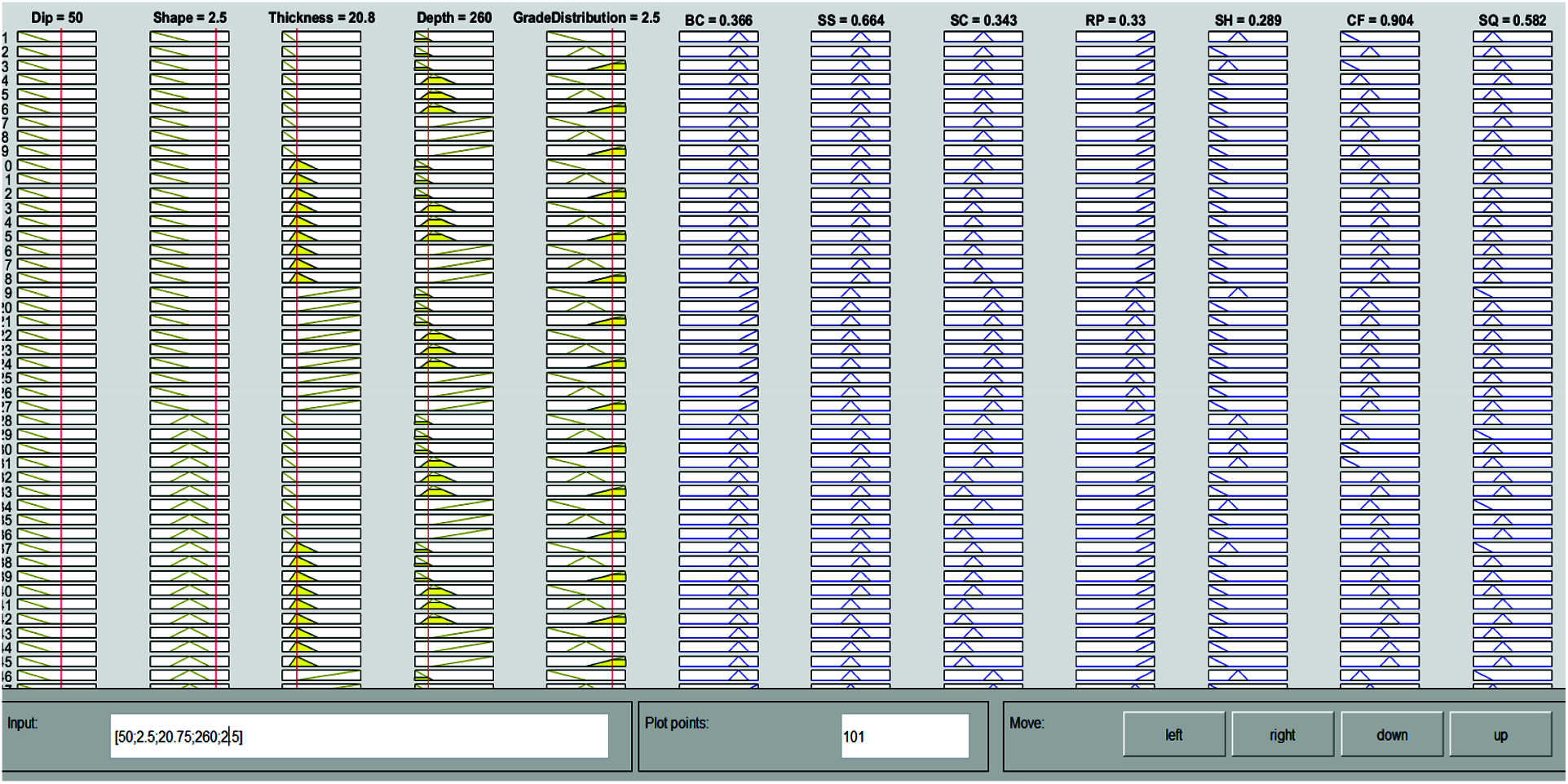
Figure 5: Scores of seven mining methods for turamdih mine
As underground mining method selection is based on multiple criteria, it it very difficult for the mining engineers to select proper mining method for extraction of the minerals. In this study, fuzzy logic-based underground metal mining method selection is developed. The five input parameters dip, shape, thickness, depth, and grade distribution considered in the study are uncertain and ambiguous in nature. This ambiguity is achieved through the fuzzy logic by considering the triangular membership function. A total of seven underground metal mining methods, namely block caving, sublevel stoping, sublevel caving, room and pillar, shrinkage stoping, cut and fill stoping, and square set stoping are selected for various geological conditions. The developed fuzzy logic-based model is also validated by two Indian mines. The results obtained from the developed model are the same with the mining methods used by the two specified mines.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. J. Deshmukh, “Elements of mining technology,” Vidyasewa Prakashan, I Edition, Dennet Co, Nagpur, India, 2014. [Google Scholar]
2. B. C. Balusa and J. Singam, “Underground mining method selection using WPM and PROMETHEE,” Journal of Institution of Engineers India Series, vol. 99, pp. 165–171, 2018. [Google Scholar]
3. S. Alpay and M. Yavuz, “A decision support system for underground mining,” in Int. Conf. on Industrial, Engineering and other Applications of Applied Intelligent Systems, Springer, Berlin, Heidelberg, pp. 334–343, 2007. [Google Scholar]
4. B. C. Balusa and A. K. Gorai, “Design of a multi-criteria decision making model using fuzzy-aHP for selection of appropriate underground metal mining method,” International Journal of Mining and Mineral Engineering, vol. 9, no. 4, pp. 259–301, 2018. [Google Scholar]
5. S. Gupta and U. Kumar, “An analytical hierarchy process (AHP)-guided decision model for underground mining method selection,” International Journal of Mining, Reclamation and Environment, vol. 26, no. 4, pp. 324–336, 2012. [Google Scholar]
6. B. C. Balusa and A. K. Gorai, “Sensitivity analysis of fuzzy-analytic hierarchical process (FAHP) decision-making model in selection of underground metal mining method,” Journal of Sustainable Mining, vol. 18, no. 1, pp. 8–17, 2019. [Google Scholar]
7. T. A. Thakre, O. K. Chaudhari and N. Dhawade, “A fuzzy logic multi criteria approach for evaluation of teachers performance,” Advances in Fuzzy Mathematics, vol. 12, no. 1, pp. 129–145, 2017. [Google Scholar]
8. C. V. Altrock and B. Krause, “Multi criteria decision making,” Fuzzy Sets and Systems, vol. 63, pp. 375–380, 1994. [Google Scholar]
9. B. Paterson, A. Jarre, C. L. Moloney, T. P. Fairweather and C. D. Van der Lingen, “A fuzzy-logic tool for multi-criteria decision making in fisheries: The case of the South African pelagic fishery,” Marine and Freshwater Research, vol. 58, no. 11, pp. 1056–1068, 2007. [Google Scholar]
10. L. A. Zadeh, “Fuzzy sets information and control,” The Journal of Symbolic Logic, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]
11. A. Aryanfar, A. Gholami, M. Pourgholi and M. Zandi, “Multicriteria wind potential assessment using fuzzy logic in decision making: A case study of Iran,” Wind Energy, vol. first Online, pp. 1–23, 2021. [Google Scholar]
12. B. C. Balusa and A. K. Gorai, “A comparative study of various multi-criteria decision-making models in underground mining method selection,” Journal of Institution of Engineers India Series, vol. 100, pp. 105–121, 2019. [Google Scholar]
13. B. C. Balusa, A. K. Gorai and S. Jayanthu, “Design of decision-making techniques using improved AHP and VIKOR for selection of underground mining method,” Recent Findings in Intelligent Computing Techniques, vol. 1, pp. 495–504, 2018. [Google Scholar]
14. B. C. Balusa and A. K. Gorai, “Analysing the role of safety level and capital investment in selection of underground metal mining method,” International Journal of Mining and Geo-Engineering, vol. 55, pp. 125–131, 2021. [Google Scholar]
15. B. C. Balusa and A. K. Gorai, “Hierarchical fuzzy-AHP-based multi-criteria decision making approach for selection of underground metal mining method,” Intelligent Decision Technologies, vol. Pre-press, no. Pre-press, pp. 1–16, 2021. [Google Scholar]
16. L. Miller-Tait, R. Pakalnis and R. Poulin, “UBC mining method selection,” in Proc. of the Mine Planning and Equipment Selection Symposium, Calgary, Canada, pp. 163–168, 1995. [Google Scholar]
17. Y. Lva, Q. Zhoua, Y. Li and W. Li, “A predictive maintenance system for multi-granularity faults based on adaBelief-bP neural network and fuzzy decision making,” Advanced Engineering Informatics, vol. 49, pp. 1–12, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |