Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023524
Article

Actuator Fluid Control Using Fuzzy Feedback for Soft Robotics Activities

K. Karnavel1,*, G. Shanmugasundaram2, Satish S. Salunkhe3, V. Kamatchi Sundari4, M. Shunmugathammal4 and Bal Krishna Saraswat5

1Anand Institute of Higher Technology, Chennai, 603103, India
2Sri Manakula Vinayagar Engineering College, Puducherry, 605107, India
3Computer Engineering Department, Terna Engineering College, 400706, India
4SRM Institute of Science and Technology, Ramapuram, Chennai, 600089, India
5Faculty of Engineering & Technology, SRM Institute of Science & Technology, NCR Campus, Uttar Pradesh, 201204, India
*Corresponding Author: K. Karnavel. Email: treseofkarnavel@gmail.com
Received: 11 September 2021; Accepted: 22 October 2021

Abstract: Soft robotics is a new field that uses actuators that are non-standard and compatible materials. Industrial robotics is high-throughput manufacturing devices that are quick and accurate. They are built on rigid-body mechanisms. The advancement of robotic production now depends on the inclusion of staff in manufacturing processes, allowing for the completion of activities that need cognitive abilities that are now beyond the scope of artificial networks. Hydrostatic pressure is used to achieve high deflections of structures that are based on the elastomeric in Fluid Actuators (FAs). Soft actuators based on the fluid are a popular choice safe for humans and lightweight robots. However, owing to a deficiency of durable, accurate, and affordable sensors that can be combined with actuator systems that are highly deformable and that use low-cost materials and production, closed-loop management of such actuators remains difficult. Such actuators, in combination with hydrodynamic force feedback, form a series-elastic actuation (SEA), which eliminates virtually friction from all driving-point. Fuzzy control is a smart computing analysis technique that enables complex systems to be controlled independently of a mathematical model. Fuzzy logic is used to optimize the parameters of a Fuzzy Logic Controller (FLC’s) function to find the best rational controller for an automated robot. Because discontinuous endpoint friction is undetectable to the pressure of the fluid internally, feedback from traditional external force using force/tactile sensing is preferred. As a result, a fuzzy-based control using linear feedback was developed and used to test the integrated system’s response dynamically and location accuracy.

Keywords: Fluid Actuators; Fuzzy Logic Controller (FLC); Linear Feedback; soft robotics

1  Introduction

Recently, human-friendly robots are involved in many business sectors for regularizing their commercial and basic activities quick and accurate. Especially, the industrial manufacturing units the usage of robots are inevitable for increasing production process with accurate completion of activities that brings cognitive abilities that are beyond the scope of artificial systems. Thereby, a new breed of the robotic system has emerged, with architecture and control techniques based on the potential to execute stable physical human-robot encounters. However, it provides flexibility of including an advancement of modular robotic devices such as serial elastic actuators are capable for high-throughput devices have aided the advent of new structures with sufficient protection and engagement goals. Moreover, it is still rigid connection robots with control and sensing capabilities that enable them to operate quite safely in diverse societies [1]. It is termed as “soft robotics”. It takes a step far to use mechanical enforcement for protection; again, it leads a complicated task for approaching the extraordinary capacities of advanced life forms. Soft wearable robotics is a new field that uses soft, mobile, and structural flexible in the materials fabrication. It produces distortion less output by soft actuators, as well as the apparent capability to various conditions because of material compliance, are the main aspects of this technique [2]. Although several emerging actuation methods such as Electro Active Polymers (EAPs), Shape Memory Alloys actuators, etc. are being used in soft robots whereas fluid pressure namely pneumatic and hydraulic remain the most widely used actuation system [3]. Elastomeric frameworks with integrated chambers support to modify their volume depending on the input pressurized fluid supply in Flexible Fluidic Actuators (FFAs). Furthermore, the actuator deforms is created based on the chamber’s position and displacement. In additionally, Bend-based Flexible Fluidic Actuators (B-FFAs) are a common sub-category that converts the shift in chamber volume into a bending movement. Thereby, it forms continuous snake-like robotic actuator which has potential of robotic manipulation role in the confined surrounding. The enhancement of soft robotics requiring external risks includes rescue zones [4] or Minimally Invasive Operation [5] is growing rapidly. However, the system model is necessary to ensure safe before interaction of objects from external environmental. According to dynamic model, the input pressure of actuator is linearly adjusted by monitoring open-loop pressure-driven soft actuators [6]. Conversely, a closed-loop feedback scheme is involved visual or magnetic detection systems based on location input given by outside localization sensors [7]. An appropriate feedback control is ensembles by embedded sensors that allow for precise recovery of the actual actuator model. The enhancement of soft-bodied actuators requires unique sensing methods than the rigid-bodied counterparts such as motor encoders face the challenges during the sensor integration [8]. Similarly, fuzzy decision modeling is really support the identification of uncertainty present in the unknown weight measurement [9]. Consequentially, 2-tuple spherical fuzzy linguistic operators are highly influencing a model for providing accurate estimation of unknown geometric weights [10]. However, efficiency of the operation is further improves by introducing interval-valued picture fuzzy variable for group linguistic decision marking [11,12] which enhance the aggregation operators. A protective layer in liquid droplets is made up of hydrophobic particles that ensure no wetting property. Thereby, liquid marbles are considered active droplets and are made of composite material [13]. Furthermore, varies friction, surface tension, or viscosity on a liquid’s surface serve as a stimulus for such actuators. A fluid-based actuator has several drawbacks as opposed to a solid-material actuator which has limited consistency of leakage due to minute particles caught in the fluid, causing efficient material transfer impossible. While interacting with other fluids, there is a complex inflow of fluid and can combine in unpredictable ways. Fluids are therefore particularly vulnerable to such environmental circumstances, and small amounts can evaporate, preventing their use in versatile actuators.

2  Literature Survey

Fuzzy control is a fundamental method that relates to professional systems and enables complex systems to be controlled without the use of theoretical equations. Due to this new property, fuzzy control is well suited to dynamic systems that are hard to analyze analytically, often due to a lack of understanding of the system or the inability to define the innovative technique owing to the unquantifiability of the method outputs and inputs. As a result, this method can be viewed as a method for converting a linguistic control scheme dependent on an operator’s experience into an automated control policy [14]. A fuzzy logic controller in comparison with other features provides quick and accurate dynamic behavior, allows for knowledge analysis using a false and true scale. It is relatively stable and resistant to noise and imprecision present in the data input. The principles include the arbitrary order and membership function number or form can be changed to control the programming of Fuzzy controller logic [15].

The fuzzy logic controller has been extensively used by scientists to create controllers for a broad array of applications in various fields since its inception. The smart medicine dispenser [16] is analyzed based on information flow from a body temperature of a patient; evaluation of asthma data is performed using a robust fuzzy algorithm; identify the individual reasoning ability at a various precision rate by utilizing terms and linguistic expressions and Wireless Sensor Networks (WSNs) include five inputs namely energy, base station distance, centrality, and hops and node density count are obtained using clustering algorithm is fault-tolerant. The parameter in regards to controlling the functioning of Unmanned Aerial Vehicle (UAV) has to be properly selected [17]; the car encloses a pendulum in an inverted manner has to be stabilized; for an uncertain, non-linear, and chaotic Multi-input Multi-output (MIMO) systems uses this controlling methodology; implementation of a standard PID controller into an optimization technique depending on fuzzy norms [18]; control of unpredictable strict-feedback in non-linear systems restrict asymmetric output depending on the changes in input saturation at a various time; humanoids are recovered by using the type-1 fuzzy logic-based controller; Adaptive Neuro-Fuzzy Inference System (ANFIS) controller is used to control the navigation of individual and numerous mobile robot in heavily cluttered environments. In robotic systems, fuzzy logic-based control methods are generally determined using location and speed data collected from sensors placed in every joint part of the robot [19].

In soft wearable robotics, embedded sensors must endure extremely large distortion while maintaining the high adherence of the corresponding actuator. The field of expandable electronics is becoming increasingly common in this context [20]. This method aims to create electronic circuits that can be reproduced on a variety of soft, foldable, expandable, and even biocompatible materials. The creation of elastomeric-based curve and stretch sensors that respond to actuator distortion while interacting with basic motion mechanics and the method includes microchannels packed with fluid conductors embedded in the actuator system. The variation in electric potential is caused due to the deformation in the cross-section of the microchannel, which uses a functionalized sodium chloride (NaCl) solvent as a conductive fluid to provide sensing channels that can sense the stretching structure of the actuator. [21], describes a simplified soft actuator stage sensing device. The size of a pneumatic artificial muscle (PAM) is calculated in this study by wrapping a wise conductive insulated wire around the actuator that raises its inductance with the simultaneous reduction in the actuator [22]. The above sensing methods have a high degree of form customization, making it easier to tailor the sensor’s form to a wide range of soft robot models, at the expense of extremely complex manufacturing processes, that have a significant impact on sensor efficiency and consistency.

3  System Model

In soft wearable robots, the proposed fluid actuators provide a fuzzy-based optimization and linear feedback controller. The fluid-driven technique is the most widely used form of actuation in soft industrial robotics. To tempt motion or produce force, this technique employs fluidic pressurization of complex cavities inside soft actuators. Deformable fluids are used to produce adjustable stiffness throughout complex actuators in flexible fluidic actuators (FFAs) driven systems.

3.1 Fuzzy Based Optimization

Fuzzy-based optimization in the fluid actuator is considered as the main functional membership parameter, even granularity and number of rules enables us to provide the best solution to most of the challenges encountered during the development of the soft wearable robots. Fuzzy control is a smart computing analysis technique that enables complex systems to be controlled independently of a mathematical model. Fig. 1 shows the architecture of the fuzzy logic controller. The fuzzy-based optimization control is well suited to dynamic systems that are hard to analyze analytically, perhaps due to inadequate understanding of the system or the inability to define the empirical approach due to the unquantifiability of the method inputs and outputs. In soft wearable robots, fuzzy logic-based optimization control algorithms are usually determined using location and speed data acquired from sensors placed on every robot joint. The following are typical technical advancements that use location and speed concerning time by deriving the error and first error are mentioned as a linguistic term in an optimization based on fuzzy logic: (1) Hybrid information systems, which include fuzzy-PID, force or position, and motion or force; (2) Fuzzy optimization technique with obstacle detection and dynamic instability; (3) Fuzzy optimization technique for effective scalability. (4) Fractional derivative fuzzy controller-based optimization; (5) Dynamic fractional PID control scheme; (6) Feedback linearization methods depend on PID structures to control extremely nonlinear industrial systems, even when variable fluctuations, noise, and instabilities are present.

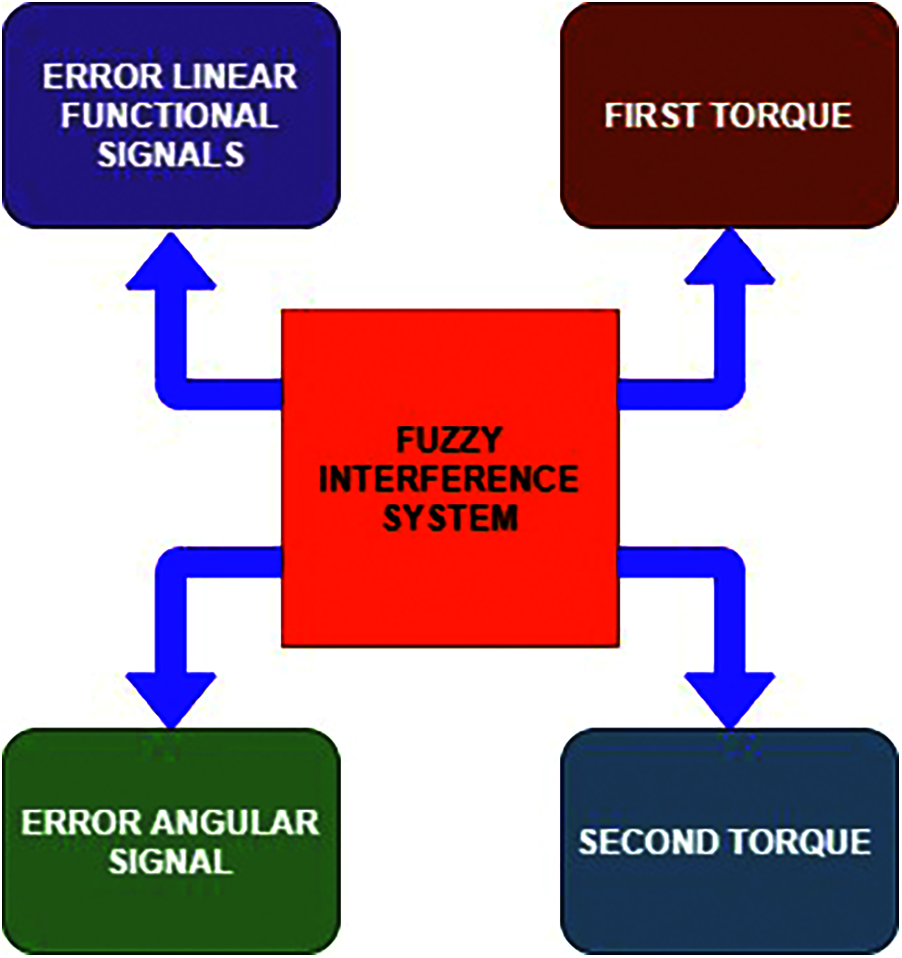
Figure 1: Architecture of FLC (Fuzzy Logic Controller)

Fuzzy Logic Controllers (FLC) based optimization is of different types namely FLC-PD, FLC-PI, and FLC-PID. Based on the selection of the fuzzy-based optimization the corresponding input data such as error e, change in error Δ e, and the average errors ∑e are used for robotics development. The traditional Flexible Liquid Crystal Polymer (FLC-P) based proportional fuzzy controller is derived as follows,

u=kp⋅e(k) (1)

Here, the proportional gain coefficient is denoted as kp and the control output is denoted as u. In optimization-based P-FLC, e=Aiandu=Bj . Here, the linguistic variables are represented as AiandBj,i,j=1,2,…..,n.

A Proportional-Differential (PD) FLC based optimization is enhanced by utilizing error and change in error model is represented in the following expression,

u=kp⋅e+kd⋅Δe (2)

Here, the coefficient of the proportional is denoted as kp and coefficient of the differential gain is denoted as kd . The control output is represented as u. In the optimization-based FLC-P, e=AiandΔe=Bj so that u=Ck . Here, the linguistic variables are presented as Ai,BjandCk . i=1,2,…..,n1,j=1,2,…..,n2andk=1,2,…..,n3 . The expression for the optimization-based conventional FLC-PI is given below,

u=kpe+kl∫edt (3)

Here, the proportional gain coefficient is denoted as kp and the integral gain coefficient is denoted as kl . The control output is denoted as u. In FLC-PI, e=Aiand∑e=Bj so that u=Ck . Here, the linguistic variables are presented as Ai,BjandCk . This kind of Fuzzy logic controller-based optimization has high efficiency in the stable state and decreases error but still, it has a longer rise fall times. The function of the integral controller produces certain undesirable features, even though the integrator is implemented solely to address the problem of errors in a static situation. Fuzzy logic Controller (FLC) is identical to PID. Thus, PID enable to improve the output in regards to the rise fall time, errors in a stable state, as well as overshoot, is being represented in the following expression,

uPID=kp⋅e+kd⋅Δe+kl∫0t⁡e.dt (4)

The FLC-PID includes the conditions such as e=Ai,Δe=Bjand∑e=Ck so that u=Dl . Here, i=1,2,…..,n1,j=1,2,…..,n2andk=1,2,…..,n3andl=1,…,m .

A PD fuzzy controller-based optimization cannot eradicate error in the static condition whereas PI-fuzzy controller-based optimization can solve the challenges. According to the integral terms in the dependent variables, it seems to have a slower response. An FLC-PID is proposed to satisfy the functional requirement including a quick rise time, lesser settling time, 0 static status errors, and minimal overshoot. Fuzzy logic controller-PID is usually four-dimensional in which it contains three inputs and one output device with error e, change in error ∆e , and a sum of errors ∑e are regarded as their control measures. Nonetheless, an FLC encourages a long processing period, resulting in an unnecessarily delayed reaction, which is incompatible with tasks that require a fast response, such as joint trajectory regulation of the 2-DoF manipulator robot is achieved. Conversion of PID-FLC into an FLC-PD is parallel connected with different fuzzy gains, integral fuzzy controllers, fuzzy integrators, predetermined fuzzy controllers. FLC-PD includes the controls gain in steady-state, integral action, and gain controller.

The evaluation effects of joint trajectory prediction in manipulator robots are contrasted with the outcomes obtained from traditional fuzzy-PID controllers, such an option enables representative changes. It should be remembered that using the second derivative error in the approved fuzzy controller-based optimization becomes unique and thus contributes to the regulation of manipulator robots. The proposed novel approach is used to monitor the joint trajectory monitoring of a 2-DoF planar robot and the corresponding simulation is produced by utilizing MatLab or Simulink tools. The performance of the fuzzy controller with the traditional PID controller is evaluated.

In the manipulator robot model, to acquire the conceptual framework of a 2-DoF planar of i = 1, 2,…, n. q generalized coordinates and joints are determined with the below-recommended notation.

 τ=M(q)q..+C(q,q.)+G(q)+F(q.) (5)

Here, the generalized forces vector is denoted as τ , inertia matrix is denoted as M , centrifuge and Coriolis force vectors is denoted as C , the gravitational force vector is denoted as G , the frictional force vector is denoted as F , joint acceleration vector is q¨ , joint position vector is denoted as q and the joint speed vector is denoted as q˙ . The position of the centroids of every connection is determined using a 2-DoF planar in a manipulator robot. The systematic analysis of the manipulator can be represented depending on the Lagrange-Euler formulation is expressed below,

M=[M11M21M12M22] (6)

M11=m1⋅lc12+m2⋅[l12+lc22+2⋅l1⋅lc2⋅cos(θ2)]+I1+I2 (7)

M12=m2⋅l1⋅lc2⋅cos(θ2)+m2⋅lc22+I2 (8)

M21=m2⋅l1⋅lc2⋅cos(θ2)+m2⋅lc22+I2 (9)

M22=m2⋅lc22+I2 (10)

C=[C11C21] (11)

C11=−m2⋅l1⋅lc2⋅sin(θ2)⋅θ˙22−2⋅l1⋅lc2⋅sin(θ2)⋅θ˙1⋅θ˙2 (12)

C21=m2⋅l1⋅lc2⋅sin(θ2)⋅θ˙12 (13)

G=[G11G21] (14)

G11={m1⋅lc1⋅cos(θ1)+m2⋅[l1⋅cos(θ1)+lc2⋅cos(θ1+θ2)]}⋅g (15)

G21=[m2⋅lc2⋅cos(θ1+θ2)]⋅g (16)

F=[F11F21] (17)

Here, the mass of the first link and second link are represented as m1andm2 , length of the first and second link is represented as l1andl2 , length from the origin of the first and second link to its centroid is represented as lc1andlc2 , and moment of inertia of the first and second link concerning the z-axis is represented as I1andI2 .

3.2 Linear Feedback Controlled Fluid Actuators

The two pressure-driven flexible fluid actuators (FFAs) are evenly positioned concerning the central line in the soft wearable robotic elastomeric structure of the module. A flexible fluid actuator has a dual cylinder container with an in-extensible loop inserted into the elastomeric element along the channel longitudinal wall for radial reinforcement. As of press, the chamber structure permits it to stretch longitudinal direction with limited lateral extension to the central axes. The module’s ability to fold around steady radius curves is determined by the perfect elongation of one Flexible fluid actuators (FFA) at a period. A Degree of Freedom (DoF) present within the module is in terms of kinematics, which is defined as the plane y-z with bending angle produced by the pressurized Flexible fluid actuators (FFA) at a period. Based on two Flexible fluid actuators (FFA) is enabled, the angle may be negative or positive. The two actuators are parallel pressurized at a similar time will provide an increased DoF, resulting in a 30% elongation of the module longitudinally. The power exerted in enabling the pressurization of at least one FFA at a period ignores the DoF extension module. An evenly controlled two combined small latching valve and main pressure line in between main regulated pressure line and FFA chambers are used to manipulate FFAs pressure. The integrated latching valves are enabled by an embedded wireless microcontroller along with a Printed Circuit Board (PCB) in response to the main systems commands. The pressure in the mainline is regulated by a relative pressure transducer, and wireless contact with the support of module microcontrollers using a temporized control scheme. The module consists of an inner broadcast channel for potential deployment on a multi-module soft wearable robotic design that enables path communication between the main pressure lines with other modules.

Impedance monitoring based on system Flexible fluid actuators uses a velocity trigger actuator namely fluid servo-valve, in which the torque source is obtained from an electric motor to regulate fluid flow and also friction to make the desired impedance. Flexible fluid actuators (FFAs) are engineered to have very weak mechanical impedance but still the friction in the transmission, joints, and motor shaft bearings. The force in linear feedback control in FFAs is used to optimize the mechanical impedance in a straightforward process. 1-DOF inertia-spring-damper mechanism with dynamical friction Ff(x,x˙) uses a simple proportional force feedback Fa(t)=KfFe(t) in which Kf is the constant gain of force feedback. The motion for a closed-loop system is being represented as follows,

mx.. +bx.+kx+Ff(x,x.)=Fa+Fe=(Kf+1)Fe (18)

The above equation is rearranged into an equivalent system as follows,

m(Kf+1)x⃛+b(Kf+1)x.+k(Kf+1)x+Ff(Kf+1)(x,x.)=Fe (19)

If there is an increment in Kf , then the system’s inertia, stiffness, nonlinear friction, and damping all decrease proportionally. This method can mathematically be seen to be passive for any Kf≥−1 , in which “passive” corresponds to a stable system in the presence of any possible surrounding impedance. An actual device usually has certain internal degrees of freedom, either intentional or unintentional resulting in a condition where sensing and actuation terminals are not in synchronization.

The passivity range for 1-DOF event of Kf≥−1 is a part of the surrounding passive condition via the utilization of linear damping estimations and linear stiffness for nonlinear friction of the actuator (k,b). End-effectors (ke,be) is applicable to force feedback via the internal force Fa(t)=KfFp(t) . Lead to lack of internal actuator motion or inherent physical resonance for DOF feedback port such as 1-DOF case or the 2-DOF internal feedback force case might lead to the tighter passivity restriction −1≤Kf≤1 . In reality, passivity limits can be deliberately ignored to obtain lower terminal impedance if the surrounding situation provides a known set of impedances. Unstable environmental interactions such as static surface interaction as well as coupling to high inertia must be avoided. In the linear model for the manipulator device, the target impedance is passively made by internal as well as external force feedback. These findings are typical, demonstrating that at specific frequencies, force external feedback normally improves force internal feedback. Force Internal feedback is especially unreliable when the endpoint friction is high, but it is satisfactory when the endpoint mass is wide enough (me >> m). Passivity constraints mean that no kind of force feedback can increase frequency and impedance outside the passive event.

With the conservative passivity range Kf=1 , it is possible to obtain the target endpoint impedance of force feedback internally at the lower frequency range:

lims→0⁡Z(s)|Kf=1=(k+2ke)ks+kke(2ks+k)s (20)

Identify the conditions in which the actuator is not back-driven k≫ks,ke Force feedback internally cannot lower the end impedance dynamically in such a situation:

lims→0⁡Z(s)|Kf=1,k≫{ks,ke}=(ks+ke)s (21)

If the actuator is back-driven, then the transmission resistance is greater than the moving and end friction ks≫k,ke ,

lims→0⁡Z(s)|Kf=1,ks≫{k,ke}=(12k+ke)s (22)

The force feedback internally is involved in reducing to half of the driving point friction dynamically.

Force feedback structure includes a force feedback filter that substitutes the proportionate force gain Kf→Kf(s) model-based force control, Natural Admittance Control (NAC), and the distortion observer control (DOB) system are techniques implemented to increase impedance correction performance besides basic proportional force feedback. Instead of implementing force feedback control ability equally for all frequencies in the methods enable maximum force feedback to an endpoint at lower frequencies. The system’s stiffness, friction, and damping prevail independently of attempting to minimize inertia at high frequency, exceeding causality and passivity limits. Fig. 2 shows the feedback control within the closed-loop model.

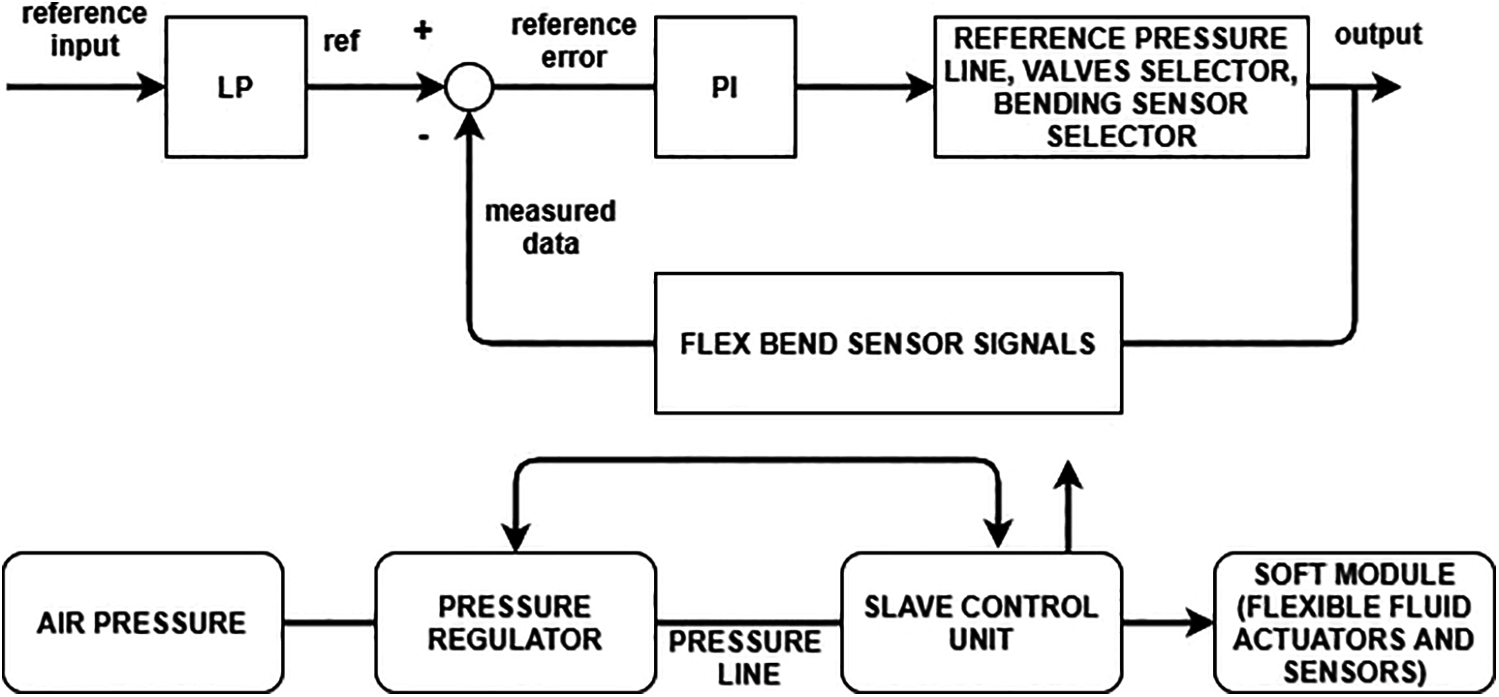
Figure 2: Linear feedback controller in a soft wearable robotic structural model

Flexible fluid actuators have a high force density that permits a low-end point mass in serial-chain exploiters with several degrees of freedom. An intentional sequence of elasticity and damping is tuned by changing the fluid conformity and transmitting the internal geometry hoses. The joint torques can be estimated by measuring the internal pressure in the mainline of fluid actuators. Internal pressure calculations do not reveal the endpoint static friction. Exterior contact forces can be determined with high accuracy by using internal fluid pressure parameters and soft-continuum fluid actuators depending on the material elastic modulus and non-rubbing membrane closures but still, these are not required for endpoint wiring.

4  Result and Discussion

The outcomes of the proposed controller and actuators to stabilize the mobile robot are presented in this section. The suggested controller is used to monitor the physical dimensions of a flexible manipulator. Simulation experiments are performed for the sake of contrast. To demonstrate the controller’s robustness.

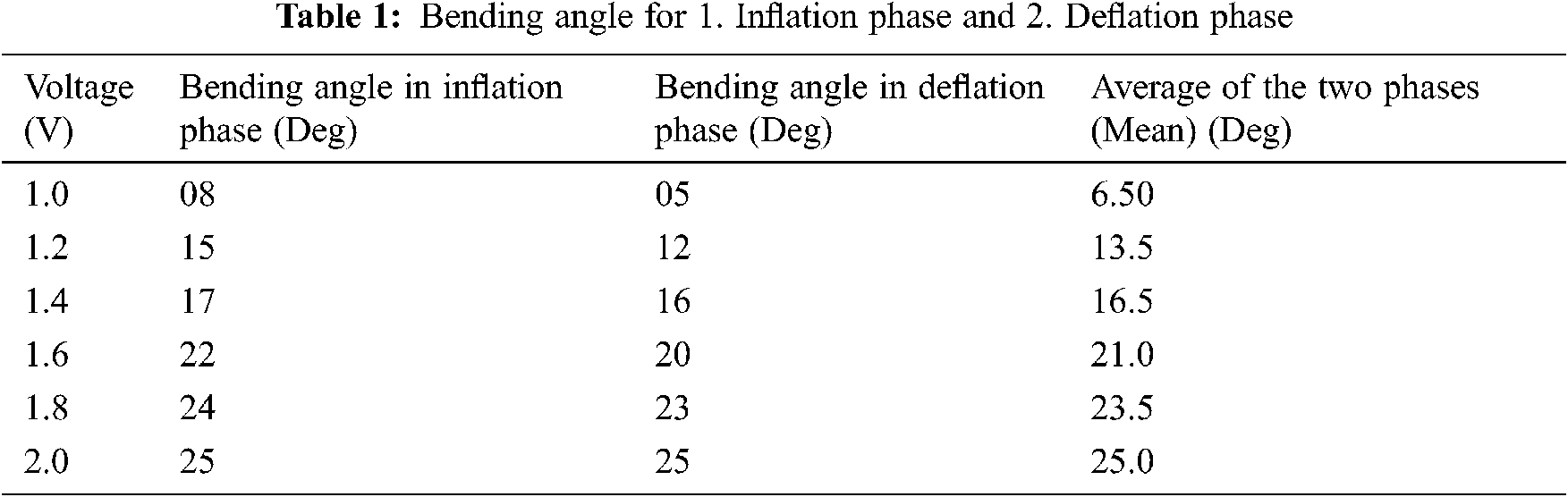
Tab. 1 indicates the values obtained when fitting the calibration curve with the sensors. The Root mean Square Error (RMSE) obtained for the inflation phase is 0.22, the deflation phase is 0.056 and for the average phase is 0.182. The measurement original data includes the three calibration curves which are being estimated via inflation stage, deflation stage, and average two stages effectively measure the bending angle. These curves are produced by utilizing a smoothing curve fit, with a 0.99 index value of R-square is being validated for all fits. The inflation curve has a Root Mean Square Error (RMSE) of 1.17 degrees and the deflation curve has an RMSE of 1.2 degrees concerning the mean curve.

The signal of the GT method is contrasted to the measured sensor’s reaction utilizing an average curve to assess the accuracy of the calibration protocol and the appropriateness of the chosen sensors. With angles higher than 5 degrees, this contrast reinforces the flex fold sensors with higher precision and repeatability. The RMSE among these two curves is observed to be 1.3 degrees and involved in ensuring the estimated accuracy value depending on the RMSE value.

Tab. 2 shows the soft module’s dynamic response when provided with the reference signal. A mechanism similar to stick-slip and mechanical static friction causes the delay between both the actual and nominal responses. The module does not begin to shift until the pressure reaches those limits for every equilibrium point. As a result, a consistent delay of around 0.3 seconds affects the module’s transient performance.

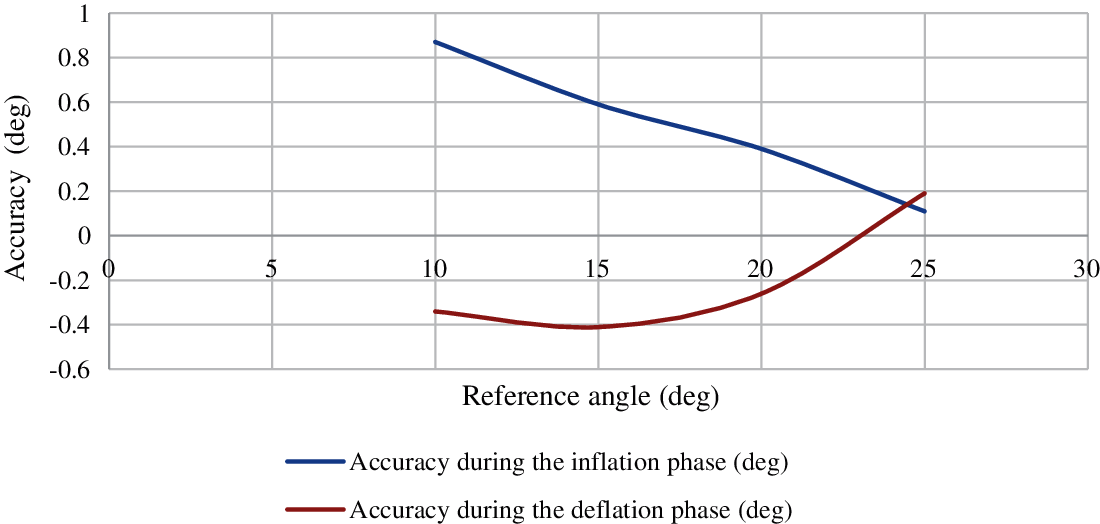
Figure 3: Evaluation of the system accuracy during the inflation and deflation phase

The above Fig. 3 shows the accuracy of the system examined with four different reference angles during the path of cyclic excitation. The excitation path is separated into the phase of inflation and the phase of deflation. The linear model for the soft wearable robots includes the endpoint impedance is passively made by force feedback internally as well as externally. The obtained results are typically demonstrated at low–mid frequencies displays that the external force feedback generally performs better than internal force feedback. If the endpoint friction is high, then internal force feedback is especially ineffective but still, it is superior when the endpoint mass is wide adequate. Passivity range represents that no other kind of force feedback can increase high-frequency impedance outside the passive event.

5  Conclusion

In this paper, the soft wearable robot with fuzzy-based optimization and linear feedback-controlled fluid actuators is discussed. The activation functions of soft robot has controlled through trajectory monitoring on the kinematics and dynamic performance output of the model. The secured human friendly interaction has risen dramatically with help of soft wearable robotics that attempt to meet the need of utilizing the shock-absorbing properties of the components. Moreover, it has significantly improved the accuracy of perceptive sensing that would do from efficient linear fuzzy feedback controllers of the FFAs. The convergence of flex bend sensors into a soft bending framework is being actuated by pressure-controlled FFAs. Comparatively, Non-back-driven actuators weaken endpoint estimation in fluid-actuated models despite specific endpoint detection. However, proposed model has produced a reliable endpoint state evaluation is dependent on driving-point state input and internal pressure.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Schaffer, A. Eiberger, O. Grebenstein, M. Haddadin, S. Ott et al., “Soft robotics: From torque feedback controlled lightweight robots to intrinsically compliant systems,” IEEE Robotics and Automation Magazine, vol. 15, no. 3, pp. 20–30, 2008. [Google Scholar]

 2.  D. Rus and M. T. Tolley, “Design, fabrication and control of soft robots,” Nature, vol. 521, no. 7553, pp. 467–475, 2015. [Google Scholar]

 3.  C. Laschi and M. Cianchetti, “Soft robotics: New perspectives for robot body ware and control,” Bionics and Biomimetics, vol. 2, pp. 3, 2014. [Google Scholar]

 4.  M. Cianchetti, T. Ranzani, G. Gerboni, T. Nanayakkara, K. Althoefer et al., “Soft robotics technologies to address shortcomings in today’s minimally invasive surgery: The stiff-flop approach,” Soft Robotics, vol. 1, no. 2, pp. 122–131, 2014. [Google Scholar]

 5.  G. Gerboni, T. Ranzani, A. Diodato, G. Ciuti, M. Cianchetti et al., “Modular soft mechatronic manipulator for minimally invasive surgery: Overall architecture and development of a fully integrated soft module,” Meccanica, vol. 50, no. 11, pp. 2865–2878, 2015. [Google Scholar]

 6.  C. D. Onal and D. Rus, “Autonomous undulatory serpentine locomotion utilizing body dynamics of a fluidic soft robot,” Bioinspiration & Biomimetics, vol. 8, no. 2, pp. 026003, 2013. [Google Scholar]

 7.  B. Chang, A. Chew, N. Naghshineh and C. Menon, “A spatial bending fluidic actuator: Fabrication and quasi-static characteristics,” Smart Materials and Structures, vol. 21, no. 4, pp. 045008, 2012. [Google Scholar]

 8.  P. Polygerinos, Z. Wang, J. T. Overvelde, K. C. Galloway, R. J. Wood et al., “Modeling of soft fiber-reinforced bending actuators,” IEEE Transactions on Robotics, vol. 31, no. 3, pp. 778–789, 2015. [Google Scholar]

 9.  S. Ashraf, S. Abdullah and S. Khan, “Fuzzy decision support modeling for internet finance soft power evaluation based on sine trigonometric Pythagorean fuzzy information,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 2, pp. 3101–3119, 2021. [Google Scholar]

10. S. Abdullah, O. Barukab, M. Qiyas, M. Arif and S. A. Khan, “Analysis of decision support system based on 2-tuple spherical fuzzy linguistic aggregation information,” Applied Sciences, vol. 10, no. 1, pp. 276, 2020. [Google Scholar]

11. M. Qiyas, S. Abdullah, Y. D. Al-Otaibi and M. Aslam, “Generalized interval-valued picture fuzzy linguistic induced hybrid operator and TOPSIS method for linguistic group decision-making,” Soft Computing, vol. 25, no. 7, pp. 5037–5054, 2021. [Google Scholar]

12. A. B. Khoshaim, M. Qiyas, S. Abdullah, M. Naeem, Muneeza et al., “An approach for supplier selection problem based on picture cubic fuzzy aggregation operators,” Journal of Intelligent & Fuzzy Systems, vol. 40, no. 5, pp. 10145–10162, 2021. [Google Scholar]

13. M. Naeem, M. A. Khan, S. Abdullah, M. Qiyas and S. Khan, “Extended TOPSIS method based on the entropy measure and probabilistic hesitant fuzzy information and their application in decision support system,” Journal of Intelligent & Fuzzy Systems, vol. 40, no. 6, pp. 11479–11490, 2021. [Google Scholar]

14. C. Lee, M. Kim, Y. J. Kim, N. Hong, S. Ryu et al., “Soft robot review,” International Journal of Control, Automation and Systems, vol. 15, pp. 1–13, 2015. [Google Scholar]

15. F. Z. Baghli, E. L. Bakkali and Y. Lakhal, “Multi-input multi-output fuzzy logic controller for complex system: Application on two-links manipulator,” Procedia Technology, vol. 19, no. 3, pp. 607–614, 2015. [Google Scholar]

16. V. Bhatia, V. Kalaichelvi and R. Karthikeyan, “Application of a novel fuzzy logic controller for a 5-dof articulated anthropomorphic robot,” in Proc. of the 2015 IEEE Int. Conf. on Research in Computational Intelligence and Communication Networks (ICRCICNKolkata, India, pp. 208–213, 2015. [Google Scholar]

17. P. Ghanooni, A. M. Yazdanib, A. Mahmoudi, Z. S. Mahmoud, M. A. Movaheded et al., “Robust precise trajectory tracking of hybrid stepper motor using adaptive critic-based neuro-fuzzy controller,” Computers & Electrical Engineering, vol. 81, no. 2, pp. 106535, 2020. [Google Scholar]

18. N. Lu and S. Yang, “Mechanics for stretchable sensors,” Current Opinion in Solid State and Materials Science, vol. 19, no. 3, pp. 149–159, 2015. [Google Scholar]

19. C. Majidi, R. Kramer and R. Wood, “A non-differential elastomer curvature sensor for softer-than-skin electronics,” Smart Materials and Structures, vol. 20, no. 10, pp. 105017, 2011. [Google Scholar]

20. J. B. Chossat, Y. L. Park, R. J. Wood and V. Duchaine, “A soft strain sensor based on ionic and metal liquids,” IEEE Sensors Journal, vol. 13, no. 9, pp. 3405–3414, 2013. [Google Scholar]

21. S. Russo, T. Ranzani, H. Liu, S. Nefti-Meziani, K. Althoefer et al., “Soft and stretchable sensor using biocompatible electrodes and liquid for medical applications,” Soft Robotics, vol. 2, no. 4, pp. 146–154, 2015. [Google Scholar]

22. W. Felt, K. Y. Chin and C. D. Remy, “Contraction sensing with smart braid mckibben muscles,” IEEE/ASME Transactions on Mechatronics, vol. 21, no. 3, pp. 1201–1209, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.