DOI:10.32604/iasc.2022.023570

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023570 |  |
| Article |
Bacterial Foraging Based Algorithm Front-end to Solve Global Optimization Problems
División Académica de Ciencias y Tecnologías de la Información, Universidad Juárez Autónoma de Tabasco, Cunduacán, Tabasco, 86690, México
*Corresponding Author: Oscar Chávez-Bosquez. Email: oscar.chavez@ujat.mx
Received: 13 September 2021; Accepted: 14 October 2021
Abstract: The Bacterial Foraging Algorithm (BFOA) is a well-known swarm collective intelligence algorithm used to solve a variety of constraint optimization problems with wide success. Despite its universality, implementing the BFOA may be complex due to the calibration of multiple parameters. Moreover, the Two-Swim Modified Bacterial Foraging Optimization Algorithm (TS-MBFOA) is a state-of-the-art modification of the BFOA which may lead to solutions close to the optimal but with more parameters than the original BFOA. That is why in this paper we present the design using the Unified Modeling Language (UML) and the implementation in the MATLAB platform of a front-end for the TS-MBFOA algorithm to calibrate the algorithm parameters faster and with no need for editing lines of code. To test our proposal, we solve a numerical optimization problem with constraints known as tension/compression spring, where 30 independent executions were conducted using the TS-MBFOA and then compared with an earlier version called MBFOA. The runtime configuration and the parameter tuning were fluent using our front-end, and the TS-MBFOA obtained the better results. To date, there is no other user-friendly implementation of this specific algorithm in an open-source code, and the front-end is flexible enough to include other numerical optimization problems with minimal effort.
Keywords: Metaheuristics; optimization; user interface
There are optimization problems considered complex due to their high dimensionality and their dynamic nature. An optimization problem is also known as a general non-linear programming problem and can be defined as:
Minimize or Maximize
Subject to:
In this definition,
These types of optimization problems are complex, and although they can be solved by mathematical programming, they can be complicated to implement. Currently, metaheuristics are efficient methods that allow to solve optimization problems with or without constraints, combinatorial or numerical, in an approximate way. That is, they generate one or more feasible solutions close to the optimum in reasonable times.
Some of these techniques emulate natural or evolutionary processes (grouped into the called bio-inspired algorithms), which are part of the bio-inspired computation field [1]. These algorithms rise with the motivation of improving search techniques and of solving optimization problems through the simulation of intelligent and collaborative processes.
According to the natural phenomenon base of their design, bio-inspired algorithms are classified into two groups: Evolutionary Algorithms (EAs) who operate emulating the natural evolution process and the survival of the fittest [2], and the Collective Intelligence Algorithms (CIAs), which base their operation on cooperative behaviors on certain simple yet intelligent organisms, such as bees [3], ants [4], bacteria [5], and birds [6], among others.
1.1 Bacterial Foraging Algorithm (BFOA)
Among CIAs we have the Bacterial Foraging Optimization Algorithm (BFOA) [5]. This particular algorithm has been less studied and analyzed to solve optimization problems, with and without constraints, using different techniques for handling constraints such as feasibility rules, penalty function, special operators, among others [7].
The natural process of BFOA is based on the fact that each bacterium tries to maximize its own energy obtained per unit of time used in the foraging process while it also evades harmful substances. Moreover, bacteria can communicate with each other by segregating substances. These characteristics are represented in four main processes in the BFOA: chemotaxis (swim-tumble), swarming, reproduction, and elimination-dispersion. Bacteria are potential solutions to the problem, and their location represents the values of the decision variables of the problem. Bacteria can move (generate new solutions) through the chemotaxis cycle, a movement is also generated by attracting solutions in promising areas to other solutions in the search space, reproduction of the best solutions is allowed, and those bacteria located in areas of poor quality are finally removed from the swarm.
The Modified Bacteria Foraging Optimization Algorithm (MBFOA) is a BFOA based algorithm. The modifications of the BFOA include a reduction in the parameters of the original BFOA by grouping in a generational cycle the four basic processes of the algorithm (initially an independent loop) and a mechanism for handling constraints based on feasibility rules [8], which are: 1) between two feasible solutions, the one with the best objective function value is selected; 2) between a feasible solution and an unfeasible one, the feasible one is selected; 3) between two non-feasible solutions, the one with the lowest Constraint Violation Sum (CVS), is selected. The CVS is calculated using the following equation:
In order to improve the performance of MBFOA to solve CNOPs, the Improved Modified Bacterial Foraging Optimization Algorithm (IMBFOA) was proposed. IMBFOA implements a skew mechanism to create the initial population, two swim operators, dynamic step sizes, and the Sequential Quadratic Programming (SQP) local search engine. This search engine aims to bring or introduce bacteria into the feasible region or take bacteria out of a local optimum and move them to another place within the feasible region [10].
Finally, the most recent adaptation is the Two-Swim Modified Bacterial Foraging Optimization Algorithm (TS-MBFOA), where two swims are added in the chemotaxis process: the first is the original swim (except for the step size, which is randomized), and the second swim includes the mutation operator used in evolutionary algorithms. Both swims are included with the objective of improving the exploration and exploitation capabilities of the algorithm [11]. This proposal has recently been successfully used to solve engineering design problems such as tension/compression spring [12], and menu planning [13].
Swarm intelligence algorithms and even evolutionary algorithms are widely used among the scientific community. However, in most cases only their pseudocodes or source codes are distributed. Coding, implementing and executing a metaheuristic algorithm may be a difficult task for end users unfamiliar with complex algorithms in programming languages. Specifically, the algorithm based on the foraging of bacteria is one of the popular ones in solving constraint numerical optimization problems. However, it is not common to find in the state of the art or specialized literature a graphical user interface that may allow end users to calibrate the algorithm parameters, run it, and view its results on some known test problems, all of this without need to edit lines of code.
A front-end for the TS-MBFOA may help the end-user perform the optimal calibration of parameters with minimum effort and time. In the context of human-computer interaction, a front-end consists of a software interface (such as a user interface, UI) designed to enable user-friendly interaction with a computer. That is why the implementation of the algorithm plus the UI is of the utmost importance for those who have the need to use the algorithm. Also, since the UI isolates the source code from the end user, he/she does not need of programming knowledge to interact directly with the calibration of the parameters and, therefore, in the execution of the algorithm.
In the specialized literature, there are several proposals developing UIs for the implementation of BFOA in particular problems; some of these are described below.
In [14], the optimization of flexible manufacturing systems is carried out using conventional and evolutionary approaches. The authors developed optimization procedures based on three approaches: Genetic algorithm, Differential evolution, and BFOA. In the proposal, a MATLAB-based user interface was developed using version 7.1, allowing the user to properly adjust the problem parameters to be solved before the software execution.
In another work, BFOA has been implemented for planning route strategies for ships to avoid collisions. The UI has general-purpose components to facilitate the adjustment of the problem parameters: navigation direction, speed, longitude, and latitude. Also, this proposal displays a list showing a series of results and a graph corresponding to the possible collision [15].
A BFOA-based factorial order controller for a multi-area automatic generation control system with capacitive energy storage was proposed in [16]. The proposal investigates the effectiveness of a fractional-order controller and the optimal gain configuration of the controllers. The simulations of the test system are carried out in the MATLAB environment, and visualization graphs validate the dynamic performance of the controller.
In another work, BFOA was applied for the comparative analysis of the double watermark technique based on safe medical images [17]. The authors present a UI designed in MATLAB 7.1 as an integral tool capable of performing watermarks and different analyzes, as the user requires. This tool aims is to allow the user to have ease of operation to load the image, mark it, and encrypt it.
To improve the recognition rate of a fingerprint verification system, BFOA was implemented along with a UI developed in MATLAB 7.11 in [18], where it allows the end-user to load the fingerprint to make the biometric analysis.
In [19], a UI based on BFOA for lung cancer diagnosis is implemented through the fusion of support vector machines and a neural network of backward propagation, where the simulation of performance is conducted in a MATLAB environment 7.10. The UI has a series of parameters to select a specific task on the image of the lung.
In another work, BFOA was adapted for to optimize of multiple objectives to treat a medical image using a watermark and thus avoid damaging it. The proposal presents a UI that allows the user to manipulate the image easily [20].
In a previous work, we implemented TS-MBFOA for menu planning generating healthy menus. A UI was designed in language M under MATLAB R2009b, where the end-user inputs the personal data, and the healthy menu is automatically generated [13].
According to the revised proposals that implement BFOA with the help of a graphical interface, it is noticed that the typical development platform is MATLAB. All authors use the UI to enter the input data for the problem to be solved and show the results in graphs and tables that MATLAB can generate. In none of the cases reviewed, the UI is used to introduce and calibrate the algorithm input parameters. Furthermore, neither the performance of the algorithm is displayed using no performance metrics or graphs such as convergence. Finally, none of the proposals allow configuring a custom problem to be solved.
That is why the main objective of this article is to present the design and development of a front-end for the efficient adjustment of parameters of the TS-MBFOA in solving CNOPs.
2 TS-MBFOA: Two-Swim Modified Bacterial Foraging Optimization Algorithm
TS-MBFOA is an algorithm derived from MBFOA, and adaptation of BFOA proposed specifically to solve CNOPs [11]. In this variant, a bacterium i represents a potential solution and is denoted as θi(j, G), into a swarm of bacteria Sb, where j is the chemotaxis cycle. G is the generational loop that includes chemotaxis, swarming, reproduction and elimination-dispersion processes and ends up reaching a maximum number of generations (GMax) or using a number of evaluations, defined by the user, calculated as:
In the chemotaxis process, two swims are interspersed; in each cycle, only one of exploitation or exploration swims is performed. The process begins with the exploitation swim (classic swim). However, a bacterium will not necessarily intersperse exploration and exploitation when swimming, since if the new position of a given swim, θi(j + 1, G) has a better aptitude (based on the rules of feasibility) than the original position θi(j, G), then another swim in the same direction will take place in the next cycle. Otherwise, a new tumble will be calculated. The process stops after Nc attempts.
The exploration swim operator uses the mutation between bacteria and is calculated using:
where
The exploitation swim operator is calculated using:
where ϕ(i) is calculated with the original BFOA tumble operator defined in Eq. (3).
where Δ(i)T is a random vector generated with elements within an interval [−1, 1].
C(i, G) is the random step size of each bacterium updated using:
where Θ(i) is a uniformly distributed random vector of size n with elements within the range of each decision variable: [Uk, Lk], k = 1, ….n, and R is a user-defined parameter to scale the step size, this value must be close to zero. The initial C(i, 0) is generated using θ(i). This random stepsize allows bacteria to move in different directions within the search space and prevents premature convergence as suggested in [21].
In the middle loop of the chemotaxis process, the swarming operator defined in Eq. (5) is applied, where β is a positive parameter between (0, 1) as defined by the user.
where θi(j + 1, G) is the new position of bacterium i, (θB(G) is the current position of the best generational bacterium, and β is a parameter called scaling factor, which regulates how close bacterium i will be to the best bacterium θB. However, if a solution violates the limit of the decision variables, a new solution of x1 is generated randomly between the lower and upper limits Li ≤ xi ≤ Ui of the decision variables.
In the reproduction process, bacteria are ordered according to the constraint-handling technique based on the feasibility rules, eliminating the worst bacteria Sb − Sr and duplicating the best ones every certain number of cycles, defined by the user via the Repcycle parameter.
In the elimination-dispersion process, the worst bacterium of the population w(j, G) is eliminated (based on the feasibility rules), and a new one is randomly generated.
Although a bias mechanism is used in the original TS-MBFOA proposal to generate the initial random population and a local search engine, this paper does not use these mechanisms to reduce computational cost. The pseudocode of TS-MBFOA is presented in Algorithm 1.

Like all metaheuristic algorithms, TS-MBFOA has user-defined parameters (Sb, R, β, Nc, Sr, Repcycle, and the number of evaluations). However, the optimal calibration of these parameters is a challenging activity, and several experiments are necessary to find the combination of values that allows a better performance of the algorithm in the particular problem to be solved.
Some algorithms are sensitive to their parameters, and this complicates the calibration. It is worth mentioning that the values of a parameter can be an integer or a real number. Usually, the authors of an algorithm mention the range values recommended for each parameter to solve a particular problem giving only an idea of the possible values that we can use.
The main goal of this work is to implement the TS-BFOA along with a front-end to be used by any researcher or academic interested in bacterial foraging algorithms. After the analysis phase, we create the corresponding design diagrams, implement the algorithm, and finally develop the UI. The development environment used was MATLAB R2018a.
To code TS-MBFOA and the front-end, a modular programming paradigm has been used to separate each individual process of the algorithm into independent modules to have clean programming of each process implementing functions and procedures.
We designed the prototype using the UML (Unified Modeling Language), a tool that captures the idea of a system through a set of symbols and diagrams [22]. UML is used to visualize, specify, build, and document the components of a software system [23].
To develop the TS-MBFOA front-end, we designed an activity diagram (Fig. 1), a package diagram (Fig. 2), and a sequence diagram (Fig. 5). Each diagram will be explained in the corresponding section.

Figure 1: TS-MBFOA activity diagram

Figure 2: TS-MBFOA front-end package diagram
The activity diagram in Fig. 1 describes the functioning of our TS-MFOA implementation.
3.2 Modular Programming of the TS-MBFOA
Modular programming provides many advantages, e.g., simplifying the design, decreasing the coding complexity, saving programming time (as it promotes the reusability of the code), favors teamwork, ease of debugging, testing, maintenance, and structuring of specific libraries. Moreover, this technique allows designing the solution of a problem based on modularization or segmentation, given a top-down approach [24].
This modularization or segmentation, in turn, can be repeatedly divided into smaller problems until the problems are easily solved. Each subproblem is desirable to be independent of the others and is called a module. The original problem is solved within the main program (also called driver or main) and subproblems (modules) through subprograms: procedures and functions [25].
An easy-to-understand programming language due to its practical syntax is the M language. This high-level language allows users to group frequently used sentences within a program that can be invoked later.
In this work, each of the processes of the TS-MBFOA algorithm is modulated for a quick understanding and easy adaptation, as shown in the package diagram in Fig. 2. Sub-package UI contains all elements corresponding to the user interface. TS-MBFOA sub-package includes all modules related to the TS-MBFOA. Results sub-package includes code related to the results obtained by the algorithm. Finally, ProblemDefinition sub-package is where the CNOP is defined; in this case, a default problem known as Tension/compression spring problem is included, and it will be detailed in Section 4.1.
The TS-MBFOA UI consists of two windows. The first window is for the calibration of parameters, information regarding the state of execution of the algorithm, and an option for data visualization. In the second window, results are presented.
Fig. 3 describe the elements of the first UI:

Figure 3: Configuration UI
• File menu: includes options to run a new execution, load a previous configuration and show general information of the front-end.
• Action buttons: the first button allows to save the configuration, the second one to start the algorithm's execution, the third button stops the current execution, and the fourth one is enabled when the execution ends and displays the second UI.
• Run settings: the left panel allows the user to name the test, choose the optimization problem, and set the number of iterations.
• Parameter calibration: this is the main panel and allows the user to set the number of bacteria (Sb), step size (R), scaling factor (β), chemotaxis cycle (Nc), bacteria to reproduce (Sr), frequencies of the reproduction cycle (Repcycle), and the number of evaluations. It validates the input values and offers a correct range of values for each parameter.
• Process: the right panel shows the execution time of the algorithm.
Fig. 4 depicts the second UI. In this window, the output of the algorithm is presented. Results are shown in 5 panels:

Figure 4: Results UI
• General configuration: shows the configuration and calibration of parameters for this execution.
• Results: this table shows the best solution found in each of the executions of the algorithm. Each solution shows the value of the variables along with the value of the objective function and the Constraint Violation Sum (CVS).
• Statistics: this panel presents the basic statistics such as: better, average, median, standard deviation, and worse value of the set of solutions in the Final results table. In addition, performance measures of the algorithm are presented, such as the feasibility rate, success rate, and successful performance [26].
• TS-MBFOA convergence: this graph shows the algorithm's convergence for the median value of the set of solutions. It is helpful to show the behavior of the algorithm.
• Export data: it allows to export results to a spreadsheet file.
The sequence diagram in Fig. 5 shows the interaction between all the modules of the front-end. This diagram shows the sequence that the user must perform to execute the algorithm and obtain the results.
To test our front-end, we chose the CNOP known as the Tension/Compression Spring. For this specific problem, the best optimal value known in the state of the art is 0.012681. In this case, we compare the results of the TS-MBFOA and the MBFOA when solving this problem. For the comparison of results, we used the non-parametric test Wilcoxon Signed Rank test.
We use MATLAB R2018b to conduct the test on a laptop with an Intel(R) Core i5 CPU@1.60 GHz processor, 8GB RAM, and 64-bit Windows 10 Operating System.
In the Tension/compression spring problem, the aim is to minimize the weight of a tension/compression spring (see Fig. 6) subject to constraints of minimum deviation, cut-off tension, surge frequency, and limits on the outside diameter; this on the design variables. The function to be optimized in the TS-MBFOA has the following design variables: Cable diameter d(x1), Roll diameter D(x2), and the number of rolls involved N(x3). Formally, the problem can be expressed as follows:

Figure 5: TS-MBFOA front-end sequence diagram
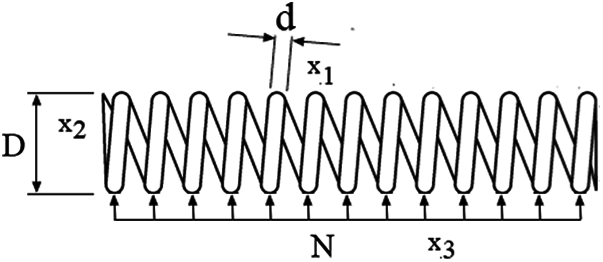
Figure 6: Representation of the design problem
Minimize
Subject to:
where:
Fig. 6 shows a representation of the Tension/compression spring problem.
4.2 Algorithm Configuration and Calibration
The values of the TS-MBFOA parameters were bacteria (Sb) = 50, step size (R) = 0.001, scaling factor (β) = 1.9, chemotaxis cycle (Nc) = 40, bacteria to reproduce (Sr) = 1, frequencies of the reproduction cycle (Repcycle) = 100, and number of evaluations = 30,000. These same parameters were used to execute MBFOA in 30 independent executions to make a fair performance comparison. These values were calibrated in a set of a priori experiments.
Tab. 1 shows the results of each of the 30 independent executions. All solutions were feasible; the best one is shown in bold. We ran the algorithm for 25 s.

The best solution found, and the basic statistical values of all the 30 independent executions are presented in Tab. 2, where the best solution was obtained during execution number 24, as highlighted in Tab. 1. We can notice that the standard deviation is very close to zero, which indicates that all the solutions obtained in each of the 30 executions are similar. Furthermore, notice that each solution is similar to the global optimum or best-known solution. This can be confirmed by the feasibility rate, success rate, and success performance [27] where the 30 independent executions obtained feasible and equal or better solutions than the global optimum known in the state of the art. Finally, about 15,314 evaluations are required to obtain a feasible and optimal solution for this problem with this algorithm.

The convergence of an algorithm occurs when a solution remains unchanged for a number of iterations until the end of the algorithm execution. This solution can be feasible or not feasible, a local or global optimum. Fig. 7 shows the convergence of the TS-MBFOA using execution number 15, which corresponds to the median of the 30 executions. In this execution, the TS-MBFOA has a progressive and continuous convergence before 15,000 generations. After these generations, the algorithm remains unchanged. That is, it converges in a local optimum because the result of this execution has a value of 0.012682678, very similar to the best optimal value known in the state of the art: 0.012681. The convergence in a good quality solution for this problem is obtained between approximately 10,000 to 15,000 generations, according to Fig. 7 and the value of the metric Success performance.

Figure 7: Convergence of a TS-MBFOA execution
Tab. 3 shows the results obtained from the 30 independent executions performed by the TS-MBFOA and the MBFOA. The Wilcoxon Signed Rank test uses this data to know if there is a significant difference between both groups of solutions.

Tab. 4 presents a comparison of the results obtained by the TS-MBFOA and the MBFOA. Results of both algorithms were generated using the same configuration of parameters. According to the values reported, TS-MBFOA is the algorithm that obtains the best results in each statistic when solving the test problem.
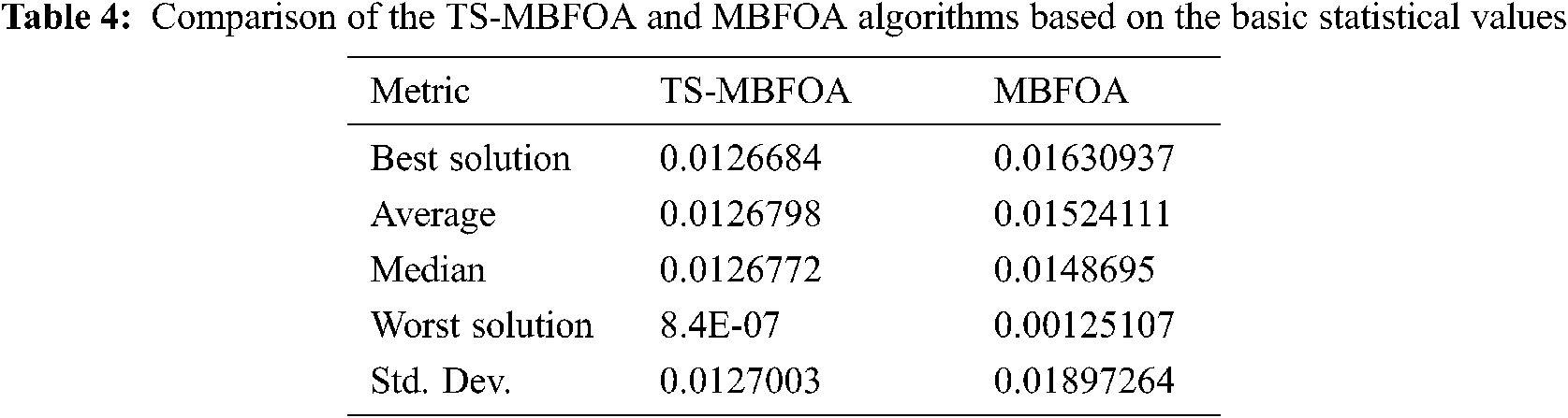
The Wilcoxon Signed-Rank test was configured with a significance level of 0.05 using an online calculator [28], obtaining a p-value value less than 0.00001. This indicates a significant difference between the results of the TS-MBFOA and the MBFOA.
In general, TS-MBFOA performed better than MBFOA. In addition, the UI allows the end-user to configure, calibrate parameters, and view the algorithm results with no additional effort.
This paper proposes an intuitive implementation of the TS-MBFOA along with a front-end for the easy solution of constraints numerical optimization problems. The main objective is to make the algorithm more straightforward in terms of parameter calibration and visualization of results. In the literature, the solutions based on the BFOA only show the algorithm's pseudocode or the code released in some programming language. However, there is no visual tool that allows to use of the algorithm in a fast way and to implement it in any problem.
The TS-MBFOA was developed following the previously designed UML diagrams. The front-end consists of two windows. In the first one, the end-user can configure the execution and calibrate the algorithm parameters. In the second one, results obtained by the algorithm are displayed in graphs and tables, in addition to exporting results to a spreadsheet file. The main advantages of our proposal to the end-user are the saving of time and effort in the calibration of parameters, the control and order of the executions to be conducted, and a clear and well-distributed display of the results.
The UI and the implementation of the TS-MBFOA were tested in solving the Tension/compression spring problem in 30 independent runs. We also compare the performance of the TS-MBFOA against the MBFOA using basic statistics and the Wilcoxon Signed Rank Test. MBFOA turned out to be the best algorithm. Our front-end is open-source software freely available at https://github.com/garcialopez/TS-MBFOA-GUI.
Future work is intended to provide an open-source graphical interface for recent swarm intelligence algorithms found in the specialized literature, such as those based on the Monarch butterfly, Earthworm, Elephant herding, Moth search, Slime mould, or Harris hawks, to name a few.
Acknowledgement: To CONACYT (Ministry of Science in México) for supporting the National System of Researchers.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. P. Engelbrecht, Fundamentals of Computational Swarm Intelligence, John Wiley & Sons, USA, 2006. [Google Scholar]
2. A. Eiben and J. E. Smith, Introduction to Evolutionary Computing, Natural Computing Series, Springer-Verlag, DE, 2003. [Google Scholar]
3. D. Karaboga and B. Basturk, “Powerful and efficient algorithm for numerical function optimization: Artificial Bee colony (ABC) algorithm,” Journal of Global Optimization, vol. 9, no. 3, pp. 459–471, 2007. [Google Scholar]
4. M. Dorigo, V. Maniezzo and A. Colorni, “The ant system: Optimization by a colony of cooperating agents,” IEEE Transactions of Systems, Man and Cybernetics-Part B, vol. 26, no. 1, pp. 29–41, 1996. [Google Scholar]
5. K. M. Passino, “Biomimicry of bacterial foraging for distributed optimization and control,” IEEE Control Systems Magazine, vol. 22, no. 3, pp. 52–67, 2002. [Google Scholar]
6. J. Kennedy and R. C. Eberhart, Swarm Intelligence, Morgan Kaufmann, UK, 2001. [Google Scholar]
7. B. Hernández-Ocaña, M. P. Pozos-Parra and E. Mezura-Montes, “Stepsize control on the modified bacterial foraging algorithm for constrained numerical optimization,” in Proc. of the 2014 Conf. on Genetic and Evolutionary Computation, GECCO ‘14, New York City, NY, USA, pp. 25–32, 2014. [Google Scholar]
8. K. Deb, “An efficient constraint handling method for genetic algorithms,” Computer Methods in Applied Mechanics and Engineering, vol. 186, no. 2–4, pp. 311–338, 2000. [Google Scholar]
9. E. Mezura-Montes and B. Hernández-Ocaña, “Modified bacterial foraging optimization for engineering design,” in Proc. of the Artificial Neural Networks in Engineering Conf. (ANNIE’2009St. Louis, MO, USA, 2009, pp. 357–364. [Google Scholar]
10. B. Hernández-Ocaña, M. P. Pozos-Parra and E. Mezura-Montes, “Improved modified bacterial foraging optimization algorithm to solve constrained numerical optimization problems,” Applied Mathematics and Information Sciences, vol. 10, no. 2, pp. 607–622, 2016. [Google Scholar]
11. B. Hernández-Ocaña, J. Hernández-Torruco, O. Chávez-Bosquez, M. B. Calva-Yáñez and E. A. Portilla-Flores, “Bacterial foraging-based algorithm for optimizing the power generation of an isolated microgrid,” Applied Sciences, vol. 9, no. 6, 1261. [Google Scholar]
12. B. Hernández-Ocaña, M. P. Pozos-Parra, E. Mezura-Montes, E. A. Portilla-Flores, E. Vega-Alvarado et al., “Two-swim operators in the modified bacterial foraging algorithm for the optimal synthesis of four-bar mechanisms,” Computational Intelligence and Neuroscience, no. vol. 2016, pp. 1–18, 2016. [Google Scholar]
13. B. Hernández-Ocaña, O. Chávez-Bosquez, J. Hernández-Torruco, J. Canul-Reich and P. Pozos-Parra, “Bacterial foraging optimization algorithm for menu planning,” IEEE Access, no. 6, pp. 8619–8629, 2018. [Google Scholar]
14. A. V. S. Sreedhar Kumar, V. Veeranna, B. Durgaprasad and B. Dattatraya Sarma, “A MATLAB GUI tool for optimization of FMS scheduling using conventional and evolutionary approach,” International Journal of Current Engineering and Technology, vol. 3, no. 5, pp. 1739–1744, 2013. [Google Scholar]
15. H. Liu, S. Liu and L. Zhang, “Ship collision avoidance path planning strategy based on quantum bacterial foraging algorithm”, in 2015 2nd Int. Conf. on Electrical, Computer Engineering and Electronics, Kuala Lumpur, Malaysia, 2015, pp. 612–621. [Google Scholar]
16. A. Pappachen and A. Peer Fathima, “BFOA based FOPID controller for multi area AGC system with capacitive energy storage,” International Journal on Electrical Engineering and Informatics, vol. 7, no. 3, pp. 429–442, 2015. [Google Scholar]
17. C. H. Venugopal Reddy and P. Siddaiah, “Comparative analysis of dual secure based medical image watermarking technique to increase security of watermark data using BFOA,” International Journal of Computer and Communication Engineering, vol. 5, no. 6, pp. 381, 2016. [Google Scholar]
18. H. S. Brar, “Fingerprint Image Recognition using Bacterial Foraging Optimization Algorithm (BFOA),” M. S. thesis, Computer Science and Engineering Department, Thapar University, Patiala, Punjab, India, 2014. [Google Scholar]
19. G. Kaur and H. Singh, “An intelligent system for lung cancer diagnosis using fusion of support vector machines and back propagation neural network,” International Journal of Science and Research, no. vol. 4, pp. 87–91, 2015. [Google Scholar]
20. C. H. Venugopal Reddy and P. Siddaiah. “Bacterial foraging optimization algorithm (BFOA) optimized adaptive hybrid DWT-SVD watermarking with encryption,” International Journal of Applied Engineering Research, vol. 9, no. 24, pp. 30911–30933, 2014. [Google Scholar]
21. A. Kasaiezadeh, A. Khajepour and S. L. Waslander, “Spiral bacterial foraging optimization method: Algorithm, evaluation and convergence analysis,” Engineering Optimization, vol. 46, no. 4, pp. 439–464, 2014. [Google Scholar]
22. M. Fowler, UML Distilled: A Brief Guide to the Standard Object Modeling Language, Addison-Wesley Professional, USA, 2004. [Google Scholar]
23. G. Booch, J. Rumbaugh and I. Jacobson, Unified Modeling Language Reference Manual. Pearson Education, Addison-Wesley, USA, 2004. [Google Scholar]
24. Department of Mathematics and Statistics University of Maryland. “An introduction to MATLAB programming,” USA: Baltimore, 2021. [Online]. Available: https://www.umbc.edu/circ/hosting/math426summer08/lct4.pdf. [Google Scholar]
25. C. S. Lent, Learning to Program with MATLAB: Building GUI Tools, Wiley, USA, 2013. [Google Scholar]
26. J. J. Liang, T. P. Runarsson, E. Mezura-Montes, M. Clerc, P. N. Suganthan et al., “Problem definitions and evaluation criteria for the CEC 2006 special session on constrained real-parameter optimization,” In Technical Report 8, School of EEE Nanyang Technological University, Singapore, 2006. [Google Scholar]
27. B. Hernández-Ocaña, J. Hernández-Torruco, O. Chávez-Bosquez, J. Canul-Reich and L. G. Montané-Jiménez, “Bacterial foraging optimization algorithm with mutation to solve constrained problems,” Acta Universitaria, vol. 29, pp. 1–16, 2019. [Google Scholar]
28. Social science statistics. “The Wilcoxon signed-rank test calculator”. 2021. [Online]. Available: https://www.socscistatistics.com/tests/signedranks/default.aspx. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |