DOI:10.32604/iasc.2022.023105

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023105 |  |
| Article |
A Machine-Learning Framework to Improve Wi-Fi Based Indoorpositioning
1CSE, SRC, SASTRA Deemed to Be University, Thanjavur, 613401, India
2CSE, SOC, SASTRA Deemed to Be University, Thanjavur, 613401, India
*Corresponding Author: K. R. Manjula. Email: manjula@cse.sastra.edu
Received: 28 August 2021; Accepted: 10 November 2021
Abstract: The indoor positioning system comprises portable wireless devices that aid in finding the location of people or objects within the buildings. Identification of the items is through the capacity level of the signal received from various access points (i.e., Wi-Fi routers). The positioning of the devices utilizing some algorithms has drawn more attention from the researchers. Yet, the designed algorithm still has problems for accurate floor planning. So, the accuracy of position estimation with minimum error is made possible by introducing Gaussian Distributive Feature Embedding based Deep Recurrent Perceptive Neural Learning (GDFE-DRPNL), a novel framework. Novel features from the dataset are through two processing stages dimensionality reduction and position estimation. Initially, the essential elements selection using the Gaussian Distributive Feature Embedding technique is the novel framework. The feature reduction process aims to reduce the time consumption and overhead for estimating the location of various devices. In the next stage, employ Deep Recurrent multilayer Perceptive Neural Learning to evaluate the device position with dimensionality reduced features. The proposed Deep-learning approach accurately learns the quality and the signal strength data with multiple layers by applying Deming Regressive Trilateral Positioning Model. As a result, the GDFE-DRPNL framework increases the positioning accuracy and minimizes the error rate. The experimental assessments with various factors such as positioning accuracy minimized by 70% and 60%, computation time minimized by 45% and 55% as well as overhead by 11% and 23% compared with PFRL and two-dimensional localization algorithm. Through the experiment and after analyzing the data, verify that the proposed GDFE-DRPNL algorithm in this paper is better than the previous methods.
Keywords: Indoorfloor planning; positioning system; dimensionality reduction; gaussian distributive feature embedding; deep recurrent multilayer perceptive neural learning; deming regressive trilateral positioning model
The industrial paradigm is widely utilized in indoor positioning research. The Indoor positioning systems use various technologies that consist of distance measurement to neighbouring anchor nodes such as Wi-Fi access points, Bluetooth beacons or Ultra-Wideband beacons. The positioning system has many applications ranging from commercial, military, retail to stock tracking industries. Many techniques and devices aid in locating the indoor positioning system. In this regard, for an accurate wireless indoor positioning system, a Particle Filter based Reinforcement Learning (PFRL) technique was designed [1]. The PFRL technique provides exact localization with minimum error. But the computation overhead did not minimize. To attain a more precise model parameter evaluation using particle swarm optimization two-dimensional Localization Algorithm was developed [2]. The algorithm designed failed to consider a novel path loss model and also, building the floors and walls that influence RSSI for accurate positioning of devices.
In order to decrease the location error and execution time, a new deep-learning-based indoor fingerprinting system was designed in [3] and the organized deep-learning approach did not reduce the performance of the above computation. In [4], an ensemble learning scheme was introduced to estimate the room level in the indoor localization of smart buildings. Yet, the designed plan did not minimize the time consumption of indoor localization through dimensionality reduction. The statistic and deep-learning techniques were employed in [5] to estimate indoor position that relies on significant feature extraction from data sources and to reduce the time complexity of position estimation. A clustering technique was developed in [6] to increase the accuracy of indoor positioning system. An Extreme Learning Machine (ELM) produced in [7] for the construction of the system that leads to high positioning accuracy. But the designed work did not use any efficient method for position estimation when the device was turning round or incline.
A deep-learning-based approach was presented in [8] for indoor localization considering the received signal strength and channel state information. Though the system minimizes the localization error, time complexity analyses did not perform. The least-square lateration method based on the signal strength was designed [9] for reducing the accuracy error. But machine learning technique did not achieve high accuracy of indoor localization.
A Back Propagation Neural Network optimized with Particle Swarm Optimization (BPNN-PSO) was employed in [10] to train the signal strength distance measure to minimize the positioning error. However, continuous positioning with high precision is complex to perform. A standard probabilistic method was developed in [11] to improve the accuracy and consistency of localization through the received signal strength of the device. In [12], a dimensionality reduction scheme with low computation cost was introduced for an indoor positioning system. But then the designed method failed to consider the path loss to achieve high precision indoor positioning system.
The issues reviewed from the above existing floor positioning works are computed overhead that did not minimize during the localization process—the machine learning technique like PFRL technique introduced for a robust wireless indoor positioning system. PFRL technique comprises a particle filter component and a reinforcement learning-based re-sampling method. The zone prediction method combines dissimilar individual predictors in a Hidden Markov Model (HMM) by an ensemble learning algorithm. A particle filter approach was developed to provide accurate localization of failure problems with a reinforcement on learning-based re-sampling method. Yet, it did not enhance the computation overhead. So, a Two-dimensional Localization Algorithm was introduced to accomplish more accurate parameter estimation by applying particle swarm optimization. The parametric model is used to strengthen the two-dimensional (2D) positioning to position the users with the weighted K-Nearest Neighbour algorithm. Still, it did not improve positioning accuracy. The existing method underwent many hitches to perform continuous positioning with high precision. Accurate position estimation was not attained during the designed scheme and it is not considered a path loss to achieve higher accuracy for the indoor positioning system. Further, the existing localization techniques did not reduce accurate dimensionality. Hence, there is a need to introduce the GDFE-DRPNL framework to address these problems
The paper presents the development of a novel GDFE-DRPNL framework and summarizes their significant contributions, introduces a novel deep-learning framework GDFE-DRPNL by combining feature selection and position estimation process. To achieve the goal, GDFE-DRPNL framework is created through Gaussian Distributive Embedding Feature and Deep Recurrent multilayer Perceptive Neural Learning. By applying Gaussian distributive feature embedding technique [GDFE-DRPNL] framework, the overall computation time and overhead is reduced. Then, it minimizes the dimensionality of the dataset by selecting principle features. DRPNL is used to increase the positioning accuracy as well as to minimize the error. In the proposed deep recurrent learning, the Deming Regressive Trilateral Positioning Model [13] is utilized to analyze the signal strength and to identify the exact coordinate of the device.
To facilitate the process of cell planning that involves locating and configuring infrastructure for mobile networks a system using cluster techniques was proposed in [14]. A new hybrid method was proposed in [15] to increase the accuracy of an indoor positioning system using a hybrid of BLE fingerprinting and PDR. A balanced approach for the multifactor dimensionality reduction (BMDR) method was proposed in [16] to increase the estimates of the prediction accurately for the error rate in the small samples.
This article is divided into various sections. In the second section, the novel indoor positioning framework and its description are presented with a neat diagram. The third section presents different tests conducted using the dataset and the results are compared with related works—finally, the fourth section offers conclusion.
With the extensive growth of information technology, the indoor positioning system has rapidly increased to identify mobile devices, people, and equipment. The Wi-Fi-based dynamic environment is not perfect and robust as the device is not capable of adapting signal oscillations, noises, and radio signal instabilities. Therefore, the proposed work has introduced deep learning as an innovative strategy to handle traditional learning problems. The main aim of the indoor positioning and localization is based on the strength of the wireless signals. The Gaussian distributive feature embedding technique increases dimensionality reduction performance. Further, it combines the Gaussian distributive function and Kernel Principal Component Analysis concept to select the principle features precisely with lower time complexity. Besides, the Deep Recurrent Multilayer Neural Network and Deming Regressive Trilateral Positioning Model are used in the proposed technique to improve the performance of indoor floor planning with higher positioning accuracy. On the contrary, Deep Recurrent Multilayer Neural Network handles a large number of Wi-Fi devices simultaneously. The overall system for Wi-Fi-based positioning and localization of various devices consists of fixed wireless access points. They are displayed in Fig. 1.
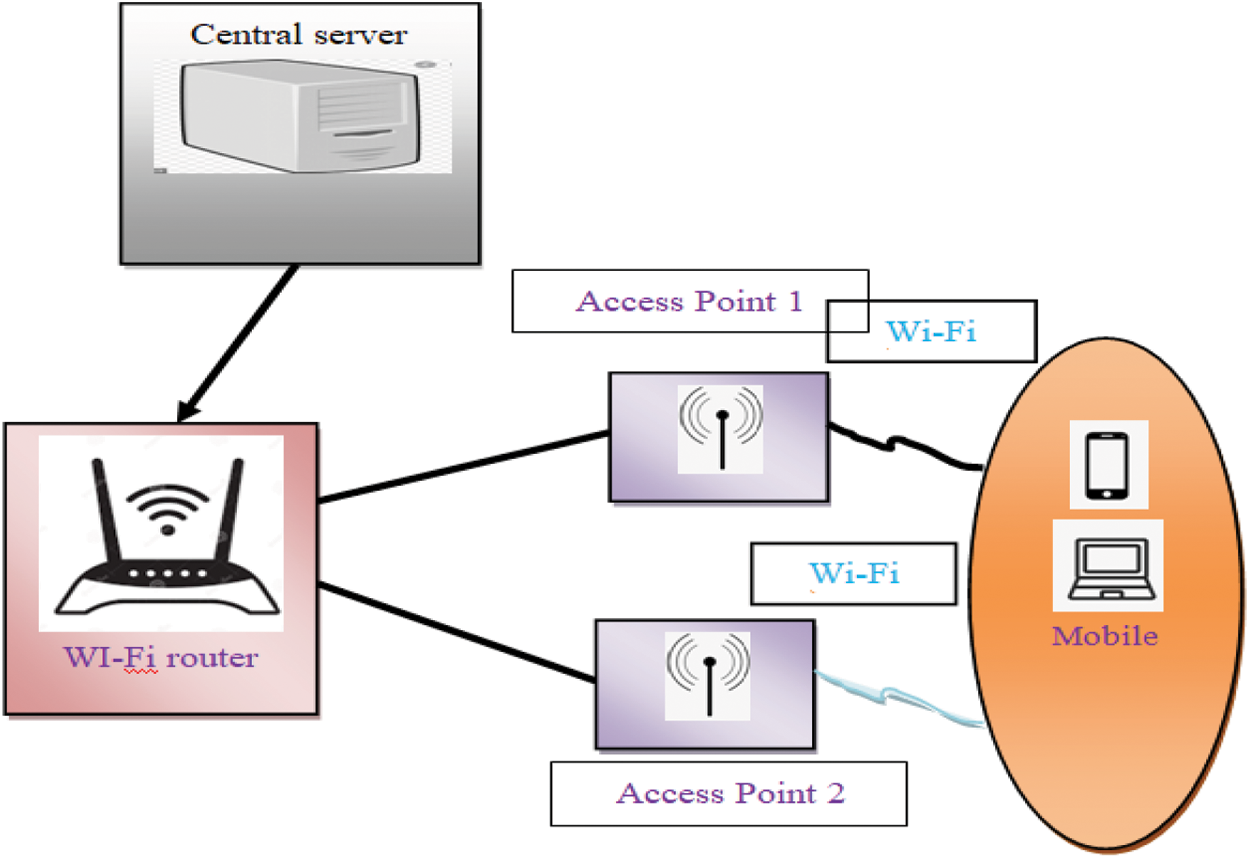
Figure 1: Indoor floor planning based on Wi-Fi devices
Fig. 1 illustrates a block diagram of the indoor floor planning with various Wi-Fi devices such as laptops, mobile, etc. The input signal is received from the central server and it finds the list of Access Points (s). The indoor floor planning utilises the IPIN dataset. Also, it comprises a total of 816 access points (APs). The dataset includes 26 log files, 17 log files are employed for training. Since everyone has a Wi-Fi-connected mobile or laptop, the Wi-Fi routers are available and deployed in most buildings. The positioning of these devices is essential to locate the objects within the building. The positioning of the various Wi-Fi devices is used for efficient indoor floor planning. This process achieves by performing two different functions, such as feature selection and position estimation. The proposed GDFE-DRPNL framework illustrates the architecture in Fig. 2.
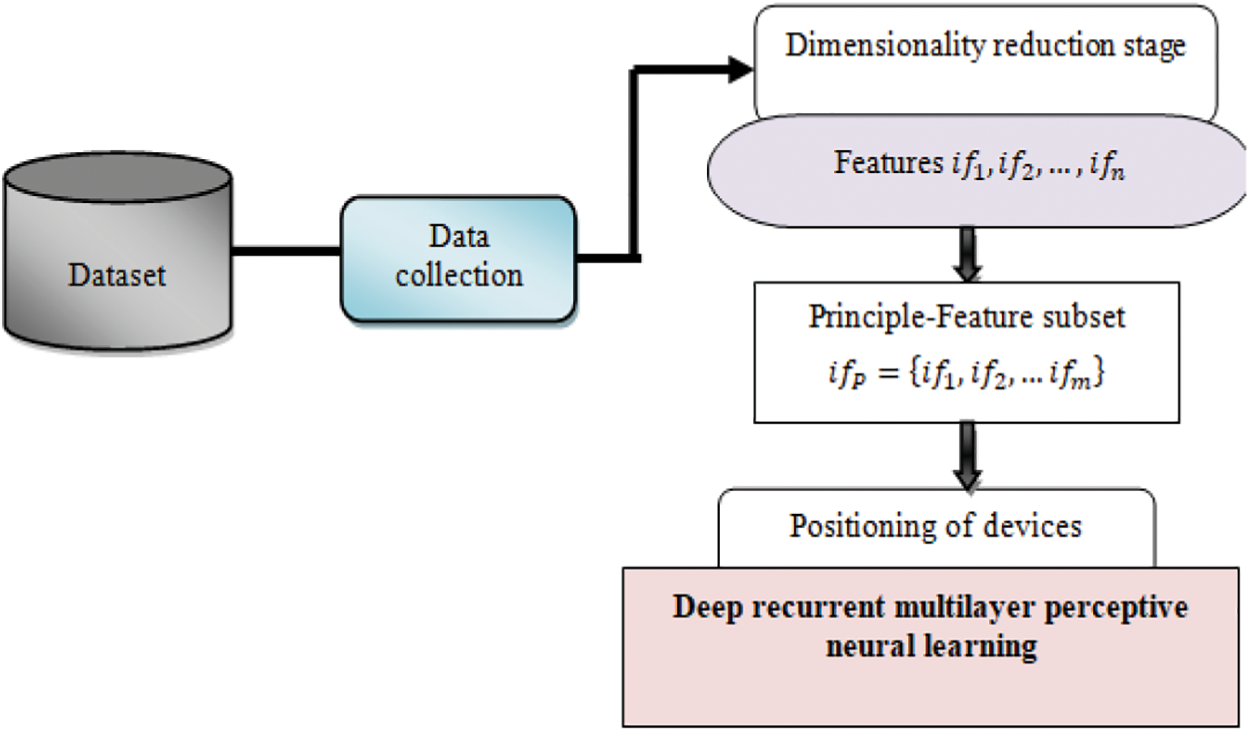
Figure 2: Architecture of the proposed GDFE-DRPNL framework
Fig. 2 illustrates the architecture of the proposed GDFE-DRPNL framework, which comprises two stages. It performs two tasks with the collected dataset. At the initial step, a machine learning technique called Gaussian distributive feature embedding applies dimension reduction in the dataset. Next, the positioning process using Deep Recurrent multilayer Perceptive Neural Network, a deep-learning method, is performed with high accuracy and minimum error. An explanation of these two processes of the proposed GDFE-DRPNL framework is presented in the following sections.
2.1 Gaussian Distributive Feature Embedding Technique (Dimensionality Reduction)
The proposed GDFE-DRPNL framework initially performs dimensionality reduction. It then removes the random variables and selects a set of essential variables. Then, to improve learning performance, appropriate principle features are selected for data modeling that reduces computational time or required resources, and high-dimensional input to decrease the curse of dimensionality. The feature selection is to choose a set of principle features that provide the best positioning estimation with a classifier. Based on this motivation, the proposed GDFE-DRPNL framework uses the Gaussian distributive feature embedding technique to perform a dimension reduction by selecting the fewest features from the dataset.
Consider the feature vectors from the given dataset ‘
The proposed technique initially calculates the probabilities using the Gaussian distribution function relative to the similarity of objects. The probability is expressed as follows:
From (1), ‘PROB(ifi, ifj)’ stands for the probability of identifying the principal features from the given feature vector, ‘D’ symbolizes Gaussian standard deviation and ||ifi − ifj|| designates Euclidean distance similarity between the two features ifi and ifj in the feature vector. The estimated probability value lies between zero and one. Then, the predefined threshold sets to map the feature vector. If the calculated probability result is higher than the predefined threshold (φ = 0.5) then, it is mapped into the principle-feature subset; otherwise, the redundant features map into the other subgroup. Based on the probability value, at first maps input features vectors ‘ifi = {ifi ∈ ifN|i = 1, …, N}’ into dimensional space ‘Z’ by way of nonlinear mapping ‘φ’ associated with kernel function ‘ω’. The mapping process perform as,
By using Eq. (2), then covariance matrix ‘δ’ is obtained with the help of below equation,
In Eq. (4), ‘φ’ is the non-linear map (i.e., feature space) whereas ‘T’ stands for a transformation matrix. Here, ‘N’ refers to the total number of features vector ifi. Subsequently, non-linear PCA [18] in ‘F’ determines eigenvectors. Then, corresponding Eigenvalues evaluate through the equation,
From Eq. (5), ‘α’ symbolizes the eigenvectors. Here, ‘λ’ point outs Eigenvalues of features vectors in dimensional space ‘φ(ifi)’. After that, eigenvectors are determined utilizing a linear combination of ‘φ(ifi)’ with the support of the following expression,
By applying Eqs. (4) and (5) to (6) and multiplying φ(ifi)T on both sides, the following equation is obtained:
In Eq. (7), ‘ω ∈ ifN×N’ refers to the Gram matrix where ‘a’ stands for normalized Eigenvectors of ‘ω’. The gram matrix is determined as an inner product form to identify principle-feature subset using the equation below:
Next, the proposed technique identifies eigenvectors with greater Eigen values to find out principal feature subset αp ⊂ α with the support of kernel function using the following:
From Eq. (9), ‘Z ∈ ifN’ and ‘ap ⊂ a’, where ‘n’ designates the set of principle features that provide the best positioning estimation. Eq. (9) projects the principle components into a low dimensional space. When the parts with less importance are removed, the principle-feature subset chooses to minimize the computation time and overhead.
2.2 Deep Recurrent Multilayer Perceptive Neural Learning (Increase Positioning Accuracy)
Once the principle features are identified from the dataset, the proposed GDFE-DRPNL framework begins to perform the positioning of Wi-Fi devices in the indoor floors. A high positioning accuracy is obtained with the proposed GDFE-DRPNL framework and employs DRPNL and considers the building of floors and walls that have influence on RSSI for the corresponding MAC address of the devices. The indoor environmental aspects such as multi-path, path loss and person movement affects the collected RSSI samples. So, the received RSSI values are dissimilar even in the same device. Similarly, location and different times, also considerably affect the accuracy of localization. Therefore, the proposed deep recurrent multilayer perceptive neural learning also measures the path loss between the floor and the wall for the accurate localization of devices.
The Deep recurrent multilayer Perceptive neural network is a machine learning technique. This technique uses cascading of layers to acquire the principle features and their information directly from the dataset. The structure of a deep recurrent multilayer perceptive neural network includes three layers, namely input, two, or more hidden layers, and output layer. The function of the input layer is to collect the series’ type of information with no predetermined size from the dataset and transfer it to the hidden layer. The feature learning process is carried out repetitively in the hidden layers, and it provides accurate results at the output layer. The proposed deep-learning model uses a unit delay for repetitively learning the features that are fed back into its input layer. The input layer in deep-learning techniques is fully linked with the output layer by adjustable weight connections.
The Deep recurrent multilayer Perceptive neural network is schematically presented in Fig. 3. The network system consists of artificial neuron-like nodes connected with layers for finding out the input. The input comprises the principle-feature value
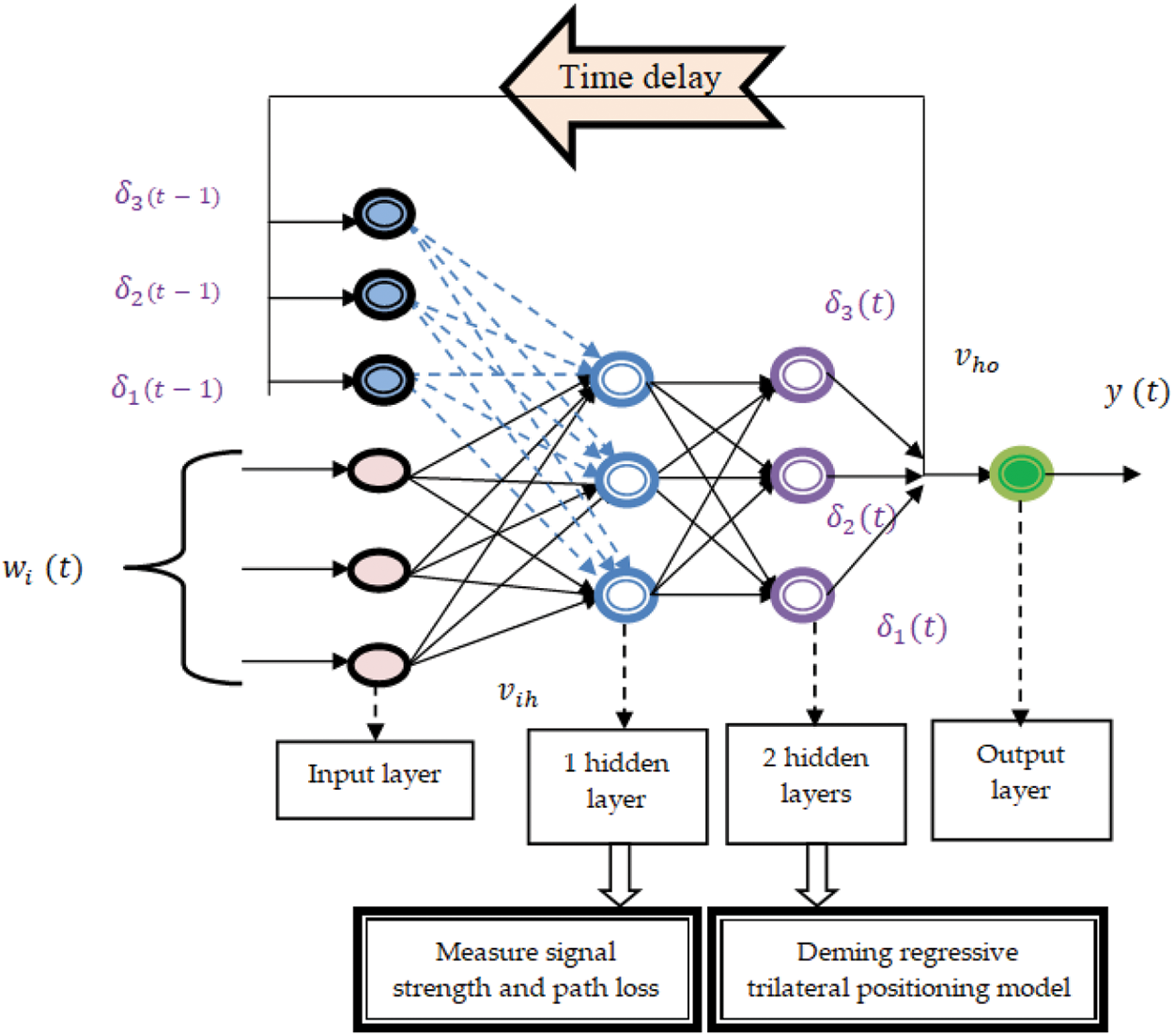
Figure 3: Representation of deep recurrent multilayer perceptive neural network
From (10), ‘X(t)’ indicates the input layer used for collecting the data at a time ‘t’, and ‘wi’ denotes input, where ‘vi’ refers to weight and ‘ b’ represents the bias that is used to adjust the output with the weighted sum of the information to the neuron. In the first hidden layer, the received signal strength of various devices is collected from the access point APi. The signal strength [19] for the corresponding MAC address of the device that predicts the path losses between a transmitting and a receiving antenna with the assumption that they are in the line of sight and is calculated as given below:
As given in the above equation, the two antennae possess different heights, the signal strength ssR posses two components, ‘Gt’ and ‘Gr’ symbolize a transmitter and receiver gain. Besides, the distance ‘d’ between the antennas is said to be relative to the height of the antenna. That is the size of the access point ‘
From the above Eq. (12), the path loss between the floor ‘f’ and wall ‘w’ are represented as PLfw. The path loss between the floor and wall is based on the penetration loss. It is at a distance of ‘1’ meter and denotes by PL0 and PLfk which stands for the attenuation. It is of the floor ‘f’ to the ‘kth’ traversed floor and PLwk denotes the attenuation due to the wall ‘w’ to the ‘kth’ traversed wall. The dataset comprises the measurement of several inbuilt sensors of smartphones. These smartphones are used to position the devices. Therefore, the signal strength of smartphones [20] is significant for receiving and sending information. If the space between sender and receiver is higher, the path loss [21] would occuron the floors and walls due to the attenuation focuses. Hence, for accurate floor planning, devices with higher signal strength and lower path loss between the floors and walls are considered in the proposed work. At the second hidden layer, the Deming regression function is applied to analyse the input signal strength of the Wi-Fi devices. The Deming regression is a statistical method that is used to find the best-fitted position of devices with the help of the trilateral process. This trilateral process uses signal strength information with the geometry of encircles and it finds the exact coordinate of the Wi-Fi device. The trilateration process is as shown in the Fig. 4.
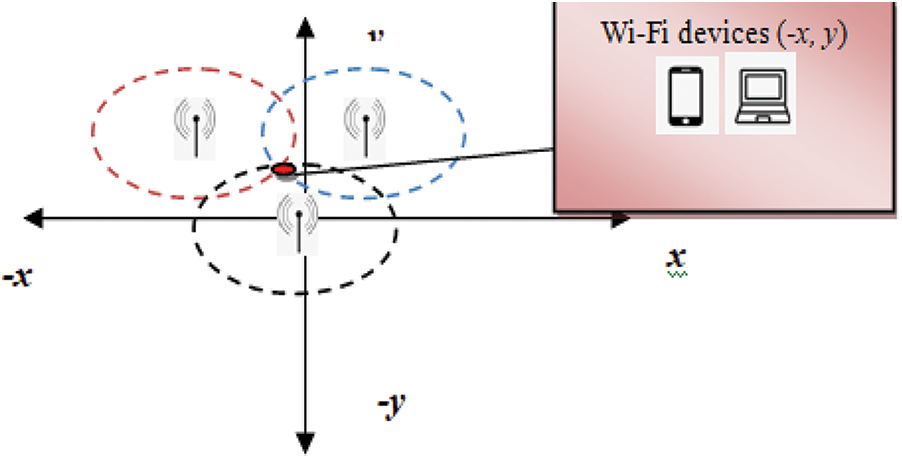
Figure 4: Deming regressive trilateral positioning model
Fig. 4 illustrates the process of the Deming regressive trilateral positing model where three
where ‘E’ stands for error in the position estimation, ‘A(t)’ denotes precise estimation output, and ‘Y(t)’ indicates the predicted outcome. Based on the error value, the weight between the layers vih,
where F indicates the gradient descent function to minimize the error ‘E’ and ‘arg min’ denotes argument of the minimum position. The recurrent procedure of deep learning is expressed as follows:
where ‘R(t)’ symbolizes the output of the hidden layer at time t, ‘δ(t − 1)’ signifies the time delay unit of hidden layer and vhh denotes the weight of the hidden layers, ‘vih’ indicates adjustable value between input and hidden layer and wi(t) represents the input. The recurrent process of deep learning repeats until the error gets minimized. The hidden layers with recurrent results are fed into the output layers. The exact coordinate for the positioning device is correctly identified at the output layer ‘y(t)’.
The goal of algorithmic process of deep recurrent multilayer perceptive neural network is to achieve accuracy and minimum error. The deep-learning network system receives the principle features and gives it to the next layer where the signal strength of various devices are analyzed utilizing the Deming regressive positioning model. The regression function minimizes the error and finds the exact coordinate for positioning multiple devices. For each result obtained, regression function determines the error and consequently updates all the weights on the network and thereby finds out the minimal error using gradient descends function. The process mentioned below iterates until the error gets minimized. Finally, the exact output is displayed in the output layer.
The algorithmic steps of the proposed deep recurrent multilayer perceptive neural learning are described as follows:

The experimental evaluation of the proposed GDFE-DRPNL framework without GDFE, PFRL, and a two-dimensional localization algorithm are possible through Java. The indoor floor planning is through the IPIN 2016 competition dataset [22]. The dataset features sensors data—feature selection is based on these files. The components are some columns in the dataset, where the attributes identify the location. In the dataset, ten principle components are selected for indoor floor planning.
Multiple data are gathered from four different buildings with different time stamps. In the dataset, 2971 Wi-Fi fingerprints are constructed by associating every Wi-Fi fingerprint with the nearest (in terms of timestamps) ground truth. The dataset comprises the measurement of several inbuilt sensors of smartphones (i.e., Wi-Fi, Magnetometer, Accelerometer, Barometer, Gyroscope, etc., with timestamps).
The IPIN dataset includes the tuples containing many grounds truth for particular timestamps due to those different sensors has different sampling rates. The samples were collected with their timestamps and also obtained from various sensors and synchronized with each other. The IPIN dataset comprises a total of 816 access points (APs). The dataset includes 26 log files. Among these, 17 log files and 9 log files were used for training and evaluate the work. Here, the first column comprises the sequence number of the log files. The second column denotes the building-id, where the data of log files are collected. Similarly, the third and fourth columns indicate the number of floors and landmarks involved in managing the data of these log files. Finally, the fifth column denotes the smartphone used to capture the data of specific log files.
In this section, the performance of the GDFE-DRPNL framework and the other three related approaches, namely without GDFE, PFRL and two-dimensional localization algorithm are analyzed with different quantitative metrics such as positioning accuracy, positioning error, computational time and computational overhead.
3.1.1 Impact of Positioning Accuracy
It is used to find how the proposed framework accurately estimates the position for different iterations. In other words, the positioning accuracy is calculated as the ratio of successful trials to the total number of shots taken as input. The formula is expressed as follows:
where ‘PosAcc’ represents the positioning accuracy, ‘Freq(ST)’ indicates a successful trial obtained and ‘Freq(T)’ denotes the number of trials taken as input for conducting the experiments. The position accuracy measures in terms of percentage (%). For each resultobtained using a deep recurrent multilayer perceptive neural network, the proposed framework measures error is occurring in the position estimation process. Here, the error determines the squared difference between the actual and predicted results. Based on the error value, the proposed framework decides whether the trial is a success or failure. Whenever the error value is very minimal, an accurate estimation of position is obtained. According to the error value involved during the position estimation process, a trial's success or failure is determined.
The performance results of GDFE-DRPNL frameworks and the other three related approaches, namely without GDFE, PFRL and two-dimensional localization algorithm are discussed in this subsection with table and graphical representation. Initially, the positioning accuracy measures are concerned with the number of trials. Totally ten iterations are considered for fair computation of accuracy using the three methods.
While considering a simulation environment with 50 Wi-Fi devices and trials, the proposed GDFE-DRPNL framework attains nine successful trials and one failed trial, whereas the one existing Without GDFE gets to earn eight successful trials and two failed trials. Besides, conventional PFRL gains seven successful trials and three failed trials, whereas the existing Two-dimensional localization algorithm acquires six successful trials and four failed trials. Based on the simulation result of successful practices and failed attempts are determined for ten iterations, positioning accuracy measures are presented in Tab. 1.
In GDFE-DRPNL Framework, the experimental results of the Wi-Fi device positioning accuracy and the other three related approaches, namely without GDFE, PFRL and two-dimensional localization algorithm are reported in Tab. 2. As shown in Tab. 2, accuracy results are obtained with various iterations. The results obtained from the three methods indicate that the GDFE-DRPNL framework outperforms to achieve high accuracy than the other three related approaches. The significant improvement of the proposed framework is to use the deep recurrent multilayer perceptive neural network. The proposed deep-learning framework analyses the principle features extracted from the dataset in the hidden layer with the Deming regressive trilateral process. The tripartite process finds the exact is to coordinate for positioning the Wi-Fi devices. This process of the GDFE-DRPNL framework achieves high accuracy. As depicted in Tab. 1, the accuracy is found to be higher for all the iterations using the GDFE-DRPNL framework.
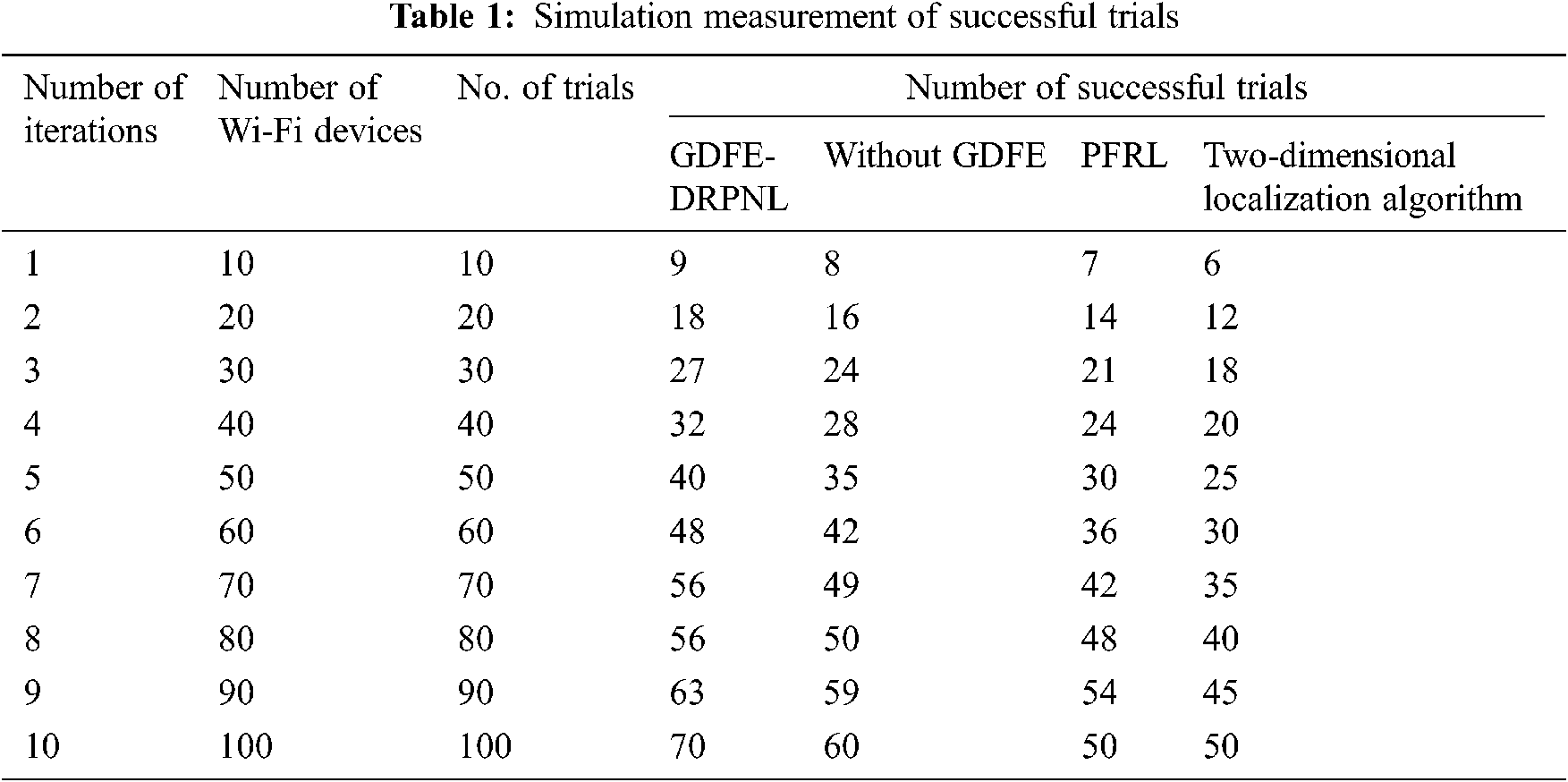
In the first iteration, ten trials are considered while computing the Wi-Fi device’s positioning accuracy. For each test has various sizes of floors view, the positioning of devices are accurately found in different sizes of the floors. As shown in Tab. 2, the GDFE-DRPNL framework observed a ‘9’ successful trial out of ten trials considered as input that achieves 90% of positioning accuracy. In the case without GDFE, ‘8’ successful attempts were obtained from ten tests and gained 80% of positioning accuracy. By using conventional PFRL and two-dimensional localization algorithm, ‘7’ and ‘6’ successful trials were obtained from ten tests and it has achieved 70% and 60% of positioning accuracy respectively. Similarly, the remaining iterations were performed and the statistical analysis reveals that the GDFE-DRPNL framework provides relatively better performance than the existing approaches. Analyzing the number of successful trials, results are demonstrated as in Tab. 1, it is evident that the proposed GDFE-DRPNL framework outperformed in comparison with the other three algorithms namely, without GDFE, PFRL and two-dimensional localization algorithm.
3.1.2 Impact of Computational Time
The computational time measures the amount of time consumed by object localization within the building. Accordingly, computational time (from 17) counts as follows:
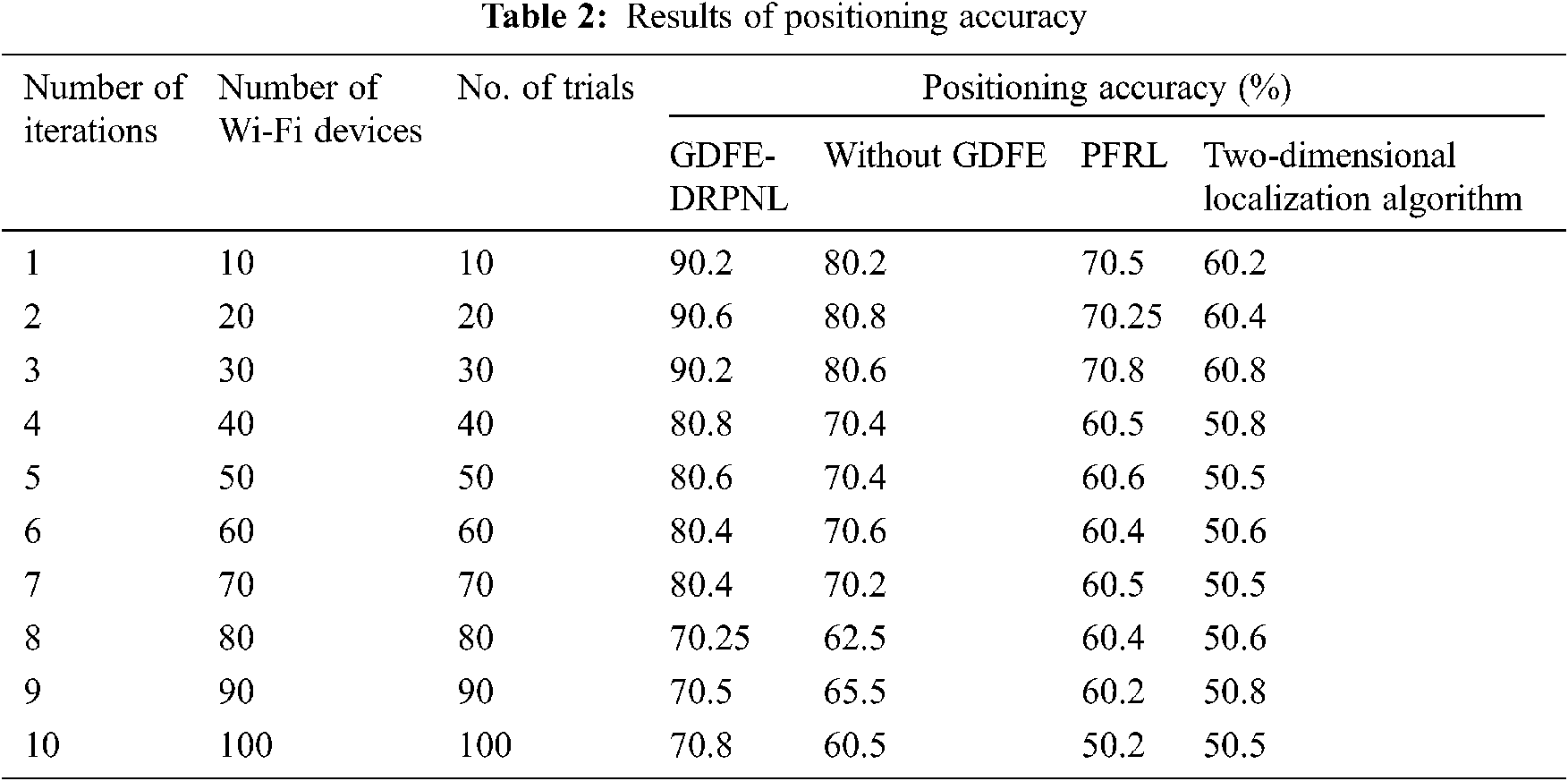
where ‘CT’ indicates computational time, ‘Time(w)’ denotes an amount of time required to localize a single object whereas ‘Size(n)’ represents some objects localized within the building. The computation time evaluations of three methods vs. several trials are illustrated in Tab. 3.
Tab. 3 presents the performance comparison of computation time concerning different trials. Totally ten practices are considered for each method. The observed results illustrate the computation time to be higher using the GDFE-DRPNL framework when compared with other methods. This improvement is achieved by selecting the principal features from the dataset. The GDFE-DRPNL framework uses the Gaussian distributive stochastic neighbour embedding technique for minimizing the dimension of the dataset. First, the Gaussian distribution function is used to compute the probabilities. The probability value lies among zero and one—next, the predefined threshold set to map the feature vector. If the probability result is maximum than that of the predefined threshold (φ = 0.5) [it is the mean of maximum and minimum value] then, it is mapped into the principle-feature subset. Also, the Deming regression provides accurate estimation results with the obtained principle features. This process consumes the minimum time for the positioning of the devices. All the ten results of the GDFE-DRPNL framework are compared with the existing ones without GDFE, PFRL, and two-dimensional localization algorithm. The average of ten products confirms that the computational time of the GDFE-DRPNL framework is minimized by 30%. Later, it is compared with and without GDFE it is found to be 45% and in comparison with PFRL it is 55%, when compared with the two-dimensional localization algorithm.
3.1.3 Impact of Computational Overhead
Computational overhead refers to the amount of memory consumed for object localization in indoor floor planning. The overall computational overhead (from 18) is mathematically defined using the following expression:
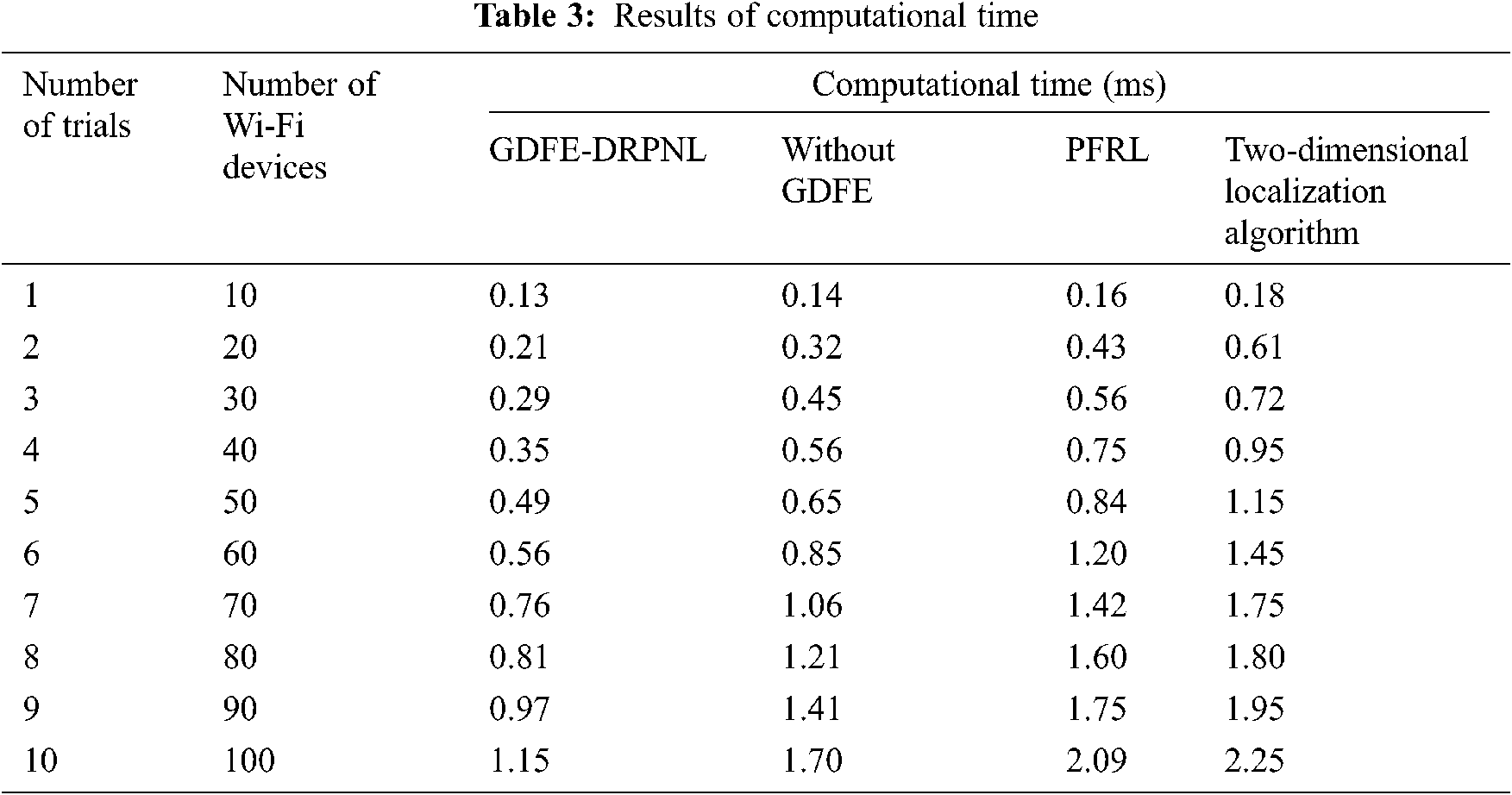
where ‘CO’ denotes computational overhead, ‘MEM(w)’ represents the memory consumed for localization of objects, ‘Size(f)’ indicates the number of floors considered for conducting the experimental evaluation. The overall computational overhead is measured in terms of kilobytes (KB). The computational overhead measures are related to the number of trials. The statistical results of the three methods report in Fig. 5.
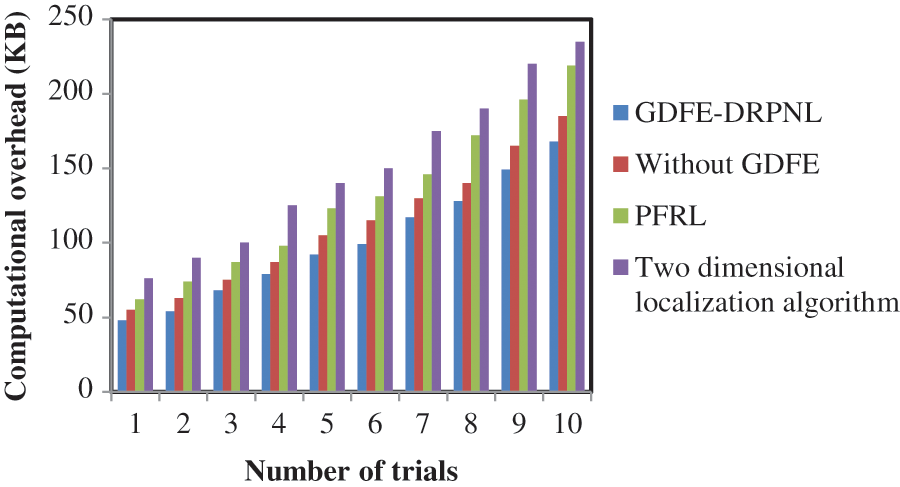
Figure 5: Graphical representation of computational overhead
Fig. 5 depicts the performance comparison of computational overhead for many trials. The graphical results demonstrate the amount of space utilized for floor planning that are significantly minimized by the GDFE-DRPNL framework. The proposed GDFE-DRPNL framework maps the principle feature into a subset in the first hidden layer of deep learning. With the obtained principle features, Wi-Fi device positioning is carried out in the hidden layer. As a result, the positioning of various devices is performed with a smaller number of features that results in the reduction of computational overhead. For each trial, multiple sizes of the floors are considered and quantitative analysis was made. The observed results of the GDFE-DRPNL framework compare to the effects of existing methods. The comparison of results proves that the average computational overhead is found to be significantly reduced by 11% when compared to that of without GDFE, it is 23% when compared with PFRL, it is 34% when compared with two-dimensional localization algorithms.
This work has proposed the GDFE-DRPNL framework for efficient wireless indoor positioning system. The GDFE-DRPNL framework is validated on distributed machine learning-based network architecture that comprises feature selection and position estimation. The feature selection achieves better positioning accuracy using the Gaussian Distributive feature Embedding technique. Followed by this, an efficient deep recurrent learning approach achieves high positioning system performance by integrating the selected features with the Deming regression learning technique through RSS signal measure. The results obtained demonstrate that the proposed framework is suitable for a robust indoor positioning system with minimum error. The localization framework is evaluated with two existing approaches in terms of different performance metrics. The observed evaluation results show that our proposed GDFE-DRPNL framework gives more accurate localization results with minimum positioning accuracy by 70% and 60%, time consumption is minimized by 45% and 55%, as well as overhead is reduced by 11% and 23% than PFRL and two-dimensional localization algorithms. In future, to enhance the accuracy and also reduce computational overhead the positioning of Wi-Fi devices for indoor floor planning could be carried out using ensemble learning techniques.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Villacrés, Z. Zhao, T. Braun and L. Zan, “A particle filter-based reinforcement learning approach for reliable wireless indoor positioning,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 11, pp. 2457–2473, 2019. [Google Scholar]
2. H. Guo, L. Huixia, J. Xiong and M. Yu, “Indoor positioning system based on particle swarm optimization algorithm,” Measurement, vol. 134, no. 4, pp. 908–913, 2019. [Google Scholar]
3. X. Wang, L. Gao, S. Mao and S. Pandey, “CSI-based fingerprinting for indoor localization: A deep learning approach,” IEEE Transactions on Vehicular Technology, vol. 66, no. 1, pp. 763–776, 2017. [Google Scholar]
4. Z. Zhao, J. L. Carrera, T. Braun and Z. Pan, “Conditional probability-based ensemble learning for indoor landmark localization,” Computer Communications, vol. 145, no. 2, pp. 319–325, 2019. [Google Scholar]
5. A. B. Hernández, G. H. Peñaloza, D. M. Gutiérrez and F. Alvarez, “Swiblux: Multi-sensor deep learning fingerprint for precise real-time indoor tracking,” IEEE Sensors Journal, vol. 19, no. 19, pp. 3473–3486, 2019. [Google Scholar]
6. T. Arsan and M. M. N. Hameez, “A clustering-based approach for improving the accuracy of UWB sensor-based indoor positioning system,” Mobile Information Systems, vol. 2019, no. 5, pp. 1–13, 2019. [Google Scholar]
7. Y. Chen, W. Guan, J. Li and H. Song, “Indoor real-time 3-d visible light positioning system using fingerprinting and extreme learning machine,” IEEE Access, vol. 8, no. 3, pp. 13875–13886, 2019. [Google Scholar]
8. C. Hsieh, J. Chen and B. Nien, “Deep learning-based indoor localization using received signal strength and channel state information,” IEEE Access, vol. 7, no. 4, pp. 33256–33267, 2019. [Google Scholar]
9. T. Dag and T. Arsan, “Received signal strength based least-squares lateration algorithm for indoor localization,” Computers & Electrical Engineering, vol. 66, no. 4, pp. 114–126, 2018. [Google Scholar]
10. G. Li, E. Geng, Z. Ye, Y. Xu, J. Lin et al., “Indoor positioning algorithm based on the improved RSSI distance model,” Sensors, vol. 18, no. 5, pp. 1–15, 2018. [Google Scholar]
11. X. Tian, R. Shen, D. Liu, Y. Wen and X. Wang, “Performance analysis of RSS fingerprinting based indoor localization,” IEEE Transactions on Mobile Computing, vol. 16, no. 10, pp. 2847–2861, 2017. [Google Scholar]
12. A. Abed and I. Qader, “RSS-Fingerprint dimensionality reduction for multiple service set identifier-based indoor positioning systems,” Applied Science, vol. 9, no. 2, pp. 1–22, 2019. [Google Scholar]
13. N. Guan, Z. Wen and K. Sun, “Research on indoor positioning algorithm based on trilateral positioning and taylor series expansion,” Int. Conf. on Computational Modeling, Simulation and Applied Mathematics, Bangkok, Thailand, pp. 1–6, 2016. [Google Scholar]
14. L. F. Ibrahim, H. A. Salman, S. Y. Sery and Z. Taha, “Using clustering techniques to plan indoor femtocell base stations layout in multi-floors,” The Computer Journal, vol. 62, no. 6, pp. 919–930, 2019. [Google Scholar]
15. V. S. Devi, T. Ravi and S. B. Priya, “Cluster based data aggregation scheme for latency and packet loss reduction in WSN,” Computer Communications, vol. 149, no. 4, pp. 36–43, 2020. [Google Scholar]
16. C. H. Yang, Y. D. Lin and L. Y. Chuang, “Class balanced multifactor dimensionality reduction to detect gene–gene interactions,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 17, no. 1, pp. 71–81, 2020. [Google Scholar]
17. W. Yongdong, X. Dong-Wei, P. Peng, L. Yi, Z. Gui-Jun et al., “Kernel PCA for road traffic data non-linear feature extraction,” IET Intelligent Transport Systems, vol. 13, no. 8, pp. 1291–1298, 2019. [Google Scholar]
18. M. Sivasathya and S. MaryJoans, “Image feature extraction using non-linear principle-component analysis,” Procedia Engineering, Elsevier, vol. 38, no. 3, pp. 911–917, 2012. [Google Scholar]
19. C. Saravanakumar, “An authentication technique for accessing de-duplicated data from private cloud using one time password,” International Journal of Information Security and Privacy, vol. 11, no. 2, pp. 1–10, 2017. [Google Scholar]
20. P. Mohan, M. Sundaram, S. Satpathy and S. Das, “An efficient technique for cloud storage using secured de-duplication algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 41, no. 2, pp. 2969–2980, 2021. [Google Scholar]
21. A. Vinothini and B. P. Sankarlingam, “Survey of machine learning methods for big data applications,” in Int. Conf. on Computational Intelligence in Data Science (ICCIDS) IEEE, India, pp. 1–5, 2017. [Google Scholar]
22. K. Balasaravanan, “Detection of dengue disease using artificial neural network based classification technique,” International Journal of Engineering and Technology UAE, vol. 7, no. 1.3, pp. 97–103, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |