DOI:10.32604/iasc.2022.023038

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023038 |  |
| Article |
Identification of Bio-Markers for Cancer Classification Using Ensemble Approach and Genetic Algorithm
1Department of Computer Science and Engineering, K.S.Rangasamy College of Technology, Namakkal, Tamil Nadu, 637 215, India
2Department of Information Technology, K.S.Rangasamy College of Technology, Namakkal, Tamil Nadu, 637 215, India
*Corresponding Author: K. Poongodi. Email: poongodikksr@gmail.com
Received: 26 August 2021; Accepted: 25 November 2021
Abstract: The microarray gene expression data has a large number of genes with different expression levels. Analyzing and classifying datasets with entire gene space is quite difficult because there are only a few genes that are informative. The identification of bio-marker genes is significant because it improves the diagnosis of cancer disease and personalized medicine is suggested accordingly. Initially, the parallelized minimum redundancy and maximum relevance ensemble (mRMRe) is employed to select top m informative genes. The selected genes are then fed into the Genetic Algorithm (GA) that selects the optimal set of genes heuristically, which uses Mahalanobis Distance (MD) as the distance measure. This proposed method (mRMRe-GA) is applied to four microarray datasets using Support Vector Machine (SVM) as a classifier. The Leave One out Cross Validation (LOOCV) method is used to analyze the performance of the classifier. Comparative study of the proposed mRMRe-GA method is carried out with other methods. The proposed mRMRe-GA method significantly improves the classification accuracy with less number of selected genes.
Keywords: mRMR; mRMRe; microarray; gene expression data; GA; feature selection; SVM; cancer classification; mRMRe-GA
Identification and selection of informative genes is the main challenge in analyzing high-dimensional microarray data. The measurement of the expression levels of genes in DNA microarray facilitates the researchers to address the issues in cancer classification and paves way for personalized medicine. The cancer datasets are usually vast and the number of features mainly influences the analytical accuracy. Lack of a powerful method to analyze the data for all genes simultaneously is the most difficult challenge. Therefore, the entire dataset can be reduced to a set of a minimal number of differentially expressed genes that classifies the samples into cancer vs. normal cases. Identification of differentially expressed genes is the primary task in microarray analysis [1].
Gene selection methods are grouped into i) filter methods, ii) wrapper methods and iii) hybrid methods [2]. Filter methods select genes by searching and ranking genes individually or as a subset of genes. Different measures are developed for filtering features such as information, distance, similarity, consistency, and statistical measures. Univariate feature filters select single feature at a time while multivariate filters evaluate a subset of features jointly. Wrapper methods search through entire feature space and evaluate all the possible feature subsets based on the machine learning algorithm. Subsets are evaluated based on the classifier performance for classification and clustering algorithm performance (e.g., K-means) for clustering. The performance is good for particular models at the cost of increased computational complexity.
Hybrid methods combine different strategies to construct the optimal subset. The dimension of feature space is reduced using filter methods and then employs the wrapper method to identify the best candidate subset which leads to high accuracy and efficiency. Several interesting hybrid methodologies were proposed in literature such as random forest based feature selection [3], dynamic genetic algorithm [4], adaptive ant colony optimization [5], and cuckoo search algorithm [6].
The proposed work aims to identify the bio-marker genes and develop an efficient classification model which provides good accuracy in diagnosing the disease with less number of genes. The proposed mRMRe-GA method comprises of two stages for gene selection. The optimal subset of genes is selected through the first stage employing mRMRe method. The top m genes are selected from this subset by using the subsequent stage of gene selection method, which consists of GA with Mahalanobis Distance as the distance measure. The correlation between features are considered in Mahalanobis distance when compare to other methods. Finally, the classification model is built using SVM classifier as it shows reduced computational complexity and increased classification accuracy when compared to any other non-linear classifier [7]. The schematic of the proposed mRMRe-GA method is depicted in Fig. 1.

Figure 1: The schematic of the mRMRe-GA method
Four microarray benchmark datasets are tested with the mRMRe-GA method, and the statistical significance of the proposed method is demonstrated. The remainder part of the paper is divided into six sections. The works relevant to the proposed method are described in Section 2 while Sections 3 and 4 describe the concepts of mRMRe and GA respectively. In Section 5, mRMRe-GA method is described. Sections 6 and 7 present the performance evaluation of the proposed method and conclusion of the work respectively.
Mutual information (MI) based ranking criteria is widely used to study the relationships among genes for feature selection. MI is a joint measure which tells the relationship between two multidimensional variables and helps to split large datasets into groups for construction of the classification model. Information theoretic ranking criteria [8,9] exploit the relationships among variables and provide the basic theoretic foundation for many research works based on filter methods. The MI plays a significant role in feature selection as it has a unified theoretical foundation when compared to other heuristic methods. MI is calculated with its class labeling, and important features are identified [10]. An MI based group oriented feature selection model is proposed for microarray dataset [11]. Relevant features are identified by studying and analyzing the hidden relations between features. The SVM based classification model is proposed using the LOOCV method [12]. Genes are ranked and selected based on the MI value.
Due to the multidimensional nature of microarray data, traditional empirical MI based gene selection algorithms suffer from the data sparseness issue. To overcome this issue, multivariate Gaussian generative model was proposed to estimate the average information content of class variables for feature selection. In this approach, entropy was calculated for class variables instead of data [13]. In Wang et al. [14] the authors studied the effect of combining different feature selection algorithms and classification models.
Random Forest algorithm was proposed using an ensemble of classification trees for gene selection problems [3]. Genetic Bee Colony algorithm was proposed for analyzing microarray data by combining Genetic and Artificial Bee Colony algorithms [15]. Initially, the exploration space was reduced by mRMR then Artificial Bee Colony algorithm was used, which enhances the gene exploration process.
Correlation and mRMR based artificial bee colony algorithms with SVM classifier were proposed for the gene selection process [16,17]. To remove the redundant non-informative genes, in Peng et al. [18] the authors proposed a GA based model with SVM classifier. The results obtained were further tuned by recursive feature elimination (RFE) method. Modified Particle Swarm Optimization (PSO) based SVM classifier model was proposed to enhance the gene prediction performance [19]. The basic PSO was modified in which few particles were stochastically selected, and the performance of each particle was tested using pre-determined fitness value.
In Abdi et al. [20] the authors proposed an mRMR based gene selection model using weighted PSO-SVM approach. Genes were given with different weights, and PSO tuned its parameters based on these weights to optimize the selection process. An Adaptive Ant Colony (AACO) optimization was used with SVM classifier 5. The classification outcomes were used as the feedback for optimization process for feature convergence. In Akadi et al. [21] the authors used an mRMR filter approach to enhance the gene selection process of GA with SVM classifier. Gene selection based on statistical approaches was proposed in Gunavathi et al. [22]. These approaches were combined with GA-SVM/kNN to select biomarker genes. The cuckoo search optimization algorithm was used over the statistical approaches to increase the effectiveness of the gene selection process 6.
A dynamic GA was proposed with SVM classifier to rank the important features. 4 Chromosome size, recombination operator probability value and the selection mechanism were dynamically varied because these parameters made GA more effective to reach the global optimum in a time effective manner. Two optimization algorithms, namely Cuckoo and Harmony Search (HS) were combined with mRMR technique to enhance the gene selection process [23]. The output of mRMR was used as the input for COA-HS, and SVM classifier was used for classification. Cost values were also calculated and compared with other methods. Classification model based on fuzzy rough set was proposed for cancer biomarker identification [24]. The prediction performance was studied with semi-supervised learning techniques.
3 Minimum Redundancy and Maximum Relevance Ensemble (mRMRe) Method
Analyzing and interpreting huge volume of genomic data is particularly important in biological understandings to develop predictive models. The performance of predictive models is mainly based on inter-correlational relations of data. Identifying and marking relevant genes in high-dimensional datasets is particularly very important. The mRMR is an interesting feature selection method because of its low computational cost [25]. The mRMR uses the MI value to select relevant features that have minimal redundancy and maximal relevance criterion. However, the performance of mRMR is not stable as it picks a totally different feature set when there is a small change in the sample size.
To alleviate this problem, the minimum Redundancy and Maximum Relevance ensemble (mRMRe) was introduced employing parallel computing, in which multiple feature set has been built rather than a single feature set [26]. An ensemble learning approach was used in the basic mRMR to better search out the feature space with the advantage of parallel computing and built robust predictors. The mRMRe can be useful for applications such as high-throughput genomic data analysis which requires more thorough feature space exploration with lower bias and lower variance.
The mRMR provides functions to search through the entire sample space to select non-redundant, relevant, informative genes. The relevance and redundancy among genes can be calculated using MI as
where p and q are the two random variables, and ρ represents the correlation coefficient.
Let q be the input variable and p = {p1, . . . ., pn} be set of input features. The feature set F is framed based on the calculated MI value between features and output variable.
Initially, the feature pi with maximum relevance and minimum redundancy with the class label was added to F. The maximization criterion is as follows,
The above step was repeated until the desired feature set had been achieved.
GA is a biological evolution model that finds the best solutions in a large search space [27]. The algorithm starts with the initial population, which consists of randomly generated solutions that represent chromosomes. The population size depends on the number of chromosomes in one generation. Each chromosome was coded as a vector of variables with finite length of binary alphabet, as shown in Fig. 2. The chromosomes within the population were moved iteratively from another population called generations. GA uses genetic operators to retain genetic diversity in its evolution. Genetic diversity is important for evolution. Genetic operators are corresponding to the things which occur in real world biological evolution. The operators are,
i) Selection: fitness value was calculated based on the quality of the chromosome, and the chromosomes with maximum fitness value were moved to the subsequent generations.
ii) Crossover/Recombination: The selected set of chromosomes was combined to create a new set of chromosomes as shown in Fig. 3.
iii) Mutation: Random modifications were carried out over the binary representation of chromosomes, as shown in Fig. 4. This maintains diversity among the population and avoids the issue of premature solutions.

Figure 2: Chromosome representation
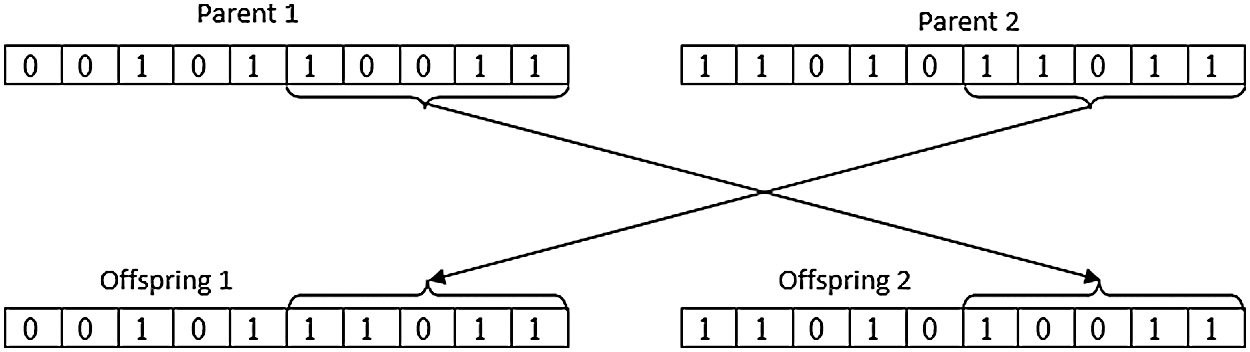
Figure 3: Crossover representation

Figure 4: Mutation representation
The pseudo code for the algorithm is given below.
Begin
Initialize the population with random solutions
Calculate fitness value as the quality measure for each individual
Rank the solutions based on fitness values according to the problem (either maximization or minimization)
For j = 1 to N (generation count)
Choose an operator randomly (crossover/mutation)
If (crossover)
Select any two parent solutions randomly
Create offspring via crossover
Else if (mutation)
Select a parent solution randomly
Create offspring via mutation
End if
Calculate the new fitness value
Replace the worst solution in the population with this offspring
Next j;
Check for stopping criteria
End
This section describes the methodology for identifying and selecting bio-marker genes using the proposed mRMRe–GA method. A flowchart of the mRMRe–GA method is shown in Fig. 5. The mRMRe was used to identify top m informative minimum redundant maximum relevance (mRMR) genes. This method works in parallels so the computational complexity is reduced
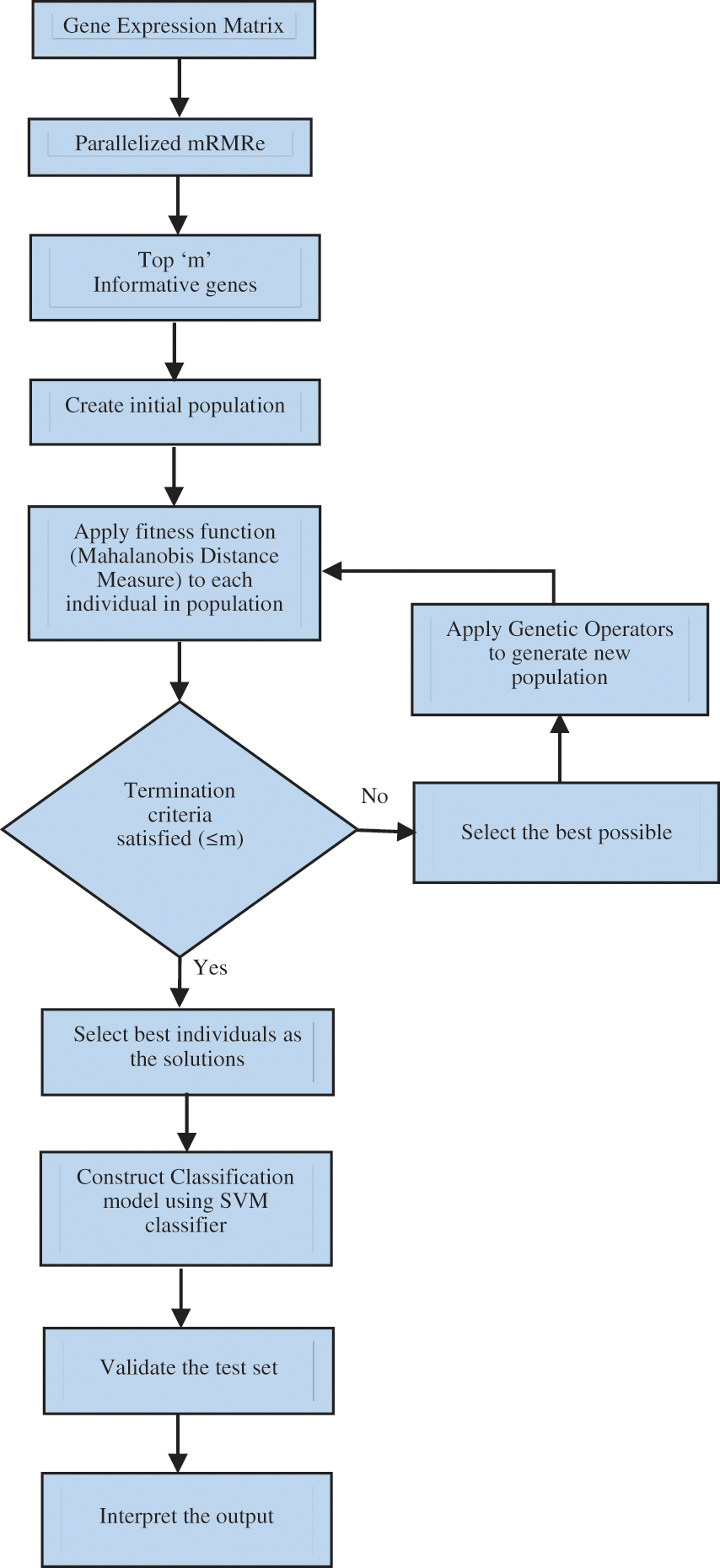
Figure 5: Flowchart of the proposed mRMRe–GA method
The mRMRe was used to identify top m informative minimum redundant maximum relevance (mRMR) genes. This method works in parallels so the computational complexity is reduced.
In maximum relevance method, strongly correlated genes with the classification label were identified by maximizing MI value as given in Eq. (2). The highly correlated genes may strongly depend on other genes as well. Therefore, the redundancy has to be removed so that the informative genes are effectively identified [25]. The top m informative genes were obtained by removing the redundancy among genes, and these were the input to the GA. The initial population for the GA was generated from these top m informative genes. The fitness function of this algorithm used mahalanobis distance as the distance measure, and it calculated the mahalanobis distance for each individual with the class label in the population.
The mahalanobis distance is calculated as follows [28],
where,
MD-Mahalanobis distance; x-Vector of a sample in a dataset
C-Covariance matrix of variables in a dataset; m-Vector of mean of variables in a dataset
Finally, GA returned the best individual, and from this, the classification model was built using SVM as a classifier. The proposed method was applied on four microarray datasets, and the LOOCV method was used to evaluate the performance of the proposed mRMRe-GA method. The benefit of LOOCV is its ability to avoid “over fitting” [29]. From each iteration in LOOCV approach, only one sample among n samples was used as the validating sample, and remaining samples were considered as training samples. This procedure was repeated ‘n’ times over the entire sample space. The implementation of mRMRe, GA and statistical analysis of the result was done using R programming language _ R version 3.6.1 [30] to make the result statistically valid, the model was executed by varying the number of input genes and SVM kernels on each microarray cancer dataset.
6 Experimental Setup and Results
Let N × M represent the microarray dataset where N and M represent the number of rows and columns respectively. The rows correspond to samples, columns correspond to genes and spots denote the expression value of a gene for the particular sample in a particular experiment. The performance evaluation of the proposed mRMRe-GA method was carried out over four publically available benchmark microarray gene expression datasets. These datasets were obtained from ELVIRA Biomedical Data Set Repository. All the datasets were high-dimensional, and the dimensional scope ranged from 2000 to 12600. The details of the dataset considered for evaluation are shown in Tab. 1.
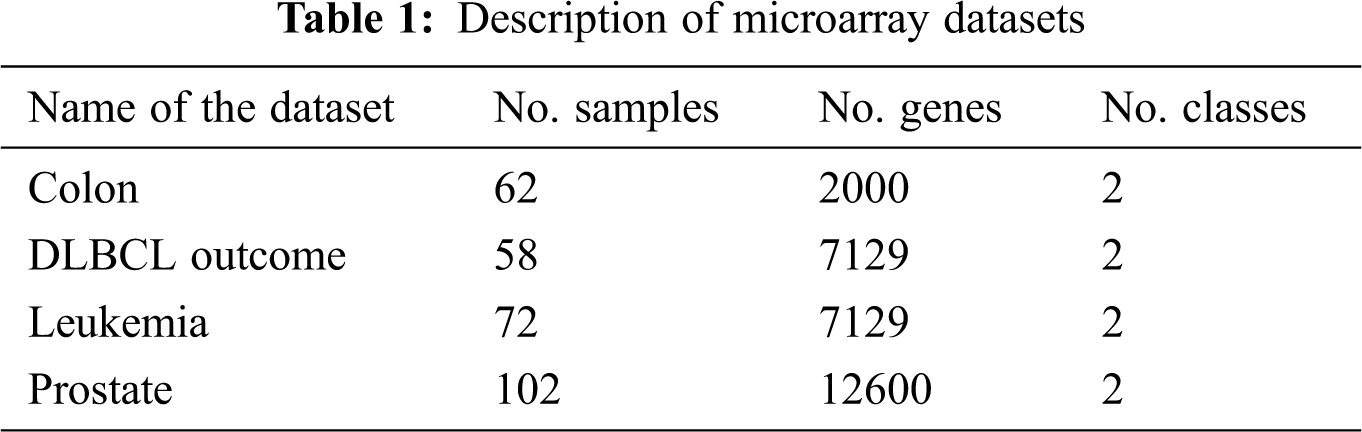
The colon cancer microarray dataset consists of 22 healthy and 40 tumor samples, and each sample is defined by 2000 genes. The DLBCL outcome contains 32 samples from cured patients and 26 from cancer patients, and each sample is defined by 7129 genes. The leukemia dataset is comprised of 47 ALL, and 25 AML samples and each sample is defined by 7129 genes. The prostate cancer dataset has 6033 gene expression profiles for 102 observations with 52 cancer and 50 healthy cases.
The proposed mRMRe-GA method combines mRMRe with GA. The SVM is used to build the final classification model. SVMs are very sensitive to the type of the kernel parameters. The different types of kernels used in SVM are represented as
where K is the kernel function defined as K(xi, xj ) = φ(xi).φ(xj) which transforms non-linear sample data points to higher dimension space for better predictions and Xi, Xj are n dimensional inputs. The parameters of the genetic algorithm were initialized and represented in Tab. 2.

The first parameter is the maximum number of generations which varies from 1 to 100. The random population of size n was generated during the initial evolution process. So the solution at step t = 0 is {s1(0), s2(0), s3(0), …, sn(0)}. At step t, the fitness value of individual member of the population,
The performance study of the proposed mRMRe-GA method was carried out with other existing algorithms. The classification accuracy was calculated against the number of genes and compared with different algorithms. The accuracy was calculated as the ratio between correct decisions and total samples in the given microarray gene expression dataset. It gave the overall accuracy of the classifier. The various performance parameters considered for the analysis of mRMRe-GA method is given in Tab. 3.
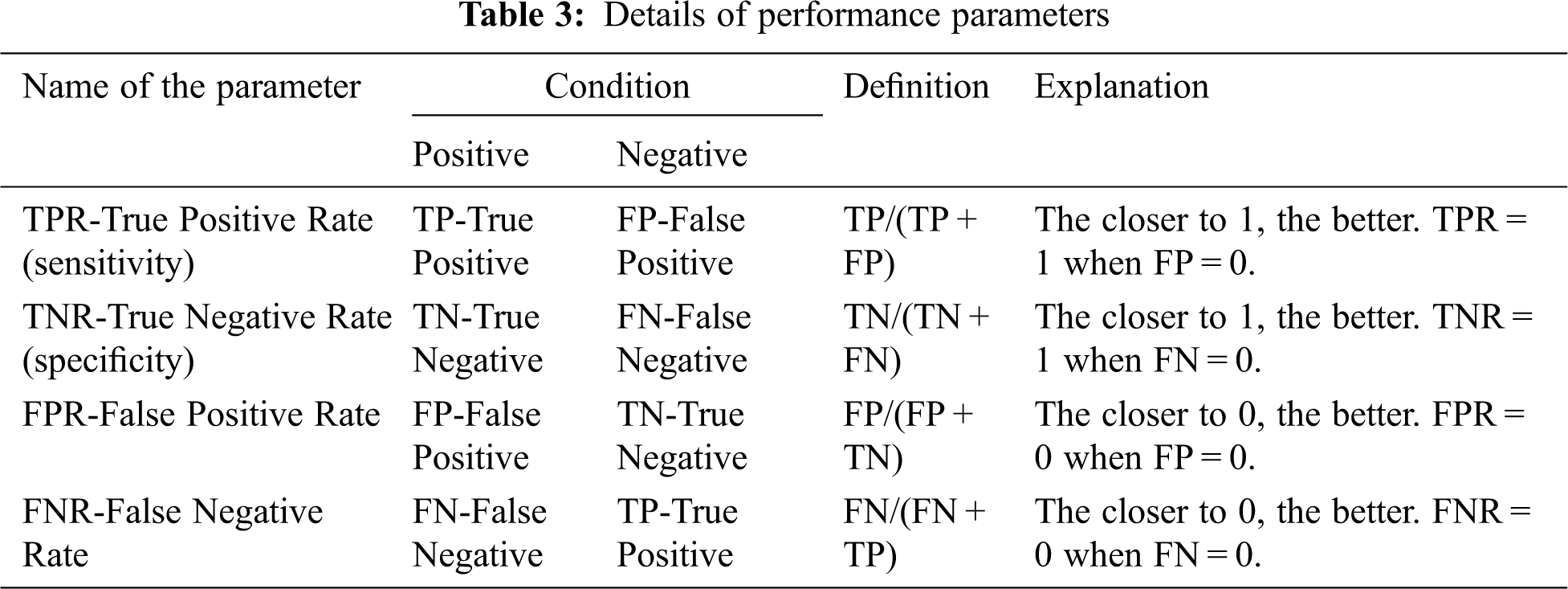
Based on these parameters, the classification accuracy was defined in terms of positives and negatives as
The mRMRe was used to select the topmost informative genes from four microarray benchmark datasets, and SVM classifier was employed for classification, which resulted in highest accuracy. To implement the SVM, the package ‘e1071’ was used. The model was assessed using the LOOCV method. The accuracy of the SVM classifier with different kernel functions against the number of selected genes is given in Tab. 3. From the experiment, it was observed that the RBF kernel performed better for microarray classification, but in Nahar et al. [7]. The authors used polynomial kernel as the kernel function for their experiment because it out performed well for eight out of nine datasets. From the results, it was observed that for high-dimensional dataset, RBF kernel outperformed which was better than polynomial kernel although cancer classification is non-linear. The performance of the SVM classifier with different kernel functions is given in Tab. 4.
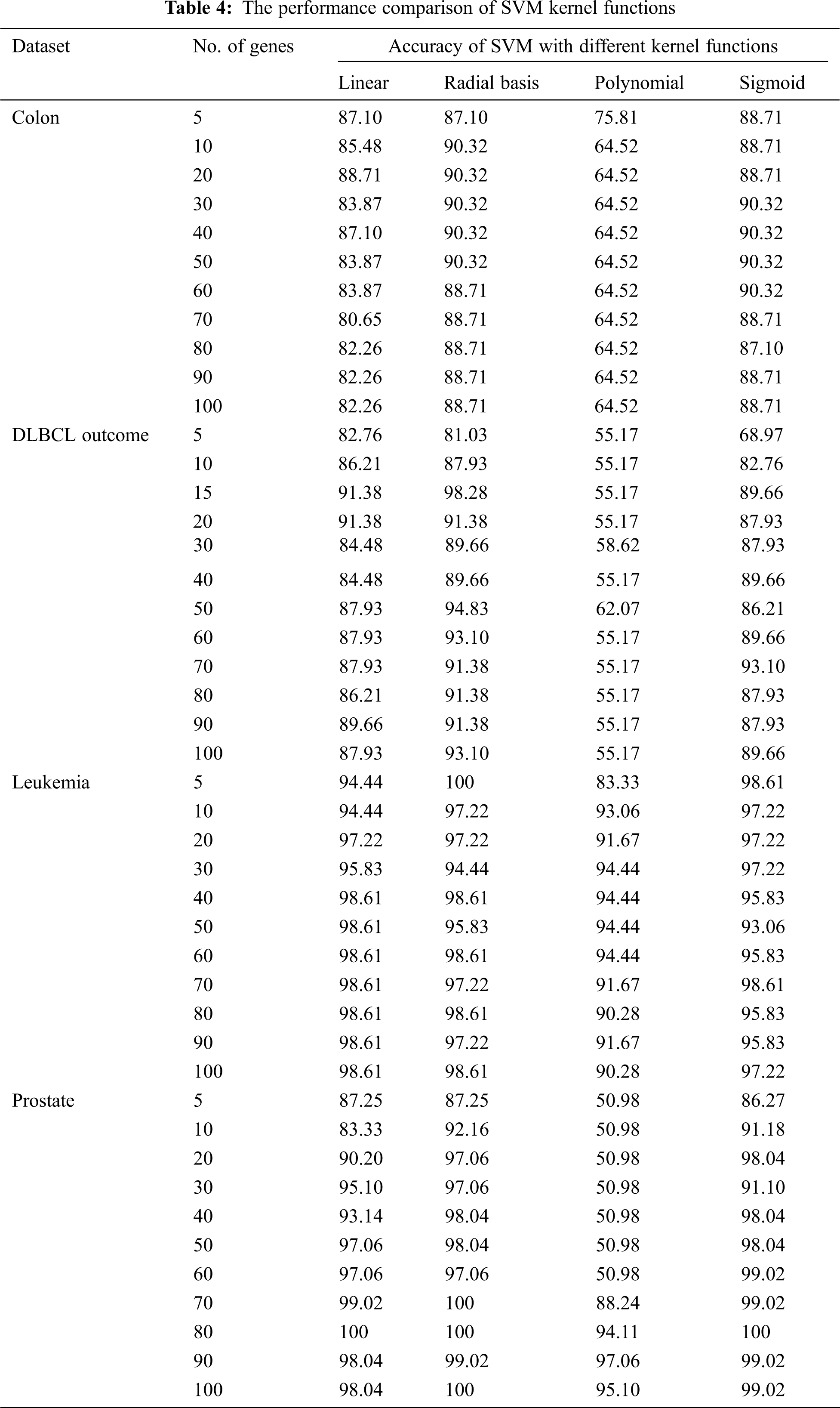
The performance of the SVM classifier with genes selected from mRMRe is shown in Fig. 6. The top 100 informative genes were selected from the original set of genes using mRMRe. These genes were fed into GA to obtain the best set of informative genes that produced the highest accuracy. The samples were classified using SVM classifier, and the LOOCV method was used to measure the classifier accuracy.
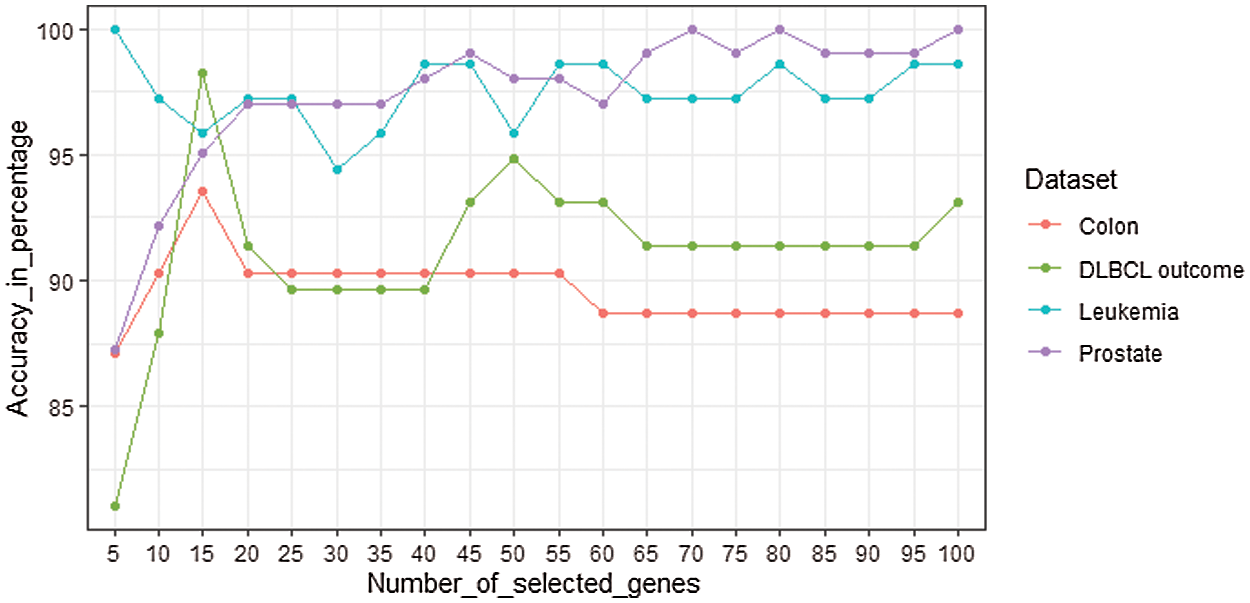
Figure 6: The performance of the SVM classifier with genes selected from mRMRe
In common, the classification accuracy increased with the number of selected genes, but in some cases, it decreased. For Leukemia dataset, the classifier gave 100% accuracy with 5 genes whereas the accuracy decreased while increasing number of genes. For prostate, the classifier provided 100% accuracy for top 70 and 80 genes, but for top 75 genes, it provided 99.02%. For DLBCL data set, the classifier produced the highest accuracy as 98.28% for top 15 genes. It decreased to 91.38% as the number of genes increased to 20. For colon data set, the highest accuracy 93.55% was observed at top 15 genes. Finally, these top informative genes were given as the input to the GA to identify the bio-marker genes that could classify the cancer data at its best.
The performance of the mRMRe-GA method is compared with other gene selection methods for four microarray datasets as given in Fig. 7. For Colon, mRMRe-GA gives 100% accuracy with only 3 selected genes whereas mRMRe provides a maximum of 93.55% with 15 genes. The GA produces a maximum of 93% accuracy with 10 genes, whereas mRMR-GA gives a maximum of 95% with 5 genes. The mRMR gives a maximum of 85% with 5 genes.
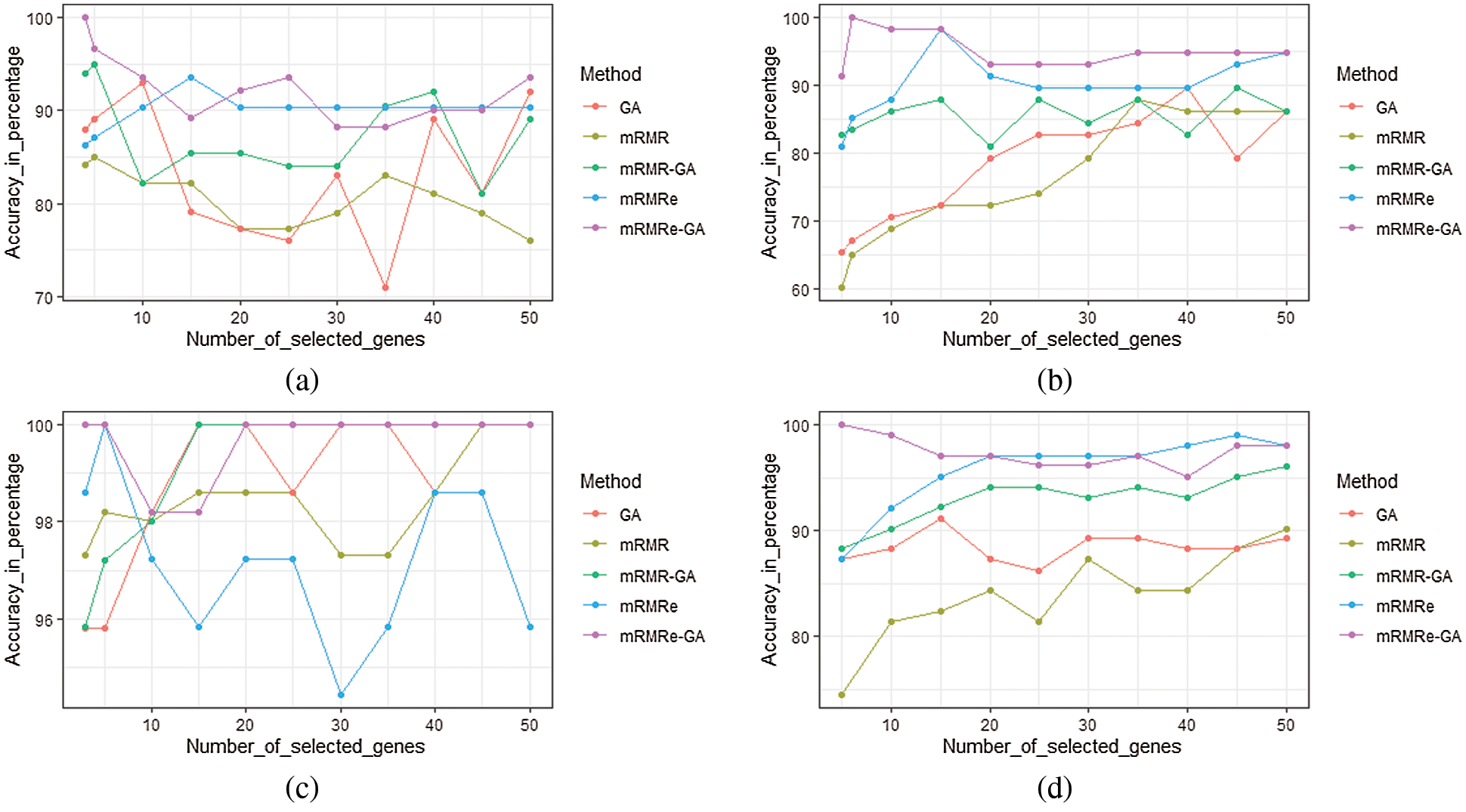
Figure 7: Comparison of the mRMRe-GA method with other gene selection methods for four microarray datasets (a) Colon (b) DLBCL outcome (c) Leukemia (d) Prostate
For DLBCL outcome dataset, mRMRe-GA gives 100% accuracy with only 5 selected genes whereas mRMRe produces a maximum of 98.28% with 15 genes. The GA produces a maximum of 90% accuracy with 40 genes whereas mRMR-GA gives a maximum of 90% with 45 genes. The mRMR gives a maximum of 85% with 5 genes. For Leukemia, mRMRe-GA gives 100% accuracy with only 3 selected genes, whereas mRMRe provides 100% with 5 genes. The GA and mRMR-GA provide 100% accuracy with 15 genes, whereas mRMR gives 100% with 45 genes. For Prostate dataset, mRMRe-GA gives 100% accuracy with only 5 selected genes, whereas mRMRe produces a maximum of 99.02% with 45 genes. The GA provides a maximum of 91.18% accuracy with 15 genes, whereas mRMR-GA gives a maximum of 96.08% with 45 genes. The mRMR gives a maximum of 90.20% with 50 genes.
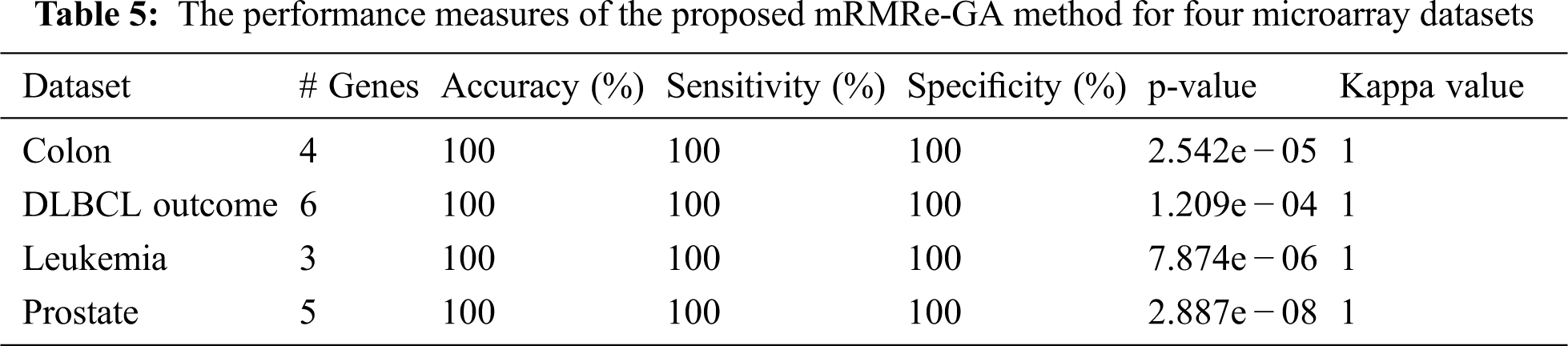
The various performance measures of the proposed mRMRe-GA method is given in Tab. 5. It is that the method has achieved 100% classification accuracy for all datasets considered in this study with the minimum number of selected genes. Similarly, it has achieved 100% sensitivity and specificity. The p-value and kappa value indicate the significance of the proposed method.
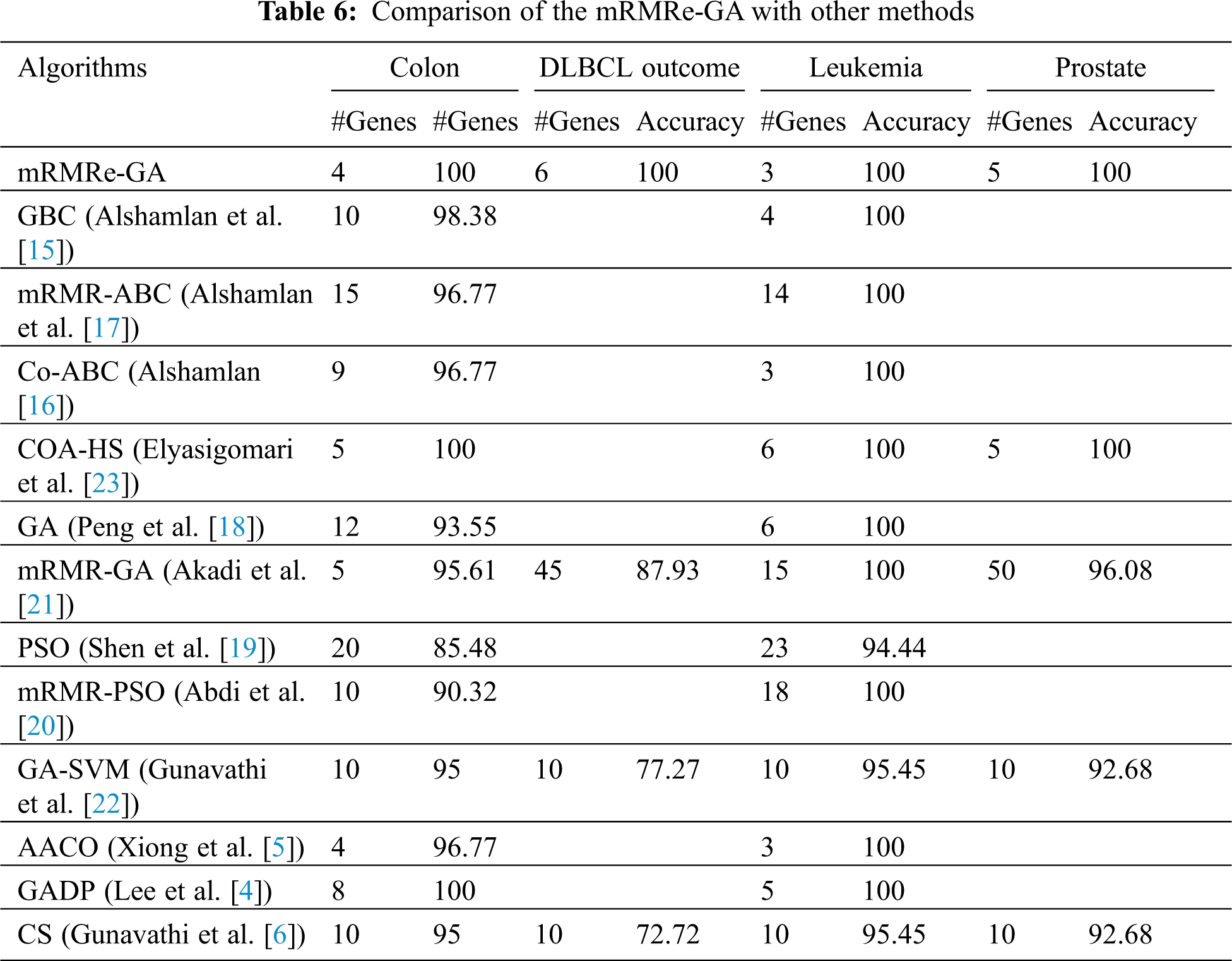
Tab. 6 presents the results of the mRMRe-GA method and other cancer classification methods for four microarray datasets. For Colon dataset, the mRMRe-GA method achieves 100% classification accuracy with 4 genes, whereas the COA-HS and GADP methods achieve 100% classification accuracy for 5 and 8 genes respectively. For Leukemia dataset, the mRMRe-GA method achieves 100% classification accuracy with 3 genes, whereas other works select more genes to give the same accuracy except for AACO method. AACO method also achieves 100% accuracy for 3 genes. For Prostate and DLBCL outcome datasets, the proposed method outperforms the existing methods and gives 100% classification for 5 and 6 genes respectively. The COA-HS method shows similar performance with the proposed method for 5 genes.
In this paper, a new gene selection method combining mRMRe and GA is proposed which produces 100% classification accuracy for four microarray datasets with the minimum number of selected genes. Initially, mRMRe gene selection technique is used to extract useful genes which have a minimum redundancy and maximum relevance with the class label. The extracted genes are then fed into to GA, which uses Mahalanobis distance as the distance measure, and it calculates the Mahalanobis distance for each chromosome with the class label in the population. This identifies the highly informative genes, and then the classification model is built using SVM classifier. The performance of the developed model is analyzed using the LOOCV method. The results are compared with other methods for four microarray datasets. The proposed mRMRe-GA method achieves better accuracy over other methods and attains optimal biological interpretations.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. M., Mutch, A., Berger, R. Mansourian, A., Rytz and M. A. Roberts, “Microarray data analysis: A practical approach for selecting differentially expressed genes,” Genome Biology, vol. 2, preprint0009.1, 2001. [Google Scholar]
2. Z. M. Hira and D. F. Gillies, “A review of feature selection and feature extraction methods applied on microarray data,” Advances in Bioinformatics, vol. 2015, no. Article ID 198363, 2015. [Google Scholar]
3. R. D. Uriarte and S. A. D. Andres, “Gene selection and classification of microarray data using random forest,” BMC Bioinformatics, vol. 7, no. Article number: 3, 2006. [Google Scholar]
4. C. P. Lee and Y. Leu, “A novel hybrid feature selection method for microarray data analysis,” Applied Soft Computing, vol. 11, no. 1, pp. 208–213, 2011. [Google Scholar]
5. W. Xiong and C. Wang, “Feature selection: a hybrid approach based on self-adaptive ant colony and support vector machine,” in Proc. IEEE Int. Conf. on Computer Science and Software Engineering, Wuhan, China, pp. 751–754, 2008. [Google Scholar]
6. C. Gunavathi and K. Premalatha, “Cuckoo search optimisation for feature selection in cancer classification: A new approach,” International Journal of Data Mining and Bioinformatics, vol. 13, no. 3, pp. 248–265, 2015. [Google Scholar]
7. J. Nahar, S. Ali and Y. P. Chen, “Microarray data classification using automatic SVM kernel selection,” DNA and Cell Biology, vol. 26, no. 10, pp. 707–712, 2007. [Google Scholar]
8. H. Peng, F. Long and C. Ding, “Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy,” IEEE Transaction on Pattern Analysis Machine Intelligence, vol. 27, no. 8, pp. 1226–1238, 2005. [Google Scholar]
9. J. R. Vergara and P. A. Estevez, “A review of feature selection methods based on mutual information,” Neural Computing and Applications, vol. 24, pp. 175–186, 2014. [Google Scholar]
10. C. H. Yang, L. Y. Chuang and C. H. Yang, “IG-GA: A hybrid filter/wrapper method for feature selection of microarray data,” Journal of Medical and Biological Engineering, vol. 30, no. 1, pp. 23–28, 2010. [Google Scholar]
11. J. Tang and S. Zhou, “A new approach for feature selection from microarray data based on mutual information,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 13, no. 6, pp. 1004–1015, 2016. [Google Scholar]
12. C. D. A. Vanitha, D. Devaraj and M. Venkatesulu, “Multiclass cancer diagnosis in microarray gene expression profile using mutual information and support vector machine,” Intelligent Data Analysis, vol. 20, no. 6, pp. 1425–1439, 2016. [Google Scholar]
13. S. Zhu, D. Wang, K. Yu, T. Li and Y. Gong, “Feature selection for gene expression using model-based entropy,” EEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 7, no. 1, pp. 25–36, 2010. [Google Scholar]
14. Y. Wang, I. V. Tetko, M. Hall, E. Frank, A. Facius et al., “Gene selection from microarray data for cancer classification-a machine learning approach,” Computational Biology and Chemistry, vol. 29, no. 1, pp. 37–46, 2005. [Google Scholar]
15. H. M. Alshamlan, G. H. Badr and Y. A. Alohali, “Genetic bee colony (GBC) algorithm: A new gene selection method for microarray cancer classification,” Computational Biology and Chemistry, vol. 56, no. c, pp. 49–60, 2015. [Google Scholar]
16. H. M. Alshamlan, “Co–ABC: Correlation artificial bee colony algorithm for bio marker gene discovery using gene expression profile,” Saudi Journal of Biological Sciences, vol. 25, no. 5, pp. 895–903, 2018. [Google Scholar]
17. H. M. Alshamlan, G. H. Badr and Y. A. Alohali, “mRMR-ABC: A hybrid gene selection algorithm for cancer classification using microarray gene expression profiling,” BioMed Research International, vol. 2015, no. Article ID 604910, 2015. [Google Scholar]
18. S. Peng, Q. Xu, X. B. Ling, X. Peng, W. Du et al., “Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines,” FEBS Letters, vol. 555, no. 2, pp. 358–362, 2003. [Google Scholar]
19. Q. Shen, W. M. Shi, W. Kong and B. Ye, “A combination of modified particle swarm optimization algorithm and support vector machine for gene selection and tumor classification,” Talanta, vol. 71, no. 4, pp. 1679–1683, 2007. [Google Scholar]
20. M. J. Abdi, S. M. Hosseini and M. Rezghi, “A novel weighted support vector machine based on particle swarm optimization for gene selection and tumor classification,” Computational and Mathematical Methods in Medicine, vol. 2012, no. Article ID 320698, 2012. [Google Scholar]
21. A. E. Akadi, A. Amine, A. E. Ouardighi and D. Aboutajdine, “A new gene selection approach based on minimum redundancy-maximum relevance (mRMR) and genetic algorithm (GA),” in Proc. Int. Conf. on Computer Systems and Applications, Rabat, Morocco, pp. 69–75, 2019. [Google Scholar]
22. C. Gunavathi and K. Premalatha, “Performance analysis of genetic algorithm with KNN and SVM for feature selection in tumor classification,” International Journal of Computer and Information Engineering, vol. 8, pp. 1490–1497, 2014. [Google Scholar]
23. V. Elyasigomari, D. A. Lee, H. Screen and M. A. Shaheed, “Development of a two-stage gene selection method that incorporates a novel hybrid approach using the cuckoo optimization algorithm and harmony search for cancer classification,” Journal of Biomedical Informatics, vol. 67, pp. 11–20, 2017. [Google Scholar]
24. D. Chakraborty and U. Maulik, “Identifying cancer biomarkers from microarray data using feature selection and semisupervised learning,” IEEE Journal of Translational Engineering in Health and Medicine, vol. 2, no. Article ID 4300211, pp. 1–11, 2014. [Google Scholar]
25. C. Ding and H. Peng, “Minimum redundancy feature selection from microarray gene expression data,” Journal of Bioinformatics and Computational Biology, vol. 3, no. 2, pp. 185–205, 2005. [Google Scholar]
26. N. D. Jay, S. P. Cavanagh, C. Olsen, N. E. Hachem, G. Bontempi et al., “mRMRe: An R package for parallelized mRMR ensemble feature selection,” Bioinformatics, vol. 29, no. 18, pp. 2365–2368, 2013. [Google Scholar]
27. D. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning. Menlo Park, California, United States: Addison Wesley, 1989. [Google Scholar]
28. A. Sankhya, “On the generalised distance in statistics,” Reprint of: Mahalanobis, P.C. (1936), vol. 80, pp. 1–7, 2018. [Google Scholar]
29. A. Y. Ng, “Preventing “overfitting” of cross-validation data,” in Proc. Int. Conf. on Machine Learning, Tennessee, United States, pp. 245–253, 1997. [Google Scholar]
30. R Core Team. “R: A language and environment for Statistical Computing,” in R Foundation for Statistical Computing, Vienna, Austria: The R Development Core Team, 2019. [Online]. Available: https://www.R-project.org/. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |