DOI:10.32604/iasc.2022.023702

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023702 |  |
| Article |
Distribution Network Reconfiguration Using Hybrid Optimization Technique
Department of EEE, Sona College of Technology, Salem, Tamilnadu, 636005, India
*Corresponding Author: S. Arun Kumar. Email: arunkumarak0806@gmail.com
Received: 17 September 2021; Accepted: 22 November 2021
Abstract: Energy management carried in a power system by configuration process is a difficult activity. So, reconfiguration has been introduced to solve this problem. Numerous optimization topologies have been utilized to solve this problem so far. However, they exhibit some drawbacks such as convergence, etc. Hence to overcome this issue, this work formulated a new hybrid optimization topology Genetic Algorithm Enabled Particle Swarm Optimization (PSOGA) to solve the energy configuration problem with low power loss in the Distribution System (DS). The proposed topology’s effectiveness was evaluated on the IEEE 33 bus Distribution System, and the results were compared to methods reported in the literature. As a result, the suggested technique appears to be more successful than other approaches, and the power loss in buses is minimised and hence exhibits an enhanced voltage profile. Hence, it is concluded that the proposed PSOGA can be a promising topology for reconfiguration as well as energy management in DS.
Keywords: Energy management; distribution system (DS); network re-configuration (NR); distributed generation (DG); genetic algorithm enabled particle swarm optimization (PSOGA); power loss
Energy management plays a vital role in DS. Thus, to maximize the efficiency of energy management, proper configuration of DS is essential. The improper configuration may lead to increased loss of power, poor voltage. Henceforth, the network should be restructured to have less power loss with improved voltage levels [1].
To minimize the power loss over DS, numerous methodologies such as NR, DG, and optimal placement of capacitor have been adopted so far [2]. NR is the most widely used of these since it is more cost-effective. It is a method of altering the configuration of feeders in a distribution system by opening and closing sections and tie switches in accordance with system limits. Thus, the reconfiguration in DS is obtained by turning ON/OFF of the switches present in the network [3].
This turning ON/OFF condition mainly depends on the objective function formulated by the user [4]. Hence, it is necessary to implement an effective algorithm to solve this optimal NR to obtain
(i) Power loss minimization
(ii) Improvement in Voltage profile and enhance the efficiency of the DS [5].
As a result, several studies have been conducted to solve this distribution network reconfiguration (DNR) [6] three different topologies were adopted, namely
a) Traditional Multi-layer Perceptron (MLP) algorithm
b) Artificial intelligence (AI) based techniques and
c) Heuristic algorithms
Among those, Metaheuristic algorithms like Particle Swarm Optimization (PSO), Evolutionary Programming (EP), and Genetic Algorithm (GA) are becoming more popular to solve NR in DS. The NR is carried out with multiple objectives such as power loss minimization, voltage stability, and load margin. Rao et al. [7] formulated a Harmony Search Algorithm (HSR) for NR and to find the optimal locations of DG units in a DS. The Plant Growth Algorithm was proposed to solve NR in DS system [8]. This is designed for the reduction of loss and to balance the load. Here, the NR was attained by turning ON/OFF few of the switches present in the system. An evolutionary PSO (EPSO) was formulated to minimise power loss in DS [9]. The result of this method is compared with conventional PSO to prove its effectiveness. Gravitational search algorithm was tailored to solve NR [10] to find an alternating network topology until the power loss is minimized.
Prasad et al. 2007 formulated GA to find a solution for NR and balancing load condition in DS. The tie switches and section status are altered according to the load state and thus the NR is performed. Shirmohammadi et al. [11] made use of a heuristic algorithm to reconfigure the network system. It reduces the line losses (resistive) under normal condition. Three DR programs were formulated to solve the NR problem [12] to increase its controllability; it utilized a mixed-integer 2nd order cone program to minimize the operational cost of the system which is subjected to both financial and technical constraints. A multi-objective biased random key GA is utilized for meter allocation [13]. Thus, it reduces the energy loss in DS. After NR, it also helps to avoid the degradation of the estimator accuracy of the system [14].
DG placement [15–18], optimal capacitor location [19], and DNR [20] can be carried out to obtain optimal NR. Among these, DNR exhibits lower power loss and the enhanced voltage across the buses. DNR with DG and capacitor is so effective in reducing Active Power Loss. Thus, so far numerous studies have been carried out to obtain optimal NR. But the time taken for convergence by the existing topologies is comparatively high.
This work introduced a hybrid method (combination of PSO and GA) with the aim of attaining NR with reduced power loss and a faster convergence time. Thus, it utilizes the divergence property of PSO with the strengthening of GA, to modify the configuration of existing network. As a result, its quick convergence characteristic establishes its superiority over alternative topologies.
This section labels the hybrid PSOGA developed for solving NR problems.
The basic concept of GA has formulated based principles of Charles Darwin and finds the persistence of the fittest. PSO is a population-based optimization topology, which is stimulated by the behaviour of a flock of birds. Though these two methods are utilized for finding the optimal solution, they exhibit some drawbacks. GA has no memory capacity to store data. Similarly, PSO have poor individuals but exhibits memory capacity. So, the thinking capability of PSO and local search capability of GA together formulated a hybrid topology called PSOGA algorithm and it is shown in Fig. 1.
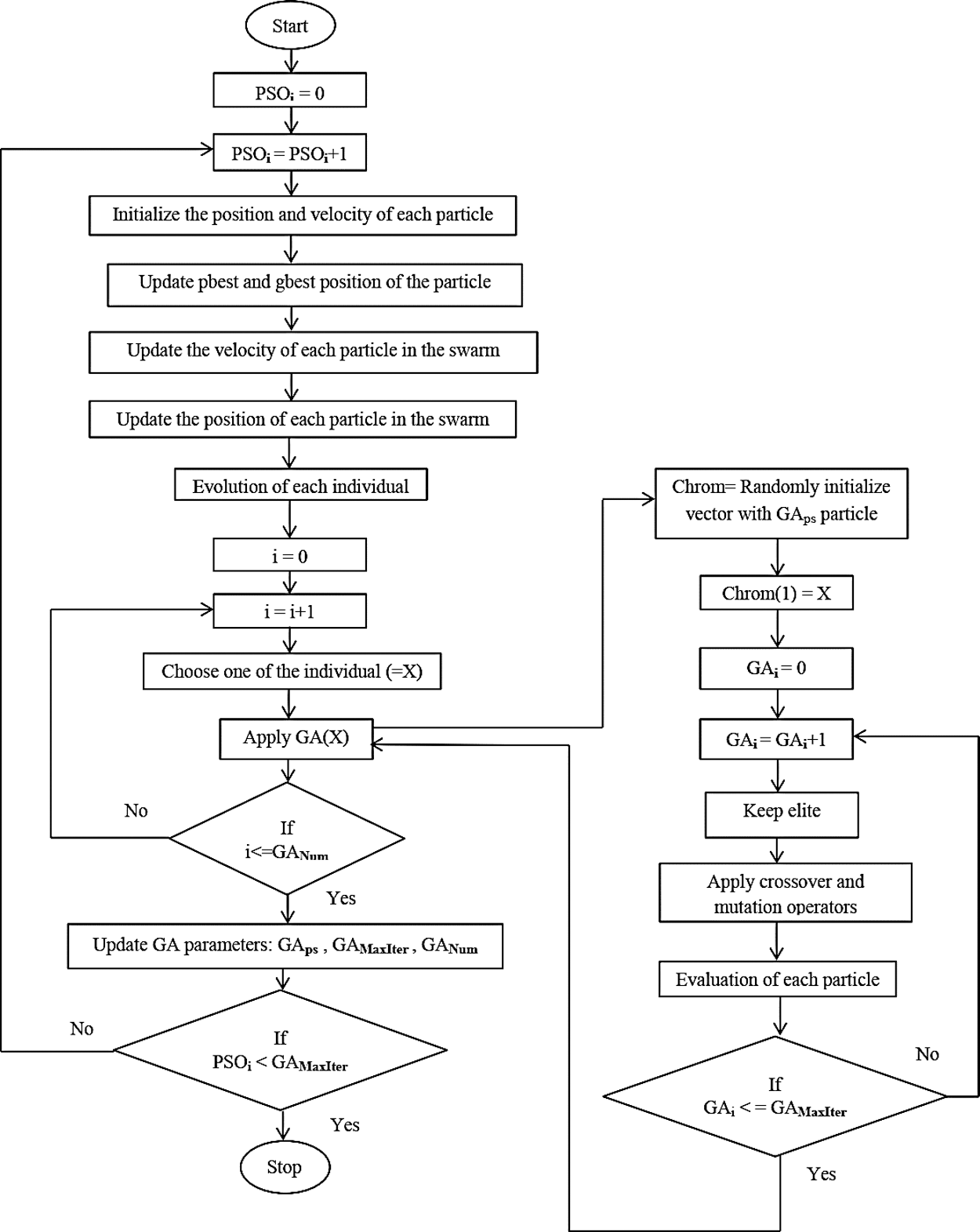
Figure 1: Hybrid PSO-GA algorithm
The algorithm adopted to find the fitness function (minimization of power loss) is depicted below.
Step 1: Input the parameters (both electrical and topology).
Step 2: Generate both initial positions and velocity randomly.
Step 3: Execute load flow calculation.
Step 4: Evaluate the objective function, update velocity and check for all the constraints.
Step 5: If the constraint is not satisfied, execute GA.
Step 6: Finally compare the previous iteration.
Step 7: Finally, the termination criteria are verified. If maximum iterations are achieved, results are drawn; otherwise go to step 2.
The parameter configuration utilized for PSO is depicted below,
Acceleration coefficients (C1, C2) = 1.6
Weight (Wmax and Wmin) = 0.9 & 0.38
Similarly for GA,
Crossover rate = 0.88,
Mutation rate = 0.02
The NR is being carried out; the key objective functions are power loss minimization and voltage profile improvement.
where,
F-Fitness Function
Wr, Wx and Wv-Weight factor
PL-Power Loss (Active)
QL-Power Loss (Reactive)
CVD-Cumulative Voltage Deviation function
CVD-Sum of deviation of gain value from its original value.
Normally, sum of all these should be equal to 1. (i.e., Wr + Wx + Wv = 1)
Voltage limit should be,
Vmin < Vi < Vmax
Vi-Voltage at node ‘i’;
Reactive power limit can be given as
Qc Total < Qd
Qc Total–Compensated KVAr in capacitor bank
Qd-Load KVAr (demand side)
Apparent power limit should be represented as Sk < S max
where
Sk-‘kth’ line power flow
Smax-Maximum allowable power flow
In this work, the standard IEEE 33-bus system depicted in Fig. 2, is deliberated as a test system. It comprises 32 sectionalizing switches and 5 tie switches at branches (33, 34, 35, 36, and 37).
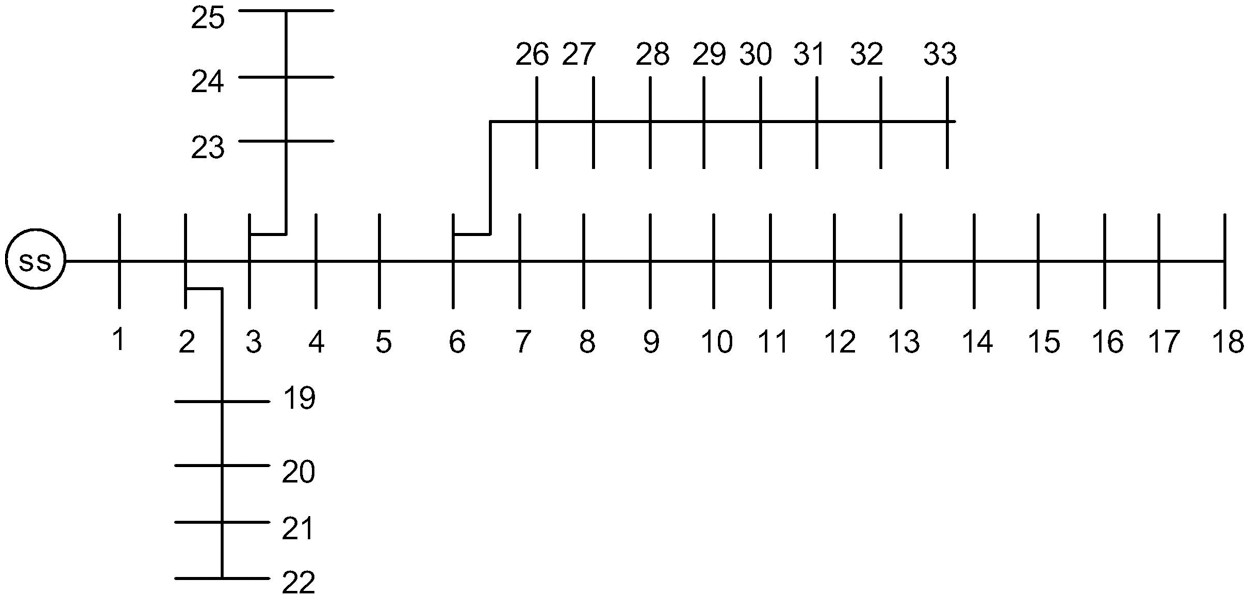
Figure 2: IEEE 33 bus system
To verify the effectiveness of this proposed topology, three different types of load conditions are considered in this study are discussed below
Case (i): Light load = 0.5 pu,
Case (ii): Normal load = 1.0 pu,
Case (iii): Heavy load = 1.3 pu.
Thus, the analysis of this system before optimization is tabulated in Tab. 1 and its voltage profile is depicted in Fig. 3.
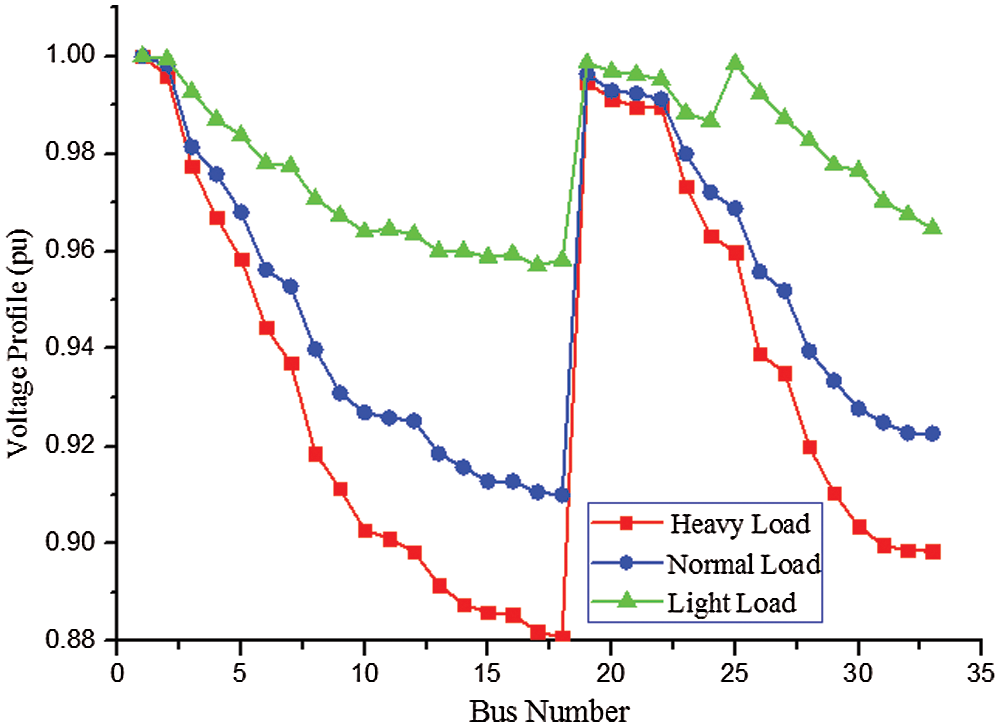
Figure 3: Voltage profile of a system (base case)

Thus, under normal condition, the minimum voltage level of a bus is about 0.9130 pu When it is lightly loaded, it is around 0.9585 pu. Under the heavy loaded condition, it is equal to 0.8808 pu.
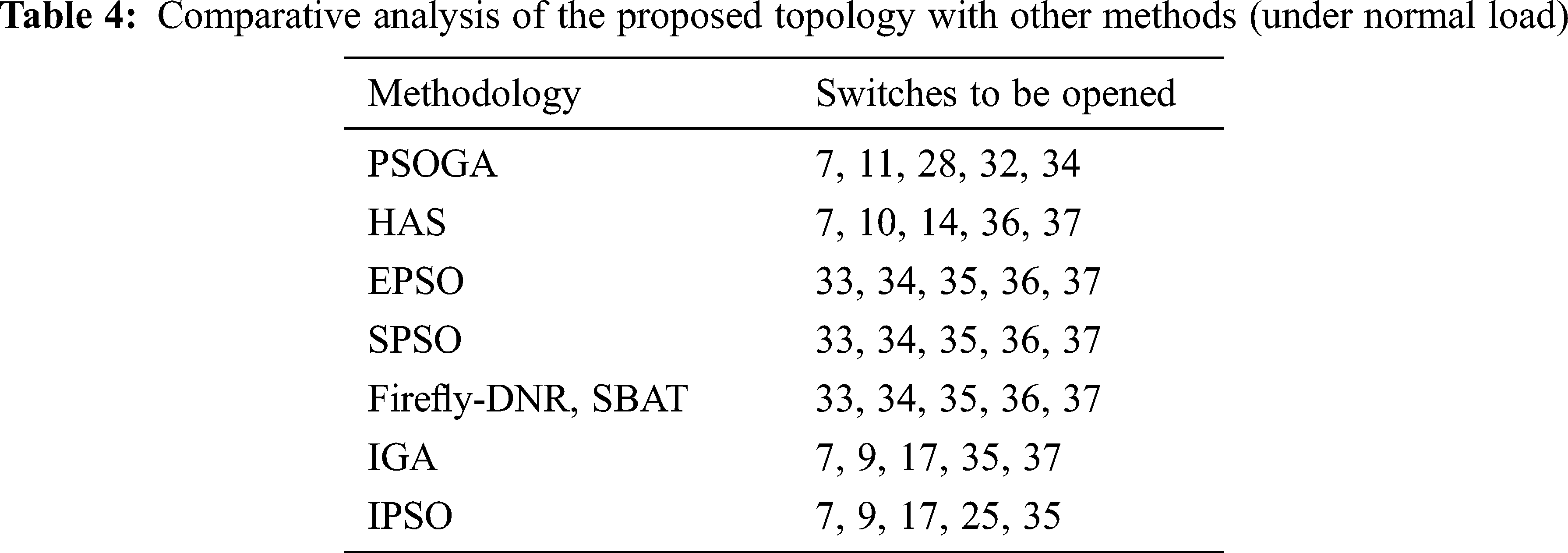
In this, tie switches mentioned above are reconfigured using the proposed topology and its results are represented in Tab. 2 Cases (i–iii).

4.2.1 Performance Analysis of Case (i)
Half of the usual load level is applied in this state. Thus, the system voltages after and before NR is depicted in Fig. 4. Thus, the minimum voltage after and before NR is about 0.9715 and 0.9585 pu. Thus, with an NR, the voltage of the system gets enhanced.
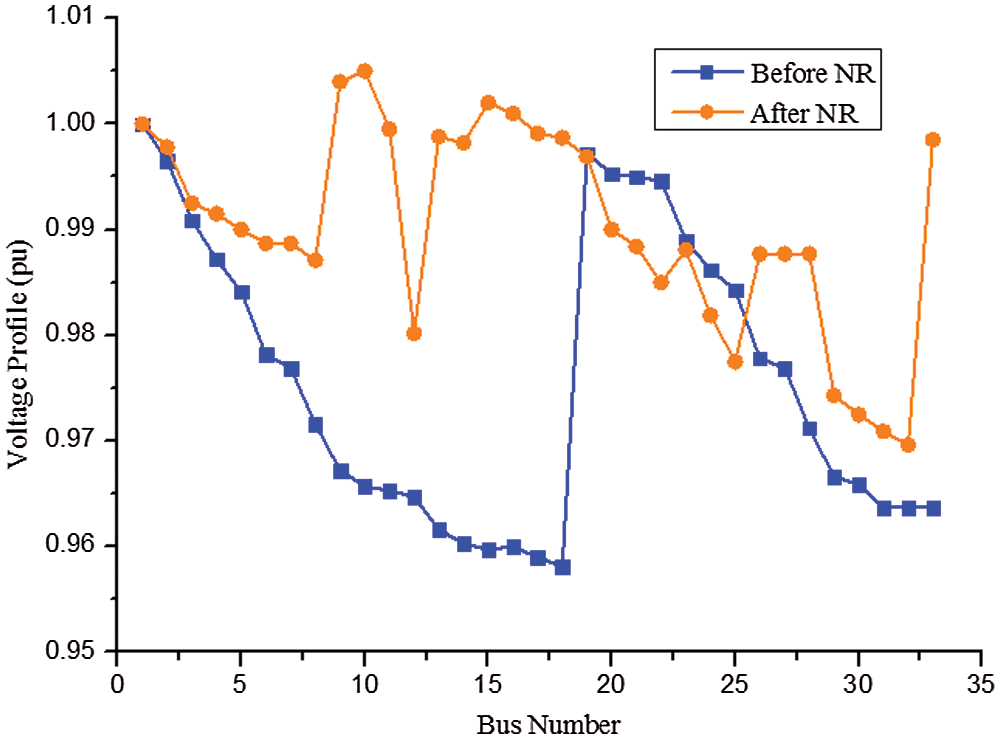
Figure 4: Voltage of test system (light load)
Similarly, the real power loss across the system gets decreases to 31.99 kW when compared to the base case value of about 47.2 kW. Thus, the power can be saved using this topology when compared to the base case condition. The tie switches 33, 35, 36 and 37 remain closed, and switches 7, 11, 28, 32, and 34 remain open under this proposed topology.
4.2.2 Performance Analysis of Case (ii)
The system voltage profile after and before reconfiguration under case (ii) is represented in Fig. 5. The minimum voltage after and before NR is about 0.940 and 0.9130 pu. Thus, with the NR, the voltage of the system gets enhanced.
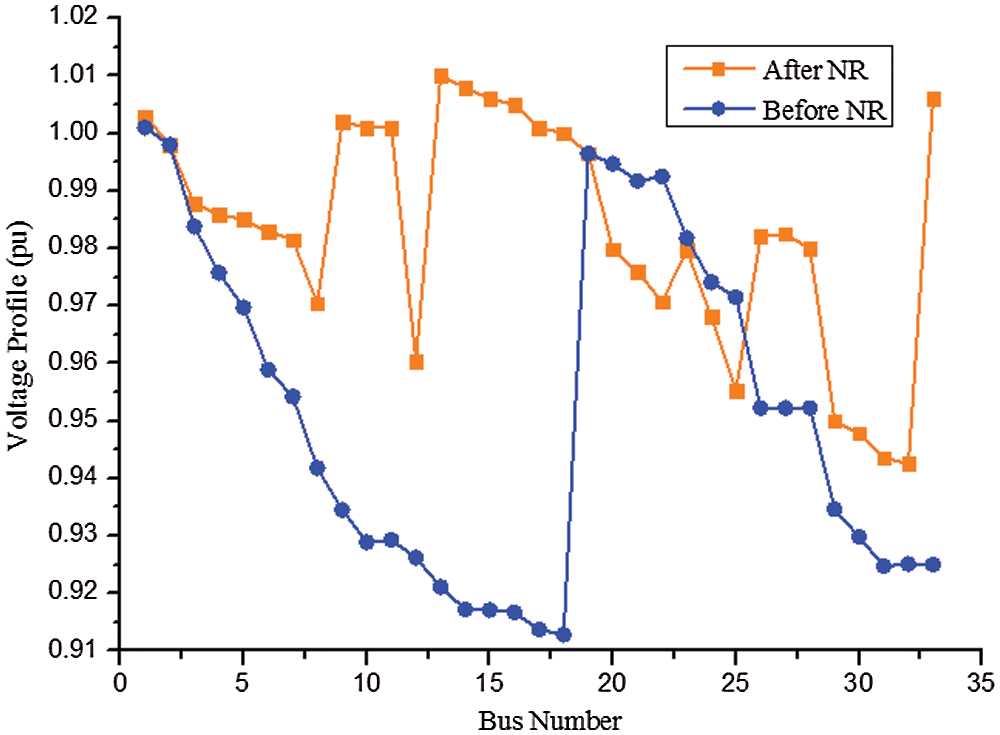
Figure 5: Voltage profile of test system (normal load)
Similarly, the power loss (real) across the system gets decreases to 109.48 kW when compared to the base case value of about 202.40 kW. Thus, the power can be saved using this topology when compared to the base case condition.
The tie switches 33, 35, 36, and 37 remain closed and switches 7, 11, 28, 32, and 34 remain open under this proposed topology.
4.2.3 Performance Analysis of Case (iii)
Under case (iii), the load is increased by about 130% of the nominal load. The system’s voltage profile after and before NR is shown in Fig. 6. Thus, after and before the NR, the minimum voltage is 0.9245 and 0.8841 pu respectively. Thus, with the NR, the voltage profile of the system gets enhanced.
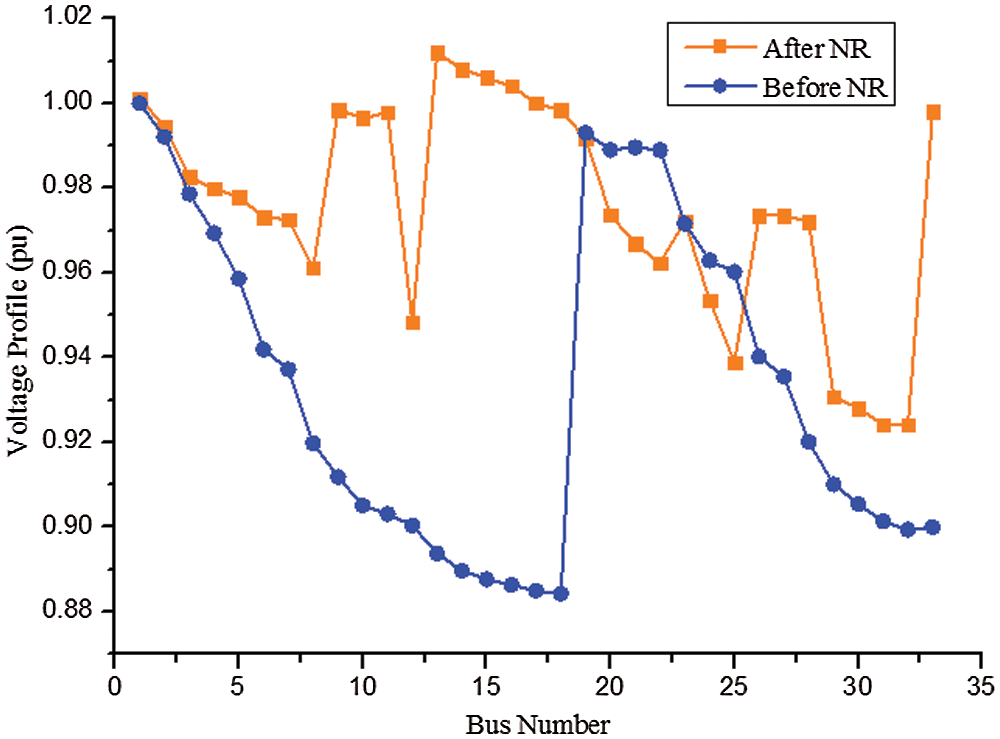
Figure 6: Voltage profile of test system (heavy load)
Similarly, the real power loss across the system gets decreases to 224.63 kW when compared to the base case value about 358 kW. Thus, the power can be saved using this topology when compared to the base case condition.
The tie switches 33, 35, 36, and 37 remain closed and switches 7, 11, 28, 32, and 34 remain open under this proposed topology.
Thus, the power loss reduction achieved by the PSOGA algorithm under different load scenarios is depicted in Fig. 7a and similarly, the minimum voltage at different load scenarios is presented in Fig. 7b.
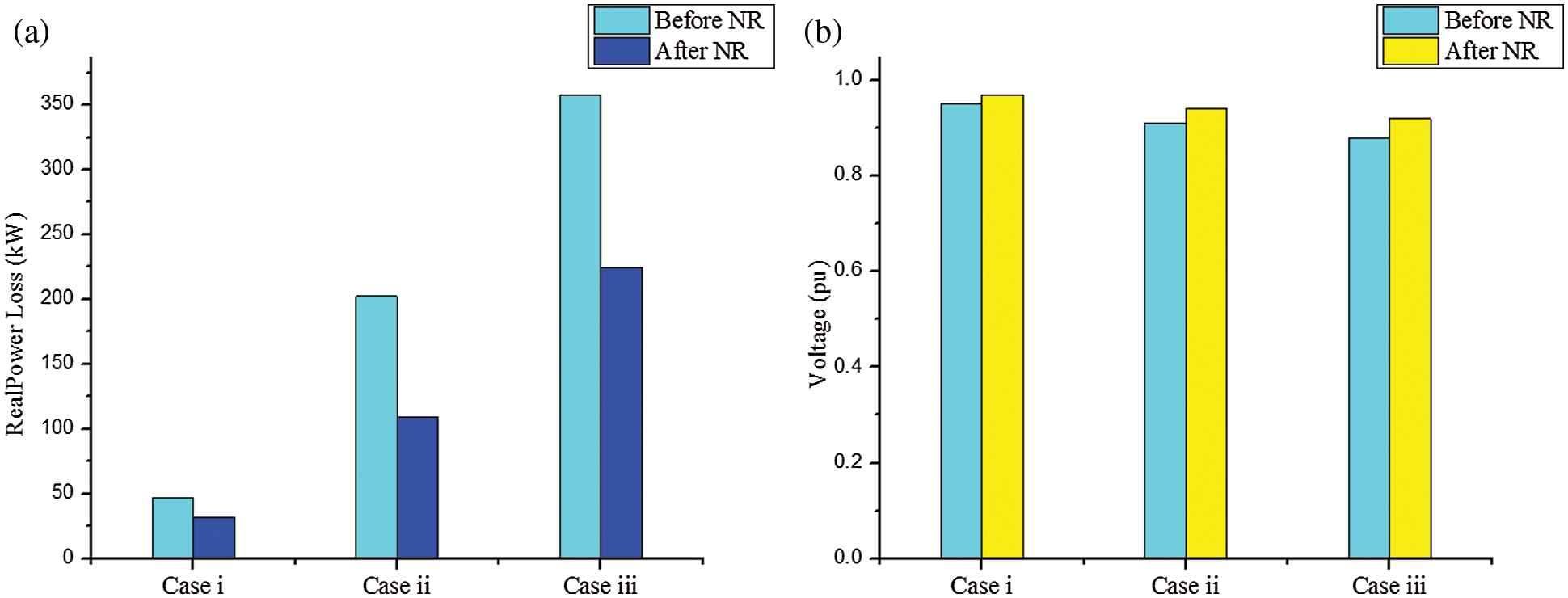
Figure 7: (a) Power loss under different load condition, (b) voltage at different load variations
From above Figs. 7a and 7b, the formulated PSOGA provides better NR irrespective of different load effects over DS.
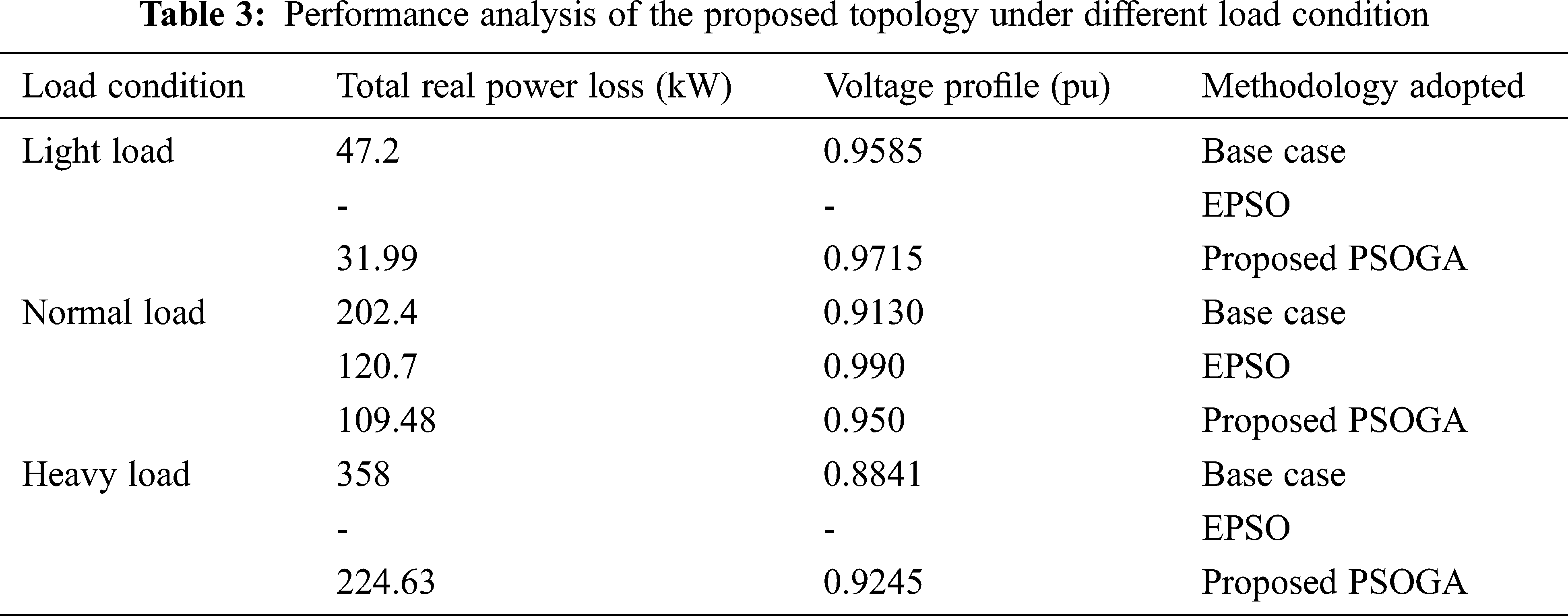
The effectiveness of the proposed topology with power loss reduction and in voltage enhancement is tabulated in Tab. 3 and hence, it is proven that the proposed topology exhibits an efficient energy management system [21,22]. Thus, the test system obtained after NR using this proposed topology is depicted in Fig. 8.

Figure 8: Test system after NR
Similarly, to prove the efficacy of the proposed algorithm, a comparative study has been made with the existing topologies which utilized IEEE 33 bus as a test system. This study is carried out under normal load condition and their results are tabulated in Tab. 4 and Fig. 9.
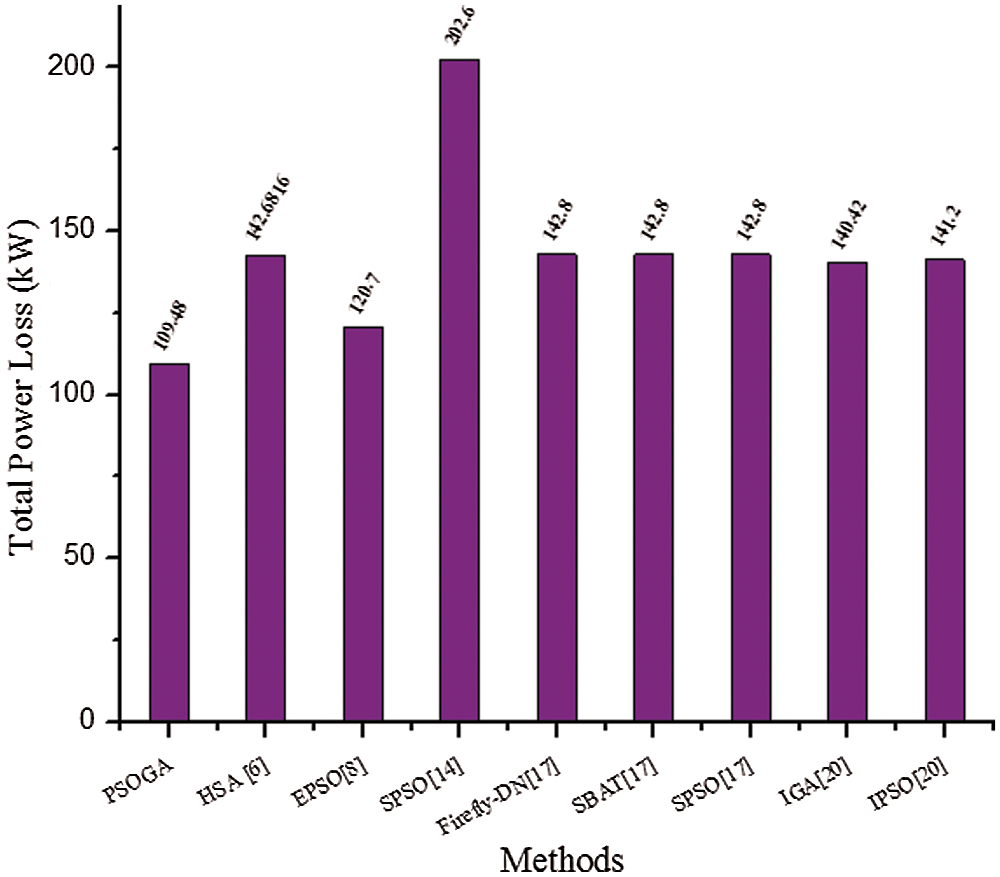
Figure 9: Comparative analysis of proposed topology with other methods (under power loss condition)
These comparison findings show that the suggested algorithm (PSOGA) achieves better results than the other optimisation algorithms, reducing total power loss and it shows effective energy management.
Similarly, it improves the minimum voltage level from 0.8804 to 0.9510 pu irrespective of load variations in the system. Similarly, the real power was improved about 99.34%, 97.28% and 95.38%, respectively for three different kinds of load considered in this work. (Light, normal and heavy load).
Fig. 10 depicts the variation of optimal real power loss with the iteration number for case (ii). The results depict that increase in iterations results in minimised objective function. From Fig. 10, it is deliberated that the computational time of PSOGA significantly less than that of PSO.
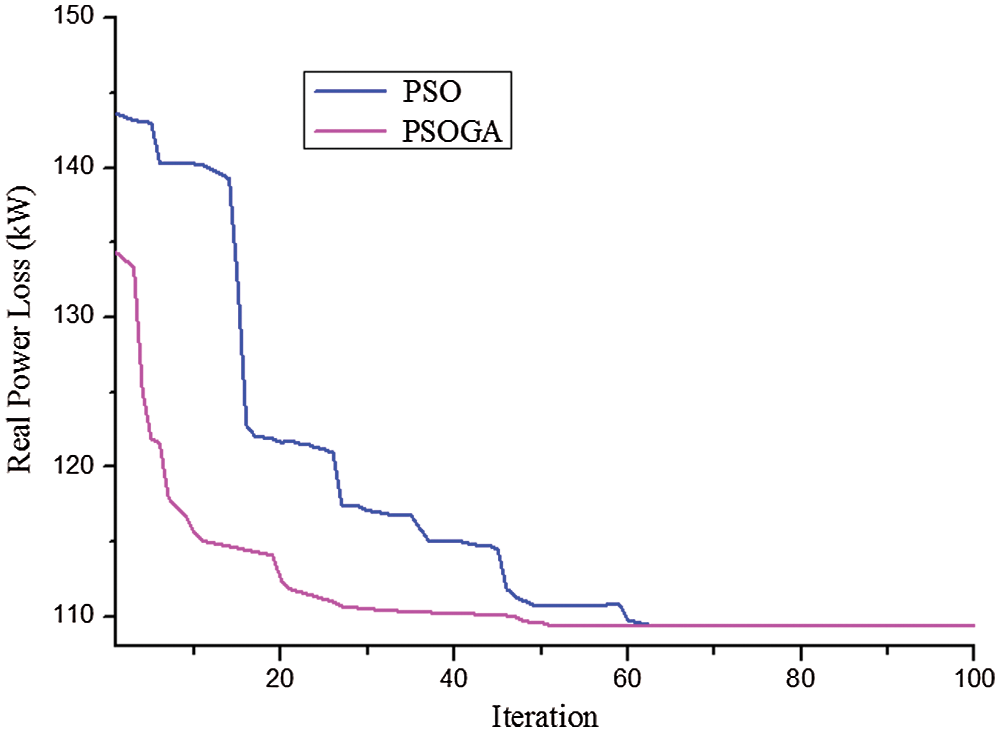
Figure 10: Convergence characteristic (minimization of power losses)
The efficiency of every optimization topology is evaluated with the convergence time also. Better convergence time results in better results. A comparative study has been made in terms of execution timein Tab. 5.
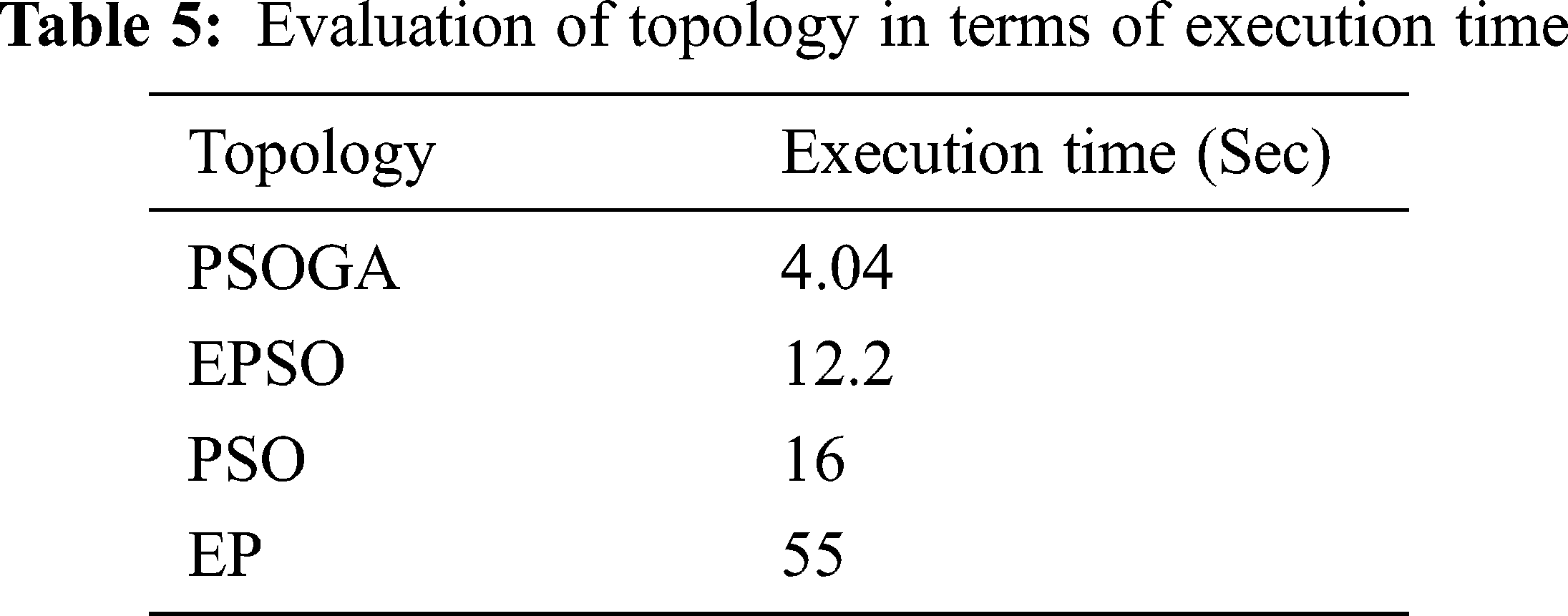
From the above Tab. 5 and Fig. 11, it is proven that the proposed PSOGA algorithm requires an average execution time of 4.04 s to obtain the optimal solution. It is comparatively lesser than EP, EPSO, and PSO [23–25]. Thus, from the overall results, it is verified that the NR carried out using the PSOGA algorithm exhibits optimal solution to that of the existing methods [26–32].
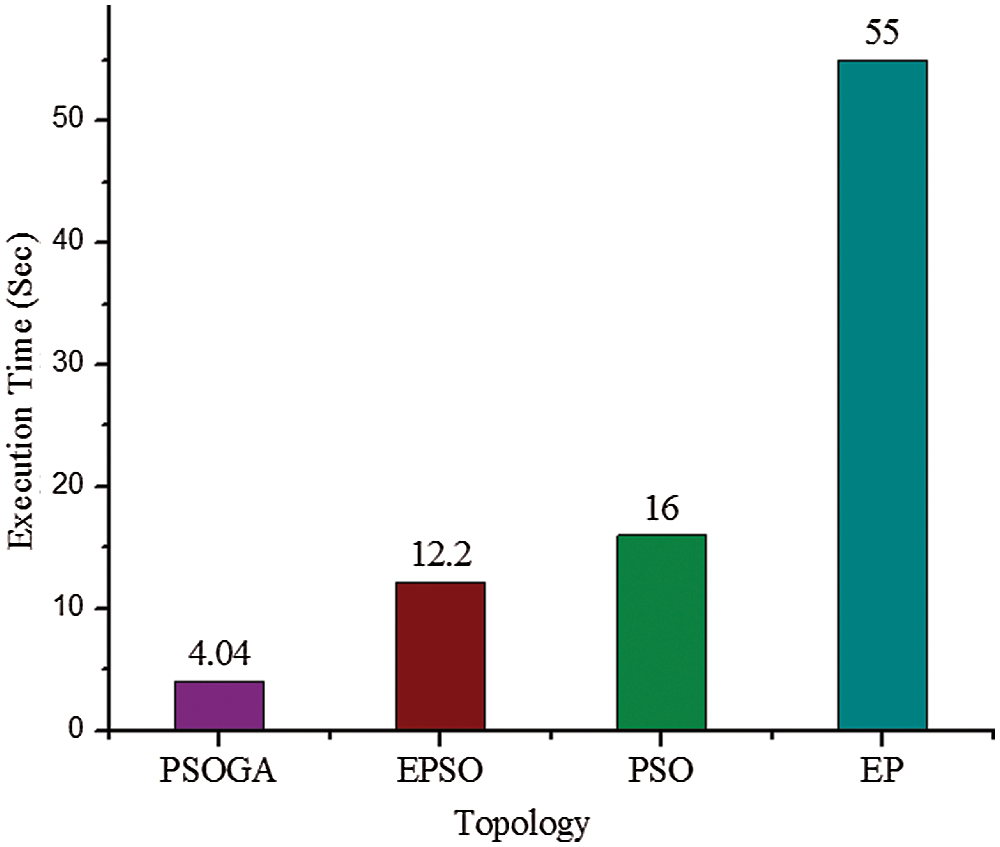
Figure 11: Evaluation of topology in terms of execution time
From the above analysis, the objective work for minimum power losses and improved voltage profile attain with least number of iterations has been observed. Therefore, it’s proved that the effectiveness of the proposed system better than the other existing optimization topology.
The PSOGA topology was effectively used to address the NR problem in this study. Its main objective is to reduce the power loss and voltage enhancement in DS. To examine the efficacy of the PSOGA algorithm, IEEE 33 bus is utilised as a test system. From the results, it is observed that the minimum voltage level of the system was improved to 0.95 p.u irrespective of load variations in the system. Similarly, the real power was improved by about 99.34%, 97.28%, and 95.38%, respectively for three different kinds of load considered in this work. (Light, normal, and heavy load). Thus, acquired results have proven the efficacy of the proposed topology for the NR problem in DS. It results in a better reduction in loss and voltage enhancement than other popular topologies. It helps to minimize the loss and the cost of energy tracking. Hence enhanced energy management can be obtained in DS. Therefore, the proposed topology is one of best method for finding a solution to large-scale NR in DS.
Acknowledgement: The authors would like to thank Anna University and also, we like to thank Anonymous reviewers for their so-called insights.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Y. Mon, “Design and calculation of 5 MVAR shunt capacitor bank at 33 kV bus in distribution substation,” International Journal of Scientific Engineering and Technology Research, vol. 3, no. 15, pp. 3259–3263, 2014. [Google Scholar]
2. R. Magadum and T. Timsani, “Minimization of power loss in distribution networks by different techniques,” International Journal of Science and Engineering, vol. 3, no. 5, pp. 521–527, 2012. [Google Scholar]
3. R. Syahputra, I. Soesanti and M. Ashari, “Performance enhancement of distribution network with DG integration using modified PSO algorithm,” Journal of Electrical Systems, vol. 12, no. 1, pp. 1–19, 2016. [Google Scholar]
4. D. A. Bitew, A. O. Salau and Y. Gebru, “Load flow and contingency analysis for transmission line outage,” Archives of Electrical Engineering, vol. 69, no. 3, pp. 273, 2020. [Google Scholar]
5. A. E. A. Elanien and K. B. Shaban, “Modern network reconfiguration techniques for service restoration in distribution systems: A step to a smarter grid,” Alexandria Engineering Journal, vol. 57, no. 4, pp. 3959–3967, 2018. [Google Scholar]
6. R. S. Rao, S. V. L. Narasimham, M. R. Raju and A. S. Rao, “Optimal network reconfiguration of large-scale distribution system using harmony search algorithm,” IEEE Transactions on Power Systems, vol. 26, no. 3, pp. 1080–1088, 2011. [Google Scholar]
7. P. R. Rao, S. Sivanagaraju and P. V. Prasad, “Network reconfiguration for loss reduction using plant growth simulation algorithm,” in Proc. Int. Conf. on Power, Control and Embedded Systems, Allahabad, India, pp. 1–4, 2010. [Google Scholar]
8. M. F. Sulaima, M. H. Jali, W. M. Bukhari, M. N. M. Nasir and H. I. Jaafar, “Power distribution network reconfiguration by using EPSO for loss minimizing,” Applied Mechanics and Materials, vol. 699, pp. 809–815, 2015. [Google Scholar]
9. Y. M. Shuaib, M. S. Kalavathi and C. C. A. Rajan, “Optimal reconfiguration in radial distribution system using gravitational search algorithm,” Electric Power Components and Systems, vol. 42, no. 7, pp. 703–715, 2014. [Google Scholar]
10. P. V. Prasad, S. Sivanagaraju and N. Sreenivasulu, “Network reconfiguration for load balancing in radial distribution systems using genetic algorithm,” Electric Power Components and Systems, vol. 36, no. 1, pp. 63–72, 2007. [Google Scholar]
11. D. Shirmohammadi and H. W. Hong, “Reconfiguration of electric distribution networks for resistive line losses reduction,” IEEE Transactions on Power Delivery, vol. 4, no. 2, pp. 1492–1498, 1989. [Google Scholar]
12. A. Appathurai and P. Deepa, “Design for reliablity: A novel counter matrix code for FPGA based quality applications,” in Proc. Asia Symp. on Quality Electronic Design, Kula Lumpur, Malaysia, pp. 56–61, 2015. [Google Scholar]
13. M. Sedighizadeh, G. S. Shahr, M. R. Aghamohammadi and M. Esmaili, “A new optimal operation framework for balanced microgrids considering reconfiguration and generation scheduling simultaneously,” International Transactions on Electrical Energy Systems, vol. 30, no. 4, pp. 12302, 2020. [Google Scholar]
14. A. A. M. Raposo, A. B. Rodrigues and M. D. G. D. Silva, “Robust meter placement for state estimation considering distribution network reconfiguration for annual energy loss reduction,” Electric Power Systems Research, vol. 182, pp. 106233, 2020. [Google Scholar]
15. T. F. Agajie, A. O. Salau, E. A. Hailu, M. Sood and S. Jain, “Optimal sizing and siting of distributed generators for minimization of power losses and voltage deviation,” in Proc. Int. Conf. on Signal Processing, Computing and Control, Solan, India, pp. 292–297, 2019. [Google Scholar]
16. C. Gerez, L. I. Silva, E. A. Belati, A. J. S. Filho and E. C. M. Costa, “Distribution network reconfiguration using selective firefly algorithm and a load flow analysis criterion for reducing the search space,” IEEE Access, vol. 7, pp. 67874–67888, 2019. [Google Scholar]
17. R. S. Rao, K. Ravindra, K. Satish and S. Narasimham, “Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation,” IEEE Transactions on Power Systems, vol. 28, no. 1, pp. 317–325, 2012. [Google Scholar]
18. G. Prathiba, M. Santhi and A. Ahilan, “Design and implementation of reliable flash ADC for microwave applications,” Microelectronics Reliability, vol. 88, pp. 91–97, 2018. [Google Scholar]
19. R. T. Juarez and E. E. Juarez, “Reconfiguration of radial distribution networks by applying a multi-objective technique,” in Proc. Int. Conf. on Artificial Intelligence, USA, pp. 131–137, 2015. [Google Scholar]
20. N. Kanwar, N. Gupta, K. R. Niazi and A. Swarnkar, “Improved meta-heuristic techniques for simultaneous capacitor and DG allocation in radial distribution networks,” Electrical Power and Energy Systems, vol. 73, pp. 653–664, 2016. [Google Scholar]
21. S. H. Mirhoseini, S. M. Hosseini, M. Ghanbari and M. Ahmadi, “A new improved adaptive imperialist competitive algorithm to solve the reconfiguration problem of distribution systems for loss reduction and voltage profile improvement,” International Journal of Electrical Power & Energy Systems, vol. 55, pp. 128–143, 2014. [Google Scholar]
22. A. M. Imran and M. Kowsalya, “A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using fireworks algorithm,” International Journal of Electrical Power & Energy Systems, vol. 62, pp. 312–322, 2014. [Google Scholar]
23. S. Golshannavaz, S. Afsharnia and F. Aminifar, “Smart distribution grid: Optimal day-ahead scheduling with reconfigurable topology,” IEEE Transactions on Smart Grid, vol. 5, no. 5, pp. 2402–2411, 2014. [Google Scholar]
24. S. Esmaeili, A. A. Moghaddam, S. Jadid and J. M. Guerrero, “Optimal simultaneous day-ahead scheduling and hourly reconfiguration of distribution systems considering responsive loads,” International Journal of Electrical Power & Energy Systems, vol. 104, pp. 537–548, 2019. [Google Scholar]
25. Y. Wu and Q. Song, “Improved particle swarm optimization algorithm in power system network reconfiguration,” Mathematical Problems in Engineering, vol. 2021, pp. 1–10, 2021. [Google Scholar]
26. W. Haider, S. Hassan, A. Mehdi, A. Hussain, G. O. M. Adjayeng et al., “Voltage profile enhancement and loss minimization using optimal placement and sizing of distributed generation in reconfigured network,” Machines, vol. 9, no. 1, pp. 20, 2021. [Google Scholar]
27. M. Dhivya and A. J. Renoald, “Fuzzy grammar based hybrid split-capacitors and split inductors applied in positive output Luo-converters,” International Journal of Scientific Research in Science, Engineering and Technology, vol. 3, pp. 327–332, 2017. [Google Scholar]
28. K. Santhiya, M. Devimuppudathi, D. Santhosh Kumar and J. R. Albert, “Real time speed control of three phase induction motor by using Lab view with fuzzy logic,” Journal on Science Engineering and Technology, vol. 5, no. 2, pp. 21–27, 2018. [Google Scholar]
29. J. R. Albert and A. A. Stonier, “Design and development of symmetrical super-lift DC–AC converter using firefly algorithm for solar-photovoltaic applications,” IET Circuits Devices & Systems, vol. 14, no. 3, pp. 261–269, 2020. [Google Scholar]
30. K. Thenmalar, J. R. Albert, D. Muhamadha Begam and P. Madhumathi, “Power quality improvement in modular multilevel inverter using for different multicarrier PWM,” European Journal of Electrical Engineering and Computer Science, vol. 5, no. 2, pp. 19–27, 2021. [Google Scholar]
31. A. J. Renoald, V. Hemalatha, R. Punitha, M. Sasikala and M. Sasikala, “Solar roadways-The future rebuilding infrastructure and economy,” International Journal of Electrical and Electronics Research, vol. 4, no. 2, pp. 14–19, 2016. [Google Scholar]
32. J. R. Albert and D. S. Vanaja, “Solar energy assessment in various regions of indian sub-continent,” Solar Cells, IntechOpen, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |