DOI:10.32604/iasc.2022.023831

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023831 |  |
| Article |
A Resource-Efficient Convolutional Neural Network Accelerator Using Fine-Grained Logarithmic Quantization
Department of Computer Engineering, Kocaeli University, Kocaeli, 41380, Turkey
*Corresponding Author: Hadee Madadum. Email: hadee.madadum@kocaeli.edu.tr
Received: 23 August 2021; Accepted: 22 November 2021
Abstract: Convolutional Neural Network (ConNN) implementations on Field Programmable Gate Array (FPGA) are being studied since the computational capabilities of FPGA have been improved recently. Model compression is required to enable ConNN deployment on resource-constrained FPGA devices. Logarithmic quantization is one of the efficient compression methods that can compress a model to very low bit-width without significant deterioration in performance. It is also hardware-friendly by using bitwise operations for multiplication. However, the logarithmic suffers from low resolution at high inputs due to exponential properties. Therefore, we propose a modified logarithmic quantization method with a fine resolution to compress a neural network model. In experiments, quantized models achieve a negligible loss of accuracy without the need for retraining steps. Besides this, we propose a resource-efficient hardware accelerator for running ConNN inference. Our design completely eliminates multipliers with bit shifters and adders. Throughput is measured in Giga Operation Per Second (GOP/s). The hardware utilization efficiency is represented by GOP/s per block of Digital Signal Processing (DSP) and Look-up Tables (LUTs). The result shows that the accelerator achieves resource efficiency of 9.38 GOP/s/DSP and 3.33 GOP/s/kLUTs.
Keywords: Convolutional neural network; logarithmic quantization; FPGA; resource efficiency
Edge devices such as low-end FPGA have limited resources, but ConNN models require large amounts of multipliers and extensive storage [1]. Resource utilization is challenging in deploying the ConNN model to FPGA devices. Several works have proposed a quantization for neural networks to address this issue. Compressing a model to low bit-width precision greatly improves resource utilization. In quantization scheme, ConNN models can be transformed from 32-bit to lower precision, for example 8-bits [2], binary-bits [3] or fixed-point format [4]. A resource efficiency can also be improved by replacing the complexity of multiplication with bitwise operations such as XNOR-Net [5,6].
However, compressing a model from 32-bits to lower precision suffers accuracy degradation. The quantized model needs to be retrained to recover accuracy close to the original accuracy. But the retraining process can be time-consuming and require additional computations. Moreover, some of the original training datasets are not accessible due to privacy or ownership. For example, the data in healthcare systems and user data in applications collected by companies.
A Post-training scheme has been introduced to address the issue by quantizing the model without retraining [7,8]. Recent works relied on linear quantization which provides an equal quantization level. However, linear quantization still requires multiplication to compute model inference. On the other hand, base-2 logarithmic encoding scheme is more hardware-friendly since multiplication can be replaced with a bit shift operation. But, using non-uniform quantization as a logarithmic method without retraining may not achieve the optimal accuracy.
For this reason, we investigate a modified logarithmic quantization to overcome the issues mentioned above. We then propose an efficient hardware architecture for running model inference on resource-constrained device. The main contributions of this work consist of following features:
• We present a modified logarithmic quantization for compressing a ConNN model to very low bit-width. We use different quantization methods for weights and activations to fit different distributions. Our design achieves to convert models to lower bit-width without the retraining.
• We also propose a resource-efficient accelerator for running the ConNN inference on Zynq XC7Z020. The proposed processor uses only adders and shifters for computing convolution. Experiment results show that our work achieves resource efficiency of 9.38 GOP/s/DSP and 3.33 GOP/s/kLUTs.
This section provides a review of related work in literature. Quantization has been proposed in many works to address the computational complexity and high memory requirement issues of neural network model by compressing an original 32-bit model to a lower precision. Logarithmic quantization is one of the efficient methods that can compress models to very low bit-width precision without significant deterioration in performance. Logarithmic quantization was proposed in [9] to quantize activations and weights to 4 bit-width. The results show that logarithmic quantization outperforms linear quantization and only a few accuracies degradation.
To improve the quantization levels, the logarithmic base-
The logarithmic scheme is non-uniform quantization with a low resolution at high-level input. To address this issue [12,13] proposed a logarithmic-based quantization for weights and activations through the addition of power-of-two values with scalable parameters. To address the resolution issue, [14] proposed a method to present quantized value using real numbers instead of rounding them to integers. This design decreases the step-size resulting in higher resolution. The authors [15] presented the fixed-point quantization into logarithmic method for activations to reduce the step-size when the bit-width increases.
Several works have shown that the weights in layers of the neural networks follow a bell-shaped and long-tailed distribution. A large number of weights are around the mean and a few of weights have high absolute values. This is well motivated to use a logarithmic quantization because it has a high number of quantization levels around the mean. In other words, the logarithmic quantization provides high resolution at low-level input. Due to unequal quantization levels, logarithmic scheme on the other hand has a low resolution at high input. In the logarithmic scheme, quantized values are represented using integers in the log domain. The step-size increases exponentially from low to high-level input. Although the distribution of weights indicates that a few weights have a high value, but high value weights can have a strong connection and have a high impact on accuracy.
To address the unbalanced quantization levels issue, we propose a modified logarithmic quantization that uses real numbers for quantization levels in the log domain. This method reduces the spacing between integers in log domain. Therefore, it provides a greater number of quantization levels at high inputs. Since logarithmic method has a high resolution at low input, we therefore continue to use integers for quantization levels at low-level input. In this way, our method provides high resolution across all input levels.
Fig. 1 shows the weight distribution after applying a naive logarithmic (Log.) and the proposed logarithmic with Qset (LogQ.) using 4 and 6 bit-width respectively. The proposed method offers fine-grained quantization levels at the tail area as shown in Fig. 1b. Moreover, Fig. 1c shows that increasing bit-width can improve the resolution. This method can also be used to quantize the activations. However, defining the interval for the set of real numbers requires a sample of data. Our goal is to quantize activations and weights without involving sample data. Therefore, we adopt the fixed-point into logarithmic method from [15]. This method is similar to our design but using a fixed-point number to represent the quantized value. These quantization methods are then proposed together to quantize models without a retraining process. Additionally, the advantage of logarithmic quantization is that it is hardware-friendly as multiplications can be replaced with addition and bit-shift operations. In this context, we also present a resource-efficient processor for running neural networks inference on low-end FPGA devices.

Figure 1: Logarithmic and the proposed logarithmic quantization. The naive logarithmic quantization has high resolution around the mean only (a) The proposed method provides a more reasonable resolution (b) In addition, the resolution can be higher by increasing the bit-width (c)
This approach is mostly used in previous work to map a 32-bit floating-point to a lower bit-width such as binary, ternary, and fixed-point formats. This method is uniform quantization which the quantization levels are equally spaced. The quantization parameters are full scale range (FSR) and word length (W). The fixed-point quantization function (
where the clip function (Clip(.)) is defined as:
Fixed-point format is denoted by ap_fixed (W, FL), where W is the total bit-width including an integer-bit (IL) and a fractional bit (FL). To quantize 32-bit floating-point to fixed-point format using linear quantization, the parameters are defined as:
The quality of the quantization depends upon the number of bit-width. Increasing the bit-width linearly increases the number of quantization level and gives a higher resolution. However, it requires more memory space, and the cost of computation is expensive. On the other hand, using the lower bit-width takes less memory but the accuracy degradation is a trade-off.
4.1.2 Logarithmic Quantization
This method converts a floating-point number to lower bit-width by mapping a number in log domain. Logarithmic quantization is non-uniform quantization in which the quantization levels are unequal and involves the logarithm to represent a quantized value. The logarithmic quantization parameters are full scale range and total bit-width (W). With w-bit representation, the logarithmic quantization function (
where
Unlike fixed-point quantization, the logarithmic scheme gives a high number of quantization levels (high resolution) around the mean and lower resolution for other regions. The weights in a layer of the neural network can be considered a bell-shaped distribution. Therefore, the logarithmic quantization performs better than the fixed-point scheme when quantizing using very low bit-width. Moreover, the advantage of logarithmic quantization is that it is hardware-friendly as multiplications can be replaced with a bit-shift operation. For instance, given quantized weights (
where
Applying logarithmic quantization directly to weights can result in a loss of accuracy. Obviously, the weights in the layers of the neural network have different effects on accuracy. Larger absolute values affect accuracy more than smaller ones. The disadvantage of logarithmic scheme is the use of integer format in log domain. Because of the exponential property, the number of quantization levels decreases for high-value inputs. In other words, logarithmic scheme does not work well when absolute input is large. To address the quantization levels issue, we take the inspiration from this work [14] that uses real numbers to represent quantized values instead of rounding to an integer in the log domain. We further improve this method by using both integers and real numbers for quantization levels. The logarithmic quantization with Qset function (
where
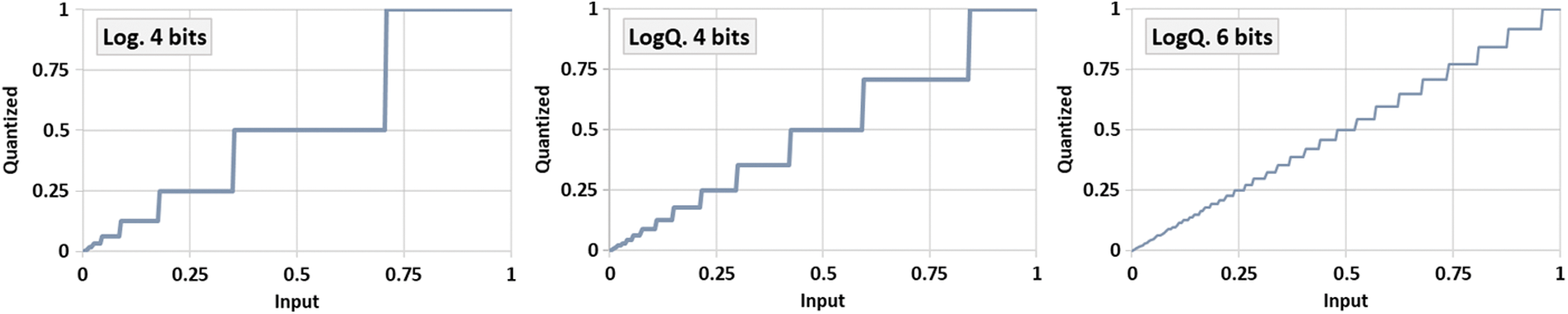
Figure 2: Quantization of unsigned inputs to 4 and 6 bit-width using naive logarithmic and logarithmic with Qset. The naive logarithmic quantization (left) suffers from quantizing large inputs with low resolution. The proposed method (middle) provides higher resolution at high values. The quantization level becomes more fine-grained by increasing the bit-width quantization (right)
The quantized weight
where
where M =
The idea of Qset is to represent the quantized value using real numbers or integers. Absolute weights greater than s takes real numbers for the representation levels, otherwise the quantized value is represented by integers. In the set p1, the interval starts from 0 to
The parameter S is used to define the range of set p1. In our experiments, we set S to 0.01 to provide a high resolution quantization levels for absolute weights of 1 to 0.01. The parameter R is a positive real number and is used to set the step-size of representation levels. A larger R provides a wider representation range but will reduce the resolution. Parameter R must be greater than
Fig. 2 shows a comparison of quantization levels using naive logarithmic and the proposed logarithmic quantization. The proposed logarithmic scheme has a more reasonable resolution at high values. In addition, the proposed method shows that increasing bit-width can reduce the step-size and provides higher number of quantization levels.
There are challenges in applying logarithmic quantization to activations when the activations of each layer has a different shape of the distribution. Using the quantization with Qset may lead to sub optimal because the activations value is not constant and depend on the input. Thus, we cannot determine the optimal parameter R for the range of Qset. For this reason, we use another method for quantizing activations. We adopt this [15] to compress the activations using a fixed-point into logarithmic quantization. This method uses fixed-point numbers to represent the quantized value instead of integers. The fixed-point into logarithmic quantization function (
where
The quantization step

Figure 3: The histogram of activations of convolutional layer 2 in ResNet-18. The order from top to bottom is: (original activations, after naive logarithmic quantization, after fixed-point into logarithmic quantization)
6.1 Performance of Quantization
This section presents the performance of quantization method. The goal of quantization is to compress values into smaller bit-width with less distortion. We use the signal-to-quantization-noise (SQNR) to evaluate each quantization method. Let
where
Fig. 4 shows the SQNR of different quantization methods in each layer of ResNet-18. In this result, we apply the function

Figure 4: Performance of quantization for weights and activations in ResNet-18 on imageNet dataset. (a) SQNR of weight quantization (b) SQNR of activations quantization
The performance of quantization for activations is shown in Fig. 4b. We compare the proposed fixed-point into logarithmic (Flog.), naive logarithmic (Log.) and fixed-point quantization (Fixed.) using different bit-width. The results show that the proposed quantization (Flog.) outperforms other methods when using 4 bit-width activations. Fixed-point quantization gives better results when increasing bit-width. In the experiment, we have to increase bit-width for fixed-point quantization to 8 bits to achieve acceptable accuracy. On the other hand, fixed-point into logarithmic quantization using only 6 bit-width can produce better results in most layers compared to the fixed-point scheme using 8 bit-width.
6.2 Quantized Models Accuracy Results
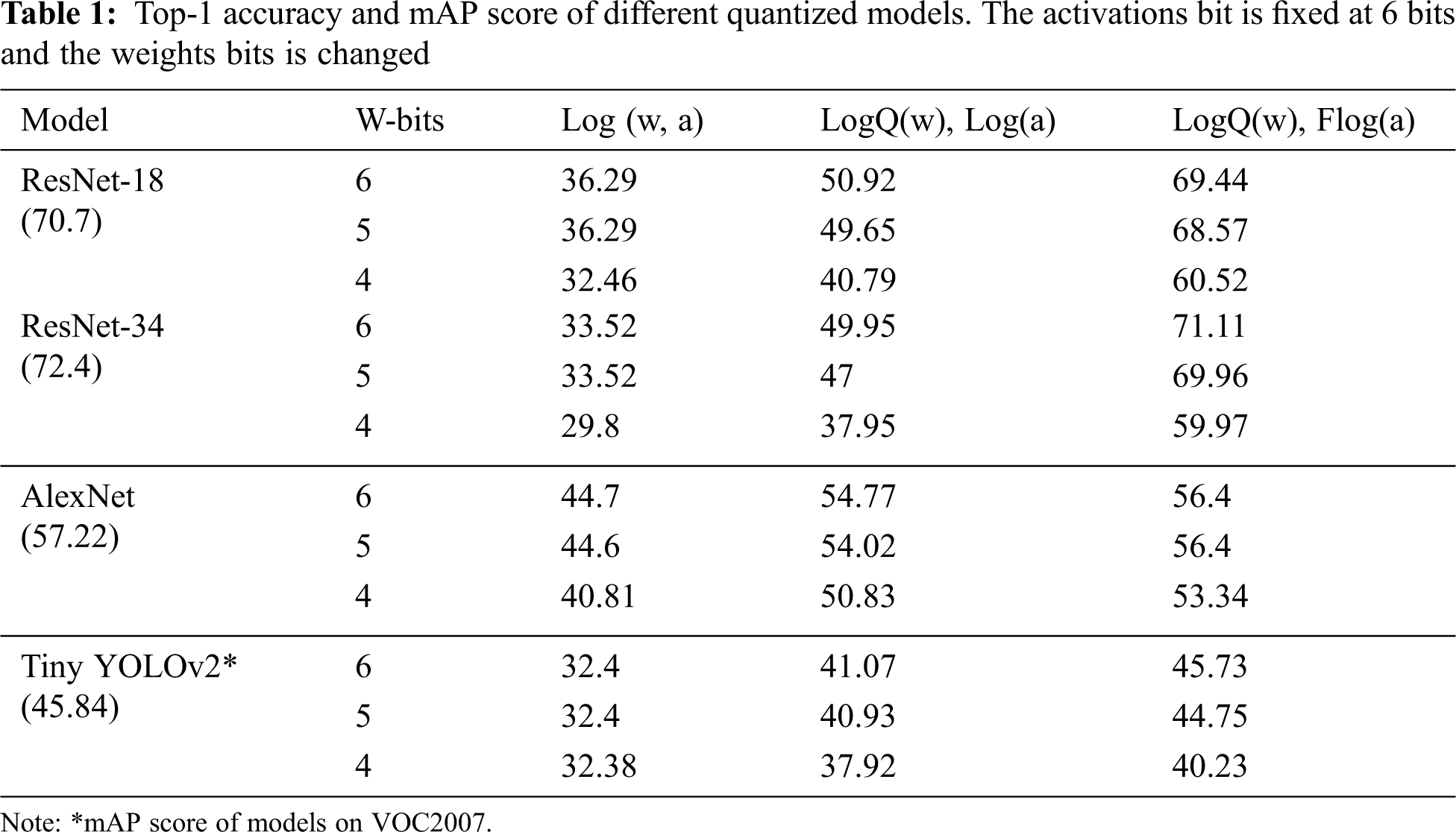
We evaluate the proposed quantization method on different models and datasets. To present the improvement, we apply only naive logarithmic method and the proposed logarithmic quantization to weights. We also implement naive logarithmic and fixed-logarithmic quantization for activations. Tab. 1 shows the performance of quantized models using 3 different combinations. Log(.) denotes the use of naïve logarithmic quantization. LogQ(.) denotes the use of logarithmic quantization with Qset. Flog(.) denotes the use of fixed-point into logarithmic quantization. W-bits represents the bit-width of weights. We evaluate different models using a Top-1 score for the image classification on ImageNet dataset. In addition, we apply the proposed quantization to an object detection model named TinyYOLOv2 and evaluate it using mean Average Precision (mAP) on Pascal Visual Object Classes 2007 (VOC2007) dataset.
For the weights compression, using LogQ(w) with Flog(a) can increase almost 2
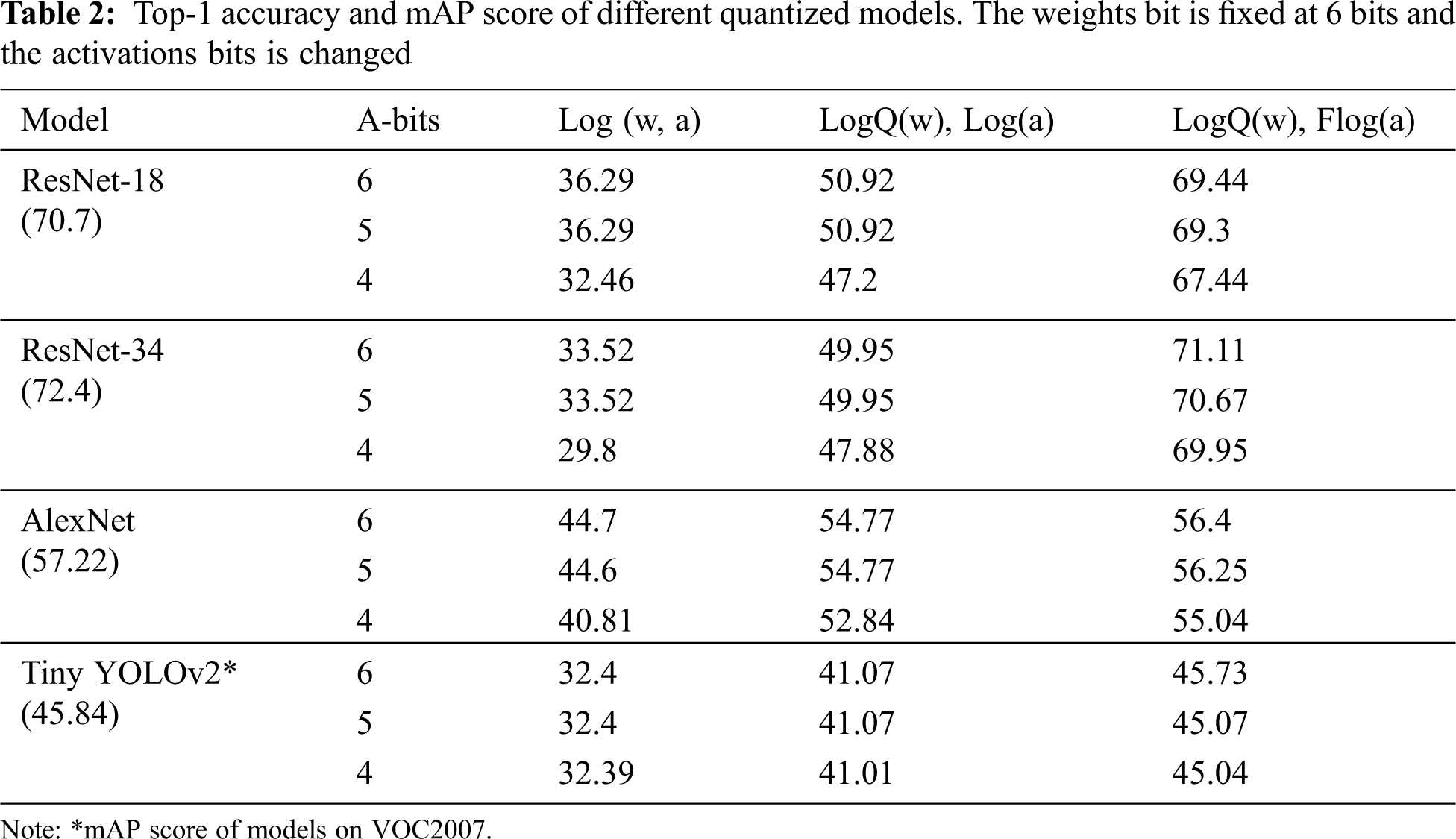
The results of quantization for activations are shown in Tab. 2. A-bits represent the bit-width of activations. Using Flog(a) quantization significantly improves accuracy compared to naive logarithmic method. With 6 bit-width weights, using Flog(a) scheme for 4 bit-width activations can result in a loss of around 2% of original accuracy. Unlike weight quantization, increasing bit-width in Flog(a) quantization can slightly increase the accuracy. The 5 bits activations models have approximately 1%–2% higher accuracy than 4 bits activations. This is because weights quantization has a greater impact on accuracy than activations quantization.
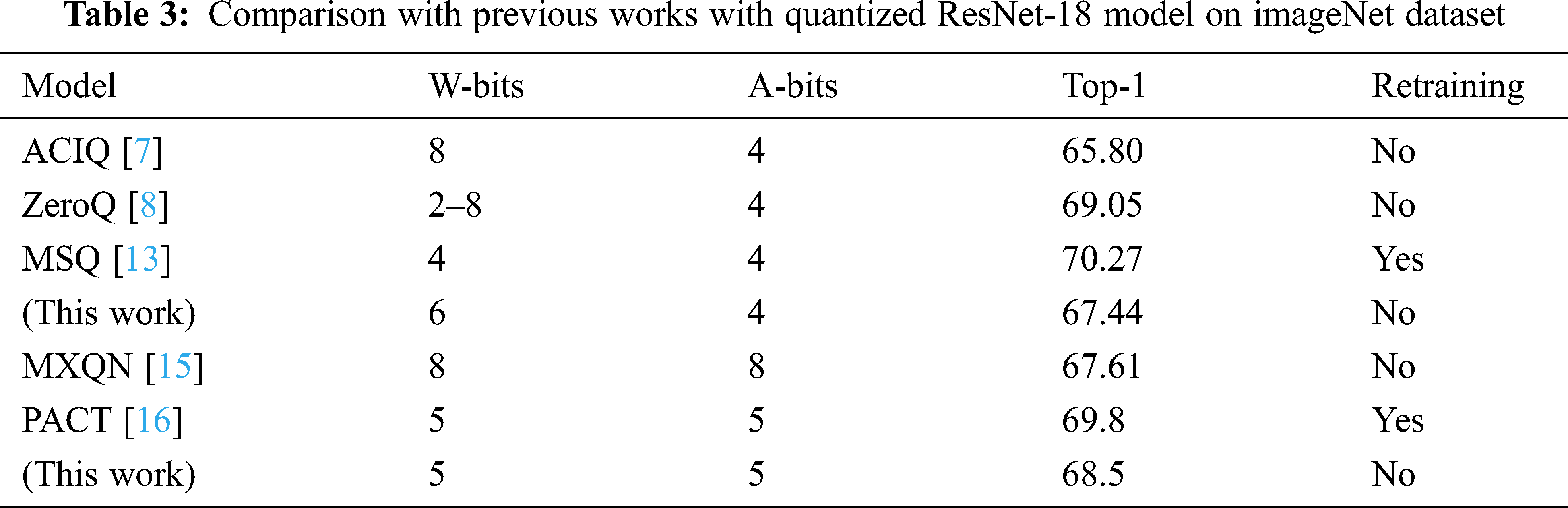
6.3 Comparison to Previous Implementations
Tab. 3 shows a comparison of the performance of our design with other existing works. The results show that our work performs better than [7] with lower bit-width weights. Our work achieves accuracy 2% lower than mixed-precision quantization for weights [8] and around 3% lower accuracy than this work [13] that requires a retraining process. In 5 bit-width precisions, our work outperforms this [15] which uses both logarithmic and fixed-point quantization for activations. Our work achieves 1.3% less accuracy than [16]. However, their method requires retraining process.
This section presents the hardware accelerator for running quantized neural networks inference on FPGA. The Zedboard Zynq7000 based FPGA is used as an edge device for the hardware experiment. This board includes a dual-core ARM Cortex A9 and a Zynq XC7Z020-based FPGA chip. The trained weights are stored on the SD card. The accelerator is implemented in the programmable logic (PL) part. Fig. 5 illustrates a hardware-integrated design for the accelerator in FPGA. The details of each component are described in the following section:
• Zynq Processor: We use this processor to control the workflow of ConNN inference. To start ConNN inference, the processor initializes the necessary peripherals. After that, the processor loads the trained weights from the SD card to the DRAM memory using DDR control module. When the framework requires convolutional computation, zynq processor will send configuration parameters, weights and activations addresses in DRAM and then enable the accelerator to perform convolution.
• Logarithmic Accelerator: This is the hardware core for running neural network inference. The accelerator consists of a processing element (PE) for multiplication and accumulation. There are multiple PEs in a single accelerator and all PEs runs simultaneously to support parallel computation. The details of this module are described in the next section.
• Internal memory: Typically, FPGA does not have enough on-chip memory to store all parameters. Therefore, we design memory buffer for weights and activations. These buffers are generated by 36 Kb block RAM (36 Kb-BRAM) resource in FPGA.
• Advanced eXtensible Interface (AXI): The AXI is used for sending configurations parameters from the processor to the accelerator. The Memory AXI (M_AXI) is built for the accelerator to access external memory. Thus, the accelerator can control load/store instructions.

Figure 5: Block diagram of the proposed hardware accelerator for neural networks inference in FPGA
We implement the convolution computation based on the General Matrix Multiplication (GEMM). The activations and weights are stored in the DRAM by Zynq. The runtime workflows start with loading the input activations and the weights of the first layer into the on-chip memory in the accelerator. The processing elements then compute the convolution and stores the output activations in the output buffer. After completing the convolution, the accelerator writes output activations back to the DRAM memory. Then the accelerator starts the process again for computing convolution for the next layer.
In general, a processor for computing convolution consists of a set of multipliers and adders. In this work, the quantized value is expressed as the power of base 2. Therefore, we can replace the multiplier with bit-shift operator in convolution. We simplify the multiplication of quantized activations and weights on the log domain. The algorithm can be expressed as:
where
In the hardware-level implementation, we avoid using multipliers by storing all multiplications
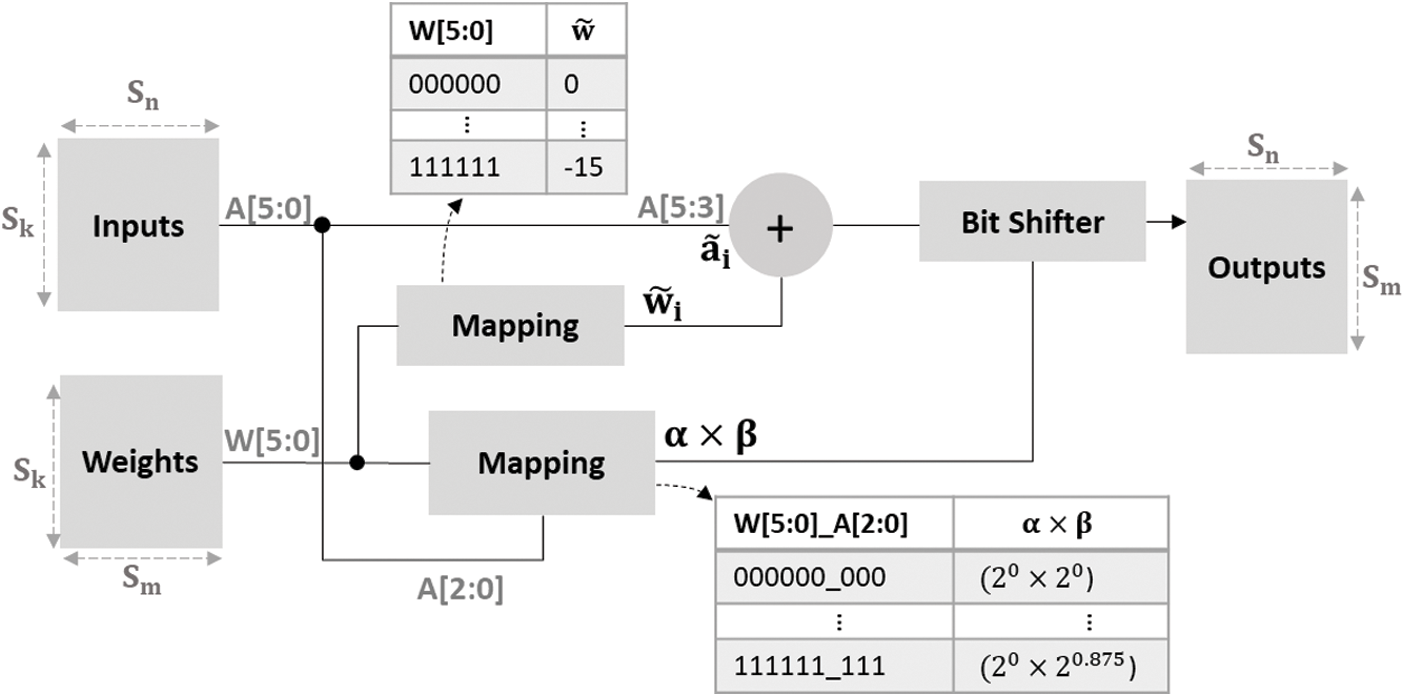
Figure 6: The architecture of proposed logarithmic accelerator for running the quantized model inference when using 6 bit-width weights and activations
Since weights are stored as indexes of Qset, we use look-up table to convert the index to integer part of quantized weights (
To accelerate the computation, we implement multiple PEs to support parallel computation. The maximum number of PEs is
FPGA devices consist of Digital Signal Processing (DSP) blocks, Look-up Tables (LUTs), Flip-Flops (FFs) and Block RAM memory (BRAM). These resources, particularly DSP and LUTs, are very limited in edge FPGA devices. For this reason, we constraint the resource usage by setting the amount of storage available. This defines the structure of the accelerator as mentioned in section 7.2. We instantiate the structure of the accelerators as:
The size of parameter is another important factor in mapping ConNN to hardware. A larger bit-width requires a high number of resources. However, bit-width and accuracy are trade-off. The quantized model evaluation results show that weight quantization has a high impact on accuracy. Therefore, we focus on using 6 bit-width for weights quantization, whereas bit-width for activations is changed. Tab. 4 shows the results of resource requirements for the accelerator core using different bit-width. Below the column name displays the number of available resources on the device. We present resource usage in terms of amount and percentage. In addition, we present an accelerator for computing fixed-point convolution to observe improvements in resource utilization.
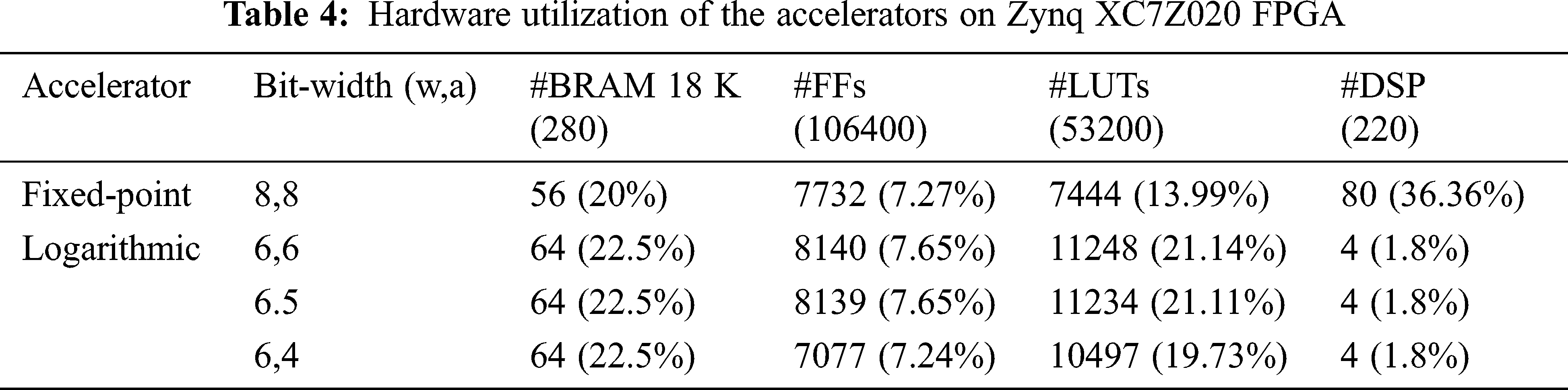
Using a multiplier requires DSP and LUTs, whereas a bit shifter requires only LUTs. Therefore, the proposed hardware significantly reduces the number of DSP 20
7.4 Hardware Accelerator Comparison
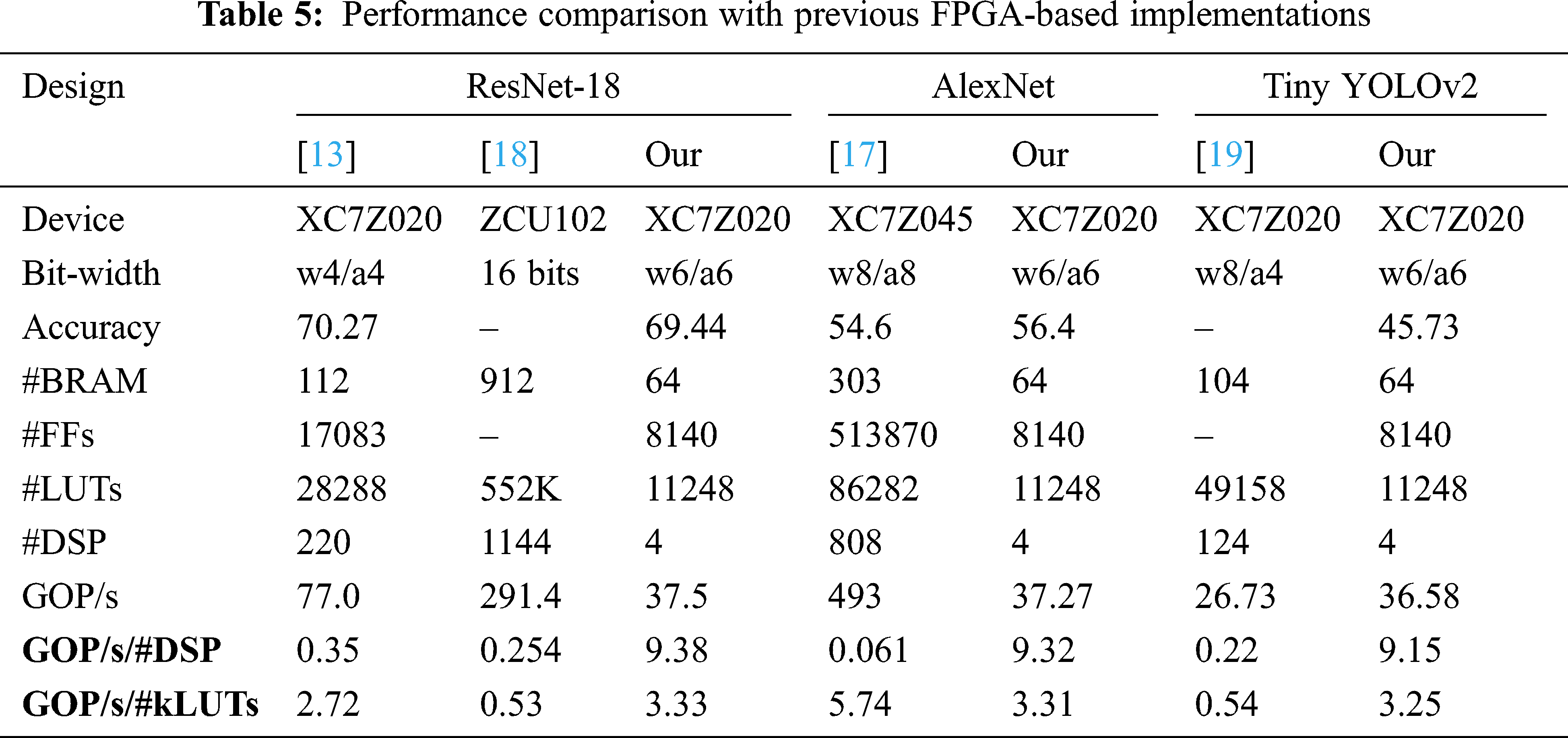
This section presents a performance comparison with other prior designs. In this implementation, the Zynq XC7Z020-based FPGA is used under 150 MHz operating frequency. We run different neural network models on the device to evaluate the proposed accelerator. Our goal is to run complex neural networks on a resource-constrained FPGA device. We therefore concentrate on the efficient use of resources. The throughput is also a key factor for running the model in a real-world environment. We capture the actual execution time of the accelerator and calculate the throughput using Giga Operation Per Second (GOP/s) metric. However, the throughput and resource usage are trade-off. For this reason, we evaluate the performance of the accelerator using resource efficiency metrics, which are the ratio of GOP/s per number of DSP and GOP/s per number of LUTs.
The performance of the proposed accelerator and its comparison with other prior works are presented in Tab. 5. The results show that our proposed hardware significantly reduces the number of DSP and achieves about 9
This article presents a modified logarithmic quantization to compress convolutional neural networks without retraining process. We propose a simple but effective method for solving low resolution at high-level input issues of logarithmic quantization. Different logarithmic-based methods are performed for quantizing weights and activations. As a result, quantized models achieve comparable accuracy to floating-point models. Additionally, we propose an efficient hardware accelerator for ConNN inference on low-end FPGA devices. With the advantages of logarithmic compression, we present the hardware processor that computes convolution using bit shifters and adders. The proposed hardware design is resource efficient and suitable for use on embedded devices. For future work, we recommend to further study the optimal bit-width quantization for each layer in ConNN, as each layer has a different distribution.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Madadum and Y. Becerikli, “FPGA-based optimized convolutional neural network framework for handwritten digit recognition,” in 1st Int. Informatics and Software Engineering Conf. (UBMYK), Ankara, Turkey, pp. 1–6, 2019. [Google Scholar]
2. R. Krishnamoorthi, “Quantizing deep convolutional networks for efficient inference: A whitepaper,” arXiv preprint arXiv: 1806.08342, 2018. [Google Scholar]
3. Y. Umuroglu, N. J. Fraser, G. Gambardella, M. Blott, P. H. W. Leong et al., “FINN: A framework for fast, scalable binarized neural network Inference,” in Proc. of the 2017 ACM/SIGDA Int. Sym. on Field-Programmable Gate Arrays, Monterey, CA, USA, pp. 65–74, 2017. [Google Scholar]
4. R. Goyal, J. Vanschoren, V. Van Acht and S. Nijssen, “Fixed-point quantization of convolutional neural networks for quantized inference on embedded platforms,” arXiv preprint arXiv:2102.02147, 2021. [Google Scholar]
5. M. Rastegari, V. Ordonez, J. Redmon and A. Farhadi, “XNOR-Net: ImageNet classification using binary convolutional neural networks,” in European Conf. on Computer Vision (ECCV 2016), Amsterdam, The Netherlands, vol.9908, pp. 525–542, 2016. [Google Scholar]
6. E. H. Lee, D. Miyashita, E. Chai, B. Murmann and S. S. Wong, “LogNet: Energy-efficient neural networks using logarithmic computation,” in 2017 IEEE Int. Conf. on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, pp. 5900–5904, 2017. [Google Scholar]
7. R. Banner, Y. Nahshan and D. Soudry, “Post training 4-bit quantization of convolutional networks for rapid-deployment,” in Advances in Neural Information Processing Systems 32: Annual Conf. on Neural Information Processing Systems 2019, Vancouver, Canada, pp. 7948–7956, 2019. [Google Scholar]
8. Y. Cai, Z. Yao, Z. Dong, A. Gholami, M. W. Mahoney et al., “ZeroQ: A novel zero shot quantization framework,” in 2020 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 13166–13175, 2020. [Google Scholar]
9. D. Miyashita, E. H. Lee and B. Murmann, “Convolutional neural networks using logarithmic data representation,” arXiv preprint arXiv:1603.01025, 2016. [Google Scholar]
10. J. Xu, Y. Huan, Y. Jin, H. Chu, L. R. Zheng et al., “Base-reconfigurable segmented logarithmic quantization and hardware design for deep neural networks,” Journal of Signal Processing Systems, vol. 92, no. 11, pp. 1263–1276, 2020. [Google Scholar]
11. S. Vogel, M. Liang, A. Guntoro, W. Stechele and G. Ascheid, “Efficient hardware acceleration of CNNs using logarithmic data representation with arbitrary log-base,” in Proc. of the Int. Conf. on Computer-Aided Design, New York, USA, pp. 1–8, 2018. [Google Scholar]
12. Y. Li, X. Dong and W. Wang, “Additive powers-of-two quantization: An efficient non-uniform discretization for neural networks,” in 8th Int. Conf. on Learning Representations, Addis Ababa, Ethiopia, pp. 1–15, 2020. [Google Scholar]
13. S. E. Chang, Y. Li, M. Sun, R. Shi, H. K. H. So et al., “Mix and match: A novel FPGA-centric deep neural network quantization framework,” in IEEE Int. Sym. on High-Performance Computer Architecture, Seoul, South Korea, pp. 208–220, 2021. [Google Scholar]
14. J. Cai, M. Takemoto and H. Nakajo, “A deep look into logarithmic quantization of model parameters in neural networks,” in Proc. of the 10th Int. Conf. on Advances in Information Technology, New York, USA, pp. 1–8, 2018. [Google Scholar]
15. C. Huang, P. Liu and L. Fang, “MXQN: Mixed quantization for reducing bit-width of weights and activations in deep convolutional neural networks,” Applied Intelligence, vol. 51, no. 7, pp. 4561–4574, 2021. [Google Scholar]
16. J. Choi, Z. Wang, S. Venkataramani, P. I.-J. Chuang, V. Srinivasan et al., “PACT: Parameterized clipping activation for quantized neural networks,” arXiv preprint arXiv: 1805.06085, 2018. [Google Scholar]
17. J. Wang, Q. Lou, X. Zhang, C. Zhu, Y. Lin et al., “Design flow of accelerating hybrid extremely low bit-width neural network in embedded FPGA,” in 28th Int. Conf. on Field Programmable Logic and Applications, Dublin, Ireland, pp. 163–169, 2018. [Google Scholar]
18. C. Zhu, K. Huang, S. Yang, Z. Zhu, H. Zhang et al., “An efficient hardware accelerator for structured sparse convolutional neural networks on FPGAs,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 28, no. 9, pp. 1953–1965, 2020. [Google Scholar]
19. T.-Y. Lu, H.-H. Chin, H.-I. Wu and R.-S. Tsay, “A very compact embedded CNN processor design based on logarithmic computing,” arXiv preprint arXiv:2010.11686, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |