DOI:10.32604/iasc.2022.024023

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.024023 |  |
| Article |
A Novel Medical Image Encryption Using Rössler System
1Department of CSE, Alagappa Chettiar Government College of Engineering and Technology, Karaikudi, 630003, India
2School of Computer Science and Engineering, Vellore Institute of Technology, Vellore, 632014, India
*Corresponding Author: K. Sundara Krishnan. Email: sundarakrishnank@gmail.com
Received: 30 September 2021; Accepted: 08 November 2021
Abstract: The technological advances made possible by the Internet, coupled with the unforeseen critical circumstances set in motion by the Covid-19 pandemic, have greatly increased the generation and transmission of medical images every day. Medical image transmission over an unsecured public network threatens the privacy of sensitive patient information. We have, in this paper, designed a new secure color medical image encryption algorithm based on binary plane decomposition, DNA (deoxyribonucleic acid) computing, and the chaotic Rössler dynamical system. At first, a bit-by-bit swap is performed on twenty four binary planes of the input image and encoded using DNA encoding rules. Thereafter, the Rössler system is used to modify the pixel values of the encoded image, which is subsequently decoded. Finally, the ciphered image is obtained by pixel-by-pixel permutation using position sequences. An innovative approach is used to compute keys from the color components of the input image. Extensive performance experiments of the proposed technique is conducted with metrics such as key sensitivity, key space, correlation coefficients (horizontal, diagonal and vertical directions), histograms, information entropy, number of pixel changes rate (NPCR), information entropy, unified average changing intensity (UACI), and encryption time. Comparative analyses have demonstrated that the proposed algorithm is fast, robust and competitive.
Keywords: DNA Computing; bit-plane decomposition; permutation; encryption; chaos
Owing to brilliant advancements in medical imaging technology, Internet use by medical practitioners has seen a massive push, particularly for the end-to-end transmission of medical images. While such public network transmission cuts the time and expense involved, it threatens the very confidentiality of vital patient data. Further, disease diagnosis based on falsified medical images is fraught with difficulty. Thus, robust security is imperative to protect patients’ image data and ensure privacy during transmission. Encryption, which renders the contents of images unintelligible, best addresses these challenges in medical image transmission. The voluminous size and adjacent correlations that are intrinsic features of medical image data differ vastly from those of text. Therefore, traditional algorithms such as the International Data Encryption Algorithm (IDEA), Data Encryption Standard (DES) and Advanced Encryption Standard (AES) are poorly equipped to secure medical images [1,2].
Researchers have successfully used the advantages of DNA computing technology, such as parallelism and ultra-low power consumption, in image cryptosystems. Zhang et al. [3] presented an image cipher that applies DNA subsequence operations. The algorithm only uses DNA operations to scramble the location and value of pixels, leading to weak security. The authors have proposed encryption techniques based on a 2D logistic map and DNA computing [4,5]. The algorithms use the map for confusion and DNA rules to encode images. Chai [6] designed a novel image cryptosystem based on DNA computing and a 3D dynamical system. The algorithm introduces a 3D DNA matrix for pixel scrambling and diffusion operations. Dagadu et al. [7] proposed a scheme that uses DNA encoding to achieve high-level diffusion. The algorithm offers good security, though the encryption process is slow. The nested chaotic map and DNA computing were combined to create an effective encryption solution. The technique produces complex and large key streams [8]. Wang et al. [9] created a cryptosystem for images that uses the DNA plane and pseudorandom bit sequences. Liu et al. [10] presented a color image cipher by employing four-dimensional hyper-chaos and dynamic DNA encoding. The block-based dynamic DNA diffusion of this scheme enhances randomness in cipher images. Akkasaligar et al. [11] proposed a selective image cipher utilizing DNA computing and hyper-chaos. Their unique DNA structure-based encryption significantly reduces computational complexity and time. Liu et al. [12] designed a robust color image cipher using dual chaos and DNA coding which performs bit-level diffusion using DNA computation.
Zhu et al. [13] introduced an image encryption scheme that executes the permutation process at the bit-level rather than the pixel level. Zhou et al. [14] presented an algorithm for image encipherment based on the decomposition of parametric bit-planes and the P-Fibonacci transform. Tang et al. [15] designed a lossy multiple image cipher wherein the permutation is done using bit-planes in the form of bit-blocks. A 3D bit-plane-based scrambling method was proposed by Gan et al. [16]. A technique for a parallel image cryptosystem, based on bit-planes, was developed by Mozaffari [17]. Som et al. [18] proposed a novel partial image encryption scheme by adopting a tent map and selective bit-planes. Zhang et al. [19] introduced an image cryptosystem that combined the logistic map, Chen system, and bit-plane decomposition.
Cao et al. [20] designed a lossless medical image cryptosystem using binary edge maps, which showed significant resistance against differential attacks. Shahriyar et al. [21] introduced an enciphering scheme by utilizing the Advanced Encryption Standard and elliptic curve cryptography. The algorithm offers adequate security with a high computational cost and hence is not appropriate for real-time applications. Zahmoul et al. [22] created a new beta map and designed an encryption scheme. Cavusoglu et al. [23] propounded an efficient design for image encryption that employs a novel s-box and a simple encryption operation. However, it performs poorly against noise attacks. Broumandnia [24] introduced a color image encryption technique based on a 3D modular chaotic map and a modular arithmetic-based multiplicative reversible operation. Banik et al. [25] presented a multiple medical image cipher by employing the Mersenne-Twister pseudorandom sequence generator and EIGamal algorithm. The EIGamal algorithm utilizes Cartesian space coordinates bounded by a positive modulo for enciphering. Ke et al. [26] posited a medical image encryption method with linear piecewise chaos. The method avoids prediction errors by preprocessing images using an error location map. Cheng et al. [27] proposed an efficient color image cipher by applying a 5D multi-wing hyper-chaotic system. The approach realizes block permutation by mixing three color components which resist grey image attacks. A selective image cryptosystem, based on the Henon map and the 2-level discrete wavelet transform, was presented by Lisungu et al. [28] to reduce redundancy and offer high security.
Maria [29] introduced a scheme for image encipherment based on a q-deformed chaotic logistic map, which maximizes key spaces despite low dimensions. Ibrahim et al. [30] designed an efficient scheme by combining a chaotic system and the S-box to resist PRING reset attacks. Madhusudhan et al. [31] suggested a simple technique, using the Arnold map to secure medical images, where key generation is not a dynamic process. Gafsi et al. [32] designed a robust and fast cipher by employing the chaos-based PRING. The results have shown that correlation decreases and randomness increases in encrypted medical images. Sasikaladevi et al. [33] developed a medical image encryption approach based on hyper-chaotic elliptic curves. The prime field-based curve used in this scheme increases key size. Sahasrabuddhe et al. [34] proposed a 3D scrambling and chaotic system-based image cryptosystem. The 3D image formed from the input images undergoes rotation and permutation in three axes to handle occlusion attacks. Rehman et al. [35] utilized the concept of chaos and a pseudo rotor cylinder to build a cryptosystem. Their innovative design performs well against histogram equalization transmission impairments. Javeed et al. [36] used chaotic differential equations to develop an image cipher. Their lightweight scheme designed substitution boxes based on the Duffing oscillator. Wang et al. [37] designed a novel method for achieving image encryption based on time delay chaotic system. However, the results obtained have not been analysed. Using ordinary differential equations and substitution-boxes, Liu et al. [38] proposed an adaptive dual-image cryptosystem. To acquire the system’s initial values, the technique makes use of ambient noise. The approach creates a vast key space that is resistant to quantum computer attacks. Tutueva et al. [39] devised a new adaptive map and applied it to the creation of a random sequence generator. The adaptive coefficients increase the period length of chaotic sequences dramatically. The literature survey reveals algorithmic shortcomings such as a smaller key space, high computation overhead and an inability to resist plaintext and chosen cipher-text attacks. Further, the algorithms can be applied to encrypt only grayscale medical images.
Binary bit-plane-level scrambling alters the location of the bits and effectively modifies the pixel values as well. DNA computing has enormous parallelism and ultra-low energy consumption capabilities. Chaotic systems generate real random sequences and are highly sensitive to the initial seeds. Driven by the above, we propose an encryption algorithm for medical images based on DNA computing, binary bit-plane decomposition and a chaotic system. In this work, a new permutation-encoding-substitution-decoding-permutation encryption framework is implemented. An innovative approach is used to compute keys from the color components of the input image. We choose the DNA encoding rule dynamically for the encoding process, and the Rössler system is used to create random sequences that are efficiently pre-processed before being used in the pixel-level permutation phases..
The paper is structured as follows. Section 3 introduces the basic theory of binary bit-plane decomposition, DNA encoding and the Rössler system. Section 4 presents the key generation process and the proposed algorithm. The detailed experimental findings are described in Section 5 and a comparative analysis carried out in Section 6. Section 7 concludes our work.
A single DNA sequence is composed of the four nucleic acid bases of Adenine (A), Cytosine (C), Guanine (G) and Thymine (T). The Watson-Crick rules of complementary pairs state that thymine and adenine are complementary, as are guanine and cytosine. In the binary number system, since 1 and 0 are complementary, the binary pairs of 11 and 00, as well as 01 and 10, are also complementary. If we use the four nucleic acid bases to denote the four binary number pairs 00, 01, 10, 11 (that is, A→00, C→01, G→10, T→11), 24 (4! permutations) DNA coding rules are obtained. Of the 24 rules, only 8 satisfy the Watson-Crick legal complementary pairing summarized in Tab. 1 Applying the rules, an 8-bit pixel value can be expressed as a single color component and transformed into a DNA sequence of length four (For instance, the binary equivalent for a grayscale value of 151 is 10010111, with which we obtain the DNA sequence ‘TAAG’, using rule7). The DNA decoding rule is the reverse of the DNA encoding rule.
DNA computing chiefly includes the XOR, subtraction and addition operations. Tab. 2 summarizes the three operations above in accordance with rule1, wherein the base of every row or column is unique. Thus, it is concluded that the DNA operations guarantee the uniqueness of the bases, support high-level parallelism and consume minimal energy. Inspired by these attractive characteristics, we use the DNA rules in our encryption technique to encode the color components of images.


Bit-planes are a notable property of digital images. They represent binary images, formed from the binary values of every pixel in the same position in the image. Tab. 3 shows a representation of the positional weight of a single pixel (an 8-bit grayscale) in the digital image. A gray image can be split into 8 binary bit-planes, ranging from bit-plane1 (for the least significant bit) to bit-plane8 (for the most significant bit). As the weight of each binary bit-plane is different, the percentage of information contained in each also differs. The percentage of information in each bit-plane is computed using Eq. (1) and the results are presented in Tab. 4.


It is seen from Tabs. 3 and 4 that the percentage of information contained in the bit-planes gradually increases from low to high (i.e., from the 1st to the 8th). The lower 4 bit-planes (from the 1st to the 4th) contain only 5.8882% of the total information, whereas the higher 4 (from the 5th to the 8th) contain the remaining 94.118% of the information. The 24 binary planes of test Image1 are depicted in Fig. 1.

Figure 1: Binary bit-planes of an input color medical image
3.3 Chaotic Rössler Dynamical System
Chaos is aperiodic, random behavior of dynamical systems, where even minor changes in the initial seeds lead to completely different outcomes after a particular point. Such dependence on the initial seeds of deterministic chaotic dynamical systems is used to enhance the security strength of image encryption. The Rössler system, proposed by Otto Rössler, is defined by the following Eq. (2) [40].
where a, b and c are non-negative system parameters. The Rössler system exhibits chaotic behavior for the parameter values a = 0.2, b = 0.2 and c = 5.7, as shown in Fig. 2. Key properties of the Rössler system, such as stable equilibrium points and the Lyapunov exponent, are presented below:
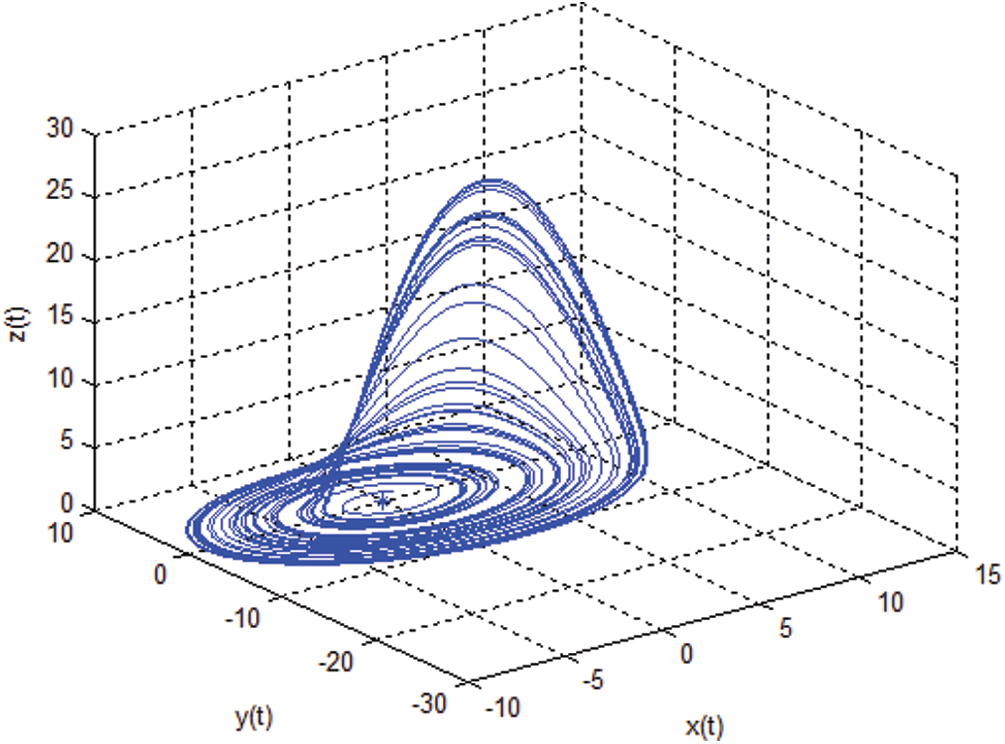
Figure 2: Trajectory of the Rössler system
3.3.1 Stability of Equilibrium Points
The equilibrium points of the Rössler system are obtained as follows:
From Eq. (3),
Substitute Eq. (8) in Eqs. (6) and (7),
Case 1: If c2 > 4ab is true, there exists two equilibrium points,
The Equilibrium point EP1 is not stable and EP2 is locally asymptotically stable [41].
Case 2: If c2 = 4ab is true, there is only equilibrium point
The Equilibrium point EP is non-hyperbolic .
Case 3: If c2 < 4ab is true, no equilibrium point exists.
The Lyapunov exponent, which measures the sensitivity of a deterministic dynamical system with respect to small changes in the initial seeds, is useful for revealing the chaotic behaviour of a dynamical system. If a Lyapunov exponent from the spectrum is positive, the nature of the system is chaotic. The domain of all exponents is referred to as the Lyapunov spectrum. Given that the Lyapunov spectrum of the Rössler system is LE1 = 0.0714, LE2 = 0 and LE3 = –5.3943, the Rössler system is chaotic and useful for encryption. Fig. 3 shows the Lyapunov spectrum of the Rössler system.
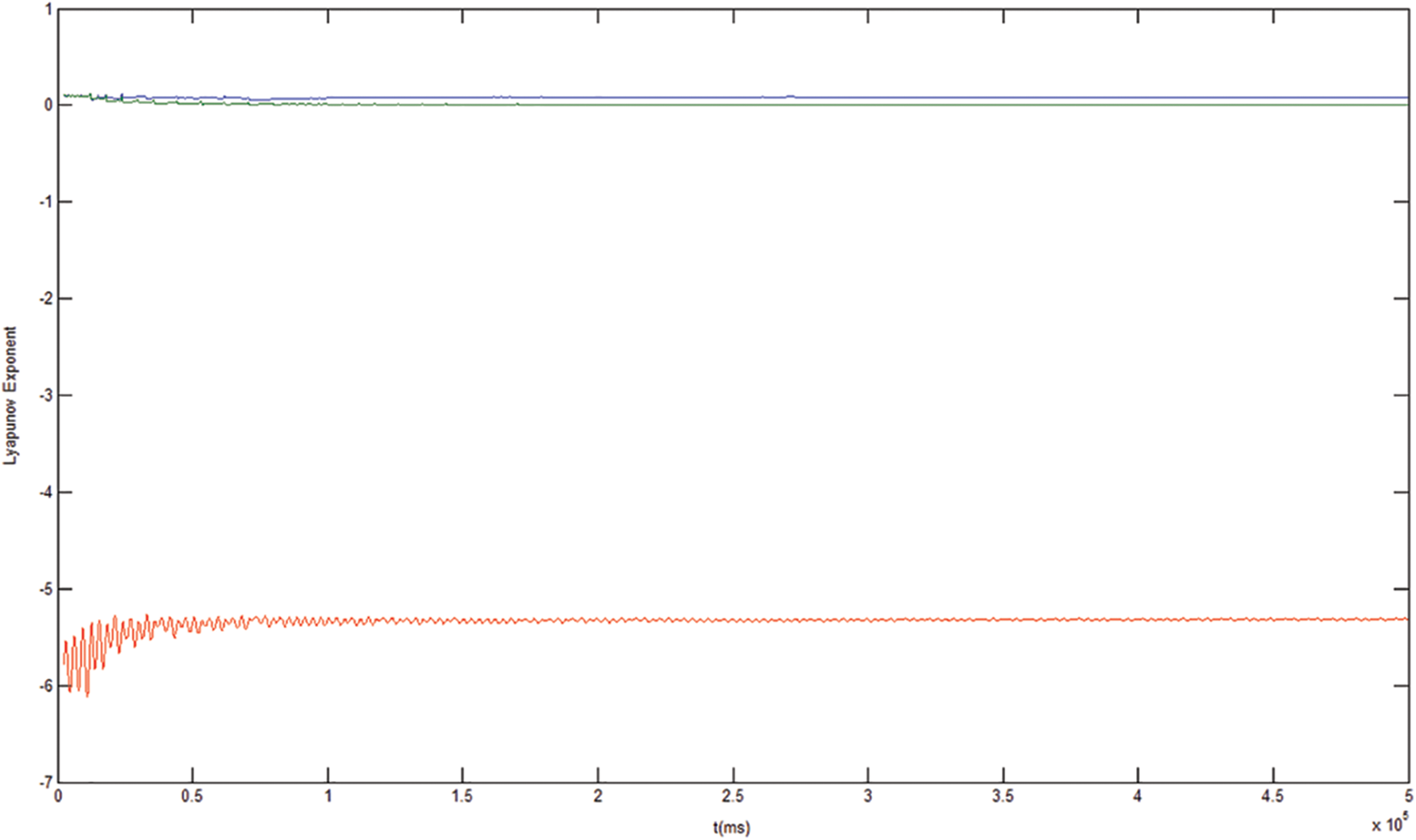
Figure 3: Lyapunov exponents of the Rössler system
Bifurcation is a term used to describe changes in the qualitative behaviour of a dynamical system caused by a tiny smooth change in the bifurcation parameter. Fig. 4 shows the bifurcation diagram for the Rössler system with regard to parameters a, b, and c, which exhibit a period doubling path to chaos.
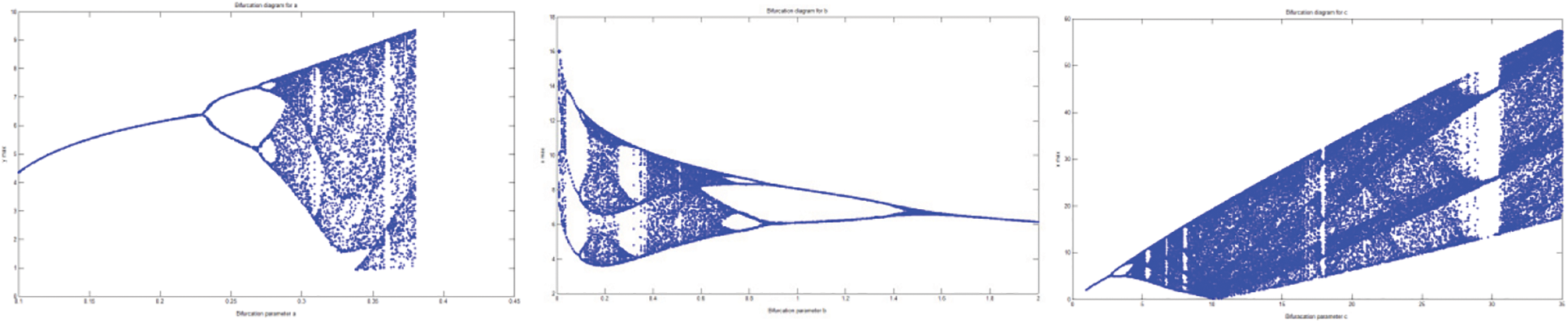
Figure 4: Bifurcation with respect to system parameters (a, b and c)
A general block diagram of the proposed encryption scheme is depicted in Fig. 5. Confusion and diffusion are two intrinsic properties of secure encryption algorithms, which are achieved by means of the substitution and permutation operations in the proposed cipher. Descriptions of the key generation and encryption algorithm follow below:
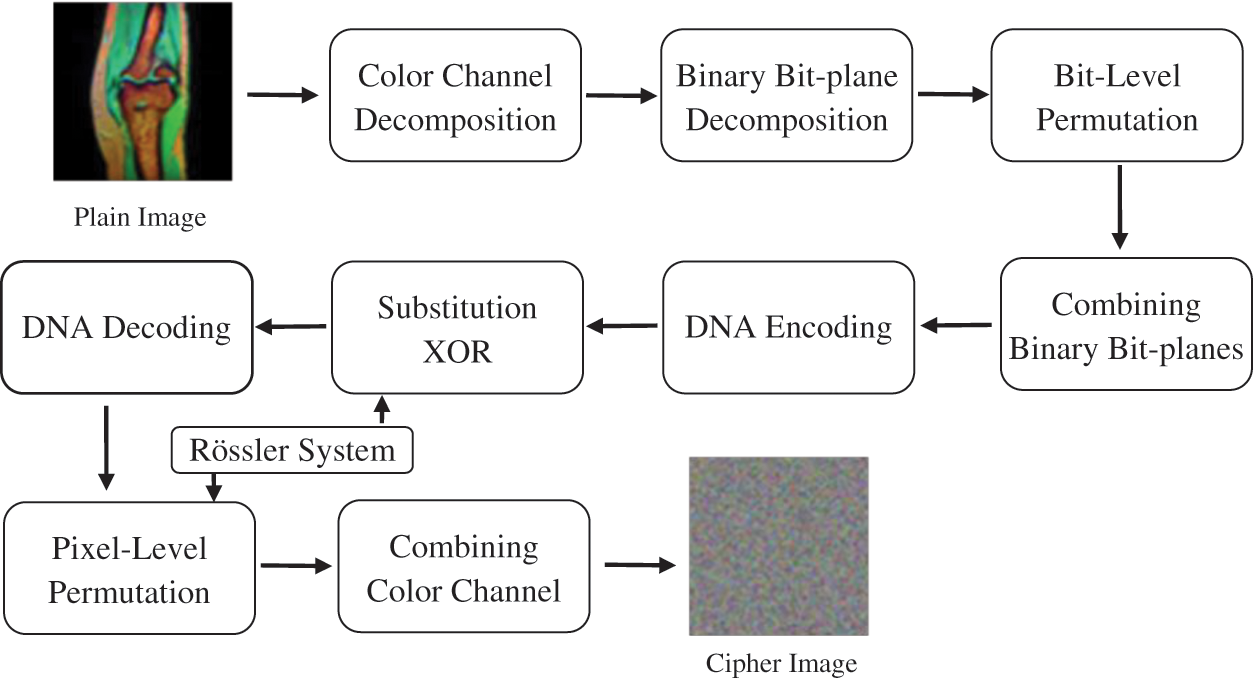
Figure 5: Block diagram of the proposed algorithm

Figure 6: Key generation process
The Rössler system’s initial seeds are employed as the secret-key in the proposed technique. To find the secret-key, firstly the input color image (size M x N) is decomposed into three color components and then it is obtained using Eqs. (11)–(13). Fig. 6 shows a key generation example.
where R(i, j), G(i, j) and B(i, j) represent the pixel value in the ith row and jth column of the red, green and blue components, respectively. The color component-based initial values cause the cipher to be more sensitive to the plain image.
Step 1: Input a color medical plain image (P) of R and C dimensions, where R is the number of rows and C the number of columns.
Step 2: Set the initial values and parameters of the Rössler system and iterate the system using the Runge-Kutta technique (step distance 0.0001). Next, iterate the Rössler system L times to obtain three float-valued chaotic sequences (where L=R×C+3000, and the first 3000 values are ignored to remove the transient effect). Preprocess the sequences using Eq. (14), where s1i, s2i, and s3i are three float-valued chaotic sequences.
Step 3: Separate the input image into three gray images corresponding to the three color channels, R, G and B. Encrypt each color component image, in parallel.
Step 4: Divide the color components into 8 binary bit-planes by using the binary plane decomposition technique.
Step 5: In the bit-level permutation process, change the positions of the bits in the bit-planes with the bit planes of another component at the same level through circular bit-swapping.
Step 6: Recombine the binary bit-planes of the corresponding color components to create permuted grayscale images.
Step 7: Encode the permuted grayscale images into three DNA sequences by using the selected DNA base coding rule.
Step 8: Transform the three random, chaotic sequences produced in Step 2 into DNA sequences (DS1i, DS2i, and DS3i) using the DNA encoding rules. Perform the substitution operation by using the bit-wise logical exclusive-or operation between the grayscale DNA sequences and chaotic DNA sequences as follows:
where DRpi, DGpi, and DBpi are three DNA sequences
Step 9: Decode the three DNA sequences obtained in Step 8 using the DNA decoding rules selected and transform them into three color components.
Step 10: In the pixel-level permutation process, sort the random sequences produced in Step 2 in ascending order to obtain three position-index sequences. Shuffle the pixels in the color components, based on the position sequences.
Step 11: Merge the components to form the final encrypted image (C).
5 Investigation Results and Performance Analysis
This section presents the results of a detailed investigation of the proposed cipher. Further, its performance in terms of security is analyzed and compared with five similar encryption techniques. The plain image set used in our investigation consists of five color medical images with dimensions of size 256 × 256 (named “Image1”, “Image2”, Image3”, “Image4” and “Image5”). All investigations are conducted on a 2.50 GHz Intel Processor with a 4GB RAM, using the MATLAB tool.
The key space of a cipher should be greater than 2100 for high security and strong resistance against brute force attacks. The three initial values of the Rössler system form the key space of the proposed scheme. The IEEE-754 standard double precision is used for the initial value representation, which provides 252 key spaces to each value. As a result, the total space is 2156, owing to which our scheme has the key space necessary to withstand key-based attacks.
A good encryption technique must produce an entirely different cipher image even if an insignificant change is made in the key. The sensitivity of the decryption process of the proposed cipher is tested by using the slightly modified key (x0 = 0.043100000000000000000001, y0 = 0.0989, z0 = 0.0872), instead of the correct key (x0 = 0.0431, y0 = 0.0989, z0 = 0.0872), to decrypt the cipher image. The sensitivity test result, presented in Fig. 7, shows that the deciphered medical image is entirely random and different from the original medical image.

Figure 7: Key sensitivity result. (a) Decrypted image2 with the keys (x0 = 0.0431, y0 = 0.0989, z0 = 0.0872), (b) Decrypted image2 with the keys (x0 = 0.043100000000000000000001, y0 = 0.0989, z0 = 0.0872)
A histogram offers a visual display of the distribution of pixel intensity levels in an image, which can be analyzed and exploited by means of statistical attacks. Fig. 8 shows the histograms of five input images and their corresponding encrypted images. The histograms reveal that encrypted image pixels are distributed in uniform patterns, whereas input image pixels are concentrated at certain intensity levels. Thus, the proposed cipher conceals statistical information leakages most effectively.

Figure 8: Histogram of input images and their corresponding encrypted images
It is well known that a high degree of correlation exists between adjoining pixels in medical images. Attackers can use the correspondence between pixels to obtain quantitative information; therefore, correlation in cipher images should be very low. The correlation coefficient is measured for 3500 randomly selected pixels using Eq. (16). Fig. 9 and Tab. 5 display the correlation coefficients obtained from the input and encrypted images in diagonal, vertical, and horizontal directions. The correlation coefficient is negative when the association between neighbouring pixels changes in the opposite direction. The results show that the correlations in cipher images are significantly minimized in all three directions.
where rxy is the correlation coefficient between the adjacent pair of pixels x and y, E(x) is the variance of x, D(x) is the expectation of x and N is the total number of selected pixels.

Figure 9: Correlation coefficient of image 4

Entropy represents the amount of randomness existing in information. If the entropy is nearly 8, the values of the cipher image pixels are more randomly distributed. Entropy is measured using Eq. (19), and the results listed in Tab. 6 indicate that the entropy values of the cipher images are optimal.
where gi represents the gray levels and p(gi) the probability of the gray levels, gi.

The peak signal-to-noise ratio (PSNR) metric is used to check the quality of the encrypted image. The PSNR is computed between the input and ciphered images using Eq. (20). The low PSNR values in Tab. 7, which are indicative of the very poor quality of the cipher images, show that the proposed encryption technique is good.
wherein, P(i,j), C(i,j) are the input and the ciphered images pixel values of the location (i, j), and h and w are the image dimensions.

Encryption speed is a critical measure that tests the practical applicability of an algorithm. Tab. 8 displays the encryption speed (in seconds) of the proposed technique. Components that take up the most time in the proposed algorithm include DNA encoding, decoding and chaotic sequence generation.

The input image sensitivity test that is carried out observes the effect of the changes in the ciphered image after an insignificant change (typically a single bit) is made to the pixel value of the input image. Metrics like the number of pixel changing rate (NPCR) and unified averaged changed intensity (UACI) are utilized to undertake the sensitivity analysis. The NPCR represents the number of pixels between two different same-sized images. The NPCR is calculated for the two ciphered images (C1 and C2), and the corresponding input images differ in terms of exactly one bit. The UACI specifies the difference in the degree of pixel intensity values between two same-sized images. The best UACI and NPCR values are approximately 33.5% and 99.6%, respectively. Tab. 9 presents the NPCR and UACI test results obtained, which are ideal. The NPCR and UACI are defined as follows:
wherein, d(i,j) is
C1(i, j) and C2(i, j) are pixel values at locations (i, j) of the two ciphered images and the width and height are the dimensions of the image.

The NIST SP 800-22 test is a standard way to randomness testing. It is a collection of fifteen statistical tests that determine the genuine randomness of cryptographic sequences. P > 0.01 in the NIST test indicates that the sequence passes the test and is truly random [43]. The randomness of the encrypted image was checked, and the results are shown in Tab. 10. It can be seen from the table that the encrypted image passes all tests.

The strength of any effective cryptosystem design is its anti-disturbance capacity against noise and clipping attacks. To see how well the proposed method works, the encrypted images are subjected to noise and pixel clipping attacks.
During the transmission, the ciphered image has a high probability of being distorted by different kinds of noises. It is natural that these noises would directly impact the quality of the deciphered image. If the cryptosystem is noise sensitive, a tiny change in the encrypted image caused by noise may make it difficult to restore the original image after decryption. To execute noise attack, several densities of salt and pepper noise (0.01, 0.04, and 0.07) are introduced to the enciphered image, and the test results are shown in Fig. 10. The proposed algorithm has good anti-noise performance, as can be shown in the Fig. 10.
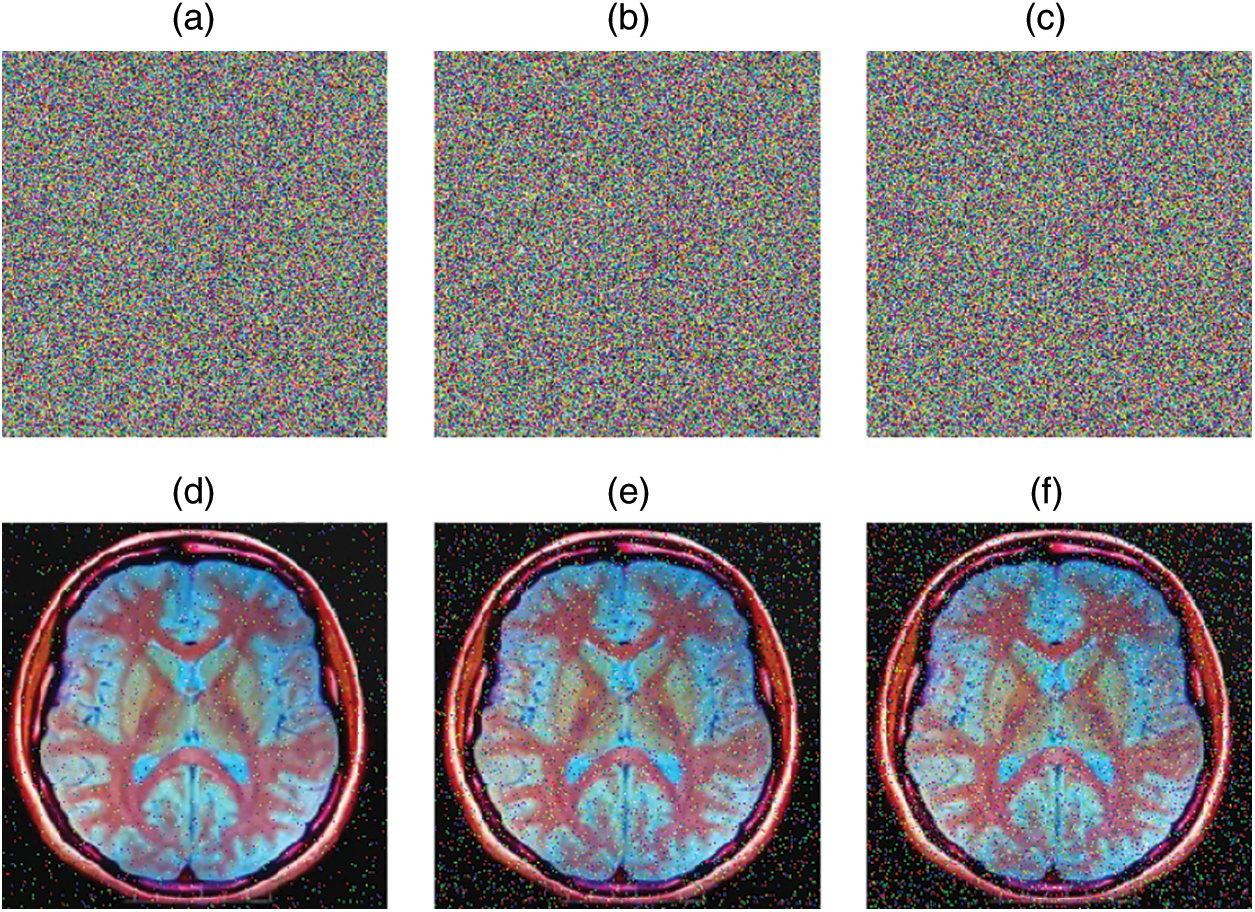
Figure 10: Decryption results with different noise density levels. (a) Cipher image with 0.2 salt and pepper noise, (b) Cipher image with 0.5 salt and pepper noise, (c) Cipher image with 0.1 salt and pepper noise, (d) Decrypted image corresponding to (a), (e) Decrypted image corresponding to (b), (f) Decrypted image corresponding to (c)
To test the clipping attack, the encrypted image of input image1 is cropped by size 32 × 32, 64 × 64, and 96 × 96 blocks before being decrypted. Fig. 11 depicts the outcomes of the experiment. The decryption technique can fairly reconstruct the primary information even if a piece of the encrypted image is destroyed, as seen in Fig. 11.
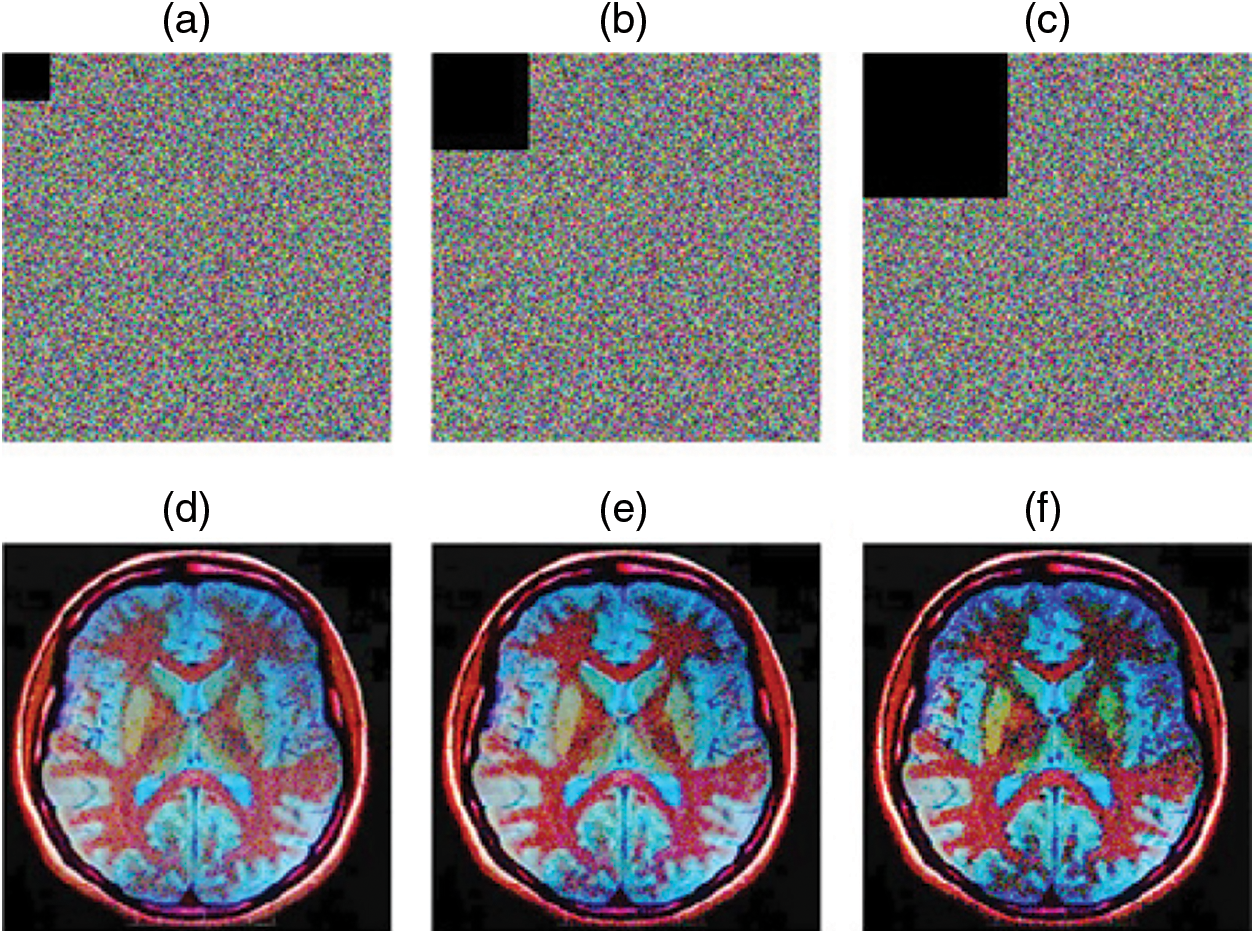
Figure 11: Decryption results with different degree of clipping attacks. (a) 32 × 32 size block cropped attack, (b) 64 × 64 size block cropped attack, (c) 96 × 96 size block cropped attack, (d) Decrypted image corresponding to (a), (e) Decrypted image corresponding to (b), (f) Decrypted image corresponding to (c)
The new technique is compared, performance-wise, with five recently proposed algorithms in terms of safety and visual quality. Tab. 6 shows that our scheme obtained optimal entropy values (average of 7.99902) compared to other methods. The results of the PSNR test, shown in Tab. 7, indicate that the quality of the encrypted image produced by the proposed algorithm is poor. An analysis of the correlation coefficient reveals that the proposed system significantly reduces the correlation of the adjacent pixels in all three directions. As can be seen from Tab. 9, our method yielded an ideal UACI (average of 33.41756) and NPCR (average of 99.519) when compared to other algorithms. Our technique offers better results overall in all tests than the other four methods.
In this paper, we have presented a new robust encryption technique for color medical images. The permutation-encoding-substitution-decoding-permutation architecture is adopted for increased security. The starting seeds of the Rössler system are calculated from input medical images that significantly strengthen the proposed algorithm against chosen and known plaintext attacks. It is observed from the experimental results that the new scheme has obtained a key space of 2156, sufficient to withstand key-based attacks. The histograms of the encrypted images are evenly distributed and visually unintelligible; therefore, no significant pattern can be derived. To demonstrate the competence of the suggested algorithm, comparisons are made with four recent algorithms. From the analysis, it is evident that our algorithm produced optimal NPCR (avg ≈ 99.519), UACI (avg ≈ 33.4175), correlation coefficient (close to zero) and PSNR (avg ≈ 9.2623) values as compared to the other four techniques. Hence, it is demonstrated that our technique can stand up strongly to differential and statistical attacks.
Acknowledgement: We would like to thank Rittmat ELES for the English language editing of this manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. X. Chen and C. Hua, “Adaptive medical image encryption algorithm based on multiple chaotic mapping,” Saudi Journal of Biological Sciences, vol. 24, no. 8, pp. 1821–1827, 2017. [Google Scholar]
2. Y. Chen, C. Tang and R. Yeb, “Cryptanalysis and improvement of medical image encryption using high-speed scrambling and pixel adaptive diffusion,” Signal Processing, vol. 167, no. 22, pp. 107286, 2020. [Google Scholar]
3. Q. Zhang, X. Xue and X. Wei, “A novel image encryption algorithm based on DNA subsequence operation,” Scientific World Journal, vol. 2012, no. 6736, pp. 1–10, 2012. [Google Scholar]
4. X. Chai, Y. Chen and L. Broyde, “A novel chaos based image encryption algorithm using DNA sequence operations,” Optics and Lasers in Engineering, vol. 88, no. 2, pp. 197–213, 2017. [Google Scholar]
5. X. Wang, Y. Zhang and Y. Zhao, “A Novel image encryption scheme based on 2D logistic map and DNA sequence operations,” Nonlinear Dynamics, vol. 82, no. 3, pp. 1269–1280, 2015. [Google Scholar]
6. X. Chai, “A novel image encryption algorithm based on the chaotic system and DNA computing,” International Journal of Modern Physics C, vol. 28, no. 4, pp. 1750069, 2017. [Google Scholar]
7. J. C. Dagadu, J. Li and E. O. Aboagye, “Medical image encryption based on hybrid chaotic DNA diffusion,” Wireless Personal Communications, vol. 108, no. 1, pp. 591–612, 2019. [Google Scholar]
8. N. P. Slimane, N. Aouf, K. Bouallegue and M. Machhout, “An efficient nested chaotic image encryption algorithm based on DNA sequence,” International Journal of Modern Physics C, vol. 29, no. 7, pp. 1850058, 2018. [Google Scholar]
9. X. Wang, H. Zhao, Y. Hou, C. Luo, Y. Zhang et al., “Chaotic image encryption algorithm based on pseudo-random bit sequence and DNA plane,” Modern Physics Letters B, vol. 33, no. 22, pp. 1950263, 2019. [Google Scholar]
10. Z. Liu, C. Wu, J. Wang and Y. Hu, “A color image encryption using dynamic DNA and 4D memristive hyper-chaos,” IEEE Access, vol. 7, pp. 78367–78378, 2019. [Google Scholar]
11. P. T. Akkasaligar and S. Biradar, “Selective medical image encryption using DNA cryptography,” Information Security Journal: A Global Perspective, vol. 29, no. 2, pp. 91–101, 2020. [Google Scholar]
12. Q. Liu and L. Liu, “Color image encryption algorithm based on DNA coding and double chaos system,” IEEE Access, vol. 8, pp. 83596– 83610, 2020. [Google Scholar]
13. Z. Zhu, W. Zhang, K. Wong and H. Yu, “A chaos-based symmetric image encryption scheme using a bit-level permutation,” Information Sciences, vol. 181, no. 6, pp. 1171–1186, 2011. [Google Scholar]
14. Y. Zhou, K. Panetta, S. Agaian and C. L. P. Chen, “Image encryption using p-fibonacci transform and decomposition,” Optics Communications, vol. 285, no. 5, pp. 594–608, 2012. [Google Scholar]
15. Z. Tang, J. Song, Z. Zhang and R. Sun, “Multiple-image encryption with bit-plane decomposition and chaotic maps,” Optics and Lasers in Engineering, vol. 80, pp. 1–11, 2016. [Google Scholar]
16. Z. Gan, X. Chai, D. Han and Y. Chen, “A chaotic image encryption algorithm based on 3D bit-plane permutation,” Neural Computing and Applications, vol. 31, no. 11, pp. 7111–7130, 2019. [Google Scholar]
17. S. Mozaffari, “Parallel image encryption with bitplane decomposition and genetic algorithm,” Multimedia Tools and Applications, vol. 77, no. 19, pp. 25799–25819, 2018. [Google Scholar]
18. S. Som, A. Mitra, S. Palit and B. Chaudhuri, “A selective bit-plane image encryption scheme using chaotic maps,” Multimedia Tools and Applications, vol. 78, no. 3, pp. 10373–10400, 2018. [Google Scholar]
19. L. Zhang and X. Zhang, “Multiple-image encryption algorithm based on bit planes and chaos,” Multimedia Tools and Applications, vol. 79, no. 29-30, pp. 20753–20771, 2020. [Google Scholar]
20. W. Cao, Y. Zhou, C. L. P. Chen and L. Xia, “Medical image encryption using edge maps,” Signal Processing, vol. 132, no. 9, pp. 96–109, 2017. [Google Scholar]
21. T. Shahryar, M. H. Fathi and Y. A. Sekhavat, “An image encryption scheme based on elliptic curve pseudo random and advanced encryption system,” Signal Processing, vol. 141, no. 1, pp. 217–227, 2017. [Google Scholar]
22. R. Zahmoul, R. Ejbali and M. Zaied, “Image encryption based on new beta chaotic maps,” Optics and Lasers in Engineering, vol. 96, no. 3, pp. 39–49, 2017. [Google Scholar]
23. Ü. Çavuşoğlu, S. Kaçar, I. Pehlivan and A. Zengin, “Secure image encryption algorithm design using a novel chaos based s-box,” Chaos Solitons & Fractals, vol. 95, no. 11, pp. 92–101, 2017. [Google Scholar]
24. A. Broumandnia, “The 3D modular chaotic map to digital color image encryption,” Future Generation Computer Systems, vol. 99, no. 1, pp. 489–499, 2019. [Google Scholar]
25. A. Banik, Z. Shamsi and D. S. Laiphrakpam, “An encryption scheme for securing multiple medical images,” Journal of Information Security and Applications, vol. 49, no. 4, pp. 102398, 2019. [Google Scholar]
26. G. Ke, H. Wang, S. Zho and H. Zhang, “Encryption of medical image with most significant bit and high capacity in piecewise linear chaos graphics,” Measurement, vol. 135, no. 18, pp. 385–391, 2019. [Google Scholar]
27. G. Cheng, C. Wang and H. Chen, “A novel color image encryption algorithm based on hyper chaotic system and permutation-diffusion architecture,” International Journal of Bifurcation and Chaos, vol. 29, no. 9, pp. 1–17 2019. [Google Scholar]
28. L. O. Tresor and M. Sumbwanyambe, “A selective image encryption scheme based on 2D DWT, henon map and 4d qi hyper-chaos,” IEEE Access, vol. 7, pp. 103463–103472, 2019. [Google Scholar]
29. M. Muñoz-Guillermo, “Image encryption using q-deformed logistic map,” Information Sciences, vol. 552, pp. 352–364, 2021. [Google Scholar]
30. S. Ibrahim, H. Alhumyani, M. Masud, S. Alshamrani, O. Cheikhrouhou et al., “Framework for efficient medical image encryption using dynamic s-boxes and chaotic maps,” IEEE Access, vol. 8, pp. 160433–160449, 2020. [Google Scholar]
31. K. N. Madhusudhan and P. Sakthivel, “A secure medical image transmission algorithm based on binary bits and arnold map,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 5, pp. 5413–5420, 2021. [Google Scholar]
32. M. Gafsi, N. Abbassi, M. A. Hajjaji, J. Malek, A. Mtibaa et al., “Improved chaos-based cryptosystem for medical image encryption and decryption,” Scientific Programming, vol. 2020, no. 11, pp. 1–22, 2020. [Google Scholar]
33. N. Sasikaladevi, K. Geetha, K. Sriharshini and M. D. Aruna, “H3-hybrid multilayered hyper chaotic hyper elliptic curve based image encryption system,” Optics and Laser Technology, vol. 127, no. 3, pp. 106173, 2020. [Google Scholar]
34. A. Sahasrabuddhe and D. S. Laiphrakpam, “Multiple images encryption based on 3D scrambling and hyper-chaotic system,” Information Sciences, vol. 550, no. 18, pp. 252–267, 2019. [Google Scholar]
35. A. U. Rehman, A. Firdous, S. Iqbal, Z. Abbas, M. M. A. Shahid et al., “A color image encryption algorithm based on one time key, chaos theory, and concept of rotor machine,” IEEE Access, vol. 8, pp. 172275–172295, 2020. [Google Scholar]
36. A. Javeed, T. Shah and Attaullah, “Lightweight secure image encryption scheme based on chaotic differential equation,” Chinese Journal of Physics, vol. 66, no. 2, pp. 645–659, 2020. [Google Scholar]
37. B. Wang, B. F. Zhanga and X. Liu, “An image encryption approach on the basis of a time delay chaotic system,” Optik, vol. 225, pp. 165737, 2021. [Google Scholar]
38. H. Liu, A. Kadir, X. Sun and Y. Li, “Chaos based adaptive double-image encryption scheme using hash function and s-boxes,” Multimedia Tools Applications, vol. 77, no. 1, pp. 1391–1407, 2018. [Google Scholar]
39. A. V. Tutueva, E. G. Nepomuceno, A. I. Karimovc, V. S. Andreev and D. N. Butusov, “Adaptive chaotic maps and their application to pseudo-random numbers generation,” Chaos, Solitons and Fractals, vol. 133, no. 1, pp. 109615, 2020. [Google Scholar]
40. O. E. Rössler, “Continuous chaos four prototype equations,” Annals of the New York Academy of Sciences, vol. 316, no. 1, pp. 376–392, 2006. [Google Scholar]
41. R. Barrio, F. Blesa, A. Denac and S. Serrano, “Qualitative and numerical analysis of the rössler model: Bifurcations of equilibria,” Computers and Mathematics with Applications, vol. 62, no. 11, pp. 4140–4150, 2011. [Google Scholar]
42. P. Deshmukh, “An image encryption and decryption using AES algorithm,” International Journal of Scientific & Engineering Research, vol. 7, no. 2, pp. 210–213, 2016. [Google Scholar]
43. S. Hanis and R. Amutha, “Double image compression and encryption scheme using logistic mapped convolution and cellular automata,” Multimedia Tools Applications, vol. 77, no. 6, pp. 6897–6912, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |