DOI:10.32604/iasc.2022.025608

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.025608 |  |
| Article |
Gender-specific Facial Age Group Classification Using Deep Learning
1Coimbatore Institute of Technology, Coimbatore, 641014, India
2Swinburne University of Technology, Kuching, 95530, Malaysia
*Corresponding Author: Khaled ELKarazle. Email: kelkaeazle@swinburne.edu.my
Received: 30 November 2021; Accepted: 31 December 2021
Abstract: Facial age is one of the prominent features needed to make decisions, such as accessing certain areas or resources, targeted advertising, or more straightforward decisions such as addressing one another. In machine learning, facial age estimation is a typical facial analysis subtask in which a model learns the different facial ageing features from several facial images. Despite several studies confirming a relationship between age and gender, very few studies explored the idea of introducing a gender-based system that consists of two separate models, each trained on a specific gender group. This study attempts to bridge this gap by introducing an age estimation system that consists of two main components. The first component is a custom-built gender classifier that distinguishes females and males apart. The second is an age estimation module that consists of two models. Model A is trained only on female images, while model B is trained only on male images. The system takes an input image, extracts the facial gender then passes the image to the appropriate model based on the predicted gender label. Our age estimation models are based on the Visual Geometry Group (VGG16) networks and have been modified to fit the nature of our problem. The models produce accuracies of more than 85% individually, and the system achieves an overall accuracy of 80%. The proposed system is trained and tested on the UTKFace dataset and cross-validated on the FG-NET dataset to validate the performance on unseen data.
Keywords: Age estimation; age group classification; deep learning; computer vision; facial recognition; facial analysis
Automatic age estimation is the process of training a machine learning model to process an input image with an unknown age label, extract the relevant features, then produce a label representing the person’s estimated age or age group.
Whether the model is based on traditional machine learning or deep learning architecture, the creation, training and testing processes remain the same. Before training, the initial step is finding a suitable labelled facial images dataset for training and evaluation. Several benchmark datasets such as the Adience [1] or the UTKFace [2] have been widely used for age estimation research. The second step is pre-processing the samples in which the images are cropped and rotated to eliminate unnecessary background noises that may interfere with the training process. The next step is extracting the relevant facial features from the training samples. This step can be carried out using deep learning methods such as convolutional neural networks or manually configured filters like local binary patterns [3] or Sobel [4] filters. The next and final step in building the model is training a particular machine learning algorithm on the extracted feature maps. The defined model attempts to produce a mapping function
Although age estimation studies such as [5,6] have confirmed a direct correlation between age and gender, there has been insufficient research into the concept of estimating age based on the subject’s gender. In addition, other studies such as [7,8] have stated that the rate of ageing and ageing patterns varies based on the subject’s gender. Based on these studies, which have demonstrated a relationship between age and gender, we consider the lack of research into building gender-specific age estimation models a significant gap in the current work of literature. We attempt to solve the abovementioned issue by introducing a gender-specific age estimation system that consists of two models. Each model is based on the Visual Geometry Group (VGG16) [9] architecture and trained on the UTKFace dataset. Model A is only trained on images of female subjects, while model B is only trained on images of male subjects. We use the letters “A” and “B” for labelling purposes. In addition, a custom-built gender estimation model is employed to detect the gender of the subject from an input image and produces a label that is then used to load the appropriate age model. We divide the images into four age classes: 0–12, 13–19, 20–59 and 60+ and test our implementation on a testing portion of the UTKFace dataset, which was not included in the training phase. The proposed system is also cross-validated on the FG-NET [10] dataset to confirm whether gender separation affects performance. Our results demonstrate an improvement in the classification accuracy when two separate models are trained compared to a single model. Our contributions are summarized as follows:
1) We propose a novel gender-based age classification system consisting of two age classifiers, where each model is trained on a specific gender group.
2) We introduce a robust custom-built facial gender classifier that produces a gender label responsible for loading the appropriate age model.
3) We propose two modified VGG16 networks to estimate age groups from input images.
The study’s novelty and the main contribution to the literature is the system architecture that segregates the training process between males and females. To the best of our knowledge, none of the current work has introduced a similar design but instead focused on either introducing new age estimation algorithms or optimizing existing ones. The typical age estimation process is illustrated in Fig. 1.

Figure 1: An overview of the training process of age estimation models
This paper is organized into six sections. Section one is the introduction in which we introduce the problem and a high-level explanation of the proposed method. Section two covers the latest work that has been done to solve the problem of age estimation. Section three presents a thorough explanation of our proposed method. Section four presents both our experimental and comparative results. Section five discusses the results and why these accuracies were obtained. The sixth and final section concludes the study and provides our plans for future works.
A typical age estimation model is usually based on either regression or classification. On the one hand, regression-based models learn to output a single value representing the estimated age. In contrast, classification-based models attempt to produce a label representing the subject’s age group.
In a study conducted by [11], the authors presented a set of pre-trained models combined with K-Fold validation to estimate facial age. The authors employed three pre-trained networks, namely the VGG16, Residual Networks (ResNet50) [12] and the Squeeze-and-Excitation (SENet50) [13]. The authors claim that these models were decided on after a few experiments.
All the three networks used Visual Geometry Group Face (VGGFace) [14] weights as they were trained on facial recognition, which is a task that is close to age estimation. All three models were fine-tuned to produce the best possible accuracies. The fine-tuning of the networks is carried out by adding five more layers at the end of each network. The first layer flattens the feature map into a 1D vector, and the three subsequent layers are fully connected. The fifth and final layer is an output layer that maps the features to eight age classes. In addition, the authors froze all the layers in all networks except the ones that were added. The networks were trained on the UTKFace dataset, where the age classes were divided into eight groups: 0–2, 4–6, 8–12, 15–20, 25–32, 38–43, 48–53, 60+.
The UTKFace dataset was divided into 9300 images for training, 2300 images for testing and 330 images for validation. Each model was trained for 20 epochs for 5 h with a batch size of 32 and optimized using the Adam optimizer with a learning rate of 0.001. Additionally, every network was trained with a 5-fold cross-validation technique to counter overfitting. The authors reported accuracy of 71.84% from the ResNet50 network, 65.31% from the VGG16 network and 61.96% from the SENet50 network.
In another study, [15] experimented with five pre-trained models, namely, the extreme version of Inception (Xception) [16], ResNet50, VGG16, Visual Geometry Group (VGG19) and InceptionV3 [17]. Prior to training, the training samples are cropped, rotated and resized to 224 × 224. This step is crucial to ensure that only the faces are extracted without the unnecessary background noises. The authors used a large-scale dataset denoted as MORPH, which contains more than 40,000 images to train and test all five models. The authors focused primarily on investigating the effects of freezing and unfreezing the layers in each network on the accuracy of estimating age. The experimental results of their study demonstrated that the Xception model is the most accurate, with a comparatively low Mean Absolute Error (MAE) of 2.35 when 100% of its layers were frozen. However, the model produces the worst mean absolute error of 15.5 among all the five models when all layers are unfrozen. The InceptionV3 model produced an MAE of 2.47 when all layers were frozen and 15.4 when 0% were frozen.
The ResNet50 model performed slightly better than the other two abovementioned, with an MAE of 2.53 with 100% frozen layers and 8.95 with all layers unfrozen. The VGG models, on the other hand, were incapable of producing better accuracies than the ResNet50, InceptionV3 and Xception. The lowest MAE obtained by the VGG16 model was 4.43, with all the layers remaining unfrozen. A higher MAE of 9.32 was obtained when 25% of the layers were frozen. The fifth and final model, VGG19, produced an MAE of 3.14, with 75% of the layers frozen. However, this value increased to 9.32 when 25% of the layers were frozen. Despite the obtained accuracies, the authors insisted that the training samples did not resemble real-life scenarios where images are taken in various conditions.
Another study [18] proposed a multi-stage system that detects gender and age from a given facial image. The first component in the proposed system is an encoder-decoder saliency detection network that extracts regions of interest. In this study, regions of interest are denoted as “people”, and unwanted background noises are denoted as “others.” The encoder of the network consists of 14 convolutional layers, each followed by one max-pooling. On the other hand, the decoder contains six convolutional layers, five unpooling layers, and a single output layer. The second module in the proposed system is a regression-based model which predicts age and gender. The prediction model is based on the VGG19 architecture due to its robustness and efficiency. The saliency network was trained on a modified PASCAL visual object challenge 2012 dataset [19] since the authors did not have access to a dataset with samples of pixel-level saliency. The modification of this dataset was done by manually labelling regions of interest and backgrounds. The authors trained and tested the entire system on three benchmark datasets: FG-NET, Adience and Cross-Age Celebrity Dataset (CACD) [20]. The system produced an MAE of 2.97 on the FG-NET, 2.08 on the Adience dataset and 5.94 on the CACD dataset.
Despite the numerous studies discussed in this section, there has been little to no attention given to investigating the effect of gender on the accuracy of age estimation models. Therefore, the fundamental hypothesis discussed in our study is that gender influences the accuracy of age estimation models, so the primary gap we attempt to bridge is the relationship between age and gender.
This section explains our proposed system and provides information on replicating the method for future research. Our method consists of two main components. The first component is a gender estimator, that groups input images based on their facial gender. The second component is an age estimation module which consists of two VGG16 models. The first model is denoted as model A, and it is trained only on images of female subjects. The second model is denoted as model B, and it is trained only on male subjects. The labels A and B are only used to refer to the models. We use the UTKFace and FG-NET datasets to test and train our age estimation models and the Kaggle gender dataset [21] to train our gender classifier. We choose an entirely different dataset to train our gender estimation model to minimize biases that might arise if we train it on the age estimation dataset. An overview of the process is illustrated in Fig. 2.
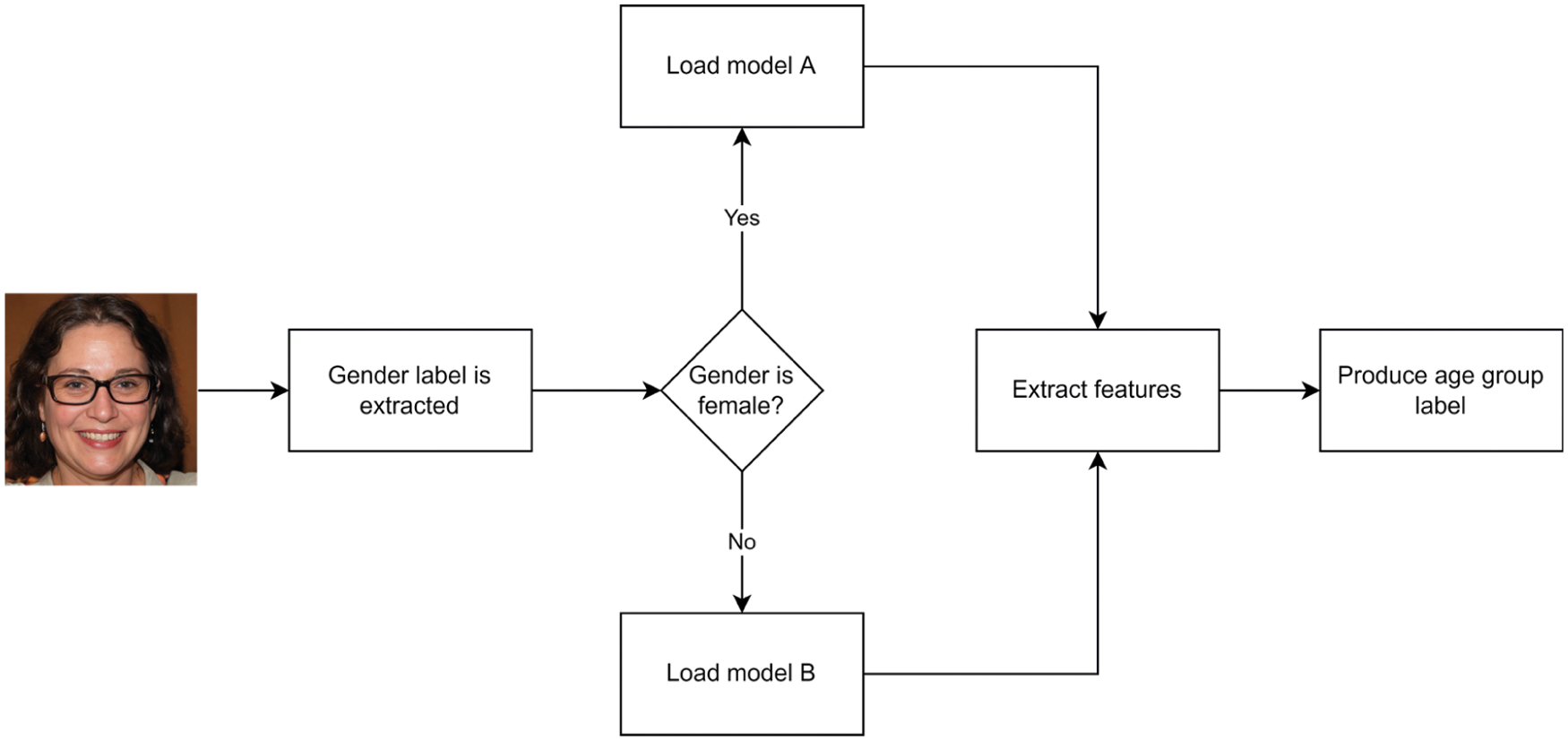
Figure 2: Overview of the proposed system
Before training the gender and age estimation models, we first pre-process the samples to ease the training process. We begin by running a face detection algorithm based on the C++ Deep Learning Library (dlib) and OpenCV to detect faces in a given image. The detected faces are cropped and separated from the rest of the entire image. Next, the positions of both left and right eyes are detected using dlib and the coordinates are extracted. The coordinates are then used for reference to align and rotate the image. The alignment is carried out using Eq. (1):
where xi and yi represent the coordinates of the left eye, and xj and yj represent the coordinates of the right eye. The rotation angle is denoted as θ. After preparing the images for training, we segregate them into classes. We separate the images in the UTKFace dataset based on their gender labels for age estimation, resulting in two training datasets. One dataset contains only males, and the other is only females.
Our gender estimation model is created and trained from scratch due to the simplicity of the gender prediction task compared to age estimation. The model is a binary classifier with a sigmoidal output between 0 and 1. For labelling purposes during training, images of males are assigned “0”, and images of females are denoted as “1”. This output is produced after a given image x is fed to the model. We describe the sigmoid function [22] in Eq. (2):
We use the binary cross-entropy loss function [23] to optimize the model. The function is defined in Eq. (3) as follows:
where y is the gender label, p(yi) is the probability of the image being of class A while log(1 − p(y)) is the probability that the image is of class B and N is the total number of samples. The network takes an input RGB image of size 96 × 96. The network consists of four hidden layers and two fully-connected layers. The hidden layers are defined as follows:
1) The first convolutional layer consists of 64 filters with a kernel size of 3 × 3, followed by batch normalization and max-pooling layer.
2) The second layer consists of 128 filters with a kernel size of 3 × 3, followed by a batch normalization layer and max-pooling layer.
3) The third layer consists of 256 filters of kernel size of 3 × 3, a batch normalization layer and a max-pooling layer.
4) The final layer contains 512 filters with a kernel size of 3 × 3, followed by batch normalization and max-pooling layers.
Each convolutional layer is activated using the Rectified Linear Unit (ReLU) function, and each max-pooling layer has a pool size of 2 × 2. The fully-connected portion consists of two layers, each with 512 neurons, activated using the ReLU function and followed by a dropout layer with a rate of 0.5. The final output layer consists of two neurons, producing the gender label. The network is optimized using the Adam optimizer and trained for ten epochs. The model’s architecture is presented in Fig. 3.

Figure 3: Gender classifier’s architecture
Model A and Model B are both pre-trained, fine-tuned VGG16 networks. The networks are initially pre-trained on the ImageNet dataset [24], containing around 1.2 million images. The VGG16 design is comparatively deep and robust, and it has been employed in several challenging tasks besides age estimation. We modify the model to fit our task by replacing the default input layer with an input layer that accepts an image size of 96 × 96 × 3. The input size is adjusted to 96 × 96 to reduce the network’s complexity and training time.
Moreover, we do not freeze any of the layers during training. The second adjustment we make to the model is adding a single dense layer with 512 neurons after the last convolutional layer. This dense layer is activated using the ReLU function and followed by a single dropout layer with a rate of 0.5. This dense layer finally maps to an output softmax layer which maps to four age classes. In total, the number of trainable parameters becomes 22,386,757 from 138 million. Since we are using the softmax activation for the output layer and cross-entropy as a loss function, we define these in Eqs. (4) and (6):
We define
During training, the number of epochs is set to 100; however, early stopping is implemented to ensure that the models do not overtrain. The addition of early stopping stops the training process of model A on the 30th epoch and model B on the 20th epoch. Both models are optimized using the adam optimizer with a learning rate of 0.001. In Fig. 4, we summarize the overall design of both age estimation models.
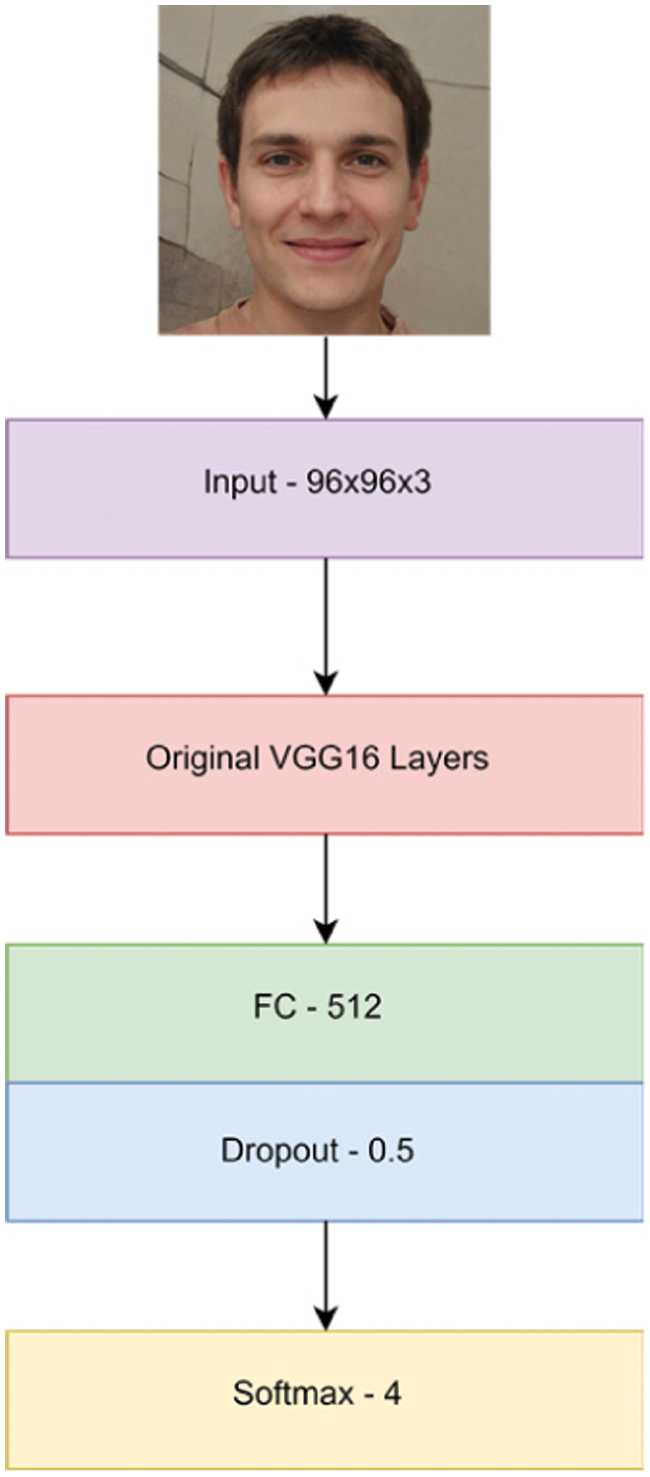
Figure 4: Overview of the age estimation model
This section presents the accuracy of both models, the system’s overall accuracy, a comparative evaluation with similar methods, and a breakdown of the datasets.
In this study, we use the following datasets:
1) UTKFace [2]: This is a large-scale dataset with over 20,000+ facial images of subjects between 0 and 100 years old. In addition to age, the dataset is also labelled by gender, making it more suitable to train our system. We divide this dataset into two portions. The first portion is training and testing, which is used to train and validate models A and B. This portion consists of 22,508 images. The second portion is only used to test both models and the whole system, and it contains 1164 images. We use 80% of the images for training and 20% for validation for the first portion. The dataset can be downloaded through this link.
2) Kaggle Gender Dataset [21]: The Kaggle gender dataset is available for research purposes on Kaggle. This dataset contains 47,009 training images, out of which 23,766 are of males, and the remaining are of females. We use this dataset to train our gender classifier. The dataset is designed for facial analysis tasks and can be accessed through this link.
3) FG-NET [10]: The FG-NET dataset has been widely used in age estimation tasks, and it is relatively smaller in size. The dataset contains 1009 facial images, and it is used to further validate the performance of our implementation. Out of these images, we use 200 random images for testing. The dataset is available for research purposes on this link.
Tabs. 1 and 2 present the breakdown of our age classes and the number of male and female images in each dataset. In addition, the breakdown of the gender dataset is presented in Tab. 3.



In Figs. 5 and 6, we present both models’ learning and loss curves. In addition, we present the confusion matrix of models A and B in Figs. 7 and 8, respectively.
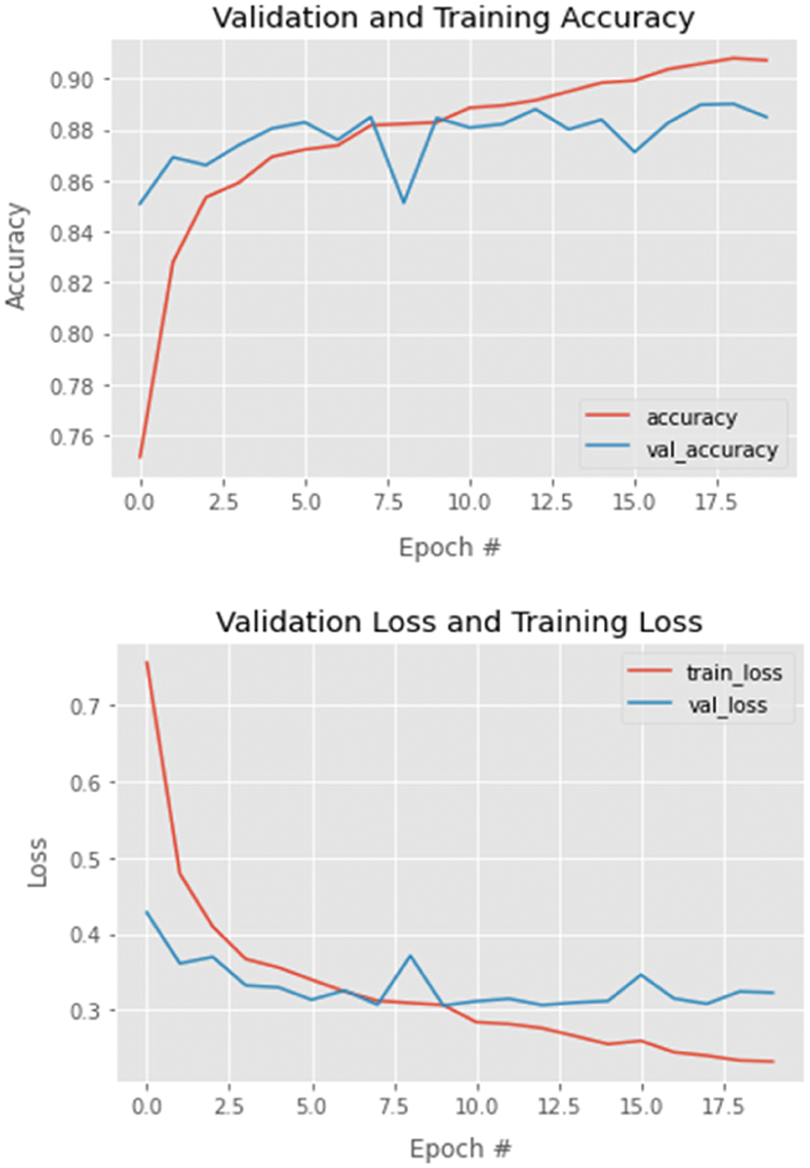
Figure 5: Training and validation loss/accuracy–model B

Figure 6: Training and validation loss/accuracy–model A
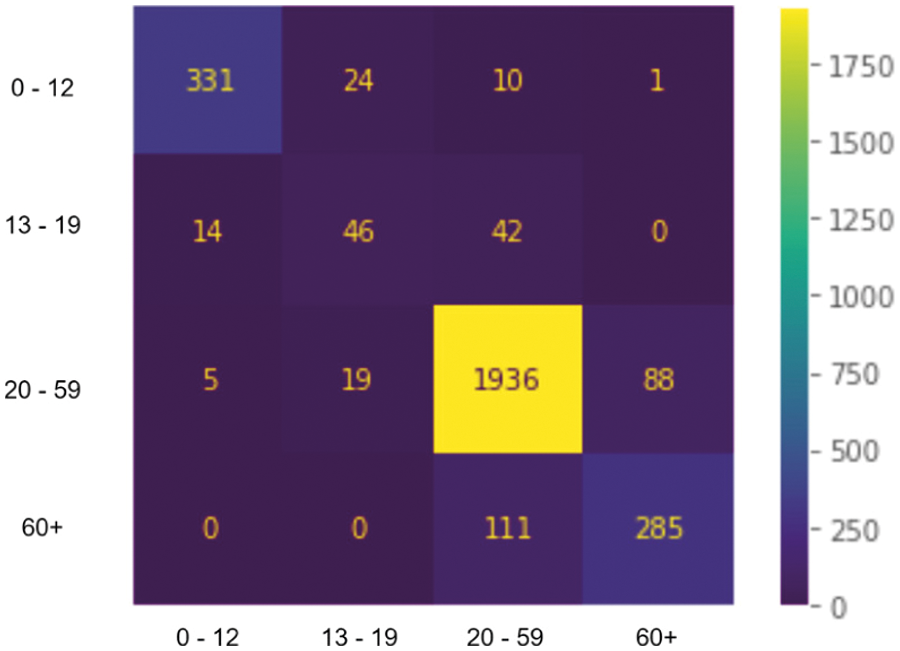
Figure 7: Confusion matrix-model B
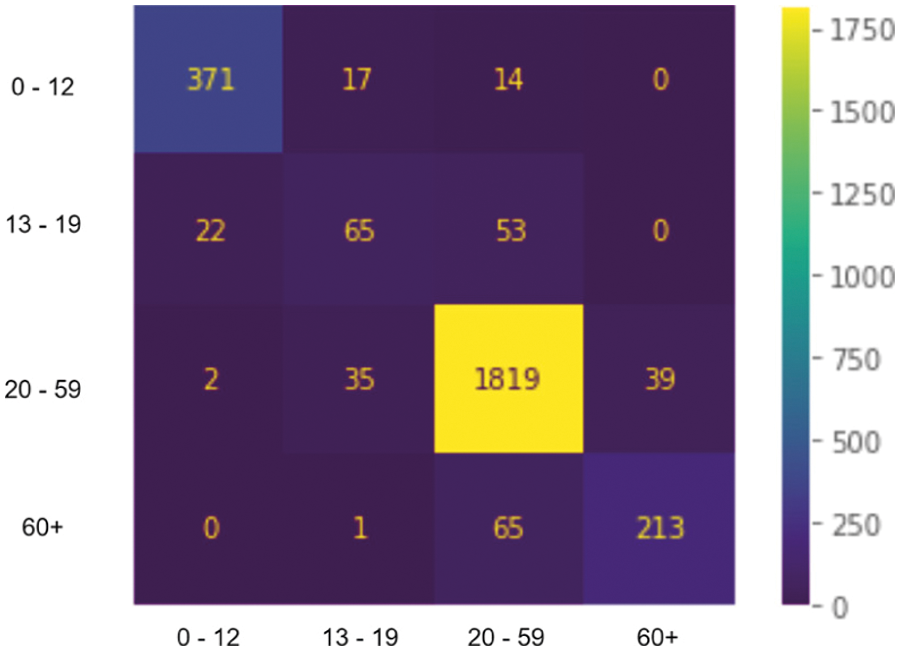
Figure 8: Confusion matrix-model A
Since our age estimation model is classification-based, we use the formula presented in Eq. (2) as a metric to produce the accuracy. In Tab. 4, we present the accuracies of each model separately. In addition, in Tab. 5, we present the entire system’s accuracy when tested on the FG-NET dataset and the UTKFace test portion. Tab. 6 presents the accuracy of a single model that has been trained on the entire dataset without separating the genders. Moreover, in Tab. 7, we compare our method with existing pieces of literature. In Fig. 9, we present several misclassified samples from the FG-NET and the UTKFace datasets. The number of correctly classified and misclassified images is obtained using Eqs. (7) and (8):

Figure 9: Misclassified samples of females (top), males (bottom)




In Eq. (7), the objective is to find the number of correctly classified images where the predicted label equals the ground-truth label. On the other hand, Eq. (8) objective’s is to find the total number of outputs where the predicted label is not equal to the ground-truth label.
To justify our choice of using a modified VGG16 network, we present the performance of three well-known pre-trained models that have been configured similarly to our original age classifier. The accuracies of the VGG19, ResNet50 and the Densely Connected Convolutional Networks (DenseNet121) [31] are presented in Tab. 8.

Upon conducting several experiments, we concluded that the most suitable network architecture for our problem is the VGG16 design. We notice that pre-trained models other than the VGG16 tend to overfit easily with our configurations, as demonstrated in Tab. 8. We theorize that overfitting happens due to the complexity of the models and the small number of training samples; therefore, ResNet50 or DenseNet121 models may outperform the VGG16 network if more training images are acquired.
A significant observation from our study is that separating the images based on their facial gender improves the classification accuracy. This observation is illustrated in the results presented in Tabs. 4–6. It is evident from the results in these tables that training two different models increases the overall accuracy by roughly 10%.
We hypothesize that the accuracy increases because each model will no longer have to learn the gender features; therefore, the models will solely focus on extracting and learning the ageing features. The early stopping mechanism backs this hypothesis since model A stops training on the 30th and model B stops training on the 20th. Based on Tab. 4, it is observed that despite the number of female and male subjects being almost similar, model B produces lower accuracy compared to model A. The theory for the difference in accuracy is that images of males may contain more features than those of females. Features such as facial hair in male subjects might explain why the model struggles to produce an accurate class prediction.
The number of age classes was decided on after several experiments. The age classes chosen represent the four main age categories: Childhood (0–12), Teenage (13–19), Adulthood (20–59), Senior Citizens (60+). This grouping of age labels was preferred to cover all the possible age groups, which studies like [11,25,26] lack. The age gaps and number of classes seemed to affect the accuracy of both models and the entire system. Based on our experiments, the accuracy worsens when we decrease the age gap and increase the number of age classes. This issue occurs as some age classes might have overlapping features with subsequent classes. For example, subjects in 0–5 and 6–10 age groups would be difficult to classify as their facial features look similar.
The gender classifier is the first entry point to our system; therefore, we aim to produce a robust gender estimation model that works on unrestrained facial images while remaining as lightweight as possible. We achieve this objective by proposing the design shown in Fig. 3. Batch normalization is utilized for regularization and to reduce overfitting. In addition, max-pooling layers are employed to reduce the dimensionality of the feature map, thus reducing the number of parameters. To further prevent overfitting, we add dropout layers with a rate of 50% after each fully-connected layer. The number of convolutional layers, kernel size and filter size was decided based on several experiments. These experiments aimed to maximize accuracy and reduce complexity as much as possible. Our system has several limitations that could be solved if more training samples are added. The first limitation is that the system struggles to classify age and gender when given grayscale images similar to the ones shown in Fig. 9.
Moreover, low-resolution samples pose a significant challenge to our system as several ageing features like wrinkles or the face’s texture become unclear to capture. Finally, images of toddlers are mostly misclassified during the gender filtering process since it is difficult to know a toddler’s gender based on their face. These limitations are primarily encountered when the system is evaluated on the FG-NET dataset.
This study introduces a gender-specific age estimation system based on two components. The first component is a gender estimation model which labels incoming input facial images. The second component is an age estimation model, consisting of two main VGG16 classifiers denoted as models A and B. Model A is trained only on female subjects. In contrast, model B is trained only on male subjects. Based on the label produced by the facial gender estimator, the appropriate age model is loaded and used to predict the facial age class. We bundle the age groups into four classes: 0–12, 13–19, 20–59 and 60+. We use the UTKFace and FG-NET datasets to train and test the age estimation models and the Kaggle gender dataset to train the gender classifier. The presented results demonstrate that separating age estimation models based on gender increases the classification accuracy; however, there are several limitations to the proposed system which need to be addressed in future research. For future work, we are interested in exploring the integration of generative adversarial networks (GANs) to generate more training samples since the lack of enough data is one of the significant limitations.
Acknowledgement: The authors would like to thank Swinburne University of Technology (Sarawak Campus) for providing the necessary resources to carry out this study
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. T. Hassner, S. Harel, E. Paz and R. Enbar, “Effective face frontalization in unconstrained images,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Boston, USA, pp. 4295–4304, 2015. [Google Scholar]
2. Z. Zhang, H. Qi and Y. Song, “Age progression/regression by conditional adversarial autoencoder,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Hawai, USA, pp. 4352–4360, 2017. [Google Scholar]
3. K. Song, Y. Yan, W. Chen and X. Zhang, “Research and perspective on local binary pattern,” Acta Automatica Sinica, vol. 39, no. 6, pp. 730–744, 2013. [Google Scholar]
4. N. Kanopoulos, N. Vasanthavada and R. L. Baker, “Design of an image edge detection filter using the sobel operator,” IEEE Journal of Solid-State Circuits, vol. 23, no. 2, pp. 358–367, 1988. [Google Scholar]
5. S. Al-Shannaq and L. A. Elrefaei, “Comprehensive analysis of the literature for age estimation from facial images,” IEEE Access, vol. 7, pp. 93229–93249, 2019. [Google Scholar]
6. R. Angulu, J. Tapamo and A. Adewumi, “Age estimation via face images: A survey,” Journal of Image Video Processing, vol. 42, no. 2, pp. 1–35, 2018. [Google Scholar]
7. O. Ekiz, G. Yuce, S. Ulaşli, F. Ekiz, S. Yuce et al., “Factors influencing skin ageing in a Mediterranean population from Turkey,” Clinical and Experimental Dermatology, vol. 37, no. 5, pp. 492–496, 2012. [Google Scholar]
8. M. A. Farage, K. W. Miller, P. Elsner and H. I. Maibach, “Intrinsic and extrinsic factors in skin ageing: A review,” International Journal of Cosmetic Science, vol. 30, no. 15, pp. 87–95, 2008. [Google Scholar]
9. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Int. Conf. on Learning Representations, San Diego, USA, pp. 1130–1150, May 2015. [Google Scholar]
10. Y. Fu, T. Hospedales, T. Xiang, Y. Yao and S. Gong, “Interestingness prediction by robust learning to rank,” in European Conf. on Computer Vision, Zurich, Switzerland, pp. 448–503, 2014. [Google Scholar]
11. S. Uddin, M. Morshed, M. Prottoy and A. Rahman, “Age estimation from facial images using transfer learning and K-fold cross-validation,” in 3rd Int. Conf. on Pattern Recognition and Intelligent Systems, Bangkok, Thailand, pp. 33–36, 2021. [Google Scholar]
12. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in 29th IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, USA, pp. 770–778, 2015. [Google Scholar]
13. J. Hu, L. Shen, S. Albanie, G. Sun and E. Wu, “Squeeze-and-excitation networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 8, pp. 2011–2023, 2020. [Google Scholar]
14. Q. Cao, L. Shen, W. Xie, O. Parkhi and A. Zisserman, “VGGFace2: A dataset for recognising faces across pose and age,” in 13th IEEE Int. Conf. on Automatic Face & Gesture, Xian, China, pp. 67–74, 2018. [Google Scholar]
15. A. Othmani, A. Taleb, H. Abdelkawy and A. Hadid, “Age estimation from faces using deep learning: A comparative analysis,” Computer Vision and Image Understanding, vol. 196, no. 1, pp. 102961, 2020. [Google Scholar]
16. F. Chollet, “Xception: Deep learning with depthwise separable convolutions,” in IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, USA, pp. 1800–1807, 2017. [Google Scholar]
17. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens and Z. Wojna, “Rethinking the inception architecture for computer vision,” in IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, USA, pp. 2818–2826, 2016. [Google Scholar]
18. J. Fang, Y. Yuan, X. Lu and Y. Feng, “Muti-stage learning for gender and age prediction,” Neurocomputing, vol. 334, no. 2, pp. 114–124, 2019. [Google Scholar]
19. M. Everingham, L. Gool, C. Williams, J. Winn and A. Zisserman, “The pascal visual object classes (VOC) challenge,” International Journal of Computer Vision, vol. 88, no. 2, pp. 303–338, 2010. [Google Scholar]
20. B. Chen, C. Chen and W. Hsu, “Face recognition and retrieval using cross-age reference coding with cross-age celebrity dataset,” IEEE Transactions on Multimedia, vol. 17, no. 6, pp. 804–815, 2014. [Google Scholar]
21. KAGGLE, https://www.kaggle.com/cashutosh/gender-classification-dataset, 2019. [Google Scholar]
22. J. Feng and S. Lu, “Performance analysis of various activation functions in artificial neural networks,” Journal of Physics: Conference Series, vol. 1237, no. 2, pp. 111–122, 2019. [Google Scholar]
23. S. Mannor, D. Peleg and R. Rubinstein, “The cross-entropy method for classification,” in Machine Learning, Proc. of the Twenty-Second Int. Conf., Bonn, pp. 561–568, 2005. [Google Scholar]
24. J. Deng, W. Dong, R. Socher, L. Jia, K. Li et al., “ImageNet: A large-scale hierarchical image database,” in IEEE Conf. on Computer Vision and Pattern Recognition, Miami, USA, pp. 248–255, 2009. [Google Scholar]
25. G. Levi and T. Hassner, “Age and gender classification using convolutional neural networks,” in IEEE Workshop on Analysis and Modeling of Faces and Gestures (AMFG), Boston, USA, pp. 34–42, 2015. [Google Scholar]
26. Z. Qawaqneh, A. Mallouh and B. Barkana, “Deep convolutional neural network for age estimation based on VGG-face model,” arXiv preprint arXiv, 2017. [Google Scholar]
27. T. Kim, “Generalizing MLPs with dropouts, batch normalization, and skip connections,” arXiv preprint arXiv, 2021. [Google Scholar]
28. K. Zhang, C. Gao, L. Guo, M. Sun, X. Yuan et al., “Age group and gender estimation in the wild with deep RoR architecture,” IEEE Access, vol. 5, pp. 22492–22503, 2017. [Google Scholar]
29. L. Hou, D. Samaras, T. Kurc, Y. Gao and J. Saltz, “Convnets with smooth adaptive activation functions for regression,” in Int. Conf. on Artificial Intelligence and Statistics, Lauderdale, USA, pp. 430–439, 2017. [Google Scholar]
30. R. Rothe, R. Timofte and L. Van Gool, “Deep expectation of real and apparent age from a single image without facial landmarks,” International Journal of Computer Vision, vol. 126, no. 2, pp. 144–157, 2018. [Google Scholar]
31. G. Huang, Z. Liu and K. Weinberger, “Densely connected convolutional networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, USA, pp. 4700–4708, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |