Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.024682
Article

Another View of Weakly Open Sets Via DNA Recombination

Samirah Alzahrani1,*, A.I. El-Maghrabi2 and M.S. Badr3

1Department of Mathematics and Statistics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Mathematics, Faculty of Science, Kafrelshikh University, Kafrelshikh, Egypt
3Department of Mathematics, Faculty of Science, New Valley University, El Kharga, Egypt
*Corresponding Author: Samirah Alzahrani. Email: mam_1420@hotmail.com
Received: 27 October 2021; Accepted: 17 January 2022

Abstract: The generalized structure of deoxyribonucleic acid (DNA) is based on the rules of topological spaces. DNA recombination is one of the most important processes within DNA, as it is essential in the pharmaceutical industry as well as in gene therapy. In this paper, we are discussing the relationship between rough sets, nano topological spaces (N τs ), nano Z open (N Z0 ) sets, and DNA recombination. We also created a new recombination mapping using the properties of the DNA recombination process. Further, by using the process of cutting and sticking of a sequence of genes, new topological structures are constructed and some of their properties and characterizations are investigated. Moreover, we study recombination operators in the statement “Sticky Ends”. Furthermore, we use nano topological structures to prove the validity of the mathematical model of the recombination process and the extent to which the topological mathematical properties correspond to the biological properties. Finally, we use nano Z-open sets to study many topological characteristics of the neighborhood, closure, interior, limit points, frontier, border and exterior.

Keywords: DNA recombination; sticky ends; nano Z-open; operator

1  Introduction

Liellis Thivagar [1] invented the notion of nano topological spaces (short for Nτs )), which define a subset of a universe using upper, lower approximations and a boundary region defined by an equivalence relation on it. Nano open (nano closed, nano-interior and nano-closure) sets (briefly, N0,Nc,Nint and Ncl ) as being defined by him. El-Maghrabi and Mubarki [2] defined Z-open sets in topological structures and investigated several of their features. The concept of nano Z-open sets plays a role in topological structures and their applications in domains such as mathematics, biology and other aspects of life. The goal of this research is to look at how mathematics is used in biological applications (DNA recombination) and prove the validity of the mathematical model of the recombination process using nano topology and NZ0 . The extent to which the topological mathematical properties correspond to the biological properties. We also use nano Z-open sets to study many topological characteristics of the neighborhood, closure, interior, limit points, frontier, border and exterior.

Proposition 1.1. [3] If (U,R) is an approximation space and X,Y⊆U , then

(i) LR(X)⊆X⊆UR(X) ,

(ii) LR(φ)=UR(φ)=φ and LR(U)=UR(U)=U ,

(iii) UR ( X∪Y )= UR(X)∪UR(Y)) ,

(iv) UR ( X∩Y ) ⊆UR(X)∩UR(Y)) ,

(v) LR ( X∪Y ) ⊇LR(X)∪LR(Y) ,

(vi) LR ( X∩Y )= LR(X)∩LR(Y) ,

(vii) IfX⊆Y then LR(X)⊆LR(Y) and UR(X)⊆UR(Y) ,

(viii) UR(Xc)=[LR(X)]c and LR(Xc)=[UR(X)]c ,

(ix) URUR(X)=LRUR(X)=UR(X) ,

(x) LRLR(X)=URLR(X)=LR(X) .

Definition 1.2 [1] Let H⊆U and (U,τR(X)) be a Nts . Then H is a nano regular open ( Nro ) if H=Nint(Ncl(H)).

Definition 1.3 [4] If H⊆U and (U,τR(X)) be a Nts . Then the nano θ -interior(resp. nano θ closure) of H is defined by NNintθ(H)=∪{E:EisaNθ set and Ncl(E)⊆H} (resp. Nintθ (H)= ∪{x∈E:Ncl∩H≠∅ , E is a Nθ set, x∈E} .

Definition 1.4 [4] A subset H of U is said to be a nano θ open ( Nθ0 )(resp. nano θ -closed( Nθ )) set if H= (resp. Hc is a nano θ open set ).

Definition 1.5 [5] If H⊆U and (U,τR(X)) is Nts , then the nano δ -interior(resp. nano δ closure) of H is defined by Nintδ (H)= ⋃{x∈E:Nroset,E⊆H} (resp. Nclδ (H)= ∪{x∈U:Nint(Ncl(H))∩H≠∅ , E is a No set, x∈E} .

Definition 1.6 [5] A subset H of U is said to be a nano δ open ( Nδo )(resp. nano δ -closed( Nδc )) set if H= Nintδ (H) (resp. Hc is a nano δ open set ).

Definition 1. 1 Let K⊆U and (U,τR(X)) be a Nts . Then K is said to be:

(i) nano δ -preopen [5] (briefly, Nδ P0)set if K⊆Nint(Nclδ (K),

(ii) nano δ -semiopen [5] (briefly, Nδ S0)set if K⊆Ncl(Nintδ (K),

(iii) nano e-open [6] (briefly, N e0)set if K⊆Nint(Nclδ (K) ∪Ncl(Nintδ (K),

(iv) nano θ -semiopen [6] (briefly, NθSO set if Ncl(Nintθ (K),

1.1 DNA Recombination

DNA recombination is one of the most important processes within DNA, as it is essential in the pharmaceutical industry as well as in gene therapy. Bacteria can acquire new genes by incorporating environmental DNA into their genomes [7], and the recombination process may be used for gene reproduction or tissue culture, and defects in homologous recombination may lead to a gastric cancer mutation [8]. However, recombination is not accurate [9]. Since the adoption of computer programmes depends on mathematics and the description of operations before their implementation, making a simulation of any problem requires a mathematical model of the problem, so we made a mathematical model of the recombination process and verified the validity of the mathematical model using nano-topological structure and nano Z-open and we also made a conclusion. Some mathematical results on nano Z-open.

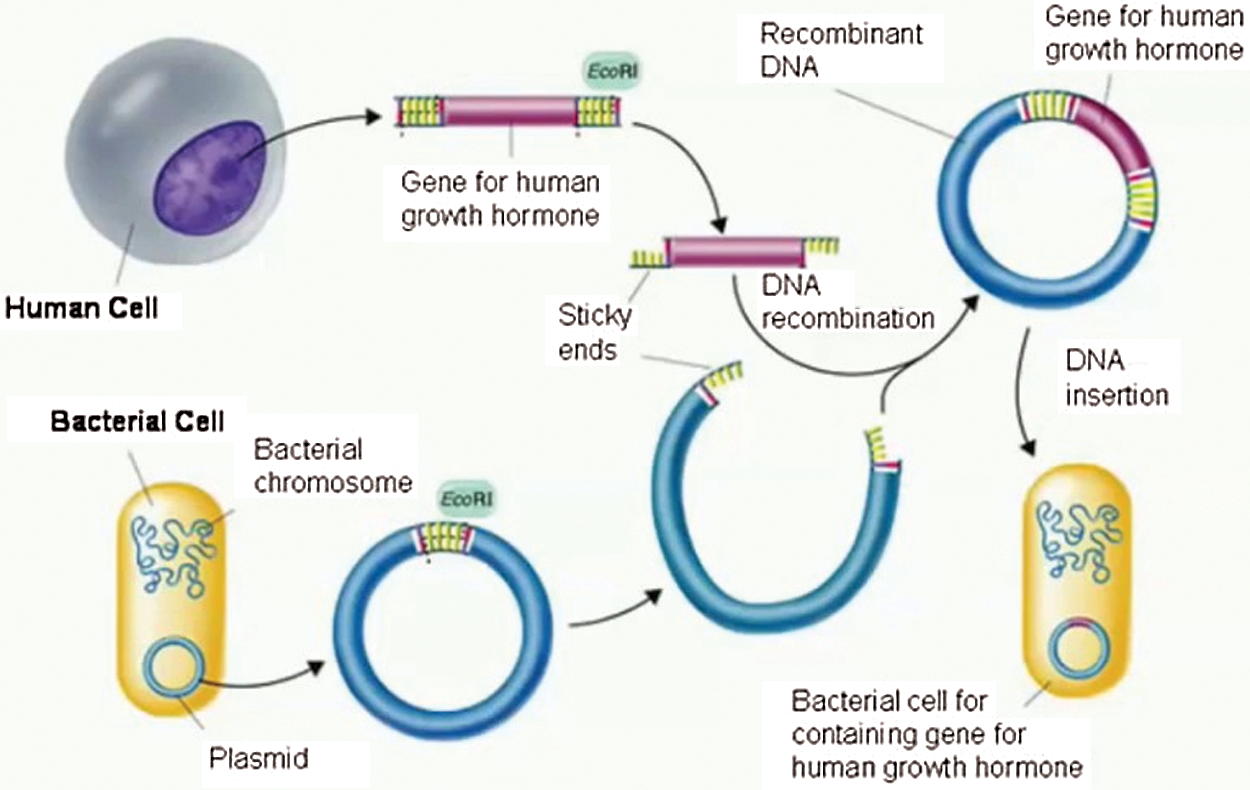
Fig. 1 depicts the steps involved in creating recombinant DNA as:

•   Treat the DNA taken from both sources with the same restriction end nuclease.

•   The restriction enzyme is an enzyme that cleaves DNA into fragments at or near specific recognition sites, such as sticky ends (EcoRI recognizes the sequence G ↓ AATTC CTTAA ↑ G) and at blunt ends for example (HpaI restriction enzyme recognizes the sequence GTT ↓ AACCAA ↑ TTG.

•   Sticky ends are an overhanging segment of single-stranded DNA at the cut's ends.

•   These sticky ends can base pair with any complementary sticky end-containing DNA molecule.

•   When put together, complementary sticky ends can form a pair.

•   A DNA ligase is used to covalently join the two strands of recombinant DNA into a molecule.

•   Recombinant DNA must be copied several times before it can be used.

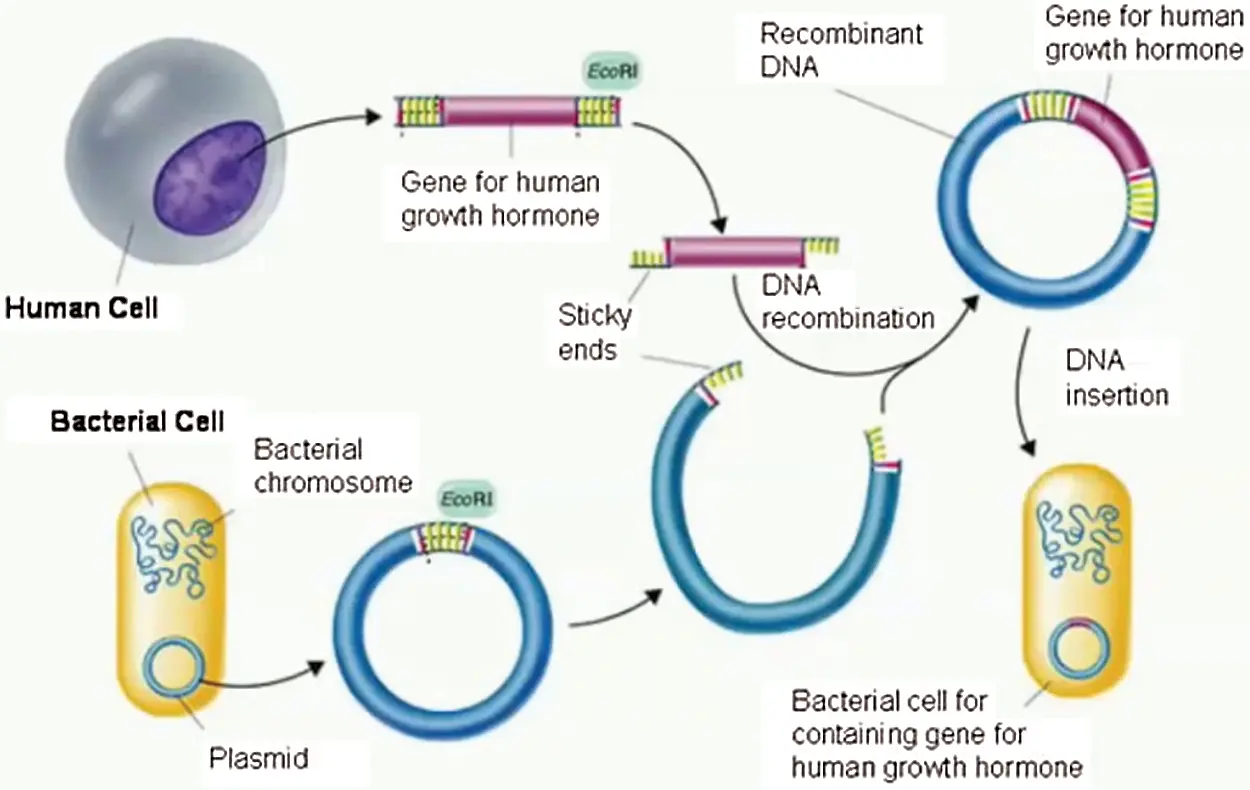
Figure 1: Recombinant DNA process

1.1.1 Mathematical of DNA Recombination

Mathematical modelling of biological processes is very useful in identifying the processes and designing programs that help in investigating possible solutions and avoiding errors. These models have helped in the development of other sciences and mathematics. Representing the problem of life or any process does not stop when building the mathematical model, but continues to prove the validity of the mathematical model and match the mathematical solution with the practical solution (to solve the problem of life). To prove the validity of the model, we use mathematical methods (topological, numerical analysis, differential equations, etc.). But during our work, we use topological methods more than any other branch of mathematics. Recombination is the production of offspring with combinations of hits that differ from those found in either parent. Stadler & Stadler [10,11] had defined the recombination process (most applications are inherited) and had problems with the definition, since the recombination of R(x, x) will not always give the x. Therefore, we will build on the definition of Stadler & Stadler definition of genetic re-synthesis, which is more commonly used in the manufacture of medicine and gene therapy. The DNA recombination process makes it possible to cut different strands of genotypes with a restriction enzyme (sticky ends) and join the genotypes together via complementary base pairing [12–14]. In this study, we consists of mathematical modelling of the recombination process. Also, we consider a method for generating nano topologies by (recombination operator deduce the equivalence classes) rough set theory via one of the biological applications (DNA recombination processes). We will investigate the topological properties of nano Z-open sets using nano topological structures. Finally, we explore the extent of the match between mathematical and biological results.

1.2 The DNA Recombination Operator

“A new mathematical representation is proposed for the configuration structure induced by recombination. It consists of the mapping of pairs of objects to a power set of all objects in the search space. The mapping assigns to each pair of parental (genotypes) the set of all recombinant genotypes obtainable from the parental ones.”

Definition 1.3.1 [10] Let X be any set of types “strings of bites, vectors, DNA, ribonucleic acid (RNA) sequence …etc.” A recombination operator on X that is defined by F:A×A→P(A) the following condition holds ∀h,k∈A :

(i)F(h,k)=F(k,h)

(ii)F(h,h)={h}

(iii){h,k}⊆F(h,k)

(iv)‖F(h,v)‖=‖F(h,k)‖,∀v∈F(h,k).

2  Topological Spaces of DNA Recombination

By constructing a new recombination mapping based on the properties of the recombination process, we aim to use topological concepts to build flexible mathematical models in biomathematics. In addition, we investigate the topological qualities of the newly formed map as well as the topological structures of DNA that are related to it. We study the properties of recombination mapping, new topological structures, and characterizations by using the new concepts “Cut and Sticks” for sequences of genotypes. Further, we define recombination mathematically by a matrix where enzymes can be cut and the integration of two “types” introduces the meaning of the process of recombination, and as a result of improved optimization of this definition, more than once, it’s a description of the recombination process is more accurate. The process of recombination consists of three elements: a gene, an enzyme, and plasma to form the mathematical model and then replace the enzyme with the slicing Boolean matrix. The functions (gene slicing and plasma slicing) and recombination composition were explained well by the way recombination between genes occurs. We have greater accuracy and better places to cut the injured part from the rest of the injured part.

Definition 2.1

Let X be a set of types “strings of bites, vectors, DNA, RNA sequence …etc.” and the span of X contains all the linear combination elements of X as well as recombinant. Then the topological DNA recombination operator Rs:X×X→spanX , is defined by

Rs (x,y) =⋃i=1n{ci∗x5′3′+cn−i∗y1,cj∗x3′5′+cn−j∗y2} , Since, Ci∗=(I⋯I⋮⋱I⋮I⋯I)

Ci∗=(1000…0100…000…000…⋮⋮000⋮000…1⋮…⋮⋮000⋮000…⋮…)

where “ I∈{0,1} and the matrix represents the unity of level i×n , O a zero matrix, Ci∗ is called the matrix slicing and Ci∗∈Mn(f) [Boolean matrix] and the sense strand of DNA X5′3′ , the antisense strand of DNA X3′5′ .”

We will conduct a new topological study on DNA recombination in which recombination between types x and y occurs, where x is the first gene and y is the plasmid.

Proposition 2.2 Let Rs:X×X→spanX be the recombination operator, defined by

Rs(x,y)=⋃i=1n{ci∗x5′3′+cn−i∗y1,cj∗x3′5′+cn−j∗y2} , Rs(x,y) consists of (offspring) can be induced by x,y and it satisfies the following:

•    {x,y}∈Rs(x,y) .

•    Rs(x,y)≠Rs(y,x) .

•    ∀z∈Rs(x,y)⇒‖Rs(x,z)‖ ≤‖Rs(x,y)‖∀x,y,z∈X .

•    Rs(x,x)=2x

•    Rs(x,y)⊆Span{x,y} .

Proof. Obvious.

In this section, we present the definition of closure recombination space by using a recombination function.

Definition 2.3 Let A⊆X . We take TRs∗(A) represents the closure recombination (“sticky end”) operator, since TRs∗(A)=⋃x,yRs(x,y).

We work with the topological recombination (“sticky ends”) operator. The closure recombination space from the recombination operator Rs is denoted by (X,TRs∗) .

Theorem 2.4 The closure recombination structure (X,TRs∗) arising from recombination operator

satisfies:

•    TRs∗(φ)=φ ,

•   If H is a group of genes, then H⊆TRs∗(H) ,

•   If H⊆K , then TRs∗(H)⊆TRs∗(K) ,

•    TRs∗(H)∪TRs∗(K)=TRs∗(H∪K) and TRs∗(H)∩TRs∗(K)⊇TRs∗(H∩K) ,

•    TRs∗(TRs∗(H))⊇TRs∗(K) .

Proof. Obvious.

A space (X,TRs∗) , is called Rs DNA recombination structure useful for DNA recombination.

2.1 The Upper and The Lower Approximation on DNA Recombination

In the following, we study the connection between rough sets [15] concepts and DNA recombination. Also, we investigate new definitions of the class of elements depend on definitions of recombination sets that result from the definition of recombination function, which identifier as follows, Rs:X×X→spanX . Since Rs(x,y)=⋃i=1n{ci∗x5′3′+cn−i∗y1,cj∗x3′5′+cn−j∗y2} .

Definition 2 .1.1 Set of all recombination products can be done or (offspring can be obtained) caused by x,y, let’s call it Rs(x,y) .

Definition 2.1.2 Let Rs (x,y) be a recombination set. Then the recombination class of x can be defined as [x]Rs={y∈U:y∈Rs(x,y)} and the lower and the upper approximation of a subset X of U are defined as:

R_s(X)={x∈U:[x]Rs⊆X}.

R¯s(X)={x∈U:[x]Rs∩X≠∅}.

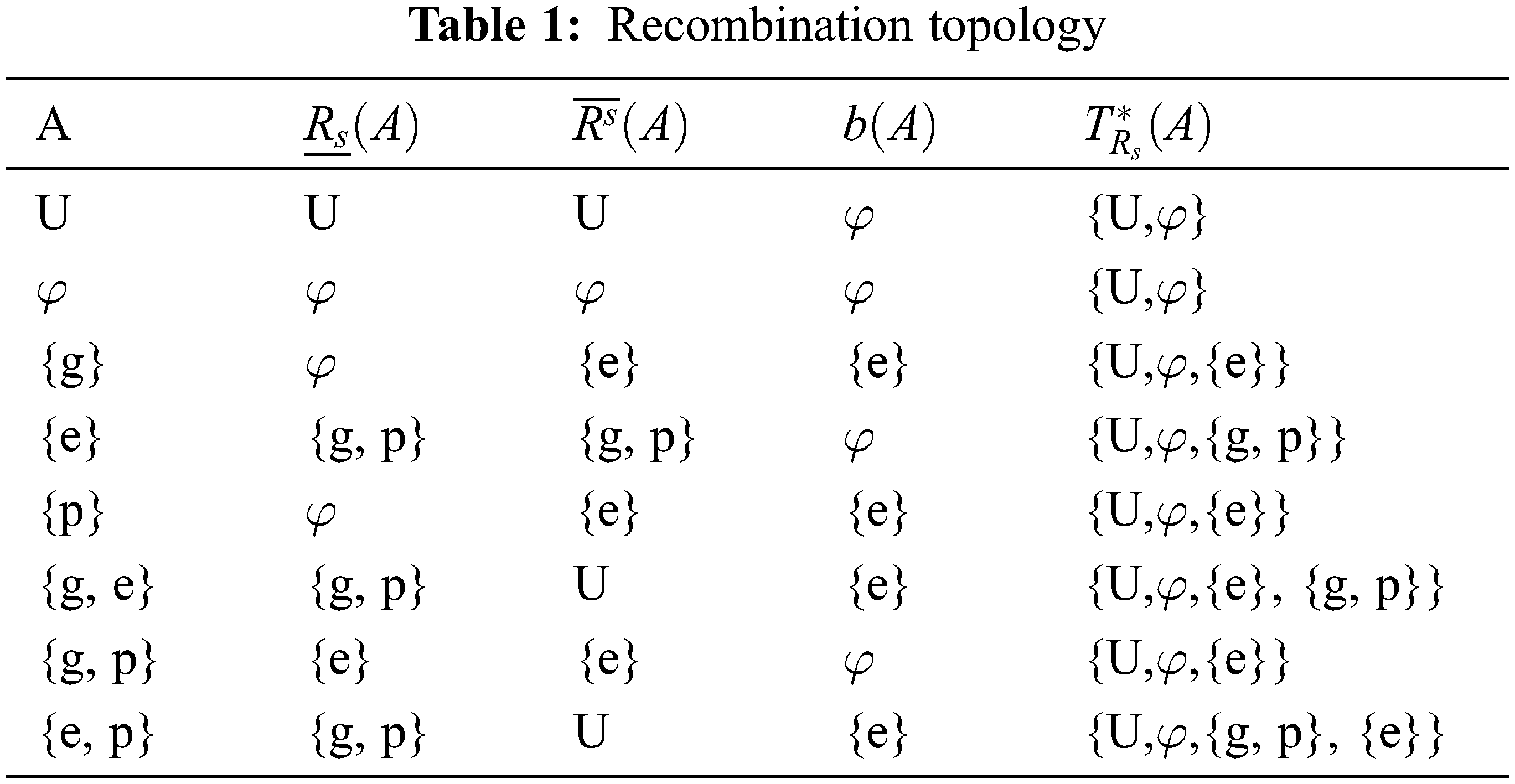
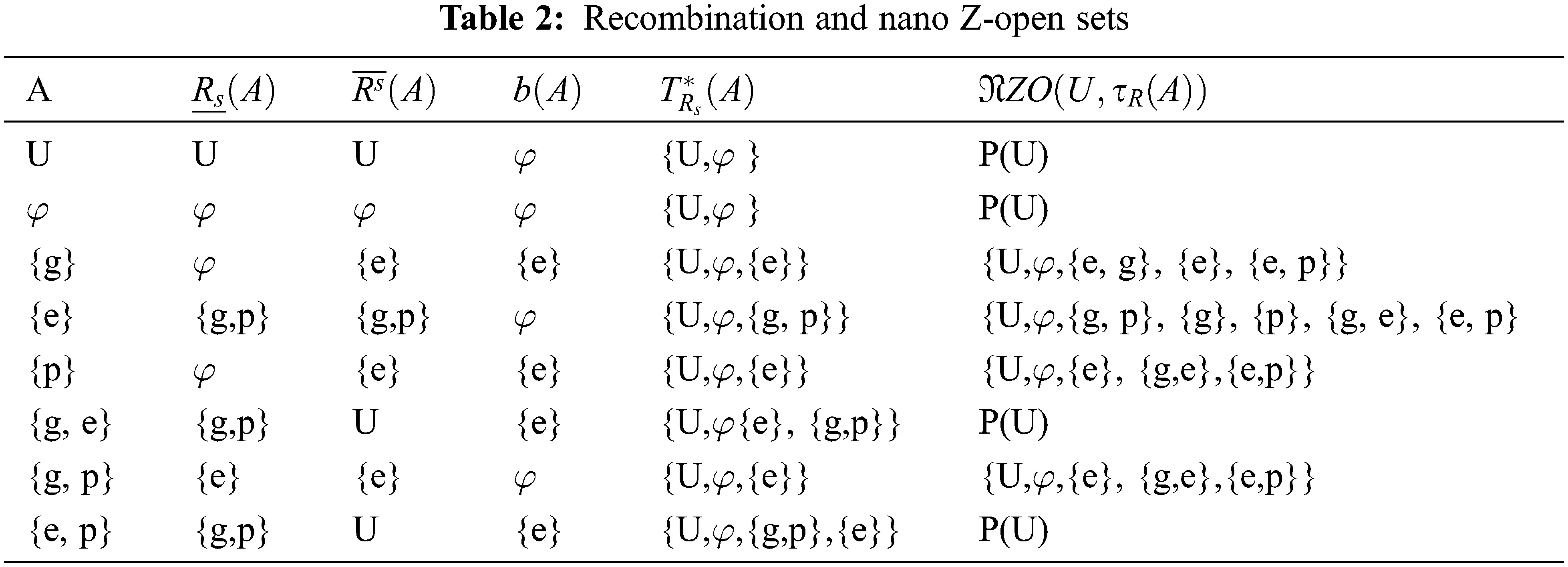
Example 2.1.3 Let the recombination process consists of three key pillars are: genes (g), plasmids(p), enzymes(e) and elements of recombination process (U) i.e. U = {g , e, p}, the recombination class of gene [g]R ={e},[p]R = {e} and [e]R = {g, p} and A any subsets of U (see, Tab. 1)

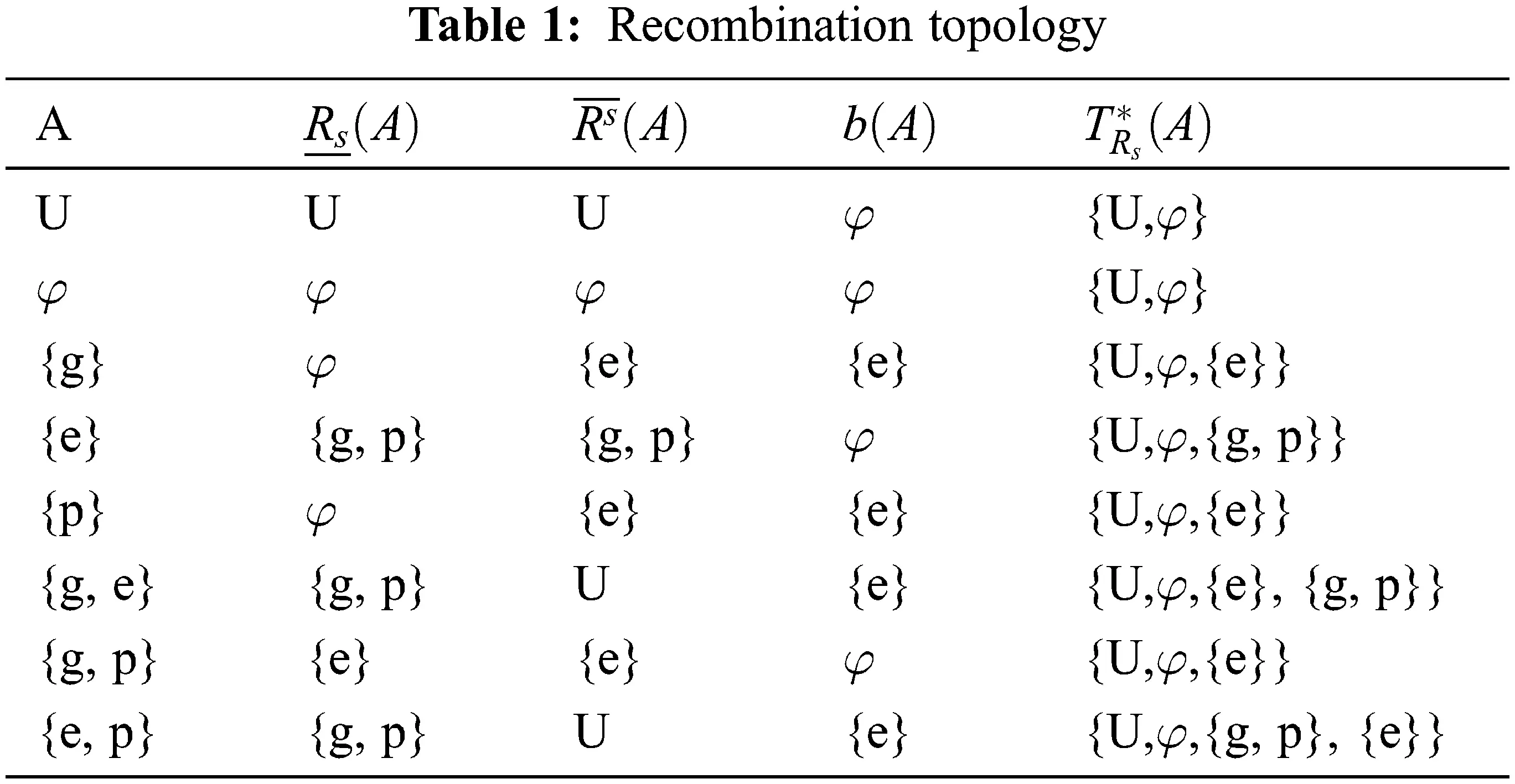
From Tab. 1, the set of all recombination open (closed) sets consists of the indiscrete recombination space when using the general topology, and this result applies to the nano topological structure defined on the set U (enter all items of DNA recombination). But when using the nano topology, more than one topology appears. For example, when using the enzyme, only group B appears, as the effect of the enzyme is practically on the gene and the plasm. When using the gene or the plasma only, the enzyme appears, and this applies as a cofactor. These results are consistent with the biological results.

Proposition 2.1.4 let (U,TRs∗) be an indiscrete recombination space, H⊆U .Then the limit point of H is given by

H′= { ∅if H=∅U−{ p }if H={P}U if H contains more then one element  

Proof. Obviously

These results mean that:

1.    That there is always an end point to the process.

2.    There is an output of the process of recombination, and this is applicable to the biological concept.

Remark 2.1.5 Every subset of an indiscrete recombination space is dense. The sense that it produces a very large number of plasma carrying the gene The aim of the following proposition is to describe any item in the recombination process.

Proposition 2.1.6 Every indiscrete recombination space is a regular space. We note that from Tab. 1, the appearance of more than nano topology structures, but it appears one topological structure.

3  Nano Z-Open Sets

“Throughout this paper (U,τR(X)) is a Nts with respect to X where X⊆U and R is an equivalence relation on U. Then U/R denotes the family of equivalence classes of U by R.' [1,3,15]

Definition 3.1 [1] If H⊆U and (U,τR(X)) is a Nts , then H is a nano Z -open(briefly, N Zo) (resp. nano Z-closed(briefly, N Zc)) set if H⊆Nint(Ncl (H) ∪Ncl(Nintδ (H), (resp. H ⊇Nint(Nclδ (H) ∩Ncl(Nint (H)). The family of all N Zo (resp. N Zc) sets are denoted by N Z O(U,τR(X) (resp. N Z C(U,τR(X)) .

Definition 3.2 If H⊆U and (U,τR(X)) is a Nts , then H is a nano e∗ -open(briefly Ne∗ o) set if H⊆Ncl(Nint(Nclδ (H))). The family of all Ne∗o sets are dented by Ne∗O(U,τR(X)) .

Example 3.3 From Example 2.1.3.

From Tab. 2 the set of all nano Z-open sets to nano topological structure defined on the set U(enter all items of DNA recombination) is the discrete recombination space.

Definition 3.4 [16] If H⊆U and (U,τR(X)) is a Nts , then a nano Z-interior of H is the union of all N Zo sets contained in H (briefly, NZint(H) .

Definition 3.5 [16] Let H⊆U and (U,τR(X)) be a Nts . Then a nano Z-closure of H is the intersection of all N Zc sets containing H (briefly, NZcl(H)) .

Remark 3.6 Every N Z-open set is N b-open (resp. e-open and e∗ -open ).

Lemma 3.7 Let G be a subset of a space U . Then the following statement are satisfied:

(1) N P intδ ( NPcl(G ))= NPcl(G )) ∩Nint(Nclδ (G)),

(2) N P clδ ( NPint(G ))= NPint(G )) ∪Ncl(Nintδ (G)).

Proof. (1) Since, N P intδ ( NPcl(G )) = NPcl(G)∩Nint(Nclδ(NPcl(G))=NPcl(G)∩Nint(Nclδ(G∪Nint(Ncl(G))=NPcl(G)∩Nint(Nclδ(G))

(2) It follows from (1).

Definition 3.8 [17] A subset Zx⊆U is called a nano Z (resp. nano e∗ ) neighbourhood (briefly, N ZNbd (resp. Ne∗Nbd )) of a point x∈U if there exists H∈NZO(U,τR(X)) (resp. x∈H⊆Zx and a point x is called N ZNbd (resp. Ne∗Nbd ) point of the set H. The family of all N ZNbd (resp. Ne∗Nbd ) of a point x⊆U is called N ZNbd (resp. Ne∗Nbd ) system of x (briefly, N ZNbd S(x)) (resp. Ne∗Nbd S (x)).

Theorem 3.9 An arbitrary union of N ZNbd (resp. Ne∗Nbd ) of a point x∈U is again NZNbd (resp. Ne∗Nbd ) of a point x∈U .

Proof. Let {Hi:i∈I} be an arbitrary collection of N ZNbd of x∈U . Since ∀i∈I , Ai is N ZNbd of x, ∃Li∈N ZO (U,τR(X)) such that. x∈Li⊂Hi , but for each i∈I , Hi⊆∪Hi , therefore x∈Hi⊂∪Ai which implies that ∪Hi is again N ZNbd of x. The other cases are similar.

Lemma 3.10 The intersection of N ZNbd (resp. Ne∗Nbd ) of a point x∈U is not a N ZNbd (resp.) of the p Ne∗Nbd oint x∈U in general.

Example 3.11 From Example 3.3. and Tab. 2, let A={e} . Then the Nts τR(X) = {U,φ,{g,p}} . In the Nts , (U,τR(X)) , the sets {g,e} and {e,p} are N ZNbd (e) but {g,e} ∩{e,p}={e} is not a N ZNbd (e).

Theorem 3.12 If (U,τR(Y)) is a Nts , then

1.     EveryNδNbd(y)isNNbd(y),∀y∈U,

2.     EveryNδNbd(y)isNZNbd(y),∀y∈U,

3.     EveryNδSNbd(y)isNZNbd(y),∀y∈U,

4.     EveryNPSNbd(y)isNZNbd(y),∀y∈U,

5.     EveryNZNbd(y)isNbNbd(y),∀y∈U,

6.     EveryNZNbd(y)isNeNbd(y),∀y∈U,

7.     EveryNZNbd(y)isNe∗Nbd(y),∀y∈U,

Proof. (3) Let A be an arbitrary NδSNbd of y∈U. T hen∃H∈NδSO(U,τR(X)) such that y∈H⊆A . Since every NδSo is NZo , then H NZo , therefore y∈H⊆A . Then A is NZNbd of y. The other cases are similar.

Definition 3.13 Let H⊆U and (U,τR(X)) be a nano topological structure. Then H is called nano Z (briefly, NZ )-dense subset if NZ cl(H) = U.

Definition 3.14 A nano topological structure is said to be a nano Z-extremally disconnected space (briefly, NZEDS ) if the nano Z-closure of NZo set is NZo set for each NZo subset of U.

Definition 3.15 A nano topological space is called nano Z-submaximal (briefly, NZE ????) if each NZ -dense subset of U is NZo set.

Remark 3.16 A nano topological space is NZEM and NZEDS , then every NZNbd is NδSNbd and NPNbd of x∈U .

Theorem 3.17 For any point x∈U , NZNbd S(x) satisfies

(1) NZNbd S(x) ≠φ .

(2) if H⊆U and H∈NZNbd S(x), then x∈H .

(3) if H⊆U and H∈NZNbd S(x), H⊆C then C∈NZNbd S(x).

(4) if H⊆U and H∈NZNbd S(x) then ∃B∈NZNbd S(x)S(x) such that B⊆H , H∈NZNbd S(y), ∀y∈B .

Proof. (1) Since, ∀x∈U and U is a NZo set, Then x∈U implies that U is NZNbd of x. Then U∈NZNbd S(x) ⇒NZNbd S(x) ≠φ .

(2) Let H∈NZNbd S(x). Then H is a NZNbd of x implies that ∃B∈NZO(U,τR(X)) ⇒x∈B⊆H . Thus x∈H .

(3) Let H∈NZNbd S(x). Then that ∃B∈NZO(U,τR(X)) ⇒x∈B⊆H and H⊆C ⇒x∈B⊆H⊆C . Therefore C∈NZNbd S(x).

(4) From (3) it is obvious.

Theorem 3.18 Let NZ O (U,τR(X)) be closed under finite intersection, H be NZ c subset of U and x∈U−H . Then there exists a NZNbd A of x such that H∩A=φ .

Proof. Let H be a NZ c set. Then U−H is a NZoNZo set. Therefore U−H is NZNbd of each of its points. If x∈U−H , implies that A∈NZo , since x∈A⊆U−H , then H∩A=φ .

Definition 3.19 [2] A point x∈U is called a nano Z- limit point of H , if for each K∈NZ O (U,τR(X)) containing x satisfies K ∩(H−x)≠∅ .

Definition 3.20 The set of all nano Z-limit points of H is a nano Z-derived set (briefly, NDZ(H) ).

Theorem 3.21 If H and K are subsets of a space U , then the following are hold.

(1) NDZ(ϕ)=ϕ ,

(2) if x∈NDZ(H) , therefore x∈NDZ(H−x) .

Proof. (1) Suppose that x∈U and Gx∈NZ O (U,τR(X)) . Therefore (G−x)∩φ=φ⇒x∉NDZ(ϕ) , then ∀x∈U , x∉NDZ(ϕ) . Thus NDZ(ϕ)=ϕ.

(2) If x∈NDZ(H) ⇒G∩(H−x)≠φ and ∀Gx∈NZO(U,τR(X)) and contains at least one point other than x of H−x . Thus x∈NDZ(H−x) .

Theorem 3.22 If H⊆U and (U,τR(X)) is a N ts, then:

1.    If NZ ZC (U,τR(X)) is closed under arbitrary union, then H∪NDZ(H) is NZ c set,

2.     N Zcl(H) = H∪NDZ(H) .

Proof. To show that H∪NDZ(H) is a NZ c set, we want to prove U−(H∪NDZ(H)) is a NZ o set,we have two cases:

Case 1: Let U−(H∪NDZ(H)) . Then the result is clear.

Case 2: Let U−(H∪NDZ(H))≠ϕ . Then x∈U−(H∪NDZ(H)) implies that x∉(H∪NDZ(H)) and hence x∉H , x∉NDZ(H)⇒Gx∈NZO(U,τR(X)) . Since G∩(H−x)=φ such that x∉H⇒G∩H=φ implies x∈G⊆U−H . Thus G∩NDZ(H) = φ implies x∈G⊆U−NDZ(H) . Then x∈G⊆(U−H)∩(U−NDZ(H)) = U−(H∪NDZ(H)) implies that x∈G⊆U−(H∪NDZ(H)) . Therefore U−(H∪NDZ(H)) ) is a NZbd of each of its points. U−(H∪NDZ(H)) is a NZ o set and then (H∪NDZ(H)) is NZ c.

(2) By (1), if H∪NDZ(H) is a NZ c set, then H∪NDZ(H) is a NZ c set containing H. Therefore NZ cl(H) ⊆H∪NDZ(H) and H⊆NZ cl(H), implies that NDZ(H)⊆NDZ(NZcl(H)⊆NZ cl(H) because NZcl(H) is NZc . Hence H∪NDZ(H)⊆NZ cl(H). Thus NZ cl(H)= H∪NDZ(H)

Theorem 3.23 If H⊆U and (U,τR(X)) is a N ts, then the following holds:

1.     NZ cl(H) is the smallest NZc super set of H,

2.    H is a NZc set iff NZcl(H)=H .

Proof. (1) Let {Fi:i∈I} , Fi⊆U , Fi be a NZc set and H⊆Fi ∀i∈I . Then NZ cl(H) =∩{Fi:i∈I} , hence ∩{Fi:i∈I} is a NZc set. Therefore NZ cl(H) is a NZc set. Also, H⊆Fi , ∀i∈I⇒H⊆∩{Fi:i∈I} = NZ cl(H). Then NZ cl(H) is a NZc set containing H such that NZ cl(H) = ∩{Fi:i∈I} , therefore NZ cl(H) ⊆Fi , ∀i∈I . Consequently, NZ cl(H) is the smallest NZc superset of H.

(2) Let H be a NZc set. Then NZc is the superset of H and hence NZ cl(H)= H. Thus H is a NZc set. Then H is a NZc set iff NZ cl(H)= H.

Proposition 3.24 If H and K are two subsets of a space U , then the following properties hold:

(1) If NZc(U,τR(X)) is closed under finite union, then NZ cl (H∪K)= NZcl (H) ∪NZcl( K) for every H,K∈NZc(U,τR(X)) ,

(2) If Nec(U,τR(X)) is closed under finite union, then Necl(H∪K)=Necl(H)∪Necl(K) for every H,K∈Nec(U,τR(X)) .

Proof. (1) Let H and K be N Zc sets in U. By hypothesis, H∪K is NZc . Thus NZcl(H∪K)=H∪K=NZcl(H)∪NZcl(K)

(2) Likewise (1).

Theorem 3.25 If H and K are two subsets of a space U , Then the following are holds:

1.     NZin(H) is the largest NZo set contained in H.

2.    H is a NZo set iff H = NZin(H) .

3.     NZint(φ)=φ and NZin(U)=U .

4.     NZint ( NZint(H)) ) = NZint(H) .

Proof. (1) Let B∈NZo(U,τR(X)) , B⊆H . If x∈B , therefore x∈B⊆H , B∈NZo(U,τR(X)) , Then H is NZbd of x and hence x∈B⇒x∈NZint(H) . Therefore every NZo subset of H is contained in NZint(H) . Hence NZint(H) is the largest NZo set contained in H.

(2) Let H∈NZO(U,τR(X)) , H⊆H and H be the largest NZo subset of H. By (1), NZint(H) is the largest NZo subset of H. Hence H = NZint(H) .

(3) It is clear.

(4) By (2), H is a NZo set iff H= NZint(H) and by (1), NZint(H) is the largest NZo set contained in H. Then NZint ( NZint(H)) ) = NZint(H) .

Theorem 3.26 If H and K are two subsets of a space U , then NZint(H)=H−NDZ(U−H).

Proof. Let x∈(H−NDZ(U−H))⇒x∈Handx∉NDZ(U−H). Then ∃Gx∈NZO(U,τR(X)) such that Gx∩(U−H)=∅⇒Gx⊆H. Hence x∈G⊆H⇒x∈NZin(H) . Then H−NDZ(U−H)⊆NZin(H) .

If x∈NZin(H)⇒x∈H and NZin(H) , x∈NZin(H)∩(U−H) . Therefore x∉NDZ(U−H) ). Then x∈(H−NDZ(U−H)) . Hence NZin(H)⊆H−NDZ(U−H) . Then NZin(H) = H−NDZ(U−H).

Theorem 3.27 For H,T⊆U , then NZin(H−T)⊆NZint(H)−NZint(T) .

Proof. Let NZin(H−T)=NZin(H∩(U−T))⊆NZint(H)∩NZint(U−T)⊆NZint(H)∩(U−NZint(T))=NZint(H)−NZint(T).

4  Nano Z-Exterior, Eorder and Frontier Sets

Definition 4.1 For H⊆U , then a nano Z exterior (briefly, NZEr \x9D\x96\x97) of H is defined as N Zint\x9D\x96\x97(H) = N Zint (U−H) .

Definition 4.2 [17] For H⊆U , then a nano Z border (briefly, NZBr \x9D) of H is defined as NZBr \x9D\x96\x97 (H) = H - NZint(H) .

Theorem 4.3 If H and K are two subsets of a space U , then the following are satisfied:

1.     NE ???? δS(H)⊆NZE ???? (H) ,

2.     NE ???? P(H)⊆NZE ???? (H),

3.     NZE ???? (H)=U−NZcl H),

4.     NZE ???? (H∪K)=NZE ???? (H)∩NZE ???? (K) ,

5.     NZint(H),NZE ???? (H)aremutuallydisjointandU=NZE ???? (H)∪NZint(H) ,

6.     H∩NZE ???? (H)=∅ ,

7.     NZE ???? (H)⊆U−H

8.     NZE ???? (H)⊆NZint(Hc) ,

Proof. (1) For K⊆U , NSintδ(K)⊆NZint(K) . Put K=U−H , then NSintδ(U−H)⊆NZint(U−H) . This implies NE ???? δS(H)⊆NZE ???? (H) .

(2) For K⊆U , NPint(K)⊆NZint(K) Put K=U−H , then NPint(U−H)⊆NZint(U−H) . This implies NE ???? δS(H)⊆NZE ???? (H) .

(3) By the definition of NZEr(H)=NZint(U−H)=U−NZcl(H).

(4) Consider NZEr(H∪K)=NZint(U−(H∪K))=NZint((U−H)∩(U−K))⊇NZint(U−H)∩NZint(U−K)=NZE ???? (H)∩NZE ???? (K) . That is, NZE ???? (H∪K)⊇NZE ???? (H)∩NZE ???? (K).(1)