DOI:10.32604/iasc.2022.025655

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.025655 |  |
| Article |
Performance Analysis of PTS PAPR Reduction Method for NOMA Waveform
1Department of Computer Science & Engineering, JECRC University, Jaipur, 303905, India
2Department of Electrical and Computer Engineering, Kennesaw State University, GA, USA
3Department of Computer Engineering, College of Computers and Information Technology, Taif University, 11099, Saudi Arabia
4Department of Computer Science, College of Computers and Information Technology, Taif University, 11099, Saudi Arabia
5Department of Electronics and Communication Engineering, JECRC University, Jaipur, 303905, India
*Corresponding Author: Arun Kumar. Email: arun.kumar1986@live.com
Received: 01 December 2021; Accepted: 13 January 2022
Abstract: Cellular systems utilize single and multicarrier waveforms for high-speed data transmission. The Fifth-Generation (5G) system proposes several techniques based on multicarrier waveforms. However, the Peak to Average Power Ratio (PAPR) is one of the significant concerns in advanced waveforms as it degrades the framework's efficiency. Non Orthogonal Multiple Access (NOMA) can provide massive connectivity, which is the crucial requirement of the Internet of Things (IoT). The 3rd generation tested NOMA applications in downlink and uplink transmission. However, NOMA uplink transmission in the power domain has performance degradation and is not considered a possible technique in 3rd generation power projects (3GPP). Presently, NOMA is not just a concept but has been introduced as a standard method in various transmission schemes. NOMA suffers from a high peak to average power ratio (PAPR), which forces the power amplifier (PA) to shift into a nonlinear region. The high value of PAPR leads the power amplifier of the multicarrier technique into a nonlinear region. As the performance of the power amplifier degrades, the overall system performance goes down. In this work, we suggest different methods to overcome the issue of PAPR in multicarrier techniques such as Selective Mapping (SLM) and Partial Transmit Sequence (PTS). The simulation results reveal that the performance of the proposed PTS is better than that of the conventional SLM and PTS.
Keywords: PTS; 5G; PAPR; SLM
The deployment of 5G is ongoing worldwide, and the selection of advanced waveforms is considered one of the crucial tasks for the regularisation of 5G and beyond. In the present scenario, Orthogonal Frequency Division Multiplexing (OFDM) is the commercially available waveform that has been utilized in several applications [1]. However, OFDM is not a popular choice for the advanced radio framework due to several concerns, such as loss of spectrum and PAPR. In [2], it is seen that the utilization of the Cyclic Prefix (CP) results in a loss of 11% spectrum. In [3], it is experimentally proven that PAPR severely degrades the performance of the power amplifier of the radio framework. However, PAPR can be reduced by applying some of the algorithms discussed in [4]. However, it cannot be nullified. In recent years, there have been numerous waveforms investigated and recommended for advanced radio systems, including NOMA [5], Filter Bank Multi Carrier (FBMC) [6], and Universal Filter Bank Multi Carrier (UFMC) [7]. NOMA has gained so much popularity and attracted the attention of researchers and academicians. NOMA's characteristics, such as fast data rate, low latency, support for massive device integration, and compatibility with other advanced techniques, make it a viable candidate for a 5G radio network. The NOMA waveforms are available in two different forms, namely code domain and power domain (P-NOMA) waveforms. NOMA utilizes time and frequency resources to modulate the signal on a common channel for multiple users. It utilizes the gains of several users to achieve an excellent throughput. The structure of P-NOMA mainly consists of Super Coding (SC), Successive Interference Cancelation (SIC), and Fourier Transforms. SC guarantees the failure allocation of resources to all users, and SIC detects the signals of a particular user. The ability to support users with poor channel gain lowers the probability of outrage. However, despite several advantages of NOMA, PAPR is considered a significant problem in NOMA [8]. PAPR is a common problem in all multicarrier techniques. However, due to the different structural arrangements, the PAPR algorithms designed for OFDM cannot be directly applied to the advanced waveforms [9]. In [10], the authors introduced a three-stage PAPR algorithm to decrease the PAPR of FBMC. The study reveals that the system's performance can be efficiently scaled by scaling the maximum amplitudes of the FBMC signals. The peak power problem in the FBMC framework is overcome by applying a clipping algorithm [11]. The experimental study reveals that the proposed algorithm outperforms the conventional clipping technique. The PAPR of the FBMC waveform is decreased by applying the Companding Transformation method. The study's outcome reveals that the Mu-Law is one of the most efficient algorithms [12]. In [13], conventional PAPR algorithms are applied to evaluate the Bit Error Rate (BER) and PAPR of the FBMC framework. It was noted that the conventional algorithms could not be directly applied to the advanced waveforms. It degrades the performance and increases the complexity of the framework. In [14], the authors presented a comprehensive study on NOMA performance and its key parameters. The experiment outcomes demonstrate that the NOMA is better than the existing waveforms. On the other hand, the complex receiver is concerned with implementing the NOMA receiver. A comprehensive survey of the NOMA waveform was presented in [15]. The article outlines the problems and the role of NOMA in the advanced wireless framework. It was concluded that the deployment of NOMA will enhance the performance and can satisfy the demands of different applications. In [16], the PAPR of NOMA is reduced by applying a hybrid algorithm. The SLM and PTS algorithms were combined with the wavelet transform. The experimental outcomes indicated that the presented algorithm outperforms the conventional PTS and SLM. The Dummy Sequence Insertion (DSI) algorithm was applied to the NOMA-OFDM structure to overcome the complexity and PAPR problem [17]. The work results show that the proposed hybrid method has lower complexity and a higher PAPR gain than the existing SLM. The authors proposed a hybrid method integrating SLM and circular transformation methods for 5G waveforms. It is noted that the proposed algorithm enhanced the gain of the 5G radio [18]. In [19], the authors introduced novel peak shrinking and interpolation methods to lower the effect of high peak signals in NOMA. It is implemented by scaling the maximum amplitude of the signal, reinserting and transmitting the scaled signal. It is noted that the proposed method achieved efficient performance and high throughput. In [20], a PAPR precoding algorithm is suggested to mitigate the effect of PAPR in NOMA. The proposed method exploits the characteristics of PAPR in an advanced waveform. The results reveal that the presented method outperforms the non-precoding algorithms. The key objectives of the projected article are as follows:
• We propose advanced PTS and SLM algorithms for the NOMA waveform and evaluate the PAPR and BER estimation framework.
• The complexity of the PAPR techniques is analyzed, and it is seen that the projected algorithm has low computational intricacy as compared with conventional SLM and PTS.
• The power gain performance of the PAPR algorithms is computed, and it is seen that the projected algorithm achieved a power saving of 66.9%.
The block diagram of the NOMA waveform is represented in Fig. 1. The resource blocks are allocated to the users by using SC and SIC. SC is used at the transmitter to form composite signals for all the users at the same time. At the same time, SIC is performed at the receiver to decode the signals for their respective users.
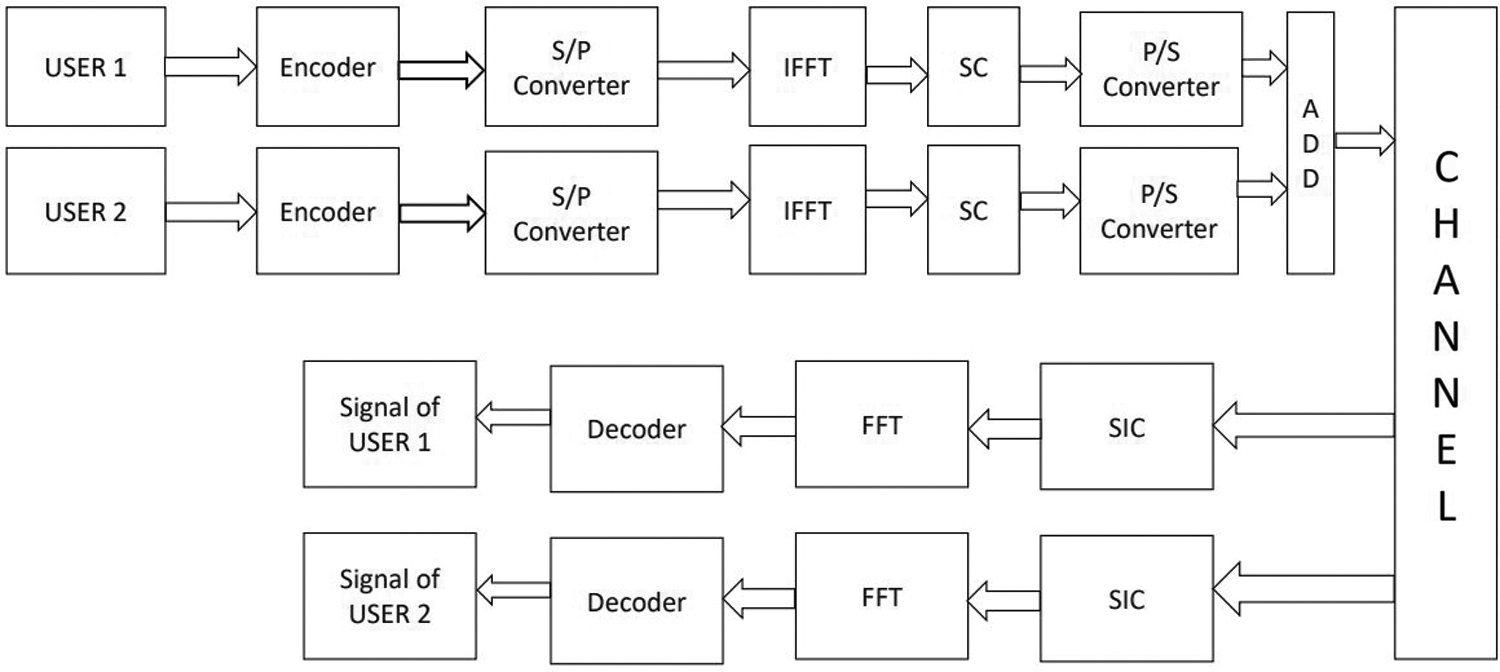
Figure 1: NOMA
The signal from user one is encoded using an encoder. The encoded signal is converted in parallel before sending it to the Inverse Fast Fourier Transform (IFFT) block. Signals will be converted from frequency domain to time domain by the IFFT block. In NOMA, Superposition Coding (SC) is performed at the transmitter to form a composite signal simultaneously transmitted to all the users. Then, a successful interference cancellation mechanism is applied at the receiver to decode the signals for their respective users properly. After SIC, the Fast Fourier Transform (FFT) of the signals is taken to convert them from the time domain to the frequency domain. Finally, the decoder will use its decoding algorithm to retrieve the original signal [21].
Selective mapping (SLM) is an encouraging PAPR reduction technique. The basic principle of SLM is to have Z alternative transmit sequences from a similar data source, and the signal with the lowest PAPR will be transmitted [22]. Fig. 2 shows the basic block diagram of selective mapping. Here the PAPR is analyzed by the sequences of transmitting data vectors. Consider the L original signals, which are given as:
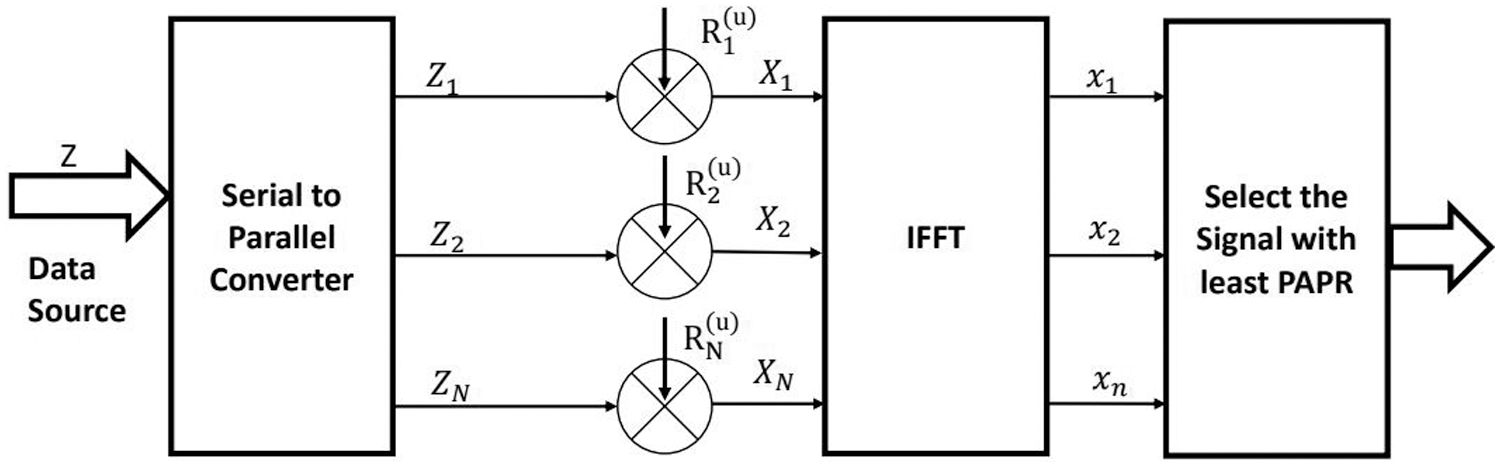
Figure 2: SLM
These signals are multiplied with independent phase sequences such as
where u = 0, 1, 2 ….U–1.
Note that the length of input bits and phase sequences is the same, i.e., (L = U). Then, the IFFT of the sequences is taken to convert them from the frequency domain to the time domain. The signal with the least PAPR is identified by the last block and transmitted in the last step.
2.2 Partial Transmit Sequence (PTS)
PTS is one of the most promising techniques to reduce the value of PAPR given in Fig. 3. However, the computational complexity of PTS is higher than the previous techniques like SLM, etc. In this technique, the first input data block is divided into sub-blocks with no common element. Then each sub-block is sent to the IFFT to transform signals from the frequency to the time domain. After the conversion multiplication of each sub-block with a phase factor is performed to generate the candidate signal, we combined all the received signals [23].
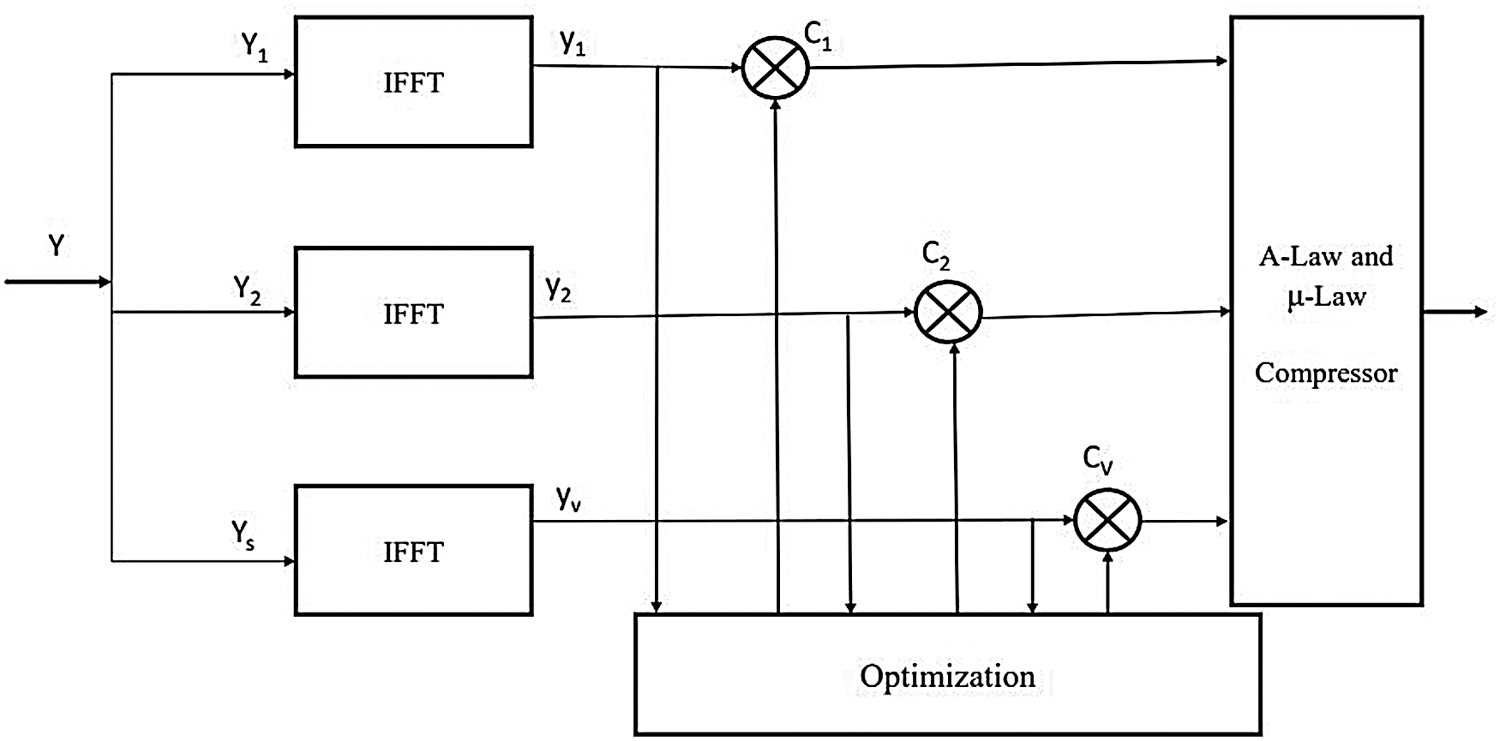
Figure 3: PTS
Firstly the input data is converted to a sub-block. Let us consider that the input data is represented by:
After conversion, the sub-block of the input data is given by
R is the no of sub-blocks, r is given as [1, 2, 3, … R].
In order to convert the input data into sub-blocks, many techniques are used, such as interleaving, adjacent and pseudo-random numbers. In phase factors, the generally used vectors are ± 1 or sometimes (± 1, ± j). Phase factor vector is represented as [24]:
From the given Eq. (5) can be obtained by:
cv is the phase rotation vector; X is a number of allowed phase factors. The time-domain input y can be obtained after the IFFT operation, and it is represented by
The final signal is expressed as:
In this work, the PAPR of an advanced waveform is studied and evaluated using Matlab-2014. The PAPR and BER parameters of NOMA are plotted, and the results are analyzed. The parameters utilized in the simulation of the projected work are given in Tab. 1. The complexity of the system is indicated in Tab. 2. It is concluded that the proposed algorithms require fewer additions, multiplications, and Fourier transformations than other algorithms.
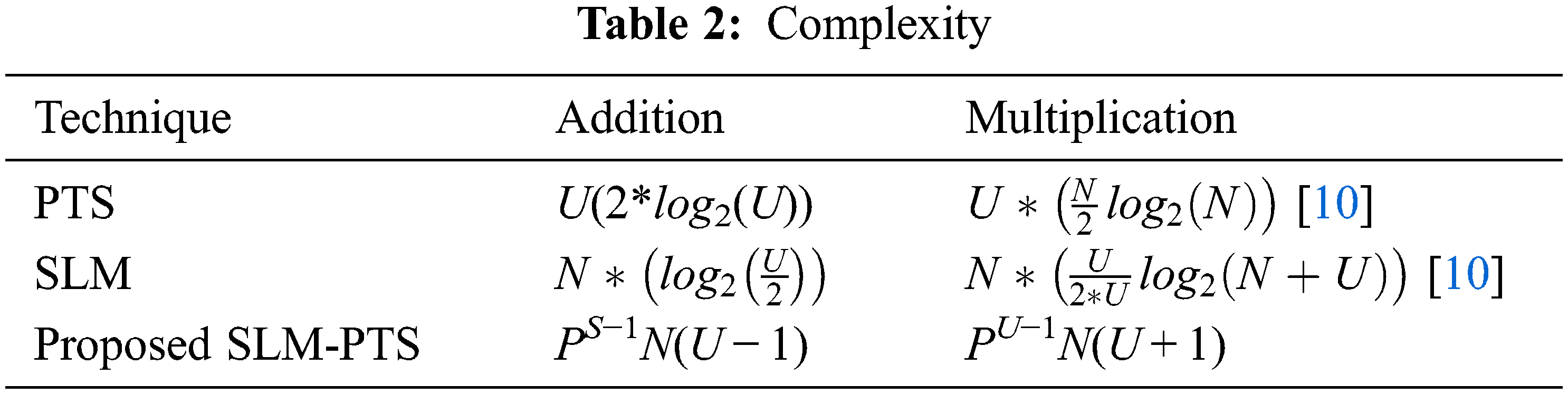
The PAPR performance of the PTS algorithm in NOMA is given in Fig. 4. The peak power can be efficiently reduced by varying the values of sub-carriers (u) and phase factor (w). By increasing the values of u and w, the desired performance can be obtained. The PAPR of the NOMA signal is 13 dB at the Complementary Cumulative Distribution Function (CCDF) of 10−3. The conventional PTS reduces the PAPR to 10.1 dB, achieving a gain of 2.9 dB. However, the optimal performance is obtained at PTS (u = 16 and w = 32). Therefore, it is concluded that the projected PTS achieved a gain of 8.8 and 5.9 dB compared with the original NOMA signal and conventional PTS.
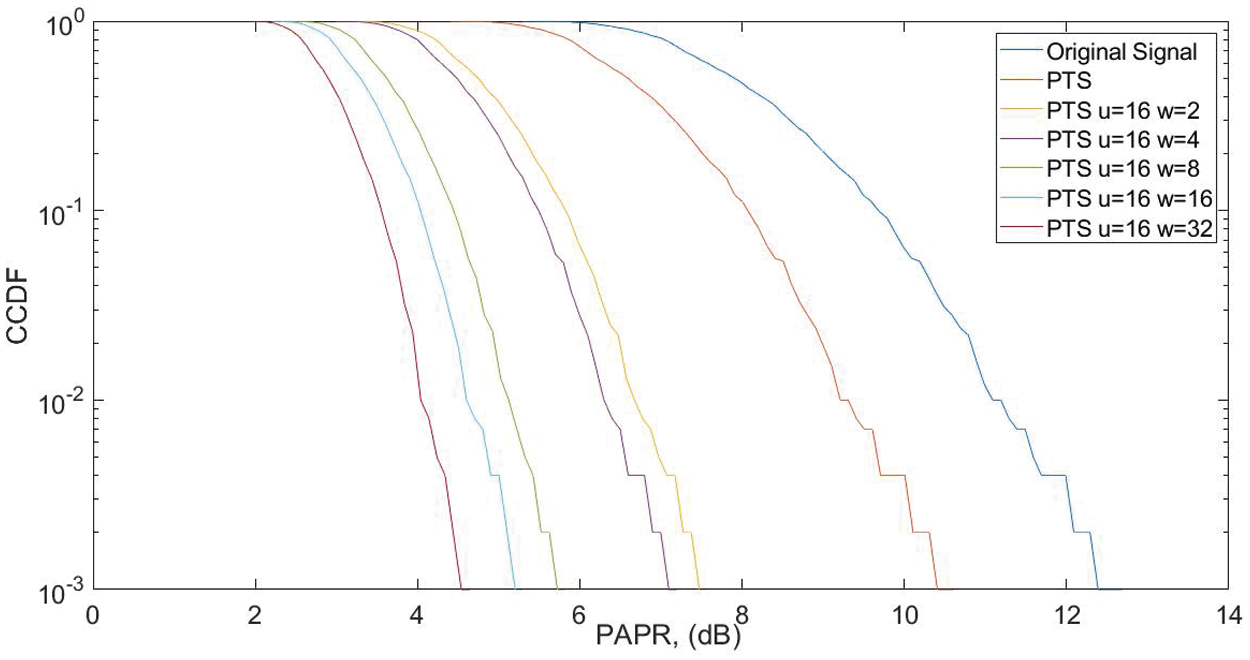
Figure 4: PAPR
The BER performance of the NOMA signal is given in Fig. 5. It analyzes the throughput of the NOMA. It is seen that the proposed PTS algorithm efficiently enhances the throughput of the system. The original BER (10−3) is obtained with a Signal-to-Noise Ratio (SNR) of 13 dB, which is further reduced to 10, 6.2, 5.8, 4.2, 3.8, and 2.1 dB for different combinations of the PTS method.
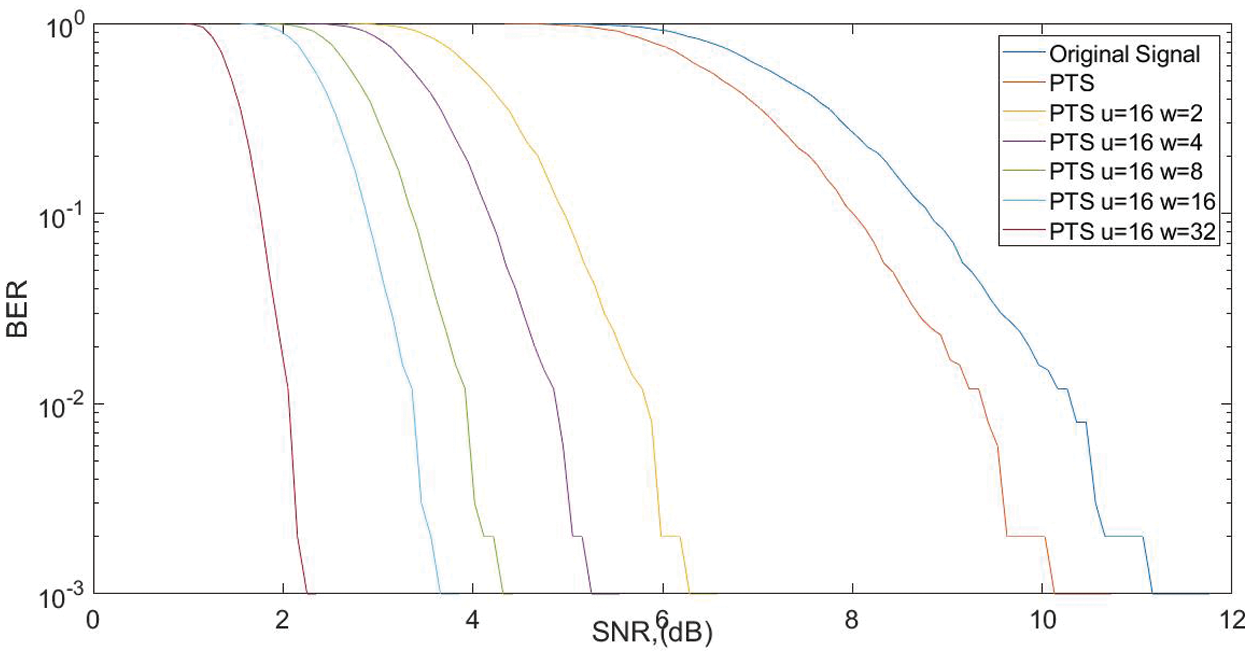
Figure 5: BER analysis
The PAPR performance of the SLM and PTS is compared in Fig. 6. The PAPR of the NOMA waveform at 10−3 CCDF for conventional SLM and PTS is 7.8 and 7.6 dB. The proposed PTS reduces the PAPR to 4 dB. The procedure achieves a gain of 3.8 and 3.6 dB compared with the existing algorithms.
Figure 6: PAPR comparison
By reducing PAPR levels, power savings can be achieved in wireless communication. It is an essential point as in the uplink scenario, the inbuilt antenna/transmitter uses the device's battery, so power saving becomes more important in that case. The gain of the NOMA system is expressed by investigating the PAPR of various signals indicated in Tab. 3. The gain of the systems is defined as:
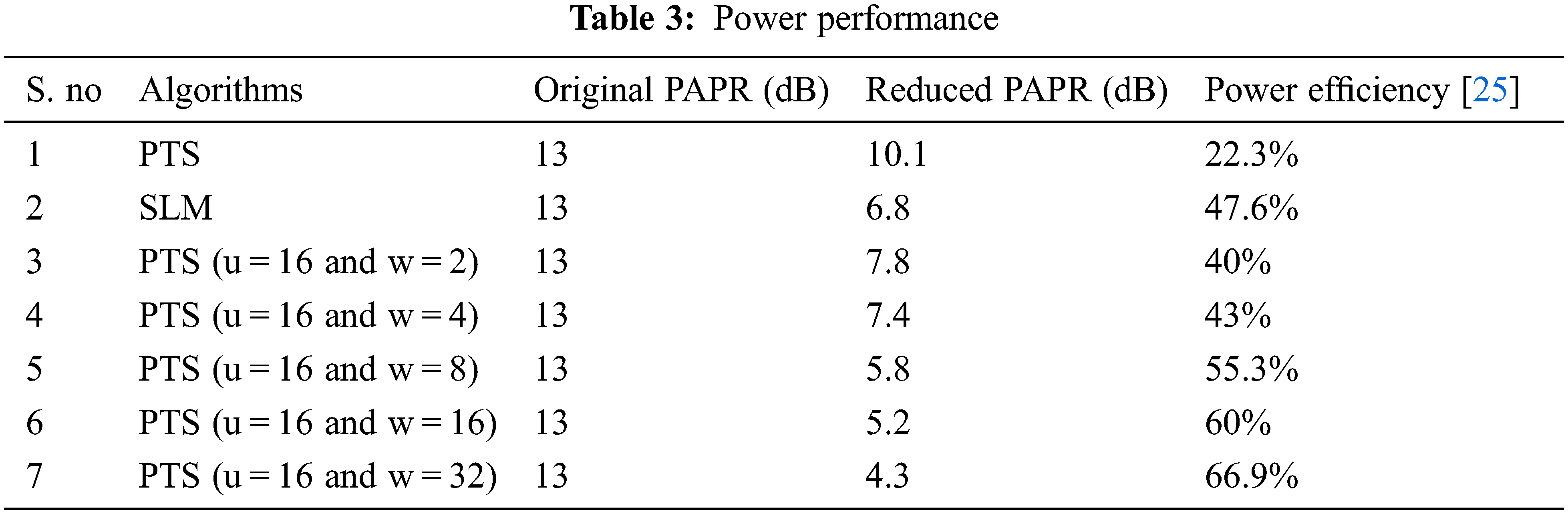
Over the last three decades, many multicarrier techniques have been proposed and analyzed. Significant efforts have been dedicated to introducing new modes of multiple access techniques to simultaneously share the resources with multiple users. The latest technology is known as NOMA, and it has two different dimensions, such as power-domain and code-domain NOMA. In the power domain of NOMA, the multiplexing of the resource block is done based on the power levels of the users. At the same time, the code is used to provide the resource block to a particular user in the code domain NOMA. PAPR is the most significant drawback of multicarrier techniques, such as OFDM, UFBMC, and NOMA. PAPR is hugely degrading the system performance of all the multicarrier techniques. In this paper, SLM and PTS techniques are proposed to eliminate the PAPR problem. It is demonstrated in the experimental results that the proposed scheme is significantly better than the other techniques used in NOMA. The simulation results indicate that the projected algorithm achieved a significant gain in BER and PAPR as compared with the existing SLM and PTS.
Acknowledgement: We would like to give special thanks to Taif University Research supporting Project Number (TURSP-2020/214), Taif University, Taif, Saudi Arabia.
Funding Statement: This work was supported by Taif University Researchers Supporting Projects (TURSP). Under Number (TURSP-2020/214), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Kumar, “PAPR reduction of fbmc using hybrid and k-hybrid techniques,” Radio Electronics Communication System, vol. 62, pp. 501–509, 2019. [Google Scholar]
2. A. Kumar and M. Gupta, “A review on activities of fifth-generation mobile communication system,” Alexandria Engineering Journal, vol. 57, no. 2, pp. 1125–1135, 2018. [Google Scholar]
3. A. Kumar and H. Rathore, “Modified DSLM technique for paper reduction in fbmc system,” Radio Electronics Communication System, vol. 62, pp. 416–421, 2019. [Google Scholar]
4. F. Sandoval, G. Poitau and F. Gagnon, “Hybrid peak-to-average power ratio reduction techniques: Review and performance comparison,” in IEEE Access, vol. 5, pp. 27145–27161, 2017. [Google Scholar]
5. M. M. Şahin and H. Arslan, “Application-based coexistence of different waveforms on non-orthogonal multiple access,” in IEEE Open Journal of the Communications Society, vol. 2, pp. 67–79, 2021. [Google Scholar]
6. R. Zakaria and D. Le Tuyet, “Theoretical analysis of the power spectral density for fft-fbmc signals,” in IEEE Communications Letters, vol. 20, no. 9, pp. 1748–1751, 2016. [Google Scholar]
7. T. Padmavathi, P. Udayasree, C. Kusumakumari and R. Madhu, “Performance of universal filter multicarrier in the presence of carrier frequency offset,” in 2017 Int. Conf. on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai INDIA, pp. 329–333, 2017. [Google Scholar]
8. A. Kumar, M. A. Albreem, M. Gupta, M. H. Alsharif and S. Kim, “Future 5g network-based smart hospitals: Hybrid detection technique for latency improvement,” in IEEE Access, vol. 8, pp. 153240–153249, 2020. [Google Scholar]
9. S. Prasad and R. Jayabalan, “PAPR reduction in OFDM systems using modified slm with different phase sequences,” Wireless Personal Communication, vol. 110, pp. 913–929, 2020. [Google Scholar]
10. H. F. Abdalla, E. S. Hassan, M. I. Dessouky and A. S. Elsafrawey, “Three-layer paper-reduction technique for fbmc based vlc systems,” in IEEE Access, vol. 9, pp. 102908–102916, 2021. [Google Scholar]
11. Z. Kollar and P. Horvath, “PAPR reduction of fbmc by clipping and its iterative compensation,” Journal of Computer Networks and Communications, vol. 2012, pp. 1–11, 2012. https://doi.org/10.1155/2012/382736. [Google Scholar]
12. I. A. Shaheen, A. Zekry, F. Newagy and R. Ibrahim, “Performance evaluation of paper reduction in fbmc system using nonlinear companding transform,” ICT Express, vol. 5, no. 1, pp. 41–46, 2019. [Google Scholar]
13. A. Kumar and H. Rathore, “Reduction of paper in fbmc system using different reduction technique,” Journal of Optical Communications, vol. 42, no. 2, pp. 1–7, 2018. https://doi.org/10.1515/joc-2018-0071. [Google Scholar]
14. M. Hussain and H. R. Sheed, “Nonorthogonal multiple access for next-generation mobile networks: A technical aspect for research direction,” Hindawi Wireless Communications and Mobile Computing, vol. 2020, pp. 1–17, 2020. https://doi.org/10.1155/2020/8845371. [Google Scholar]
15. A. Akbar, S. Jangsher and F. A. Bhatti, “Noma and 5g emerging technologies: A survey on issues and solution techniques,” Computer Networks, vol. 190, no. 2021, pp. 1–40, 2021. https://doi.org/10.1016/j.comnet.2021.107950. [Google Scholar]
16. M. K. Sharma and A. Kumar, “PAPR reduction in NOMA by using hybrid algorithms,” Computers Materials & Continua, vol. 69, no. 1, pp. 1391–1406, 2021. [Google Scholar]
17. R. Sayyaria, J. Pourrostam and H. Ahmadib, “Efficient paper-reduction scheme for ofdm-noma systems based on dsi & precoding methods,” Physical Communication, vol. 47, no. 2021, pp. 1–11, 2021. https://doi.org/10.1016/j.phycom.2021.101372. [Google Scholar]
18. A. Kumar, “A novel hybrid paper-reduction technique for noma and fbmc system and its impact in power amplifiers,” Iete Journal of Research, 2019. https://doi.org/10.1080/03772063.2019.1682692. [Google Scholar]
19. S. Mohammady, R. Farrell, D. Malon and J. Dooley, “Performance investigation of peak shrinking and interpolating the paper-reduction technique for lte-advance and 5g signals,” Information, vol. 11, no. 1, pp. 1–22, 2020. https://doi.org/10.3390/info11010020. [Google Scholar]
20. A. Baig, “A Precoding-based multicarrier non-orthogonal multiple access scheme for 5g cellular networks,” in IEEE Access, vol. 5, pp. 19233–19238, 2017. [Google Scholar]
21. J. Li, X. Zeng, C. Yin, Q. Luo and G. Li, “A low-complexity CRC-based decoding algorithm for slm-ml OFDM systems,” in IEEE Wireless Communications Letters, vol. 10, no. 6, pp. 1144–1147, 2021. [Google Scholar]
22. H. Chen and K. Chung, “A low complexity pts technique using minimal trellis in OFDM systems,” in IEEE Transactions on Vehicular Technology, vol. 67, no. 1, pp. 817–821, 2018. [Google Scholar]
23. A. K. Bairagi, M. S. Munir, M. Alsenwi, N. H. Tran, S. S. Alshamrani et al., “Coexistence mechanism between eMBB and uRLLC in 5g wireless networks,” in IEEE Transactions on Communications, vol. 69, no. 3, pp. 1736–1749, 2021. [Google Scholar]
24. M. Mounir, M. M. El, S. Berra, G. S. Gaba and M. Masud, “A novel hybrid precoding-companding technique for peak-to-average power ratio reduction in 5G and beyond,” Sensors, vol. 21, no. 4, pp. 1410, 2021. [Google Scholar]
25. A. Kumar, S. Ambigapathy, M. Masud, E. S. Jaha, S. Chakravarty et al., “An efficient hybrid PAPR reduction for 5G NOMA-FBMC waveforms,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2967–2981, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |