DOI:10.32604/iasc.2022.026308

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.026308 |  |
| Article |
A Neuro Fuzzy with Improved GA for Collaborative Spectrum Sensing in CRN
1Department of Computer Science and Engineering, Vel Tech Multi Tech Dr.Rangarajan Dr. Sakunthala Engineering College, Chennai, 600062, India
2Department of Computer Science and Engineering, R.M.D. Engineering College, Chennai, 601206, India
3Department of Computer Science and Engineering, School of Engineering and Technology, Christ University, Bengaluru, 560029, India
*Corresponding Author: S. Velmurugan. Email: velmurugan@veltechmultitech.org
Received: 22 December 2021; Accepted: 25 January 2022
Abstract: Cognitive Radio Networks (CRN) have recently emerged as an important solution for addressing spectrum constraint and meeting the stringent criteria of future wireless communication. Collaborative spectrum sensing is incorporated in CRNs for proper channel selection since spectrum sensing is a critical capability of CRNs. According to this viewpoint, this study introduces a new Adaptive Neuro Fuzzy logic with Improved Genetic Algorithm based Channel Selection (ANFIGA-CS) technique for collaborative spectrum sensing in CRN. The suggested method’s purpose is to find the best transmission channel. To reduce spectrum sensing error, the suggested ANFIGA-CS model employs a clustering technique. The Adaptive Neuro Fuzzy Logic (ANFL) technique is then used to calculate the channel weight value and the channel with the highest weight is selected for transmission. To compute the channel weight, the proposed ANFIGA-CS model uses three fuzzy input parameters: Primary User (PU) utilization, Cognitive Radio (CR) count and channel capacity. To improve the channel selection process in CRN, the rules in the ANFL scheme are optimized using an updated genetic algorithm to increase overall efficiency. The suggested ANFIGA-CS model is simulated using the NS2 simulator and the results are investigated in terms of average interference ratio, spectrum opportunity utilization, average throughput, Packet Delivery Ratio (PDR) and End to End (ETE) delay in a network with a variable number of CRs.
Keywords: Cognitive radio; spectrum sensing; channel selection; spectrum assignment; improved genetic algorithm
Cognitive Radio (CR) has emerged as a viable communication strategy for making full use of constrained spectrum resources in an opportunistic manner [1,2]. It makes good use of the available spectrum. Spectrum sharing, spectrum management, spectrum sensing and spectrum mobility are the four aspects of CR technology. Spectrum sensing detects idle spectrums and distributes them to another user. Following that, the optimal portion that meets the user’s transmission requirements. In order to have an effective spectrum, constant transmission needs are maintained during the spectrum mobility process. The third phase provides a feasible spectrum scheduling strategy for coexisting users [3]. Several issues, such as multipath fading, shadowing and the receiver uncertainty problem, have a significant impact on the detection efficiency of the spectrum sensing process in real-time. To prevent these challenges, cooperative sensing is suggested to boost sensing effectiveness by observing spatially distributed CR users. Fig. 1 depicts the structure of CR networks (CRN).
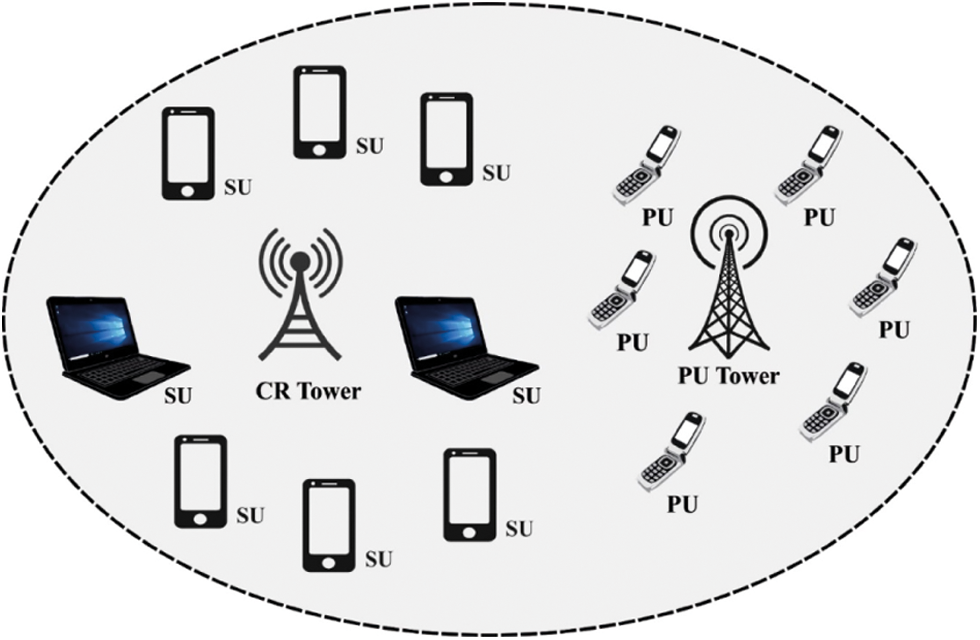
Figure 1: Architecture of CRN
The spectrum assignment function of CR handles how Secondary Users (SUs) can resourcefully utilize the unused licensed spectrum without interference and on a lease basis at some point throughout the entire spectrum [4]. The primary goal of CRN is to optimize specific network utilities such as the allocation of existing channels to SUs. Channel selection is vital in CRN because it allows the CR to choose the best channel among the available detected channels. The current channel selection research activities are based on recent observations of the channel state as a basic information to select the channels. However, a channel used by the Primary User (PU) could not be used for CR transmission. As a result, if PU arrives, the CR should stop the transmission and look for another channel to restart it. These CR transmission distributions have an impact on the Quality of Service (QoS) performance of CR consumers. Several models are created in [5] to address these issues. In this case, the CR will forecast the arrival of PU on various channels and select the one with the lowest PU utilization for broadcast (PUU). The goal of these techniques is to eliminate interference between CR and PUs. However, other aspects that must be considered while choosing the best channels are channel state and the CR’s QoS requirements. All of these aspects are considered by an effective channel selection model.
CRN’s spectrum assignment strategies include game theory, pricing and auction mechanisms and local bargaining. In [6] an optimal channel and power allocation model for a multi-channel environment is created based on the probability of channel accessibility. The spectrum allocation problem is treated as an NP-hard Graph Coloring Problem (GCP) in [7,8] and a Color Sensitive Graph Coloring (CSGC) strategy is proposed to solve it. In [9], an improved graph coloring theory-based technique is created with CSGC spectrum usage of least simulated time. In [10], graph coloring and bidding theory techniques are used to allocate channels in a novel distributed collusion mechanism. The channel selection procedure is carried out by Genetic Algorithm (GA) based models described in [11] by considering the bit error rate, modulation, bandwidth, power and frequency. The objective function is converged to the optimum value and the stopping criteria are met based on the desired criteria. It provided a thorough evaluation of the channel selection process without taking the PUU into account.
Despite the fact that numerous spectrum sensing models are available in the literature, the concealed terminal problem occurs when the cognitive user is shadowed while the main user (PU) operates nearby. To address the concealed terminal issue, collaborative spectrum sensing is employed, which alleviates the problem of corrupted detection by utilizing inbuilt spatial variety to reduce the chance of interferences with the PUs. According to this viewpoint, this study introduces a new Adaptive Neuro Fuzzy Logic with Improved Genetic Algorithm-based Channel Selection (ANFIGA-CS) technique for collaborative spectrum sensing in CRN. The ANFIGA-CS approach aids the CR in determining available spectrum slots/channels in the radio band. The ANFIGA-CS technique primarily employs a clustering technique to reduce spectrum sensing inaccuracy. Furthermore, the Adaptive Neuro Fuzzy Logic (ANFL)-based channel weight selection technique is used and the channel with the highest weight is picked for transmission. To improve the channel selection process in CRN, the rule optimization in the ANFL scheme is performed using the Improved Genetic Algorithm (IGA) to increase overall performance. The suggested ANFIGA-CS model is simulated using the NS2 simulator and the outcomes are evaluated using several metrics.
The remainder of the paper is organized as follows. Section 2 summarizes the available channel selection approaches in the literature. Section 3 covers the ANFIGA-CS model’s operation, while Section 4 examines its experimental validation. Finally, in Section 5, the important findings of the ANFIGA-CS model are summarized.
This section examines some of the most recently established channel selection strategies for CRNs. A fully distributed channel selection technique is devised to facilitate the existence of LTE devices or systems in the unlicensed 5 GHz band [12]. For channel allocation, the game theory and Q-learning models are used. The performance of this model is validated in terms of signaling requirements, convergence time and error. The overhead issue associated with many SUs is addressed in [13], which delivers examinations to the fusion centre by dividing a network into a series of clusters. Through the usage of cluster heads, the cluster transmits observations to the fusion centre (CHs). They are created using the machine learning affinity propagation technique. The construction of an infrastructure-based model becomes simple in such a way that the fusion centre remains static regardless of the movement of SUs. This strategy does not consider ad hoc scenarios. The simulation of channel conditions is regarded as a critical operation in [14]. The channel states are described using stochastic processes with a joint distribution that the user is aware of.
A backward propagation training strategy using Neural Network (NN) is given for predicting future channel state from past data [15]. GA is used to avoid the local optima problem while decreasing aggressive structural patterns and optimizing the structure of a NN. Sumathi et al. [16] create an effective support vector machine model for identifying likely free channels for SU transmission. It employs four input variants for successful channel selection, which is utilized to determine the channel preference list for SUs to carry out channel switching. It manages two queues using the M/M/1 queueing technique to reduce the channel switching count and poison distribution is used to determine the SU count coming in a certain time span.
Because of channel dynamics, the study underlines the difficulties that SUs confronts in determining the best sensing and transmission protocols. The reinforcement learning technique, namely the Double Deep-Q Network [17], is used to develop a unique transmission strategy for SU. It is used to determine the sensing order of channels as well as the cooperative sensing partner selection. When compared to traditional Q learning models, deep reinforcement learning algorithms have a faster learning rate and a larger performance gain. Soft and hard decision recognition are used in the fusion centre to detect the existence or absence of PUs [18]. When it comes to sensing, soft decision recognition often outperforms hard decision sensing. It is realised in order to provide a better compromise between cost and sensing efficiency.
For CR, an Intelligent Fuzzy based Dynamic Spectrum Allocation (IDSA) approach with bandwidth flexibility is designed [19]. The presented IDSA model yielded better results in terms of delay, packet loss and service rate. A dynamic GA is designed for channel allocation in CRN [20]. It is based on better crossover and mutation operators and it provides a new technique for allocating spectrum to Pus and SUs. [21] proposes a Best Fit Channel Selection (BFC) technique for distributed channel selection. For channel selection, it takes primary channel and CR traffic activities into account. The CR nodes determine the PU’s traffic activity and the channel condition. It also forecasts how long the channel will be idle. Despite the fact that numerous models are available in the literature, there is still a need to create an appropriate channel selection mechanism for CRNs.
3 The Proposed Channel Selection Methodology
The proposed ANFIGA-CS model comprises of several process such as node deployment, clustering, channel weight determination and rule optimization. The overall working principle of the ANFIGA-CS model is illustrated in Fig. 2. Once the nodes are deployed and clusters are constructed, the channel weights are determined using ANFL scheme. It involves three fuzzy input parameters namely PUU, number of CRs (NCR) and Channel Capacity (CC) to determine the channel weight. The channel with maximum weight will be chosen for data transmission. Finally, the rules generated using the ANFL scheme are optimized using IGA and thereby the efficiency can be further improved. The detailed operation of this process is given in the subsequent subsections.
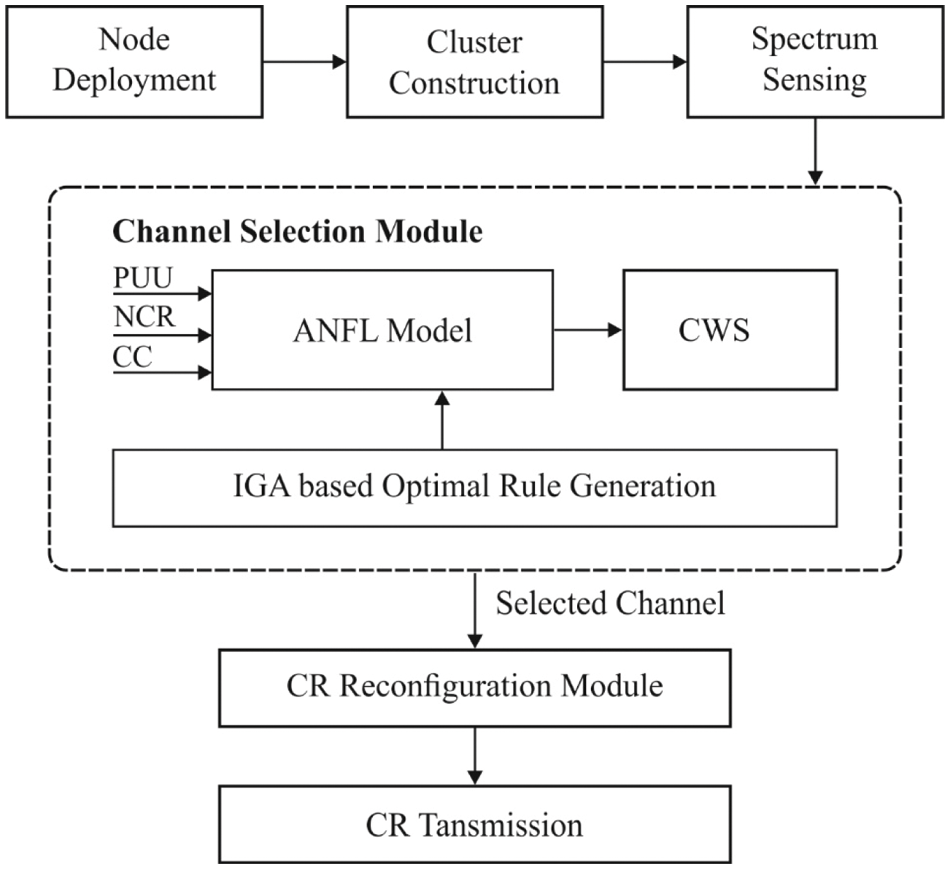
Figure 2: Workflow of proposed ANFIGA-CS model
A CRN with a set of PU and CR nodes is considered. The PU nodes are the approved clients who have first priority access to the channels that are not disrupted by CR node transmission. The network is supposed to operate in a different fashion, with the CR nodes performing networking functions such as spectrum sensing and channel selection. The ability of CR and PU is discovered to be sampled. The primary distinction between CR and PR is that the PR owns a band that may be used everywhere, but the CR can only access the idle frequency band. When the CR detects a PU signal, it quickly exits the designated spectrum. CR has a single transceiver that allows it to perceive or communicate on only one channel at a time. By using a multi-transceiver, it reduces the processing cost of the CRs and removes the possibility of interference. Each CR node performs spectrum sensing on a regular basis. The CRN’s effectiveness is primarily determined by the PU’s activity throughout the channels. The CR user will only use the spectrum resource if the PUs does not use it. When the CR uses an idle channel, the PU can arrive at any time and the CR must then stop the conversation and vacate the existing channel. The PU activity is based on Poisson modelling with an exponential distribution of inter-arrivals.
3.2 Cluster Construction Phase
Earlier in the process, cognitive sensors are deployed to operate as SU in the RF environment. In this situation, the relevant sensors are regarded as static and an adaptive spectrum-based clustering technique is employed to achieve rapid spectrum creation in a dynamic environment with constraints. In this case, the weighted clustering technique is used to choose the CHs, resulting in the formation of clusters. The development of a clustering topology aids in the effective sharing of spectrum and the efficient use of existing spectrum.
3.3 ANFL Based Channel Weight Selection Phase
The ANFL model combines the fundamental concepts of Fuzzy Logic (FL) with Artificial Neural Network (ANN) (ANN). It supports a set of Membership Functions (MF) as well as if/then rules. To alter weights, the ANFL use a trapezoidal MF. These MFs are used in conjunction with the product inference rules during the fuzzification stage. The ANFL model contains three inputs: PUU, NCR and CC and one output: Channel Weight Selection (CWS). The minimizing of interference caused by PUs and between CRs is a major challenge that exists to improve the efficiency of the CRN. As a result, the optimal channel with low PUU, low CR user congestion and high CC must be selected. The output assigns a channel weight based on three parameters, which are defined below: PUU, NCR and CC.
a. Primary user’s utilization
PUU denotes the fraction of time at which channel i is in ON state, that is used by PUs. Channel utilization [22] u can be determined using Eq. (1). A major necessity of CRN is that there should be zero inference between the CRs and Pus transmission. Hence, the optimum channel will be the one with minimum PUU rate.
where,
b. Number of CRs
By using the channel, an effective channel selection process will choose the channel with the fewest CR neighbors. The lowest possible CR reduces interference between CRs, increasing transmission rate, resource utilization and throughput. It also lowers packet loss and latency. Every CR node will use the Common Control Channel (CCC) mechanism to investigate the nearby nodes in order to determine the NCR.
c. Channel capacity
CC defines the data rate per Hertz of the spectrum band utilized [23]. The expected normalized capacity of a user k in spectrum band i can be determined as follows.
where Ci(k) denotes spectrum capacity, ci(k) is the normalized channel capacity of spectrum band i in bits/sec/Hz, τ is the spectrum switching delay, γi is the spectrum sensing efficacy and
Each individual input makes use of the three MFs. The TakagiSugeno type model, which consists of 27 rules, is then employed. The first portion of the rule represents the fuzzy subspace, while the second part computes the output in the fuzzy subspace. In general, the ANFL system is a five-layer FFNN with supervised learning. The five layers are labelled as fuzzy, Tnorm, normalized, defuzzy and aggregated, in that order. Fig. 3 [24] depicts the structure of an ANFC. The first and fourth layers are dynamic, whereas the rest are static. The TakagiSugeno fuzzy inference model generates a set of 27 if then rules for the three inputs PUU, NCR and CC with CWS output [24]. These rules are
where high and low are the MFs or the linguistic parameters of the inputs. Xi, Yj, Zk are linear parameters of then part (consequent) of the Takagi-Sugeno fuzzy inference model.
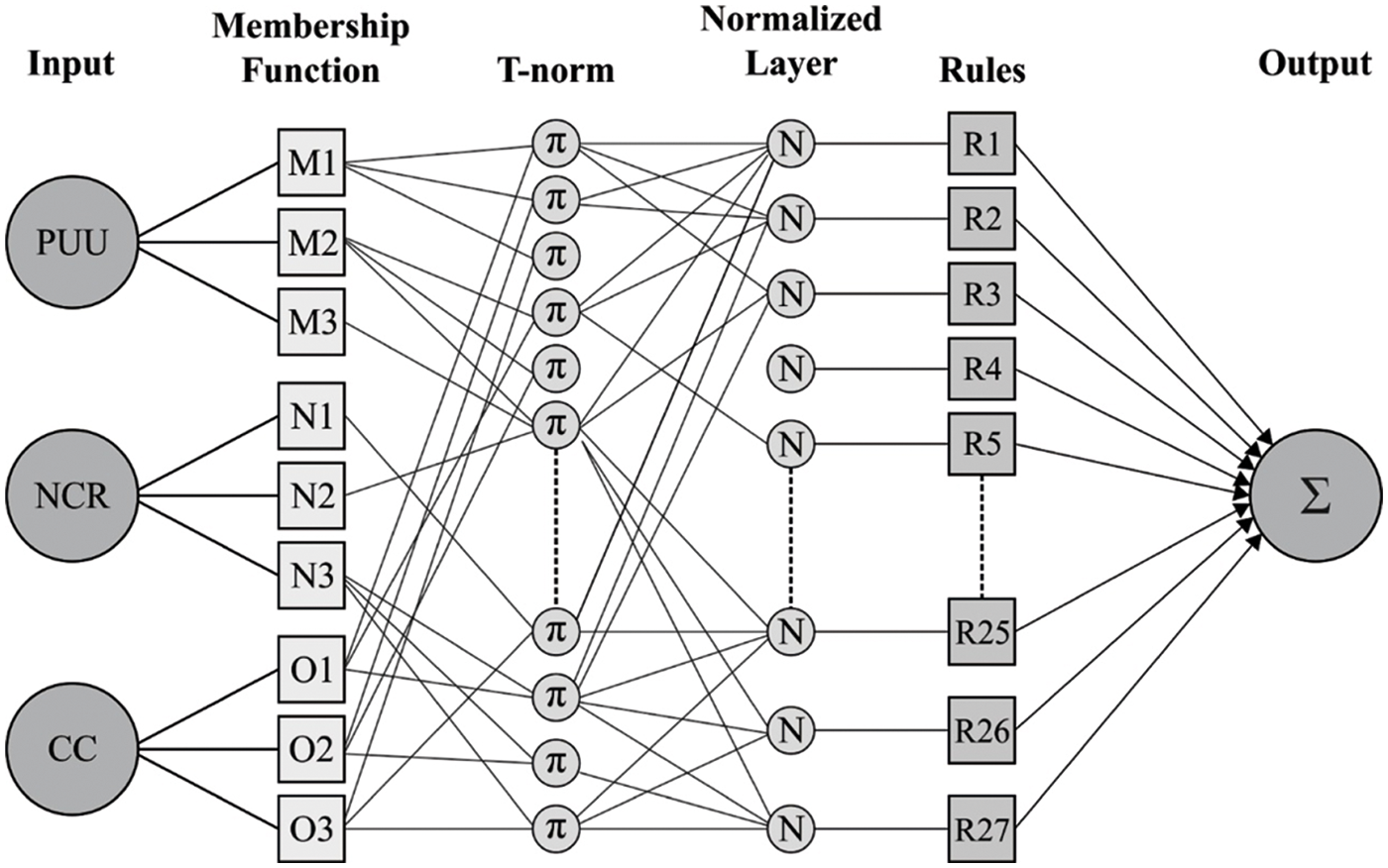
Figure 3: Structure of ANFC model
Fuzzy Layer: It explains the flexible behaviors of the node, based on the backward pass which resembles every individual input parameter related to the MF. The MF graph is plotted for every adaptable node to define its output. The MF follows Gaussian distribution as defined in Eq. (3) or generalized bell-shaped MF (see Eq. (4)).
where M is the input node to α and μMi, μ, μoi are the degree of MF corresponding to linguistic parameters Mi, Ni and Oi and {di, ei, fi} are denoted as a parameter set of the MF. The bell-shaped MF differs along with the values of the principal parameter set.
T-Norm Layer: Here, every individual node is static and named as rule node. It represents the firing strength of the rules linked to it. For determining the outcome of every individual node, the multiplication of all the MF signals comes to the node. The T-norm operator makes use of generalized AND to compute the antecedent/output at subsequent layer of the rule.
where Tα is the outcome of every individual node denoting the firing strength of every rule.
Normalized Layer: The nodes in the normalized layer are static and are called normalized nodes. The outcome of all nodes is the determination of the proportion among αth rule’s firing strength to the summary of firing strength of every rule. The outcome at the 3rd layer or normalized output is defined by
De-fuzzy Layer: It comprises of the nodes with dynamic essence. The outcome will be the multiplication of the normalized firing strength and individual rule. Its output can be represented as
where
Aggregated Output Layer: It comprises of one consolidated node which acts as output and is static in nature. It provides details about the outcome of the whole system determined by totaling the approaching signals at this layer from the preceding node. Σ is utilized in a circle for representing the aggregated output node. The outcome of the 5th layer can be determined as follows.
The ANFL scheme is divided into two stages: forward and backward passes. The input signal is transferred to the 4th layer during the forward pass (layer-wise). They are static and the least mean squares model is used to update the sequential measures. Following the achievement of output data at the fourth layer, the data is compared by the original outcome and error. The error caused by the forward pass outcome and the original output are transferred to the dynamic node of the first layer in the backward pass. As a result, the best CWS value will be chosen. The IGA is used for optimal rule generation to boost the efficiency of the ANFL model even further.
3.4 IGA Based Rule Optimization Phase
The rules produced by the ANFL model are optimized by IGA. Its goal is to ensure the implementation of optimum rules for effective performance. All 27 rules are sent into the IGA, which selects the best rules through a process of selection, fitness evaluation, crossover, mutation and elite retention. GA has been discovered to be a common strategy for locating optimal solutions to a variety of situations. In this paper, IGA is derived for ANFL rule optimization. The population initialization procedure occurs at the beginning in a random manner in preparation for further genetic manipulation. For a simpler training set, a maximum of three hidden layers are sufficient to achieve higher performance. Because binary coding is a widely used coding technique in GA, the node count in the three buried layers is directly encoded as binary chromosomes. It defines a network structure with three hidden levels, each with six bits. Each each bit’s value will be a binary number, either ‘0’ or ‘1’. The translated decimal value represents the number of neurons in the layer. The allowed neuron count in the hidden layer can be anywhere between the input and output layers. As a result, when the population is initialized, the node count in each layer is guaranteed to be less than the input feature count and greater than the output feature count.
The selection procedure tries to pick superior chromosomes from the current population and to develop crossover and mutation models. As a candidate’s fitness improves, so does his or her chances of being chosen. Furthermore, a roulette wheel selection approach based on proportional fitness assignment (also known as the Monte Carlo method) is used. However, one significant restriction is that adopting an arbitrary number may result in the exclusion of individuals with the highest fitness [25]. As a result, the IGA is designed to select individuals with better fitness values to ensure that they advance to the next stage and to select the remaining individuals using the roulette idea. This improvement demonstrates that only the best people are kept.
The Partially Matched Crossover (PMC) model is then used, which interchanges arbitrarily picked regions from two nearby chromosomes. However, when two neighboring chromosomes are picked at random, they stay intact following the crossover procedure. Therefore, interval crossover is employed in IGA as defined in Eq. (9). For instance, when n chromosomes are available, the initial one is crossed with (n/2 + 1) th, the subsequent one with (n/2 + 2) th, etc.
where c signifies the individuals created next to the intersection. The utilization of this approach avoids the local optima; therefore, the diversity of the subsequent generation can be improved and the convergence rate can be enhanced.
The mutation procedure is then performed to change a specific bit in the chromosome. It might make use of the mutation operator’s arbitrary search capability. When the operational outcome is closer to the optimum solution neighborhood, it quickly converges to the optimum solution. The process of crossover and mutation may result in the loss of ideal individuals in the subsequence round. For preventing this issue, an ‘‘elite retention’’ strategy is employed. Next to the process of every mutation, the optimal individual A in this generation undergoes comparison to the optimal individual B which existed in the evolution process. If B exceeds A, B will replace the worst individual in the present round and moves to the subsequent round, A moves to the subsequent round straightaway. If A is equal or greater than B, A goes to the succeeding generation directly, as given in Eq. (10).
where C signifies the one which drives to the succeeding round. The processes involved in the IGA based rule optimization is given as follows [26].

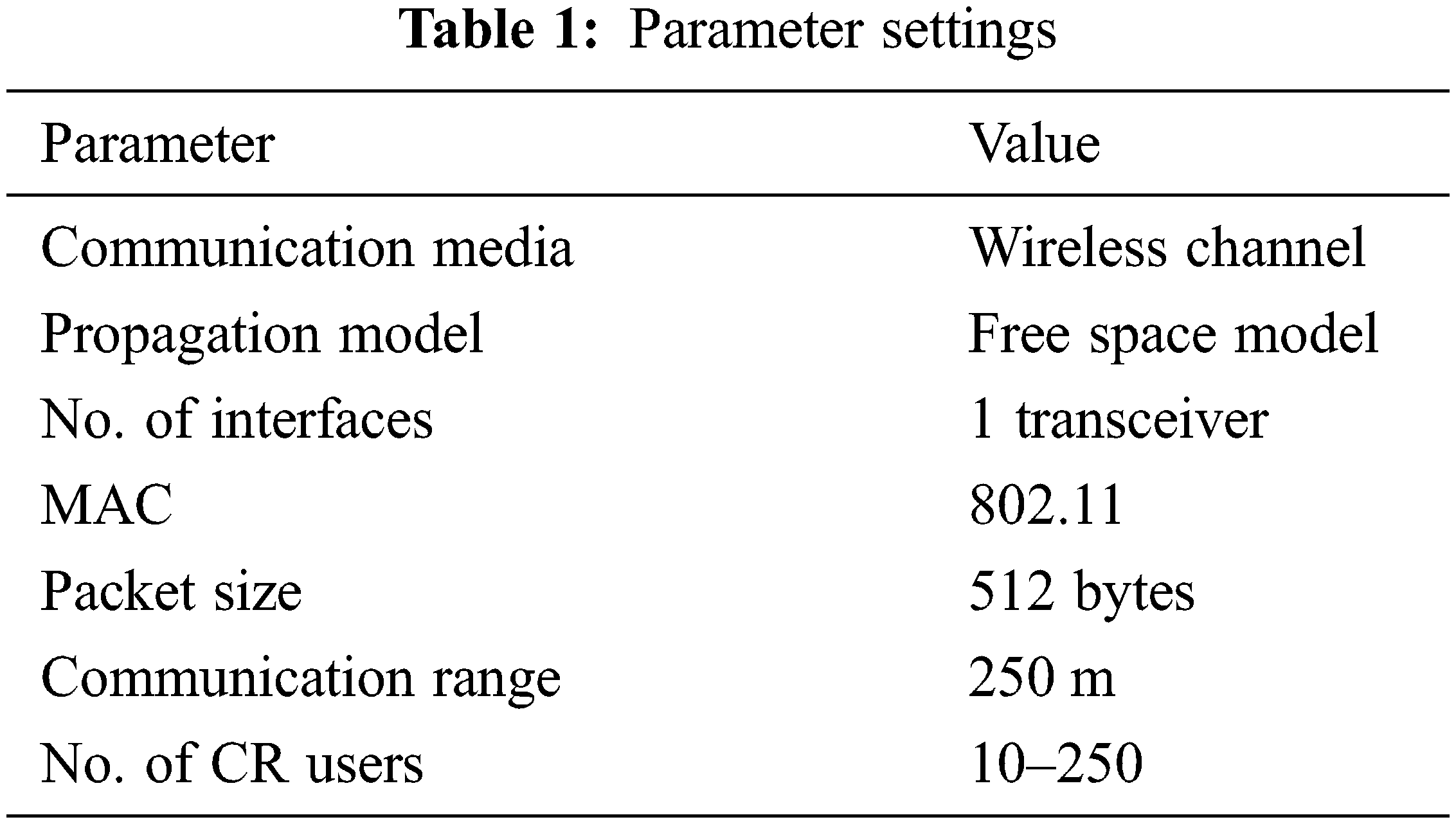
To validate the effective performance of the ANFIGA-CS model, a series of simulations are run and the results are examined at CR with varied numbers of available channels. Tab. 1 shows the parameter settings for the simulation process.
In Tab. 2, a detailed comparative result analysis of the ANFIGA-CS model with other existing approaches is performed in terms of Average Inference Ratio (AIR) and average throughput. Fig. 4 displays the AIR analysis of the ANFIGA-CS model with varied numbers of accessible channels at each CR. According to the graph, the LITC model suffers from strong interference between CR and PUs despite having a greater AIR than the other techniques. Furthermore, the GA and BFC models attempted to outperform the LITC model by lowering the AIR. Similarly, the ICSSS model produced a respectable result with a reasonable AIR, whereas the ILFCS model produced an even better performance. The ANFIGA-CS model, on the other hand, has demonstrated improved performance by achieving the lowest possible AIR. The experimental results revealed that the ANFIGA-CS model produced the lowest AIR of 0.1371 while the ILFCS, ICSSSS, GA, BFC and LITC models produced higher AIRs of 0.1996, 0.2394, 0.4210, 0.4609 and 0.6978, respectively.
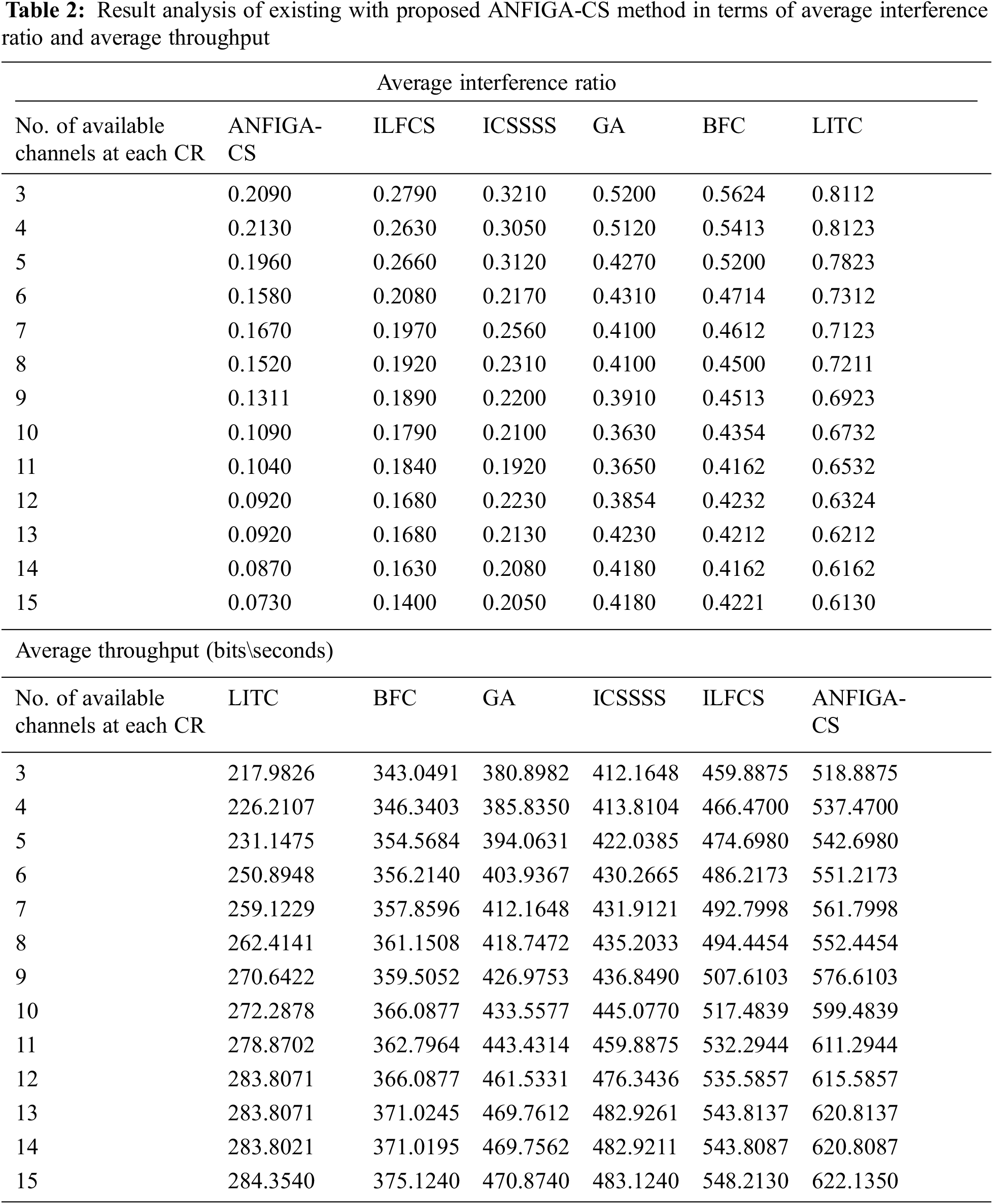
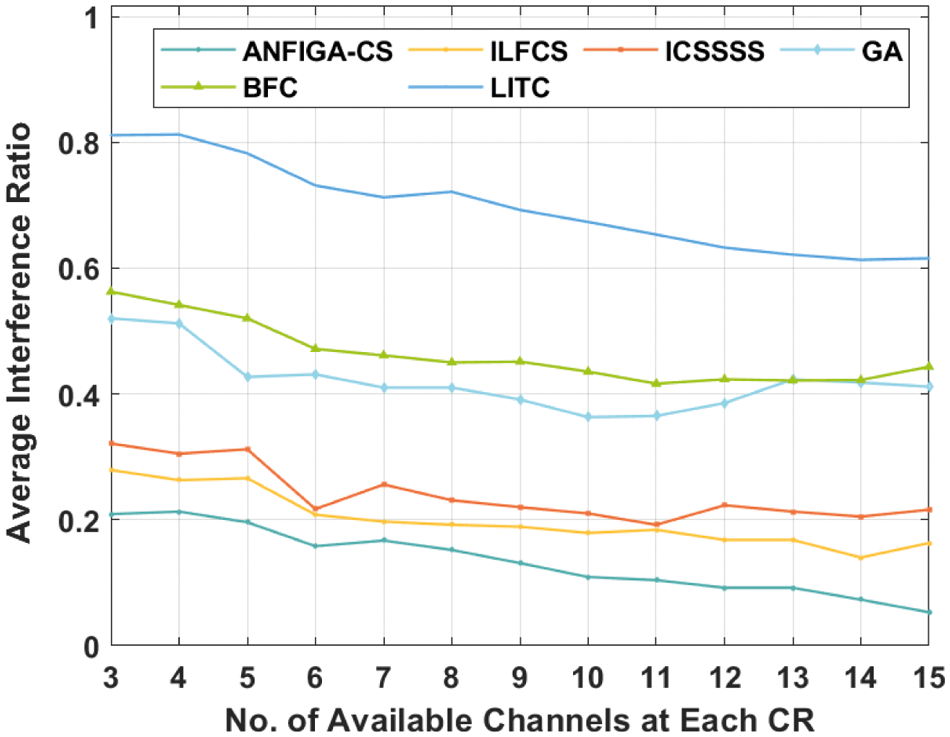
Figure 4: AIR analysis of the ANFIGA-CS with other existing models
The average throughput analysis of the ANFIGA-CS model with varied numbers of accessible channels at each CR is depicted in Fig. 5. The graph shows that the LITC model achieved the lowest average throughput compared to the other techniques. Similarly, the GA and BFC models outperformed the LITC model in terms of efficiency, achieving a slightly higher average throughput. Similarly, the ICSSS model outperformed the previous methods in terms of results. Despite reporting competitive average throughput, the ANFIGA-CS model surpassed the other approaches with the highest average throughput. The ANFIGA-CS model, for example, has a higher average throughput of 579.3269 bits/s, but the ILFCS, ICSSSS, GA, BFC and LITC models have lower average throughputs of 261.9494692, 360.8328615, 428.5795308, 447.1172231 and 507.9482846 bits/s, respectively.
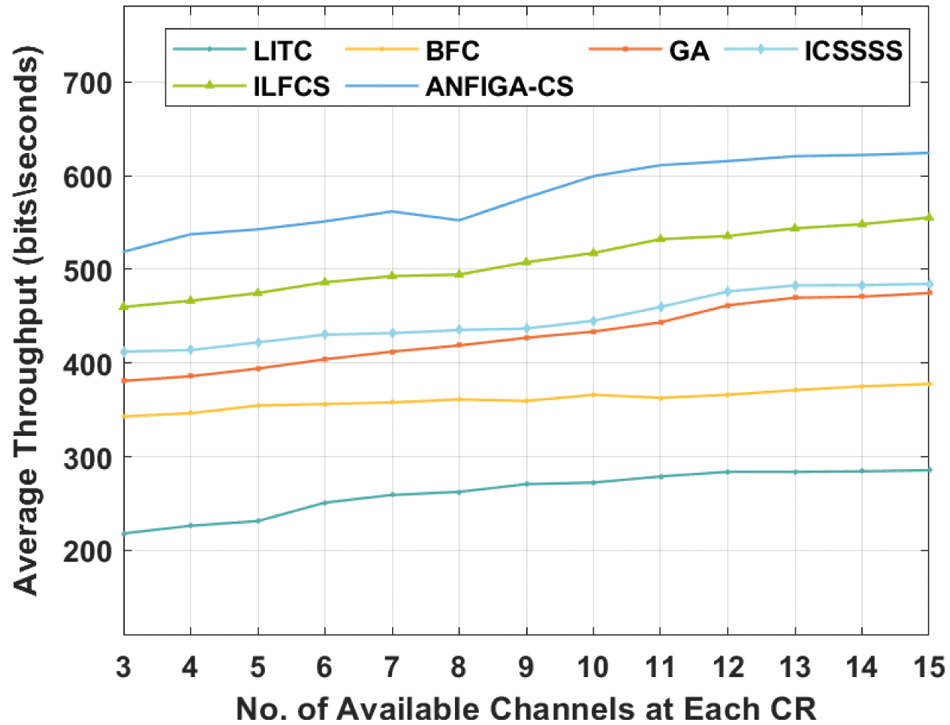
Figure 5: Average throughput analysis of the ANFIGA-CS with other existing models
Tab. 3 and Fig. 6 examine the SOU analysis of the ANFIGA-CS model with comparable approaches at each CR using different accessible channels. The importance of SOU in the construction of an effective channel allocation model cannot be overstated. The experimental results demonstrate that the LITC technique performed poorly, achieving the lowest SOU, whereas the BFC and GA techniques achieved significantly higher results. Additionally, the ICSSSS and ILFCS models outperformed all other techniques except the ANFIGA-CS model. However, the provided ANFIGA-CS model produced an effective result by achieving a maximum SOU of 0.953585, whereas the other techniques, such as ILFCS, ICSSSS, GA, BFC and LITC models, produced a lower average SOU of 0.0908, 0.6152, 0.6553, 0.8647 and 0.9341, respectively.
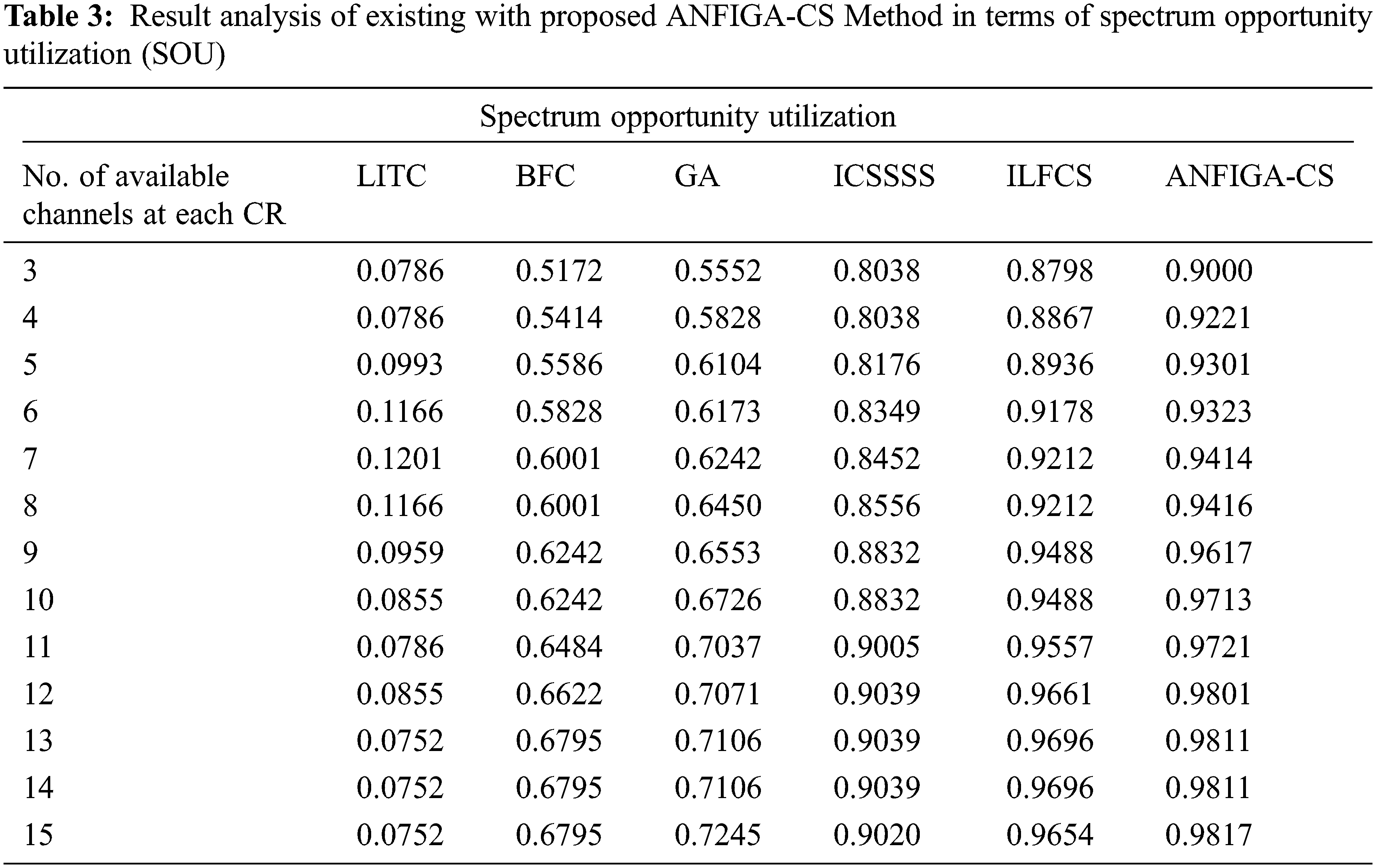
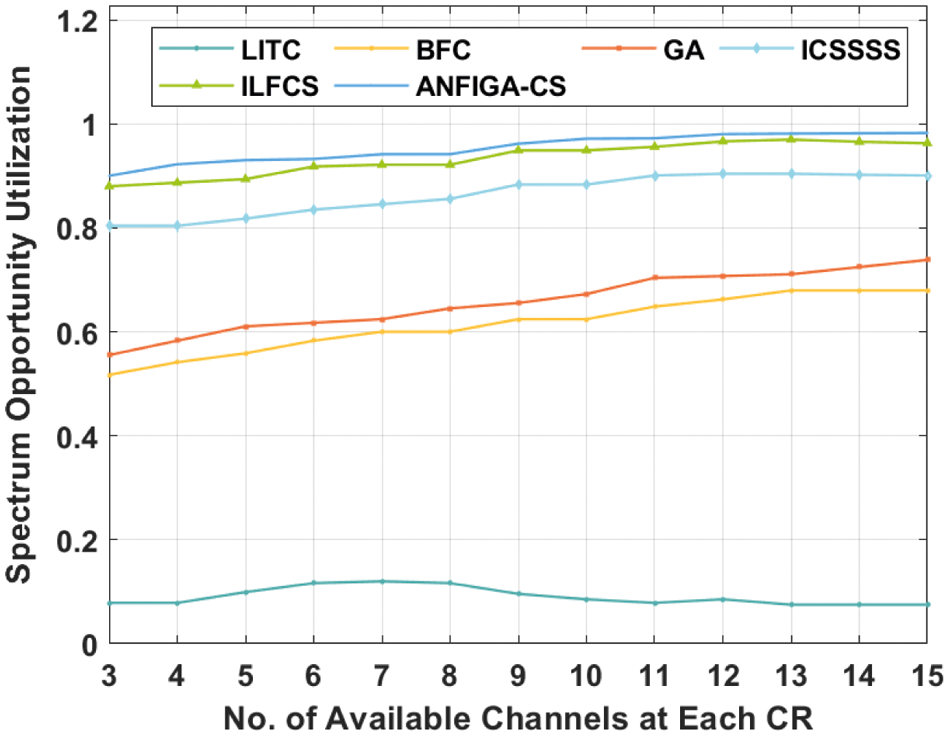
Figure 6: SOU analysis of the ANFIGA-CS with other existing models
Tab. 4 and Fig. 7 compare the PDR analysis of the given ANFIGA-CS model to other available approaches. The importance of PDR in the construction of an effective channel allocation model cannot be overstated. The results show that the LITC model outperformed the other compared methods in terms of PDR. Simultaneously, the BFC and GA models resulted in a somewhat higher PDR than the LITC model. Finally, the ICSSSS and ILFCS models outperformed all other techniques save the ANFIGA-CS model in terms of PDR. However, as compared to other current approaches, the ANFIGA-CS model ensured a higher PDR. The ANFIGA-CS model, for example, has an average PDR of 93.41%, but the LITC, BFC, GA, ICSSSS and ILFCS models have lower average PDRs of 45.10%, 62.778%, 78.26%, 85.69% and 92.04%, respectively.
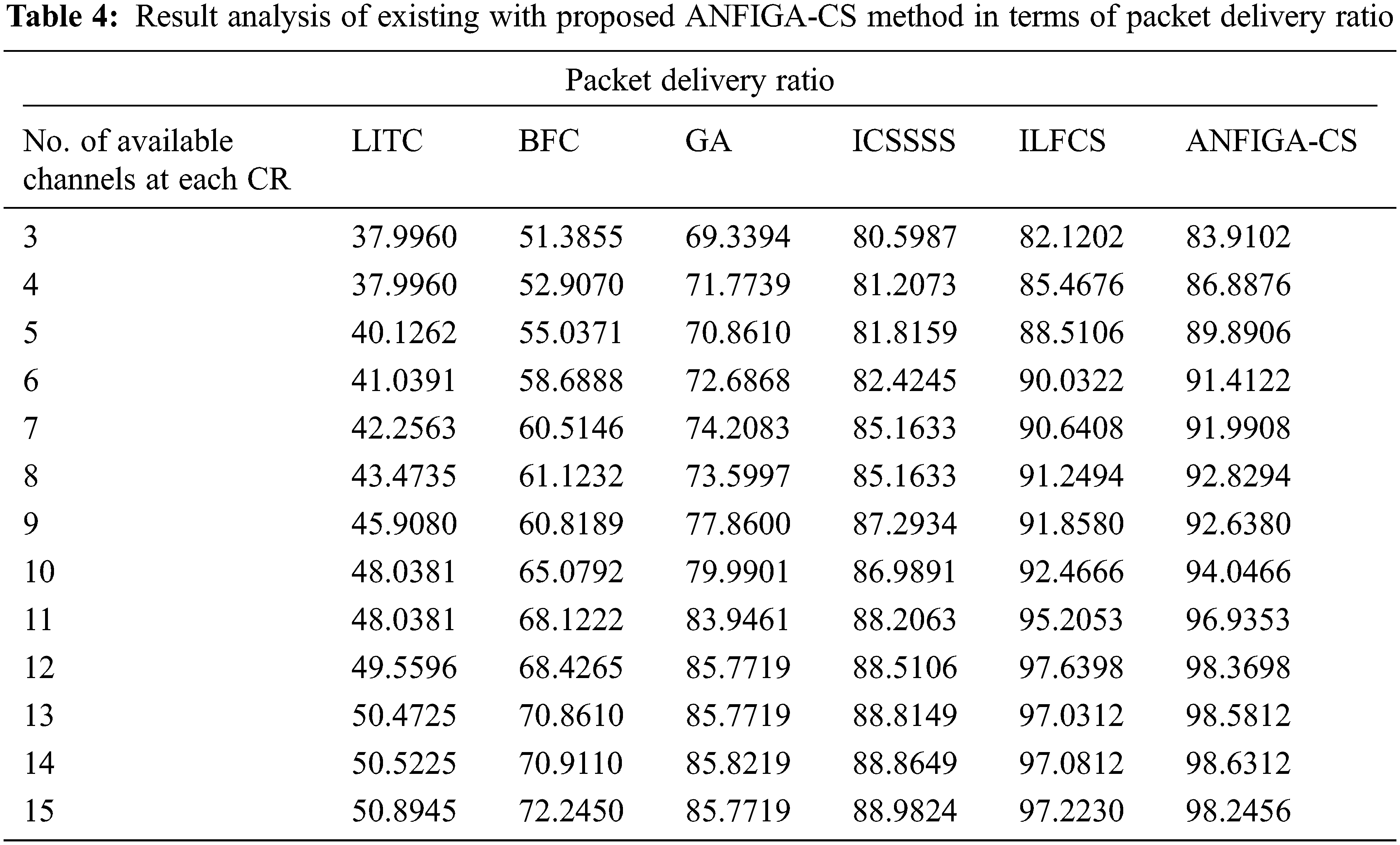
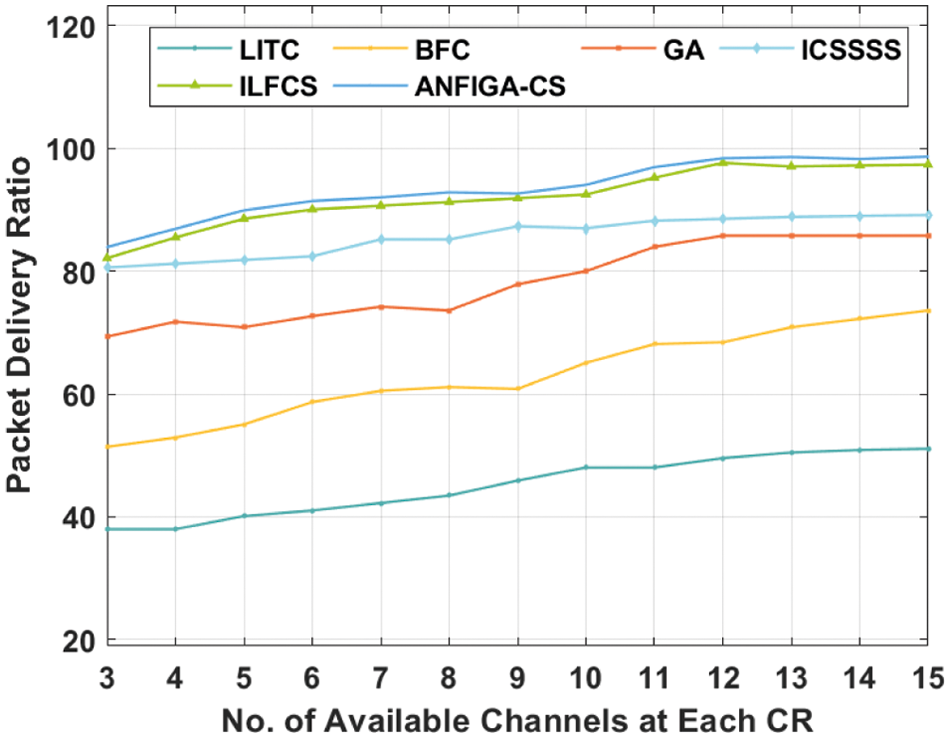
Figure 7: PDR analysis of the ANFIGA-CS with other existing models
Tab. 5 and Fig. 8 compare the ETE delay analysis of the ANFIGA-CS model to other existing approaches with varied numbers of accessible channels at each CR. For an effective channel allocation strategy, the ETE delay must be kept to a bare minimum. According to the results, the LITC technique resulted in inferior channel selection performance by achieving a maximum ETE delay, whereas the BFC technique resulted in marginally improved performance. Simultaneously, the GA and ICSSSS models revealed considerable ETE delay. It should also be noted that the ILFCS model has a shorter ETE delay. However, the proposed ANFIGA-CS model has achieved an effective result by achieving the shortest ETE delay. The ANFIGA-CS model, for example, had the shortest average ETE delay of 0.1264 s, but the ILFCS, ICSSSS, GA, BFC and LITC models had longer average ETE delays of 0.1574, 0.3249, 0.4060, 0.5570 and 0.6580 s, respectively.
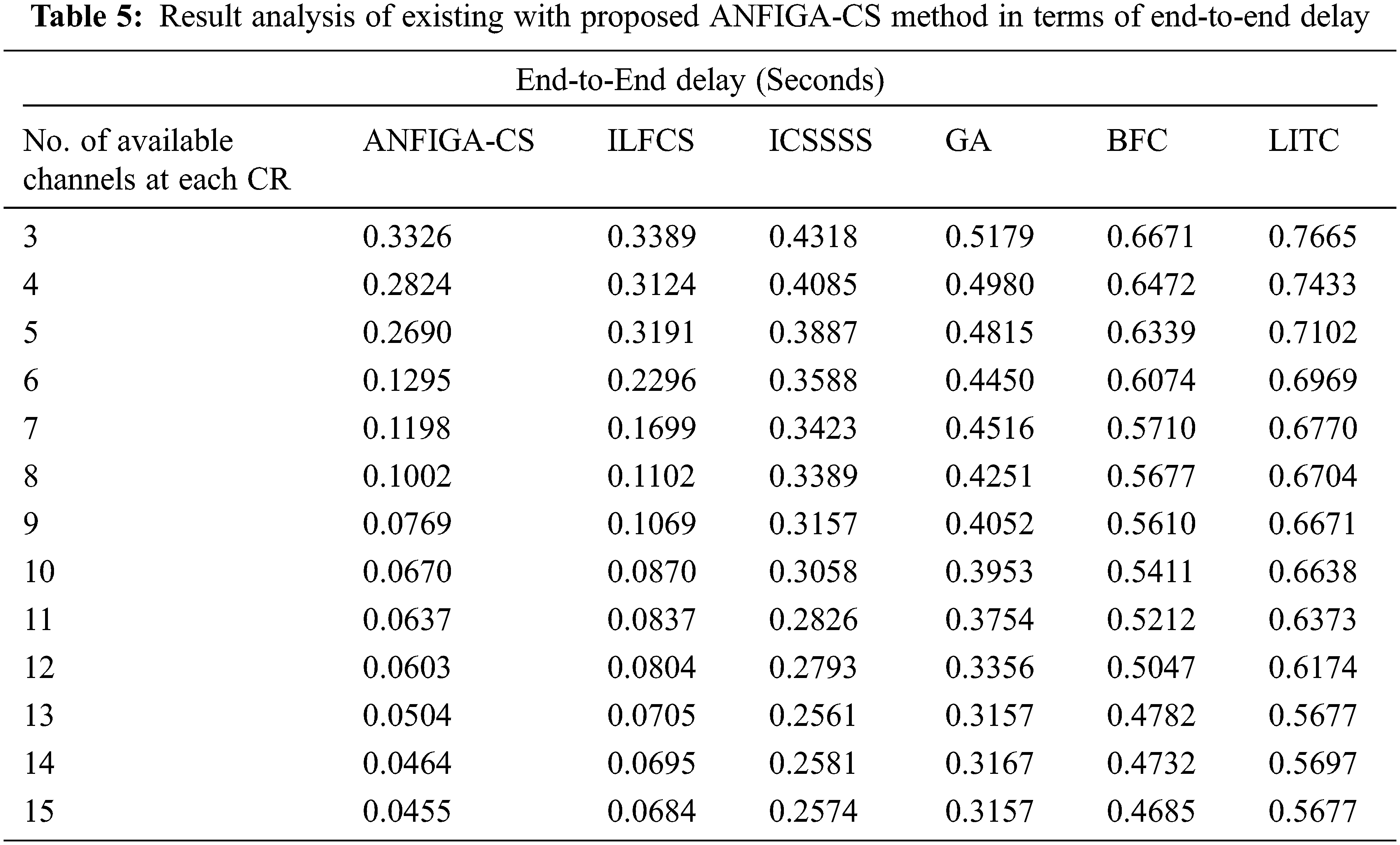
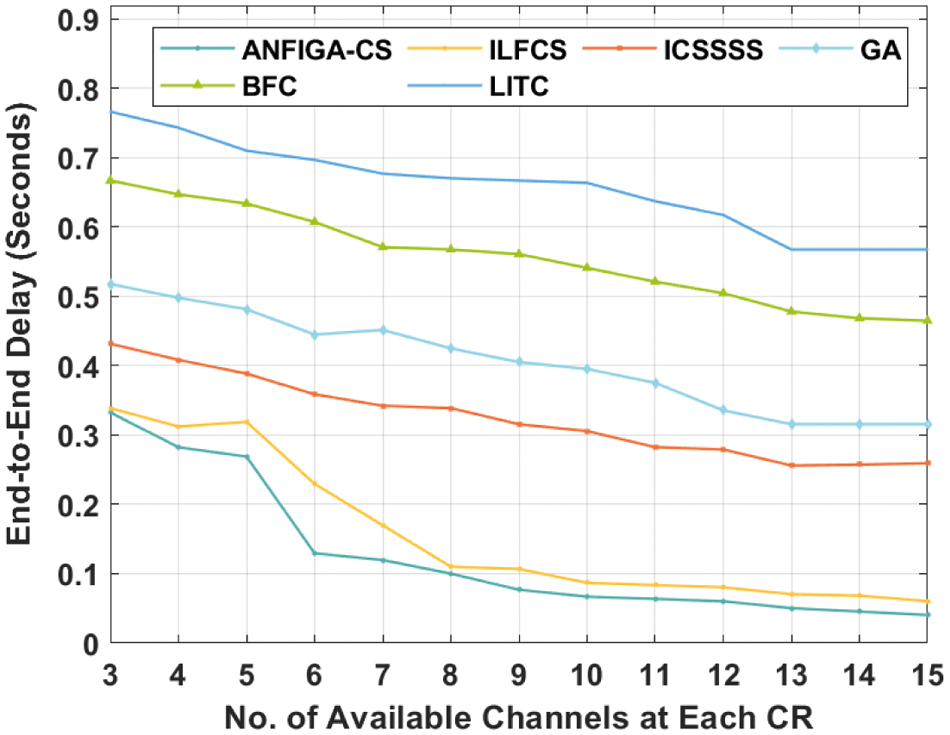
Figure 8: ETE delay analysis of ANFIGA-CS with other existing methods
From the above-mentioned tables and figures, it is evident that the presented ANFIGA-CS model has outperformed all the other existing methods under varying number of available channels at CRs.
In this study, a new ANFIGA-CS approach for collaborative spectrum sensing in CRN was established. The ANFIGA-CS technique given here allows the CR to locate accessible spectrum slots/channels in the radio band. The proposed ANFIGA-CS model includes several stages of operations, including node deployment, clustering, channel weight determination and rule optimization. The ANFIGA-CS technique is primarily subjected to a clustering technique in order to reduce spectrum sensing inaccuracy. The ANFL-based channel weight selection technique is then used and the channel with the highest weight is selected for transmission. Finally, the IGA is used to optimise the rules generated by the ANFL scheme in CRNs. A large number of simulations were run to demonstrate the increased performance of the ANFIGA-CS model. A thorough comparison results study ensured that the ANFIGA-CS model improved in terms of diverse measures. The performance of channel selection in CRN can be improved in the future by combining advanced Deep Learning (DL) architectures with learning rate scheduling approaches. Statement of Funding: This study was not funded in any way by the authors.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Haykin, “Cognitive radio: Brain-empowered wireless communications,” IEEE Journal on Selected Areas in Communications, vol. 23, no. 2, pp. 201–220, 2005. [Google Scholar]
2. C. Pretty Diana Cyril, J. Rene Beulah, N. Subramani, P. Mohan, A. Harshavardhan et al., “An automated learning model for sentiment analysis and data classification of twitter data using balanced CA-SVM,” Concurrent Engineering Research and Applications, vol. 29, no. 4, pp. 386–395, 2021. [Google Scholar]
3. S. Neelakandan, A. Arun, R. Bhukya, B. M. Hardas, T. Ch et al., “An automated word embedding with parameter tuned model for web crawling,” Intelligent Automation & Soft Computing, vol. 32, no. 3, pp. 1617–1632, 2022. [Google Scholar]
4. Q. Zaho and B. M. Sadler, “A survey of dynamic spectrum access: Signal processing, networking and regulatory policy,” IEEE Signal Processing Magazine, vol. 55, no. 5, pp. 2294–2309, 2017. [Google Scholar]
5. L. Yang, C. Lili and Z. Haitao, “Proactive channel access in dynamic spectrum networks,” Physical Communication, vol. 1, no. 2, pp. 103–111, 2008. [Google Scholar]
6. D. Paulraj, “A gradient boosted decision tree-based sentiment classification of twitter data,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 18, no. 4, pp. 1–21, 2020. [Google Scholar]
7. M. Prakash and T. Ravichandran, “An efficient resource selection and binding model for job scheduling in grid,” European Journal of Scientific Research, vol. 81, no. 4, pp. 450–458, 2012. [Google Scholar]
8. C. Peng, Z. Haitao and Y. Z. Ben, “Utilization and fairness in spectrum assignment for opportunistic spectrum access,” Mobile Networks and Applications, vol. 11, no. 4, pp. 555–576, 2006. [Google Scholar]
9. J. Wang, H. Yuqing and J. Hong, “Improved algorithm of spectrum allocation based on graph coloring model in cognitive radio,” in 2009 WRI Int. Conf. on Communications and Mobile Computing, Harbin, China, vol. 3, pp. 353–357, 2009. [Google Scholar]
10. Y. Liu, X. Guisen and T. Xuezhi, “A novel spectrum allocation mechanism based on graph coloring and bidding theory,” in IEEE Int. Conf. on Computational Intelligence and Natural Computing, Wuhan, China, pp. 155–158, 2009. [Google Scholar]
11. J. Moung, S. H. Sohn, H. Ning, Z. Guanbo, M. K. Young et al., “Cognitive radio software testbed using dual optimization in genetic algorithm,” in 2008 3rd Int. Conf. on Cognitive Radio Oriented Wireless Networks and Communications (CrownCom 2008), Singapore, pp. 1–6, 2008. [Google Scholar]
12. A. Castañe, J. Pérez-Romero and S. Oriol, “On the implementation of channel selection for LTE in unlicensed bands using Q-learning and game theory algorithms,” in IEEE 2017 13th Int. Wireless Communications and Mobile Computing Conf. (IWCMC), Valencia, Spain, pp. 1096–1101, 2017. [Google Scholar]
13. D. M. Saqib, A. Saleem, C. Abdul and S. Kashif, “Clustering formation in cognitive radio networks using machine learning,” AEU-International Journal of Electronics and Communications, vol. 114, no. 2, pp. 1–14, 2020. [Google Scholar]
14. G. Reshma, C. Al-Atroshi, V. K. Nassa, B. Geetha, N. Subramani et al., “Deep learning-based skin lesion diagnosis model using dermoscopic images,” Intelligent Automation & Soft Computing, vol. 31, no. 1, pp. 621–634, 2022. [Google Scholar]
15. P. Mohan and R. Thangavel, “Resource selection in grid environment based on trust evaluation using feedback and performance,” American Journal of Applied Sciences, vol. 10, no. 8, pp. 924–930, 2013. [Google Scholar]
16. D. Sumathi and S. S. Manivannan, “Machine learning-based algorithm for channel selection utilizing preemptive resume priority in cognitive radio networks validated by ns-2,” Circuits, Systems and Signal Processing, vol. 39, no. 2, pp. 1038–1058, 2020. [Google Scholar]
17. W. Ning, H. Xiaoyan, Y. Kun, W. Fan and L. Supeng, “Reinforcement learning enabled cooperative spectrum sensing in cognitive radio networks,” Journal of Communications and Networks, vol. 22, no. 1, pp. 12–22, 2020. [Google Scholar]
18. A. M. Judith and S. B. Priya, “Multiset task related component analysis (M-TRCA) for SSVEP frequency recognition in BCI,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 5, pp. 5117–5126, 2021. [Google Scholar]
19. T. S. Veeramakali, S. Jayashri and S. Prabu, “Intelligent dynamic spectrum allocation with bandwidth flexibility in cognitive radio network,” Cluster Computing, vol. 20, no. 2, pp. 1575–1586, 2017. [Google Scholar]
20. R. Kamalraj, M. Ranjith Kumar, V. Chandra Shekhar Rao, R. Anand and H. Singh, “Interpretable filter based convolutional neural network for glucose prediction and classification using PD-SS algorithm,” Measurement, vol. 183, no. 8, pp. 1–12, 2021. [Google Scholar]
21. M. Sundaram, S. Satpathy and S. Das, “An efficient technique for cloud storage using secured de-duplication algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 42, no. 2, pp. 2969–2980, 2021. [Google Scholar]
22. M. H. Rehmani, V. Aline Carneiro, K. Hicham and F. Serge, “Surf: A distributed channel selection strategy for data dissemination in multi-hop cognitive radio networks,” Computer Communications, vol. 36, no. 10–11, pp. 1172–1185, 2013. [Google Scholar]
23. R. Arnous, A. I. El-Desouky, S. Amany and B. Mahmoud, “ILFCS: An intelligent learning fuzzy-based channel selection framework for cognitive radio networks,” EURASIP Journal on Wireless Communications and Networking, vol. 14, no. 1, pp. 1–18, 2018. [Google Scholar]
24. B. P. Sankaralingam, U. Sarangapani and R. Thangavelu, “An efficient agro-meteorological model for evaluating and forecasting weather conditions using support vector machine,” in Proc. of First Int. Conf. on Information and Communication Technology for Intelligent Systems, India, pp. 65–75, 2016. [Google Scholar]
25. D. Venu, A. V. R. Mayuri, G. L. N. Murthy, N. Arulkumar and N. Shelke, “An efficient low complexity compression based optimal homomorphic encryption for secure fiber optic communication,” Optik, vol. 252, no. 1, pp. 1–15, 2022. [Google Scholar]
26. P. V. Rajaram and M. Prakash, “Intelligent deep learning based bidirectional long short term memory model for automated reply of e-mail client prototype,” Pattern Recognition Letters, vol. 152, no. 12, pp. 340–347, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |