Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.026161
Article

Efficient Medical Image Encryption Framework against Occlusion Attack

May A. Al-Otaibi1,*, Hesham Alhumyani1, Saleh Ibrahim2 and Alaa M. Abbas2

1Department of Computer Engineering, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
2Department of Electrical Engineering, College of Engineering, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
*Corresponding Author: May A. Al-Otaibi. Email: may.abdullah.alotaibi@gmail.com
Received: 16 December 2021; Accepted: 05 February 2022

Abstract: Image encryption has attracted a lot of interest as an important security application for protecting confidential image data against unauthorized access. An adversary with the power to manipulate cipher image data can crop part of the image out to prevent decryption or render the decrypted image useless. This is known as the occlusion attack. In this paper, we address a vulnerability to the occlusion attack identified in the medical image encryption framework recently proposed in [1]. We propose adding a pixel scrambling phase to the framework and show through simulation that the extended framework effectively mitigates the occlusion attack while maintaining the other attractive security features. The scrambling is performed using a separate chaotic map which is securely initialized using a secret key and a random nonce to deter chosen-plaintext attacks. Moreover, we show through simulation that the choice of chaotic map used for scrambling is irrelevant to the effectiveness of the scrambling algorithm against the occlusion attack.

Keywords: Medical image encryption; occlusion attack; scrambling

1  Introduction

Image encryption continues to attract attention of researchers developing new techniques for protecting the confidentiality of image data during both storage and transmission [1]. Image encryption departs from regular text encryption due to the low entropy, high spatial correlation, and large data size [2]. Many cryptographic techniques for realizing the confusion and diffusion goals have been proposed in the literature. In the literature, chaotic maps have been used in cryptography to achieve both goals due to their deterministic behavior that is but highly sensitivity to initial conditions [3]. The uses of chaotic maps in image encryption include histogram equalization [1], pixel scrambling [4], pseudorandom number generation [5], and construction of substitution boxes (S-boxes) [6].

The medical image encryption framework recently proposed in [1] provides a generic framework with demonstrable security features that can be implemented using a wide variety of cryptographic primitives. The framework uses a generic chaotic map component for whitening the histogram of input images and breaking their naturally high spatial correlation. The dynamic S-box component is used for adding an extra layer of confusion and increase the key space beyond the limits of brute force attacks. This framework has several advantages which set it apart from other schemes found in the literature. First, the generic chaotic map is initialized with a seed derived securely from the shared key and a random nonce. This technique deters chosen-plaintext attacks as well as pseudorandom number generator (PRNG) reset attacks. Furthermore, an image-dependent dynamic S-box is applied to both the plain image and the cipher image pixels to protect the chaotic map against cryptanalysis using chosen-plaintext or chosen-ciphertext attacks. The S-box itself is securely controlled by a secret key and a nonce to fend off cryptanalysis attacks through the S-box construction algorithm. In addition to its particular security features, the framework is computationally very efficient. It achieves encryption speeds fit for real-time operation because of the simplicity of its pixel processing pipeline, which employs just an XOR and S-box substitution operations. Although the framework achieves confidentiality, the lack of scrambling operations makes it susceptible to message tampering threats. An adversary may attempt to obstruct the delivery of a portion of the image in transit over a communication channel. This is known as the occlusion attack, which aims to prevent authorized receivers from successful decryption or to render the decrypted image useless [7].

The contribution of this work can be summarized in the following points.

•   We extend the framework proposed in [1] to include a final scrambling block and visually demonstrate the effectiveness of the extended framework in mitigating the occlusion attack.

•   We design the scrambling process to be image-dependent to deter chosen-plaintext attacks from descrambling cipher images.

•   We propose a new metric for measuring robustness against the occlusion attack and use it to evaluate the improvement due to scrambling in the proposed extended framework.

•   We simulate the extended framework with various chaotic maps and demonstrate its effectiveness irrespective of the chose chaotic map.

The rest of the paper is organized as follows. Section 2 presents some background and reviews relevant literature. The proposed extended medical image encryption framework is described in Section 3. Section 4 evaluates the performance of the proposed framework. Finally, the conclusion and future work are presented in Section 5.

2  Background and Related Work

Unlike text data, image data has a large size and high spatial correlation. Since their early use [8] and demonstration of their security features [9], chaotic maps have been employed in many image encryption algorithms [10–13]. Chaotic maps are non-linear and deterministic systems which possess features that are suitable for image encryption. Namely, a chaotic system is sensitive to initial conditions and shows pseudorandom behavior [3]. This means that a slight change in the parameters leads to different output in the chaotic maps [14]. Diverse image encryption techniques have been presented in the literature based on dynamic S-boxes [15,16]. Dynamic S-boxes represent an efficient secret key dependent substitution which increases confusion and serves as nonlinear components that deter linear and differential cryptanalysis [17].

Transmitted or stored images could be subject to different security issues, e.g., modification, eavesdropping, duplication, and noise. In this work, we focus on a type of attack known as the cropping attack or the occlusion attack. In this attack, the adversary attempts to obstruct selected cipher image pixels to stop or invalidate the decryption process. A common defense mechanism against the occlusion attack is pixel scrambling. By randomly and securely shuffling pixel locations, the effect of the occlusion attack can be transformed into speckle noise that affect the decrypted image at random pixel locations. The scrambling process must be reversible to facilitate the recovery of the original pixels during decryption [18].

There are several scrambling techniques in literature. The scrambling techniques varies in methods of scrambling an image under processing [19,20]. The authors in [19] introduced a new image scramble technique. They used a hash value to initiate the value of the piece-wise linear chaotic map (PWLCM) as a key for the global scramble. Then, a local scramble is performed by the Hilbert curve and H-fractal. Finally, they used ciphertext as feedback for enhancing the characteristics of confusion and diffusion. The technique presented in [20] for image scrambling is based on hash table structure and deoxyribonucleic acid (DNA) substitution. It used a closed hash in the structure table with the value of pseudo-random sequence to generate two different sequence keys. The two keys are used in pixel-scrambling of the plain image.

As a traditional method for scrambling some researchers used chaotic maps to scramble a plain image such as [21,22]. In [21], the authors introduced an implementation of a chaotic image encryption system in a transform domain that used Baker map. The scrambling process using The Baker map is performed by splitting the plain image into squares. Then, each square is divided into N rectangles and stretched horizontally to change the positions of the pixels. Also, in [22] the authors presented chaotic image encryption that used Baker map to scramble the plain image. The disadvantage of this method is the same histogram of the plain and scrambled images. Recently, the researchers used other methods for image scrambling such as in [23]. The authors of [23] used the Josephus problem to scramble the pixels of a plain image to new positions to perform the needed confusion for encryption. In [24], the authors designed a 2-dimensional logistic modulated sine coupling logistic chaotic map (LSMCL) to scramble the plain image. The scrambling process is achieved by performing two rounds of permutation. Another image encryption system in [25] utilized a cosine transform-based chaotic system (CTBCS) to produce chaotic maps with highly dynamical behavior to perform efficient scrambling.

In [21] introduced a method for scrambling by chaotic sub-block scrambling (CSBS) based on spiral transformation. The process starts by scanning pixels for a disorder, which is a change in the position of all pixels. In the scanning methods of scrambling process, it is difficult to evade pixels that do not change their positions. To overcome this problem, they used spiral transformations with sub-block scrambling. The authors of [26] designed an encrypt image technique which scrambles a plain image by chaotic coupled sine map (CCSM). The main purpose of using the CCSM is to a degree of freedom to the secure key space. The scrambling process is based on a chaotic sequence which resists the chosen and known-plaintext attacks. The scrambling process was used at the beginning of the encryption system. Their technique showed good performance against the occlusion or data loss attacks.

3  Proposed Framework

The proposed framework extends the framework in [1] to include a pixel scrambling phase. In this section, we describe the extended framework and describe the details of the newly added scrambling algorithm.

3.1 Encryption Process

The block diagram of the encryption process of the extended framework is shown in Fig. 1. The encryption process starts by using the PRNG to generate two random nonces NS and NC . The nonce, NS , is used with the secret S-box key, KS , to construct a dynamic S-box, S . The other nonce, NC , is encrypted using the secret chaotic map key, KS , to generate the chaotic map initialization vector ( IV ). Two chaotic maps are initialized using IV , namely the masking map and the scrambling map. After setting the initial state of the chaotic maps using IV , the chaotic maps are operated to generate a sequence of points of length equal to the number of pixels in the plain image. The two chaotic sequences, which are denoted M and P , are used for performing the XOR mask and the scrambling, respectively. The plain image is then processed pixel by pixel through an encryption pipeline that consists of a substitution using the dynamic S-box S , an XOR with the corresponding element of the chaotic mask M and another substitution using S . The resulting cipher pixel is then fed back to be XORed with the next plain pixel in cipher block chaining fashion as signified by the Z−1 operation. The resulting cipher image is finally scrambled using the chaotic sequence P as will be shown in the following subsection. To enable decryption, the two random nonces, NS and NC are included in the cipher message and transmitted to the receiver.

Figure 1: Encryption process of the proposed framework with scrambling

3.2 Decryption Process

To decrypt a cipher message, the receiver uses the shared keys KS and KC to decrypt the cipher message as follows. As shown in Fig. 2, the receiver first extracts both nonces, NS and NC , from the cipher message. The receiver constructs the same S-box using KS and NS then inverts it. The receiver simultaneously calculates the initialization vector IV from KC and NC and uses it to initialize the two chaotic maps. The chaotic maps are then used to generate two chaotic sequences, M and P , of length equal to the number of cipher image pixels. Equipped with the inverse S-box, S−1 , the chaotic mask, M , and the scrambling sequence, P , the receiver is ready to decrypt the cipher image pixels. First, P is used to descramble the image, as will be shown in detail in the next subsection. Then each descrambled cipher pixel is substituted using S−1 , XORed with the corresponding mask element, again substituted using S−1 , and then XORed with the previous cipher pixel to obtain the corresponding decrypted pixel.

Figure 2: Decryption process of the proposed framework

3.3 Scrambling Algorithm

The pixel scrambling process is the major security improvement proposed to extend the medical image encryption framework. The purpose of scrambling pixel locations is to distribute the effect of occlusion attack on diverse locations of the plain image, thus preserving a portion of the information in each locality of the image that is sufficient for keeping the decrypted image useful. The proposed scrambling and descrambling processes used for encryption and decryption are illustrated in Figs. 3 and 4, respectively.

The chaotic sequence, P , generated by the encryption scheme is paired with image pixels. The chaotic value-pixel pairs are subsequently sorted according to the chaotic value, resulting in the pixels being reordered in a pseudorandom order. In Fig. 3, for instance, an example matrix of 3 × 3 pixels is converted to a column in lexicographic order and each pixel is paired with a chaotic value. When the chaotic values are sorted in ascending order, the position of each pixel follows the position of the corresponding chaotic value. Finally, the pixels are stored in the new order and reshaped back to a 3 × 3 matrix to form the cipher image.

The descrambling algorithm works in a similar fashion. After obtaining the scrambling mapping, it is inverted to obtain the descrambling mapping.

Figure 3: Scrambling technique for the proposed framework

Figure 4: Descrambling procedure for the proposed framework

4  Performance Evaluation

The proposed framework is generic in the sense that any chaotic map can be invoked to generate the chaotic sequences M and P . However, to illustrate the usability of the framework, we implement it using two specific chaotic maps. For generating the chaotic mask, M , we use Arnold's cat map defined by Eqs. (1) and (2).

xn=(2xn−1+yn−1)mod1 (1)

yn=(xn−1+yn−1)mod1 (2)

where (x0,y0) is the initial state and (xn,yn) is the state at the n th iteration.

Similar to [1], the initial state of Arnold's cat map (x0,y0) is derived from the initialization vector, IV , using Eq. (3). The chaotic map is first iterated NT=512 times to cancel the transient effect of the initial state thus increasing it key sensitivity.

(x0,y0)=2−53(∑i=053⁡2ibi,∑i=053⁡2ibi+64) (3)

where bi is the i th bit of the initialization vector, IV .

As in [1], the mask bytes ⟨mi⟩i=1L are extracted from the chaotic sequence ⟨(xi,yi)⟩i=1L , where L is the number of image pixels, using Eq. (4)

mi=(224xi+NT)mod256 (4)

For generating the scrambling sequence, P , we use Baker map defined by Eqs. (5) and (6).

xn={xn−1p,0≤xn−1<pxn−1−p1−p,p≤xn−1<1 (5)

yn={pyn−1,0≤xn−1<p1−(1−p)yn,p≤xn−1<1 (6)

where (x0,y0) is the initial state, (xn,yn) is the state at the n th iteration, and p is a parameter.

The initial state of Baker map (x0,y0) is derived from the initialization vector, IV , using the same Eq. (3) and the parameter p is set to 0.6111.

In this following subsection, the proposed scrambling technique is examined under the application of occlusion attack. Then we study the remaining security metrics of the proposed framework.

4.1 Occlusion Attack Analysis

To analyze the robustness of the proposed framework against occlusion attacks, we perform the following test. A cipher image is occluded with a black block occupying 1/2,1/4, and 1/8 of the size of the image. Then the occluded cipher image is decrypted using the usual decryption process. The top row of Fig. 5a shows three cipher images corresponding to a magnetic resonance image (MRI) plain image with 1/2, 1/4, and 1/8 of the image zeroed out. The second row or images shows the direct result of decrypting each of the occluded images using the proposed framework with scrambling. The bottom row shows the result of denoising each of the decrypted images using 3×3 median filter. In contrast, Fig. 5b shows the effect of the occlusion attack on the decryption of cipher images encrypted with the system in [1], which lacks the scrambling phase. The results indicate that the proposed technique can effectively recover a recognizable version of the image even at 50% occlusion. The decrypted images obtained from the proposed framework with scrambling have a visually satisfactory quality with respect to the percentage of occlusion. The proposed technique successfully resists this type of attack because the scrambling process distributes the pixels of the occluded area through the whole image. Figs. 5c and 5d repeats the same test for a sample computerized tomography scan (CT scan) image, which again confirm the effectiveness of scrambling in mitigating the occlusion attack.

To numerically evaluate the robustness of an encryption scheme against the occlusion attack, previous works traditionally used peak signal-to-noise ratio (PSNR) as a metric. The PSNR is defined as follows [27].

PSNR(O,R)=10log10(2k−1)2MSE(O,R), (7)

MSE(O,R)=1M×N∑i=1M⁡∑j=1N⁡[Oi,j−Ri,j]2, (8)

where k is the number of bits per pixel, M×N is the size of the image, O is the original image, and R is the decrypted image. However, we observed that the PSNR metric is inaccurate and can sometimes be misleading. So, we propose a new robustness metric denoted Median Filter Correlation (MFC). MFC is based on the correlation between the original image and the decrypted image denoised using median filter as expressed by the following formula.

MFC(O,R)=Corr(O,F(R)), (9)

where F(R) denotes the output of a 3 × 3 median filter applied to the decrypted image R , and Corr(O,D) denotes the correlation between the original image, O , and the denoised decrypted image, D=F(R) . Tab. 1 shows the results of PSNR and MFC for the proposed technique in comparison to the framework in [1], for varying occlusion ratios. It can be observed that the PSNR metric doesn't accurately reflect the achieved mitigation of the occlusion attack visually detectable from Fig. 5. On the other hand, the proposed MFC metric indicates a significant mitigation of the occlusion attack.

Tab. 2 presents a comparison between the robustness of the proposed framework and the relevant medical image encryption scheme in [28]. As evident from the results in Tab. 1, the values of the PSNR metric for the same encryption scheme depend on the choice of plain image. For the comparison to be fair, we must use the same test image used by [28], which is shown in Fig. 6. The result of the comparison demonstrates that the proposed framework is on par with related medical image encryption scheme [28].

Figure 5: Occlusion attack analysis for the proposed system (shown in (a) and (c)), in comparison to framework [1] without scrambling (shown in (b) and (d))

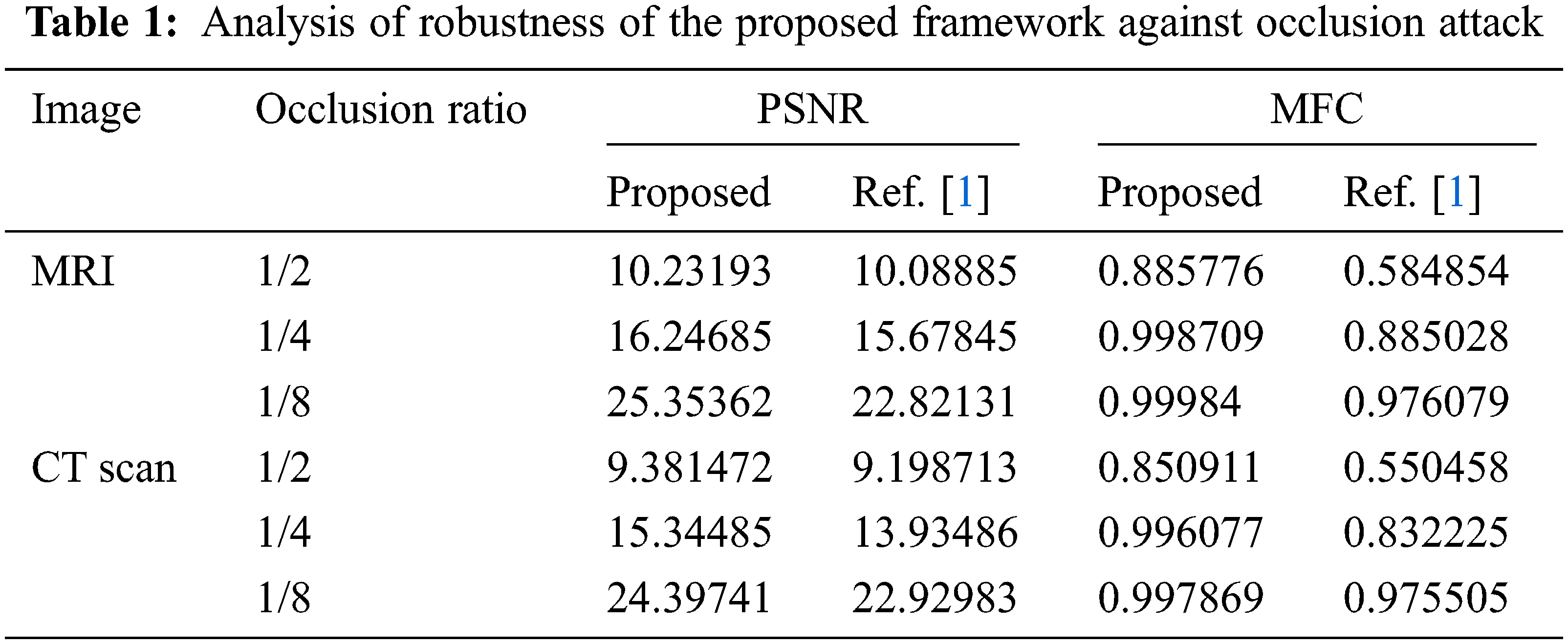
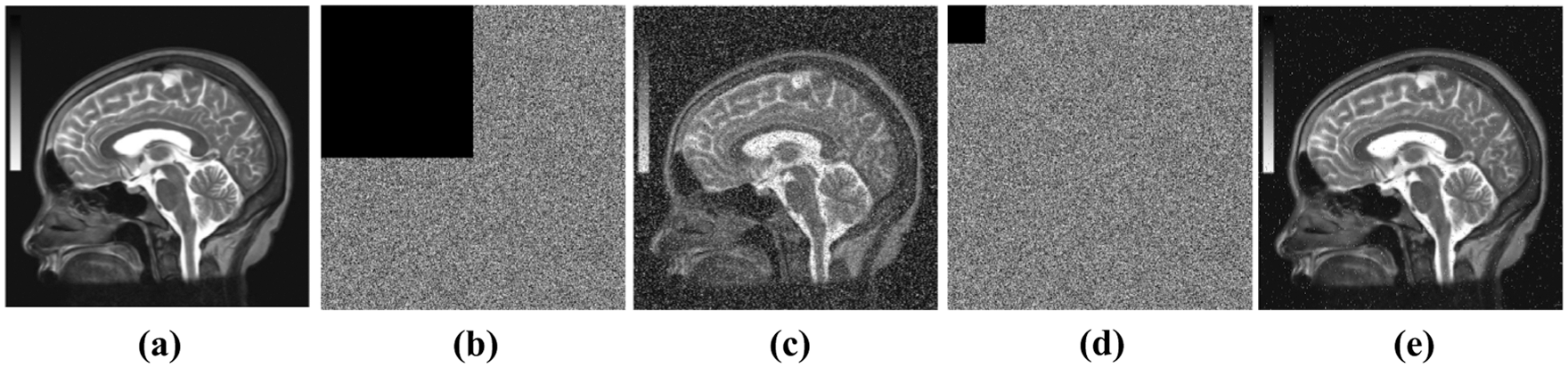
Figure 6: Image used for occlusion robustness. (a) plain image, (b) 1/4 occluded cipher image, (c) 1/4 ocluded decrypted image, (d) 1/64 occluded cipher image, (e) 1/64 decrypted image

4.2 Choice of Chaotic Maps

The results in the previous section were obtained using two specific chaotic maps for generating the whitening mask and performing the pseudorandom permutation of pixels, namely Arnold's cat map and baker's map, respectively. In this section, we demonstrate that the choice of chaotic maps doesn't affect the immunity of the framework to occlusion attacks by performing two experiments. In the first experiment, we fix the whitening chaotic map and change the chaotic map that drives the scrambling algorithm. The maps used for scrambling in this experiment are Arnold's cat map, baker map, Henon map, standard map, sine logistic map [29], 2D sine-chaotified Henon map (SCHenon) [30], 2D sine chaotified sine logistic map (SCSL) [30], and logistic-modulated-sine-coupling-logistic chaotic map (LSMCL) [31]. With each scrambling chaotic map, we perform the PSNR analysis at different ratios of occlusion. The results shown in Fig. 7 and Tab. 3 shows that at 1/2 occlusion, the PSNR is approximately 10.24 ± 0.02 regardless of the chaotic map used for whitening. Similarly, at 1/4, 1/8, and 1/16 occlusion, the PSNR are approximately 13.25 ± 0.02, 16.25 ± 0.02, and 19.25 ± 0.02, respectively.

In the second experiment, we fix the scrambling chaotic map and vary the chaotic map used for masking. The occlusion attack PSNR results are shown in Fig. 8 and Tab. 4. Like with the first experiment, the results do not show any significant variance with respect to the whitening chaotic map.

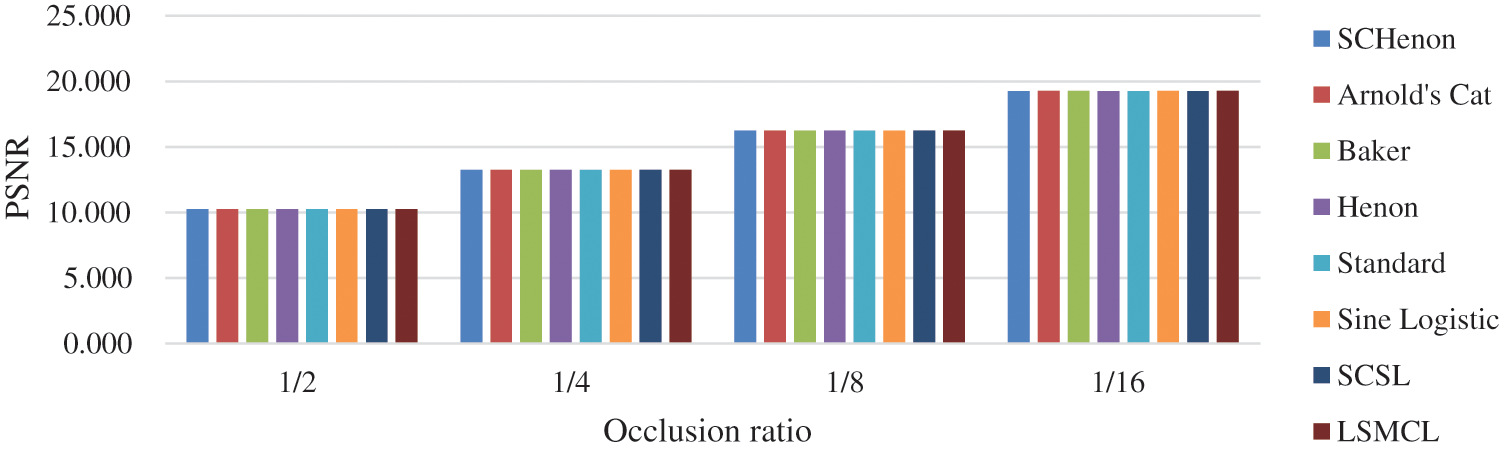
Figure 7: Effect of the scrambling chaotic map on the PSNR metric at different occlusion ratios

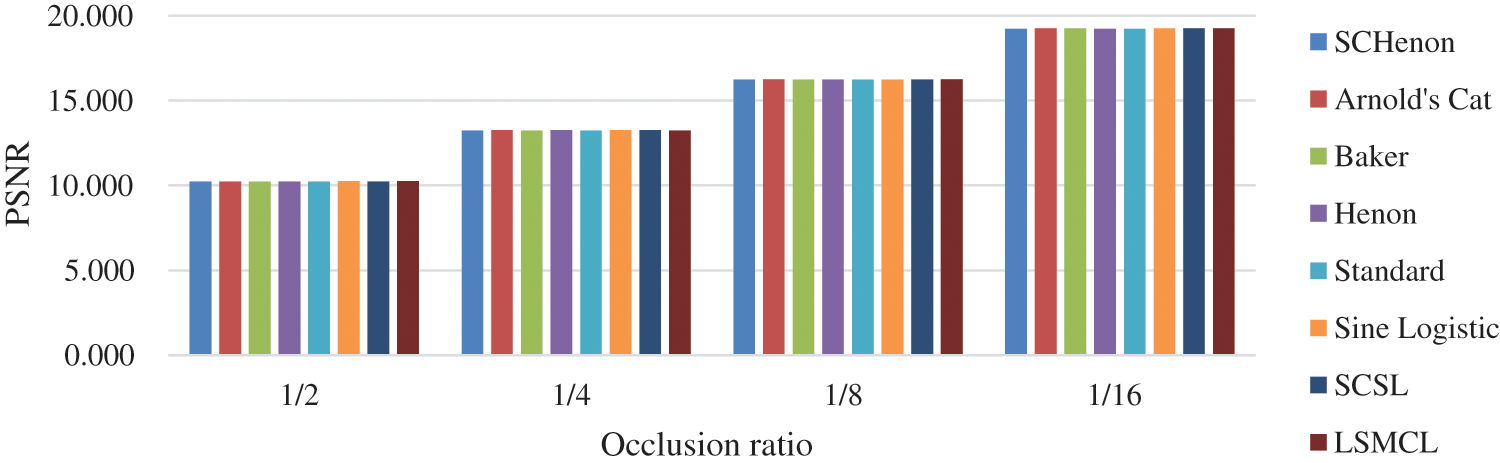
Figure 8: Effect of the whitening chaotic map on the PSNR at different occlusion ratios

4.3 Security Analysis

In this section, we summarize the results of common statistical analysis, plain image sensitivity analysis, and key sensitivity analysis for the proposed results and compare them to relevant medical image encryption scheme. The statistical analysis results in Tab. 5 show that the proposed framework is highly resistant to statistical ciphertext-only attacks. It can be observed that the spatial correlation of cipher images produced by the proposed framework is significantly better than that of [1], because of the effect of the additional scrambling phase. Differential analysis test results shown in Tab. 6 indicate that the proposed framework is highly sensitive to changes in plain images and cipher images, thus resisting differential cryptanalysis. The key sensitivity analysis results summarized in Tab. 7 indicate that the proposed framework is highly sensitive to KC and thus can resist related key attacks.

5  Conclusion and Future Work

By adding a scrambling phase to the framework in [1], the proposed framework could successfully mitigate occlusion attacks. This improvement makes the proposed framework applicable to environments where such a threat exists. One potential situation for applying the proposed scheme is when encrypted data is stored in a distributed storage system over multiple servers to reduce the damage caused by a compromised server. A scrambled cipher image generated by the proposed framework can be split into pieces, each of which is stored in a different server. If one of the servers is compromised and the adversary attempts to destroy the image data stored in the system by deleting the portion of the data stored in the compromised server, the proposed framework will successfully mitigate the data loss and partially restore the image data. The level of data loss caused by a compromised server can be limited by increasing the number of servers onto which pieces of the cipher image are stored. The results of this framework show that if a medical cipher image is split into four parts and distributed over four servers, the plain image can be successfully decrypted with correlation 99.8% after applying a median filter. An interesting future research is to study the efficiency of different scrambling techniques within the proposed framework and to compare their respective robustness against the occlusion attack.

Funding Statement: This research was funded by Taif University Researchers Supporting through Taif University, Taif, Saudi Arabis (Project Number TURSP-2020/216).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Ibrahim, H. Alhumyani, M. Masud, S. S. Alshamrani, O. Cheikhrouhou et al., “Framework for efficient medical image encryption using dynamic S-Boxes and chaotic maps,” IEEE Access, vol. 8, pp. 160433–160449, 2020. [Google Scholar]

 2.  I. F. Elashry, O. S. F. Allah, A. M. Abbas, S. El-Rabaie and F. E. A. El-Samie, “Homomorphic image encryption,” Journal of Electronic Imaging, vol. 18, no. 3, pp. 14, 2009. [Google Scholar]

 3.  W. K. S. Tang and Y. Liu, “Formation of high-dimensional chaotic maps and their uses in cryptography BT - chaos-based cryptography: Theory, algorithms and applications,” In: L. Kocarev, S. Lian (Eds.Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 99–136, 2011. [Google Scholar]

 4.  Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-Box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]

 5.  Z. M. Z. Muhammad and F. Ozkaynak, “An image encryption algorithm based on chaotic selection of robust cryptographic primitives,” IEEE Access, vol. 8, pp. 56581–56589, 2020. [Google Scholar]

 6.  S. Ibrahim and A. Alharbi, “Efficient image encryption scheme using Henon map, dynamic S-boxes and elliptic curve cryptography,” IEEE Access, vol. 8, pp. 194289–194302, 2020. [Google Scholar]

 7.  A. Belazi, M. Talha, S. Kharbech and W. Xiang, “Novel medical image encryption scheme based on chaos and DNA encoding,” IEEE Access, vol. 7, pp. 36667–36681, 2019. [Google Scholar]

 8.  J. Fridrich, “Image encryption based on chaotic maps,” in 1997 IEEE Int. Conf. on Systems, Man, And Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, vol. 2, pp. 1105–1110, 1997. https://ieeexplore.ieee.org/document/638097. [Google Scholar]

 9.  G. Jakimoski and L. Kocarev, “Chaos and cryptography: Block encryption ciphers based on chaotic maps,” IEEE Transactions on Circuits and Systems, vol.48, pp. 163–169, 2001. [Google Scholar]

10. H. Alhumyani, “Efficient image cipher based on baker map in the discrete cosine transform,” Bulgarian Academy of Sciences-Cybernetics and information Technologies, vol. 20, no. 1, pp. 68–81, 2020. [Google Scholar]

11. Z. Hua, Y. Zhou and H. Huang, “Cosine-transform-based chaotic system for image encryption,” Information Sciences, vol. 480, no. 8, pp. 403–419, 2019. [Google Scholar]

12. J. A. P. Artiles, D. P. B. Chaves and C. Pimentel, “Image encryption using block cipher and chaotic sequences,” Signal Processing: Image Communication, vol. 79, pp. 24–31, 2019. [Google Scholar]

13. Q. Liu and L. Liu, “Color image encryption algorithm based on DNA coding and double chaos system,” IEEE Access, vol. 8, pp. 83596–83610, 2020. [Google Scholar]

14. L. Kocarev, “Chaos-based cryptography: A brief overview,” IEEE Circuits and Systems Magazine, vol. 1, no. 3, pp. 6–21, 2001. [Google Scholar]

15. C. Zhu, G. Wang and K. Sun, “Cryptanalysis and improvement on an image encryption algorithm design using a novel chaos based s-box,” Symmetry, vol. 10, no. 9, pp. 399, 2018. [Google Scholar]

16. U. Hayat and N. A. Azam, “A novel image encryption scheme based on an elliptic curve,” Signal Processing, vol. 155, no. 13, pp. 391–402, 2019. [Google Scholar]

17. F. Özkaynak, “Brief review on application of nonlinear dynamics in image encryption,” Nonlinear Dynamics, vol. 92, no. 2, pp. 305–313, 2018. [Google Scholar]

18. Z. J. Huang, S. Cheng, L. H. Gong and N. R. Zhou, “Nonlinear optical multi-image encryption scheme with two-dimensional linear canonical transform,” Optics and Lasers in Engineering, vol. 124, no. 16, pp. 105821, 2020. [Google Scholar]

19. X. Zhang, L. Wang, Z. Zhou and Y. Niu, “A chaos-based image encryption technique utilizing hilbert curves and H-fractals,” IEEE Access, vol. 7, pp. 74734–74746, 2019. [Google Scholar]

20. X. Wang and L. Liu, “Image encryption based on hash table scrambling and DNA substitution,” IEEE Access, vol. 8, pp. 68533–68547, 2020. [Google Scholar]

21. E. A. Naeem, M. M. Abd Elnaby, N. F. Soliman, A. M. Abbas, O. S. Faragallah et al., “Efficient implementation of chaotic image encryption in transform domains,” Journal of Systems and Software, vol. 97, pp. 118–127, 2014. [Google Scholar]

22. H. M. Elhoseny, H. E. H. Ahmed, A. M. Abbas, H. B. Kazemian, O. S. Faragallah et al., “Chaotic encryption of images in the fractional Fourier transform domain using different modes of operation,” Signal Image and Video Processing, vol. 9, no. 3, pp. 611–622, 2015. [Google Scholar]

23. Z. Hua, B. Xu, F. Jin and H. Huang, “Image encryption using josephus problem and filtering diffusion,” IEEE Access, vol. 7, pp. 8660–8674, 2019. [Google Scholar]

24. H. Zhu, Y. Zhao and Y. Song, “2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption,” IEEE Access, vol. 7, pp. 14081–14098, 2019. [Google Scholar]

25. Z. Hua, Y. Zhou and H. Huang, “Cosine-transform-based chaotic system for image encryption,” Information Sciences, vol. 480, no. 8, pp. 403–419, 2019. [Google Scholar]

26. B. Y. Irani, P. Ayubi, F. A. Jabalkandi, M. Y. Valandar and M. J. Barani, “Digital image scrambling based on a new one-dimensional coupled Sine map,” Nonlinear Dynamics, vol. 97, no. 4, pp. 2693–2721, 2019. [Google Scholar]

27. Y. Zhang, B. Xu and N. Zhou, “A novel image compression-encryption hybrid algorithm based on the analysis sparse representation,” Optics Communications, vol. 392, no. 11, pp. 223–233, 2017. [Google Scholar]

28. X. Chai, J. Zhang, Z. Gan and Y. Zhang, “Medical image encryption algorithm based on Latin square and memristive chaotic system,” Multimedia Tools and Applications, vol. 78, no. 24, pp. 35419–35453, 2019. [Google Scholar]

29. Z. Hua, Y. Zhou, C. M. Pun and C. L. P. Chen, “2D Sine Logistic modulation map for image encryption,” Information Sciences, vol. 297, pp. 80–94, 2015. [Google Scholar]

30. Z. Hua, Y. Zhou and B. Bao, “Two-dimensional sine chaotification system with hardware implementation,” IEEE Transactions on Industrial Informatics, vol. 16, no. 2, pp. 887–897, 2020. [Google Scholar]

31. H. Zhu, Y. Zhao and Y. Song, “2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption,” IEEE Access, vol. 7, pp. 14081–14098, 2019. [Google Scholar]

32. P. T. Akkasaligar and S. Biradar, “Selective medical image encryption using DNA cryptography,” Information Security Journal, vol. 29, no. 2, pp. 91–101, 2020. [Google Scholar]

33. A. M. Abbas, A. A. Alharbi and S. Ibrahim, “A novel parallelizable chaotic image encryption scheme based on elliptic curves,” IEEE Access, vol. 9, pp. 54978–54991, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.