DOI:10.32604/iasc.2022.029657

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.029657 |  |
| Article |
Consensus Mechanism of Blockchain Based on PoR with Data Deduplication
1Engineering Research Center of Digital Forensics of Ministry of Education, School of Computer Science, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Shenzhen Research Institute, Nanjing University of Aeronautics and Astronautics, Shenzhen, 518000, China
3Department of Cyber Security at VaporVM, Abu Dhabi, 999041, United Arab Emirates
4School of Computer Engineering, Jiangsu University of Technology, Changzhou, 213001, China
*Corresponding Author: Dan Chen. Email: chen8891dan@163.com
Received: 08 March 2022; Accepted: 14 April 2022
Abstract: As the basis of cloud computing, distributed storage technology mainly studies how data centers store, organize and manage data. Blockchain has become the most secure solution for cloud storage due to its decentralization and immutability. Consensus mechanism is one of the core technologies of blockchain, which affects the transaction processing capability, security and scalability of blockchain. The current mainstream consensus algorithms such as Proof of Work, Proof of Stake, and Delegated Proof of Stake all have the problem of wasting resources. And with the explosive growth of data, cloud storage nodes store a large amount of redundant data, which inevitably increases storage overhead and computing cost. To this end, we propose to use the Proof of Retrievability with deduplication algorithm as the consensus mechanism of the blockchain system and design a blockchain consensus protocol suitable for distributed storage. First, the data integrity verification protocol in the scheme guarantees that storage nodes correctly store the data they promise to store. Second, the deduplication algorithm in the protocol can optimize data auditing, greatly reduce the need for data storage space, and improve the scalability of data transmission. In addition, the scheme uses ring signatures in the audit process to ensure user anonymity and data unlinkability, while providing highly reliable data storage, and ensuring data storage security through blockchain. Finally, we demonstrate the security of the proposed scheme and evaluate its performance. The evaluation results show that our scheme is efficient and scalable.
Keywords: Integrity verification; consensus; blockchain; deduplication
With the emergence and gradual maturity of technologies such as 5G, cloud computing, and artificial intelligence, the future will be an era of data explosion. With the emergence of massive data, how to store this data and how to use it rationally has become a problem that most companies and even experts think about. Compared with traditional storage networks, distributed storage has more advantages. The distributed system structure combines a large number of ordinary servers into a whole and uses server positioning to store information [1]. It has the advantages of high reliability, data consistency, and high performance. However, in the face of the explosive growth of massive data, it is necessary to solve the problems of data evolution from single internal small data to multiple dynamic big data, real-time data collection, and excessive data redundancy. Distributed storage will face many challenges in the future.
Peer-to-peer (P2P) architecture embodies a key concept of Internet technology, and one of its important goals is to allow all nodes on the network to provide resources, including bandwidth, storage space, and computing power [2]. This technology has been extensively researched, and users can use resources more efficiently and access data more quickly. The distributed nature of P2P network also increases failure-proof robustness by replicating data across multiple nodes. And in a general P2P network, nodes do not need to rely on a central index server to discover data, so the system will not have a single point of collapse. In fact, hundreds of well-known projects with huge user bases have already formed considerable momentum, such as Ethereum, filecoin, Fabric, etc.
Research on consensus algorithms in P2P network has started a long time ago. Bitcoin’s Proof of Work (POW) is an innovation of great significance. It cleverly integrates the functions of Bitcoin’s issuance, transaction payment and data verification through computing power competition, crossing the gap of byzantine fault tolerance in distributed systems. However, it cannot meet the needs of high throughput and timely processing of general applications. PeerCoin (PPC) first uses Proof of Stake (POS) to replace the proof of work based on hashing power in PoW, and the node with the highest stake in the system rather than the highest computing power obtains the block accounting right [3]. However, since the maximum rights and interests of nodes cannot be legally guaranteed, the PoS consensus mechanism still has the possibility of centralization. Delegated Proof of Stake (DPOS) is a democratic version of the POS consensus algorithm, and token holders can participate in voting [4]. Because they do not require high computing power, they are more scalable. However, the DPoS mechanism still needs to determine the accounting rights through voting and other processes, which will have a certain impact on the throughput. How to choose or design a suitable consensus algorithm for a specific business scenario is a major problem in the implementation of blockchain applications at this stage [5].
The current distributed storage solution cannot meet the persistent storage market demand [6]. First of all, if no other node pulls data, only the local machine has an orphaned copy of the data. Once the local machine fail, the data will be lost, and there is no data integrity monitoring and automatic data reconstruction. Second, the existing solution lacks a strong economic model, so it cannot use a large-capacity database as its service model [7]. A reliable economic model requires that at least a majority of nodes provide value to other nodes and volunteer to support the system. Therefore, an incentive mechanism is needed for participants to voluntarily provide and use resources.
Our design combines data integrity verification with the blockchain technology. Facing the persistent storage market demand, it provides a powerful economic model. As an incentive layer in distributed storage, it can better realize data storage and transactions. The main contributions are as follows:
1) We use Proof of Retrievability (POR) with the deduplication algorithm as a new consensus mechanism and design a safe and efficient distributed storage system based on blockchain. The nodes on the blockchain form a collaborative network, and the nodes can jointly maintain data verification records.
2) We use ring signature technology in the consensus protocol to achieve data owner anonymity and file unlinkability by introducing more users in the file signature process and protect user outsourced data from privacy leaks and brute force attacks.
3) We add adeduplication algorithm in the verification process to optimize the data audit and storage space of storage nodes, save network bandwidth for data transmission, and improve the scalability of the solution.
There has been a lot of research on data integrity verification and blockchain-based consensus mechanisms.
In 2007, Ateniese et al. [8] first proposed a Provable Data Possession (PDP) protocol that can verify the integrity of cloud data. This scheme uses a probabilistic strategy to complete integrity verification, while using RSA Homomorphically Verifiable Tags (HVTs) to aggregate evidence into a small value. This not only reduces the computing overhead of cloud storage, but also greatly reduces the communication overhead of the protocol due to the characteristics of signature aggregation. In 2007, Juels et al. [9] proposed another classic verification scheme, POR scheme. The scheme effectively identifies the damage of the outsourcing documents by implanting some “sentinel” checking data blocks in the outsourcing documents and uses the Reed-Solomon error correction code to perform fault-tolerant preprocessing on the outsourced files, so as to restore the damaged data files. However, in this scheme, the data owner needs to consume huge computational cost for erroneous data recovery and original data encryption. In 2013, Yang et al. [10] proposed a cloud data privacy protection protocol, which can better solve the security risk of data confidentiality in the public audit process in Compact Proofs of Retrievability (CPOR). The protocol improves the overall performance of the scheme by reducing the number of data tags by using data fragmentation technology and HVT. In 2017, Hiremath et al. [11] introduced an efficient data auditing method that uses the AES encryption algorithm and SHA-2 (Secure Hash Algorithm), utilizing a third-party auditor to perform integrity checks. In this method, the user encrypts the data using the AES algorithm and obtains a message digest of the encrypted data using SHA-2. Encrypted data is sent to the cloud server, and message digests are sent to a third-party auditor (TPA) that performs data integrity checks. In 2018, Han et al. [12] proposed a pairless integrity verification scheme based on Schnorr signatures. However, this scheme suffers from computational errors in the domain and requires a third party. In 2019, Zhang et al. [13] proposed a general construction method for PoR based on Linear Homomorphic Structure Preserving Signatures (LHSPS). The unforgeability of LHSPS ensures the authenticity and tractability of the PoR scheme. In 2020, Yu et al. [14] designed a more efficient pairing-free scheme based on blockchain. However, this scheme can only be applied to private audits.
In 2008, Satoshi Nakamoto first introduced it into the blockchain in his paper [15], which is the underlying technology of Bitcoin. Traditional transactions require a centralized and trusted institution. The confirmation and recording of transactions are completely dependent on trusted institutions, which can lead to many issues such as transaction costs, efficiency and security. PoW is the consensus algorithm used in Bitcoin. Its core idea is to allocate accounting rights and rewards through the competition of computing power among nodes. Based on the information from the previous block, different nodes calculate a specific solution to a mathematical problem [16]. This math problem is difficult to solve. The first node to solve this math problem can create the next block and be rewarded with a certain number of bitcoins. The earliest application of PoS is PPCoin. In PoS, digital currency has the concept of coin age. The coin age of a coin is its value multiplied by the time period since it was created. The longer a node holds coins, the more power it has in the network. Coin holders will also receive certain rewards based on the coin age. In the design of PPCoin, mining is also required to obtain bookkeeping rights. The formula is proof hash < coin age * target. The proof hash is the combined hash of the weight factor, the unspent output value, and the fuzzy sum of the current time [17]. With the concept of coin age, blockchains no longer rely solely on POW. This effectively solves the resource waste problem in PoW. BitShares is an example of DPoS [18]. In a blockchain with DPoS, each node can choose witnesses based on their stake. In the entire network, the top N witnesses who participate in the election and get the most votes have the right to keep accounts. The number of witnesses, N, is defined as at least 50% of voting stakeholders believe there is sufficient decentralization.
2.3 The Combination of Integrity Verification and Consensus Mechanism
In 2014, Miller et al. proposed a new scheme, Permacoin [19], which modified Bitcoin to produce highly decentralized file storage and reduce the overall waste of Bitcoin. Permacoin encourages participants to store locally, ensuring a high probability of complete data recovery, enabling robust file distribution. In 2018, Hao et al. [20] proposed a blockchain-based decentralized model called DCOM (Decentralized COllaborative verification Model). The model consists of a cooperative network of validating peers, each of which maintains a record of validation via a blockchain. Francati et al. [21] proposed a blockchain-based decentralized storage system—Audita in 2019. It can be built on multiple blockchain systems and uses an enhanced network of participants including storage nodes and block creators.
Our goal is to provide a distributed storage system with proof of retrievability and deduplication algorithms as consensus mechanisms, incentivizing a majority of nodes to participate in storage services (see Fig. 1). Because centralized storage cannot guarantee user privacy and user information is easily leaked, we use ring signatures and blockchain to achieve distributed storage. The system model consists of three entities: Data Owner (DO), Cloud Storage Provider (CSP), Third-Party Auditor (TPA).
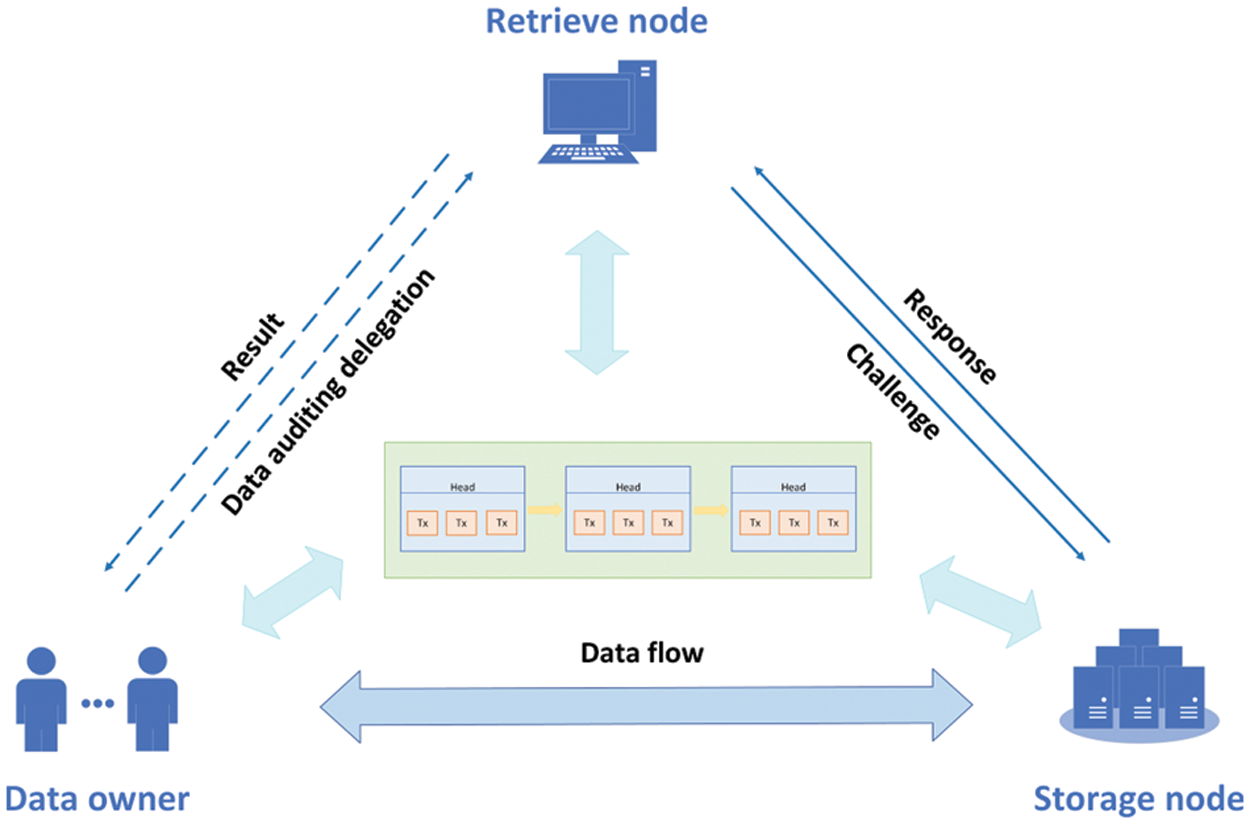
Figure 1: System model
Data owner (common node): The data owner is a node that owns a series of files that need to be stored on the cloud.
Cloud storage provider (storage node): The cloud storage provider is a node that provides cloud storage services to data owners.
Third-party auditor (retrieval node): The third-party auditor is a node that provides retrieval services for users.
The entire design includes the following functions: file storage, deduplication, privacy protection, and block election.
File storage. To store files and ensure data integrity, the data owner uses proof of retrievability and encodes the files. Then the data owner sends a storage request, agrees on a price with the cloud storage provider, and signs a contract on the blockchain [22]. Cloud storage providers accept files and are checked by retrieval nodes for the duration of the contract. The retrieval proof will be issued as a transaction, including a reference to the storage contract in the blockchain and the storage integrity proof. The retrieval node and storage node will also receive a portion of the service incentive [23].
Deduplication. In order to meet the optimization of storage capacity in cloud storage, a deduplication algorithm is added to the solution [24]. In terms of data integrity verification, duplicate identity authentication tags are not introduced, thereby ensuring that communication costs and computing costs remain unchanged. At the same time, a polynomial-time adversary without a complete data file cannot pass the verification process [25]. The algorithm greatly reduces the demand for physical storage space and brings many benefits to the entire system, such as saving the total storage cost and management cost; efficiently controlling the accelerated growth of data; increasing effective storage space and improving storage efficiency; saving network bandwidth for data transmission [26].
Privacy protection. User privacy is one of the most important aspects of privacy protection. The system model needs to effectively manage and control personally identifiable information and enhance the confidentiality of documents. To do this, we use ring signatures to construct our scheme [27].
Multiple users participate in the file storage stage. During the signing process, the public key of everyone is used to sign the file, including the storage node, which makes the file signature untraceable. Unrelated nodes in the blockchain system cannot trace the sender of the file [28]. When other nodes verify the transaction, they can only determine that the file signature is one of many public keys, but cannot locate the specific sender of the file. At the same time, Sybil attacks and outsourcing attacks initiated by some malicious storage nodes are prevented.
Election blocks. When data owners store data, they need to issue storage orders and a certain amount of blockchain tokens to reward storage nodes and retrieval nodes [29]. Storage nodes and retrieval nodes receive corresponding rewards after completing storage and retrieval services, and record transaction orders and storage proofs on the blockchain [30]. In our model, the blockchain will elect a leader based on the current storage node capacity to generate new blocks.
Inspired by the audit scheme [31], we briefly define the security model of the scheme.
Initialization: Challenger C first generates a random file and runs the algorithm to generate the file key pair (pk, sk) and the encoding block {mi}. Then, C sends the public parameter para to the adversary A.
Query: The adversary randomly selects a block mj ∈ {mi} and queries the challenger C to obtain the corresponding hash value and signature until the query time reaches qs.
Challenge: C randomly challenges A to some block Chalt that has not yet been queried. According to Chalt, generate aggregate signature σt and proof Prooft, and return them to C.
Verification: Check that σt is consistent with Proof. If they agree, A wins, otherwise, A loses.
To enhance security and privacy protection, our proposed distributed storage scheme should satisfy validity, unforgeability and privacy protection. Defined as follows:
1) Effectiveness
Validity means that for any security parameter λ and a negligible function negl( ⋅ ), all proofs generated by honest nodes must pass verification, while proofs generated by malicious nodes cannot pass verification.
2) Unforgeability
Unforgeability means that no adversary to our verification scheme can make a verifier accept a proof of retrievability protocol instance with non-negligible probability unless it responds with a correctly computed value.
3) Privacy protection
Privacy protection means that the signer of the file identification in the scheme has unconditional anonymity, that is, for any algorithm A, any set of users R = pk1, pk2, …, pkn, the probability P[pk = pk′] is all 1/2, where
4 Construction of the Proposed Consensus Protocol
4.1 Notation and Preliminaries
In the scheme we have used the following symbols (as shown in Tab. 1).

We use λ to denote the security parameter. F represents the encoded file after user preprocessing, where F = (m1, m2, …, mn). H( ⋅ ) represents a one-way hash function. G is the base point on the elliptic curve. Let A denotes an algorithm, then, the notation a ← A(x) denotes an algorithm A that takes an input x and gets an output a. e is a bilinear map in the scheme.
Let G1, G2 be additive group and multiplicative group of order g, respectively, and assume that g1 is the generator of G1. Suppose that in the group G1, G2, the discrete logarithm problem is intractable. A bilinear mapping pair can be defined as e:G1 × G1 → G2, and satisfy the following properties:
1) Double mapping.
2) Non-degenerate. If e(g1, g2) = 1, there is g2 ∈ G1, then there is g1 = O.
3) Computability. Efficient algorithms exist to compute e(g1, g2) for g1, g2 ∈ G1.
The POS scheme allows the scheme to allow user V to outsource the storage of data D to server P, and then repeatedly check whether P is still storing F. PDP and POR were introduced independently around the same time in 2007 [32]. Since then, the concept of POS has popularized PDP and PoR. The main difference between the POR model and the PDP model is that in the preprocessing stage, the use of error correction code or other codes to encode the file data can not only verify the integrity of the file, but also recover damaged data [33]. Adding the two algorithms of Encode () and Extract() to the PDP model can be extended to a POR model.
Blockchain refers to a new distributed infrastructure and computing paradigm that utilizes blockchain data structures to verify and store data, utilizes distributed node consensus algorithm to generate and update data, utilizes cryptography to ensure the security of data transmission and access, and utilizes smart contracts composed of automated script codes to program and manipulate data [34]. A blockchain is basically a series of linked blocks of data. Blocks are added to the blockchain through consensus of the majority of nodes in the system. Each block contains a block header and a sequence of transactions, each block header contains a link pointer to the block header of the previous block, the merkle root of the tree-like transaction information, and a timestamp [35]. In this way, the blocks are linked together in chronological order. Cryptographic hashing algorithms ensure that transaction data in each block is immutable and that linked blocks in the blockchain cannot be tampered with.
In 2001, Rivest et al. [36] proposed a new type of signature technique called ring signatures in the context of how to leak secrets anonymously. Suppose there are n users, and each user ui has a public key yi and a corresponding private key xi. Ring signature is a signature scheme that can realize the unconditional anonymity of the signer. It mainly consists of the following algorithms:
KeyGen. A probabilistic polynomial time (PPT) algorithm with the security parameter k as input and the public and private keys as output. Here it is assumed that KeyGen generates a public key yi and a private key xi for each user ui.
Sign. A PPT algorithm, after inputting message m and the public key L = {y1, y2, …, yn} of n ring members and the private key xs of one of the members, generates a signature R for message m, in which a parameter in R is a ring according to certain rules.
Verify. A deterministic algorithm that, after inputting (m, R), if R is the ring signature of m, output “True”, otherwise output “False”.
In this section, we describe the construction of the proposed distributed storage consensus protocol.
KeyGen:
Given the security parameter λ, the TA selects a random number
Data owner DOi randomly selects
Among them,
Setup:
Data owner DOs encodes the file F, F′ ← F, F′ = {mij}, 1 ≤ i ≤ n, 1 ≤ j ≤ t − 1. Randomly chooses the filename
Selects a signature public key set R = {spk1, spk2, …, spkn}, which contains the CSP’s signature public key for verification, randomly selects
Among them,
Chooses
where name is the content of the signature here, and the ring signature of the file name name by the data owner DOs is output as
For each file block mi, every file block generates an authentication tag
Data owner DOs stores {F′, τ, σi} into CSP.
Challenge:
To verify data integrity, the third party first uses spks to verify τ and the signature on τ. Terminate if the signature is invalid. If the signature is valid, randomly selects the pair (k1, k2) where
Prove:
CSP calculates ai = ϕ(k1, i), i ∈ c as the random index of the challenge block and
Then
The CSP finally computes
Verify:
The third-party computes
Deduplication:
The CSP randomly selects k3 ∈ ZP, computes di = ϕ(k3, i) and sends it to a third party.
After receiving D, the third party responds to the corresponding data block
The CSP then verifies the integrity of the data block by e(η′, ɛ) ⋅ ξ′ = e(σ′, g).
Theorem 1: If the data owner and the storage node honestly follow the proposed storage protocol, any challenge-response verification can pass the verification of the retrieval node. The correctness of the equation is as follows.
Proof: Based on Eq. (6), we obtain the correctness of Theorem 1.
Theorem 2: If the data owner follows the data deduplication protocol, any challenge-response verification can pass the verification of the storage node. The correctness of the equation is as follows.
Proof: Based on Eq. (7), we obtain the correctness of Theorem 2.
Theorem 3: The verifier verifies the document identity T according to the formula, and if T is correct, the verification is passed.
Proof: Based on Eqs. (8)–(12) and (13), we obtain the correctness of Theorem 3.
When i ≠ s, γi, δi can be expressed as Eqs. (9) and (10).
when i = s, γi, δi is represented as follows:
Therefore, according to the above equation, the correctness of the file identification can be verified by the Eq. (13).
Theorem 4: If the signature scheme is unforgeable and the computational Diffie-Hellman problem on bilinear groups is difficult, then any adversary to our public verification scheme for correctness cannot make the verifier accept the proof of retrievability protocol instance with non-negligible probability unless it responds with a correctly computed value.
We prove this theorem with a series of games defined in [37].
Game 0: The first game, Game 0, is simply a challenge game, similar to [37].
Game 1: Game 1 is the same as Game 0, with one difference. The challenger maintains a list of all signature tags issued as part of the storage protocol query. If an adversary submits a tag when initiating the proof of retrievability protocol or as a challenge tag, the challenger will abort if this is a valid tag that the challenger has never signed.
From the definition of games 0 and 1, it is obvious that if the opponents of games 0 and 1 have different success probabilities, we can use the opponent to construct a counterfeiter for the signature scheme.
Game 2: Game 2 is the same as Game 1, except that in Game 2, the challenger keeps a list of its responses to the opponent’s query. The challenger now observes each instance of the adversary’s proof of retrievability protocol. Suppose prf = {σ, ξ, y} is the expected response from an honest prover and Prf′ = {σ′, ξ′, y′} is the adversary’s response. The verification of prf = {σ, ξ, y} is e(η, ɛ) ⋅ e(ξ, v ⋅ ɛ−r) = e(σ, g) ⋅ e(ɛ−y, g), and the verification of prf′ = {σ′, ξ′, y′} is
Game 3: Game 3 is the same as Game 2, with the following differences: As before, the challenger observes the proof of retrievability protocol instance. Suppose the document that caused the abort was the signature {σi}, and suppose Q = (ai, bi) was the query that caused the challenger to abort, and the adversary’s response to that query was P′ = (σ′, ξ′, y′). Let P = (σ, ξ, y) be the expected response from an honest prover. We have already proved in game 2 that σ′ = σ, that is, only
Theorem 5: The signer of the file identification in the scheme has unconditional anonymity, that is, for any algorithm A, any set of users R = pk1, pk2, …, pkn, the probability P[pk = pk′] is all 1/2, where
Proof:
The output signature is obscured to any third party until the signer actively discloses all information. In the ring signature generation algorithm Aring, the Li and Ri values required to calculate ci and ei are calculated by the signer by randomly selecting the corresponding
In this section, we evaluate the experimental results in terms of storage overhead, computation overhead, and communication overhead to show the efficiency of our proposed consensus scheme. The simulated experiments were run on a laptop with Intel i7–7500U CPU @ 2.70 GHz. and 8 GB RAM. We simulated a prototype of the scheme in C language, based on the free Pairing-Based Cryptography (PBC) Library. Next, we compare the performance of the proposed scheme with Scheme [38] and Scheme [39] from the aspects of storage overhead, computational overhead, and communication overhead.
Fig. 2 shows the relationship between the number of data owners and the storage overhead between storage nodes. In our proposed consensus protocol, storage nodes keep only one file copy for duplicate data. That is, the storage node always maintains only one copy of the file, even if the number of data owners is increasing [40]. Compared with the SW scheme or other schemes, our consensus protocol has lower storage overhead.
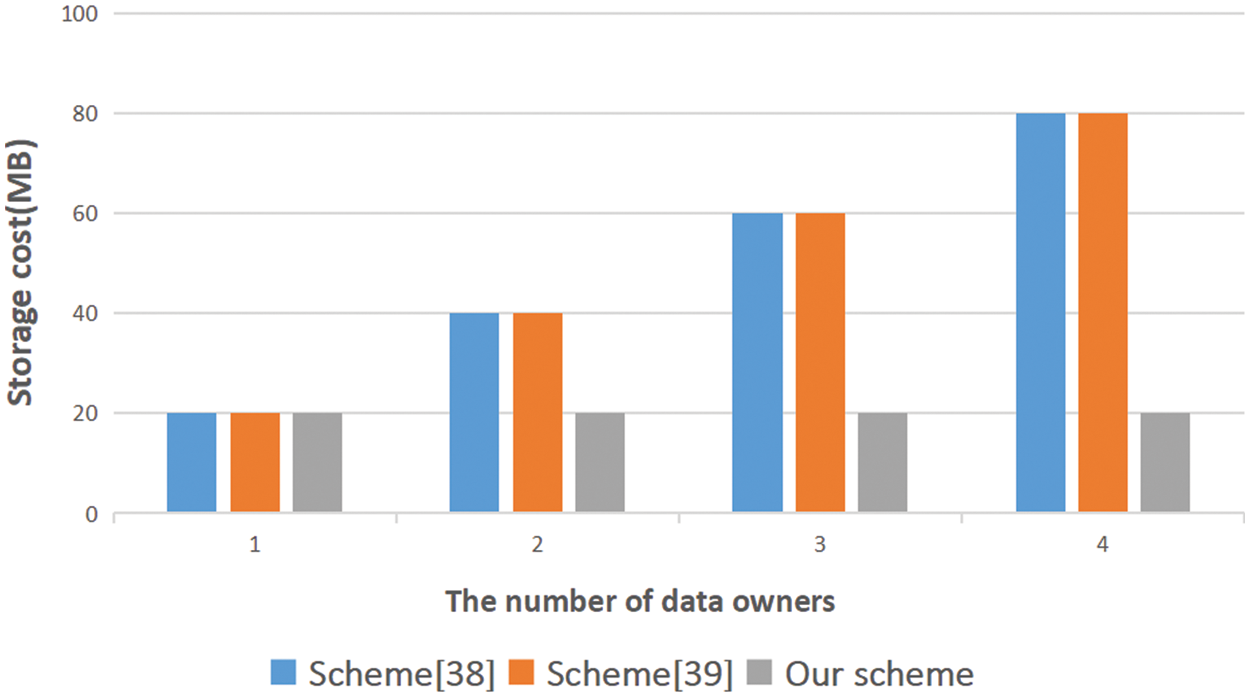
Figure 2: The relationship between the number of data owners and the storage cost
The consensus protocol we propose has three algorithms in the audit phase: Challenge, Prove, and Verify. Concepts used in the scheme we give definitions in Tab. 2 and experimental results in Fig. 3 to visually describe the computational overhead of these three algorithms. During the integrity verification audit process, the third party runs the challenge algorithm and sends the challenge information to the CSP at a negligible cost. After receiving the challenge value, the CSP performs (k + s − 1)MUL and (s + k)EXP operations to generate the storage proof. After that, the computational complexity of the third-party audit proof is O(1)MUL + O(1)EXP + O(1)Pair. In addition, in the deduplication stage, the user does not need any computational overhead, and the computational complexity of the operation that the user needs to perform is O(s + d)MUL + O(s)EXP + O(1)Pair. In the experiments, we choose to challenge the number of blocks from 1 to 1000. When the number of challenges is 1, the running time of the Challenge algorithm is the least, which is 0.016 s, and it reaches 0.216 s when the number of challenges grows to 1000. In the Prove algorithm, when the number of challenge blocks is increased from 200 to 1000, the running time increases from 0.346 s to 3.879 s. In the Verify algorithm, the running time required to challenge 1000 blocks is 10.347 s, which takes the most time among these algorithms. It can be concluded that during the audit process, the computational cost is linearly related to the number of challenge blocks [41]. Fig. 3 shows that the computational cost of the three algorithms Challenge, Prove, and Verify varies with the number of challenge blocks.
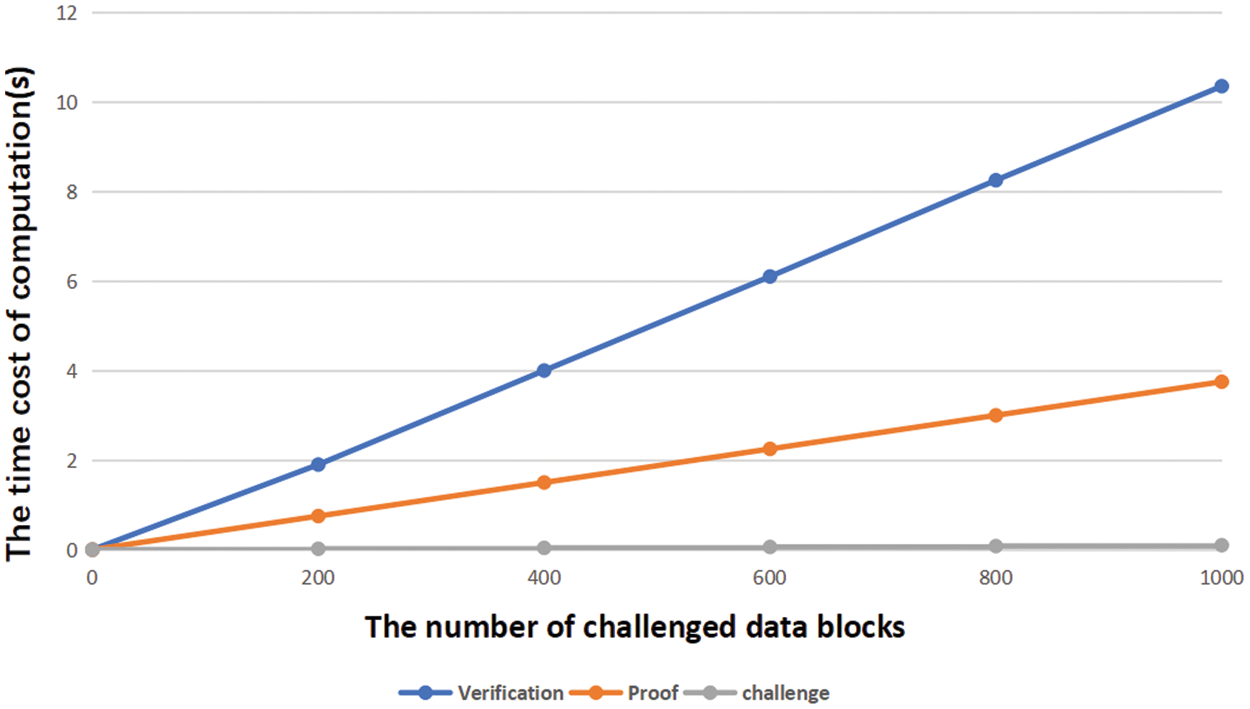
Figure 3: The relationship between computational overhead and number of challenge blocks

In our proposed consensus protocol, the algorithm in the audit phase does not bring communication overhead to users. At the same time, if the storage node has a copy of the storage file, the communication overhead with the data owner will be less than that without a copy of the storage file. Fig. 4 shows the change in communication time between the number of challenge blocks from 200 to 1000, as the number of challenge blocks increases during the audit process. Scheme [38], scheme [39] and our proposed scheme all have an upward trend in communication time, and our scheme has more advantages than them in communication time.
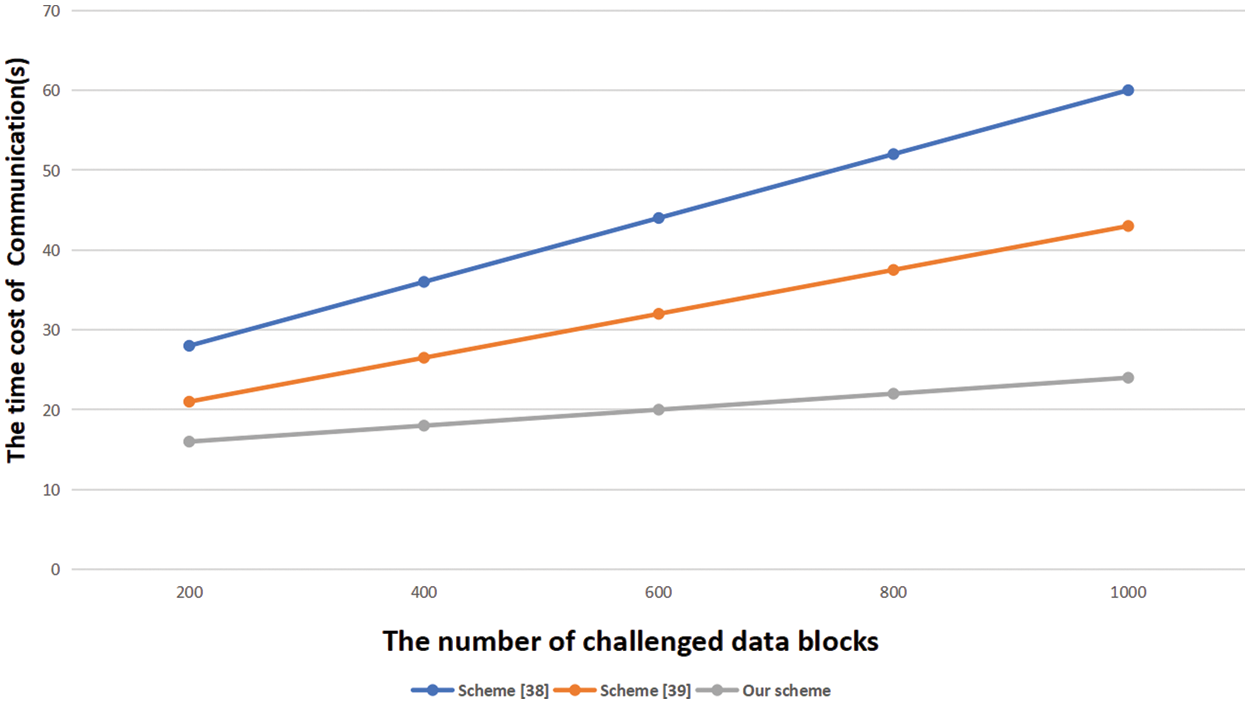
Figure 4: The relationship between communication overhead and number of challenge blocks
In this paper, we propose a blockchain consensus protocol suitable for distributed storage, which utilizes verifiable computation instead of a trust mechanism to solve the problems of existing distributed storage in blockchain platforms. In addition, the proof of retrievability with data deduplication technology can optimize data auditing and storage space while ensuring storage security, which greatly improves the efficiency and scalability of the scheme. Finally, the ring signature algorithm is used in the scheme to ensure user anonymity and file unlinkability, preventing privacy leakage and brute force attacks. In conclusion, this scheme is of great significance for improving the practicability of distributed storage services on the blockchain.
Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 62072249, 62032025), Yongjun Ren received the grant and the URLs to sponsors’ websites is https://www.nsfc.gov.cn/. This work was also supported by the Guangdong Basic and Applied Basic Research Foundation (No. 2021A1515012650). Hao Wang received the Grant and the URLs to sponsors’ websites is http://gdstc.gd.gov.cn/.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Leong, A. G. Dimakis and T. Ho, “Distributed storage allocations,” IEEE Transactions on Information Theory, vol. 58, no. 7, pp. 4733–4752, 2012. [Google Scholar]
2. X. Hei, C. Liang, J. Liang, Y. Liu and K. W. Ross, “A measurement study of a large-scale P2P IPTV system,” IEEE Transactions on Multimedia, vol. 9, no. 8, pp. 1672–1687, 2007. [Google Scholar]
3. T. Xue, Y. Yuan, Z. Ahmed, K. Moniz, G. Cao et al., “Proof of contribution: A modification of proof of work to increase mining efficiency,” in Proc. 2018 IEEE 42nd Annual Computer Software & Applications Conf. (COMPSAC), Tokyo, Japan, pp. 636–644, 2018. [Google Scholar]
4. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
5. Y. J. Ren, Y. Leng, J. Qi, K. S. Pradip, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, pp. 304–313, 2021. [Google Scholar]
6. C. P. Ge, Z. Liu, J. Y. Xia and L. M. Fang, “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable & Secure Computing, vol. 18, no. 3, pp. 1214–1226, 2021. [Google Scholar]
7. L. M. Fang, M. H. Li, Z. Liu, C. T. Lin, S. L. Ji et al.,“A secure and authenticated mobile payment protocol against off-site attack strategy,” IEEE Transactions on Dependable & Secure Computing, vol. 21, no. 8, pp. 1–12, 2021. [Google Scholar]
8. G. Ateniese, R. Burns, R. Curtmola, J. Herring, L. Kissner et al., “Provable data possession at untrusted stores,” in Proc. of the 14th ACM Conf. on Computer & Communications Security, Alexandria Virginia, USA, pp. 598–609, 2007. [Google Scholar]
9. A. Juels and B. S. Kaliski Jr, “PORs: Proofs of retrievability for large files,” in Proc. of the 14th ACM Conf. on Computer & Communications Security, Alexandria Virginia, USA, pp. 584–597, 2007. [Google Scholar]
10. K. Yang and X. Jia, “An efficient and secure dynamic auditing protocol for data storage in cloud computing,” IEEE Transactions on Parallel & Distributed Systems, vol. 24, no. 9, pp. 1717–1726, 2012. [Google Scholar]
11. S. Hiremath and S. Kunte, “A novel data auditing approach to achieve data privacy and data integrity in cloud computing,” in Proc. 2017 Int. Conf. on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT), Mysuru, India, pp. 306–310, 2017. [Google Scholar]
12. J. Han, Y. Li and W. Chen, “A lightweight and privacy-preserving public cloud auditing scheme without bilinear pairings in smart cities,” Computer Standards & Interfaces, vol. 62, pp. 84–97, 2019. [Google Scholar]
13. X. Zhang, S. Liu and S. Han, “Proofs of retrievability from linearly homomorphic structure-preserving signatures,” International Journal of Information & Computer Security, vol. 11, no. 2, pp. 178–202, 2019. [Google Scholar]
14. Y. Li, Y. Yu, R. Chen, X. Du and M. Guizani, “Integritychain: Provable data possession for decentralized storage,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 6, pp. 1205–1217, 2020. [Google Scholar]
15. S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” Decentralized Business Review, vol. 4, pp. 21260, 2008. [Google Scholar]
16. J. Wang, H. Han, H. Li, S. M. He, P. K. Sharma et al., “Multiple strategies differential privacy on sparse tensor factorization for network traffic analysis in 5G,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 1939–1948, 2022. [Google Scholar]
17. Y. J. Ren, Y. Leng, Y. P. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences & Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]
18. C. P. Ge, W. Susilo, Z. Liu, J. Y. Xia, L. M. Fang et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable & Secure Computing, vol. 18, no. 6, pp. 2787–2800, 2021. [Google Scholar]
19. A. Miller, A. Juels, E. Shi, B. Parno and J. Katz, “Permacoin: Repurposing bitcoin work for data preservation,” in Proc. 2014 IEEE Symp. on Security & Privacy, Berkeley, CA, USA, pp. 475–490, 2014. [Google Scholar]
20. K. Hao, J. Xin, Z. Wang, Z. Jiang and G. Wang, “Decentralized data integrity verification model in untrusted environment,” in Proc. Asia-Pacific Web (APWeb) and Web-age Information Management (WAIM) Joint Int. Conf. on Web & Big Data, Macau, China, pp. 410–424, 2018. [Google Scholar]
21. D. Francati, G. Ateniese, A. Faye, A. M. Milazzo, A. M. Perillo et al., “Audita: A blockchain-based auditing framework for off-chain storage,” in Proc. of the 9th Int. Workshop on Security in Blockchain & Cloud Computing, Virtual Event Hong Kong, pp. 5–10, 2021. [Google Scholar]
22. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “Revocable attribute-based encryption with data integrity in clouds,” IEEE Transactions on Dependable & Secure Computing, vol. 99, pp. 1–1, 2021. [Google Scholar]
23. J. Wang, C. Y. Jin, Q. Tang, N. X. Xiong and G. Srivastava, “Intelligent ubiquitous network accessibility for wireless-powered MEC in UAV-assisted B5G,” IEEE Transactions on Network Science & Engineering, vol. 8, no. 4, pp. 2801–2813, 2021. [Google Scholar]
24. Y. J. Ren, K. Zhu, Y. Q. Gao, J. Y. Xia, S. Zhou et al., “Long-term preservation of electronic record based on digital continuity in smart cities,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3271–3287, 2021. [Google Scholar]
25. G. Xiao, K. Li, Y. Chen, W. He, A. Y. Zomaya et al., “Caspmv: A customized and accelerative spmv framework for the sunway taihulight,” IEEE Transactions on Parallel & Distributed Systems, vol. 32, no. 1, pp. 131–146, 2019. [Google Scholar]
26. T. Xiaoyong, K. Li, Z. Zeng and B. Veeravalli, “A novel security-driven scheduling algorithm for precedence constrained tasks in heterogeneous distributed systems,” IEEE Transactions on Computers, vol. 60, no. 7, pp. 1017–1029, 2010. [Google Scholar]
27. J. Xu, L. Wang, X. Liu, X. Feng, Y. Ren et al., “Front-end control mechanism of electronic records,” Computer Systems Science & Engineering, vol. 39, no. 3, pp. 337–349, 2021. [Google Scholar]
28. Y. J. Ren, J. Qi, Y. P. Cheng, J. Wang and O. Alfarraj, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]
29. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “A verifiable and fair attribute-based proxy re-encryption scheme for data sharing in clouds,” IEEE Transactions on Dependable & Secure Computing, vol. 21, no. 7, pp. 1–12, 2021. [Google Scholar]
30. Y. J. Ren, F. J. Zhu, S. P. Kumar, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]
31. Q. Wang, C. Wang, K. Ren, W. Lou and J. Li, “Enabling public auditability and data dynamics for storage security in cloud computing,” IEEE Transactions on Parallel & Distributed Systems, vol. 22, no. 5, pp. 847–859, 2010. [Google Scholar]
32. Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 1639–1648, 2022. [Google Scholar]
33. J. Chen, K. Li, Z. Tang, K. Bilal, S. Yu et al., “A parallel random forest algorithm for big data in a spark cloud computing environment,” IEEE Transactions on Parallel & Distributed Systems, vol. 28, no. 4, pp. 919–933, 2016. [Google Scholar]
34. X. Zhou, K. Li, Y. Zhou and K. Li, “Adaptive processing for distributed skyline queries over uncertain data,” IEEE Transactions on Knowledge & Data Engineering, vol. 28, no. 2, pp. 371–384, 2015. [Google Scholar]
35. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
36. R. L. Rivest, A. Shamir, and Y. Tauman, “How toleak a secret,” in Proc. Int. Conf. on the Theory & Application of Cryptology & Information Security, Melbourne, Australia, pp. 552–565, 2001. [Google Scholar]
37. C. Liu, K. Li and K. Li, “A game approach to multi-servers load balancing with load-dependent server availability consideration,” IEEE Transactions on Cloud Computing, vol. 9, no. 1, pp. 1–13, 2018. [Google Scholar]
38. H. Shacham and B. Waters, “Compact proofs of retrievability,” in Proc. Int. Conf. on the Theory & Application of Cryptology & Information Security, Melbourne, Australia, pp. 90–107, 2008. [Google Scholar]
39. Y. Yu, M. H. Au, G. Ateniese, X. Huang, W. Susilo et al., “Identity-based remote data integrity checking with perfect data privacy preserving for cloud storage,” IEEE Transactions on Information Forensics & Security, vol. 12, no. 4, pp. 767–778, 2016. [Google Scholar]
40. Y. J. Ren, J. Qi, Y. P. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM Transactions on Internet Technology, vol. 21, no. 1, pp. 1–20, 2021. [Google Scholar]
41. T. Li, N. P. Li, Q. Qian, W. Xu, Y. Ren et al., “Inversion of temperature and humidity profile of microwave radiometer based on bp network,” Intelligent Automation & Soft Computing, vol. 29, no. 3, pp. 741–755, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |