DOI:10.32604/iasc.2022.030274

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.030274 |  |
| Article |
Selfish Mining and Defending Strategies in the Bitcoin
1Network Security and Information Office, Hohai University, Nanjing, 210098, China
2Nanjing University of Aeronautics and Astronautics, Nanjing, 210008, China
3SKEMA Business School, Lille, 59777, France
4University of Hertfordshire, Hertford, AL10 9EU, UK
*Corresponding Author: Weijian Zhang. Email: weijzhang2022@163.com
Received: 22 March 2022; Accepted: 29 April 2022
Abstract: As a kind of distributed, decentralized and peer-to-peer transmitted technology, blockchain technology has gradually changed people’s lifestyle. However, blockchain technology also faces many problems including selfish mining attack, which causes serious effects to the development of blockchain technology. Selfish mining is a kind of mining strategy where selfish miners increase their profit by selectively publishing hidden blocks. This paper builds the selfish mining model from the perspective of node state conversion and utilize the function extremum method to figure out the optimal profit of this model. Meanwhile, based on the experimental data of honest mining, the author conducts the simulation of selfish mining and discovers that selfish miners are able to acquire more revenue than honest miners when they account for more than 1/3 computing power of the whole system. Lastly, to defend the selfish mining attack, the author also summarizes the existing defending strategies and evaluates every kind of strategy briefly.
Keywords: Bitcoin; blockchain; selfish mining; markov chain
Since the 21st century, the vigorous development of Internet technology has greatly improved the quality of our daily life, which makes the Internet an indispensable guarantee for the information society. However, the Internet also faces many problems such as data leakage, hacker attack and etc. Blockchain technology [1], is a new kind of technology which includes distributed data storage, peer-to-peer transmission, encryption algorithm and other computer technology applications, and has the characteristics of decentralization, trustworthiness and etc. Therefore, blockchain technology may play an important role in computer science and finance area. Until now, the study of blockchain mainly includes the following areas: (1) blockchain consensus mechanism, (2) distributed storage technology, (3) security and privacy technology.
Bitcoin is a new kind of digital currency based on blockchain technology. Its main characteristics are as follows: (1) decentralized, (2) unforgeability, (3) non-tampering. However, there are many problems in the current Bitcoin mining system including selfish mining. Selfish mining attack is a kind of mining strategy where mining nodes selectively hide or publish discovered blocks. This strategy is a competition based on computing power. When the blockchain diverges (not the hard or soft fork used to change the consensus principle, but the one that remains the same), the longest chain is considered as legitimate mining chain [2]. While selfish miners find a new block, they can hide the discovered block and let other honest miners mine in the public chain. If selfish miners find more blocks, the selfish chain will have an advantage over the public chain and choose to keep them secret. Until the length of the public chain approaches the length of the selfish chain, selfish miners would public the selfish chain to the system.
As a result, all the efforts of honest miners are in vain. In the contrast, selfish miners can get the maximum relative profit. To the Bitcoin system, driven by profit, more and more honest miners would participate in the selfish mining. When the number of selfish miners exceeds 50% of all nodes, the system will face serious security threats or even lead to credit collapse.
The paper is organized as follows. Section 2 introduces the concept of selfish mining. The research of selfish mining is displayed in Section 3. Section 4 shows selfish mining strategy and rewards. Section 5 introduces simulation experiments. We conclude the paper in Section 6.
The stability of the Bitcoin standard protocol depends on the common interests of participating nodes. When a miner discovers a new block, it immediately broadcasts these messages to the whole system. After receiving and confirming these messages, other miners record them on the distributed ledger and begin to mine other blocks. Miners who mine a new block will be rewarded. This mechanism enables Bitcoin transactions to reach a consensus in the case of decentralization, thus maintaining the stability of the Bitcoin mining system. Therefore, the Bitcoin mining system is widely regarded as incentive compatible, that is, motivating miners to comply with the prescribed Bitcoin standard protocol [3].
However, the current standard Bitcoin protocol only considers the computing power of honest miners and ignores that of selfish miners. In 2013, foreign researcher Eyal and Sirer put forward the concept of selfish mining. Different from other cyber-attacks, selfish mining is designed to disrupt the normal functioning of the blockchain network, but purely to gain more relative profits. As a result, cryptocurrencies such as Bitcoin, are more likely to encounter selfish mining attacks than other types of cyber-attacks. Eyal mentioned the dangers of such attacks on different occasions and concluded through mathematical models that if selfish miners only own one-third of the computing power of the network, they can acquire more money than that under the standard Bitcoin protocol. Therefore, selfish mining is more attractive and easier than other attacks.
The root cause of selfish mining is the computing power of selfish miners and the adjustment of mining difficulty. Selfish miners make use of it and let mining easier and more efficient. Selfish mining behavior may lead to the increase of isolated blocks (i.e., small forks in the main blockchain system have no impact on the main chain data) in the system and a large of number of honest miners would join in the selfish mining. It is possible to result in an increase in the average time used by the transaction network to verify blocks. After mining 2016 blocks, the system will automatically ignore isolated nodes and adjust the mining difficulty [4]. Hence, selfish miners earn more per unit of time, which makes the attack profitable, and it can be said that there is no selfish mining without difficult adjustments [5].
Apart from this, blockchain researcher Kartik Nayak and Andrew Mille who are from Cornell University and the University of Maryland respectively, they further propose that selfish mining is not the best choice for large parameter space [6]. Therefore, they consider a kind of stubborn strategy, (i.e., the attacker continues to exploit his private branch, giving the public fork ahead, which is very beneficial to the attacker). Because if he happens to surpass the public chain later, he will waste even more of them. In this case, researchers calculated that the attacker’s revenue would increase by 13%. Meanwhile, researchers also showed how to further amplify his gains through a combination of non-trivial mining and cyber-attacks. Eventually, they found a strategy for distributed decentralized Eclipse attacks [7] that actually benefits honest miners [8]. Compared with research abroad, domestic research on blockchain has begun to start. However, the research on selfish mining is still insufficient, especially lacking research on selfish mining process models.
3.1 Reasons for Selfish Mining Attacks
The fundamental cause of conducting selfish mining is the improvement of computing power and the adjustment of mining difficulty. The current existing Bitcoin protocol only considers the computing power of honest miners and ignores that of selfish miners. Selfish miners make use of this to improve computing power while increasing mining efficiency. Selfish mining behavior leads to a rapid increase in the number of isolated blocks (i.e., small forks in the main blockchain system, which have no impact on the main chain data) [9]. As a result, a large number of honest mining nodes would participate in the selfish mining, which will result in an increase in the average time that the transaction network utilize to verify the block. After mining 2016 blocks, the system will automatically ignore isolated nodes and adjust the mining difficulty [10]. Although the total computing power of network remains steady, the new difficulty is lower than the original theoretical value, and the time for block verification is correspondingly reduced. Therefore, the revenue of selfish miner’s unit time has increased, which leads the attacker to be profitable. Therefore, when the difficulty of mining is adjusted, the success rate of selfish mining is higher [11].
3.2 Existing Improvement to the Bitcoin Standard Protocol
Until now, faced with selfish mining, a considerable amount of literature has been published on how to resist selfish mining. The vast majority of them adopt two kinds of strategies:
① Fundamentally change the block authentication method in Bitcoin transaction system, for example, methods raised by Bahack [12], Solat and PotopButucaru [13].
② Reduces the possibility of honest mining nodes working on selfish mining chains, for example, strategies raised by Eyal, Sirer [14] and Heilman [15].
Among these methods, we firstly introduce the Backward-Incompatible strategy raised by Bahack. When selfish miners find selfish mining behaviour in the system, it is necessary to report to the transaction system. After receiving the report, the system would confiscate the profit of selfish miners and then give 50% of the forfeited profit to the first honest miner, including block fork certification. However, this strategy would do harm to honest miners and generate another attack on the whole system. Apart from this, Solat and Potop-Butucaru [16] raise that we can use a certain number of digital signatures to prove that these excavated blocks are validated by the system. But this method does not propose the accurate number threshold of digital signatures. As a result, there is no guarantee that the system can conduct normal transactions in the next step. Therefore, there are potential risks in this scheme.
4 Selfish Mining Strategy and Rewards
As a kind of encrypted digital currency, the essence of the Bitcoin transaction is a data structure containing a set of input lists and output lists [17]. In other words, it contains the transfer records between nodes. Simply, the Bitcoin transaction process contains 6 steps, as shown in Fig. 1.
1) The miner M1 sends a transaction request to the system.
2) The system broadcasts the transaction request to the P2P network.
3) The remaining miners in the system verify the correctness of transactions.
4) Multiple transactions make up a block.
5) New blocks are added to the existing blockchain system.
6) All trades finished.
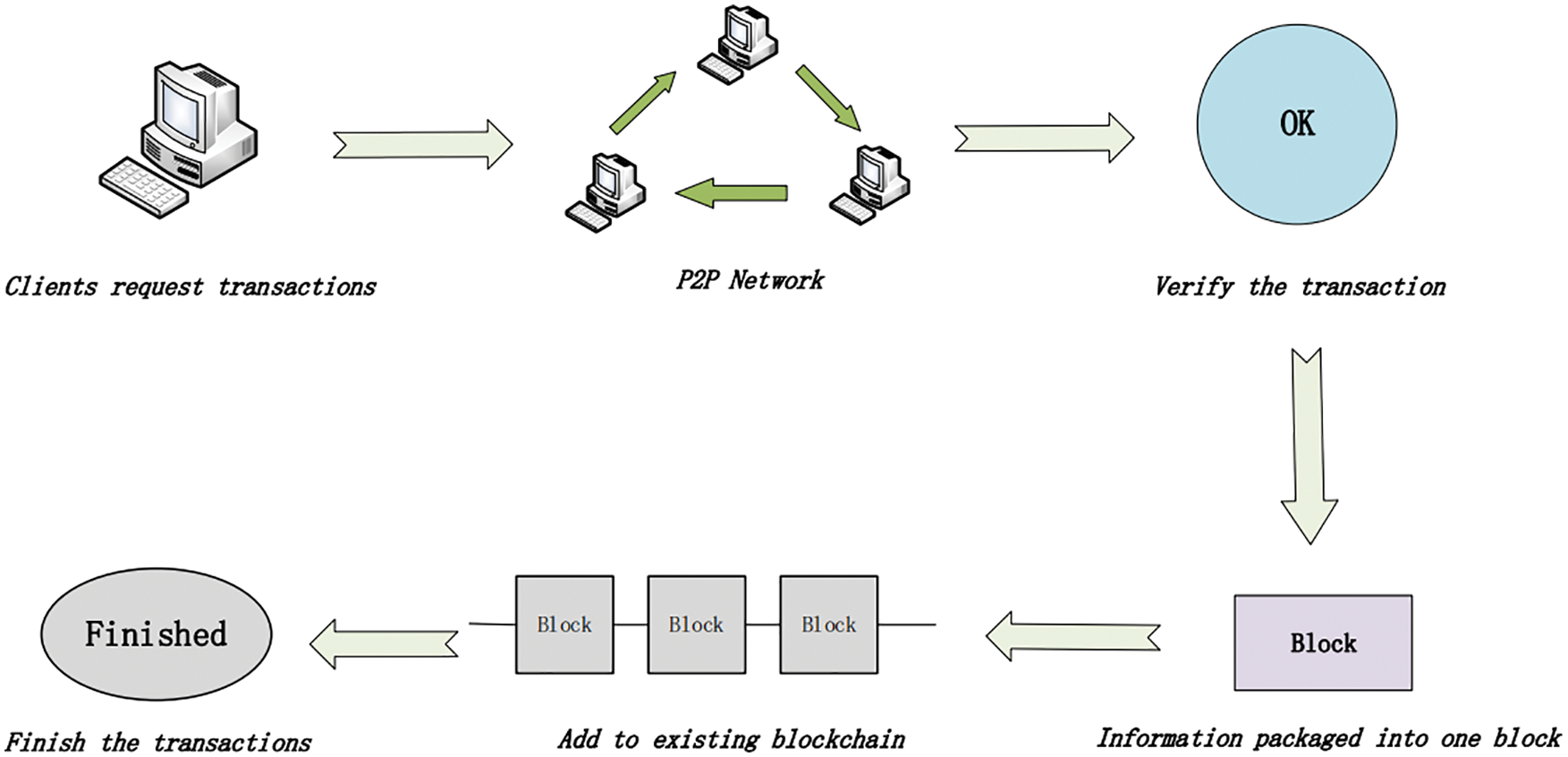
Figure 1: Bitcoin transactions progress
The validity of the bitcoin transaction is based on the signature of the deal initiator, which is used to prevent others from imitating signature and generating falsified data. After completing the transaction, the system would broadcast the transaction to the neighbor nodes. The system will sort out all transaction information over a period of time and pack the information into new blocks when the mining node works [18]. After successfully entering the blockchain system, the transaction would be confirmed by the system. However, before trading, the authenticity of the transaction needs to be verified to prevent the fraud data.
4.2 The Model of Selfish Mining
Selfish miners acquire the extra profit through hiding or publishing blocks. However, there is one key problem: when selfish miners choose to publish or hide blocks to maximize their relative profit.
According to the reference [19], we use < S, A, P, R > model to implement the behavior of selfish miners and transform the selfish mining problem into a decision problem. The objective function is a relative profit function which is a non-linear function. Because selfish miners hope to maximize their relative profits, not specific profits. In other words, they want to acquire the maximum ratio of return. Then we analyze the < S, A, P, R > model.
S is the state set of g and g = {State1, State2, State3 ⋅ ⋅ ⋅ }, we use the ternary expression {la, lh, fork} to express the spatial state of S. The first two parameters represent the length of selfish mining chain and the length of honest mining chain respectively. The third parameter represents the fork phenomenon [20].
A is the action set. A(S) represents next steps that selfish miners would take under the state S. There are 4 elements in this action set.
– Accept: It means that selfish miners give up all blocks on the selfish chain.
– Publish: When la ≥ lh, selfish miners would publish all hidden blocks.
– Hide: Selfish miners cannot publish their hidden blocks and continue to mine in their private chains.
– Match: Selfish miners choose to publish selfish mining chains of the same length as the honest miners. This is based on one premise that selfish miners must prepare one block at least in advance and conceal it.
P is the probability of transferring from the current state to the next state under the above actions.
R represents expected relative profit under the current state.
When the blockchain generates forks, the state of selfish mining is following in Fig. 2.
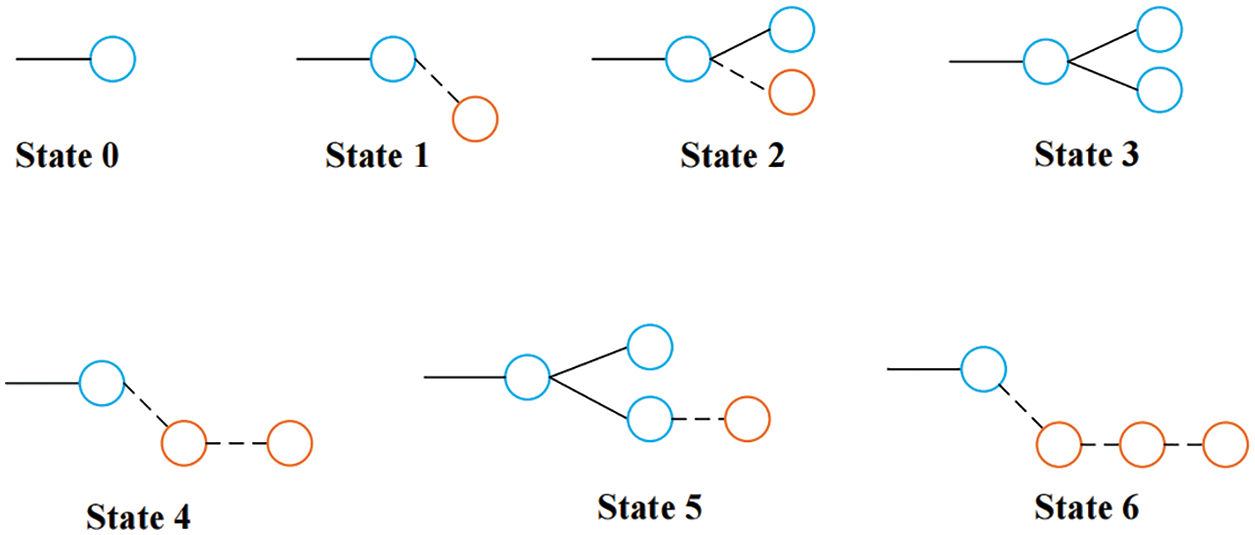
Figure 2: The state of selfish mining nodes
Where State 0 is the initial state that each miner starts from this state. State 1 is a state where the selfish miner mines one new block and hides it. State 2 indicates that the honest miner announces it has mined one new block when the selfish miner hides one block. At this time, the selfish miner should immediately announce its hidden block. Meanwhile, the state would transfer into the State 3. In this case, a part of miners would receive blocks of selfish miners and mine the next block on the basis of this block. Whether it is a selfish mining block or honest mining block, it can guarantee the profit as long as it mines successfully on the blocks found by selfish miners. In State 1, if selfish miners find one new block, the state will convert into State 4. Similarly, in State 3, the state can convert into State 5 when selfish miners find one new block, in that case, selfish miners should publish all newly mined blocks to preserve the profit from the previous mined block. Lastly, the state would transfer from State 4 to State 6.
When la = lh, some honest miners are likely to participate in the selfish mining. When selfish miners discover new blocks, they would take the next action judged by the length of the selfish mining chain and the length of the honest mining chain, the possible actions are expressed as Eq. (1).
Probability analysis of mining nodes
In this section, we analyze the probability distribution of mining nodes based on the state conversion frequency. It should be pointed out that we ignore the size of blocks and communication delay in this model.
To express intuitively, we label the mining nodes as node 0’, node 0, node 1 and so on. It is better to be represented by a state conversion diagram [21], as shown in Fig. 3.
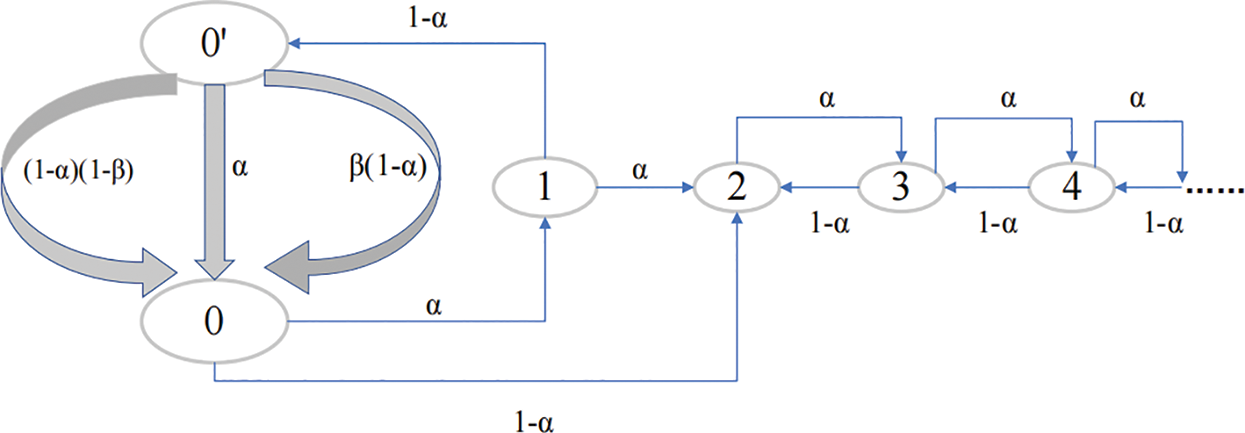
Figure 3: State conversion diagram
Where the State 0 represents that we only have one public chain. The State 0′ represents that the selfish mining chain has the same length with the honest mining chain. Besides of this, β is the proportion of honest nodes in the mining pool.
In this paper, we will equate the computing power of nodes to the transition frequency α. Through Fig. 3, if starting from the node 0′, it is possible for us to get three kinds of state transition ways [22]. The first one is that the mining pool mines a new block on the previous selfish chain with the frequency α. The second one is that other miners mine one new block on the previous selfish chain with the frequency β(1 − α). The last one is that other miners mine one new block on the public chain with the frequency (1 − β)(1 − α).
We can deduce the probability distribution of nodes through Fig. 3 and get the expression Eq. (2).
where p0,
Obviously, we can deduce Eq. (2) to get Eq. (3).
Apart from this, we already known:
We can get Eq. (5) by substituting Eq. (2) into Eq. (3).
Finally, for convenience, we use α to represent
4.3 The Analysis of Relative Profit
Our objective function is the relative profit that is a non-linear function. Because selfish miners want to acquire a higher ratio of return on the investment compared with other miners.
According to Fig. 3, we can consider the relative profit from the perspective of the node state transition frequency. The objective function is shown as Eq. (7).
where ra and rh are the profit of selfish miners and honest miners respectively.
We can research the relative profit by considering the different state of the honest mining chain and the selfish mining chain [23].
(1) The length of the selfish chain and honest chain are both 1 while generating forks. As show in Fig. 4, the selfish mining chain will be longer than the honest mining chain for one block when the selfish miner appends the new block to the private chain.

Figure 4: Condition 1
(2) The blockchain generates two forks with the same length 1. Meanwhile, selfish miners find one new block and they choose to publish all blocks on the selfish mining chain. Therefore, the selfish chain gets the profit of 2 blocks, which is shown in Fig. 5.
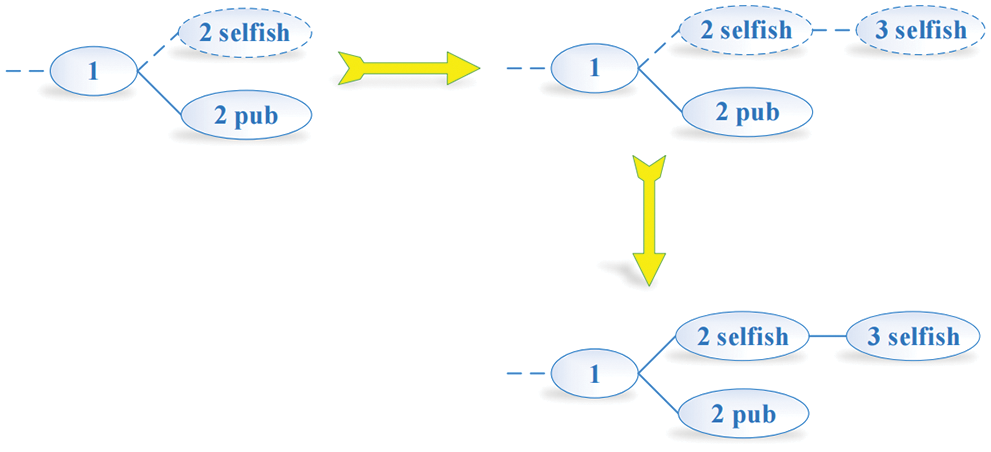
Figure 5: Condition 2
(3) When honest miners find one new block firstly and add it to the honest mining chain, in that case, selfish miners would accept them and give up all blocks on the selfish mining chain. Fig. 6 displays the condition.

Figure 6: Condition 3
(4) When honest miners find one new block firstly, they are likely to add the one new block to the selfish mining chain. As a result, honest miners and selfish miners can earn one block bonus respectively, which would lead to the subsequent profit owned by honest miners. The condition is shown in Fig. 7.

Figure 7: Condition 4
(5) The relative profit of honest miners is (1 − α) p0.
(6) In the case, when lh = la, selfish miners would take match action. Therefore, the ultimate attribution of profit depends on the result of the outcome between selfish miners and honest miners. When lh − la = 2, if honest miners add blocks that they find to the honest mining chain, then lh − la ≥ 1. The selfish mining chain would choose to publish all blocks. What they do would cause all the efforts of honest miners in vain and a part of honest miners participate in selfish mining. In that case, revenue belongs to selfish miners, which is shown in Fig. 8.
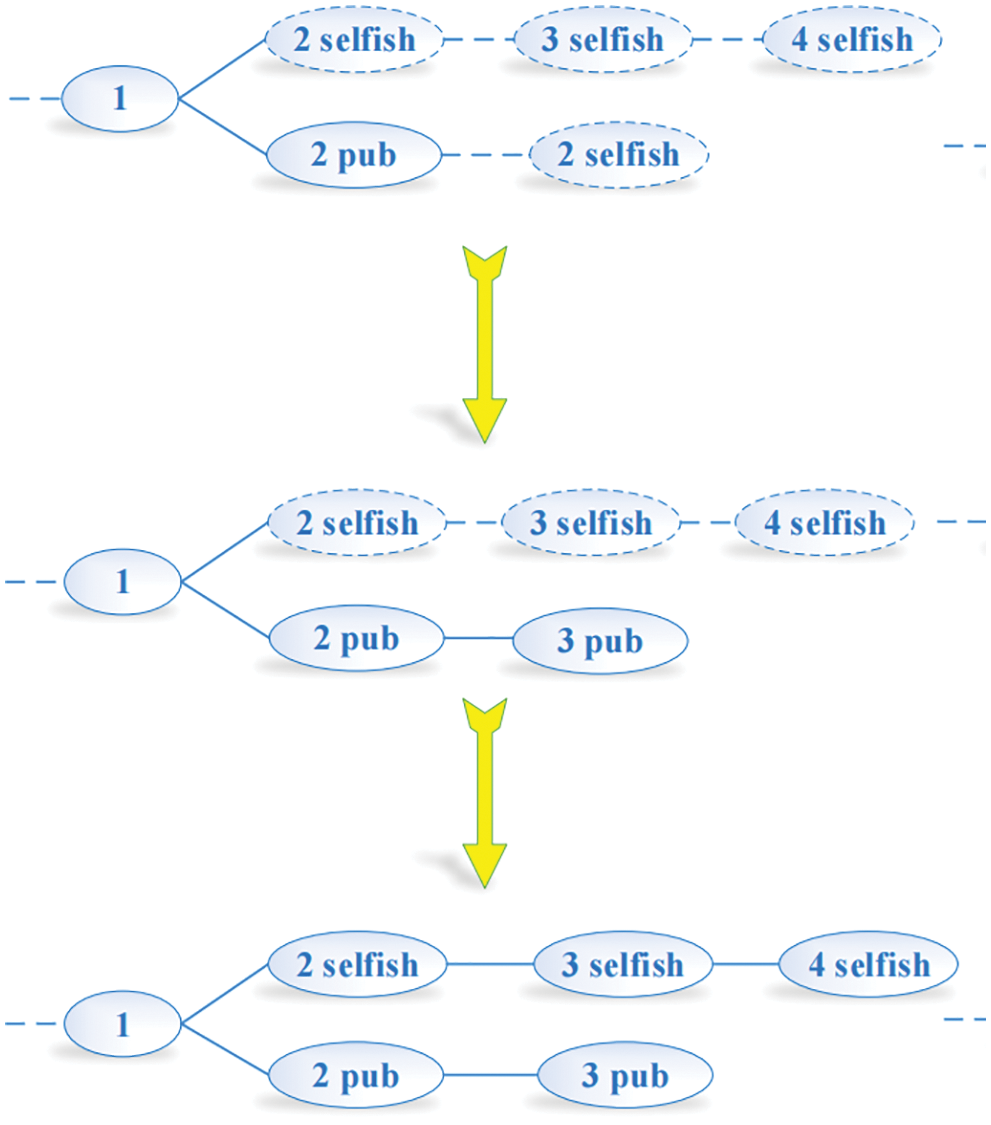
Figure 8: Condition 7
(7) The selfish mining chain decreases the lead, which remains at least two. The new block will end outside the chain once the selfish chain publishes its entire fork. However, the selfish chain now reveals only one block and obtains a revenue of one. All of these are shown in Fig. 9.
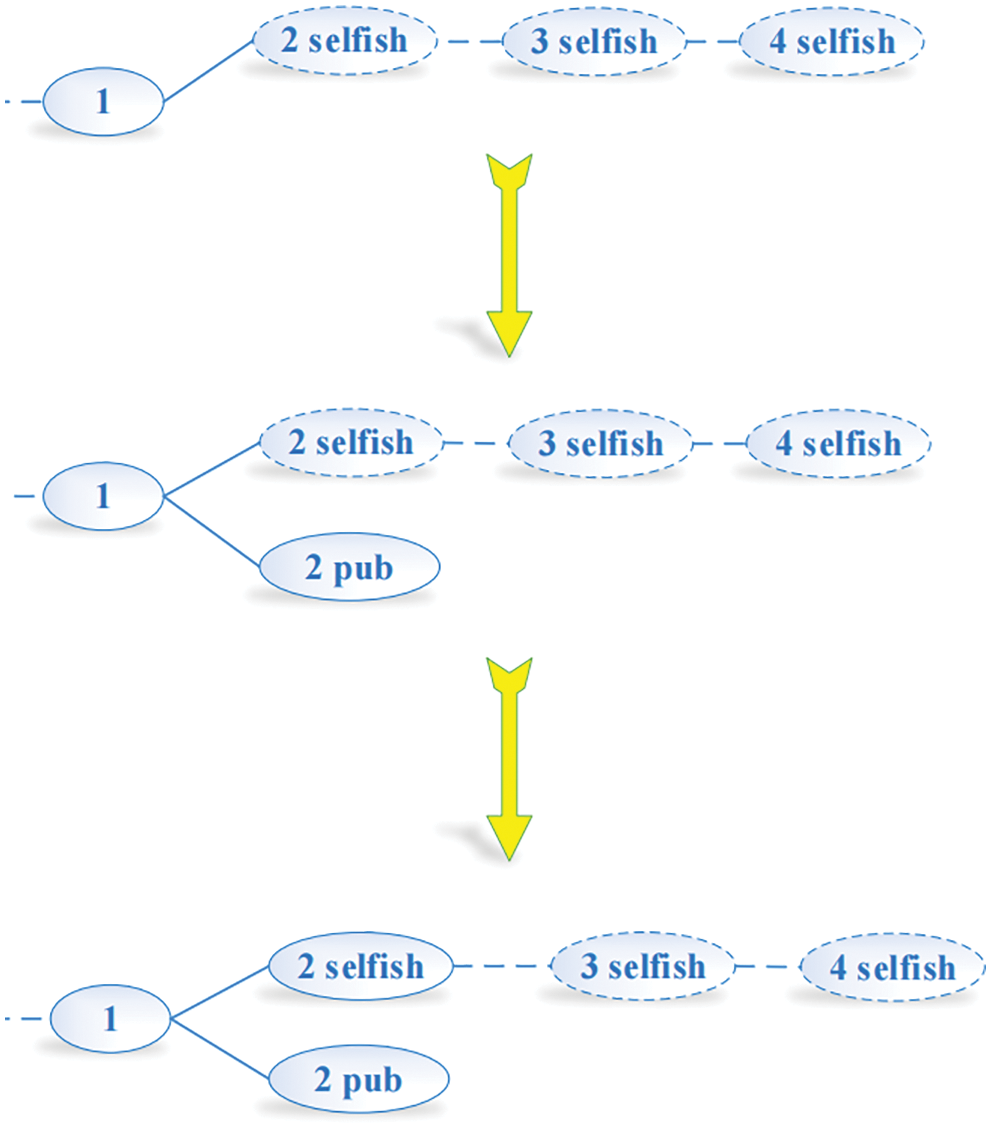
Figure 9: Condition 8
Based on the analysis of above 8 conditions, we can figure out the profit of honest miners and selfish miners respectively. Among them, the profit of condition 3, 4, 5 belong to honest miners and the profit of condition 1, 2, 3, 7, 8 belong to selfish miners. Therefore, the relative profit can be expressed as Eq. (8).
where
To simplify the function R intuitively, we create the diagram of the function R through MATLAB.
From Eq. (5) and Fig. 10, we discover that R is determined by the value of α and β. So we will turn this into a problem of finding the extremum value of R in the feasible region of α and β. According to the reference [24], we discover that selfish miners who only master more than one-third computing power of the entire network can acquire more profit than honest miners, which is corresponding to our recognition. Apart from this, when β equals to 1/2, the threshold value of 1/4. In other words, when selfish miners account for 1/2 of total miners, they can acquire more profits than honest miners as long as they master the 1/4 computing power.
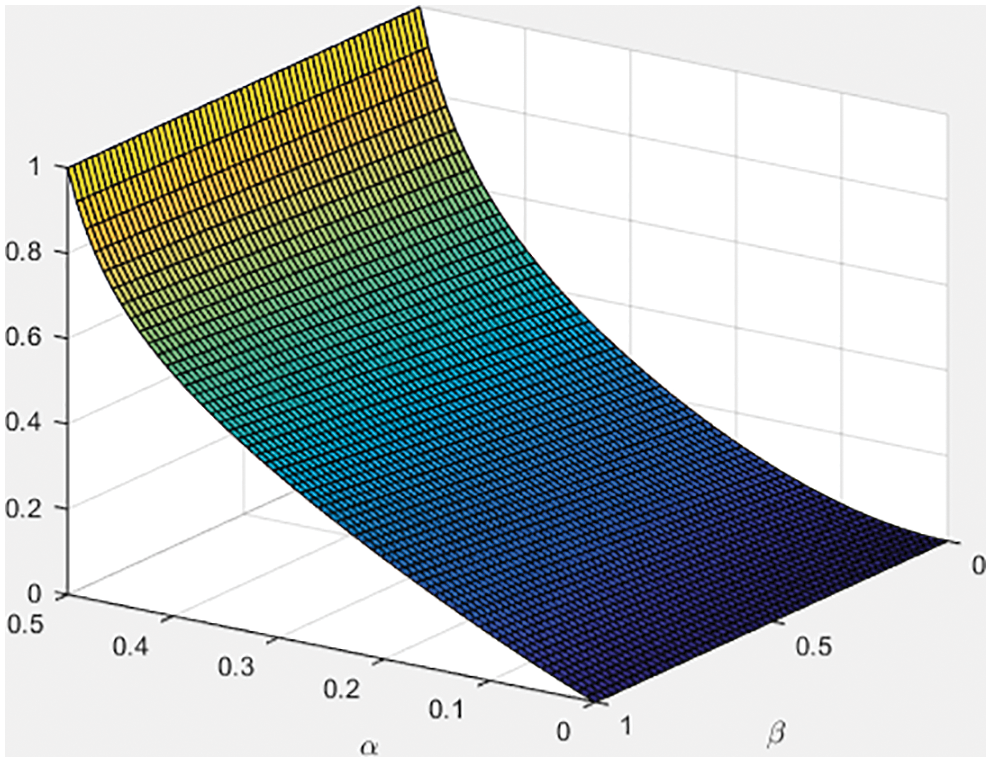
Figure 10: Profit function diagram
5.1 The Simulation of Honest Mining
5.1.1 Experimental Environment
We use Go language to implement the experiment. The simulation system is developed based on the following software and hardware environment, and then the experimental data is collected.
The hardware environment: Intel(R) Core(TM) i5-8300 CPU @ 2.30 GHz, 8G RAM.
The software environment: Ubuntu 18.04 LiteIDE X35.5 go 1.11.1.
We use terminal nodes of Linux system to simulate the miner. Mining nodes make use of broadcasting to conduct information exchange. Besides of this, the experimental data is processed by SigmaPlot and Matlab.
5.1.2 Experiment Content and Data Analysis
To simplify the experiment, we suppose that one transaction is one block. If we mine successfully, the profit would be 1 and the transaction cost is 0. In this section, we design two experiments. Two thousand simulated transactions are conducted for 6 miners with the same calculation force and 10 miners with different calculation force respectively [25]. After that, we analyze the data and get the relationship between computing power and profit.
We set 10 mining nodes with different computing power and conduct the simulation experiment for 2000 times. For the convenience of calculation, the total computing power is 8000, from M1 to M10 are 6%, 7%, 7.5%, 8.5%, 9.5%, 10.5%, 11%, 12%, 13% and 15% respectively. After 2000 times of simulation, we analyze the actual profit and then make comparison with the theoretical profit. All of data is shown in Tab. 1. From the experimental data, we find the error rate of theoretical profit and actual profit are within a reasonable range. For the sake of comparing intuitively, we select bars to represent the error rate between theoretical profit and actual profit, as shown in Fig. 11.
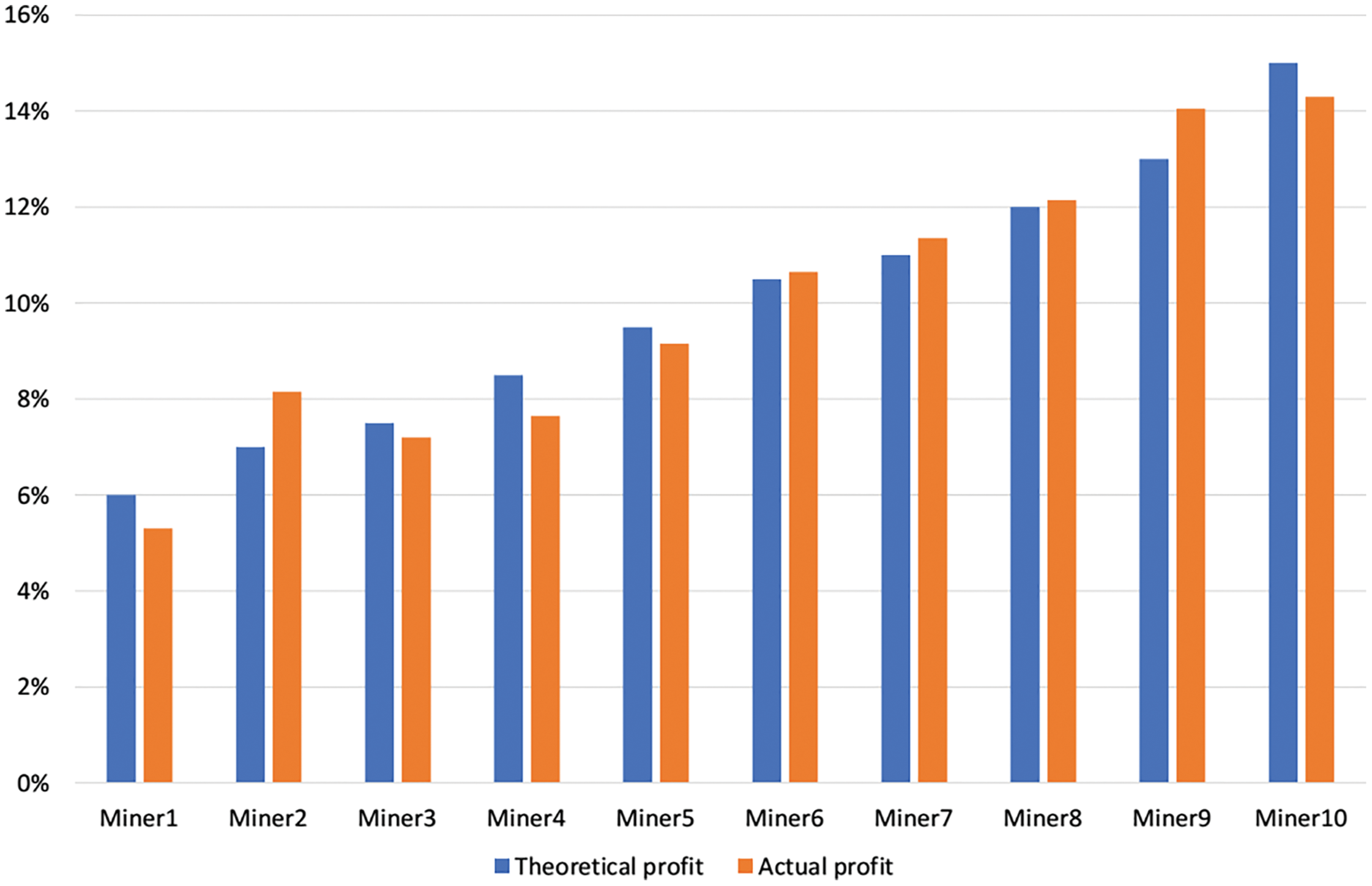
Figure 11: Honest mining diagram

From Tab. 1, we can find that the actual revenue ratio and the theoretical revenue ratio are roughly equal. Meanwhile, according to Fig. 11, we can draw the conclusion that there is a positive correlation between computing power and node profit for honest miners. In other words, if one honest node has more computing power, it would acquire more node profit.
We can analyze the lost ratio briefly. According to the reference [26], the blockchain system can generate two types of forks, including accidental fork and intentional fork. The probability of the former is 1.69%. Different from intentional fork, the accidental fork is the result of Poisson process of PoW in the system and it may cause transactions lost [27]. In the simulation of honest mining, the lost ratio is 0.1%. Furthermore, the quality of hardware may influence the lost ratio of experiment.
5.2 The Simulation of Selfish Mining
5.2.1 Experimental Environment
The selfish mining experimental environment is the same as that of the simulation of honest mining. We do not repeat it again.
5.2.2 Experiment Content and Data Analysis
In the selfish mining experiment, firstly, we build 2 selfish mining nodes with the computing power of 15000 and 27500 respectively. Then there are also 2 honest mining nodes with the same computing power of 20000.
The statistical data of selfish mining experiment is shown in Tab. 2. Where SM1 and SM2 represent two selfish miners respectively, M3 and M4 are two honest miners with the same computing power. In order to make comparison, we transfer the table into the bar chart.


According to Tabs. 2, 3 and Fig. 12, we can mainly draw two conclusions.
① When two selfish miners work together, the loss ratio trends to be smooth, which is around 30%.
② There is a significant difference in the revenue of each node because of various computing power. For example, the computing power of SM1 accounts for 18.18% of the whole system, but it only acquires 13.68% of the total profit. On the contrary, the computing power of SM2 accounts for 33.33% of the system, as a result, and the revenue reaches 37.85% of the total system. From this perspective, there is a game process with computing power as main factor between SM1 and SM2. Meanwhile, the computing power of SM1 is lower than other miners, there is also a mutual game process between honest miners and selfish miners. As for the detailed analysis of the game process between nodes, it is not the focus of this paper, and will not be discussed in detail here.
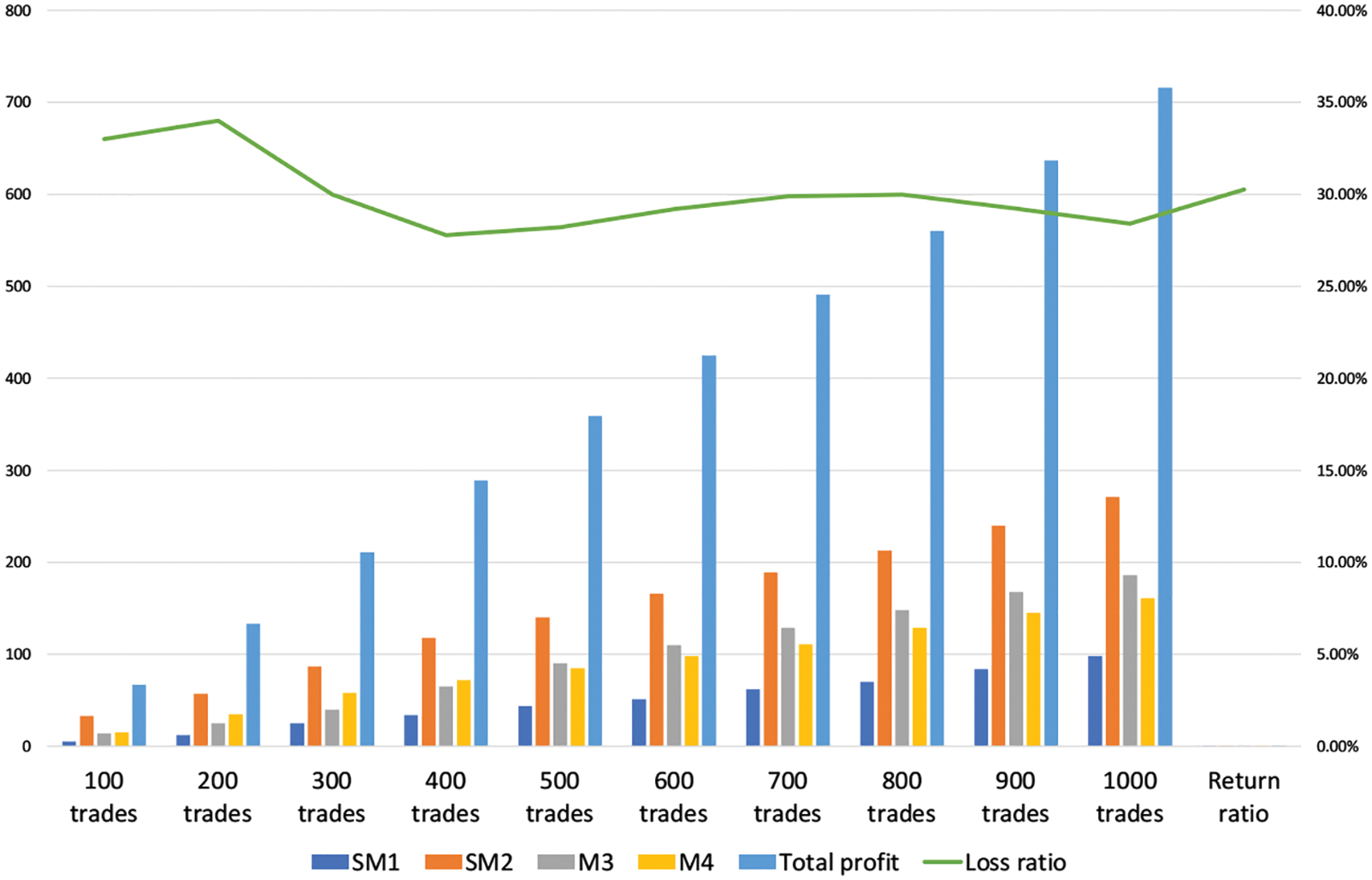
Figure 12: Selfish mining diagram
In a nutshell, the above experimental data indicates that when the nodes are conducting self-mining, if the power of the node is too small, it will be difficult to obtain additional benefits, or even less than the benefits of the honest node. When the computing power reaches 1/3 of the total system power, the self-mining node can obtain more additional benefits than the honest node. The result is in accordance with the theoretical derivation by researcher Eyal in 2013.
In this chapter, we mainly introduce some characteristics of blockchain and then lead to selfish mining attack in the current Bitcoin transaction system. We analyze the cause of selfish mining and illustrate the results of selfish mining. Furthermore, the research process of selfish mining at home or abroad is also illustrated there. We build the model of selfish mining from the perspective of node state transition diagram and derive the function expression of relative profit. Then by utilizing the function extremum method, we figure the value of optimal profit. When the computing power reaches 1/3 of the total system power, the self-mining node can obtain more additional benefits than the honest node. Overall, blockchain technology is still in development stage. There is a lot of work to do in technical level.
Funding Statement: This work was supported by the National Key R&D Program of China (Grant No. 2020YFB1005900, 2021YFB3101104, 2021YFB2700503), Hao Wang received the grant and the URLs to sponsors’ websites is https://service.most.gov.cn/.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Nofer, P. Gomber, O. Hinz and D. Schiereck, “Blockchain,” Business & Information Systems Engineering, vol. 59, no. 3, pp. 183–187, 2017. [Google Scholar]
2. X. Li, P. Jiang, T. Chen, X. Luo and Q. Wen, “A survey on the security of blockchain systems,” Future Generation Computer Systems, vol. 107, pp. 841–853, 2020. [Google Scholar]
3. A. Urquhart, “The inefficiency of bitcoin,” Economics Letters, vol. 148, pp. 80–82, 2016. [Google Scholar]
4. P. Ciaian, M. Rajcaniova and D. Kancs, “The economics of bitcoin price formation,” Applied Economics, vol. 48, no. 19, pp. 1799–1815, 2016. [Google Scholar]
5. Y. J. Ren, Y. Leng, J. Qi, K. S. Pradip, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, pp. 304–313, 2021. [Google Scholar]
6. C. P. Ge, W. Susilo, Z. Liu, J. Y. Xia, L. M. Fang et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 6, pp. 2787–2800, 2021. [Google Scholar]
7. L. M. Fang, M. H. Li, Z. Liu, C. T. Lin, S. L. Ji et al., “A secure and authenticated mobile payment protocol against off-site attack strategy,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 2, pp. 1–10, 2021. [Google Scholar]
8. J. Wang, H. Han, H. Li, S. He, P. K. Sharma et al., “Multiple strategies differential privacy on sparse tensor factorization for network traffic analysis in 5G,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 1939–1948, 2022. [Google Scholar]
9. T. Li, Q. Qian, Y. J. Ren, Y. Z. Ren and J. Y. Xia, “Privacy-preserving recommendation based on kernel method in cloud computing,” Computers, Materials & Continua, vol. 66, no. 1, pp. 779–791, 2021. [Google Scholar]
10. Y. J. Ren, J. Qi, Y. P. Cheng, J. Wang and O. Alfarraj, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]
11. Y. J. Ren, K. Zhu, Y. Q. Gao, J. Y. Xia, S. Zhou et al., “Long-term preservation of electronic record based on digital continuity in smart cities,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3271–3287, 2021. [Google Scholar]
12. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “A verifiable and fair attribute-based proxy re-encryption scheme for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 7, pp. 1–12, 2021. [Google Scholar]
13. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]
14. J. Wang, C. Y. Jin, Q. Tang, N. X. Xiong and G. Srivastava, “Intelligent ubiquitous network accessibility for wireless-powered MEC in UAV-assisted B5G,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 4, pp. 2801–2813, 2021. [Google Scholar]
15. T. Li, W. D. Xu, L. N. Wang, N. P. Li, Y. J. Ren et al., “An integrated artificial neural network-based precipitation revision model,” KSII Transactions on Internet and Information Systems, vol. 15, no. 5, pp. 1690–1707, 2021. [Google Scholar]
16. C. P. Ge, Z. Liu, J. Y. Xia and L. M. Fang, “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1214–1226, 2021. [Google Scholar]
17. Y. J. Ren, Y. Leng, Y. P. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]
18. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
19. Y. J. Ren, F. J. Zhu, S. P. Kumar, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]
20. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “Revocable attribute-based encryption with data integrity in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 4, pp. 1–12, 2021. [Google Scholar]
21. Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 1639–1648, 2022. [Google Scholar]
22. H. Vranken, “Sustainability of bitcoin and blockchains,” Current Opinion in Environmental Sustainability, vol. 28, pp. 1–9, 2017. [Google Scholar]
23. Y. Ren, X. Liu, Q. Wu, L. Wang and W. Zhang, “Cryptographic accumulator and Its application: A survey,” Security and Communication Networks, vol. 2022, no. 1, pp. 1–13, 2022. [Google Scholar]
24. S. Underwood, “Blockchain beyond bitcoin,” Communications of the ACM, vol. 59, no. 11, pp. 15–17, 2016. [Google Scholar]
25. Y. J. Ren, J. Qi, Y. P. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM Transactions on Internet Technology, vol. 21, no. 1, pp. 1–20, 2021. [Google Scholar]
26. M. Di Pierro, “What is the blockchain?,” Computing in Science & Engineering, vol. 19, no. 5, pp. 92–95, 2017. [Google Scholar]
27. H. -N. Dai, Z. Zheng and Y. Zhang, “Blockchain for internet of things: A survey,” IEEE Internet of Things Journal, vol. 6, no. 5, pp. 8076–8094, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |