DOI:10.32604/iasc.2023.024660

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.024660 |  |
| Article |
Application of Intuitionistic Z-Numbers in Supplier Selection
1Centre for Mathematical Sciences, College of Computing and Applied Sciences, Universiti Malaysia Pahang, Lebuhraya Tun Razak, Gambang, Kuantan, 26300, Pahang, Malaysia
2Faculty of Computer and Mathematical Sciences, Universiti Teknologi MARA Pahang, Jengka Campus, Bandar Tun Abdul Razak Jengka, 26400, Pahang, Malaysia
*Corresponding Author: Ku Muhammad Naim Ku Khalif. Email: kunaim@ump.edu.my
Received: 26 October 2021; Accepted: 06 December 2021
Abstract: Intuitionistic fuzzy numbers incorporate the membership and non-membership degrees. In contrast, Z-numbers consist of restriction components, with the existence of a reliability component describing the degree of certainty for the restriction. The combination of intuitionistic fuzzy numbers and Z-numbers produce a new type of fuzzy numbers, namely intuitionistic Z-numbers (IZN). The strength of IZN is their capability of better handling the uncertainty compared to Zadeh's Z-numbers since both components of Z-numbers are characterized by the membership and non-membership functions, exhibiting the degree of the hesitancy of decision-makers. This paper presents the application of such numbers in fuzzy multi-criteria decision-making problems. A decision-making model is proposed using the trapezoidal intuitionistic fuzzy power ordered weighted average as the aggregation function and the ranking function to rank the alternatives. The proposed model is then implemented in a supplier selection problem. The obtained ranking is compared to the existing models based on Z-numbers. The results show that the ranking order is slightly different from the existing models. Sensitivity analysis is performed to validate the obtained ranking. The sensitivity analysis result shows that the best supplier is obtained using the proposed model with 80% to 100% consistency despite the drastic change of criteria weights. Intuitionistic Z-numbers play a very important role in describing the uncertainty in the decision makers’ opinions in solving decision-making problems.
Keywords: Intuitionistic Z-number; fuzzy decision making; ranking function; supplier selection; sensitivity analysis
In the theory of fuzzy set, Zadeh [1] considered the real number in the interval [0, 1] to define the membership grade for a fuzzy set. The concept of the fuzzy set was then extended to a fuzzy number by Dubois et al. [2]. A fuzzy number is defined as a fuzzy subset of the real number in which its maximum membership values are surrounding the average value [2]. Many researchers have used triangular and trapezoidal fuzzy numbers to solve multi-criteria decision making (MCDM) problems.
The fuzzy set has been generalized as an intuitionistic fuzzy set by Atanassov [3]. The intuitionistic fuzzy set incorporates the membership and non-membership degrees, both taking values from the interval [0, 1]. The membership degree represents the grade of belongingness, while the non-membership degree measures the level of non-belongingness of the elements to the fuzzy sets. The concept of the intuitionistic fuzzy set has been extended to the intuitionistic fuzzy number by Grzegrorzewski [4].
In 2011, Zadeh [5] proposed a new type of fuzzy number, namely Z-number, Z = (A, R), which consists of a reliability component instead of only a restriction component. The reliability component, R, describes the level of sureness or certainty of the restriction component, A. The restriction and reliability components are usually represented by trapezoidal and triangular fuzzy numbers, respectively.
Many MCDM methods were developed based on fuzzy numbers, intuitionistic fuzzy numbers and Z-numbers. Among the prominent MCDM methods are the fuzzy analytical hierarchy process (FAHP), the fuzzy technique for order preference by similarity to ideal solution (FTOPSIS) and the fuzzy VIKOR method. Recently, Wang et al. [6] used FAHP and fuzzy weighted aggregated sum product assessment (FWASPAS) to evaluate the performance of the last-mile delivery companies in Vietnam. The same combined MCDM methods were used for online food delivery companies selection in [7]. The integrated FAHP-FTOPSIS was implemented in [8] to select the reverse logistics partners. FAHP and fuzzy VIKOR were used for logistics outsourcing in [9] and coffee bean supplier selection in [10].
Considering intuitionistic fuzzy numbers and Z-numbers, Sari et al. [11] defined the intuitionistic Z-numbers (IZNs) by refining the membership and non-membership grades of the constraint and reliability components of Z-numbers. The strength of the defined membership and non-membership grades are their ability to indicate the hesitancy of the experts for both components of Z-numbers in the decision making. The authors also proposed a defuzzification method to transform IZNs into regular fuzzy numbers. However, there was no application of IZNs in the decision making given in their literature. Since IZNs are believed to have a better capability of handling uncertainty, it is important to develop an MCDM model based on IZNs.
In this present paper, a new MCDM model based on IZNs is proposed. First, the linguistic value for each linguistic term of IZNs is given. The aggregation of decision makers’ opinions are aggregated using the trapezoidal intuitionistic fuzzy power ordered weighted average (TIFPOWA) [12]. Although many other effective MCDM methods can be used, such as FAHP, FTOPSIS and fuzzy VIKOR as in [6–10], this study focused on the ranking of alternatives using a ranking function based on centroid [13], which makes the model more time-efficient. In fact, the main purpose of the model is to illustrate the use of IZN in characterizing the decision makers’ preferences for the decision-making process. The proposed model is then implemented in the supplier selection problem.
This paper is organized as follows: the introduction of the paper is explained in Section 1, and some preliminaries on intuitionistic fuzzy numbers, Z-numbers and IZNs are given in Section 2; Section 3 proposes the MCDM model based on IZNs; Section 4 illustrates the proposed model using the supplier selection problem. Finally, results and discussion are given in Section 5, and the conclusion is presented in Section 6.
In this section, some preliminaries on the intuitionistic fuzzy numbers, Z-numbers and intuitionistic Z-numbers are reviewed.
2.1 Intuitionistic Fuzzy Number
Instead of only assigning the membership degree to each element of the fuzzy set, Atanassov [3] defined the non-membership function, which denotes the degree of non-belongingness of the element to the set. The intuitionistic fuzzy set is a generalization of a classical fuzzy set, defined as follows [3]:
Definition 1 An intuitionistic fuzzy set I in the universe of discourse U is defined by
where μI(x) is the membership function and νI(x) is the non-membership function, satisfying the condition,
A trapezoidal intuitionistic fuzzy number AI = 〈(a2, a3, a4, a5)(a1, a3, a4, a6)〉 is shown in Fig. 1. The trapezoidal intuitionistic fuzzy number is used instead of the triangular intuitionistic fuzzy number due to its capability of processing ill-defined quantities [14–16].

Figure 1: A trapezoidal intuitionistic fuzzy number
Moreover, Zadeh [5] introduced the concept of Z-numbers, which incorporate two components: the restriction component, A and the reliability component, R. Moreover, Z-numbers include the probability concept in the fuzzy knowledge since the reliability deals with the probability distribution. For simplicity, the restriction and reliability components of Z-numbers can be represented by a trapezoidal fuzzy number and triangular fuzzy number, respectively, as shown in Fig. 2.

Figure 2: A Z-number Z = (A, R)
Refining the membership and non-membership functions for both components of Z-numbers, Sari et al. [11] defined the intuitionistic Z-numbers.
Definition 2 An intuitionistic Z-number is of the form
as illustrated in Fig. 3.

Figure 3: An intuitionistic fuzzy Z-number
The defuzzification of intuitionistic fuzzy Z-numbers was also given in [11] as follows:
Step 1: Convert the reliability into a crisp value.
where τ can be any large positive number.
Step 2: Add the weight obtained in Step 1 to the restriction component to obtain the weighted Z-number.
Step 3: Convert
3 MCDM Model Based on Intuitionistic Z-Numbers
An MCDM model is developed based on IZNs, in which the trapezoidal intuitionistic fuzzy power ordered weighted average (TIFPOWA) is used as an aggregation operator. In contrast, the ranking function of intuitionistic fuzzy numbers based on centroid is used to rank the alternatives. The proposed steps of the MCDM method are as follows:
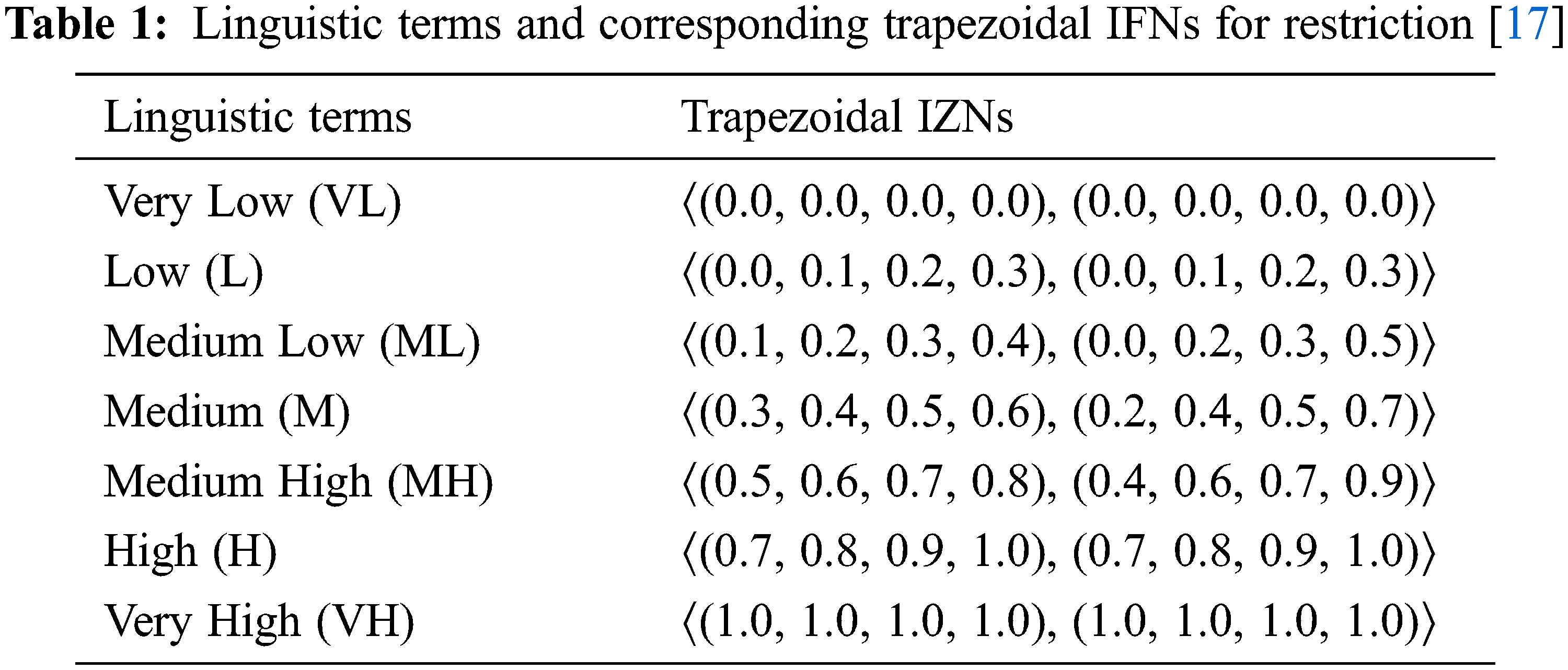
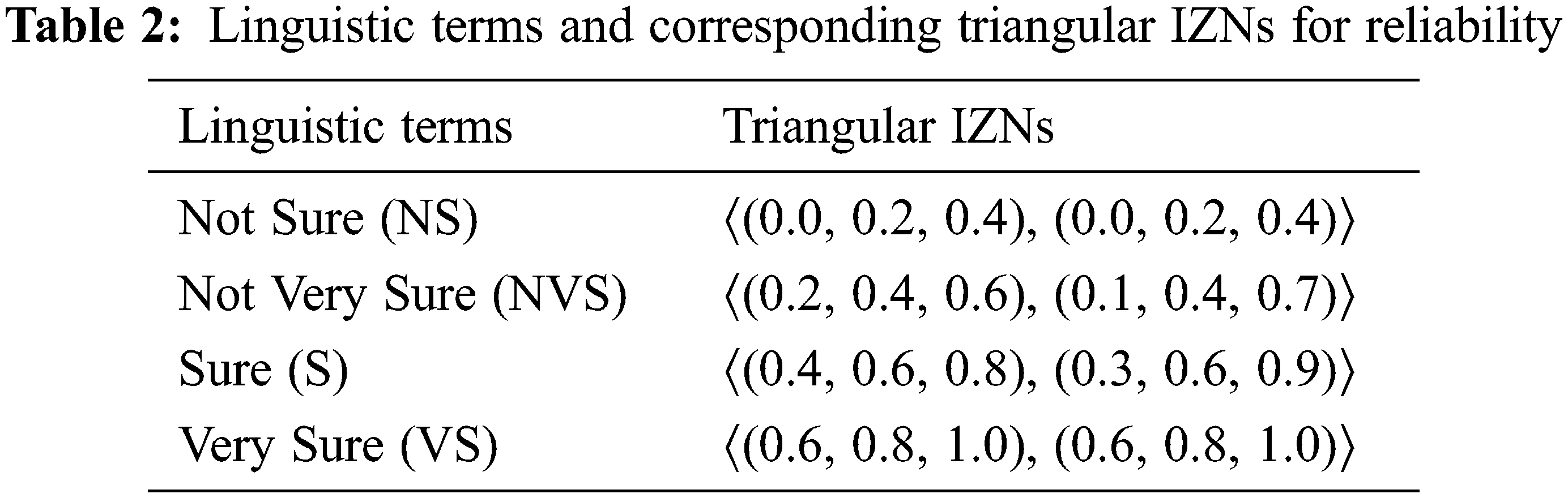
Step 1: The experts’ opinion is obtained and transformed into IZNs. The linguistic terms for the restriction and reliability components are given in Tabs. 1 and 2, respectively.
Step 2: The IZNs are then converted into intuitionistic fuzzy numbers using Eqs. (5)–(7) from the previous section.
Step 3: The evaluations from all decision-makers are then aggregated using the trapezoidal intuitionistic fuzzy power ordered weighted average (TIFPOWA) [12].
Step 4: The evaluations for all criteria are aggregated using TIFPOWA given by Eq. (8).
Step 5: The ranking function based on centroid [13] is calculated.
where
In this section, some literature regarding supplier selection in the automobile manufacturing industry is reviewed. Then, a case study adapted from [18] is implemented to illustrate the supplier selection using the model proposed in the previous section.
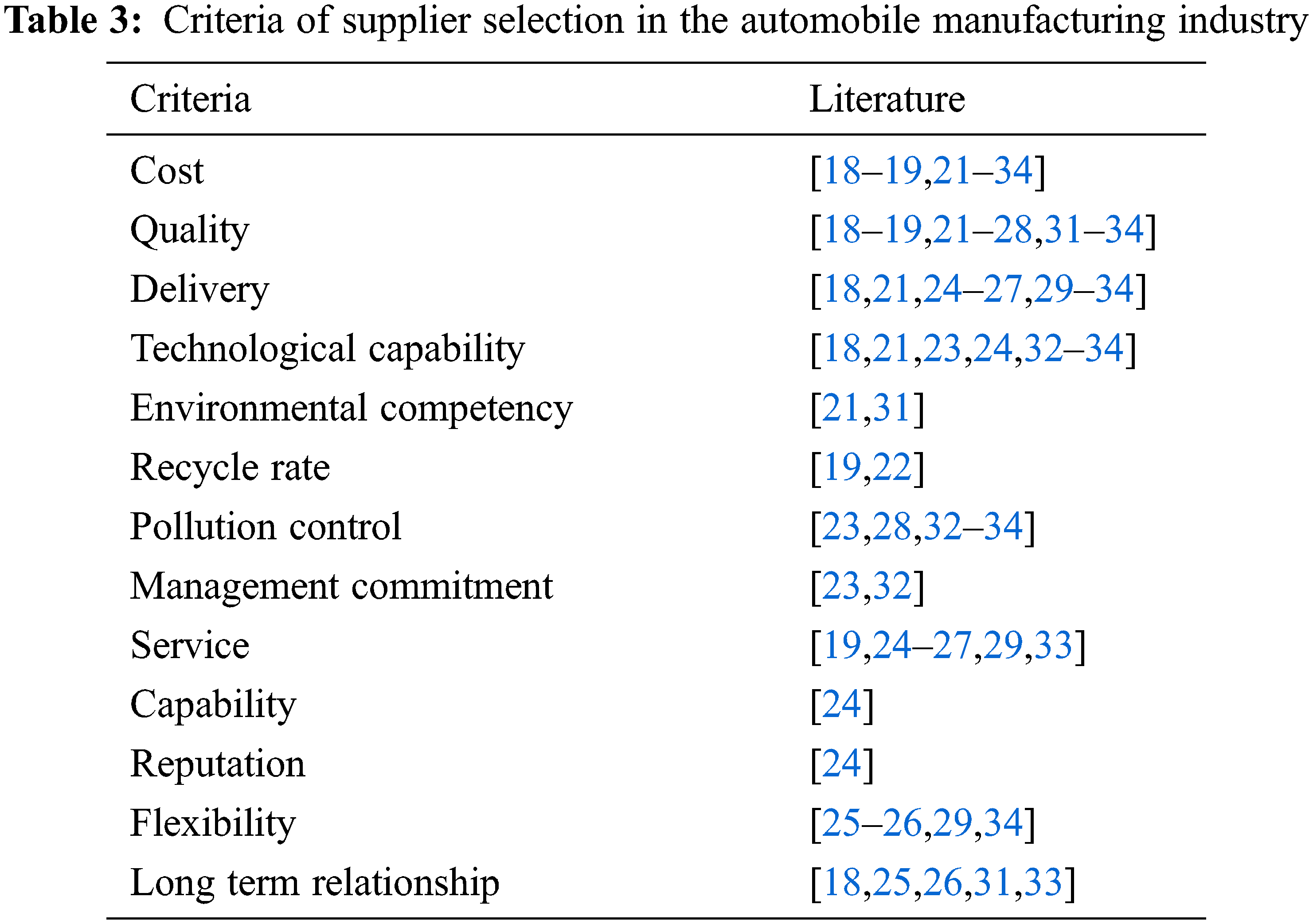
Selecting suppliers is a crucial process in supply chain management. The main objective of supplier selection is to assess available suppliers by using a set of criteria and measures [19]. Many multi-criteria decision-making (MCDM) methods have been developed to help experts in selecting the best supplier in various industries such as digital, textile manufacturing, logistics and automobile.
Furthermore, Huo et al. [20] implemented a 4-stage supplier selection method using TOPSIS to determine the quality suppliers in an automobile manufacturing enterprise. The integrated FAHP, FTOPSIS and fuzzy multi-objective linear programming methods were developed in [21]. The supplier selection in an Iranian automobile manufacturing company is implemented to illustrate the developed model. The integrated FAHP-FTOPSIS model was used for green supplier selection in the automobile industry in [22]. In most models using FAHP and FTOPSIS, the FAHP is used to evaluate the criteria weight, while FTOPSIS is to select the best alternatives.
Apart from that, Hashemi et al. [23] developed a model using the analytical network process (ANP) and Grey relational analysis (GRA) for a green supplier selection process. The automotive industry was used to demonstrate the proposed model. A fuzzy TODIM method based on interval type-2 fuzzy sets was used in [24] for a green supplier selection, in which the selection of automobile manufacturers was considered as a case study. Likewise, Yadav et al. [25] proposed a hybrid data envelopment analytical hierarchy process (DEAHP) to solve supplier selection in an Indian automobile company. They used another approach in [26], which is FAHP, to select the best supplier in a car and truck manufacturing company in India.
In 2016, Dweiri et al. [27] proposed a non-fuzzy AHP and implemented the model for supplier selection in the automotive industry. Four criteria considered were cost, quality, delivery and service and three suppliers were ranked. A modified multiplicative AHP (MMAHP) was used in [19] to select the best green supplier in an automobile manufacturing company. Other than that, Qin et al. [28] extended the TODIM technique using interval type-2 fuzzy sets and implemented the method for supplier selection in an automobile manufacturing enterprise. Ten criteria were considered to search for the best supplier to buy key components of its new automobile equipment.
The fuzzy Delphi method and the integrated AHP-DEMATEL were used in [29] to optimize supplier selection in the Indian automobile industry. Here, fuzzy Delphi was used to finalize the criteria selection, and AHP was implemented for prioritizing the criteria. Next, AHP-DEMATEL was used to determine the inter-relationship among all criteria. Besides, Rabieh et al. [30] developed a robust-fuzzy model for the purpose of supplier selection specifically under uncertainty. Finally, the developed model was applied in the automobile industry for a case study.
Moreover, Jain et al. [31] used fuzzy AHP and TOPSIS to solve supplier selection problems in the Indian automotive industry. The fuzzy AHP and TOPSIS methods were used separately to rank the alternatives. Hence different supplier ranking was obtained using different methods. However, using sensitivity analysis, they found that the AHP method is more robust than TOPSIS. Subsequently, Haeri et al. [32] combined the best worst method and fuzzy Grey relational analysis to select suppliers in the automotive industry.
A cloud TOPSIS model was used by Ramakrishnan et al. [33] to solve the green supplier selection problem for the automotive industry. In addition, Wang et al. [18] used the TOPSIS method based on Z-numbers to solve the supplier selection problem in the automobile manufacturing industry. Recently, Beiki et al. [34] proposed a novel integrated language entropy weight method and multi-objective programming method to solve the supplier selection in an automobile manufacturing company. The analysis of criteria considered from the above-mentioned literature is presented in Tab. 3 below.
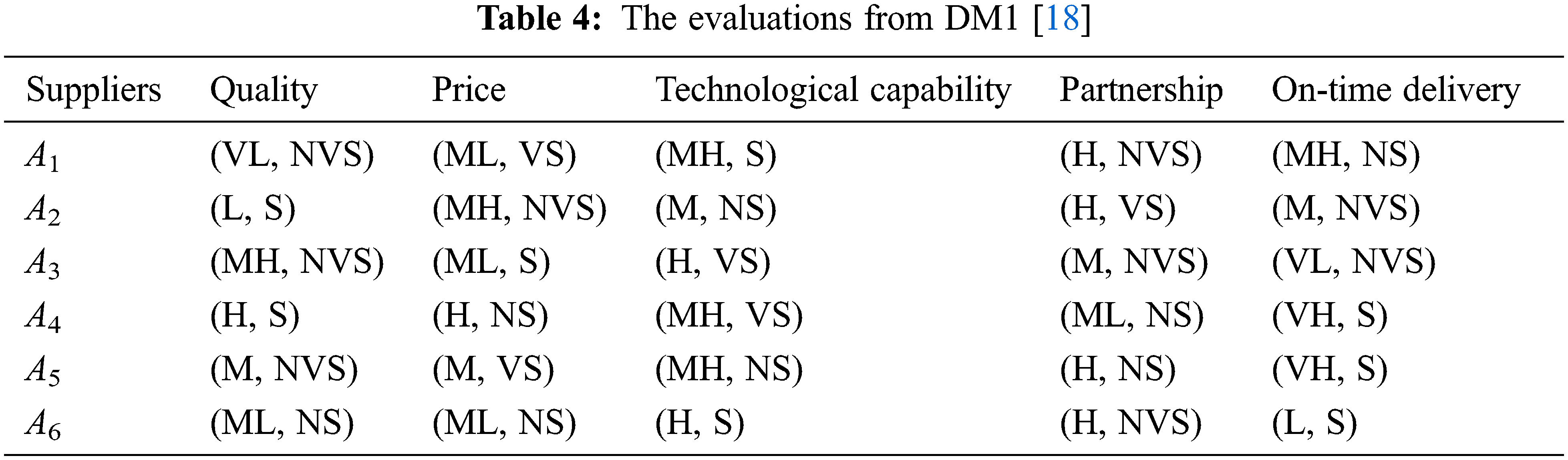
The proposed MCDM model based on IZNs is implemented in the supplier selection problem adopted from [18]. The supplier selection problem involved is concerning the automobile manufacturing company, considering five criteria: quality, price, technological capability, partnership and on-time delivery. There are six suppliers to be ranked, and three decision-makers are involved.
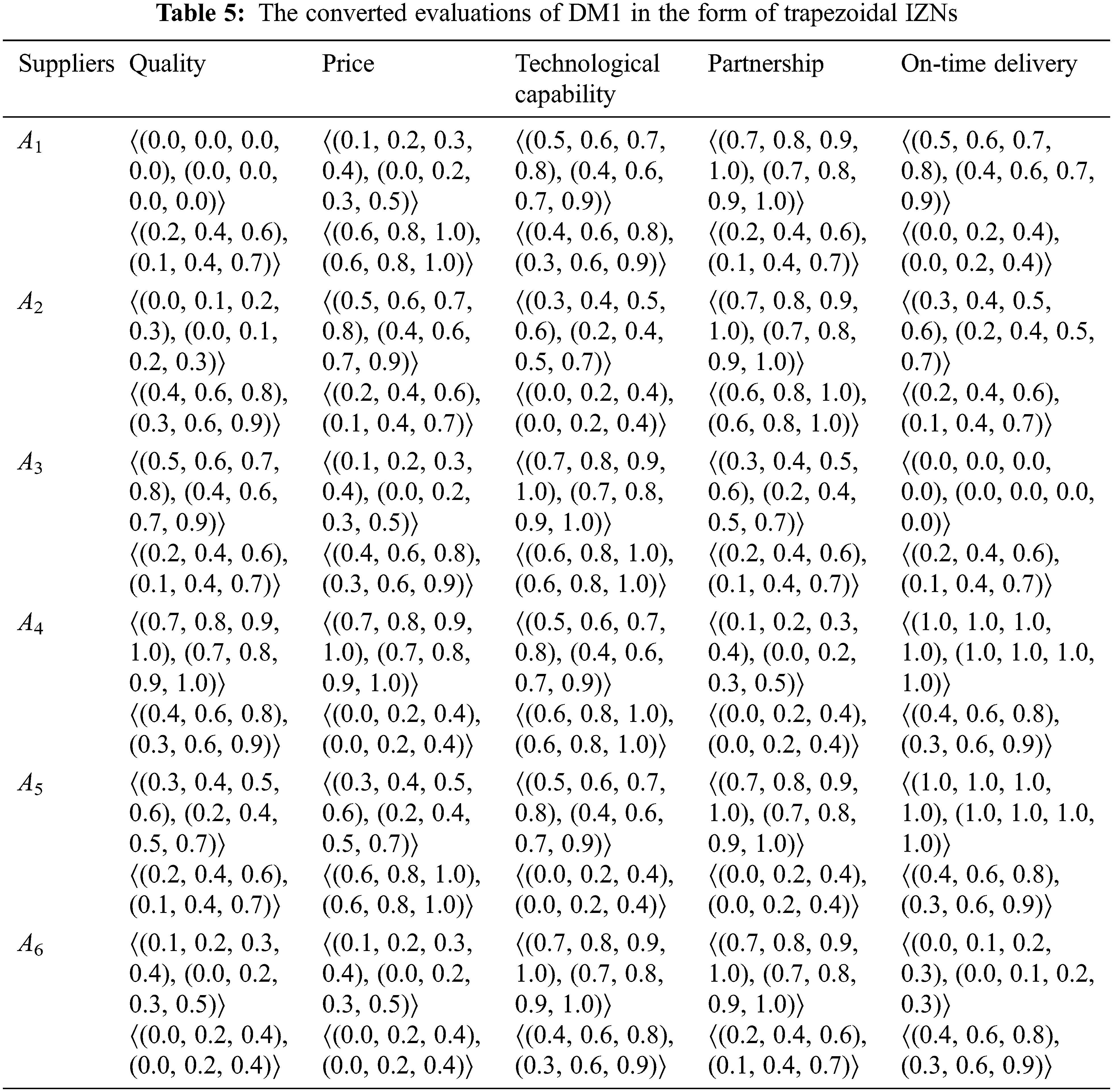
Step 1: The linguistic terms given by the three decision-makers are converted into linguistic values in the form of trapezoidal IZNs. For example, the evaluations of the first decision-maker (DM1) are given in Tab. 4, and the converted evaluations in the form of trapezoidal IZNs are given in Tab. 5.
Step 2: The trapezoidal IZNs are then converted into intuitionistic fuzzy numbers using Eqs. (5)–(7), assuming τ = 100. The value of τ is chosen based on the suggestion from [11]. Moreover, τ should be large so that the defuzzified value of the reliability part of IZN is mainly determined by the membership degrees. The presence of the smaller defuzzified value for the non-membership degree exhibits a degree of hesitancy. If τ is too big, then the non-membership degree of the reliability component will be completely ignored. Hence, choosing τ = 100 is perfect enough for the purpose of defuzzifying IZN into intuitionistic fuzzy numbers.
Step 3: The evaluations of all decision-makers are aggregated using TIFPOWA. For example, considering only criterion 1, the aggregated evaluations in the form of intuitionistic fuzzy numbers are given in Tab. 6.

Step 4: Again, using TIFPOWA, the evaluations for all criteria are aggregated, assuming the similar criteria weight for each criterion. The aggregated evaluations for each supplier are given below.
Step 5: The ranking functions are calculated, resulting
Based on the ranking functions in the proposed model, the ranking of suppliers is
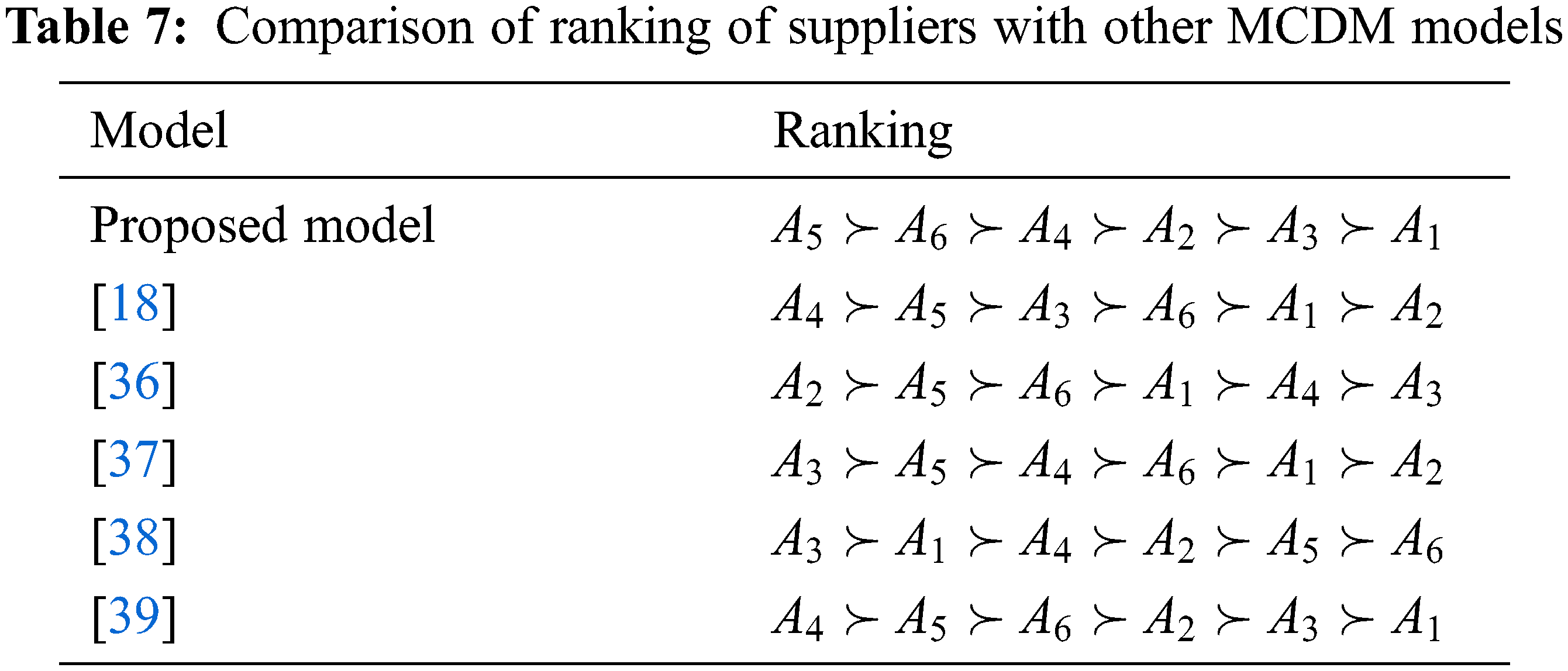
It is clearly seen that using different methods results in different rankings for the suppliers. Each of the models has its own strengths and weaknesses. However, identifying them for specific problems is quite hard [18]. The MCDM models [18,35–38] use Z-numbers, while the proposed model utilizes intuitionistic Z-numbers, which are more detailed in terms of representation of expert's evaluation. The fusion of intuitionistic fuzzy numbers concepts in the Z-numbers has a better capability of handling uncertainty arising from the lack of information when making the evaluation on the restriction and reliability components.
The model in [18] used TOPSIS and power aggregation operators to produce its ranking. The ranking fuzzy numbers method was used in [35], and the model in [36] used priority weight. The similarity measure was used in [37], and the TOPSIS method was used in [38]. In the TOPSIS method implemented in [18,38], the distance is used to measure the separation of each alternative from the positive and negative ideal solutions. In this paper, instead of using the distance measure, a ranking method was used to rank the alternatives. The use of the ranking method has skipped some steps as compared to the TOPSIS method, which makes the proposed model time-efficient.
Based on the proposed model, the supplier A5 is ranked first. The same supplier, however, is ranked second in [18,35,36,38]. The supplier A1 is ranked last in the present model, which is similar to the ranking from [38]. In fact, the ranking of the last three alternatives of the proposed model is similar to the one in [38]. The proposed model and the model from [37] give similar ranking for the third and fourth, which are A4 and A2, respectively.
To validate the ranking result obtained using the proposed method, a sensitivity analysis is used by changing the weight of each criterion into zero [39–41] and increasing by 50%, 100% and 150%. The sensitivity analysis is a well-known method in studying how the output uncertainty of a model can be attributed to different sources of uncertainty in the model input [42]. Tab. 8 below lists the ranking obtained when each criterion weight is shifted to zero. Tabs. 9–11 present the ranking obtained when each criterion weight is increased by 50%, 100% and 150%, respectively. Here, C1, C2, C3, C4 and C5 represent the criteria for quality, price, technological capability, partnership and on-time delivery, respectively.


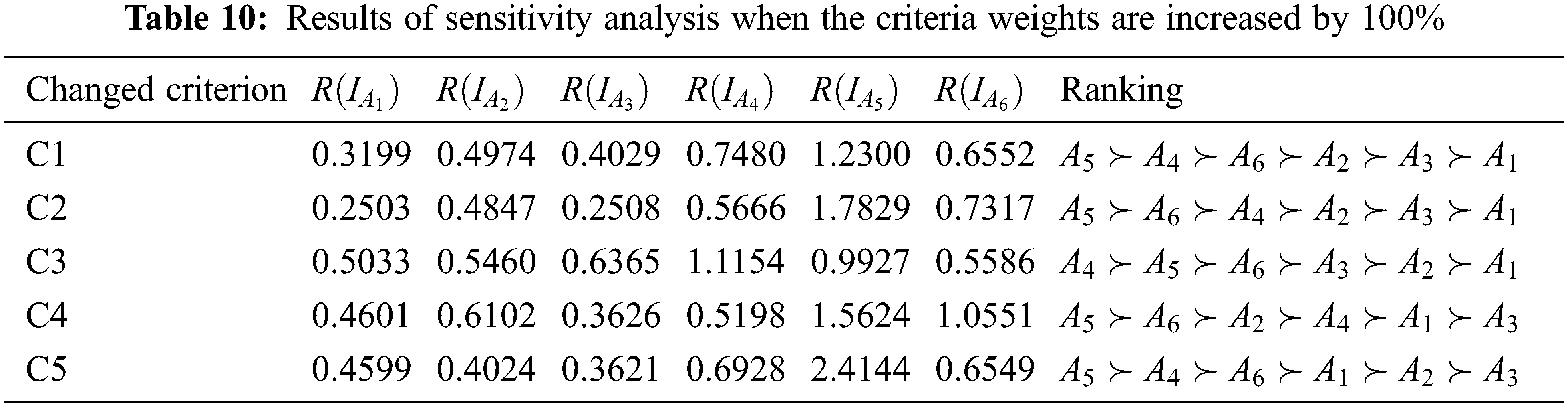
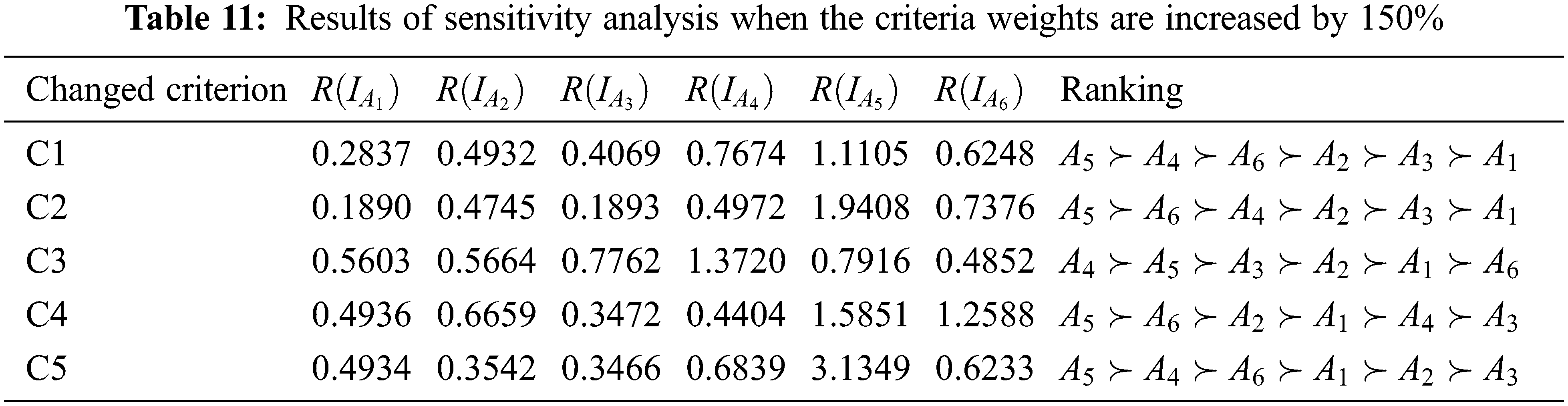
From Tabs. 8 and 9, A5 is always ranked first no matter which criterion weight is changed. When the criteria weight is increased by 100% and 150%, A5 is still ranked first except when criterion C3 is changed, as shown in Tabs. 10 and 11. As the goal of this selection problem is to identify the best supplier, this research focuses on the consistency of the first ranking. The consistency of the ranking is defined as the similarity of at least two rankings of the alternatives [43]. In this case, the first ranking obtained when the criteria weight is shifted to zero and increased by 50%, 100% and 150% is compared to the ranking obtained using the proposed model, which recommends that A5 is the best supplier. The consistency of the obtained ranking using sensitivity analysis is shown in Tab. 12.
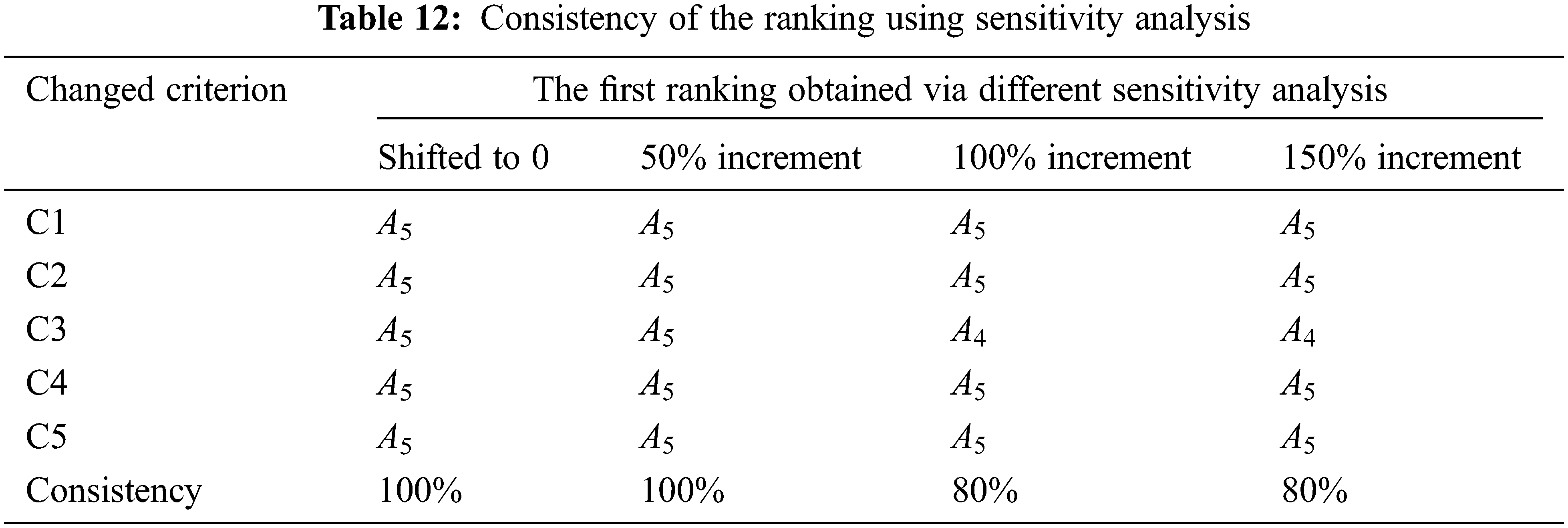
The sensitivity analysis thus suggests that A5 is the best supplier among all with an 80% to 100% consistency degree, as shown in Tab. 12. Again, a radar diagram is most suitable to support this result. Figs. 4–7 further illustrate this ranking, in which Situations 1, 2, 3, 4 and 5 represent the state where the weights of criteria quality, price, technological capability, partnership and on-time delivery are changed, respectively.

Figure 4: Radar diagram for sensitivity analysis when the criteria weights are changed to zero

Figure 5: Radar diagram for sensitivity analysis when the criteria weights are increased by 50%

Figure 6: Radar diagram for sensitivity analysis when the criteria weights are increased by 100%

Figure 7: Radar diagram for sensitivity analysis when the criteria weights are increased by 150%
From the presented radar diagrams, it is obviously seen that supplier A5 is the outermost line in all situations, recommending it to be the best supplier among all. Furthermore, the robustness of the proposed model was validated with an 80% to 100% consistency, hence supporting the fact that the intuitionistic Z-numbers play a vital role in representing the uncertainty in the decision-making process.
The ranking of alternatives always differs if different methods of the MCDM model are used. Each method has its own advantages and disadvantages. In the present paper, the MCDM model is developed based on IZNs, which combine the intuitionistic fuzzy numbers and Z-numbers. The degrees of membership and non-memberships are defined for each component of Z-numbers, where their values for linguistic terms are defined. This fusion has a better capability of handling uncertainty and vagueness arising from the lack of information during the process of experts’ evaluation. The proposed model involves the conversion of IZNs into intuitionistic fuzzy numbers, which are then evaluated using the ranking function to list the alternatives. As compared to other models which use TOPSIS, this model did not measure the nearest and furthest distance of alternatives from the positive or negative ideal solutions, respectively. Instead, the ranking function based on centroid is used. The sensitivity analysis is used to validate the obtained ranking, in which the supplier A5 is ranked first. The strength of IZNs and the ranking function plays a crucial role in the proposed model. In the future, a better defuzzification method is used in the fuzzy MCDM model to transform the IZNs into intuitionistic fuzzy numbers. Besides, it is also recommended that direct calculation on IZNs is used without needing to convert the IZNs into intuitionistic fuzzy numbers. This will avoid significant loss of information contained in the IZNs and can be implemented to solve many MCDM problems.
Acknowledgement: All the authors would like to thank Universiti Malaysia Pahang and Ministry of Higher Education Malaysia for supporting this research work.
Funding Statement: This work is funded by the Fundamental Research Grant Scheme under the Ministry of Higher Education Malaysia FRGS/1/2019/STG06/UMP/02/9.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]
2. D. Dubois and H. Prade, “Operations on fuzzy numbers,” International Journal of Sytems Science, vol. 9, no. 6, pp. 613–626, 1978. [Google Scholar]
3. K. Atanassov, “Intuitionistic fuzzy sets,” Fuzzy Sets and Systems, vol. 20, pp. 87–97, 1986. [Google Scholar]
4. P. Grzegrorzewski, “The hamming distance between intuitionistic fuzzy sets,” in Proc. of the 10th IFSA World Congress, Turkey, pp. 35–38, 2003. [Google Scholar]
5. L. A. Zadeh, “A note on Z-numbers,” Information Sciences, vol. 181, no. 14, pp. 2923–2932, 2011. [Google Scholar]
6. C. N. Wang, T. T. Dang and H. P. Hsu, “Evaluating sustainable Last-Mile Delivery (LMD) in B2C e-commerce using two-stage fuzzy MCDM approach: A case study from Vietnam,” IEEE Access, vol. 9, pp. 146050–146067, 2021. [Google Scholar]
7. N. B. T. Nguyen, G. H. Lin and T. T. Dang, “Fuzzy multi-criteria decision-making approach for online food delivery (OFD) companies evaluation and selection: A case study in Vietnam,” Processes, vol. 9, no. 8, pp. 1–20, 2021. [Google Scholar]
8. C. N. Wang, T. T. Dang and N. A. T. Nguyen, “Outsourcing reverse logistics for e-commerce retailers: A two-stage fuzzy optimization approach,” Axioms, vol. 10, no. 1, pp. 1–22, 2021. [Google Scholar]
9. C. N. Wang, N. A. T. Nguyen, T. T. Dang and C. M. Lu, “A compromised decision-making approach to third-party logistics selection in the sustainable supply chain using fuzzy AHP and fuzzy VIKOR methods,” Mathematics, vol. 9, no. 8, pp. 1–27, 2021. [Google Scholar]
10. N. B. T. Nguyen, G. H. Lin and T. T. Dang, “A two-phase integrated fuzzy decision-making framework for green supplier selection in the coffee bean supply chain,” Mathematics, vol. 9, no. 16, pp. 1–21, 2021. [Google Scholar]
11. I. U. Sari and C. Kahraman, “Intuitionistic fuzzy Z-numbers,” in Int. Conf. on Intelligent and Fuzzy Systems, Izmir, Turkey, pp. 1316–1324, 2020. [Google Scholar]
12. T. Baležentis and A. Baležentis, “Group decision making procedure based on trapezoidal intuitionistic fuzzy numbers: Multimoora methodology,” Economic Computation & Economic Cybernetics Studies & Research, vol. 50, no. 1, pp. 103–122, 2016. [Google Scholar]
13. A. A. Prakash, M. Suresh and S. Vengataasalam, “A new approach for ranking of intuitionistic fuzzy numbers using a centroid concept,” Mathematical Sciences, vol. 10, pp. 177–184, 2016. [Google Scholar]
14. T. Chaira, Fuzzy Set and its Extension, India: Wiley, 2019. [Online]. Available: https://onlinelibrary.wiley.com/doi/book/10.1002/9781119544203. [Google Scholar]
15. Q. Zhang and D. Sun, “Some notes on possibilistic variances of generalized trapezoidal intuitionistic fuzzy numbers,” AIMS Mathematics, vol. 6, pp. 3720–3740, 2021. [Google Scholar]
16. M. Kumar, “Applying weakest t-norm based approximate intuitionistic fuzzy arithmetic operations on different types of intuitionistic fuzzy numbers to evaluate the reliability of PCBA fault,” Applied Soft Computing, vol. 23, pp. 387–406, 2014. [Google Scholar]
17. J. Ye, “Expected value method for intuitionistic trapezoidal fuzzy multicriteria decision-making problems,” Expert Systems with Applications, vol. 38, no. 9, pp. 11730–11734, 2011. [Google Scholar]
18. F. Wang and J. Mao, “Approach to multicriteria group decision making with Z-numbers based on TOPSIS and power aggregation operators,” Mathematical Problems in Engineering, vol. 2019, pp. 1–18, 2019. [Google Scholar]
19. Q. Yu and F. Hou, “An approach for green supplier selection in the automobile manufacturing industry,” Kybernetes, vol. 45, no. 4, pp. 1–19, 2016. [Google Scholar]
20. H. Huo, Y. Ma and X. Shen, “Research on automotive component supplier selection process,” in Int. Conf. on Management Science and Industrial Engineering (MSIE), Harbin, China, pp. 935–939, 2011. [Google Scholar]
21. D. Kannan, R. Khodaverdi, L. Olfat, A. Jafarian and A. Diabat, “Integrated fuzzy multi-criteria decision-making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain,” Journal of Cleaner Production, vol. 47, pp. 355–367, 2013. [Google Scholar]
22. M. Yazdani, “An integrated MCDM approach to green supplier selection,” International Journal of Industrial Engineering Computations, vol. 5, no. 3, pp. 443–458, 2014. [Google Scholar]
23. S. H. Hashemi, A. Karimi and M. Tavana, “An integrated green supplier selection approach with analytic network process and improved grey relational analysis,” International Journal of Production Economics, vol. 159, pp. 178–191, 2015. [Google Scholar]
24. X. Sang and X. Liu, “An interval type-2 fuzzy sets-based TODIM method and its application to green supplier selection,” Journal of the Operational Research Society, vol. 67, no. 5, pp. 722–734, 2016. [Google Scholar]
25. V. Yadav and M. K. Sharma, “An application of hybrid data envelopment analytical hierarchy process approach for supplier selection,” Journal of Enterprise Information Management, vol. 28, no. 2, pp. 218–242, 2015. [Google Scholar]
26. V. Yadav and M. K. Sharma, “Multi-criteria decision making for supplier selection using fuzzy AHP approach,”. Benchmarking: An International Journal, vol. 22, no. 6, pp. 1158–1174, 2015. [Google Scholar]
27. F. Dweiri, S. Kumar, S. A. Khan and V. Jain, “Designing an integrated AHP based decision support system for supplier selection in the automotive industry,” Expert Systems with Applications, vol. 62, pp. 273–283, 2016. [Google Scholar]
28. J. Qin, X. Liu and W. Pedrycz, “An extended TODIM multi-criteria group decision-making method for green supplier selection in interval type-2 fuzzy environment,” European Journal of Operational Research, vol. 258, no. 2, pp. 626–638, 2017. [Google Scholar]
29. A. Kumar, A. Pal, A. Vohra, S. Gupta, S. Manchanda et al., “Construction of capital procurement decision-making model to optimize supplier selection using fuzzy delphi and AHP-DEMATEL,” Benchmarking: An International Journal, vol. 25, no. 5, pp. 1–14, 2018. [Google Scholar]
30. M. Rabieh, M. Modarres and A. Azar, “Robust-fuzzy model for supplier selection under uncertainty: An application to the automobile industry,” Scientia Iranica, vol. 25, no. 4, pp. 2297–2311, 2018. [Google Scholar]
31. V. Jain, A. K. Sangaiah, S. Sakhuja, N. Thoduka and R. Aggarwal, “Supplier selection using fuzzy AHP and TOPSIS: A case study in the Indian automotive industry,” Neural Computing and Applications, vol. 29, no. 7, pp. 555–564, 2018. [Google Scholar]
32. S. A. S. Haeri and J. Rezaei, “A grey-based green supplier selection model for uncertain environments,” Journal of Cleaner Production, vol. 221, pp. 768–784, 2019. [Google Scholar]
33. K. R. Ramakrishnan and S. Chakraborty, “A cloud topsis model for green supplier selection,” Facta Universitatis, Series: Mechanical Engineering, vol. 18, no. 3, pp. 375–397, 2020. [Google Scholar]
34. H. Beiki, S. M. Seyedhosseini, V. V. Ponkratov, A. O. Zekiy and S. A. Ivanov, “Addressing a sustainable supplier selection and order allocation problem by an integrated approach: A case of automobile manufacturing,” Journal of Industrial and Production Engineering, vol. 38, no. 4, pp. 239–253, 2021. [Google Scholar]
35. D. Mohamad, S. A. Shaharanib and N. H. Kamisc, “A Z-number-based decision making procedure with ranking fuzzy numbers,” in Proc. of the 3rd Int. Conf. on Quantitative Sciences and its Applications, Langkawi, Kedah, Malaysia, pp. 160–166, 2014. [Google Scholar]
36. B. Y. Kang, D. Wei, Y. Li and Y. Deng, “Decision making using Z-numbers under uncertain environment,” Journal of Computational Information Systems, vol. 8, no. 7, pp. 2807–2814, 2012. [Google Scholar]
37. D. Mohamad and S. Z. Ibrahim, “Decision making procedure based on jaccard similarity measure with Z-numbers,” Pertanika Journal of Science & Technology, vol. 25, no. 2, pp. 561–574, 2017. [Google Scholar]
38. N. Zamri, F. Ahmad, A. N. M. Rose and M. Makhtar, “A fuzzy TOPSIS with Z-numbers approach for evaluation on accident at the construction site,” Recent Advances on Soft Computing and Data Mining, vol. 549, pp. 41–50, 2017. [Google Scholar]
39. A. F. H. Librantz, F. C. R. Santos, C. G. Dias, A. C. A. Cunha, I. Costa et al., “AHP modelling and sensitivity analysis for evaluating the criticality of software programs,” in IFIP Int. Conf. on Advances in Production Management Systems, Iguassu Falls, Brazil, pp. 248–255, 2016. [Google Scholar]
40. I. Syamsuddin, “Multicriteria evaluation and sensitivity analysis on information security,” International Journal of Computer Applications, vol. 69, no. 24, pp. 22–25, 2013. [Google Scholar]
41. N. H. Baharin, N. F. Rashidi and N. F. Mahad, “Manager selection using fuzzy TOPSIS method,” Journal of Physics: Conference Series, vol. 1988, pp. 1–14, 2021. [Google Scholar]
42. A. Saltelli, “Global sensitivity analysis: an introduction,” in Proc. of the 4th Int. Conf. on Sensitivity Analysis of Model Output (SAMO’04), Santa Fe, New Mexico, pp. 27–43, 2004. [Google Scholar]
43. E. Roszkowska and T. Wachowicz, “The impact of decision-making profiles on the consistency of rankings obtained by means of selected multiple criteria decision-aiding methods,” Advances in Applied Data Analysis, vol. 23, no. 2, pp. 1–14, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |