DOI:10.32604/iasc.2023.027070

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.027070 |  |
| Article |
A Recursive High Payload Reversible Data Hiding Using Integer Wavelet and Arnold Transform
School of Computer Science and Engineering, Vellore Institute of Technology, Chennai, 600012, Tamilnadu, India
*Corresponding Author: Amishi Mahesh Kapadia. Email: amishimahesh.kapadia2013@vit.ac.in
Received: 10 January 2022; Accepted: 21 February 2022
Abstract: Reversible data hiding is an information hiding technique that requires the retrieval of the error free cover image after the extraction of the secret image. We suggested a technique in this research that uses a recursive embedding method to increase capacity substantially using the Integer wavelet transform and the Arnold transform. The notion of Integer wavelet transforms is to ensure that all coefficients of the cover images are used during embedding with an increase in payload. By scrambling the cover image, Arnold transform adds security to the information that gets embedded and also allows embedding more information in each iteration. The hybrid combination of Integer wavelet transform and Arnold transform results to build a more efficient and secure system. The proposed method employs a set of keys to ensure that information cannot be decoded by an attacker. The experimental results show that it aids in the development of a more secure storage system and withstand few tampering attacks The suggested technique is tested on many image formats, including medical images. Various performance metrics proves that the retrieved cover image and hidden image are both intact. This System is proven to withstand rotation attack as well.
Keywords: Reversible data hiding (RDH); integer wavelet transforms (IWT); arnold transform; payload; embedding and extraction
The world has entered a digital era with the widespread use of the internet and digital content. In this age of digital communication, where new technologies emerge on a daily basis, data security and safe communication are the key priorities, as sharing of information takes place over unsecured networks. Majority of sensitive services like healthcare, military and forensics sectors communicate using multimedia content, particularly digital images [1]. Digital images are very effective for hiding secret information as images have a huge volume of redundant pixels that can be used to hide additional data.
Watermarking and steganography are the two main types of data concealing. There are two important components in a data hiding scheme: payload and cover medium. In both the techniques data is embedded in cover media but both have varied applications and goals [2]. The key requirement for watermarking is integrity and authentication whereas primary goal of steganography is undetectability and it strives for high security and improved capacity. Steganography is a conventional data hiding scheme where primary goal is secured communication. There is a significant amount of literature on conventional schemes, which include both spatial and frequency (transform) domains. The drawback with all these methods is that, in the receiver end, the payload can be recovered exactly, but the alteration occurred to cover media cannot be undone [3].
In the case of sensitive applications like medical images which carries secret information on cover media; failing to recover the error free cover medium after extraction of secret data in it, may result in incorrect diagnosis or analysis of the patient disease. To overcome the above limitation, the Reversible Information Hiding (RDH) has come into existence.
RDH is a type of steganography that involves changing the cover medium to conceal the payload. Both the payload and the cover medium are retrieved without any data loss at the receiver end. The embedding is conducted directly on the picture pixel in spatial domain, resulting in distortion; however, the coefficient of the pixel is updated in the frequency domain [4], resulting in a more resilient and less distorted embedded image. The following strategies can be used to do reversible data hiding [5] in the spatial domain: compression-based techniques [6], difference expansion-based techniques [7], histogram shifting-based techniques [8], and prediction error-based techniques [9]. Similarly, the Integer Wavelet Transform (IWT), Discrete Cosine Transform (DCT) [10], and Fourier Transform (DFT) [11] can be used to perform RDH in the frequency domain [12]. There is also literature on hybrid combinations, which use both spatial and frequency properties to develop a more robust, secure system with enhanced embedding capacity and security [13].
To retrieve the original image without distortion, the reversible wavelet transforms, also known as the integer wavelet transform [14], which maps integer to integer, is utilized. The wavelet transformation can split a picture into a low-resolution approximation LL image and three low-frequency detail images, HL (horizontal), LH (vertical), and HH (horizontal, vertical and HH (horizontal, vertical, and horizontal, respectively) (diagonal). Xuan et al. [15] present an Integer Wavelet Transform technique for embedding undetectable data. Hidden information, histogram-modified bookkeeping data and error codes are all encoded and retrieved without loss. The embedding capacity of this technique is greater than that of previous techniques, and the resulting image is less distorted.
Xuan et al. [16] suggested a threshold-based histogram embedding technique that reduces distortion by encoding information in IWT’s high-frequency sub-bands. Small absolute value coefficients are utilized for embedding to avoid overflow and underflow concerns. To avoid overflow and underflow concerns, small absolute value coefficients are employed for embedding. By dividing the histogram into three pieces, the threshold approach is applied. Because the coefficient values of the center and end sections are less than and more than the threshold value, they are not used for embedding. The embedding is carried out on histogram pairings with the highest threshold, ensuring the necessary Peak signal-to-noise ratio (PSNR). In their study [17], Agrawal and Kumar proposed a method for partitioning an image into four non-overlapping chunks. The entropy is determined, and the embedding block with the highest entropy is chosen. The IWT is then applied to selected blocks, as well as a histogram shift utilizing the peak and zero value pairs. The peak point is increased by one while the zero bit remains constant if the secret data to be embedded is one.
Mantos and Maglogiannis [18] suggested a method for exploiting medical pictures from Digital Imaging and Communications in Medicine (DICOM). The photos are separated into two categories: the Region of Interest (ROI) and the Region of No Interest (RNI) (RONI). The ROI holds patient information, while the RONI holds the geographical map needed to retrieve ROI. The authentication data and the information to be hidden are encrypted and placed in the NROI section using the least significant scheme after the DICOM header fields have been selected. The location map, authentication data, and size of the Stego picture are all included in the image. Zear et al. [19] provide a three-level decomposition on discrete wavelet transform (DWT) and a combination of DWT, DCT and Support vector design (SVD). DCT is applied to the decomposed DWT, and the DCT coefficients are subjected to SVD. Following extraction, a back propagation neural network (BPNN) is used to improve the result by removing noise. There are many research works which uses DWT for embedding information as in for medical images including a 3D model [20] and reversible watermarking for medical audio data [21] for privacy protection.
A unique reversible data hiding system [22] suggested by Xiong, L., Xu, Z., and Shi, Y. Q. uses integer wavelet Transform, histogram shifting, and orthogonal decomposition. Histogram shifting is used on the high frequency coefficients since they have a Laplacian distribution. The orthogonal coefficients enable in the reversibility of the dada hiding operation. In this work, IWT is performed on the cover image first, and all frequency domain coefficients are encrypted; information is then embedded in the encrypted coefficients. Wavelet-based safe data concealment is proposed by Krishna et al. [23]. The secret image is first encrypted using pixel scrambling, circular shift, and swapping before being placed to the cover image. The procedure of scrambling is performed N times. As a result of the pixel-based correlation process, the image picture quality has enhanced. Because the secret image is scrambled before embedding, the suggested method is secure.
In the steganography procedure, Rima et al. [24] used two primary transforms: the Integer wavelets transform (IWT) and the Arnold transform. With integer to integer or bit to bit mapping, the IWT is applied to the cover object to alter it to disguise the hidden object. The Arnold transform is a method of image scrambling that is used to conceal the secret image. When applied to an image, it takes on a strewn appearance that makes it impossible to recognize the image. Thanikaiselvan et al. [25] proposed combining the spatial and transforms domains for data embedding. First Wavelet Transform (IWT) converts the cover image from spatial to domain. The data is hidden using a threshold-based histogram shifting method. To achieve the second level of data concealing, the generated image is interpolated to twice its original size and adaptive prediction error expansion is applied. This stego image is scrambled using a chaotic logistic map, resulting in DCT encoded with complimentary rules. After that, a hash function and a chaotic map are used to exclusive OR (XOR) the encoded image with a key image obtained by a hash function. Finally, the encrypted image is acquired by decoding the image with DWT. This study [26] proposes a dual-image RDH approach based on embedding in nonzero DCT coefficients. This method employs a dynamic allocation method to embed secret information, resulting in increased imperceptibility. DCT conversion, quantization, and entropy coding are all used in this procedure.
In RDH scheme, based on the requirement the focus is on either improving embedding capacity or imperceptibility. Robustness in RDH is still under research, not matured yet. In sensitive applications like medical images, failing to recover original cover medium may result in incorrect diagnosis or analysis of the patient disease which is unacceptable [27].
To address above challenges, a recursive multiple embedding technique is proposed which is secured, robust and reversible along with providing high embedding capacity.
Wavelet Transform in general has floating point precision which leads in lossy embedding, So Integer wavelet transform is applied for a complete reversibility [27]. Arnold Transform is applied on both cover image and secret unlike existing system, this improves the security and even the capacity. While extraction only the embedded image is required [28]. The limitation of existing system which requires additional information along with embedded image is overcome with proposed method. The suggested study investigates a new embedding approach that increases capacity and hides more information in a single cover image.
In this research we proposed a multi layered image hiding scheme using Integer wavelet transform and Arnold transform. Integer wavelet Transform gives a complete reversibility which helps to achieve a lossless retrieval of all images.
One of the most common reversible data hiding techniques is the 2D Integer Wavelet Transform. To convert a spatial image to a frequency domain image, lifting stages are used.
The basic Haar wavelet is defined [27] as in Eqs. (1) and (2)
where O: represents odd samples, E: represents even samples, A represents: Average of odd and even samples, D: Difference of odd and even samples. The above equations of Haar wavelet can be rewritten using lifting scheme and is implemented in three steps as below.
Step 1: Split
The wavelet divides the signal into odd and even samples first.
Step 2: Predict (Dual Lifting)
This step applies a filter to even samples and subtracts it from odd samples as shown in Eq. (3)
where OS represents set of odd samples
Step 3: Update (Primary Lifting)
The average of odd samples and the difference computed in Eq. (3) is calculated using Eq. (4)
where ES represents set of even samples
The inverse transform is used to recover the original data by reversing the process and flipping the signs.
Step 1: Inverse Primary Lifting: To retrieve to the original odd set of samples, subtract the predicted and updated samples. As shown in Eq. (5)
where OR represents retrieved set of odd samples
Step 2: Inverse (Dual Lifting): The addition is done on the results of the update from Eq. (5) and the result of the predictions steps from Eq. (3), and it’s shown in Eq. (6).
where ER represents retrieved set of even samples
ER = E and OR = O
Step 3: Merge: To reconstruct the data sequence, the original odd and even sets of samples are combined.
Arnold cat map or Arnold transform was first presented by Vladimir Arnold in 1960 [29]. This is a chaotic map and it scrambles the image so it becomes noisy and imperceptible.
The equation for Arnold Transform is given in Eq. (7)
where p, q ε (0, 1, 2…. N-1) where N is the order of image and p’ and q’ are new coordinates of the pixels. For each N after K iterations the original image is obtained. For example, for an image of order 256 × 256 if the Arnold map is scrambled for 192 times, original image is obtained.
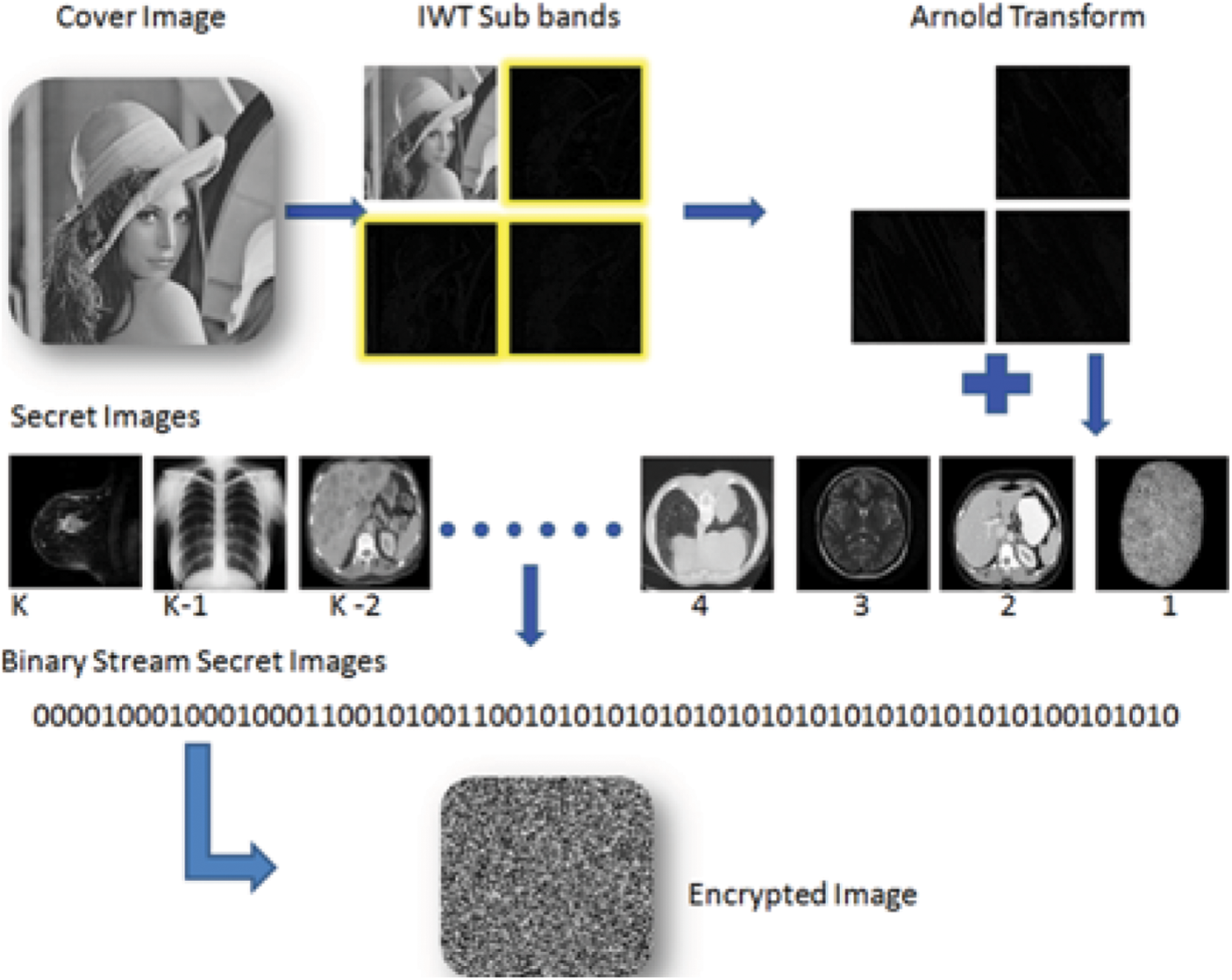
For increased security, the secret image is subjected to Arnold transform in the suggested method. The secret images are transferred to binary stream after transformation, as seen in Fig. 1. The embedding scheme of the proposed scheme is shown in Fig. 2 below; in the suggested technique, the original cover/host image is chosen, and the Integer wavelet transform is used to divide the spatial image into four sub-bands: LL, LH, HL, and HH. Except for the LL sub band, the Arnold transform is applied to the LH, HL, and HH sub bands. Because visual attacks are more resistant to this technique because there is no pattern, the result of binary streams is embedded in sub-bands using a 2-bit pseudo-LSB random embedding technique. Each block’s seed-key is buried in the block’s center rows [27]. Arnold transform is applied to the embedded sub-bands after embedding, and the remaining secret images are inserted. This procedure is repeated for K times. For example, if the cover image is of 512 × 512. Each sub band is of size 256 × 256. The cat map retrieves its original image in 192 iterations. So, a maximum of 192 times information can be stored in a single image. Arnold Transform serves two purposes one for improving security as stated above and other for embedding multiple times due to chaotic behavior. After embedding, the inverse Arnold transform and inverse integer wavelet are used to generate an encrypted image with embedded secret information.


Figure 1: Secret image conversion process
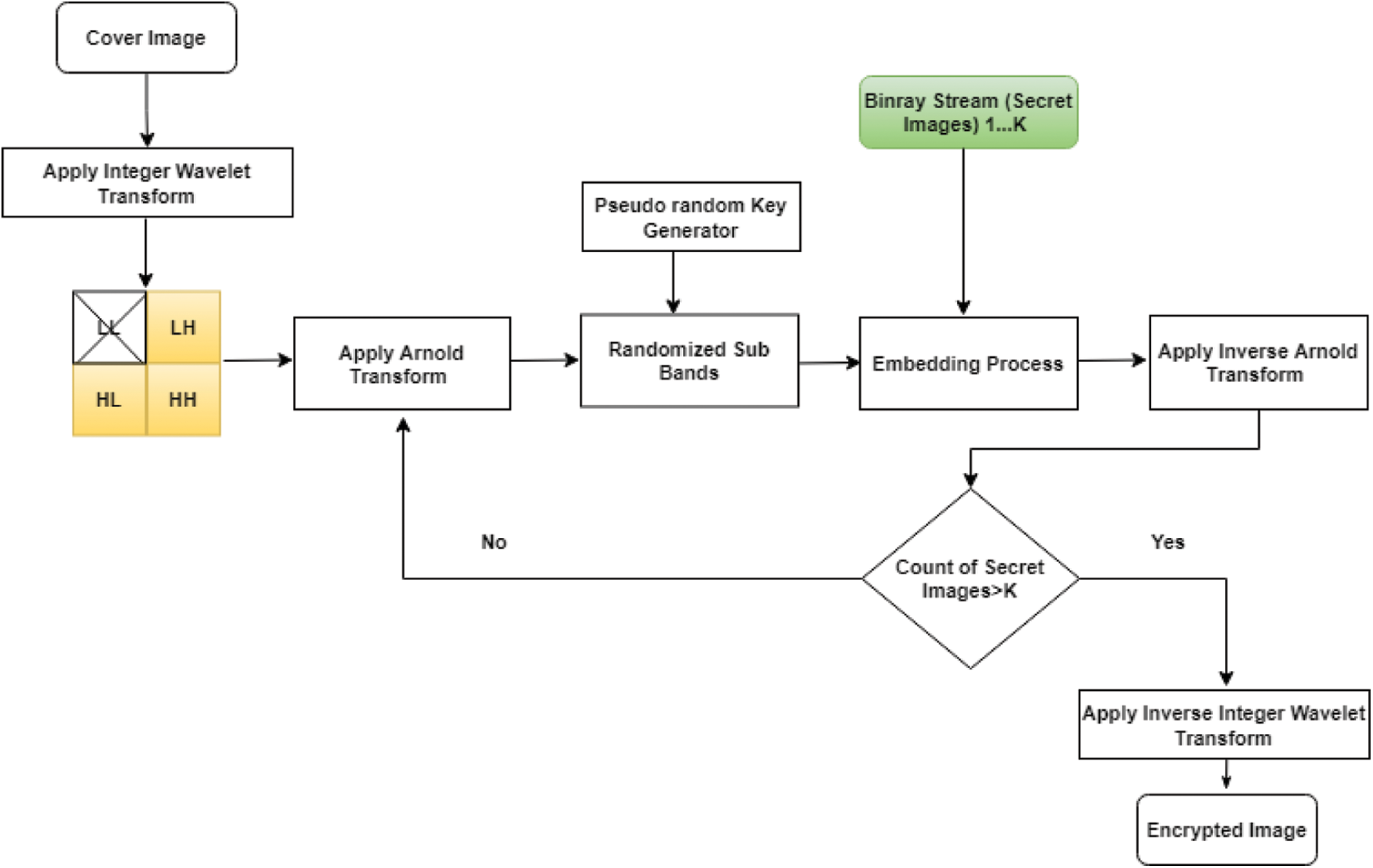
Figure 2: Embedding process
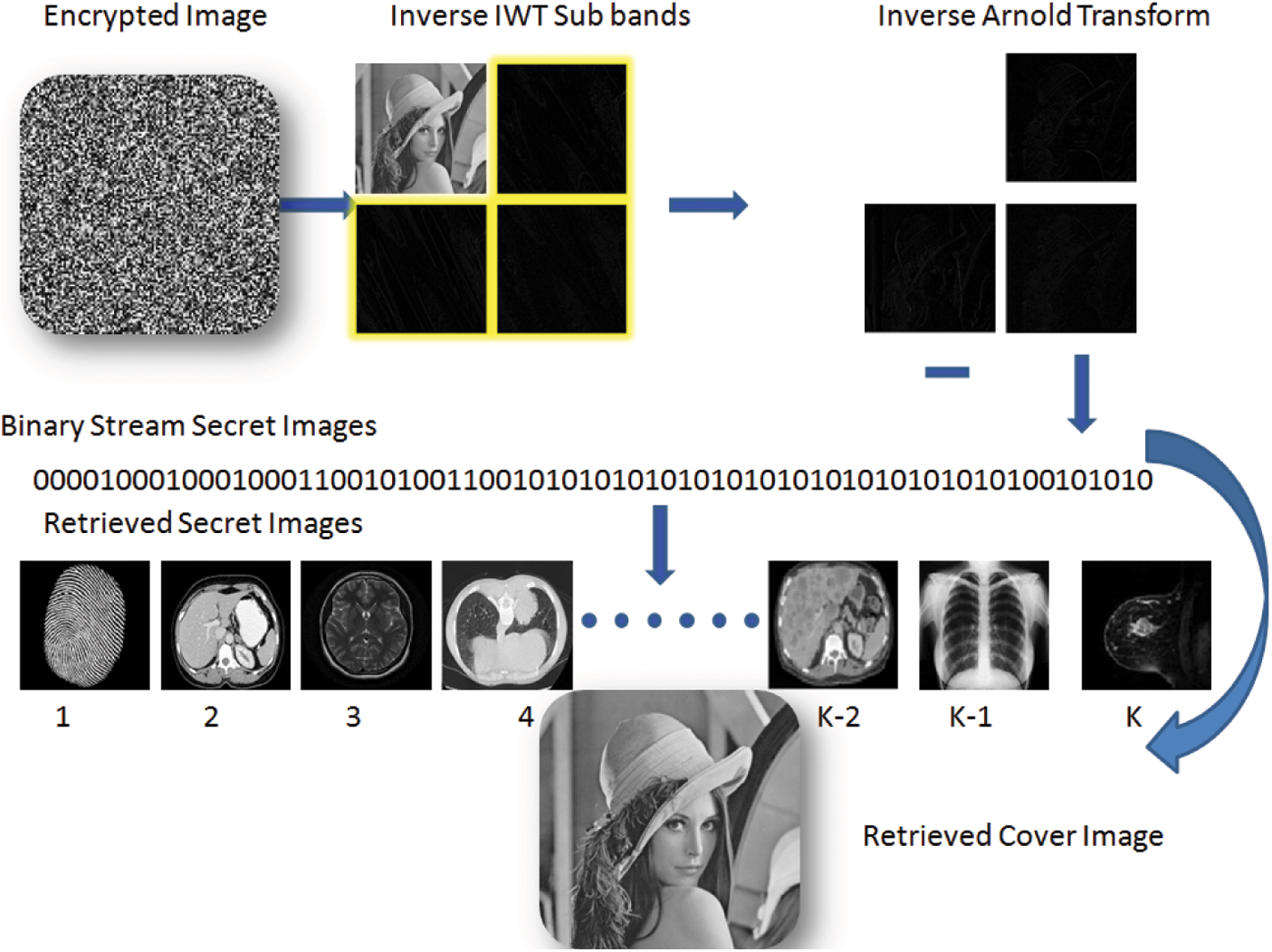
Fig. 3 depicts the extraction procedure. On the receiver end, an integer wavelet transform is used to obtain four sub-bands, and the secret image is retrieved from HH, LH, and HL sub-bands from the Kth iteration, and an Arnold transform is used at each step to reach the K-1st stage, and an inverse integer wavelet transform is used to retrieves original host image while keeping each pixel value intact. The binary stream of secret images are retrieved and converted to a 2D image, and the Inverse Arnold Transform is applied to recover them as shown in Fig. 4.

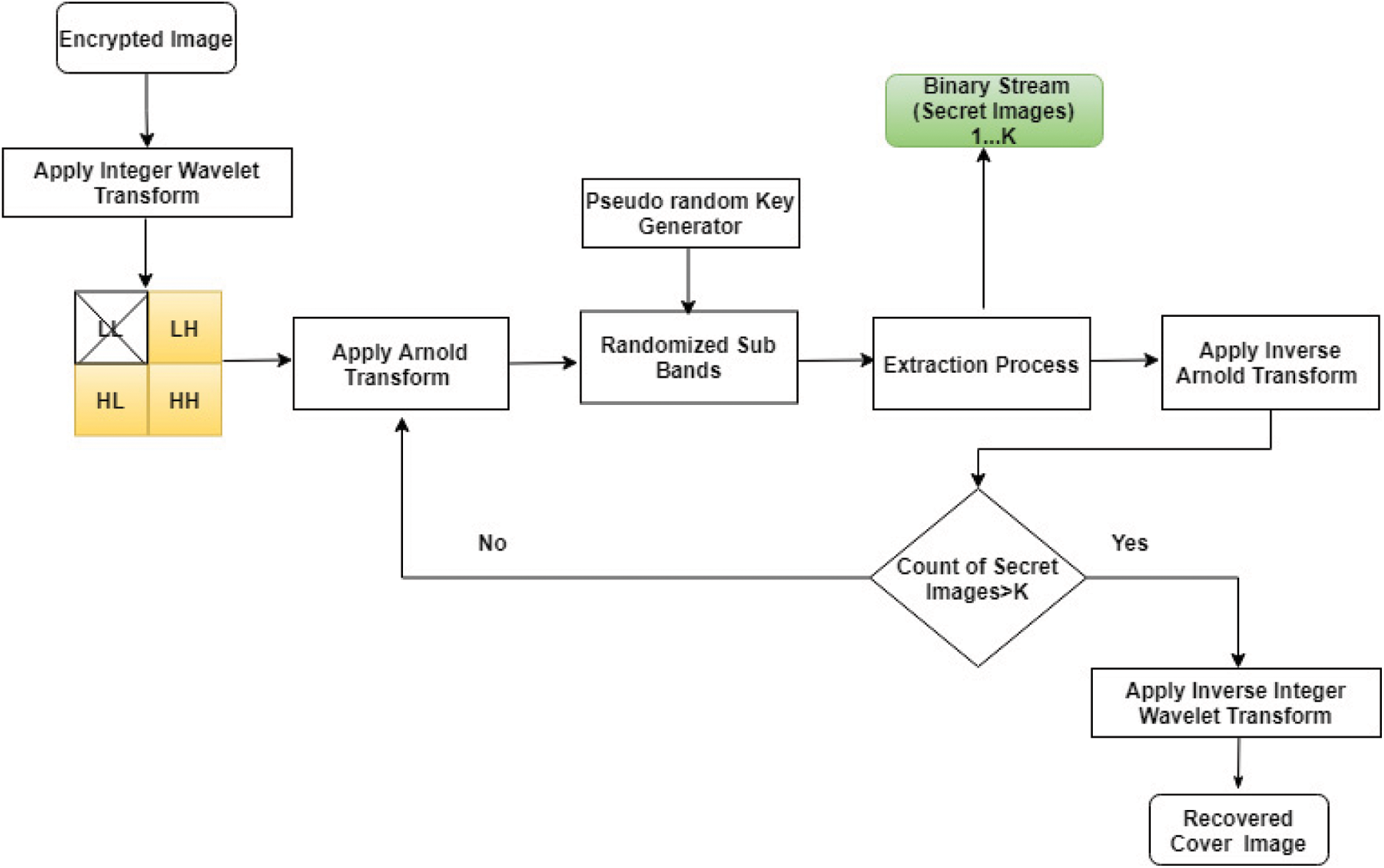
Figure 3: Extraction process

Figure 4: Retrieval of secret images
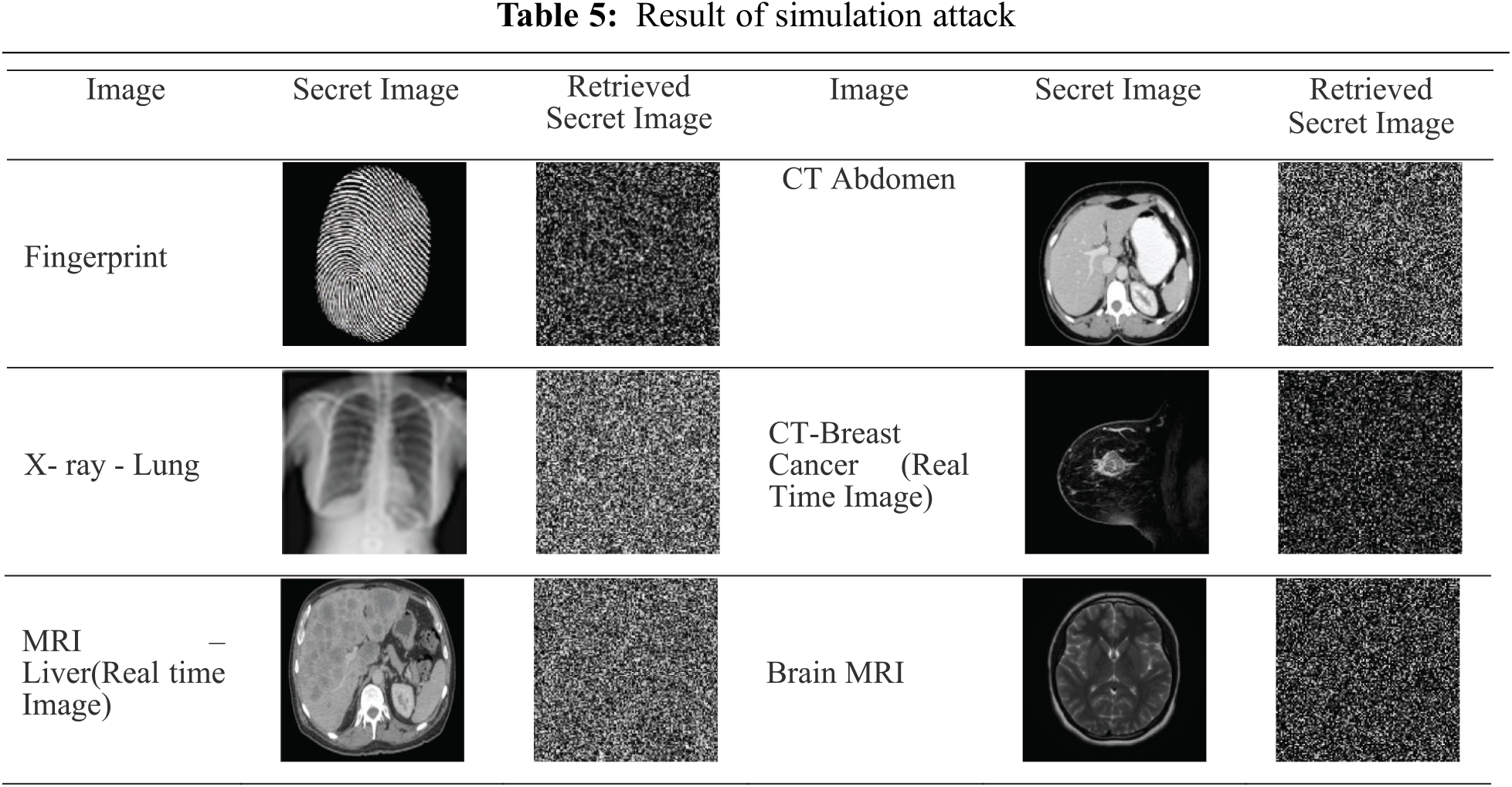
To test the feasibility of decryption by unauthorized way, a random attack is performed to assess the strength of the information’s concealment. Simulation attack [24] by varying pseudo random key carried on encrypted image but system architecture as shown in Fig. 5 is not known to attacker. The center two rows are reserved for Meta data information and the 1st row has the size of secret information embedded in 1st 4 pixels and rest of the pixels is not modified. Similarly, the pseudo random key information is stored in next row on 1st 8 pixels. For K set of images we have K set of keys generated so that it increases security level and no information can be retrieved if even a single bit of key is modified. Essentially, we have a set of three combinations of keys, first is pseudo random generator which scrambles the pixels position and performs embedding. Finally, to strengthen security, Arnold transform is performed on secret images, multi-layer Arnold transform is applied on sub-bands on outputs of the integer wavelet transform. This system is proven to decrypt information without any loss.
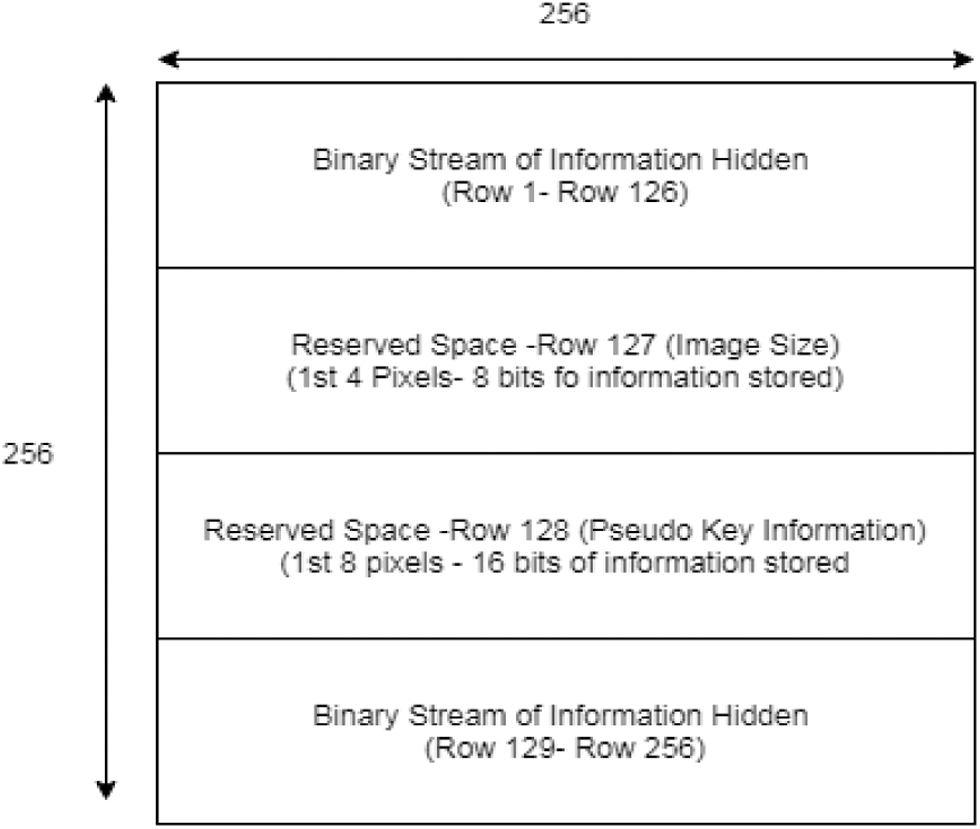
Figure 5: Metadata and payload anatomy on cover image
To begin, we have a random generator that shuffles the pixels in order to avoid sequential embedding of information. Second Arnold Transform is applied to each sub-band to further scramble the pixels and create a set of shuffled pixels. Third, in this method, we apply the Arnold transform to each secret image making it difficult for an attacker to find the exact pair of keys for retrieving information without losing any data. The second type of attacks which system is robust is a geometric attack. There are various rotations which we have performed is 90° 180°, 270°.The embedded cover image is de noised and then hidden payload retrieved is intact.
The implementation is done on mathematical laboratory (MATLAB) running on Intel (R) Core (TM) i3 CPU M 370 2.40 GHz. on MATLAB. To carry out the experiments, 512 × 512 gray scale images were taken. Initial test set consist of standard Lena, Boat, Baboon, Jet, Barbara and Man images. The maximum capacity of the cover image, i.e., the number of secret photos that can be stored in it, is 220 × 220. The experiments have been carried out with various types of images such CT scan of Breast cancer & Abdomen X-ray of Lungs and chest, magnetic resonance image (MRI) of Liver & Brain, finger print images etc. On a cover image of size 512 × 512, 192 payload/secret images of size 220 × 220 or 576 payload/secret images of size 127 × 127 can be inserted. The digital knee data set [30] and fingerprint images [31] are used for recursive embedding and the images are resized to 220 × 220 before embedding.
PSNR and SSIM are the quality metrics used to figure out the experimental activity of embedding and extraction. They are computed using Eqs. (8) and (9)
PSNR, which ranges from 0 to ∞, represents the peak error among two images, with 0 indicating bad quality and ∞ indicating an identical replica of two images.
Here max is maximum pixel value of an image.
The cover image is CI, while the stego image is SI.
The structural similarity index is used to compare the similarity of two images and is calculated using the formula indicated in Eq. (10).
The SSIM that results are graded on a 0–1 scale, with 1 indicating complete structural similarity between two sets of data. There is no structural similarity if the value is zero.
where μx is average xi
μy The average of yi
The embedding capacity is calculated using the embedding rate per pixel and is measured as in Eq. (11)
Tab. 1 exhibit few test images i.e., the cover images, recovered cover images and the difference between them. Since there is no difference in cover and recovered image pixels, it resulted in black image internally the difference in magnitude is 0 across all the pixel of both the images.

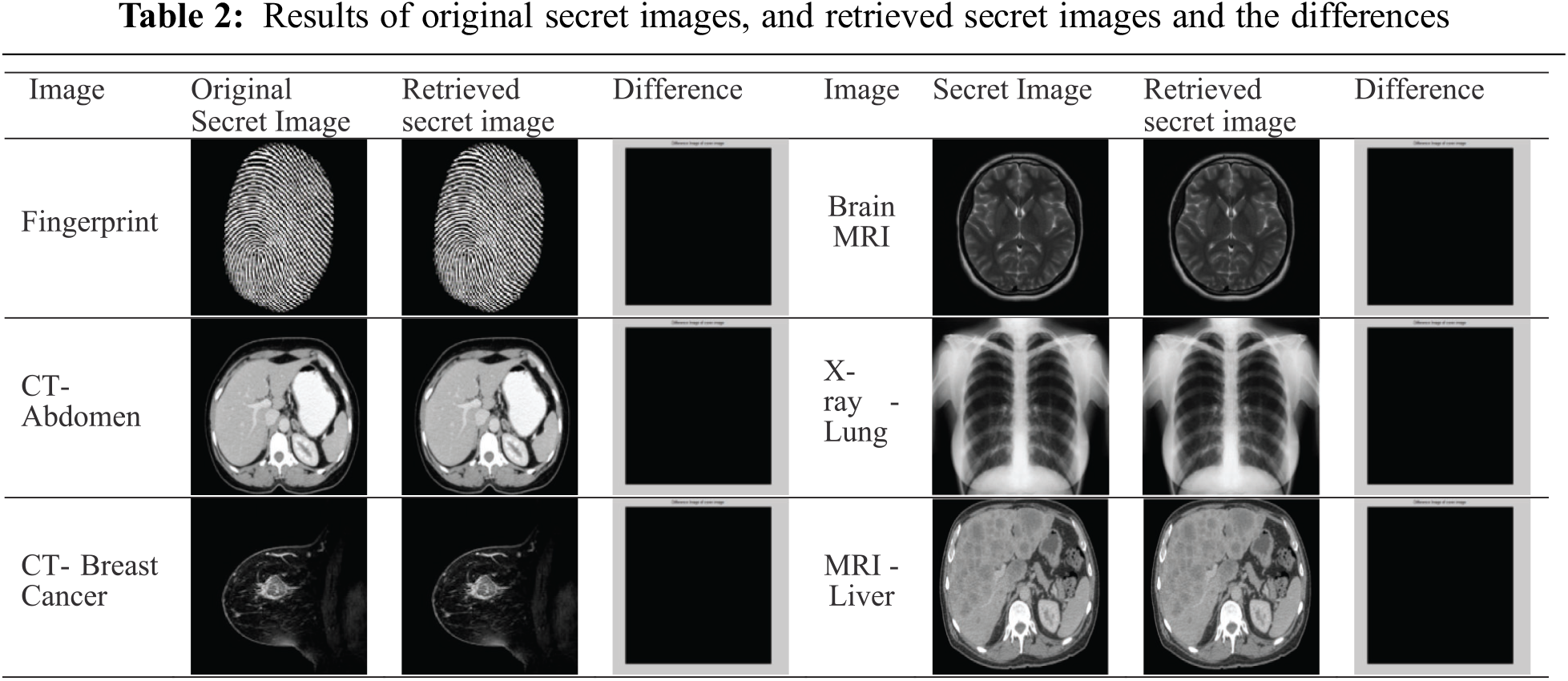
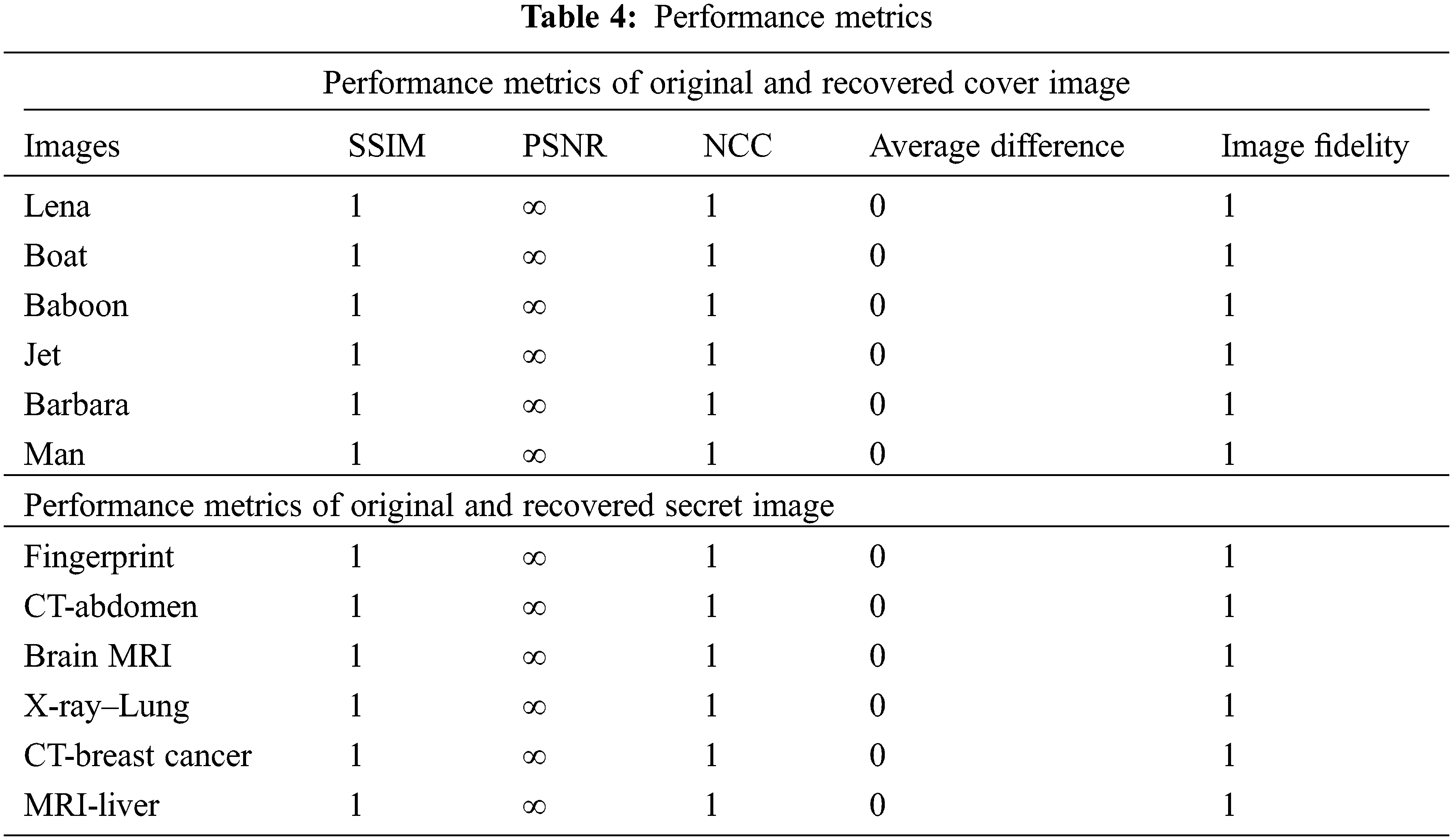
Tab. 2 depicts the comparison among the original secret images and the retrieved secret images, with each pixel having a 0-bit difference and being represented pictorially in MATLAB.
Tab. 4 has various performance metrics which has been calculated, the formula for NCC, Image fidelity are found in [32]. Structural Similarity Index Measure (SSIM), Normalize Cross Correlation (NCC) and Image fidelity metrics will be 1 if the image are exact same copy and PSNR will be ∞if both the images are intact and differences will be 0 if there are no pixel difference and the image result is shown in Tabs. 1 and 2.
The proposed approach can embed 74322432 bits, as shown in Tab. 3. The 512 × 512 pixel cover image is divided into four 256 × 256 pixel sub-bands. Only three high-level sub-bands are employed for embedding in these tests. Only three high-level sub-bands are employed for embedding in these tests. In 192 iterations, a cat map of size 256 × 256 returns to its initial place. The proposed method can embed maximum of 387096 pixels in 3 sub-bands in a single iteration. So, in total 74322432 bits can be embedded in a single image.
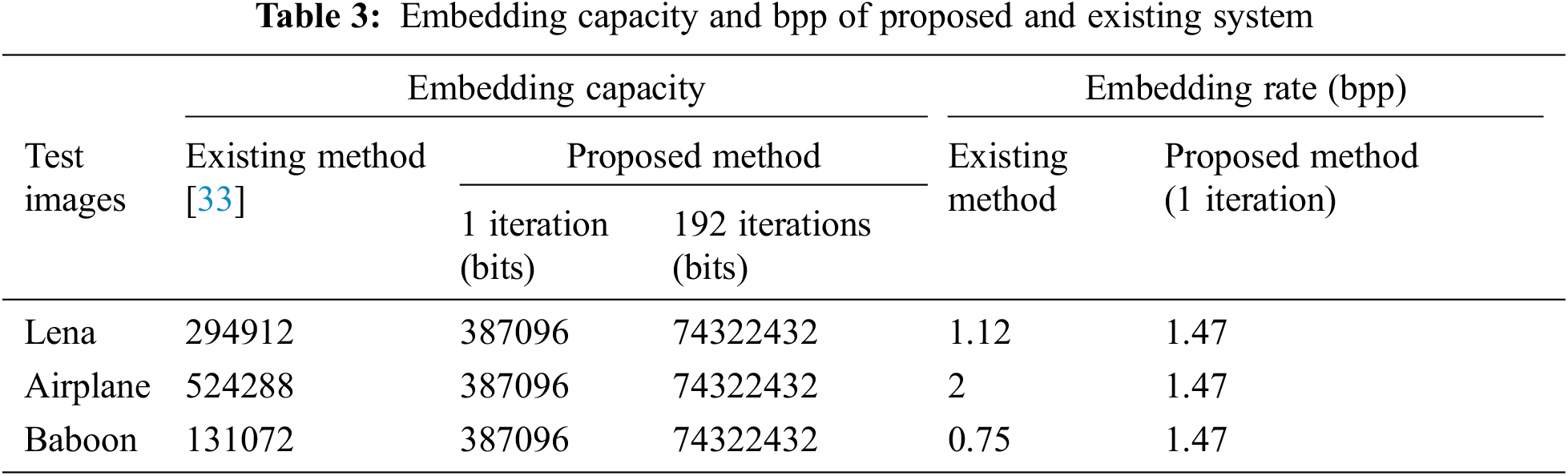
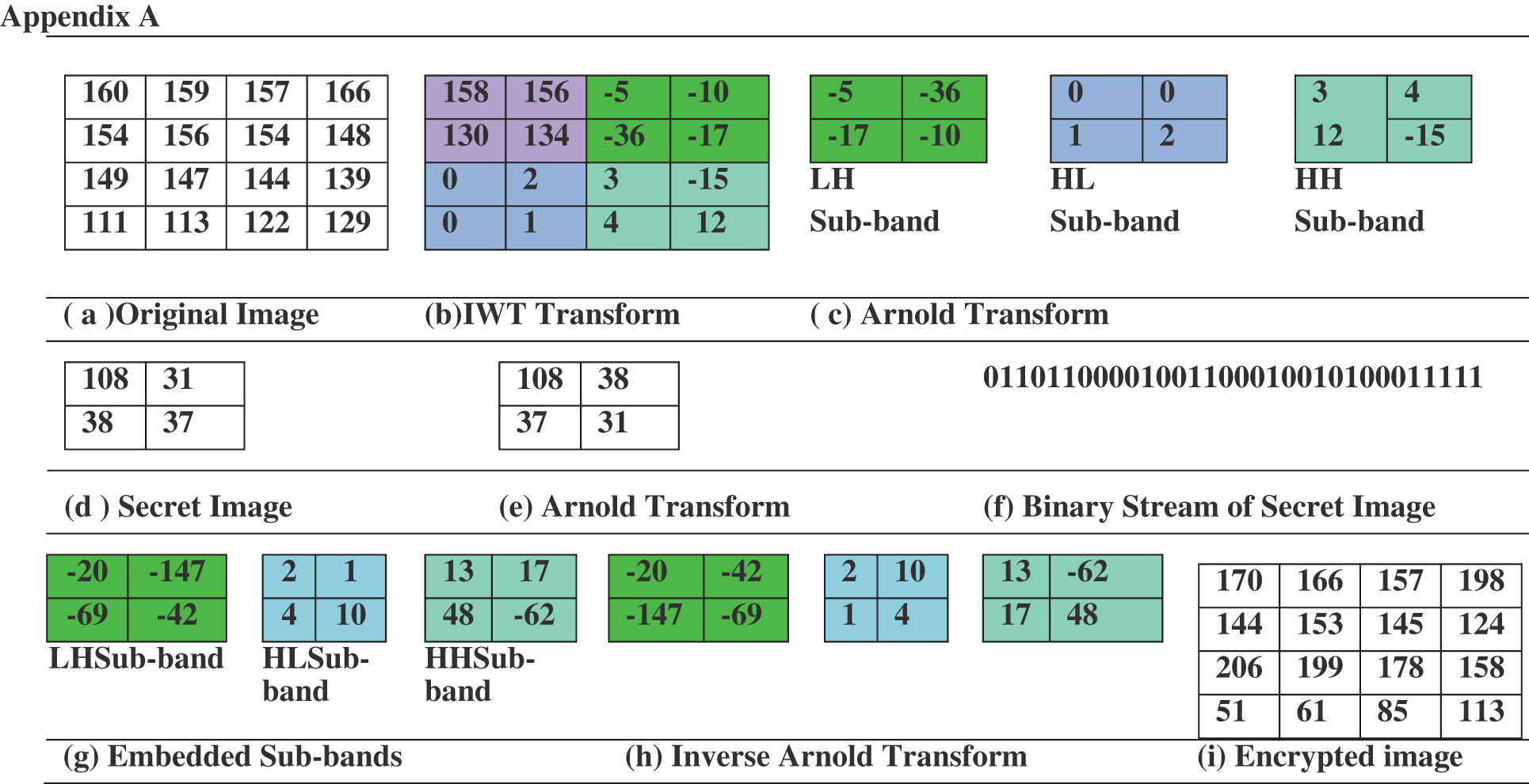
The results of extracting images at different iterations and with different key combinations are not decodable, as shown in Tab. 5. In these tests, just three high-level sub-bands are used for embedding. Tab. 6 shows the outcome of the rotation attack. The embedded image is subjected to rotations of 90°, 180° and 270°. If the image is rotated back to the original position, secret images retrieved are intact. Thus system is robust to rotation attack. As the system utilizes each and every bit for embedding, it can recover information without any loss if there is no additional noise. A single bit change will not give us desired result. This proves that the proposed system is secured for embedding and transmission of secret information. Further a pictorial representation of embedding and extraction along with a working example using a 4 × 4 matrix is depicted in Appendix section.

This study presents a high capacity and safe RDH strategy using the Integer wavelet transform and Arnold Transforms. Because the coefficients of pixels are employed instead of direct pixels of the image, the integer wavelet transform improves capacity and strengthens embedding. It also enables to recover the original image once all secret information is extracted. Arnold Transforms is used to ensure security Further Arnold transform is combined with a random method to embed information which increases security and information cannot be retrieved. Simulation attack is performed in two approaches: 1. By modifying the seed key for random embedding and 2. The key which specifies the number of iteration of Arnold transform. This concludes that it can with stand rotation attack and simulation attack and there is no means to decode the information until the combination of keys is known to the attacker. As a result, the proposed approach is a reliable medium for reversible data hiding.
In future the system can be enhanced for stronger and secured means of information hiding and transmission method by pondering machine learning techniques to train the process of hiding information including behavior of system in noisy channel.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. B. Feng, I. C. Lin, C. S. Tsai and Y. P. Chu, “Reversible watermarking: Current status and key issues,” International Journal of Network Security, vol. 2, no. 3, pp. 161–171, 2006. [Google Scholar]
2. M. U. Celik, G. Sharma, A. M. Tekalp and E. Saber, “Lossless generalized-LSB data embedding,” IEEE Transactions on Image Processing, vol. 14, no. 2, pp. 253–266, 2005. [Google Scholar]
3. I. C. Dragoi and D. Coltuc, “Local-prediction-based difference expansion reversible watermarking,” IEEE Transactions on Image Processing, vol. 23, no. 4, pp. 1779–1790, 2014. [Google Scholar]
4. O. M. Alqershi and B. E. Khoo, “An overview of reversible data hiding schemes based on difference expansion technique,” in Int. Conf. on Software Engineering and Computer Systems, Beijing, China, pp. 741–746, 2009. [Google Scholar]
5. X. Chen, X. Sun, H. Sun, L. Xiang and B. Yang, “Histogram shifting based reversible data hiding method using directed-prediction scheme,” Multimedia Tools and Applications, vol. 74, no. 15, pp. 5747–5765, 2015. [Google Scholar]
6. Z. Ni, Y. Q. Shi, N. Ansari and W. Su, “Reversible data hiding,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 16, no. 3, pp. 354–362, 2006. [Google Scholar]
7. X. Li, B. Li, B. Yang and T. Zeng, “General framework to histogram-shifting based reversible data hiding,” IEEE Transactions on Image Processing, vol. 22, no. 6, pp. 2181–2191, 2013. [Google Scholar]
8. H. W. Tseng and C. P. Hsieh, “Prediction-based reversible data hiding,” Information Sciences, vol. 179, no. 14, pp. 2460–2469, 2009. [Google Scholar]
9. X. Li, J. Li, B. Li and B. Yang, “High-fidelity reversible data hiding scheme based on pixel-value-ordering and prediction-error expansion,” Signal Processing, vol. 93, no. 1, pp. 198–205, 2013. [Google Scholar]
10. G. Xuan, J. Zhu, J. Chen, Y. Q. Shi, Z. Ni et al., “Distortion less data hiding based on integer wavelet transform,” Electronics Letters, vol. 38, no. 25, pp. 1646–1648, 2002. [Google Scholar]
11. B. Shirisha and K. Prasad, “A survey on reversible data hiding techniques,” in Int. Conf. on Data Science, Machine Learning and Applications(ICDSMLA 2019), Hyderabad, India, pp. 960–965, 2020. [Google Scholar]
12. Z. M. Lu and S. Z. Guo, “Lossless information hiding in images on transform domains,” 1st ed, London: Syngress, pp. 143–204, 2016. [Google Scholar]
13. A. M. Kapadia and N. Pandian, “A review: Reversible information hiding and bio-inspired optimization,” Artificial Intelligence and Technologies, pp. 489–506. [Google Scholar]
14. A. R. Calderbank, I. Daubechies, W. Sweldens and B. L. Yeo, “Wavelet transforms that map integers to integers,” Applied and Computational Harmonic Analysis, vol. 5, no. 3, pp. 332–369, 1998. [Google Scholar]
15. G. X. Zhu, J. Chen, Y. Quaisy and W. Su, “Distortionless data hiding based on integer wavelet transform,”. Electronics Letters, vol. 38, no. 25, pp. 1646–1648, 2002. [Google Scholar]
16. G. Xuan, Y. Q. Shi, P. Chai, J. Teng, Z. Ni et al., “Optimum histogram pair-based image lossless data embedding,” in Transactions on Data Hiding and Multimedia Security IV, Berlin, Heidelberg, Springer, pp. 84–102, 2009. [Google Scholar]
17. S. Agrawal and M. Kumar, “Reversible data hiding for medical images using integer-to-integer wavelet transform,” in IEEE Conf. on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, pp. 1–5, 2016. [Google Scholar]
18. P. L. Mantos and I. Maglogiannis, “Sensitive patient data hiding using a ROI reversible steganography scheme for DICOM images,” Journal of Medical Systems, vol. 40, no. 6, pp. 156, 2016. [Google Scholar]
19. A. Zear, A. K. Singh and P. Kumar, “A proposed secure multiple watermarking technique based on DWT, DCT and SVD for application in medicine,” Multimedia Tools and Applications, vol. 77, no. 4, pp. 4863–4882, 2018. [Google Scholar]
20. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
21. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
22. L. Xiong, Z. Xu and Y. Q. Shi, “An integer wavelet transform based scheme for reversible data hiding in encrypted images,” Multidimensional Systems and Signal Processing, vol. 29, no. 3, pp. 1191–1202, 2018. [Google Scholar]
23. R. J. Krishna, A. Singhand and V. S. Rathore, “Secure data hiding technique using secret image scrambling,” in Int. Conf. on Electronics, Communication and Aerospace Technology (ICECA), India, pp. 831–836, 2020. [Google Scholar]
24. V. G. Rima and V. S. Lakshmi, “Integer wavelet transform and arnold transform based image steganography with cryptanalysis,” in Int. Conf. on Communication and Electronics Systems (ICCES), India, pp. 673–678, 2019. [Google Scholar]
25. V. Thanikaiselvan, S. Patel and S. Sivanantham, “Secured data transmission through dual domain reversible data hiding and encryption in images,” in Int. Conf. on Inventive Computation Technologies (ICICT), San Jose, California, pp. 840–847, 2020. [Google Scholar]
26. H. Yao, F. Mao, C. Qin and Z. Tang, “Dual-JPEG-image reversible data hiding,” Information Sciences, vol. 563, pp. 130–149, 2021. [Google Scholar]
27. A. M. Kapadia and N. Pandian,“Reversible data hiding methods in integer wavelet transform,” International Journal of Information and Computer Security, vol. 12, no. 1, pp. 70–89, 2020. [Google Scholar]
28. A. M. Kapadia and N. Pandian, “Secured reversible matrix embedding based on dual image using integer wavelet and Arnold transform,” Procedia Computer Science, vol. 165, pp. 766–773, 2019. [Google Scholar]
29. G. Peterson, “Arnold’s cat map,” Math Linear Algebra, vol. 45, pp. 1–7, 1999. [Google Scholar]
30. S. S. Gornale and P. P. Dongare, “Digital knee X-ray images,” Mendeley Data, vol. 1, pp. 118–131, 2021. [Google Scholar]
31. D. Maltoni, D. Maio, A. K. Jain and S. Prabhakar, Handbook of Fingerprint Recognition (Second EditionSpringer, London, 2009 [Google Scholar]
32. A. Sharif, M. Mollaeefar and M. Nazari, “A novel method for digital image steganography based on a new three-dimensional chaotic map,” Multimedia Tools and Applications, vol. 76, pp. 7849–7867, 2017. [Google Scholar]
33. M. A. Hada, A. M. Naser and M. A. Thamary, “Hide image in image based on lsb replacement and arnold transform,” in Int. Conf. on Information Technology(ICIT 2015), Amman, Jordan, pp. 319–323, 2015. [Google Scholar]
Appendix
Working Example

 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |