DOI:10.32604/iasc.2023.027514

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.027514 |  |
| Article |
Black Widow Optimization for Multi Area Economic Emission Dispatch
1Department of EEE, Government Polytechnic College, Keelapaluvur, Ariyalur, 621707, Tamil Nadu, India
2Department of EEE, Government College of Engineering, Salem, 636011, Tamil Nadu, India
3Department of EEE, Government Polytechnic College, Uthangarai, 635207, Tamil Nadu, India
4Department of Electrical Engineering, Annamalai University, Annamalai Nagar, 608002, Tamil Nadu, India
*Corresponding Author: G. Girishkumar. Email: ggirishkumar709@gmail.com
Received: 19 January 2022; Accepted: 09 March 2022
Abstract: The optimization field has grown tremendously, and new optimization techniques are developed based on statistics and evolutionary procedures. Therefore, it is necessary to identify a suitable optimization technique for a particular application. In this work, Black Widow Optimization (BWO) algorithm is introduced to minimize the cost functions in order to optimize the Multi-Area Economic Dispatch (MAED). The BWO is implemented for two different-scale test systems, comprising 16 and 40 units with three and four areas. The performance of BWO is compared with the available optimization techniques in the literature to demonstrate the strategy’s efficacy. Results show that the optimized cost for four areas with 16 units is found to be 7336.76$/h, whereas it is 121,589$/h for four areas with 40 units using BWO. It is also noted that optimization algorithms other than BWO require higher cost value. The best-optimized solution for emission is achieved at 9.2784e+06 tones/h, and it is observed that there is a considerable difference between the worst and the best values. Also, the suggested technique is implemented for large-scale test systems successfully with high precision, and rapid convergence occurs in MAED.
Keywords: Black widow optimization algorithm; multi-objective multi-area economic dispatch; emission optimization; cost optimization
The problem of Economic Dispatch (ED) and Emission Dispatch (EmD) are significant issues in power systems. The Combined Economic and Emissions Dispatch (CEED) challenge is characterized by a collection of solutions or a compromise solution that minimizes fuel costs and environmental emissions. This solution can extend to multiple locations, which operate together on several benefits such as increasing the availability and safe operations, reducing the investments in new power generation units, decreasing the maintenance costs and improving economic resource planning. The challenge of cost-effective load shipments in multi-area systems is presented here.
One of the primary goals of the system operators is to reduce the generation costs since it lowers the customer energy expenditures and the outcomes promote welfare. Demand Side Management (DSM) is a critical component of smart grids that may provide several advantages to power system operators and customers. The DSM has possible implications on electricity generating costs by considering a thorough and practical model of individual household loads. The consumption of various house hold appliances can be changed from the typical schedules to flexible loads using varied allowable delay durations [1]. Then a modern and improved variant, Novel Symbiotic Organisms Search (NSOS) is employed to satisfy the Multi-Area CEED (MA-CEED). To solve the MA-CEED, the NSOS algorithm is modified in [2] to generate better, more stable and more accurate alternatives than the original SOS algorithm. The reduction of fuel cost and total emissions are the major aims for ED multi-area systems. Although renewable energy supplies are increasingly penetrated, a significant percentage of the plant includes thermal energy units that utilize fossil fuel increases the environmental concerns. The MAED can determine the transferred power across the various locations by optimizing the overall costs. It computes each region’s optimum cost and accomplishes the best power streams from one area to another [3].
The purpose of maintaining a balance between exploration and operation phases is discussed in [4] to achieve high efficiency. The Dantzig-Wolfe decomposition approach solves the ED issue with limits of line flows and spinning reserve in a conventional linear optimization. It solves a linear problem independently by decomposing sub-programs that may relate to the physical sections of the power network [5]. A novel Generalized Unified Power Flow Controller (GUPFC) is discussed for the multi-area multi-fuel CEED issue. A systematic total power model for GUPFC with two series converters is designed to consider the converter switching losses. Then the multi-objective issue is solved using non-dominated solutions filtering approach and a Particle Swarm Optimization (PSO) algorithm. PSO is an optimization algorithm that optimizes the challenge by periodically seeking a candidate solution through the relation to a particular quality measure [6].
The finest Artificial Bee Colony Optimization (ABCO) algorithm can solve the MAED problem with tie-line constraints in [7]. ABCO is a swarm-based algorithm developed by honey bee food foraging behavioral patterns. It considers transmission losses, multiple fuels, valve-point loading, and Prohibited Operating Zones (POZs). A unit with POZs converts the regular ED into a non-convex optimization issue where the traditional approach cannot be used. It provides the characteristics of the discontinuous input and output of the power generation. A simple and efficient way is described in [8] for incorporating the area in power transfer limitations using the unit commitment and ED process. Also, a method for dispersing savings among participating firms in a pool on an equal basis is provided.
The black widow spider genus evolutionary theory is discussed in [9] with multiple species often described as actual widows [9]. The spiders are commonly referred to as black widow spiders and brown widow spiders based on the DNA sequences from the mitochondrial gene cytochrome c oxidase subunit I. The two well-supported mutually monophyletic clades within the genus are the geometricus clade (Latrodectusrhodesiensis from Africa and its sister species, the cosmopolitan L. geometricus), the mactans clade (taxa from various localities). Although the hybrid evolutionary programming scheme is used to solve MAED issues with different fuel alternatives by evolutionary programming, the Levenberg Marquardt optimization method is designed as an essential Evolutionary Programming (EP) in [10]. It is an introductory level search that determines the best global region’s direction and finds the best solution for the MAED issues. An excellent adaption of the PSO method is described in [11] to tackle various ED issues in power systems. It includes MAED with tie-line constraints, ED with diverse fuel alternatives, CEED and ED generators with POZ.
A decomposition method to solve the issue of multi-area generation scheduling is discussed in [12]. The goal is to keep the system’s operating costs as low as possible while still meeting the network limits. Early methods did not consider the generator nonlinearities, power pool topological linkages, or tie-line restrictions. Two-layer decomposition is employed to tackle the issues since it is a large-scale mixed-integer non-linear system model. An efficient direct search approach is discussed in [13] to address the ED issue while considering transmission capacity limits. It deals with various inequality and equality restrictions and units with fuel cost functions. To improve the performance of the direct search technique, a unique strategy is integrated with multi-level convergence. It reduces the total number of iterations in the searching process.
The CEED dispatch issue is discussed in [14], accounting for cost and emission reduction. It solves the challenging conflicting-objective function problem. The goal programming approaches are best suited to such challenges. The CEED dispatch problem is tackled using linear and non-linear goal programming techniques in this case. The effectiveness of various EP strategies for all types of ED challenges is explored in [15]. The three EP approaches under consideration are Gaussian, Cauchy, and combination Gaussian–Cauchy mutations.
A unified power flow controller has an effective and reliable evolutionary-based method to reduce fuel costs [16]. It operates within limits and is associated with transmission constraints that require less CPU time than other conventional techniques. The Shuffle Frog Leaping Algorithm (SFLA) is a memetic meta-heuristic algorithm that has been intended to solve stochastic optimization issues. The SFLA is a natural memetics-inspired population based cooperative search metaphor. It does a local independent searching in each memeplex simultaneously. The first SFLA frequently converges to local optima. A novel technique that takes advantage of the Simulated Annealing (SA) method to enhance local search around the global optima is discussed in [17]. It is a meta-heuristic algorithm used to estimate global optimum in a vast search process and increases the likelihood of convergence to global optima. The SLFA described in [18] addresses the multi-objective Optimum Power Flow (OPF) problem while considering the economic and pollution. Adding the emission objective to the OPF issue makes the situation more complicated than the previous one and requires an exact algorithm to solve the problems. The power loss and voltage variation are discussed in [19]. The Distribution Feeder Reconfiguration (DFR) is the main issue in the conventional distribution systems. In the modernized distribution systems, the operating problem has virtually ignored the security difficulties caused by the distributed generation, which might threaten power system security.
A new mapping approach for quadratic 0-1 programming problems and linear equality and inequality constraints are discussed in [20]. Hopfield neural networks are performed better while addressing the combinatorial optimization tasks. The modified Gee and Prager’s approach is used to remedy the ED with transmission capacity limits. A Chaotic Global Best Artificial Bee Colony (CGBABC) method is discussed in [21]. During the search for a global optimum, chaotic sequencing from the chaotic map is mapped to provide the design variables rather than the random number generator’s sequence. The CGBABC is used to solve the MAED issue by considering valve-point effects, transmission line losses, multi-fuel sources, POZs, tie-line capacity and power transfer system’s cost across various areas and compared with Network Flow Programming (NFP), Harmonic Search (HS), Hybrid HS (HHS) and Hybrid PSO (HPSO) [21]. A PSO technique is described in [22] for tackling the ED problem in power networks in which smooth cost functions are evaluated in an operational generator. The MAED calculates the amount of electricity generated cheaply in one location and transported into another to reduce the generation in the second area. The network flow model does not compute the actual power transmission between locations. A considerable number of the issue constraints may be phrased as network-type constraints, and as a result, the technique delivers a robust and high-speed solution [23].
Black Widow Optimization (BWO) is a novel meta-heuristic method [4] appropriate for continuous non-linear optimization problems. Cannibalism is an exclusive step in this approach. As a result of this stage, species with insufficient fitness are excluded from the circle, resulting in early convergence. The BWO algorithm is tested on 51 objective functions to ensure its efficacy in generating optimal solutions. A Quasi-Oppositional Group Search Optimization (QOGSO) algorithm is discussed in [24], which addresses the multi-area dynamic ED issue with different fuels and valve-point loading. A biologically realistic approach is a group search optimization, which is inspired by animal searching behavior [25]. QOGSO is utilized in this case to increase the solution’s efficacy and quality. An enhanced Multi-Objective PSO (MO-PSO) method is designed in [26] that provides a collection of Pareto-optimal solutions. Local search is employed in the MO-PSO to improve search efficiency.
The purpose of electric power brokerage networks developed in Florida is to minimize the actual electricity generation by conducting short-term transfers between the utilities (economy energy exchanges). Nevertheless, the present procedures for determining buyers and sellers and the quantities transferred may be improved to maximize the savings [27]. The optimization approaches based on meta-heuristic processes might help the power generation policy with the objective of reducing generation costs. In this respect, this analysis aims to provide a unique strategy for addressing ED issues based on the HS algorithm and to provide a practicable alternative to the existing methods [28]. The use of meta-heuristic algorithms to successfully tackle the problem of CEED with peak load control for a medium-sized power system is discussed in [29]. The cuckoo search and grasshopper optimization algorithms are used to solve the CEED issue through a composite function of four objectives with weight ratios and the cost penalty factors. It controls the peak load condition at the generating units of expensive locations, implemented in the IEEE 30-bus system with six generating units [30]. The MAED can reduce the total generation cost in multi-area power networks by obtaining active electricity from other economic power plants. Hence, in this work, the Meta-heuristic algorithm, BWO is employed to reduce the cost based on the black widow spider’s unique matching behavior.
The main objective of this research work is to develop a meta-heuristic algorithm to optimize the cost function. Here the cost functions we have considered are generating cost and emission cost. We had utilized the proposed algorithm to reduce the objective functions. In today’s world, power generation and distribution involve many men and materials. The resources have to be effectively and intelligently used. In this regard, the meta-heuristic-based BWO algorithm is utilized. By reducing the cost, we can effectively use the precious resources. As mentioned, the fuel cost and emission are the objective functions of the underlying problem, which are defined as follow:
where Crs(Prs) is represented as cost. An electricity system with NU generating units and an R Area is deemed in various regions. Each area has Nr generating units. Trkis the tie-line power flow to area k from area r. For an area with surplus powers, it is essential to find a tie-line to transmit extra powers to a deficient area of power.
where Prsis the powers flow of generating units s from areas r; Crsis the fuel cost function related with unit r from area s, which a quadratic polynomial function can express, and Trsand fcrs are the tie-line power flow to area s from area r and its equivalent generation cost function.
where, ars, brs, crs are the factors of generating unit i in area s. ers and frs are constants of unit r from area s signifying the valve-point effects. Furthermore, the objective function is reduced subject to the subsequent limits [9]. The active powers outputs of the unit should be between their lower and upper limits.
where,
where,
The DRijand URij are the down and up ramp rate limits of unit r from s and
The real power balance constraint so the system for areas r without considerations of networks loss can be provided.
where PGr is the overall engendered power in area r, PDr is the load requirement in area r.At the point when an unsettling influence happens in the framework (e.g., cut off, trip, etc.), it might bring about the awkwardness between the power generated and the full load power. On the off chance that the complete generated power is more than the load power (counting the network misfortunes), the frequency recurrence will rise; in any case, assuming the generated power influence is not precisely the load influence, the framework recurrence will fall. In light of the different recurrence variances and the genuine activity status of the framework, the related measures, primarily including managing the generator dynamic result, breaking down the generator, crumbling the heap, etc., will be considered.
3 Valve-Point Effect (VPE) & Multi-Fuel Operations (MFO) Cost Function
The stated cost objective function description is relevant for solo fuel units. Consequently, it is not applicable for multi-fuel objective generating units. Units can have varied fuels in real life, which can be described as the equation for their respective cost function. The VPE fuel cost feature, which may be expressed as an Equation, is another popular cost function model in MAED problems.
Considering the valve-points effect of the unit, the fuel costing functions can be described as follows Eq. (6). Fmn (Pmn) is represents as Fcost
The power generation limits are as follows:
where
The real power balance are defined as
MA-CEED is a problem that optimizes two functions concurrently to minimize: Overall TotalCost [[P][T]] operations (or FuelCost [P] if transmission expenses are ignored) and emissions levels; (Emission[P]). One way of dealing with the MA-CEED issue is to make it a single target optimization problem [11].
where w is a weighting factor having [0,1] values. The FGij ratio is a scaling factor corresponding to the generator j in field i. FGij(Pij, max)/Eij. The two minimized functions (TotalCost and Emission) set competing targets. Hence, there are maximum emissions when the entire operating costs are minimized and vice versa. The two scenarios contribute to the determination of two extreme points in the space of the objectives (Total Cost, Emission). By resolving the problems of MA-ED and MA-EmD, the final points are separately defined. To acquire more points (items) from the Pareto front, which is defined as a group of non-dominated solutions in each objective is often seen as equally significant. The W factor is gradually adjusted from 0.1 to 0.9. The system operator has to select almost one operational point as a compromise between the two opposing objectives (Total Cost and Emission) [12,13]. Therefore, to help the system operator select what to do, the issue of categorizing solutions from the Pareto Front and determining the Best Compromising Solution (BCS) is recognized. Considering the Pareto-front known non-dominated solutions, this choice of BCS may be achieved via a fuzzy mechanism composed [14]. This is below:
Step 1. A value based on a linear membership function is generated for each goal I and each solution k from the P to front:
The lowest and maximal magnitude of an ith objective function is represented by fi, min and fi.
Step 2. The normalized linear membership function m*k is computed as for each non-dominated solution k.:
where P means the non-dominant number of alternatives, whereas O is the target number of functions.
Step 3. M * k max 1⁄4 max (m*k, k 1⁄4 1, 2,…, P) is the best-compromised option for this. Parameters of the non-dominated and dominated approach, the Pareto front, etc., are available in references.
Each generator, in actuality, has distinct POZs. Shaft bearing or other machine components such as pumps and boilers might harm from generating in these regions. In the operational area spectrum, the POZs are disconnected. From a technical standpoint, it is not possible or advisable to operate in POZs because the multiplication of vibrations in the shaft bearing may lead to volatile operational instability [10]. The POZs idea is created to prevent these instabilities. POZs lead to discontinuities, which are harmful to mathematical formulation such as the POZ equations 1.
The suggested method begins with previous evolutionary algorithms with an original population of spiders to make each spider possible. These first spiders attempt to replicate the new generation in pairs [15]. The man is eaten during or after the match by a female Black Widow. Then it carries in her sperm thecae stored sperms and frees them into egg sackcloth. Spreads arise from the egg sacks as soon as 11 days when they are deposited [4]. For many days to a week, they live together on the maternal orca, during which cannibalism occurs. Afterward, they go by the wind.
This technique for optimal BWO relies on three parameters: Reproductive Rate (RP), Cannibal Rate (CP), and Mutation Rate (MR). RP- By managing the generation of diverse offspring, this parameter provides additional variety and allows for a more detailed exploration of the search space. CP- It is a cannibalism operator’s regulating parameter, which excludes the incorrect individuals from the population. By agents of shifting search from global stage local and vice-versa, the appropriate parameter’s value can assure exploitation stage performance. MR- This parameter can govern the transition of search agents from the global stage to the local stage and urge them toward the optimal solution.
The breeding rate monitors the young spiders and helps to grow the search space to find a better answer. The cannibalism rate limits the lowest fit population in the iteration, while the following generation is only permitted with better fit populations [16]. The transformation rate regulates the diversity in the next generation. A pseudo-code is a simple form of describing programming that does not require any specific syntax of programming language. It can be used to develop such programming framework, which is a simple form of describing programming that does not require any specific syntax of programming language. It can be used to develop such programming framework, which is presented below in section 4.2; the principal phases of BWO have been summed up. The workflow of the BWO algorithm is shown in Fig. 1. The BWO algorithm is as follows:
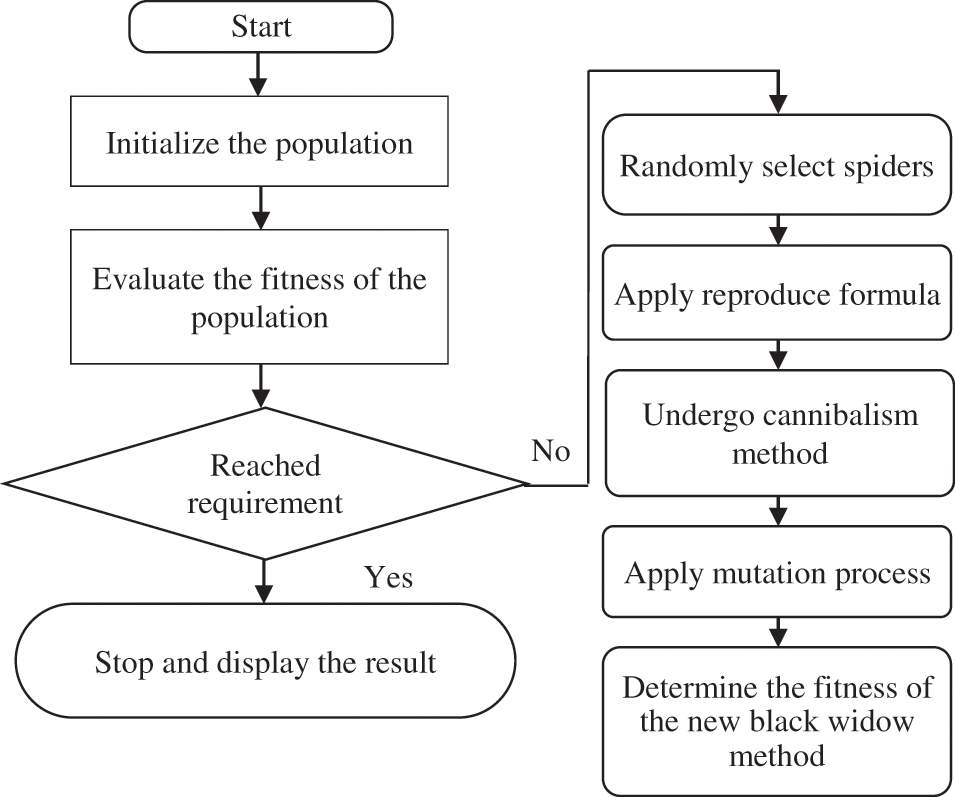
Figure 1: Flowchart of the BWO algorithm
•Step 1: Initial population:
Selecting parents randomly for the procreation stage guarantees that the search domain is explored. The examination of the search field is also emphasized while producing many children in procreation.
•Step 2: Procreate:
The step to circumvent the local optima flap is by the BWO algorithm. The BWO algorithm draws attention from local optima, as it employs many search agents to calculate global optima.
•Step 3: Cannibalism:
Eliminating unsuitable options help BWO progress exceptionally quickly to the optimal. The cannibalism step assures excellent operating performance, ensuring rapid closure of the BWO process.
•Step 4: Mutation:
The transformation process confirms the equilibrium between the phases of exploitation and research. The mutation rate of the Mute group is computed.
•Step 5: Convergence:
Three stop circumstances can be considered, like previous evolutionary algorithms: (a) The number of iterations that have been preset. (b) No observance for multiple iterations of the fitness value of the best widow. (c) The level of precision required.
The BWO algorithm relies on three important metrics: Generation Rate RP, CP, and MR. The multiplication rate, which tells the sexual reproduction effect of the female spider controls the age, growth rate of youthful bugs and gives freedoms to investigate the quest space for tracking down a superior arrangement. The sibling flesh consumption rate controls the more vulnerable fittest populace in the age, and just the fittest populaces are considered the future. The change rate controls the variety in the current reproduction to the future generations. In this research work, we thought the above three main parameters to evaluate the fittest population and thereby decide the optimization level.
4.2 Pseudo Code for the Proposed Work
Input: Maximize the number of iterations, cannibalism, Mutation rate, etc.
Output: Optimal solution for the selected objective function
Initialization:
1. Select a random value as the initial population of Black Widow spiders
2. Loop until satisfactory optimization is achieved
3. 2a. calculate the number of off-springs ‘nr’
2b. Select the best nr and its associate population as pop1
For i = 1 to nr, do
Randomly select two parents from pop1
Generate the off-spring D based on Eq. (1)
Remove the father
Randomly remove some off-spring to represent off-spring cannibalism
Save the result and name as pop2
End
4. Based on the removal (mutation), calculate the mutation rate ‘mr’
For 1to mr, Do
Select a solution from pop1
Apply mutation operation
Save the results as pop3
End
5. Update population by adding pop2 and pop3
6. Return the best solution
The performances of the BWO proposed are evaluated by the four areas, along with a 4-area system with 16 generator units and a 4-area system with 40 generating units, to demonstrate the performance and capabilities of the proposed algorithm of hybrid PSO (HPSO) that combines the traditional PSO framework with the crossover operation of a genetic algorithm using the crossover operation in PSO, it not only inhibits early convergence to the local optimum, but it also efficiently explores and uses exciting locations in the search space. To validate the efficiency of the suggested strategy, numerical experiments on a large-scale 40 units test system with valve-point effects are carried out [28].
The Teaching Learning Based Optimization (TLBO) algorithm considers the impact of a teacher on students. The optimization technique is based on phase angles rather than design variables, which allows the non-linear aspects of the issue to be treated more effectively. A new learning strategy is presented to prevent being trapped in local optima [29].
The same values are utilized in comparative algorithms for a fair comparison with similar parameters. The MATLAB 7.1 on a core i5−4110U processor with 2, 40 GHz, or 4 GB RAM is used to build comparison methods and reproduce them for all the test systems for 30 separate runs.
Case I: The total cost of generating is individually reduced as an objective function.
Case II: Emission targets are reduced as a function
Case III: Total costs and emission targets are concurrently reduced.
5.1 Test System 1: 4 Areas with 16-Unit
To demonstrate the performance of the BWO method in addressing the MAED (Case I), MA-EmD (Case II), and MA-CEED (Case III) issues, it is applied to a medium size thermal system with 16 units grouping into four zones, each with four generating units. Six tie lines link the four areas together.
Tab. 1 displays data for the cost coefficients (a, b, c), power operating limits (Prs,min, Prs,max), transmission cost coefficient (Cip), and emission coefficients (α,β, γ, δ, λ).
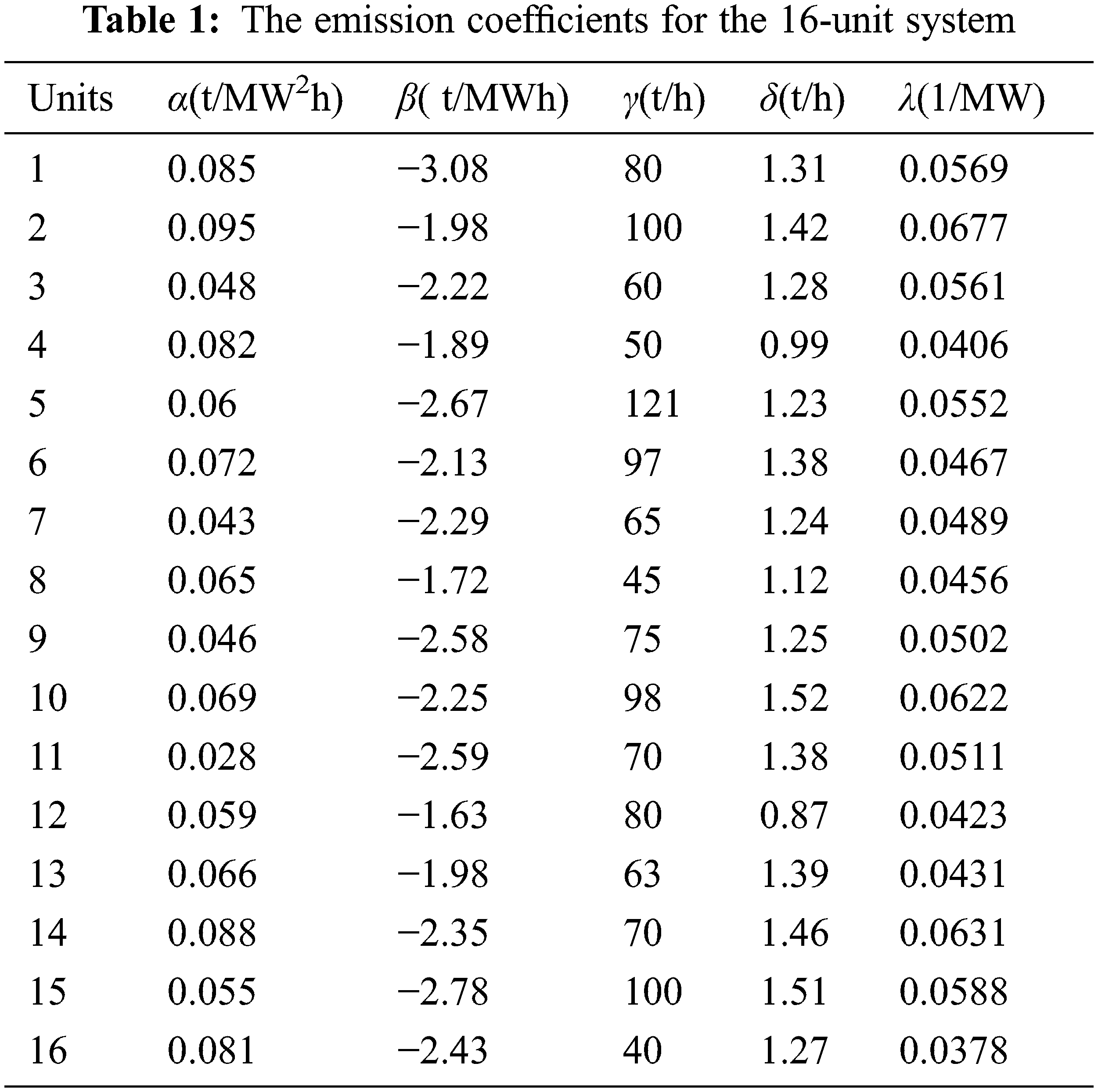
Tab. 2 provides the best answers by comparing algorithms and then the BWO receives the lowest cost of 7336. 76$/h, despite possible solutions identified by all the algorithms.
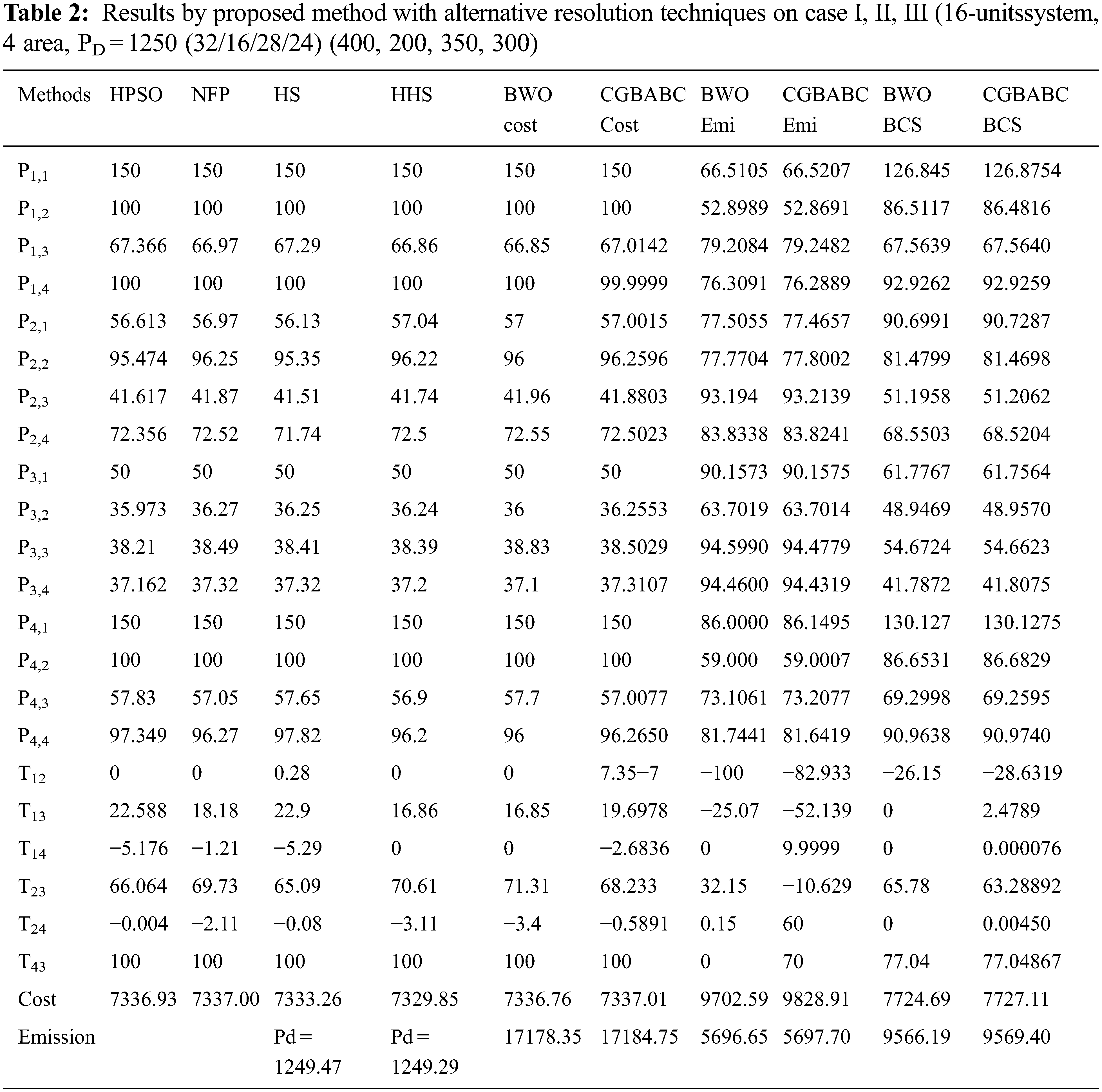
The results of the BWO are much better than those of other algorithms; compared to those of HPSO, NFP, HS, HHS and CGBABC [21], the results for reducing the emission-objective-functions. Whereas, the algorithm is superior CGBABC, which is nearer to the BWO also best compromising solution (BCS) between CGBABC and BWO are shown in Tab. 2.
Tab. 3 represents the analysis of the test system’s best, average and worst emission objective values, which provide the best, average, worst costs and BWO’s standard deviation of 30 separate runs, compared to the HPSO, NFP, HS, HHS and CGBABC. The comparative analysis shows that the BWO algorithm-based test system performs better with far smaller variations. Furthermore, in this test system, VPE, MFO and active transmission losses are considered. The capacity of the suggested method to handle various limitations of the issue is another essential aspect seen when one looks at the energy flow in ties and generator outputs in various locations. Then the existing algorithm for Case III resolution on a 16-unit test system is obtained through multi-area dispatch is comparatively shown in Tab. 4.

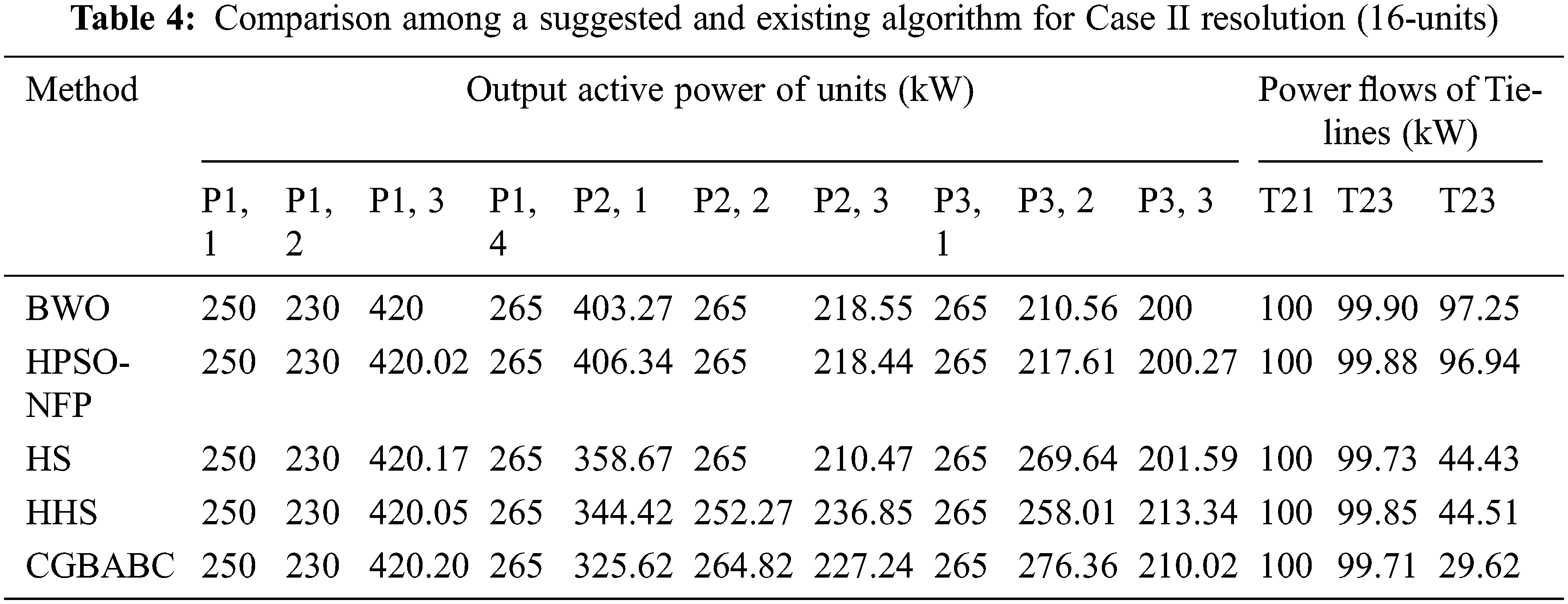
Tab. 4 illustrates the recommended technique is 30 times autonomously of each other. This table displays the best results for the presented HPSO based NFP, HS, HHS [30] and CGBABC the value of the standard emission deviation. In addition, the poorest solution of the algorithms is presented. The conversions of the test system 1 algorithm are also quicker and have better search results than other techniques, which show that the suggested methodology. Among that the two techniques has (BWO and CGBABC) superior best solution. Moreover, the generation cost of various case studies produced by the suggested approach is shown in Fig. 2.
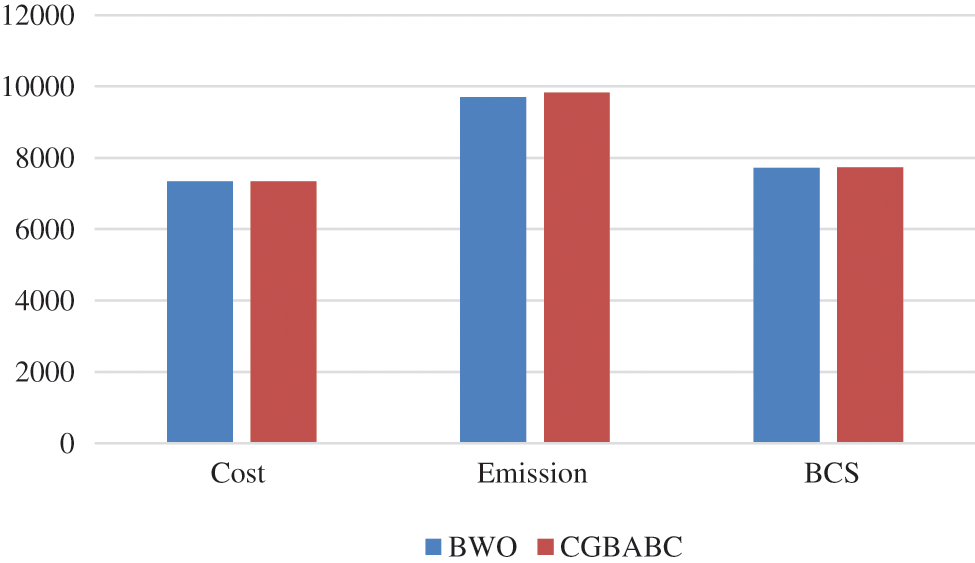
Figure 2: Analysis of test system 1
5.2 Test System 2: 4 Areas with 40-Units
There are four regions and 40 production units in the second test system. The data concerning the cost coefficients and power operating limitations are shown in Tab. 5. In addition, an ABCO, TLBO, GBABC are used in comparison with BWO to check further the effectiveness of the suggested method. Tab. 5 represents the overall Power Demand (PD) for the system is 10,500 MW, then the PD1, PD2, PD3, and PD4 are 1575, 4200, 3150 and 1575 respectively. Furthermore, the maximum flow limit of the region is 200 MW. The boundary uses 100 MW lines between regions. Whereas, the CPU time (sec) is mentioned in Tab. 6, which is the amount of time that the CPU spends processing data for a certain application or operation and it is also called as processing time. The comparative algorithms for case 2 solution methods for 40-unit test systems are shown in Tab. 6.
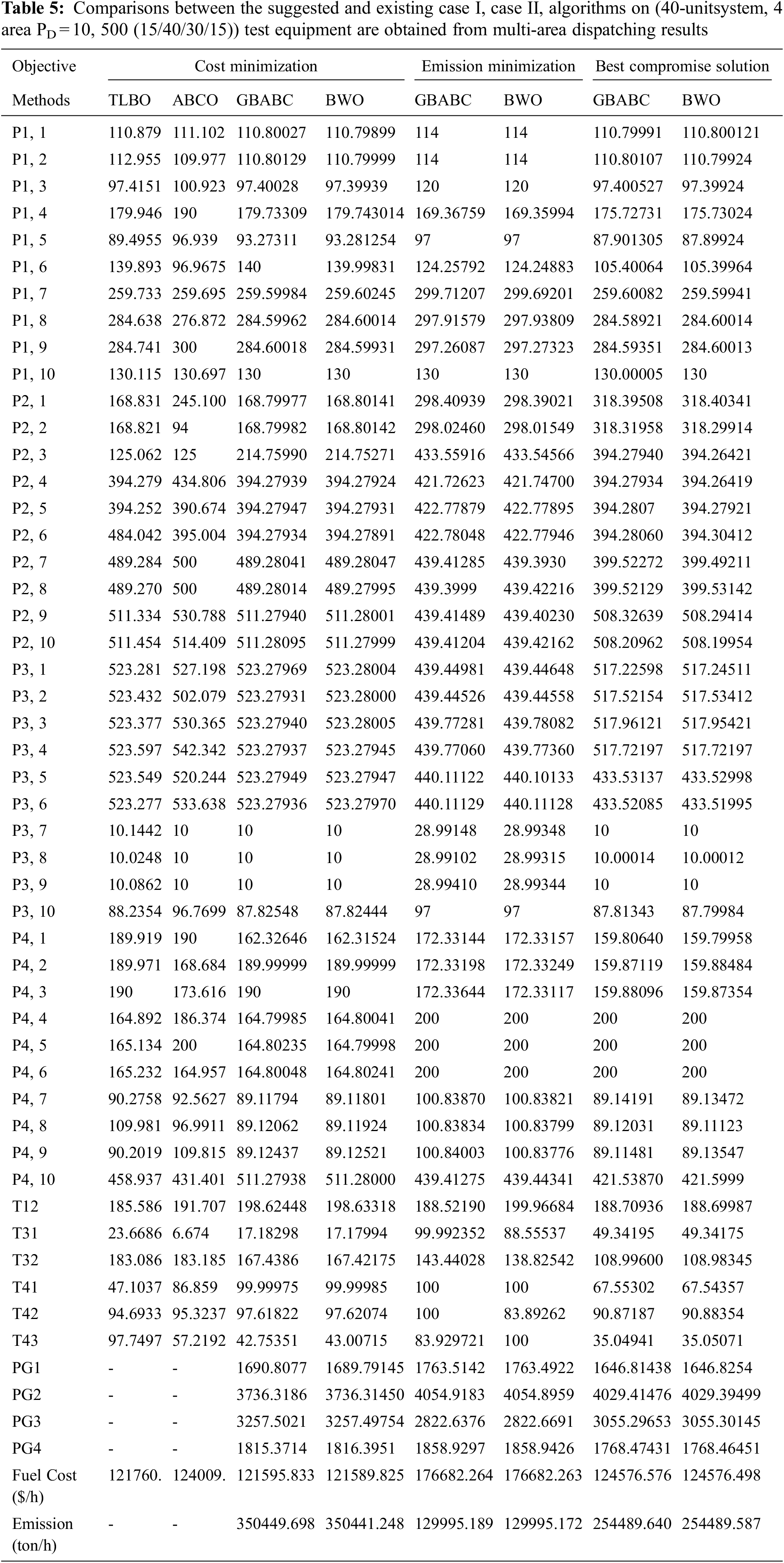
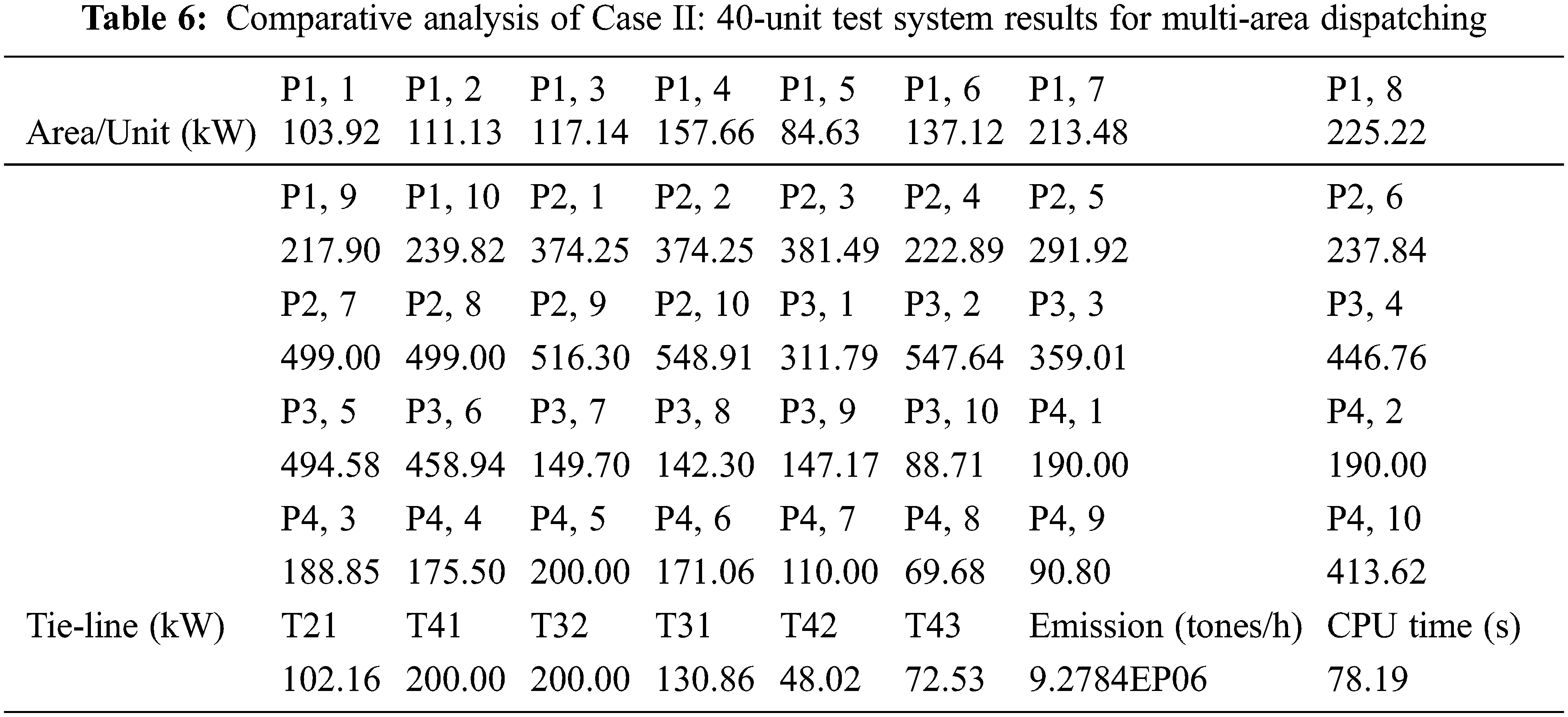
Tab. 6 illustrates the Case II 40-unit test system emission from the technique suggested and the TLBO, ABCO and GBABC methodologies. A comparison between the best, medium and worst solutions found by the proposed method, with BWO being able to converge in a better solution and being rugged than three other algorithms of optimization, is shown in Tab. 7.
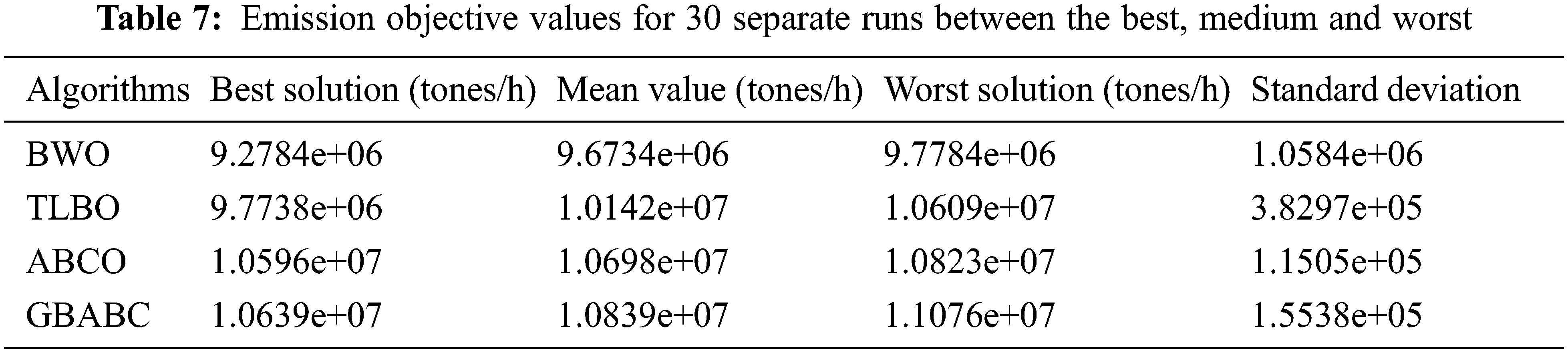
The minimal cost for fuel obtained by BWO, as seen in Tab. 5, is 121,589.8254 $/h, which is far less than the other large-scale MAED, MA-EmD solution. In particular, BWO is the least standard deviation, which indicates BWO is the most resilient of the algorithm. The BWO differs considerably from other algorithms. In addition, BWO shows higher search performance, as shown in Fig. 3.
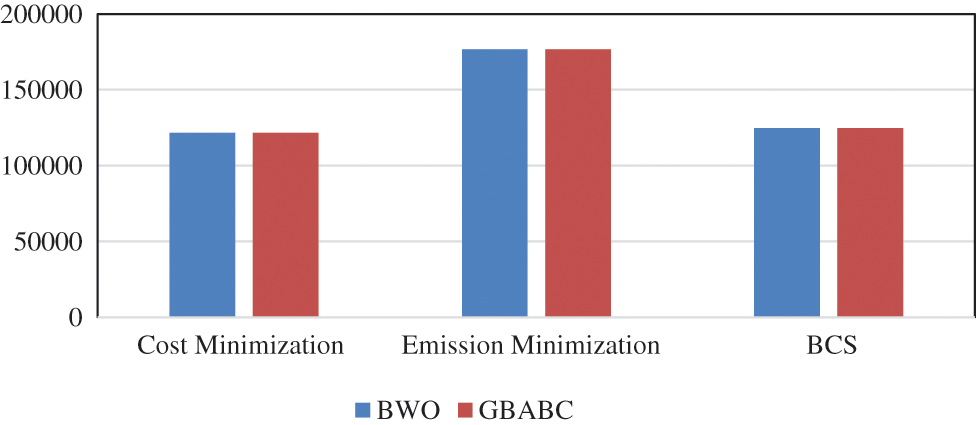
Figure 3: The cost comparison of unit 40 test system
Fig. 3 demonstrates that the proposed method may converge to a superior solution that displays the potential to resolve the suggested MAED problem globally or virtually worldwide. While BWO may achieve pretty good test system solutions, the effectiveness of the BWO has yet been considerably improved and also compared to other algorithms. It is clear that BWO converges rapidly and steadily towards optimal alternatives, showing the durability and resilience of the BWO, where the BWO has the lowest cost of 121,589 $/h among the other algorithms.
In this paper, the BWO technique is implemented for tackling the MAED issue considering the total cost for the generation and emission as multi-objective issues. It also considers the actual power system restrictions such as tie-line capacity and unit limits. In a 40-unit test system, the total cost and emission of the generation are reduced, further enhancing the optimization outcomes. In contrast, the analysis of the best, average and worst emission objective values on the 16-unit system for 30 separate runs are also provided. A comparison among the suggested and existing algorithms for a 16-unit test and 40-unit test system is also provided. The results show that the BWO algorithm outperforms conventional algorithms. The optimized cost for four areas 16 units is found to be 7336.76$/h, whereas for four areas 40 units it is found to be 121,589$/h. In the future, the MA-CEED can be solved by other techniques like genetic algorithms and cuckoo search. A new meta-heuristic optimization technique will be interesting for future studies to tackle additional complex energy-related improvements such as the demand response parameter for smart grids and production for hydroelectric plants.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. R. Narimani, J. Joo and M. L. Crow, “Dynamic economic dispatch with demand side management of individual residential loads,” North American Power Symposium, Charlotte, NC, USA, pp. 1–6, 2015. [Google Scholar]
2. D. C. Secui, “Large-scale multi-area economic/emission dispatch based on a new symbiotic organisms search algorithm,” Energy Conversion and Management, vol. 154, pp. 203–223, 2017. [Google Scholar]
3. E. Naderi, A. Azizivahed, H. Narimani, M. Fathi and M. R. Narimani, “A comprehensive study of practical economic dispatch problems by a new hybrid evolutionary algorithm,” Applied Soft Computing, vol. 61, pp. 1186–1206, 2017. [Google Scholar]
4. V. Hayyolalam and A. A. PourhajiKazem, “Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103–249, 2019. [Google Scholar]
5. V. H. Quintana, R. Lopez, R. Romano and V. Valadez, “Constrained economic dispatch of multi-area systems using the dantzig-wolfe decomposition principle,” IEEE Transactions on Power Apparatus and Systems, vol. PAS-100, no. 4, pp. 2127–2137, 1981. [Google Scholar]
6. C. V. Suresh, S. Sivanagaraju and J. V. Rao, “Multi-area multi-fuel economic-emission dispatch using a generalized unified power flow controller under practical constraints,” Arabian Journal for Science and Engineering, vol. 40, no. 2, pp. 531–549, 2015. [Google Scholar]
7. M. Basu, “Artificial bee colony optimization for multi-area economic dispatch,” International Journal of Electrical Power & Energy Systems, vol. 49, pp. 181–187, 2013. [Google Scholar]
8. R. R. Shoults, S. K. Chang, S. Helmick and W. M. Grady, “A practical approach to unit commitment, economic dispatch and savings allocation for multiple-area pool operation with import/export constraints,” IEEE Transactions on Power Apparatus and Systems, vol. PAS-99, no. 2, pp. 625–635, 1980. [Google Scholar]
9. J. E. Garb, A. González and R. G. Gillespie, “The black widow spider genus latrodectus (Araneae: TheridiidaePhylogeny, biogeography, and invasion history,” Molecular Phylogenetics and Evolution, vol. 31, no. 3, pp. 1127–1142, 2004. [Google Scholar]
10. P. S. Manoharan, P. S. Kannan and V. Ramanathan, “A novel EP approach for multi-area economic dispatch with multiple fuel options,” Turkish Journal of Electrical Engineering and Computer Science, vol. 17, no. 1, pp. 1–19, 2009. [Google Scholar]
11. D. N. Jeyakumar, T. Jayabarathi and T. Raghunathan, “Particle swarm optimization for various types of economic dispatch problems,” International Journal of Electrical Power & Energy Systems, vol. 28, no. 1, pp. 36–42, 2006. [Google Scholar]
12. C. Wang and S. M. Shahidehpour, “A decomposition approach to non-linear multi-area generation scheduling with tie-line constraints using expert systems,” IEEE Transactions on Power Systems, vol. 7, no. 4, pp. 1409–1418, 1992. [Google Scholar]
13. C. L. Chen and N. Chen, “Direct search method for solving economic dispatch problem considering transmission capacity constraints,” IEEE Transactions on Power Systems, vol. 16, no. 4, pp. 764–769, 2001. [Google Scholar]
14. J. Nanda, D. P. Kothari and K. S. Lingamurthy, “Economic-emission load dispatch through goal programming techniques,” IEEE Transactions on Energy Conversion, vol. 3, no. 1, pp. 26–32, 1988. [Google Scholar]
15. T. Jayabarathia, K. Jayaprakasha, D. N. Jeyakumarb and T. Raghunathana, “Evolutionary programming techniques for different kinds of economic dispatch problems,” Electric Power Systems Research, vol. 73, no. 2, pp. 169–176, 2005. [Google Scholar]
16. T. Niknam, M. R. Narimani, E. Farjah and B. B. Firouzi, “A new evolutionary optimization algorithm for optimal power flow in a power system involving unified power flow controller,” Energy Education Science and Technology Part A: Energy Science and Research, vol. 29, no. 2, pp. 901–912, 2012. [Google Scholar]
17. T. Niknam, M. R. Narimani and A. R. Azizipanah-Abarghooee, “A new hybrid algorithm for optimal power flow considering prohibited zones and valve point effect,” Energy Conversion and Management, vol. 58, pp. 197–206, 2012. [Google Scholar]
18. T. Niknam, M. R. Narimani, M. Jabbari and A. R. Malekpour, “A modified shuffle frog leaping algorithm for multi-objective optimal power flow,” Energy, vol. 36, no. 11, pp. 6420–6432, 2011. [Google Scholar]
19. A. Azizivahed, H. Narimani, E. Naderi, M. Fathi and M. R. Narimani, “A hybrid evolutionary algorithm for secure multi-objective distribution feeder reconfiguration,” Energy, vol. 138, pp. 355–373, 2017. [Google Scholar]
20. T. Yalcinoz and M. J. Short, “Neural networks approach for solving economic dispatch problem with transmission capacity constraints,” IEEE Transactions on Power Systems, vol. 13, no. 2, pp. 307–313, 1998. [Google Scholar]
21. D. C. Secui, “The chaotic global best artificial bee colony algorithm for the multi-area economic/emission dispatch,” Energy, vol. 93, pp. 2518–2545, 2015. [Google Scholar]
22. Z. L. Gaing, “Particle swarm optimization to solving the economic dispatch considering the generator constraints,” IEEE Transactions on Power Systems, vol. 18, no. 3, pp. 1187–1195, 2003. [Google Scholar]
23. D. Streiffert, “Multi-area economic dispatch with tie line constraints,” IEEE Transactions on Power Systems, vol. 10, no. 4, pp. 1946–1951, 1995. [Google Scholar]
24. M. Basu, “Quasi-oppositional group search optimization for multi-area dynamic economic dispatch,” International Journal of Electrical Power & Energy System, vol. 78, pp. 356–367, 2016. [Google Scholar]
25. L. Wang and C. Singh, “Reserve constrained multi-area environmental/economic dispatch based on particle swarm optimization with local search,” Engineering Applications of Artificial Intelligence, vol. 22, no. 2, pp. 298–307, 2009. [Google Scholar]
26. K. W. Doty and P. L. McEntire, “An analysis of electric power brokerage systems,” IEEE Transactions on Power Apparatus and Systems, vol. PAS-101, no. 2, pp. 389–396, 1982. [Google Scholar]
27. J. Park, Y. Jeong, J. Shin, K. Y. Lee and J. Kim, “A hybrid particle swarm optimization employing crossover operation for economic dispatch problems with valve-point effects,” in Int. Conf. on Intelligent Systems Applications to Power Systems, Kaohsiung, Taiwan, pp. 1–6, 2007. [Google Scholar]
28. T. Niknam, F. Golestaneh and M. S. Sadeghi, “θ-multi-objective teaching–learning-based optimization for dynamic economic emission dispatch,” IEEE Systems Journal, vol. 6, no. 2, pp. 341–352, June 2012. [Google Scholar]
29. M. Fesanghary and M. M. Ardehali, “A novel meta-heuristic optimization methodology for solving various types of economic dispatch problem,” Energy, vol. 34, no. 6, pp. 757–766, 2009. [Google Scholar]
30. G. R. Goyal and S. Vadhera, “Solution of combined economic emission dispatch with demand side management using metaheuristic algorithms,” International Information and Engineering Technology Association, vol. 52, no. 2, pp. 143–148, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |