DOI:10.32604/iasc.2023.028552

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.028552 |  |
| Article |
An Efficient Honey Badger Optimization Based Solar MPPT Under Partial Shading Conditions
1Department of Electrical and Electronics Engineering, Sri Ràaja Raajan College of Engineering and Technology, Sivaganga, Tamilnadu, 630301, India
2Department of Electrical and Electronics Engineering, K. L. N. College of Engineering, Sivagangai, Tamilnadu, 630612, India
*Corresponding Author: N. Rajeswari. Email: rajisugumar22@gmail.com
Received: 12 February 2022; Accepted: 24 March 2022
Abstract: Due to the enormous utilization of solar energy, the photovoltaic (PV) system is used. The PV system is functioned based on a maximum power point (MPP). Due to the climatic change, the Partial shading conditions have occurred under non-uniform irradiance conditions. In the PV system, the global maximum power point (GMPP) is complex to track in the P-V curve due to the Partial shading. Therefore, several tracking processes are performed using various methods like perturb and observe (P & O), hill climbing (HC), incremental conductance (INC), Fuzzy Logic, Whale Optimization Algorithm (WOA), Grey Wolf Optimization (GWO) and Flying Squirrel Search Optimization (FSSO) etc. Though, the MPPT is not so efficient when the partial shading is increased. To increase the efficiency and convergences in MMPT, the Honey Badger optimization (HBO) algorithm is presented. This HBO model is motivated by the excellent foraging behaviour of honey badgers. This HBO model is used to achieve the best solution in GMPP tracking and speed convergence. The HBO methodology is also compared with prior P&O, WOA and FSSO methods using MATLAB. Therefore, the experiment shows that the HBO method is performed a higher tracking than all prior methods.
Keywords: PV system; gmpp tracking; convergence; honey badger optimization; digging and honey phase
Solar energy is the most essential source to provide a clean environment and a better gain in economic. Nowadays photovoltaic (PV) systems are acted as a main solar source for electricity generation. But in the PV system, the conversion of insolation into electricity is more difficult and has minimum efficiency [1]. Solar radiation and atmospheric temperature are the environmental factors that are used for power generation in a PV system. The characteristics of power–voltage (P-V) and current-voltage (I-V) are affected by these environmental factors.
The PV array-based P-V curve has a single maximum power point (MPP) under a uniform irradiance. Also in the non-uniform irradiance, a few PV modules and also in PV cells have partial shading. The partial shading occurred due to environmental variation of clouds, trees, dust covering and buildings etc. This partial shading condition (PSC) made P–V characteristics more complex and provided multiple peaks whereas one Global peak Maximum Power Point (GMPP) and others are Local peaks Maximum Power Point (LMPP). To control these PSC, the Maximum Power Point Tracking (MPPT) techniques are developed [2]. The MPPT technique is used to achieve power availability in every operating condition.
Several MPPT techniques are developed for power stability such as perturb and observe (P&O) [3], hill climbing (HC) [4] and incremental conductance (INC) [5]. These techniques are used to track the Global Peak point under uniform irradiation conditions accurately. Though, these conventional methods are fallen easily to the LMPP that minimize solar power utilization. Therefore, there is a need of controlling the LMPP fallen point and also determine GMPP by using some efficient methods.
To improve the optimised solution for tracking a GMPP and PSC controllability, the Meta-heuristics methods are applied. The metaheuristic algorithms are based on the sources of inspiration that is categorised into different types namely Swarm Intelligence algorithms (SI), Evolutionary Algorithms (EA) and Natural Phenomenon (NP) algorithms [6]. The SI based metaheuristic is inspired by an insect or animals’ social behaviour. The EA is a method that is followed natural evolution happenings in nature. The NP based metaheuristic is motivated by using a physical and chemistry Phenomenon. In a few cases, the metaheuristic methods are motivated by the behaviour of humans that is based on neither SI nor EA respectively.
For past decades, various swarm intelligence methods are implemented for tracking GMPP. Some of the popular SI methods in MPPT are particle swarm optimization (PSO) [7], artificial bee colony (ABC) algorithm [8], firefly algorithm (FA) [9], bat algorithm [10], Grey Wolf Optimization (GWO) algorithm [11] and so on. Because of the design simplicity and easy implementation, the SI based methods are applied mostly for GMPP tracking in PV systems. In many cases, the higher settling time has occurred in SI techniques that are due to velocity and position is updated for a solution space. It may provide some inconvenience and complexity to obtain a convergence time and steady-state performance.
To overcome these issues, a SI based Honey Badger optimization (HBO) algorithm is presented for optimal GMPP tracking and fast convergence time. The HBO model is motivated by a honey badger’s excellent foraging behaviour. This HBO method is presented mathematically to solve optimization issues using a searching strategy. It carries two strategies of a honey badger with digging and honey searching strategy to provide an effective solution. This HBO provided an ample population diversity process to achieve the best solution in a larger landscape area. The HBO methodology is also validated and compared with existing techniques namely P&O, PSO, and GWO methods through simulation. The result showed that the HBO model provided a higher tracking efficiency than all prior methods.
The remaining part of the work is contributed as: Section 2 provides a related literature work based on MPPT. The preliminary of this work is presented in Section 3. It described PV model characteristics and PSC effects in it. Section 4 explored a proposed methodology of HBO techniques and its algorithm. The results and discussions are discussed in Section 5 and the work is concluded in Section 6.
In this section, the literary work based on MPPT is developed and implemented by various researchers are presented. Many works are relevant to optimization and Artificial Intelligence (AI) techniques. These methods are used to obtain a higher tracking accuracy which is explained in the following.
Lak et al. [12] presented a hybrid of zero-sequence voltage injection and dipolar variable injection methods. This method can control the DC-link capacitors voltage, and ignore voltages ripple simultaneously. The Outcomes showed that the Power Factor is unity or non-unity. The next work was an adaptive neuro-fuzzy inference system (ANFIS)-based MPPT technique developed by Ibrahim et al. [13]. This method is applied to a PV based battery charger with a greater feasibility and effectiveness verification. Figueiredo et al. [14] implemented a hybrid MPPT by combining PSO and P&O techniques. This method is used to apply in PV systems under uniform and PSC. The outcome of this hybrid method can track more effectively than the conventional PSO model.
Bharadwaj et al. [15] investigated a novel GMPPT method named a rectangular power evaluation algorithm. The basic correlation among the shading factor, GMPP and the bypass diode voltage is evaluated. The outcomes achieved a higher improvement in speed and also greater power gain. Another literature in [16], novel most valuable player (MVP) algorithm is presented by Pervez et al. It is used to track the optimal MPP from PV system in terms of tracking efficiency, tracking speed, robustness, faster convergence and lesser power fluctuations. The result experimented that all the metrics are attained a maximum value than the previous methods. Next, the Jamaluddin et al. [17] explored a duty cycle-based direct exploration method using a salp swarm optimization (SSO). This work provided a higher tracking capability of the MPP from a PV system.
Karmakar et al. [18] presented an improved DAR method using current injection (CI). The CI-based DAR method is explored and enhanced the array power that is achieved by DAR methods. Next, the JAYA method based on Lévy flight (JAYA-LF) is developed by Motamarri et al. [19]. This model can be performed as a PV array under dynamic and static conditions. The JAYA-LF attained superior efficiency and higher performance than existing. Pervez et al. [20] investigated a fuzzy logic and neural network approach for MPP tracking. It is based on stochastic search methods that achieved merits of fewer variations, sturdiness, easiness, and quicker convergence respectively.
Lyden et al. [21] presented a hybrid Simulated Annealing and P&O technique for a PV based MPPT method. This hybrid model is evaluated and compared with the sentry particle re-initialization. Thus, the Simulated Annealing and P&O obtained a more consistent GMPP tracking. Another hybrid method of P&O and modified invasive weed optimization (MIWO) is implemented by Pradhan et al. [22]. It is performed under the rapid change of weather PSC to build an efficient MPPT extraction in a PV system. Toodeji et al. [23] explored a feedback linearization-based control technique is designed for the nonlinear system. The control strategy merits are simulated in MATLAB/Simulink under several PSC by adding or ignoring PV modules.
In this section, the preliminaries for a proposed work are presented. It described a basic idea of PV model characteristics and PSC effects to obtain a tracking accuracy under uniform and non-uniform irradiance conditions.
The PV source module is given in Fig. 1a is also known as the single diode model. It is used to obtain a precise PV cell’s output characteristics for various kinds and modules. The PV Module consists of a diode, PV current (Iph), a series resistance (Rse) and a shunt resistance (Rsh) respectively. Based on these elements, the output current is expressed in the following equations.
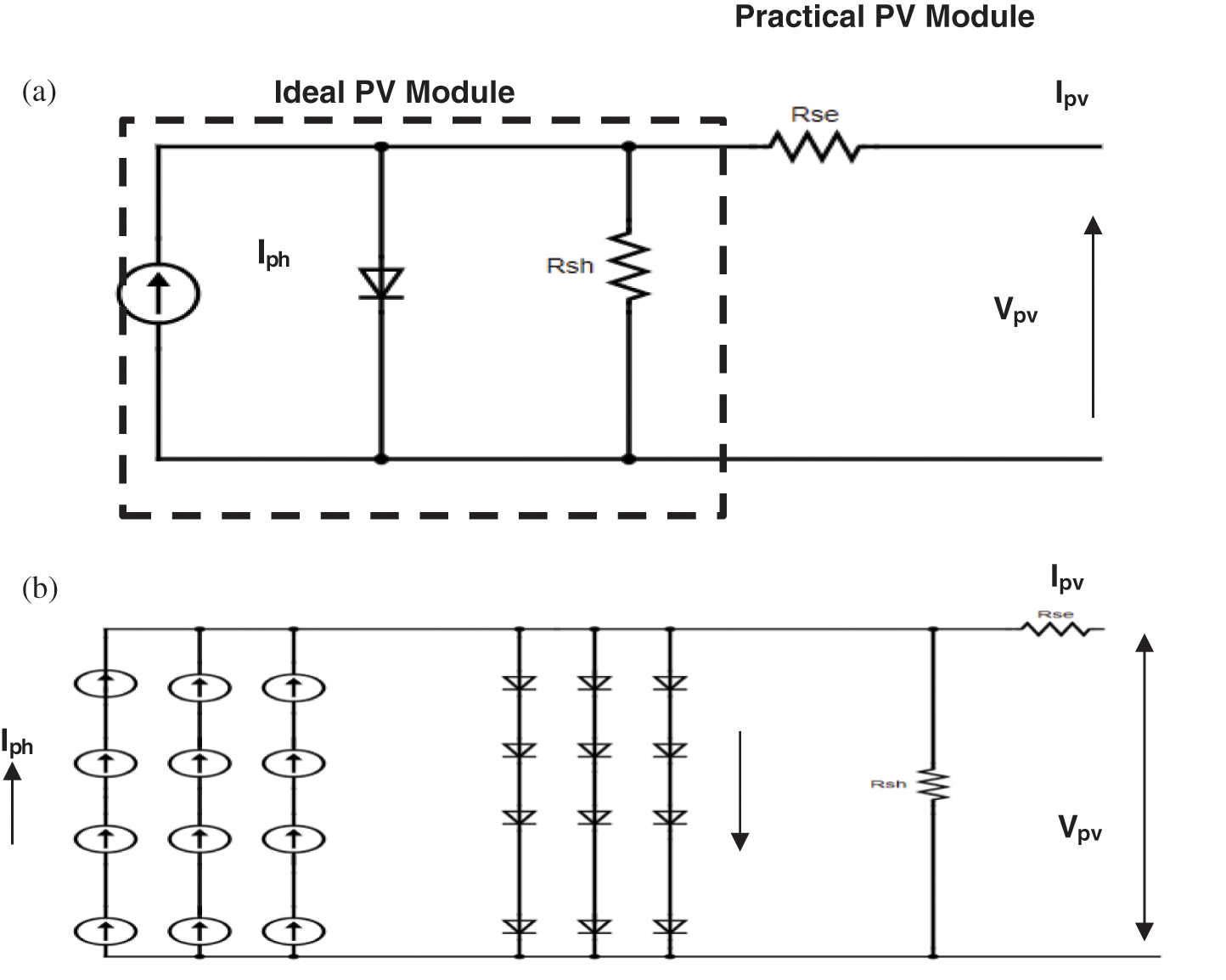
Figure 1: Equivalent circuit of PV. (a) Single diode model. (b) An array of a panel composed of series and parallel combination of modules
The output current (IPV) is expressed as
where the G indicates irradiation level, Vt denotes a thermal voltage at temperature T and Irsrepresents diode reverse saturation current. Also, Tn represents a temperature current, Gn indicates irradiance current.
The thermal voltage is evaluated based on series-connected cells (Nse) using the below Eq. (4)
The diode reverse saturation current is evaluated using Eq. (5)
where Voc,n represents an open-circuit voltage at STC(standard test condtion) temperature, Isc,n denotes a short-circuit current at STC; KI indicates short-circuit current coefficient and KV are coefficients of an open circuit voltage temperature.
To achieve a higher voltage and current, the series-parallel combinations are connected in PV modules. From Fig. 1b, the IPV is expressed in the following Eq. (6)
where
Based on the above characteristics of photovoltaic modules and their connection, the PSC is acted. If all the PV cells received a uniform irradiance under normal conditions, then the P-V curve has a single MPP shown in Fig. 2a. In the occurrence of Partial shading in any module of PV array, then the hot-spot heating is produced which does not generate more current. To overcome this issue, the external bypass diode is conducted during the solar cell is reversed biased. This may allow the unshaded cells to flow the shaded cell externally. Thus the staircase current is produced in Current-Voltage curve and also the Power –Voltage curve is categorized by multiple maxima points simultaneously as shown in Fig. 2b.
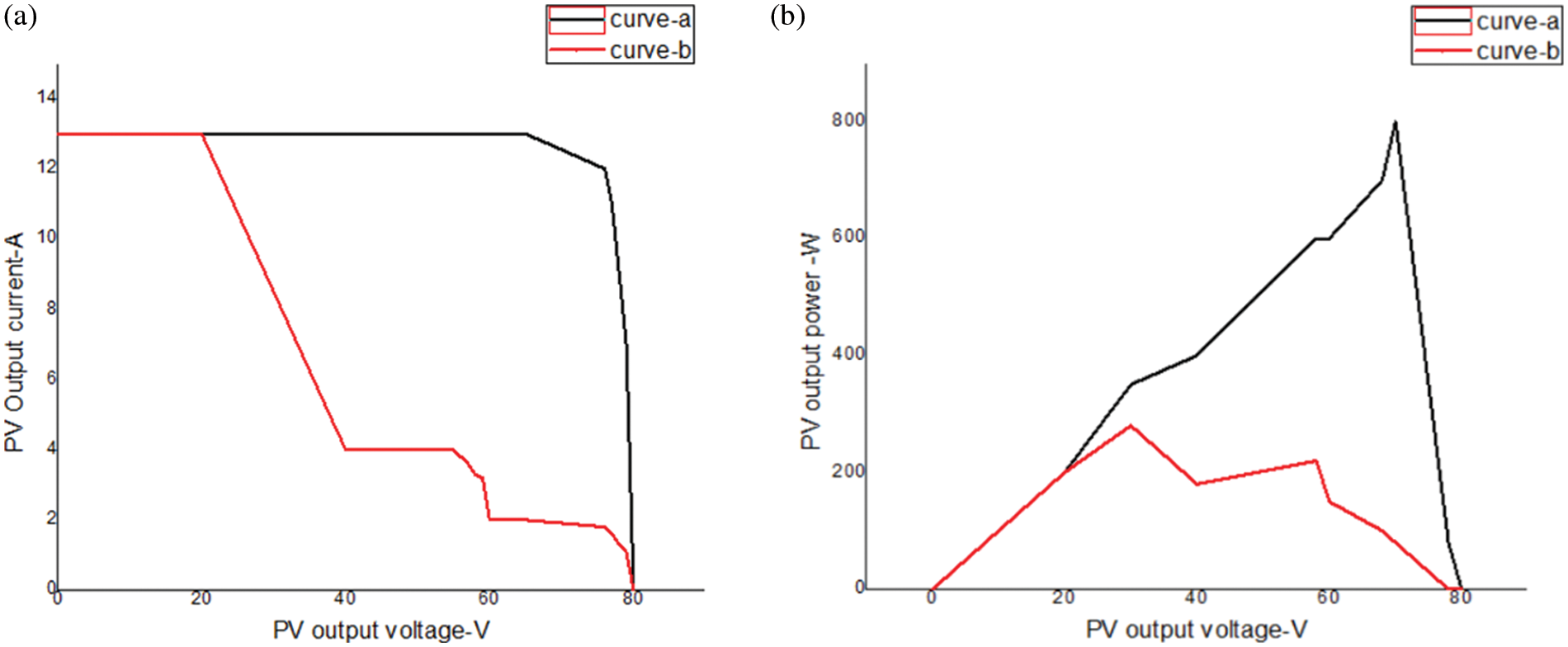
Figure 2: PV configuration. (a) Normal (b) Partial shading
In this work, the Honey Badger optimization (HBO) algorithm is implemented to track the GMPP for the photo-voltaic system under every environmental condition. This work proposed an HBO based MPPT for PV systems to provide higher accuracy and fast convergence. The connections of the PV system connected with the boost converter is shown in Fig. 3. This method can be provided with an optimal duty cycle (D) solution for a partial shading effect. Therefore, the Honey Badger optimization is described in the following.
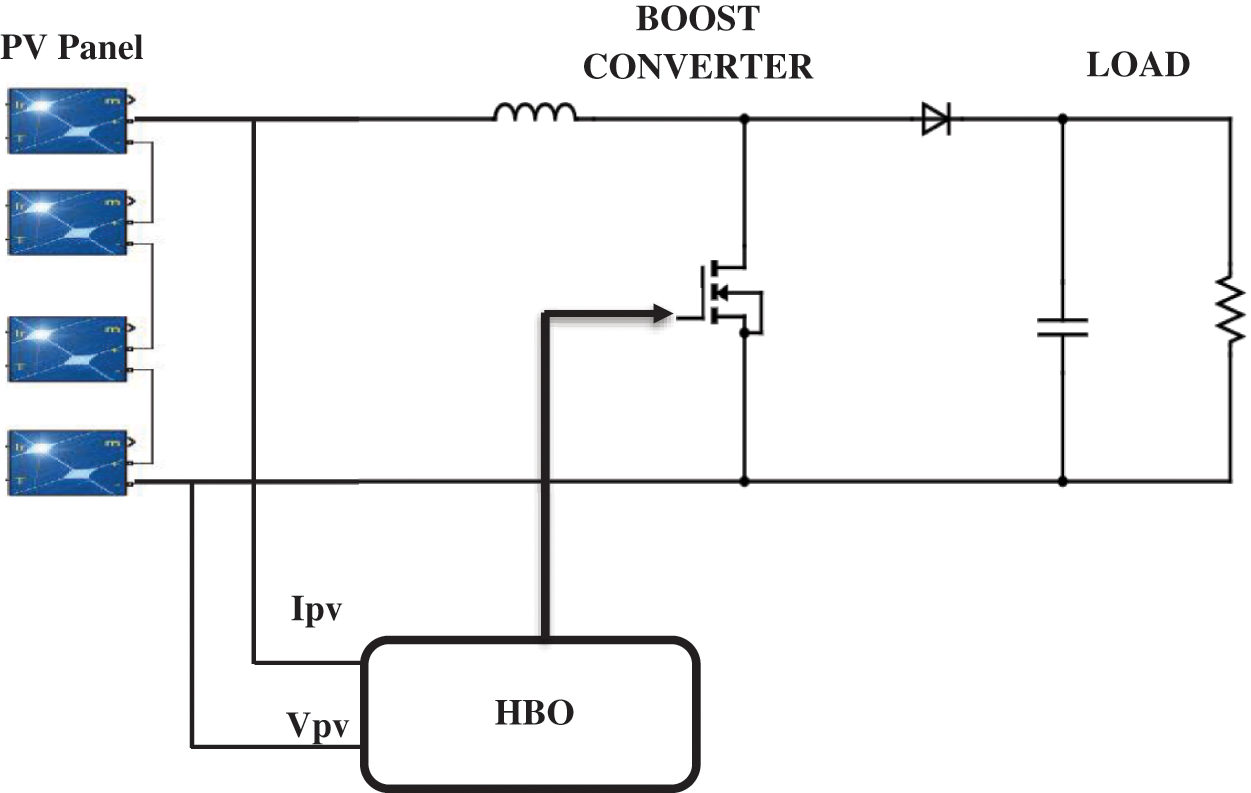
Figure 3: Block diagram of proposed MPPT algorithm
4.1 Honey Badger Optimization Algorithm
In this work, a Honey Badger optimization (HBO) algorithm is presented which is based on Swarm based algorithm. The HBO is motivated by a honey badger’s excellent foraging behaviour. This HBO method is presented mathematically to solve an optimization issue using a searching strategy. It carries two strategies of a honey badger with digging and honey searching strategy to provide an effective solution. This HBO provided an ample population diversity process to achieve the best solution in a larger landscape area. The Honey Badger Optimization is based on the foraging behaviour of Honey Badger.
Therefore, the general biology and inspiration of Honey Badger and also a mathematical model for the HBO Algorithm is presented in the following.
The Biological Behaviour of Honey Badger
Honeybadger is a black coloured white fluffy mammal often lived in areas like dry regions and forests. It is also known as a fearless mammal that seems like a dog in physics. The foraging behaviour of honey badger is fearless and very intelligent. There are more than sixty preys that are foraged by honey badger including harmful snakes. It smells and forages its prey by a slow walk. It also loves honey to eat.
Inspiration
The HBO model is inspired by the foraging behaviour of honey badgers. The foraging behaviour is based on strategies like smells, digs and follows the prey to their location. It has two stages for foraging namely the digging process and honey process. In the digging process, the honey badger has a high smelling behaviour that followed the smell location and catches the prey by digging the earth. In the honey process, it determined the beehive with the help of a honeyguide bird.
Mathematical Model
Based on the above foraging behaviour, the HBO model is derived mathematically. The HBO model is derived using two phases namely the digging phase and honey phase. Based on these phases, exploration and exploitation are performed to achieve the best optimal solution. Therefore the mathematical model is discussed in the following.
The candidate solutions population of HBO is expressed in Eq. (7).
Honey badger lth position,
Step 1: Initialize the N number of population and its positions using Eq. (8)
where
xl → lth position of Honeybadger with respect to N,
rand1 → random number among 0 and 1,
ubl → Search domain upper bounds,
lbl → Search domain lower bounds.
Step 2: Defining intensity (I) is defined as the prey concentration strength and distance among prey and lth honey badger. It is based on the smell intensity of prey that is derived using Inverse Square Law expressed in Eq. (9).
where
S = (xl − xl+1) 2, that indicated the concentration strength
dl = xprey − xl, that indicated a distance among prey and lth honey badger.
Step 3: density factor (α) is to be updated which is used to control time-varying randomization. This control is processed for an exploration to exploitation stage to smoothen the solution. It is minimized with an iteration to reduce randomization with time-based on Eq. (10).
where
tmax → Maximum number of iterations
C → Constant ≥ 1 (default = 2)
Step 4: This step is used for Escaping from the local optimum. It has a flag F that is used to alter a search direction. This direction is used to scan the search space severely by availing high opportunities for agents.
Step 5: The agent position is to be updated using the digging phase and honey phase.
In the digging phase, a Cardioid shape motion is performed by a honey badger that is expressed in Eq. (11):
where
Xprey → Position of prey
There is a flag (F) work is used to modify the direction of search that is expressed in below Eq. (12):
In the Honey phase, the beehive is obtained by using a honeyguide bird by honey badger which is given in below Eq. (13):
From Eq. (6), it is clear that the honey badger is very close to its prey location (Xprey) based on dl. The searching behaviour is used for a search in α times and also the disturbance F may be found. Thus the pseudo-code of the HBO method is given in Algorithm 1.

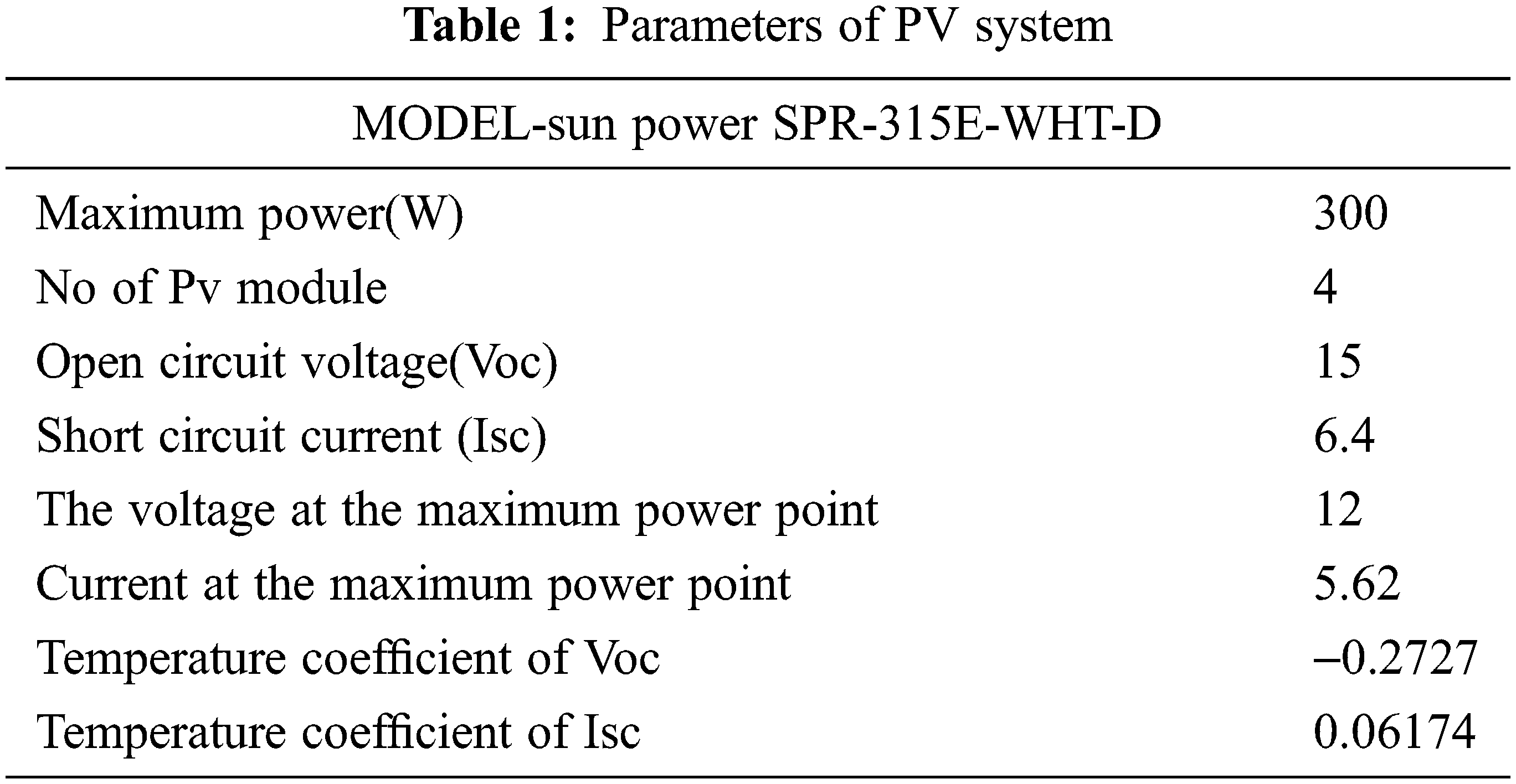
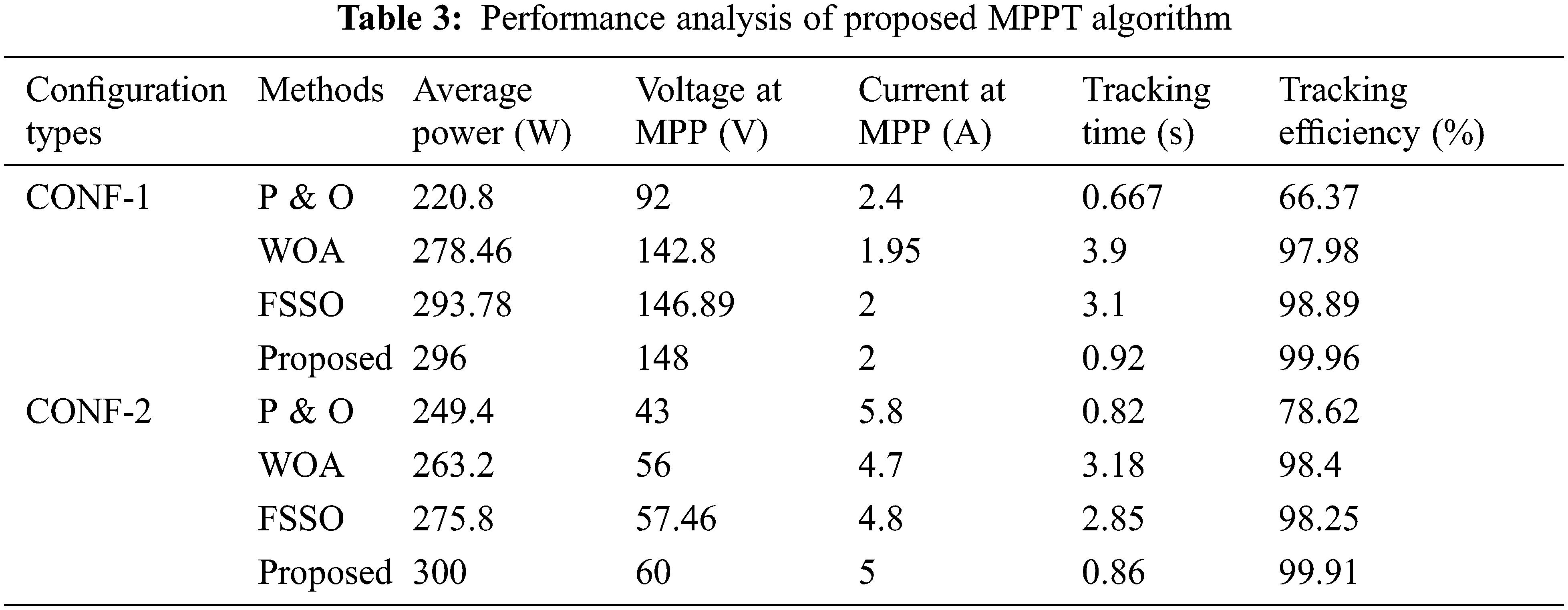
The proposed MPPT algorithm is evaluated using the MATLAB 2019a tool. For a fair comparison, the proposed algorithm compared with P&O, GWO, WOA and FSSO algorithms. The design properties used for the PV system and boost converters are given in Tabs. 1 and 2. There are two types of configurations with different partial shading conditions are considered in this work: four panels with series configuration (CONF1) and four panels with two series and two parallel configurations (CONF2).

The proposed tracking algorithm is compared in terms of tracking time and efficiency. The tracking efficiency of the proposed MPPT algorithm is calculated by the proportion of average power from the solar system at the steady-state and maximum obtainable power from the solar system partial shading.
The simulated waveform of the proposed MPPT algorithm in CONF1 is shown in Fig. 4. Tab. 3 observed that the P& O based approach traces maximum power of 220.8 W with the tracking time of 0.667 s. The WOA based approach traces maximum power of 278.46W with a tracking time of 3.9 s. The FSSO based approach traces maximum power of 293.78 W with a tracking time of 3.1 s. But, the proposed algorithm traces maximum power of 296W with a tracking time of 0.92 s.
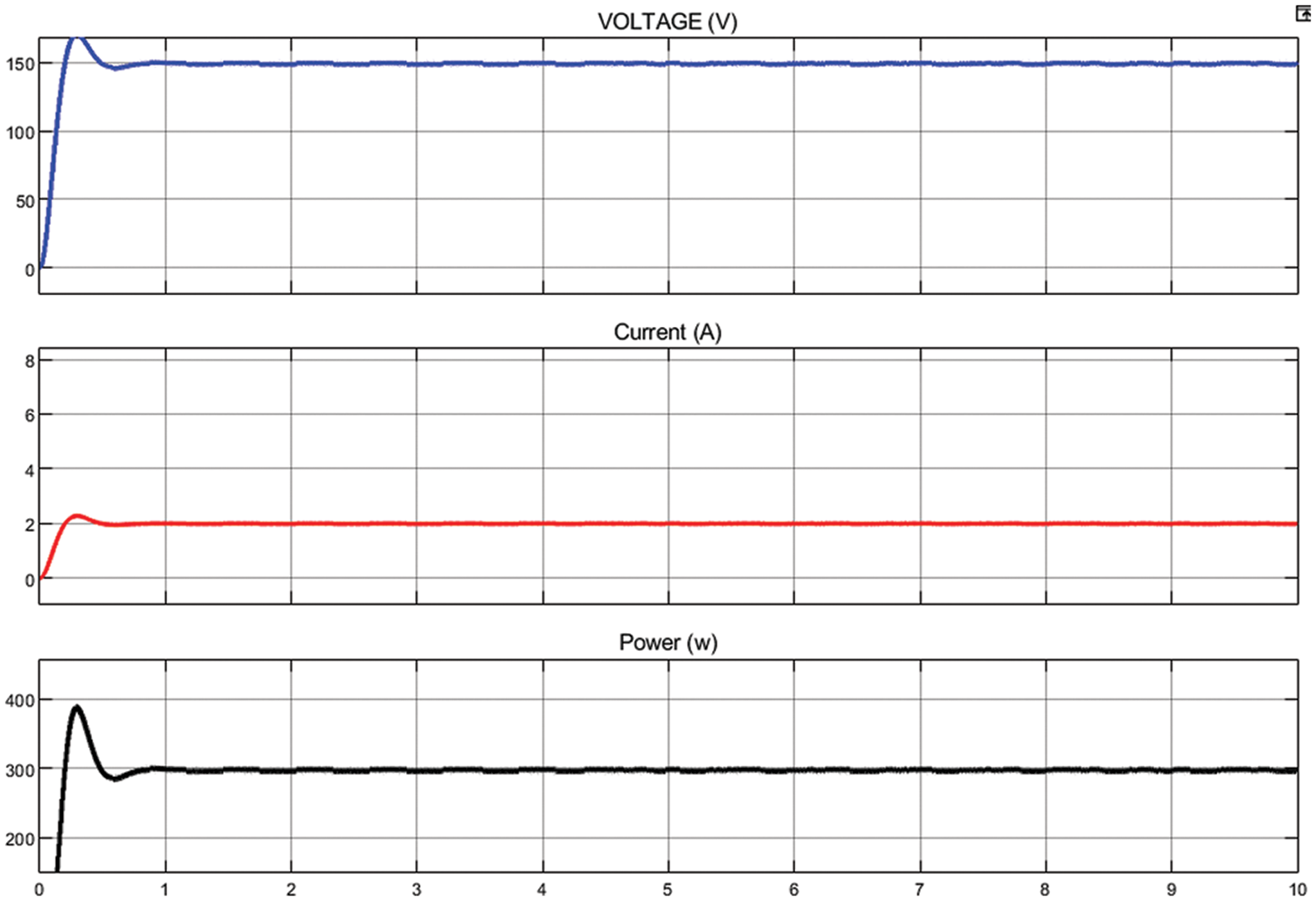
Figure 4: Output waveform for CONF-1
The simulated waveform of the proposed MPPT algorithm in CONF2 is shown in Fig. 5. Tab. 3 observed that the P & O based approach traces maximum power of 249.4 W with the tracking time of 0.82 s. The WOA based approach traces maximum power of 263.2W with a tracking time of 3.18 s. The FSSO based approach traces maximum power of 275.8 W with a tracking time of 2.85 s. But, the proposed algorithm traces maximum power of 300W with a tracking time of 0.86 s.
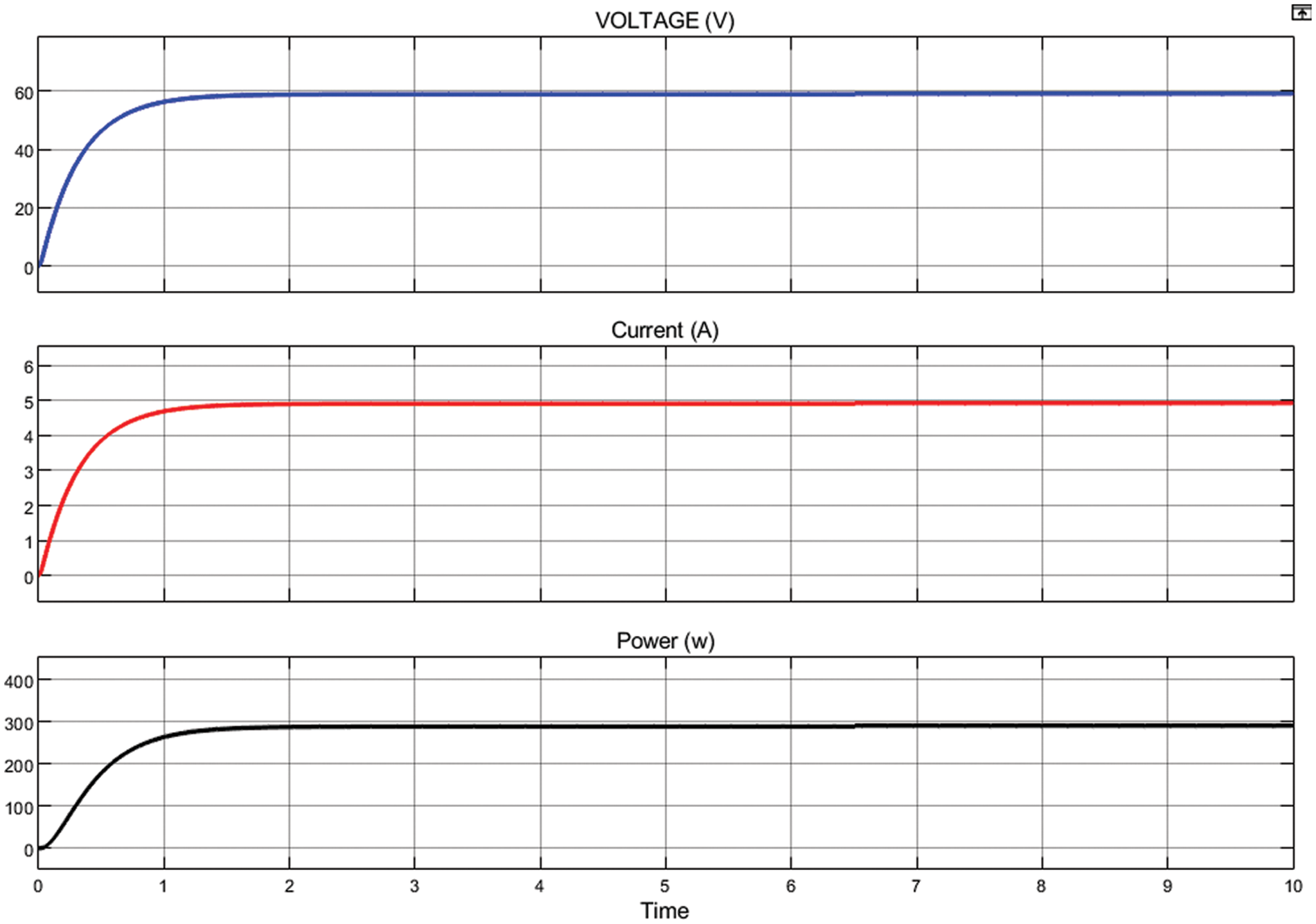
Figure 5: Output waveform for CONF-2
In this study, the HBO based MPP tracking is proposed for a global peak in the solar system. The HBO model is based on the foraging behaviour of Honeybadger that has digging and honey strategies. These phases are used to determine an optimal solution for GMPP tracking. The performance of the HBO strategy is validated in terms of power tracking efficiency and speed of convergence. The simulation result of the HBO method is compared with a conventional method such as P&O, WOA and FSSO through MATLAB software. As a result, it is attained that the HBO model provided a higher tracking efficiency than all prior methods. Also, the HBO based MPPT method has merits of higher tracking efficiency, average power and faster convergence than the prior methods respectively.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. T. Esram and P. L. Chapman, “Comparison of photovoltaic array maximum power point tracking techniques,” IEEE Transaction on Energy Conversion, vol. 22, no. 2, pp. 439–449, 2007. [Google Scholar]
2. L. Bouselham, B. Hajji and H. Hajji, “Comparative study of different mppt methods for photovoltaic system,” in 3rd Int. Renewable and Sustainable Energy Conf. (IRSEC), Marrakech, Morocco, pp. 1–5, 2015. [Google Scholar]
3. N. Femia, G. Petrone and G. Spagnuolo, “Optimization of perturb and observe maximum power point tracking method,” IEEE Trans. Aerospace Electro Systems, vol. 20, no. 4, pp. 963–973, 2005. [Google Scholar]
4. S. B. Kjaer, “Evaluation of the “hill-climbing” and the “incremental conductance” maximum power point trackers for photovoltaic power systems,” IEEE Transactions on Energy Conversion, vol. 27, no. 4, pp. 922–929, 2012. [Google Scholar]
5. A. Safari and S. Mekhilef, “Simulation and hardware implementation of incremental conductance MPPT with direct control method using Cuk converter,” IEEE Transaction on Industrial Electronics, vol. 58, no. 4, pp. 1154–1161, 2011. [Google Scholar]
6. Y. Liu, S. Huang and W. Liang, “A particle swarm optimization-based maximum power point tracking algorithm for PV systems operating under partially shaded conditions,” IEEE Transaction on Energy Conversion, vol. 27, no. 2, pp. 1027–1035, 2012. [Google Scholar]
7. K. Ishaque, Z. Salam and M. Amjad, “An improved particle swarm optimization (PSO)–based MPPT for PV with reduced steady-state oscillation,” IEEE Transactions on Power Electronics, vol. 27, no. 8, pp. 3627–3638, 2012. [Google Scholar]
8. K. Sundareswarm, P. Sankar and P. Nayak, “Enhanced energy output from a PV system under partial shaded conditions through artificial bee colony,” IEEE Transaction Sustainable Energy, vol. 5, no. 6, pp. 198–209, 2015. [Google Scholar]
9. M. Zhang, Z. Chen and L. Wei, “An immune firefly algorithm for tracking the maximum power point of PV array under partial shading conditions,” Energies, vol. 12, no. 6, pp. 3083–3090, 2019. [Google Scholar]
10. K. Kaced, C. Larbes and N. Ramzan, “Bat algorithm based maximum power point tracking for photovoltaic system under partial shading conditions,” Solar Energy, vol. 158, no. 45, pp. 590–503, 2017. [Google Scholar]
11. D. Suhardi, L. Syafaah and M. Irfan, “Improvement of maximum power point tracking (MPPT) efficiency using grey wolf optimization (GWO) algorithm in photovoltaic (PV) system. IOP Conference Series: Materials Science and Engineering, vol. 674, no. 1, pp. 12–38, 2019. [Google Scholar]
12. M. Lak, T. L. Wu and L. Lee, “A hybrid method for three-level t-type inverters to eliminate neutral point voltage ripple and control dc-link capacitors voltage for separate mppt,” IEEE Access, vol. 9, no. 5, pp. 148650–148664, 2021. [Google Scholar]
13. S. A. Ibrahim, A. Nasr and M. A. Enany, “Maximum power point tracking using anfis for a reconfigurable pv-based battery charger under non-uniform operating conditions,” IEEE Access, vol. 9, no. 6, pp. 114457–114467, 2021. [Google Scholar]
14. S. Figueiredo and R. Nayana, “Hybrid mppt technique pso-p&o applied to photovoltaic systems under uniform and partial shading conditions,” IEEE Latin America Transactions, vol. 19, no. 10, pp. 1610–1617, 2021. [Google Scholar]
15. P. Bharadwaj and V. John, “Optimized global maximum power point tracking of photovoltaic systems based on rectangular power comparison,” IEEE Access, vol. 9, no. 6, pp. 53602–53616, 2021. [Google Scholar]
16. I. Pervez, I. Shams and S. Mekhilef, “Most valuable player algorithm based maximum power point tracking for a partially shaded pv generation system,” IEEE Transactions on Sustainable Energy, vol. 12, no. 4, pp. 1876–1890, 2021. [Google Scholar]
17. M. N. Jamaludin, “An effective salp swarm based mppt for photovoltaic systems under dynamic and partial shading conditions,” IEEE Access, vol. 9, no. 3, pp. 34570–34589, 2021. [Google Scholar]
18. B. K. Karmakar and G. Karmakar, “A current supported pv array reconfiguration technique to mitigate partial shading, IEEE Transactions on Sustainable Energy, vol. 12, no. 2, pp. 1449–1460, 2021. [Google Scholar]
19. R. Motamarri and N. Bhookya, “Jaya algorithm based on lévy flight for global mppt under partial shading in photovoltaic system,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 9, no. 4, pp. 4979–4991, 2021. [Google Scholar]
20. I. Pervez, A. Pervez and A. Sarwar, “Rapid and robust adaptive jaya (ajaya) based maximum power point tracking of a pv-based generation system,” IEEE Access, vol. 9, no. 5, pp. 48679–48703, 2021. [Google Scholar]
21. S. Lyden, H. Galligan and M. E. Haque, “A hybrid simulated annealing and perturb and observe maximum power point tracking method,” IEEE Systems Journal, vol. 15, no. 3, pp. 4325–4333, 2021. [Google Scholar]
22. C. Pradhan, M. K. Senapati and S. G. Malla, “Coordinated power management and control of standalone pv-hybrid system with modified iwo-based mppt,” IEEE Systems Journal, vol. 15, no. 3, pp. 3585–3596, 2021. [Google Scholar]
23. H. Toodeji and S. Aghaei, “Domestic pv system with feedback linearization-based control strategy for module-level mppt under partial shading condition,” Journal of Modern Power Systems and Clean Energy, vol. 9, no. 6, pp. 1530–1539, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |