DOI:10.32604/iasc.2023.029299

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.029299 |  |
| Article |
Hybrid Optimization Based PID Controller Design for Unstable System
1Technical Expert, Geometric Limited, Chennai, 600096, Tamilnadu, India
2Arunachala College of Engineering for Women, Vellichanthai, 629203, Tamilnadu, India
3Trimble Information Technologies India Pvt. Ltd., Chennai, 600113, Tamilnadu, India
*Corresponding Author: Saranya Rajeshwaran. Email: srajeshwaran69@gmail.com
Received: 01 March 2022; Accepted: 01 April 2022
Abstract: PID controllers play an important function in determining tuning parameters in any process sector to deliver optimal and resilient performance for nonlinear, stable and unstable processes. The effectiveness of the presented hybrid metaheuristic algorithms for a class of time-delayed unstable systems is described in this study when applicable to the problems of PID controller and Smith PID controller. The Direct Multi Search (DMS) algorithm is utilised in this research to combine the local search ability of global heuristic algorithms to tune a PID controller for a time-delayed unstable process model. A Metaheuristics Algorithm such as, SA (Simulated Annealing), MBBO (Modified Biogeography Based Optimization), BBO (Biogeography Based Optimization), PBIL (Population Based Incremental Learning), ES (Evolution Strategy), StudGA (Stud Genetic Algorithms), PSO (Particle Swarm Optimization), StudGA (Stud Genetic Algorithms), ES (Evolution Strategy), PSO (Particle Swarm Optimization) and ACO (Ant Colony Optimization) are used to tune the PID controller and Smith predictor design. The effectiveness of the suggested algorithms DMS-SA, DMS-BBO, DMS-MBBO, DMS-PBIL, DMS-StudGA, DMS-ES, DMS-ACO, and DMS-PSO for a class of dead-time structures employing PID controller and Smith predictor design controllers is illustrated using unit step set point response. When compared to other optimizations, the suggested hybrid metaheuristics approach improves the time response analysis when extended to the problem of smith predictor and PID controller designed tuning.
Keywords: Direct multi search; simulated annealing; biogeography-based optimization; stud genetic algorithms; particle swarm optimization; SmithPID controller
Now with advancement of sophisticated industrial mechanisms arose the requirement to maintain them under certain operating circumstances. This was achieved by using a number of human operators until control theory was developed and computerized control methods were adopted. A notable illustration of this progression may be seen in the chemical sector, among others. Proportional-integral-derivative (PID) controllers, frequency domain control methods and root locus controller design are examples of such control methodologies [1]. There have been several tuning strategies proposed for PID controllers. Because the damping ratio in an under-damped unit with disruption is less than one, adjusting PID controllers for systems with under-damped responses is more difficult than tuning PID controllers for systems with over-damped responses.
PID controllers employ three distinct terminologies to describe gains: proportional, integral, and derivative. The proportionate gain is determined by the present error, the integral by previous mistakes, and the derivative by future errors. The total of those three components is then utilised to fine-tune the method. The fundamental benefit of PID controllers is that they may be used to almost any control system, even if the mathematical description of the structure is indefinite [2]. The PID controllers also enhance steady-state responses and transient. Identification of closed-loop systems has been a priority in industrial applications. The issue contains numerous options, as well as some misunderstandings, and a large range of treatments, several of which have been proposed recently. Closed-loop identification is required in these situations. A closed-loop control characterization of a transfer function model for an unstable system using either a pulse or step response of a PID controlled system could be established using an optimization technique.
Because of their simplicity of implementation, uniformity and operational simplicity, nature-inspired approaches are among the most resilient optimization strategies. Heuristic algorithms improve reaction time and capability of optimization. It may be used to generate traditional and enhanced structured controllers for a wide range of unsteady process models, regardless of model order. To improve performance, a hybrid approach combining two independent meta-heuristic algorithms can be developed, or the current algorithms can be improved by incorporating further modifications to the existing characteristics. Among researchers, heuristic algorithms are the most favoured way of controller design, followed by older approaches such as Cohen & Coon, Zeigler & Nichols and other tuning methods [3]. This is due to the fact that heuristic algorithms do not need any complex computations or modelling. It also delivers a rapid and optimum answer.
The paper is divided into sections that are well-organized. The Section 2 contains the related works. The PID controller and the Smith Predictor are discussed in Section 3. Section 4 gives a brief description of the Hybrid Metaheuristics optimization. Section 5 discusses the unstable process, including a comparison of the global optimization, local search algorithm and metaheuristic technique. Section 6 has the conclusion.
PID controller tuning is still a difficult and widely pursued issue. PID controllers’ efficacy and simplicity have demonstrated its applicability to over 95% digital controllers. As a result, the current research trend is to move away from gradient-based methods and toward the derivative-free methods. Some heuristic methods to include for derivative-free algorithms are SA, PSO, ACO, PBIL, StudGA and ES [4]. An analytical technique for building robust PID controllers for time delay procedures with the greatest sensitivity criterion is presented in the works [5]. The optimization approaches accommodate neural, fuzzy and various optimization algorithms in particular Ant Colony optimization(ACO), Particle swarm Optimization (PSO), Firefly Algorithm (FA) and so on. A new reformed and reoriented FAPSO PAB algorithm grounded on FA with position aided brightness and PSO is proposed. The study has been conducted on various stable and unstable transfer function models. The results are set side by side with FA and PSO. The proposed approach gives better out-turns than the other algorithms. The optimized results are obtained within fewer iterations and lesser errors in the case of FAPSO-PAB [6]. To build Smith predictors controllers and PID controllers, the StudG-Aalgorithm is used as a meta-heuristic strategy, while local search methods include implicit filtering (IMF), simple derivative with pattern search (SDPS) and derivative free search methods. By upgrading the StudGA with search acceleration and executing a simplex derivative pattern search on StudGA’s best solutions, the simplex derivative pattern search guided StudGA (DFSG-StudGA1) technique is created [7].
The standard SA algorithm, as well as several refined variations of SA optimization is used to create proportional-integral-derivative controller. The local search methods and direct search methods are hybridized in the way of improvement. The simplex simulated annealing (SSA) method is made by joining the simple direct search (SDS) standard simulated annealing (SA) with local search method, which has a faster convergence rate [8]. Finally, by substituting the SSA with an accelerated conditioning schedule in SSA and applying Kelley’s version of the Nelder–Mead method to the effective solutions, the direct search simulated annealing (DSSA) methodology is attained. The DSSA algorithm has been shown to be extremely dependable and efficient. Power system stabilizers for multi-machine power systems are made with PHIL (PSSs). The study examines four case studies, each of which has a unique learning rate pattern [9]. Some of the alternatives are fixed LR and simply adaptive LR [10]. A lower learning rate is proven to lead to greater algorithm exploration, resulting in more population variability at the tradeoff of slower convergence. A faster learning rate on either side in the case of fixed LR indicates more algorithm exploitation which lead to premature convergence. As the result, determining the LR necessitates a compromise between exploitation and exploration [11]. The improved approaches combined a metaheuristic method called the ACO in conjunction with derivative-free local search approaches such as Implicit Filtering and simple derivative-based pattern search.
The resultant hybrid ACO has the advantage of being able to tackle unconstrained nonlinear optimization problems and being able to be extended [12,13] to restricted optimization however, it does necessitate the provision of the constraint functions’ first order derivatives at the outset. The methodology utilizes previous objective function evaluations to determine simplex gradients or simplex Hessian techniques, which are then utilised to rearrange poll directions based on the distances they cover with the negative simplex gradient in the poll phase. To achieve the best results, the hybrid algorithm (FAPSO) was modified using a position-aided technique. That is, the brightness factor of FA firefly in FAPSO has been raised by adding the actual state of the swarms in the PSO Optimization algorithms [14–18]. As a result, FAPSO-PAB, which stands for “Position Aided Brightness,” has been given to the improved algorithm.
We apply SSA to accelerate the cooling schedule, then Kelley’s adaptation of the Nelder-Mead approach to the best solutions uncovered using the accelerated SSA method to enhance the final output and the DSA is the last method (DSSA). Extensive numerical tests on familiar operations are used to evaluate the performance of SSA & DSSA. When SSA and DSSA are compared to the performance of other meta-heuristics they are promising in actuality. To solve challenges, certain control mechanisms are presented in the section; the constraints identified in the earlier studies prompted us to perform this investigation.
PID controllers’ popularity and widespread use can be linked to its ease of use and performance features. It is used to control a variety of dynamical systems, such as industrial processes, aviation, and ship dynamics. If there is a significant disparity between the actual and desired values of the controlled variable, the gain amplifies the error, resulting in a big correction that quickly returns the output of the system to its intended destination. To avoid excessive oscillations and a substantial overshoot in the response, the gain is automatically lowered as the error decreases. . The system’s closed loop response may be effectively handled by reducing the function of error and employing proper PID controller gain parameters, specifically [KP, KI, KD]. The following Fig. 1 represents the PID controller’s structure.

Figure 1: Structure of PID controllers
The construction of the PID controller is stated as
where,
The cost function for the PID controller’s unconstrained optimization is the ISE index, as given as,
where, J is a search space valued function and S ⊂ Rn represent a cost function to reduce the ISE
3.1 Smith PID Controller Design
A dead time system tuning method is a Smith Predictor structure. A system model without dead time/fast model (Gn(s)) is used to construct the prediction at time t, and the difference between the process output is calculated and the model of the dead time is G(s) = Gn(s)(s). e-ds(s) are transmitted back and used to rectify the modelling faults as indicated in Fig. 2.

Figure 2: Smith predictor scheme
For slow variations in disturbance, k(t) ≈ k(t + d), yp(t) is a best forecast of
• Smith predictor has the following merits and disadvantages:
• A nominal set-point response is no longer affected by the dead-time effect.
• By fine-tuning the principal controller, you can get a superior achievement ratio.
• The disturbance rejection response in an open loop cannot be faster than the disturbance rejection response in a closed loop. When there isn’t a lot of dead time, this can be really useful.
4 Multi-Objective Hybrid Algorithm
When dealing with unconstraint in derivative-free optimization, an extreme barrier technique is commonly used. We can make it work by setting an extreme barrier function to MOO.
To solve the models, we propose the DMS-SA, DMS-BBO, DMS-MBBO, DMS-PBIL, DMS-StudGA, DMS-ES, DMS-ACO, and DMS-PSO hybrid multi-objective optimization methods. DMS may update solutions during the poll phase of the optimization procedure by doing a local search around nondominated solutions, and metaheuristic algorithms like SA, BBO, MBBO, PBIL, StudGA, ES, ACO, and PSO have competent global search performance.
The nondominated solutions are stored in the set NS, which is formed by connecting the SA, BBO, MBBO, PBIL, StudGA, ES, ACO, PSO, and DMS processes. In this study, the maximum size of NS is equal to the size of the population Np. When the number of non-dominated solutions in a generation exceeds the size of an NS, the sorting algorithm retains just the top Np solutions generated. NS can be updated by the SA, BBO, MBBO, PBIL, StudGA, ES, ACO, PSO, and DMS processes. The DMS method focuses exclusively on looking for new solutions via NS (Spoll). The sorting pool R is created by integrating hybrid metaheuristics or the DMS process (Spoll) with NS to create innovative solutions. After that, the R solutions are sorted by their objective values. By changing the solutions in NS with a non-dominated solutions in R, we can bring NS updated and relevant. The DMS-derived metaheuristics for SA, BBO, PBIL, StudGA, ES, PSO, and ACO are discussed in pseudo code.
Initialization: Set the list of a non-dominated points Ns and corresponding to the population size parameters of hybrid heuristics is Np.
Choosing an Iterate Point: Select (xq; αq) ∈ Lq
Search step: Calculate a finite number of points, Ladd = {(Zs; αq)}s ∈ S
To remove dominant points from Lq∪Ladd, Call Lfil = filter (Lq,Ladd). Reject the filtered list at any new non-dominated points that have not enhanced at the least one component of the objective function of points in Lq. To determine Ltri⊆Lfil, Call Ltri = select (Lfil). Set Lq+1 = Ltri and bounce the poll step if Ltri ≠ Lq declares the iteration successful.
Poll step: Pick a positive spanning set Dq from the set D.
Calculate FΩ at the set of poll points Pq = (xq + αqd∶d ∈Dq). Set Ladd = {(xq + αqd; αq), d ∈Dq}. Call Lfil = filter (Lq;Ladd) to remove dominated points from Lq∪Ladd. Remove any new nondominated points from the sorted list that have not enhanced at least one component of the objective function of points in Lq. To determine Ltri⊆Lfil, Call Ltri = select (Lfil). Declare the iteration successful if Ltri ≠ Lq and set Lk+1 = Ltrial.
Step size parameter update: If the previous iteration was successful, keep or raise the associated step size parameters: αq,new∈ (αq; γαq) and change all the new points (xq + αqd; αq) in Lq+1 by (xq + αqd; αq,new) when success comes from the poll step or (zs;αq,new) in Lq+1 by (zs;αq,new) by (zs;αq,new), when success comes from a search step.
Unstable Process Control with Time Delay: Chemical reactors and sophisticated systems are extremely volatile. Several scholars have offered approaches for adjusting time-delayed unstable systems. Take the open loop system shown the initial tunings supplied by Syrcos and Kookos given as,
In Fig. 3, the set NS, which stores the nondominated solutions, is created as the connection between the metaheuristics process and the DMS process. In this paper, we set the maximum size of NS equal to the population size Np. If the number of nondominated solutions at a generation exceeds the size of NS, only the first Np solutions obtained from the sorting method are retained. Both the metaheuristics and the DMS process can update NS. At each generation, the metaheuristics process evolves new solutions (Lq) based on the population (Pq), whereas the DMS process focuses only on searching around NS to generate new solutions (Spoll). The new solutions evolved by the metaheuristics (Lq) or the DMS process (Spoll) are combined with NS to form the sorting pool R. The solutions in R are then sorted according to their objective values. We can update NS by replacing the solutions in it with the nondominated solutions in R.

Figure 3: Flowchart of hybrid metaheuristics algorithm
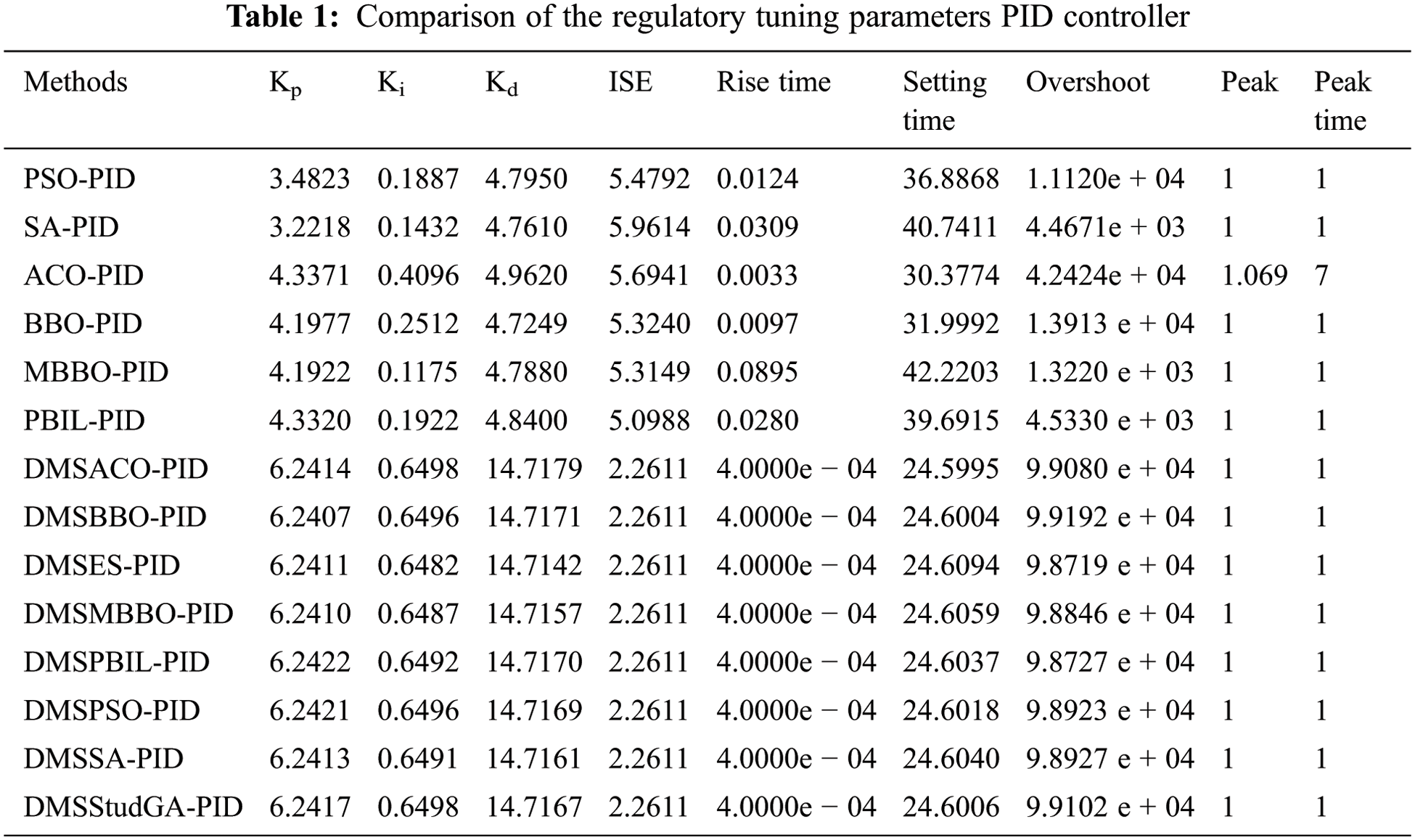
This part shows the outcomes of the experiments. The suggested work is implemented with MATLAB software, and the results are shown in tabular columns. Fig. 4 depicts the performance of a metaheuristic methods-based PID controller in controlling the regulatory output response of an unstable process in a time delay. The results demonstrate that global metaheuristic approaches fail to provide lower overshoot and DMS, however the hybrid DMS-Heuristic algorithm performs better with lower overshoot than all global approaches. Hence for easy considerate, the tabulations consistent to DMS-SA, DMS-ACO, DMS-BBO, DMS-ES, DMS-MBBO, DMS-PBIL, DMS-PSO, and DMS-StudG are referred in Tab. 1.

Figure 4: Performance analysis of regulatory output response employing a PID controller based on metaheuristic techniques
5.1 Regulatory and Servo Characteristics with PID and Smith PID Controller
5.2 Comparisons of PID Controllers
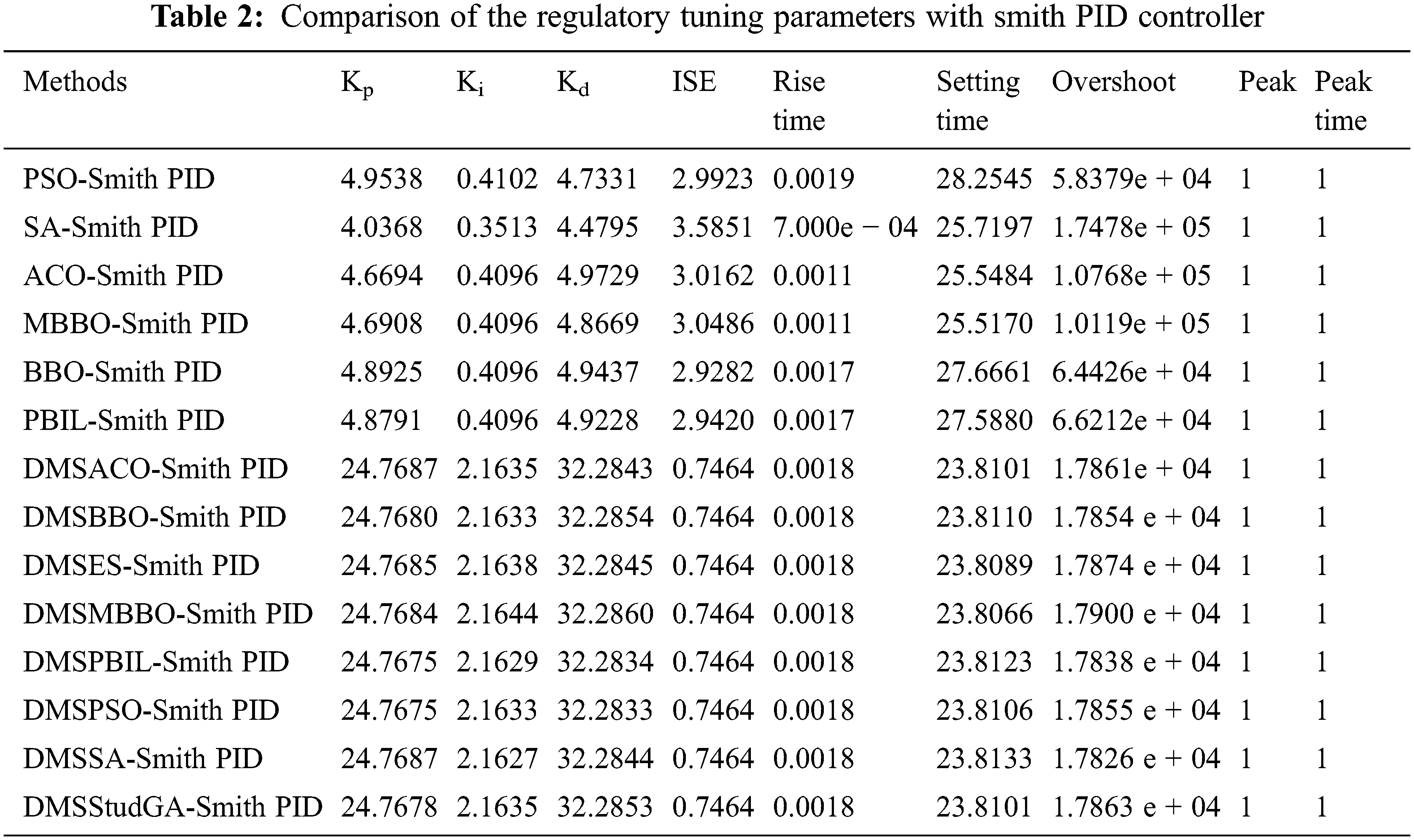
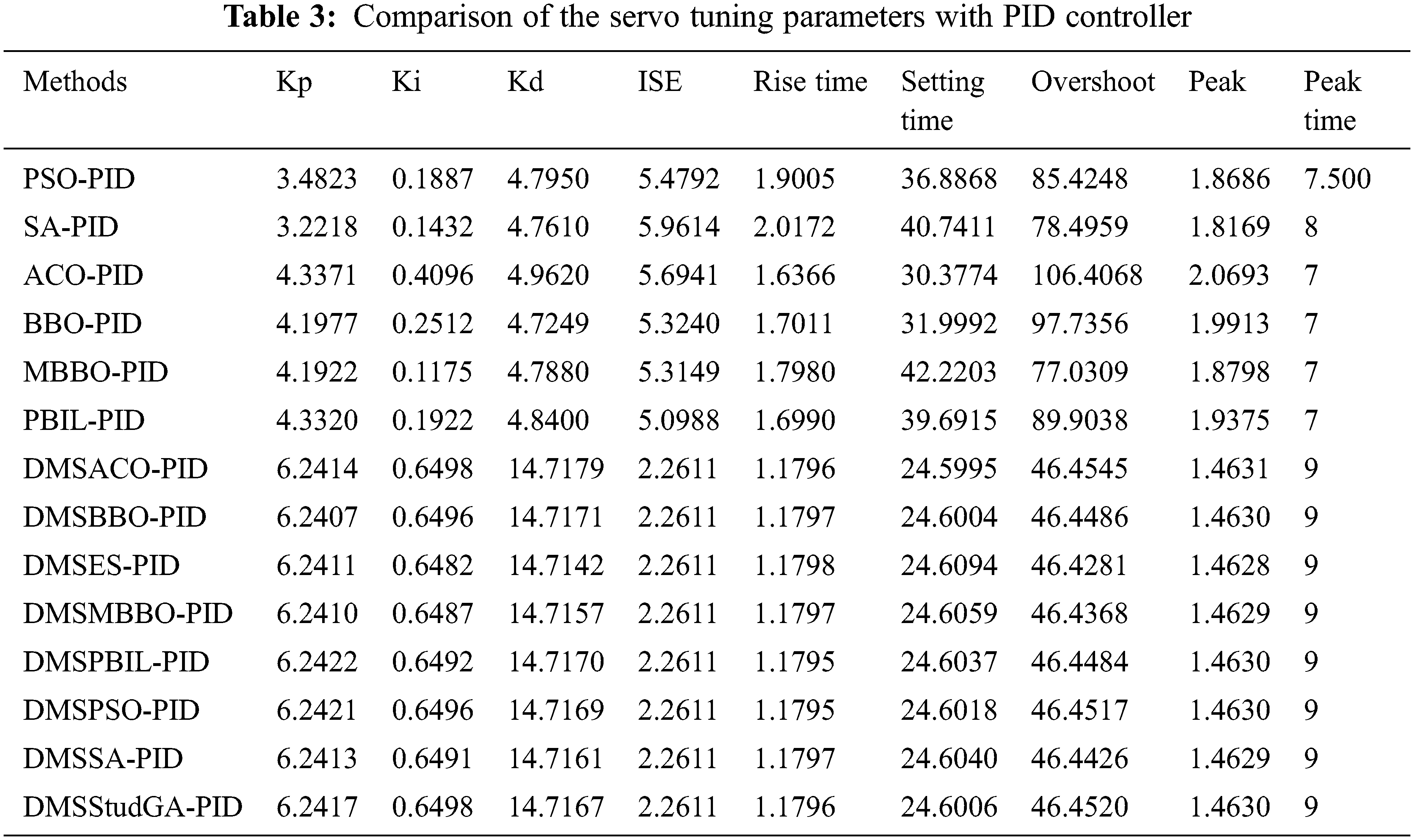
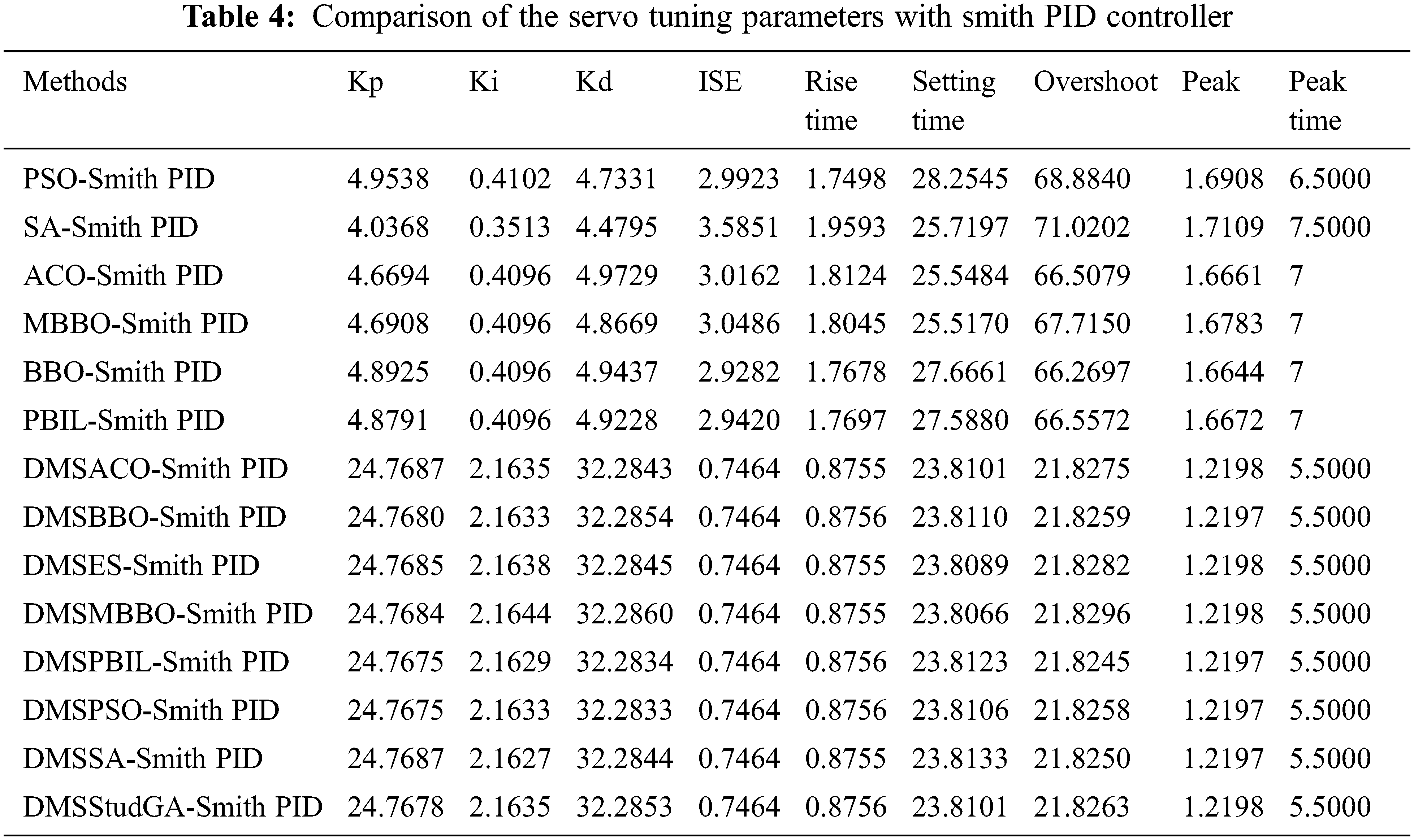
The Hybrid Heuristic algorithm exceeds all other global techniques in terms of overshoot. It is also clear that by lowering overshoot, the Smith predictor attempts to eliminate the effect of delay. Fig. 5 depicts the performance of metaheuristic approaches-based smith PID controllers in regulating the output response of an unstable process with a time delay. Fig. 6 depicts the performance of a metaheuristic methods-based PID controller in controlling the servo output respond of a time delayed unstable process. Fig. 7 shows the performance of servo output response of time delayed unstable process using metaheuristic methods-based smith PID controller. The results demonstrate that DMS based heuristic techniques do not convergence for Proportional-integral-derivative schemes, but a hybrid-heuristic system does for Smith PID and PID control systems. They also show that global approaches overreach, whereas the Smith PID controller based on a hybrid-Heuristic has less overshoot and a faster response time. Tab. 1 shows the time response characteristics and ISE values of hybrid metaheuristics.

Figure 5: Performance analysis of regulatory output response employing a smith PID controller based on metaheuristic techniques

Figure 6: Performance evaluation of servo output response employing a PID controller based on metaheuristic approaches

Figure 7: Performance evaluation of servo output response employing a smith PID controller based on metaheuristic approaches
The tuning parameters obtained by combining PID controller and Smith PID controllers were compared to those obtained by other methods as shown in Tabs. 1–4. The simulation results show that the hybrid metaheuristics-basedSmith PID controllers and PID controllers schemes produce low ISE values than the other techniques. The Hybrid metaheuristic algorithm outperforms all previous global heuristic algorithms. The performance of hybrid heuristics approaches, such as DMS-SA, DMS-ACO, DMS-BBO, DMS-ES, DMS-MBBO, DMS-PBIL, DMS-PSO, and DMS-StudG, is superior than that of other global heuristics, as shown by the ISE and other time response characteristics. When the local search technique DMS is used individually, it achieves the same results as when it is combined with Hybrid Heuristic, demonstrating the method’s effectiveness.
The Smith PID and Proportional integral derivative controller methods for a class of time delay systems are constructed by using the hybrid metaheuristics in this paper. When combined with global search algorithms such as SA, BBO, MBBO, PBIL, StudGA, ES, ACO, and PSO, DMS methods can produce the best optimal solution in the case of unstable processes. To examine the performance of several global metaheuristic techniques and hybrid metaheuristics, DMS-SA, DMS-BBO, DMS-MBBO, DMS-PBIL, DMS-StudGA, DMS-ES, DMS-ACO, and DMS-PSO are utilised. The results suggest that employing hybrid Heuristic approaches, the PID/Smith PID increases the time response analysis. Increased metaheuristic-based controller systems perform better with the time response qualities associated with servo and regulatory response of the system.
Acknowledgement: The authors with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. G. Kanthaswamy and J. Jerome, “Control of dead-time systems using derivative free local search guided population based incremental learning algorithms,” Optimization and Engineering, vol. 15, no. 2, pp. 331–354, 2014. [Google Scholar]
2. G. Kanthaswamy and J. Jerome, “Design of PID controllers for dead-time systems using simulated annealing algorithms,” International Journal of Automation and Control, vol. 4, no. 4, pp. 380–397, 2010. [Google Scholar]
3. C. A. Kumar, S. Rajeshwaran and G. Kanthaswamy, “Robust proportional integral derivative controller design for various processes using novel hybrid metaheuristic algorithms,” Journal of Dynamic Systems, Measurement, and Control, vol. 140, no. 8, pp. 1–36, 2018. [Google Scholar]
4. G. Kanthaswamy, C. A. Kumar and J. Jerome, “Optimal tuning of PID controllers for dead-time systems using stud genetic algorithms,” Journal of Vibration and Control, vol. 22, no. 10, pp. 2503–2518, 2016. [Google Scholar]
5. G. Kanthaswamy and J. Jovitha, “Control of dead-time systems using hybrid ant colony optimization,” Applied Artificial Intelligence, vol. 25, no. 7, pp. 609–634, 2011. [Google Scholar]
6. S. Meena, R. Navitha and I. Kavipriya, “Controller design using hybrid firefly and particle swarm optimization algorithm,” in Proc. 2020 Fourth Int. Conf. on Inventive Systems and Control (ICISC), Coimbatore, India, pp. 51–56, 2020. [Google Scholar]
7. F. Folly, A. Komla and K. G. Venayagamoorthy, “Effects of learning rate on the performance of the population based incremental learning algorithm,” in Proc. 2009 Int. Joint Conf. on Neural Networks, Atlanta, GA, USA, pp. 861–868, 2009. [Google Scholar]
8. H. A. Rahman and M. Fukushima, “Hybrid simulated annealing and direct search method for nonlinear unconstrained global optimization,” Optimization Methods and Software, vol. 17, no. 5, pp. 891–912, 2002. [Google Scholar]
9. L. R. D. Silva, R. C. C. Flesch and J. E. Normey-Rico, “Controlling industrial dead-time systems: When to use a PID or an advanced controller,” ISA Transactions, vol. 99, pp. 339–350, 2020. [Google Scholar]
10. I. K. Kookos and G. Syrcos, “PID controller tuning using mathematical programming,” Chemical Engineering and Processing, vol. 44, pp. 41–49, 2005. [Google Scholar]
11. R. Dhaya, R. Kanthavel, and A. Ahilan, “Developing an energy-efficient ubiquitous agriculture mobile sensor network-based threshold built-in MAC routing protocol (TBMP),” Soft Computing, vol. 25, no. 18, pp. 12333–12342, 2021. [Google Scholar]
12. J. J. Grefenstette, “Genetic algorithms for changing environments,” in Proc. of the Second Conf. on Parallel Problem Solving from Nature, Brussels, Belgium, Elsevier, pp. 137–144, 1992. [Google Scholar]
13. D. Yuan and Q. Chen, “Particle swarm optimization algorithm with forgetting character,” International Journal of Bio-Inspired Computation, vol. 2, no. 1, pp. 59–64, 2010. [Google Scholar]
14. W. Gong, Z. Cai, X. Charles and C. X. Ling, “DE/BBO: A hybrid differential evolution with biogeography-based optimization for global numerical optimization,” Soft Computing, vol. 15, no. 4, pp. 645–665, 2011. [Google Scholar]
15. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. Int. Conf. on Neural Net-Works, Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]
16. K. M. Elbayomy, J. Zongxia and Z. Huaqing, “PID controller optimization by GA and its performances on the electro-hydraulic servo control system,” Chinese Journal of Aeronautics, vol. 21, no. 4, pp. 378–384, 2008. [Google Scholar]
17. J. G. Ziegler and N. B. Nichols, “Optimum settings for automatic controllers,” Transactions of the A.S.M.E, vol. 64, no. 11, pp. 759–765, 1942. [Google Scholar]
18. M. A. Lones, “Metaheuristics in nature-inspired algorithms,” in Proc. Companion Publication of the 2014 Annual Conf. on Genetic and Evolutionary Computation, BC, Vancouver, Canada, pp. 1419–1422, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |