Journal of Renewable Materials

DOI: 10.32604/jrm.2021.016013

ARTICLE

Mechanical Properties and Constitutive Relationship of the High-Durable Parallel Strand Bamboo

Yousef Y. Sewar1, Zhancheng Zhang1, Xinmiao Meng1,*, Mohammed Y. Wahan1, Hanxiao Qi1,2, Qahtan M. Al-Shami1,3 and Shijiao Luo1

1Department of Civil Engineering, Beijing Forestry University, Beijing, 100083, China
2Department of Architecture and the Built Environment, Lund University, Lund, 22100, Sweden
3Civil Engineering Department, Amran University, Amran, Yemen
*Corresponding Author: Xinmiao Meng. Email: mengxinmiao@bjfu.edu.cn
Received: 31 January 2021; Accepted: 04 March 2021

1  Introduction

Bamboo is usually regarded as a commercial constructional material in China, Ethiopia, etc. [1,2]. Civil engineers have extended the practical application of bamboo to beams, rafters and columns [3–5]. In China, moso bamboo (Phyllostachys Pubescens) is the most popular bamboo species used in the production of engineered bamboo, while Guadua Angustifolia is widely used in South America [4]. Moso bamboo is characterized for its comparable strength and is a sustainable alternative to steel, concrete and timber [3–7]. Original bamboo, as a traditional application of building material, has been used to build green and ecological fabricated buildings and structures for a long time [8,9]. Nonetheless, the original raw bamboo suffers easy cracking and susceptibility to corrosion, so different processing method has been developed and studied such as sprayed motar-bamboo composite elements [10,11] and round bamboo culms reinforced with fiber reinforced polymer sheet or steel hose clamp [12–15]. Engineered bamboo is an alternative method fully utilizing the advantages of raw bamboo but overcoming most of its disadvantages [16]. Nowadays, many researchers are exploring engineered bamboo such as parallel strand bamboo, laminated bamboo lumber and Glubam etc. as a considerable building composite [16–19]. The mechanical performance was a significant aspect for the application of engineered bamboo, and it is also an urgent need to address the structural performance of different engineered bamboo products.

Parallel strand bamboo (PSB), also usually named as bamboo scrimber, is an important product of the engineered bamboo, and its mechanical properties including strengths and elastic modulus were tested and reported by researchers. The density was a key factor influencing its mechanical properties. Kumar A et al. [20] investigated the mechanical properties of bamboo scrimber and found that the highest modulus and strength properties, when the density is 1.2 g/cm3. Wei et al. [21] demonstrated that the increase of density was positively related to the increase of the stiffness and strength of bamboo scrimber. The bending strength with density of 0.8 g/cm3 was 120 MPa, much larger than wood-based panels [22,23]. Different processing approaches were explored through mechanical tests [24]. Li et al. [25,26] studied the effect of hot-pressing technique on the mechanical performance of bamboo scrimber and proposed stress-strain relationship models which exhibited good agreement with the experimental results. Lou et al. [27] studied mechanical properties of crack-free flattened bamboo board with bending strength high up to 101.5 MPa. Huang et al. [28,29] examined the mechanical properties of PSB and found that its strength was larger than the common timber. The stress-strain relationship with different parameters was also suggested including linear model for the tension parallel to grain and quadratic polynomial model for the elastic-plastic segment of compression parallel to grain [29]. Except for the investigation of material properties [30,31], the full size structural elements was studied and elastic eigenvalue analysis was conducted to predict the critical buckling load of long PSB columns [32,33]. The fracture analysis and size effect were also addressed to provide design reference [34,35]. The bamboo nodes was generally an imperfection for PSB material. Qi et al. [36] studied the effect of nodes on mechanical properties of bamboo fibers reinforced composite. The removal of nodes from fiber mats improved most strengths except the shear strength parallel to grain. Shangguan et al. [37] reported that bamboo scrimber achieved the best mechanical properties when the bundles of fiber were neatly fractured in the study. Despite the increased extensive research on the behavior of the engineered bamboo composite, the use of it was limited to architectural and surface purposes [38]. Nonetheless, the aforementioned studies of PSB have shown its potential application to the structural usage.

Heat treatment is a common production process for PSB material to improve its resistance to the decay [37,39,40]. The manufacturing technology has been explored and studied through physical and mechanical tests [38]. Sharma et al. [16] and Jung et al. [40] demonstrated that the temperature of thermal treatment positively increased the compression strength, bending stiffness, and the inner bond strength. Nonetheless, the heat-treated specimens experienced gradual brittle failure with the increase in temperature. Li et al. [41] studied the effect of three different treatments on the color, dimensional stability and cracking behavior of bamboo scrimber. The results showed that the color of bamboo scrimber got darker after subjecting it to all treatment conditions. Therefore, a reasonable temperature is worth being explored to keep balance between the mechanical property and the desired appearance.

The present work investigated a high-durable parallel strand bamboo (HPSB) with relative high hot-pressing temperature (140oC) to achieve full potential of engineered bamboo as a sustainable building material. The basic mechanical tests including tension, compression, shear and bending tests were conducted to evaluate its mechanical performance and make a comparison with other green building materials. Two constitutive models were proposed to describe the stress-strain relationship parallel to grain. The finite element analysis of the bending test was then conducted to assess the proposed relationship model with the software ANSYS.

2  Material and Methods

2.1 Material

The HPSB was manufactured from moso bamboo with hot-pressing process. The phenol formaldehyde resin was used to glue fiber strands together. The hot-pressing temperature was 140°C, and the pressure was 7–8 MPa. The main manufacturing procedures of HPSB material is shown in Fig. 1. The general hot-pressing temperature was between the popular 120°C and 160°C, the color gets darker while increasing the corrosion resistance. The volume faction of resin was about 15%, and the average moisture content was 6.99%. It should be noted that the measurement of moisture content took more than 24 h due to the existence of resin.

Figure 1: The schematic of manufacturing procedure of HPSB material

2.2 Specimens

In this work, a total of 105 specimens were divided into seven groups, as shown in Tab. 1. Each group contains 15 specimens. The schematic of specimens is shown in Fig. 2. The specimens were prepared through computer numerical control (CNC) machining to guarantee the precision. All specimens were placed in an environment with temperature of 20°C and relative humidity of 65% for two weeks before testing. After tests, the moisture content was immediately determined using a part of each specimen.

Figure 2: The schematic of HPSB specimens (unit: mm). (a) Tension, (b) compression, (c) shear, (d) bending

2.3 Experimental Setup and Instrumentation

The fundamental mechanical tests of tension, shear, compression and bending were carried out with respect to the corresponding standards to investigate the structural performance of HPSB as listed in Tab. 1. The standards for timber and composite materials were chosen due to the lack of specification for parallel strand bamboo. The test standards included BS 373 Methods of Testing Small Clear Specimens of Timber [42], ASTM D143 Standard Test Methods for Small Clear Specimens of Timber [43], ASTM D7078/D7078M Standard Test Method for Shear Properties of Composite Materials by V-notched Rail Shear Method [44], and GB/T 17657-2013 Test Methods of Evaluating the Properties of Wood-based Panels and Surface Decorated Wood-based Panels [45]. The monotonic loading was conducted through a WDW-100E testing machine with the maximum load of 100 kN. The displacement was measured using the linear variable displacement transducer (LVDT) and the strain was measured using strain gauges. The loading rates, referring to corresponding standards, are listed in Tab. 1. The experimental setup and instrumentation are shown in Fig. 3.

Figure 3: The test setup. (a) Tension parallel to the grain, (b) tension perpendicular to the grain, (c) compression, (d) bending, (e) shear

3  Experimental Results

3.1 Tension Parallel to Grain

The specimens were prepared as shown in Fig. 2a. Two strain gauges were adhered on both surfaces at the center of each specimen. The specimens were subjected to continuous tensile load at a rate of 1mm/min.

The schematic and photographic representation of failure modes are shown in Fig. 4a. There were two types of failure modes. The failure mode I was a rupture at the center of the specimen, and failure mode II had a diagonal fracture surface deviating from the center. The failure surface was rough and mainly perpendicular to the loading direction with respect to failure mode I occurring to 11 of 15 specimens. Similar behavior has been observed for other parallel strand bamboo materials. Although no crack was observed, a low cracking noise was heard when the load reached 70%–80% of the maximum load. The specimens suddenly fractured when the load reached the maximum value.

The load-displacement curves are demonstrated in Fig. 4b. The curves behaved almost elastically up to the maximum load. The stiffness showed a little reduction when the load reached approximately 30% of the maximum load. When the maximum load was reached, the load-carrying capacity of the specimen sharply reduced due to the fracture of bamboo fiber.

The average values for tensile strength and elastic modulus parallel to grain for HPSB were 120.7 MPa and 14.3 GPa, respectively. The experimental results showed that the tensile strength parallel to grain was mainly carried by fibers. In addition, the discreteness of values was small with coefficient of variation less than 10%.

Figure 4: Tension parallel to grain. (a) Typical failure modes, (b) load-displacement curves

3.2 Tension Perpendicular to Grain

The test of tension perpendicular to grain required special clamp as shown in Fig. 2b, and more specimens were prepared by CNC machining due to the lower precision of complex shape. The strain gauge was pasted at the critical section to measure the strain.

The typical failure modes under tensile loading perpendicular to grain can be seen in Fig. 5a. Two failure modes were observed in the tests. A total nine specimens failed at the critical section as shown in failure mode I, and the rest showed failure mode II and failed close to the critical section. The failure surface was rough and parallel to grain with no fracture of bamboo fiber. Therefore, the tensile strength perpendicular depended on the strength of resin. The load-displacement curve is shown in Fig. 5b. It was demonstrated that the specimens had linear-elastic behavior until brittle failure. Nonetheless, the specimens showed large variety in slope, leading to a large coefficient of variation of 34% for the elastic modulus. When the load reached more than 85%, a small crack could be seen accompanied with a low sound.

The mean values for tensile strength and elastic modulus of specimens under tensile perpendicular to grain are 7.7 MPa and 4.2 GPa, in which the elastic modulus of specimens were determined by the segment from 10% to 40% of maximum load. It was deduced that the large coefficient of variation resulted from the failure dominated by the relatively weak resin and the eccentric loading which attributed to complex shape of specimens.

Figure 5: Tension perpendicular to grain. (a) Typical failure modes, (b) load-displacement curve

3.3 Compression Parallel to Grain

Fifteen specimens were geometrically configured and axially loaded as shown in Fig. 2b. Two strain gauges were used to measure the corresponding strain.

Two failure modes were observed during the tests due to the microbuckling and kinking of bamboo fibers as shown in Fig. 6a. The microbukling is the buckling of fibers embedded in matrix foundation, while kinking is a highly localised fiber buckling [46]. Failure mode I had a kinking band close to one end of the specimen. However, failure mode II was kinking accompanied by splitting parallel to grain. The shape of cracking was like “Y” that splitting from the top end to the middle height and then developing to two diagonal cracks. The failure mode I was the main failure mode containing ten specimens.

The load-displacement curve of specimens is presented in Fig. 6b. The curve could be described using three stages that were elastic stage, elastic-plastic stage, and strength plateau stage. The elastic-plastic stage started from approximately 60% of the maximum load due to the developing of micro buckling of the bamboo fibers. When the load reached the maximum value, the load-carrying capacity of specimens became stable for a long time with obvious strength plateau. Therefore, it was notably demonstrated that the HPSB material under compression parallel to grain had great ductility.

The mean values for strength and elastic modulus for the specimens under compression perpendicular to grain are 121.0 MPa and 13.8 GPa, respectively. The strength was larger than other parallel strand bamboo materials mainly due to a better bonding interface to prevent the micro buckling of bamboo fibers.

Figure 6: Compression parallel to grain. (a) Typical failure modes, (b) load-displacement curve

3.4 Compression Perpendicular to Grain

The specimens and experimental setup perpendicular to grain were the same to those of compression parallel to grain. Two failure modes were shown in Fig. 7a. Most of specimens, 13 of 15 specimens, showed failure mode I. In this failure mode, a diagonal shear crack was observed for the specimens. The shear crack was often close to the end of the specimen. For failure mode II, the shear crack and the local crush of resin were blended. Regardless of the failure mode, the damage of specimens under compression perpendicular to grain existed only in the matrix.

The load-displacement relationships, as shown in Fig. 7b, were linear at the beginning. With the load increase to about the 65% of the maximum load, the stiffness of the column slightly decreased as the resin developed into plastic behavior. The elastic-plastic segment in the load-displacement relationship provided post-yield stiffness and more safety margin. It was seen that the load rapidly dropped once the shear cracking failure occurred and developed.

The mean values for strength and elastic modulus for the specimens under compression perpendicular to grain are 60.5 MPa and 4.0 GPa. The compressive strength perpendicular to grain was half of that parallel to grain, making it possible to carry the load directly perpendicular to grain.

Figure 7: Compression test perpendicular to grain. (a) Typical failure modes, (b) load-displacement curve

3.5 Shear Parallel to Grain

The parallel strand bamboo can be considered as composite material. The shear test method suggested by composite material standards is alternative except for timber standards. Fifteen V-notch specimens were prepared. A shear strain gauge was adhered in the center of the specimen to measure the shear strain.

The V-notch specimen was supposed to fail at the critical section. Nonetheless, two failure modes were actually observed during the tests as shown in Fig. 8a. The failure mode I was the expected failure for specimens. The crack parallel to grain was located at the center of the specimen. A total eleven specimens exhibited failure mode I. The rest of specimens had failure mode II due to the initial imperfection in the material. Both failure modes showed the brittle behavior once the crack occurred. Linear load-displacement relationships are shown in Fig. 8b. No visible damage was observed at the beginning of the tests. The damage firstly appeared as a fine crack in the V-notch or close to it along grain direction. After that, the cracks gradually expanded along the grain direction with the increase of load. The load had a sharp drop when the specimen was torn into two pieces.

Figure 8: Shear test parallel to grain. (a) Typical failure modes, (b) load-displacement curve

The mean values for shear strength and elastic modulus parallel to grain for the specimens are 24.0 MPa and 1.9 GPa, respectively. Therefore, the shear strength was large enough to avoid shear failure in the practice.

3.6 Shear Perpendicular to Grain

The shear test perpendicular to grain was not often required by the timber due to its much lower shear strength parallel to grain. However, the shear strength parallel to grain of HPSB material was very large, making it comparable to the shear strength perpendicular to grain. Thus, fifteen specimens were still prepared to obtain the shear strength perpendicular to grain.

Only one failure mode was observed during the tests as shown in Fig. 9a. No vertical cracks went through the V-notch section as expected. The horizontal cracks appeared adjacent to notches and developed along the fiber direction to the clamped zone. Then, the fiber in the clamped zone fractured. The load-displacement curves are shown in Fig. 9b. It was demonstrated that HPSB material behaved linearly at the beginning, and then behaved nonlinearly until the fracture failure of bamboo fiber in the fixed zone. The load-carrying capacity had a fluctuation due to the gradually splitting along fibers and local fracture of fibers. The tests were ended when the load had a sudden drop.

The mean values for shear strength and elastic modulus perpendicular to grain for specimens are 37.1 MPa and 2.1 GPa, respectively. The shear strength perpendicular to grain was just 1.55 times than that parallel to grain, so it was necessary to consider the shear failure perpendicular to grain when conducting stress analysis.

Figure 9: Shear perpendicular to grain test. (a) Typical failure mode, (b) load-displacement curve

3.7 Bending Test

The failure modes of four-point bending specimens are shown in Fig. 10a. Twelve specimens behaved as failure mode I. The fiber in the bottom surface fractured in the pure bending region between two loading rollers. Nonetheless, the failure mode II failed first under the loading roller and then developed to the pure bending region. For both failure modes, initially, no visible damage was observed, but the deflection was obvious when increasing load. Finally, when approaching the maximum load, the fracture and splitting of bamboo fiber resulted in a sudden drop in the load-carrying capacity, and accordingly, the test was terminated.

The load-displacement curve at the mid-span of specimen is presented in Fig. 10b. The deflection was obtained with a LVDT installed on the top at the mid-span. The stiffness remained constant during the elastic stage. When the upper bamboo fiber in the pure bending region was compressed to yield, the load-displacement turned into elastic-plastic stage. At the maximum value, the load-carrying capacity was reduced by about 70% due to the transverse cracking of the specimens.

The mean values for strength and elastic moduli for the specimens under bending parallel to grain are 104.4 MPa and 14.9 GPa, respectively. The tensile strength was sensitive to bamboo nodes and would be reduced a lot [36]. However, most of specimens exhibited failure mode I as shown in Fig. 10a, where the cracks developed along the nodes. The fiber fraction was located in the pure bending region, but not at the critical location under the loading roller. The failure mode I was governed by the tensile strength in the pure bending region. Thus, the bending strength was less than both tension and compression strengths due to the imperfection mainly induced by bamboo nodes in the pure bending region.

Figure 10: Four-point bending test. (a) Typical failure mode, (b) load-displacement curve

4  Analysis and Discussion

4.1 Mechanical Parameters and Comparison Test Results

The experimental data was approximately normal distribution according to statistic analysis. Tab. 2 shows all the test results of HPSB specimens and other natural materials and composites. It was found that the elastic moduli and strengths of compression and tension parallel to grain of HPSB specimens were much larger than those perpendicular to grain. The tension perpendicular to grain should be avoided in practical application, while the compression perpendicular to grain showed enough strength to bear transverse load. It should be addressed that the shear strength parallel to grain was very large due to strong bonding interface. The elastic modulus of tension perpendicular to grain showed the largest discreteness due to its sensitivity to the imprecise size even manufactured by CNC machining.

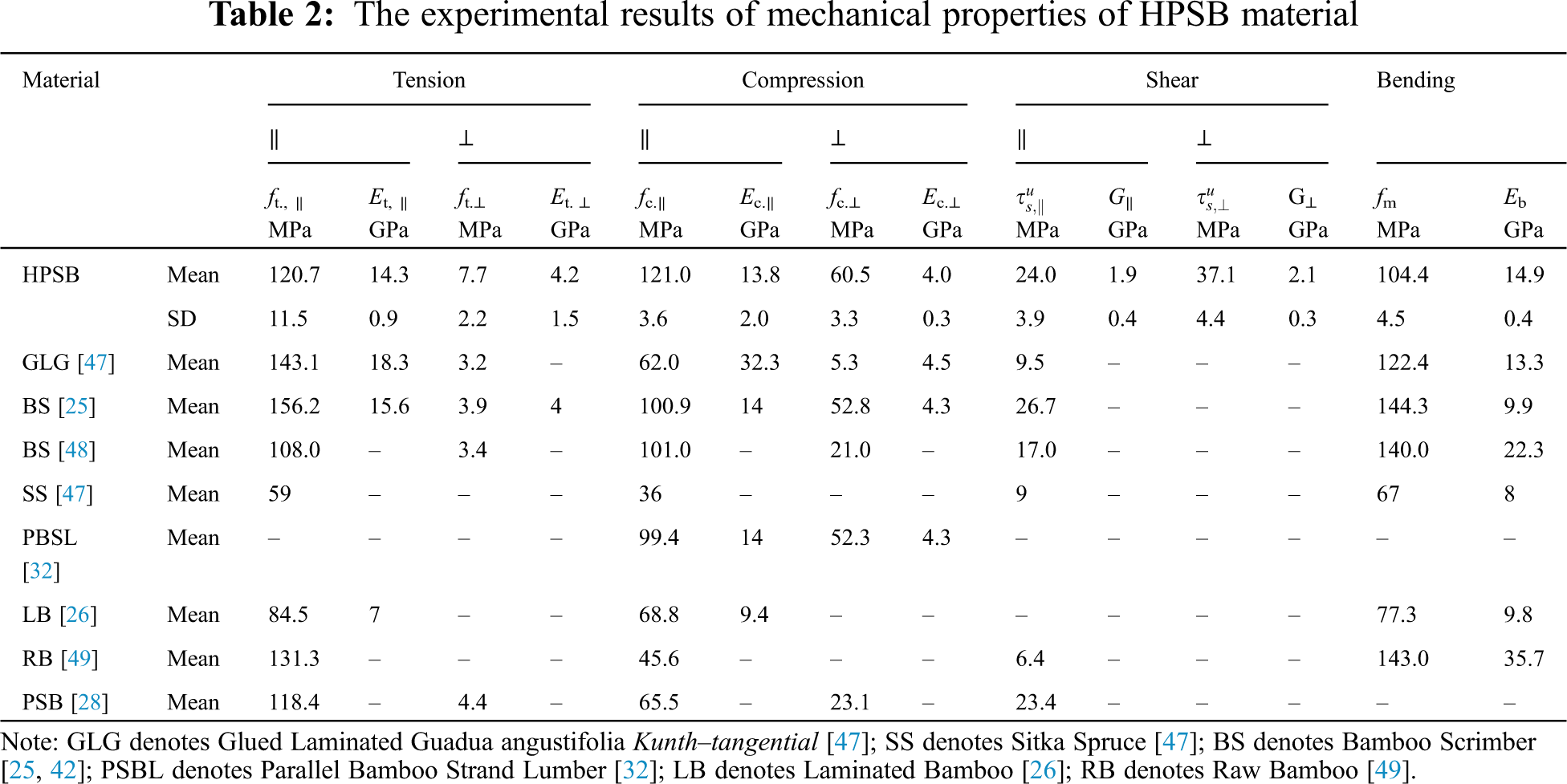
The main mechanical performance of HPSB is compared with other building materials including balsa wood, other bamboo species, laminated bamboo and bamboo composite, as shown in Tab. 2. The results demonstrated that the compression strength of HPSB material was larger than the listed wood products and bamboo products. The HPSB material also showed a balanced mechanical performance except the tension perpendicular to grain. The general hot-pressing temperature is from 120oC to 160oC. The HPSB material was processed in a moderate temperature (140oC), which means the moderate color in appearance and moderate durability due to the hot-pressing procedure. Therefore, this new HPSB material is potentially alternative for the application to structural members.

4.2 Stress-Strain Relationship of HPSB Material

Two stress-strain relationship models parallel to grain of HPSB material were proposed referring to those provided by Li et al. [25]. Both models described the mechanical behavior from uniaxial tension to compression. The compression relationships were both composed of three stages. The tension relationship shared the same slope as the linear stage of compression to benefit the finite element analysis and theoretical study, whereas the models in reference [25] had different elastic moduli between the compression and tension. The two models had different relationships in the elastic-plastic stage. The influence of the difference on the mechanical behavior would be compared with the results of experiments and finite element analysis.

4.2.1 Three-Linear Model for Stress Strain Relationship

Fig. 11a shows the three-linear model for uniaxial stress-strain relationship. The elastic-plastic stage was described as a linear segment, which was a typical method for the constitutive relationship. The three-linear model is composed of three linear stages. The stress-strain relationship of tension and the elastic stage of compression are represented by a linear segment. The slope can be obtained by the average of the elastic moduli of tension and compression. Nonetheless, the proportional point is shifted up or down after averaging the elastic moduli. Hence, the difference of elastic modulus between compression and tension should not be large to insure the accuracy of the model. As can be seen in Fig. 11c, the proposed multilinear model is smaller than the experimental results in the elastic-plastic segment.

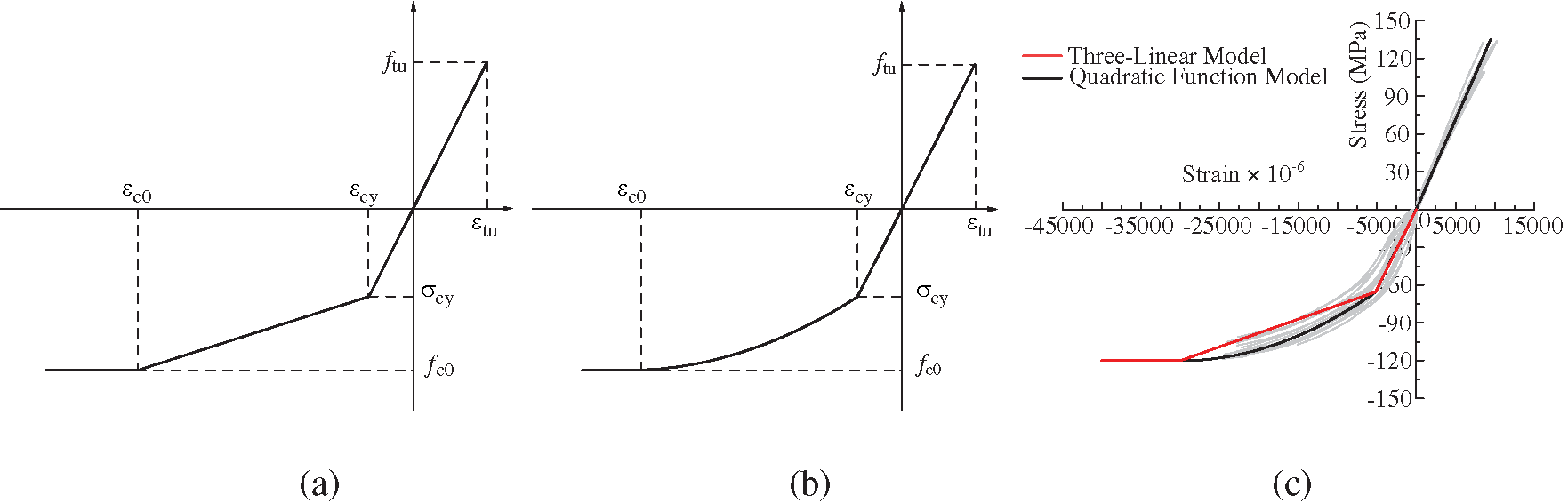
Figure 11: Stress-strain relationship models parallel to grain for HPSB material. (a) Three-linear model, (b) quadratic function model, (c) comparison with experimental results

The three-linear model can be expressed as follows:

σ={E¯ε(εcy≤ε≤εtu)fc0[1−a(1−εεc0)](εc0≤ε≤εcy)fc0(εcu≤ε≤εc0) (1)

a=kn−1(n−1) (2)

n=εcyεc0 (3)

k=E¯εc0fc0=E¯fc0εc0=E¯Ep (4)

where σ and ε are the stress and strain parallel to grain, respectively; Ec and Et are the elastic moduli of compression and tension, respectively; E¯ is the mean value of Et and Ec; Ep is the secant modulus for peak point (εc0, fc0 ); εc0 is the strain at the peak point; fc0 is the maximum compression strength; εcy is the strain of the proportional point; εcu is the ultimate compressive strain.

4.2.2 Quadratic Function Model for Stress Strain Relationship

A quadratic function curve is used to describe the elastic-plastic stage in the quadratic function model as shown in Fig. 11b. Similar to the three-linear model, the quadratic function model combines the tension relationship and elastic compression relationship with a unified elastic modulus. Compared to the three-linear model, this model showed a better agreement with the test results as can be seen in Fig. 11c.

The quadratic function model for stress-strain relationship can be similarly expressed as follows:

σ={E¯ε(εcy≤ε≤εtu)fc0[1+a(1−εεc0)2](εc0≤ε≤εcy)fc0(εcu≤ε≤εc0) (5)

a=kn−1(n−1)2 (6)

n=εcyεc0 (7)

k=E¯εc0fc0=E¯fc0εc0=E¯Ep (8)

where the parameters in the above formulas are the same as those in the three-linear model.

4.3 Finite Element Analysis

4.3.1 Modeling

To assess the constitutive relationship models, the finite element analysis (FEA) was conducted by using ANSYS software to simulate the bending process. In the finite element model (FEM), 8-node hexahedral solid element (SOLID 185) was used to simulate the parallel strand bamboo. In order to reduce the computational time, one half of the structure was modeled, as shown in Fig. 12. In addition, a mesh convergence test was conducted through element refinement, and then the element size (4 mm in depth direction and 5 mm in span direction) was determined. The boundary conditions were determined by referring to the experimental setup. The position of the specimen at support 1 was only fixed in the Y and Z directions. The load was directly applied to the nodes in the manner of displacement-control.

Figure 12: Typical meshing and boundary conditions of FEM

The elastic-plastic compressive behavior of parallel strand bamboo was considered with the orthotropic nonlinear material properties presented in Tab. 2. In order to access the accuracy of the constitutive models, both two models were chosen separately to define the compressively constitutive model in the longitudinal direction.

4.3.2 Validation

The finite element model was validated by the experimental results of bending tests. The failure modes and the load-carrying capacities were compared and discussed. It is seen that the FEM with quadratic function model shows better agreement with the experimental results than that with three linear models, as shown in Fig. 13a. The result was reasonable due to the higher precision of quadratic function model in the elastic-plastic segment. The numerical stiffness of FEM with three linear model is slightly less than the experimental stiffness due to the lower elastic modulus averaged from the values of tension and compression. In addition, the linear development of compressive stress in the elastic-plastic segment also led to the lower stiffness. The failure mode of the FEA with three linear model is shown and compared in Fig. 13b. The maximum tensile strength is 125.3 MPa at the end of the numerical load-displacement curves, which is close to the tensile fracture of parallel strand bamboo. The damage zone could be observed by the contour plot of plastic strain. Overall, the proposed finite element modelling method using three-linear model relationship is precise enough when simulating the parallel strand bamboo.

Figure 13: Results of the finite element analysis of bending tests. (a) Load-displacement relationship, (b) failure mode comparison between the experimental and numerical results

5  Conclusions

A new production method of parallel strand bamboo was used in the preparation of HPSB material. The study was carried out to investigate the characteristics of mechanical performance of HPSB as a potential material for structural application. The following conclusions can be drawn from the experimental work and analytical results:

(1) The mechanical properties of HPSB material were better than softwood timber and some other bamboo productions, especially in compression parallel to grain, which made it possible to be used as structural material. The tension perpendicular to grain should be avoided for its weakest strength. The shear stress parallel to grain required more consideration for its much improved shear strength.

(2) Two stress-strain relationship models, including three-linear model and quadratic function model, were proposed and compared with the experimental results. The tension and compression were suggested to share the same elastic modulus in both models to simplify the analytical and numerical study. The quadratic function model and the three-linear model both showed good agreements with the experimental results.

(3) Finite element models were built with the mechanical properties of HPSB material. The quadratic function model showed a better agreement with the experimental results, but the three-linear relationship was also precise enough to analyze the bending tests of HPSB material.

Funding Statement: The authors acknowledge funding supported by the Fundamental Research Funds for the Central Universities of China (No. BLX201706), and supported by Major Science and Technology Program for Water Pollution Control and Treatment (No. 2017ZX07102-001), and supported by the National Natural Science Foundation of China (Nos. 51908038 and 31770602). The authors also express their sincere gratitude and appreciation to Mohammed Sewar for his help in editing and proofreading the English manuscript and all the students who helped in the experimental program.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Chung, K. F., Yu, W. K. (2002). Mechanical properties of structural bamboo for bamboo scaffoldings. Engineering Structures, 24(4), 429–442. DOI 10.1016/S0141-0296(01)00110-9. [Google Scholar] [CrossRef]

 2.  Kibwage, J. K., Frith, O. B., Paudel, S. K. (2014). Bamboo as a building material for meeting East Africa’s housing needs: A value chain case study from Ethiopia. International Network for Bamboo and Rattan, Beijing, China. https://idl-bnc-idrc.dspacedirect.org/bitstream/handle/10625/48260/IDL-2.48260.pdf?isAllowed=y&sequence=1. [Google Scholar]

 3.  He, M. J., Li, Z., Sun, Y. L., Ma, R. (2015). Experimental investigations on mechanical properties and column buckling behavior of structural bamboo. The Structural Design of Tall and Special Buildings, 24(7), 491–503. DOI 10.1002/tal.1176. [Google Scholar] [CrossRef]

 4.  Sharma, B., Gatóo, A., Bock, M., Ramage, M. (2015). Engineered bamboo for structural applications. Construction and Building Materials, 81(2), 66–73. DOI 10.1016/j.conbuildmat.2015.01.077. [Google Scholar] [CrossRef]

 5.  Xu, M., Cui, Z., Chen, Z., Xiang, J. (2017). Experimental study on compressive and tensile properties of a bamboo scrimber at elevated temperatures. Construction and Building Materials, 151, 732–741. DOI 10.1016/j.conbuildmat.2017.06.128. [Google Scholar] [CrossRef]

 6.  Xiao, Y., Li, L., Yang, R. (2014). Long-term loading behavior of a full-scale glubam bridge model. Journal of Bridge Engineering, 19(9), 04014027. DOI 10.1061/(ASCE)BE.1943-5592.0000600. [Google Scholar] [CrossRef]

 7.  Chen, G., Li, H. T., Zhou, T., Li, C. L., Song, Y. Q. et al. (2015). Experimental evaluation on mechanical performance of OSB webbed parallel strand bamboo I-joist with holes in the web. Construction and Building Materials, 101(3), 91–98. DOI 10.1016/j.conbuildmat.2015.10.041. [Google Scholar] [CrossRef]

 8.  Chung, K. F., Yu, W. K. (2002). Mechanical properties of structural bamboo for bamboo scaffoldings. Engineering Structures, 24(4), 429–442. DOI 10.1016/S0141-0296(01)00110-9. [Google Scholar] [CrossRef]

 9.  Harries, K. A., Sharma, B., Richard, M. (2012). Structural use of full culm bamboo: The path to standardization. International Journal of Architecture Engineering and Construction, 1(2), 66–75. [Google Scholar]

10. Tian, L. M., Kou, Y. F., Hao, J. P. (2019). Axial compressive behaviour of sprayed composite mortar-original bamboo composite columns. Construction and Building Materials, 215(9), 726–736. DOI 10.1016/j.conbuildmat.2019.04.234. [Google Scholar] [CrossRef]

11. Tian, L. M., Kou, Y. F., Hao, J. P. (2019). Flexural behavior of sprayed lightweight composite mortar-original bamboo composite beams: experimental study. Bioresources, 14(1), 500–517. [Google Scholar]

12. Meng, X. M., Cao, Y. Y., Sun, H., Feng, P. (2019). The mechanical properties of cracked round bamboo reinforced with FRP sheets subjected to axial compression. Modern Engineered Bamboo Structures. CRC Press, 85–90. [Google Scholar]

13. Awaludin, A., Andriani, V. (2014). Bolted bamboo joints reinforced with fibers. Procedia Engineering, 95(1), 15–21. DOI 10.1016/j.proeng.2014.12.160. [Google Scholar] [CrossRef]

14. Meng, X. M., Cao, Y. Y., Sun, H., Feng, P. (2019). Experimental study on uniaxial compression of bamboo poles with different reinforcements. MATEC Web of Conferences, vol. 275, pp. 01023. EDP Sciences. DOI 10.1051/matecconf/201927501023. [Google Scholar] [CrossRef]

15. Meng, X. M., Yu, J. W., Zhang, Z. C., Zhai, J. Q., Feng, P. (2019). Mechanical properties of bolted bamboo culms reinforced with FRP sheets. Australia: APFIS2019. [Google Scholar]

16. Sharma, B., Gatóo, A., Ramage, M. H. (2015). Effect of processing methods on the mechanical properties of engineered bamboo. Construction and Building Materials, 83(2), 95–101. DOI 10.1016/j.conbuildmat.2015.02.048. [Google Scholar] [CrossRef]

17. Li, H. T., Zhang, Q. S., Huang, D. S., Deeks, A. J. (2013). Compressive performance of laminated bamboo. Composites Part B: Engineering. Composites Part B: Engineering, 54(7), 319–328. DOI 10.1016/j.compositesb.2013.05.035. [Google Scholar] [CrossRef]

18. Chen, G., Yu, Y., Li, X., He, B. (2020). Mechanical behavior of laminated bamboo lumber for structural application: an experimental investigation. European Journal of Wood and Wood Products, 78(1), 53–63. DOI 10.1007/s00107-019-01486-9. [Google Scholar] [CrossRef]

19. Xiao, Y. (2020). Engineered bamboo in China. Nonconventional and vernacular construction materials, pp. 625–643. Woodhead Publishing. [Google Scholar]

20. Kumar, A., Vlach, T., Laiblova, L., Hrouda, M., Kasal, B. et al. (2016). Engineered bamboo scrimber: Influence of density on the mechanical and water absorption properties. Construction and Building Materials, 127(2), 815–827. DOI 10.1016/j.conbuildmat.2016.10.069. [Google Scholar] [CrossRef]

21. Wei, J., Rao, F., Huang, Y., Zhang, Y., Qi, Y. et al. (2019). Structure, mechanical performance, and dimensional stability of Radiata Pine (Pinus radiata D. Don) scrimbers. Advances in Polymer Technology, 2019(26), 1–8. DOI 10.1155/2019/5209624. [Google Scholar] [CrossRef]

22. Barbuta, C., Blanchet, P., Cloutier, A., Yadama, V., Lowell, E. (2012). OSB as substrate for engineered wood flooring. European Journal of Wood and Wood Products, 70(1–3), 37–43. DOI 10.1007/s00107-010-0494-y. [Google Scholar] [CrossRef]

23. Francisco, A. M., Fernando, P. S., Luis, G. E. (2008). Characteristic values of the mechanical properties of radiata pine plywood and the derivation of basic values of the layers for a calculation method. Biosystems Engineering, 99(2), 256–266. DOI 10.1016/j.biosystemseng.2007.10.004. [Google Scholar] [CrossRef]

24. Yu, Y. L., Liu, R., Huang, Y. X., Meng, F. D., Yu, W. J. (2017). Preparation, physical, mechanical, and interfacial morphological properties of engineered bamboo scrimber. Construction and Building Materials, 157, 1032–1039. DOI 10.1016/j.conbuildmat.2017.09.185. [Google Scholar] [CrossRef]

25. Li, H. T., Zhang, H. Z., Qiu, Z. Y., Su, J. W., Wei, D. D. et al. (2020). Mechanical properties and stress strain relationship models for bamboo scrimber. Journal of Renewable Materials, 8(1), 13–27. DOI 10.32604/jrm.2020.09341. [Google Scholar] [CrossRef]

26. Li, H. T., Wu, G., Zhang, Q., Deeks, A. J., Su, J. (2018). Ultimate bending capacity evaluation of laminated bamboo lumber beams. Construction and Building Materials, 160(4), 365–375. DOI 10.1016/j.conbuildmat.2017.11.058. [Google Scholar] [CrossRef]

27. Lou, Z. C., Yuan, T. C., Wang, Q. Y., Wu, X. W., Hu, S. H. et al. (2021). Fabrication of crack-free flattened bamboo and its macro-/microMorphological and mechanical properties. Journal of Renewable Materials, 9(5), 959–977. DOI 10.32604/jrm.2021.014285. [Google Scholar] [CrossRef]

28. Huang, D. S., Bian, Y. L., Zhou, A. P., Sheng, B. L. (2015). Experimental study on stress-strain relationships and failure mechanisms of parallel strand bamboo made from Phyllostachys. Construction and Building Materials, 77, 130–138. DOI 10.1016/j.conbuildmat.2014.12.012. [Google Scholar] [CrossRef]

29. Huang, D. S., Zhou, A., Bian, Y. L. (2013). Experimental and analytical study on the nonlinear bending of parallel strand bamboo beams. Construction and Building Materials, 44(5), 585–592. DOI 10.1016/j.conbuildmat.2013.03.088. [Google Scholar] [CrossRef]

30. Ahmad, M., Kamke, F. (2011). Properties of parallel strand lumber from Calcutta bamboo (Dendrocalamus strictus). Wood Science and Technology, 45(1), 63–72. DOI 10.1007/s00226-010-0308-8. [Google Scholar] [CrossRef]

31. Li, X., Ashraf, M., Li, H. T., Zheng, X. Y., Al-Deen, S. et al. (2020). Experimental study on the deformation and failure mechanism of parallel bamboo Strand Lumber under drop-weight penetration impact. Construction and Building Materials, 242(9), 118135. DOI 10.1016/j.conbuildmat.2020.118135. [Google Scholar] [CrossRef]

32. Li, H. T., Qiu, Z. Y., Wu, G., Wei, D., Lorenzo, R. et al. (2019). Compression behaviors of parallel bamboo strand lumber under static loading. Journal of Renewable Materials, 7(7), 583–600. DOI 10.32604/jrm.2019.07592. [Google Scholar] [CrossRef]

33. Tan, C., Li, H. T., Wei, D. D., Lorenzo, R., Yuan, C. G. (2020). Mechanical performance of parallel bamboo strand lumber columns under axial compression: Experimental and numerical investigation. Construction and Building Materials, 231(1), 117168. DOI 10.1016/j.conbuildmat.2019.117168. [Google Scholar] [CrossRef]

34. Liu, W., Hu, X. Z., Yuan, B. Y., Xu, F., Huang, J. K. (2020). Tensile strength model of bamboo srimber by 3-p-b fracture test on the basis of non-LEFM. Composites Science and Technology, 198, 108295. [Google Scholar]

35. Xie, P., Liu, W., Hu, Y. C., Meng, X. M., Huang, J. K. (2020). Size effect research of tensile strength of bamboo scrimber based on boundary effect model. Engineering Fracture Mechanics, 107319, 239. [Google Scholar]

36. Qi, J., Xie, J., Yu, W., Chen, S. (2015). Effects of characteristic inhomogeneity of bamboo culm nodes on mechanical properties of bamboo fiber reinforced composite. Journal of Forestry Research, 26(4), 1057–1060. DOI 10.1007/s11676-015-0106-0. [Google Scholar] [CrossRef]

37. Shangguan, W., Gong, Y., Zhao, R., Ren, H. (2016). Effects of heat treatment on the properties of bamboo scrimber. Journal of Wood Science, 62(5), 383–391. DOI 10.1007/s10086-016-1574-3. [Google Scholar] [CrossRef]

38. Sharma, B., Gatoo, A., Bock, M., Mulligan, H., Ramage, M. (2015). Engineered bamboo: state of the art. Proceedings of the Institution of Civil Engineers-Construction Materials, 168(2), 57–67. DOI 10.1680/coma.14.00020. [Google Scholar] [CrossRef]

39. Yu, Y. L., Zhu, R. X., Wu, B. L., Hu, Y. A., Yu, W. J. (2015). Fabrication, material properties, and application of bamboo scrimber. Wood Science and Technology, 49(1), 83–98. DOI 10.1007/s00226-014-0683-7. [Google Scholar] [CrossRef]

40. Jung, K. H., Kim, Y. J., Roh, J. K., Park, S. J. (2003). Effect of hot-pressing time and temperature on properties of bamboo zephyr boards. Journal of the Korean Wood Science and Technology, 31(2), 77–83. [Google Scholar]

41. Li, J. P., Chen, Y. H., Xu, J., Ren, D. J., Yu, H. et al. (2018). The influence of media treatments on color changes, dimensional stability, and cracking behavior of bamboo scrimber. International Journal of Polymer Science, 2018(2), 1–7. DOI 10.1155/2018/6068589. [Google Scholar] [CrossRef]

42. BS 373 (2018). Methods of testing small clear specimens of timber. London, United Kingdom: British Standards Institution. [Google Scholar]

43. ASTM D143 (2014). 143-14 standard test methods for small clear specimens of timber. USA: ASTM International. [Google Scholar]

44. ASTM D7078/D7078M (2020). Standard test method for shear properties of composite materials by v-notched rail shear method. United States: ASTM International. [Google Scholar]

45. GB/T 17657 (2013). Test methods of evaluating the properties of wood-based panels and surface decorated wood-based panels. China: Standards Press of China. [Google Scholar]

46. Naik, N. K., Kumar, R. S. (1999). Compressive strength of unidirectional composites: Evaluation and comparison of prediction models. Composite Structures, 46(3), 299–308. DOI 10.1016/S0263-8223(99)00098-7. [Google Scholar] [CrossRef]

47. Kretschmann, D. E. (2010). Wood handbook, chapter 05: mechanical properties of wood. Madison, Wisconsin, USA: Forest Products Laboratory, Department of Agriculture Forest Service. [Google Scholar]

48. He, M. J., Zhang, J., Li, Z., Li, M. L. (2016). Production and mechanical performance of scrimber composite manufactured from poplar wood for structural applications. Journal of Wood Science, 62(5), 429–440. DOI 10.1007/s10086-016-1568-1. [Google Scholar] [CrossRef]

49. Sompoh, B., Fueangviat, V., Bauchonkol, P., Ratcharoem, W. (2013). Physical and mechanical properties of some Thai Bamboos for House Construction. http://arkn-fpd.org/index.php/publication/publication_detail/148. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.