 | Journal of Renewable Materials |  |
DOI: 10.32604/jrm.2023.022343
ARTICLE
Shear Behaviors of Steel-Plate Connections for Timber-Concrete Composite Beams with Prefabricated Concrete Slabs
Nanjing Tech University, Nanjing, 211816, China
*Corresponding Author: Huifeng Yang. Email: hfyang@njtech.edu.cn
Received: 09 March 2022; Accepted: 23 May 2022
Abstract: To promote the development of timber-concrete composite (TCC) structures, it is necessary to propose the assembly-type connections with high assembly efficiency and shear performances. This article presented the experimental results of the innovative steel-plate connections for TCC beams using prefabricated concrete slabs. The steel-plate connections consisted of the screws and the steel-plates. The steel-plates were partly embedded in the concrete slabs. The concrete slabs and the timber beams were connected by screws through the steel-plates. The parameters researched in this article included screw number, angle steel as the reinforcement for anchoring, and shallow notches on the timber surface to restrict the slip of the steel-plates. Experimental results were discussed in terms of failure modes, ultimate bearing capacities, and slip moduli. It was found that increasing the number of screws could lead to the obvious improvement on the ultimate bearing capacities and the slip moduli at the ultimate state; and the angle steel as the reinforcement showed the slight influence on the ultimate bearing capacities and the slip moduli. The application of the shallow notch can greatly improve the ultimate bearing capacities and the slip moduli. The calculation models for the ultimate bearing capacities and the slip moduli of the steel-plate connections with and without shallow notches were proposed, which showed good accuracy compared with the experimental results.
Keywords: Timber-concrete composites; steel-plate connections; prefabricated; shallow notches; push-out tests
The timber-concrete composite (TCC) beam is composed of the upper concrete slab, the bottom timber beam, and shear connections at the interface. The TCC systems were increasingly used in the construction of bridges, residential, and commercial buildings [1,2]. The concrete slab and timber beam are connected together through shear connections. Therefore, the shear connections show the significant influences on the overall structural performances of the TCC beams.
The common shear connections used in TCC structures mainly include dowel-type, notch-screw, and glued-in metal plate connections. The dowel-type fasteners mainly include the dowels, the screws, the nails, and the bolts, and so on. The inclined screws also can be considered as the dowel-type connections [3], and the inclined screws [4] and cross inclined screws [5,6] showed obvious improvements compared with vertical screws in the ultimate bearing capacities and the slip moduli, thanks to the fully utilization of the withdrawal capacity of the screws under shear-tension loading [7]. Appavuravther et al. [8] summarized the various failure modes of the vertical and inclined screw connections, considering the bending yielding of the screw and the failure of the lightweight concrete. Dias [9] and Symons et al. [10] proposed the calculations for the slip moduli of the screw connections, considering the inclination of the screw, and the interfacial plywood. In addition, the notch-screw connections [11,12] and glued-in steel-plate connections [13,14] also possessed excellent shear performances. Available experimental investigations about full-scale TCC beams/floors demonstrated that the existing shear connections can provide sufficient composite efficiency for TCC structures, and showed the great potential application in multi-storey buildings.
Timber structures were characterized by the prefabricated building, high construction efficiency, and low pollution on the construction site. However, the application of wet concrete may decline the construction efficiency, increase the pollution on the site, and need more construction matters, such as supporting formwork, binding steel bars, and pouring concrete. Therefore, the use of prefabricated concrete slabs is greatly necessary to promote the development of the TCC structures. Lukaszewska et al. [15] proposed many concepts for the TCC structures with prefabricated concrete slabs based on traditional dowel-type, notch-screw, and glued-in steel plate connections, through post-grouting and post-application of the adhesive. Khorsandnia et al. [16] also proposed several types of shear connections, which can realize the deconstruction of TCC beams. Derikvand et al. [17] proposed an innovative deconstructable screw connection that the section of the screw in the concrete slab was covered by a thin protective layer made of heat-shrink tubing. It was demonstrated that the deconstructable connection possesses the similar shear behaviors compared with the permanent connections. In addition, Crocetti et al. [18], Zhang et al. [19], and Hu et al. [20] also provided the feasible assembly-type connecting methods for TCC structures based on the dowel-type connections. Tao et al. [21] investigated shear performances of the cross inclined screw connections using prefabricated slabs through the grouting method, and obtained the expected experimental results. Wei et al. [22] investigated the bending performances of the bamboo-concrete composite beams with prefabricated concrete slabs, which were connected by glued-in steel-plate connections, and the grouting method was also adopted to assemble the bamboo beam and the concrete slab, which obtained superior bending performances.
As summarized above, the post-grouting and post-application of the adhesive methods may complicate the construction of assembly process, and the construction efficiency need to be improved further. Accordingly, the dry-dry connection for prefabricated TCC beams may be an effective solution [17]. Therefore, this experimental programme investigated the dry-type steel-plate connections for TCC beams using prefabricated concrete slabs. On this basis, different configurations of the steel-plate connections were proposed aiming to improve the shear performances. What needs to be emphasized is that the application of shallow notch to restrict the slip of the steel-plate obviously improved the ultimate load-carrying capacity and slip moduli of the shear connections, which was the most recommended structural configuration of the steel-plate connections. In addition, this article proposed the calculation methods for ultimate bearing capacities and slip moduli of the steel-plate connections with and without shallow notches, and showed acceptable accuracies.
The glulam used in the experiments was made of the Douglas fir from North America. According the Chinese Standard GB/T 50329 [23], the average values for the modulus of elasticity and compressive strength of the timber parallel to grain were tested as 13000 MPa and 34.7 MPa, respectively. The density and moisture content of the timber were 510 kg/m3 and 10.8%, respectively. For the concrete slab, the compressive strength of the concrete was tested on the basis of the standard cubic specimens with the dimension of 150 mm. The average compressive strength was tested as 40.8 MPa at the age of 28 days under the natural curing condition.
Screws in two size, designated as M6L60 and M6L70, respectively, were adopted as the fasteners between steel-plates and glulam blocks, as shown in Fig. 1. The M6L60 means that the diameter and the length of the screw were 6 mm and 60 mm, respectively. The average yield moment and strength of the screw were tested as 7445 N·mm and 206.8 MPa, respectively, according to American standard ASTM F 1575 [24], while the corresponding bending stiffness was determined as 842 N·mm2. The axial withdrawal capacity of the screw was tested as 5.8 kN for the M6L70 screws.

Figure 1: The screws adopted in the experiments
The steel-plate, with a thickness of 5 mm, were made of Q235 steel with the yield strength of 235 MPa. The detailed 2D dimensions of the steel-plates were presented in Fig. 2.
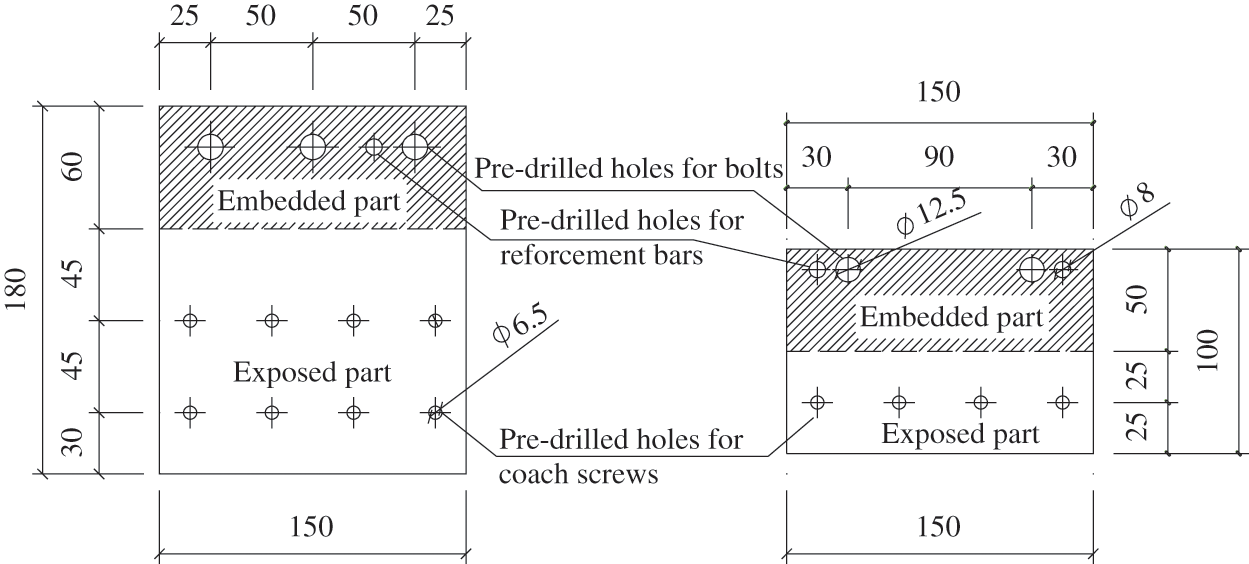
Figure 2: The diagrams of steel-plates (unit: mm)
2.2 Design of Shear Connections
Fig. 3 shows the geometry dimensions of a steel-plate specimen, taking the SP + 8S(R) as the example. The steel-plates were partly embedded in the concrete, and the steel-plates were connected with the timber block by screws, realizing the dry-dry assembly for the timber and the concrete. As shown in Fig. 3, a rebar mesh with the rebar spacing of 100 mm was placed in the concrete slab. The rebars in the transverse direction pass through the embedded part of the steel-plate.
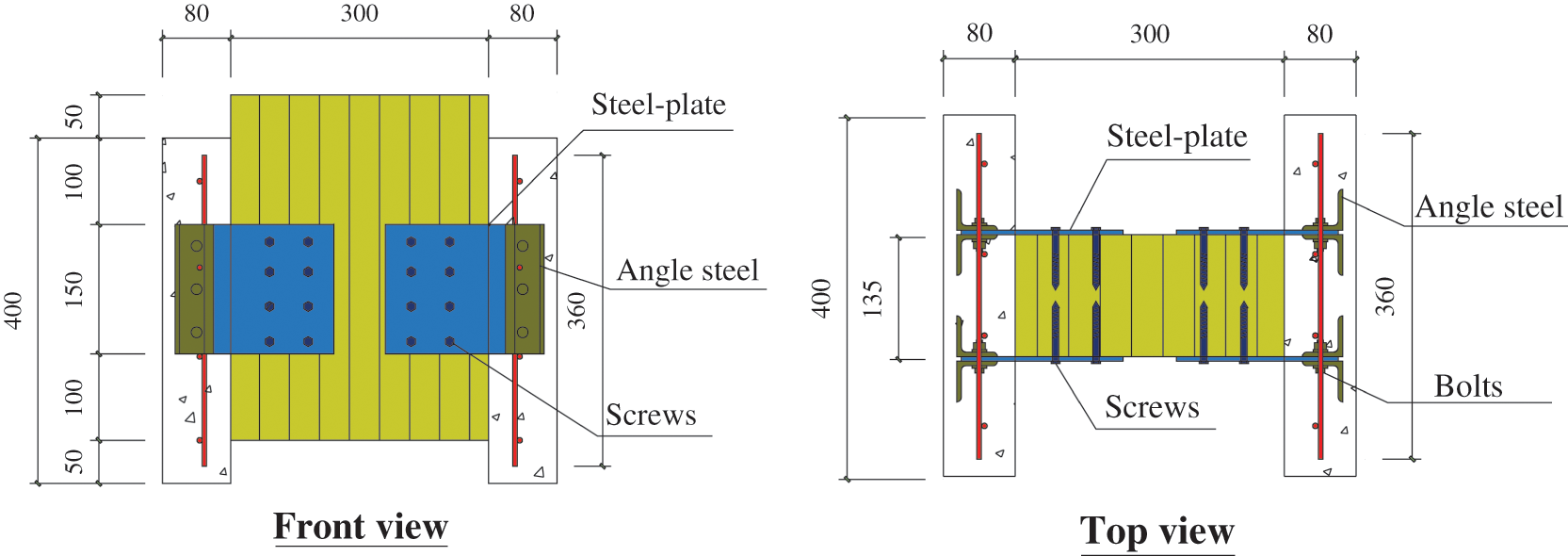
Figure 3: Dimensions of a SP + 8S(R) specimen (unit: mm)
Table 1 displays the experimental parameters of the steel-plate connections. The experimental parameters included the effect of the angle steel which was bolted to the embedded part of the steel-plate, the screw number at each steel-plate, and the timber shallow notch. The configurations of steel-plate connections were shown in Figs. 3, 4. The timber blocks with steel-plates were displayed in Fig. 5. The embedded part of the steel plate was bolted with angle steels to improve the anchorage performance (see Fig. 5a). For the SP + 8S(R) connection, the shear performances of the connection and structural behaviours in TCC beams were reported in previous investigations [25], which was demonstrated to possess sufficient shear strength and ductility. For group SP + 4S, as shown in Fig. 4b, the angle steel was not adopted aiming to simplify the fabrication process of the prefabricated concrete slabs. As illustrated in Figs. 4c and 5b, a shallow notch with the dimensions of 150 mm × 50 mm × 5 mm was formed on the surface of the timber block to restrict the rotation of the steel-plate.
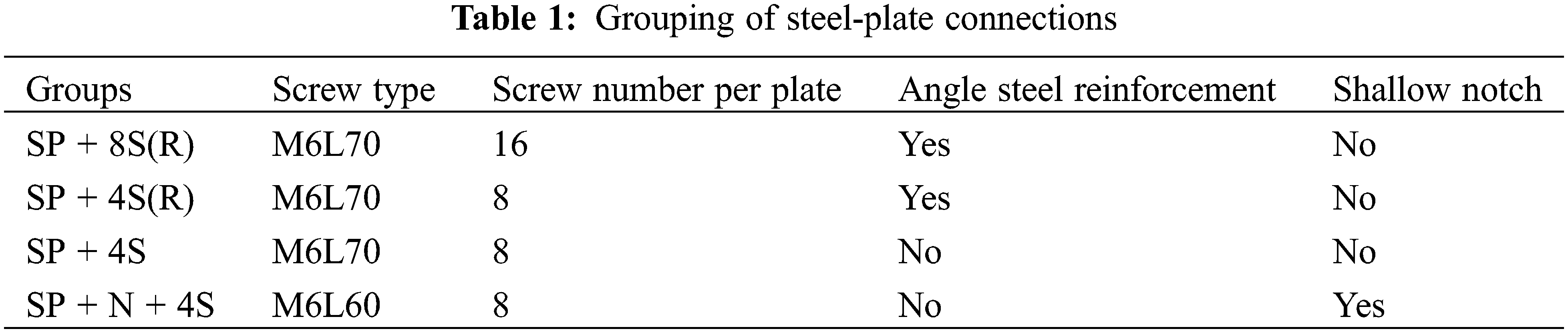
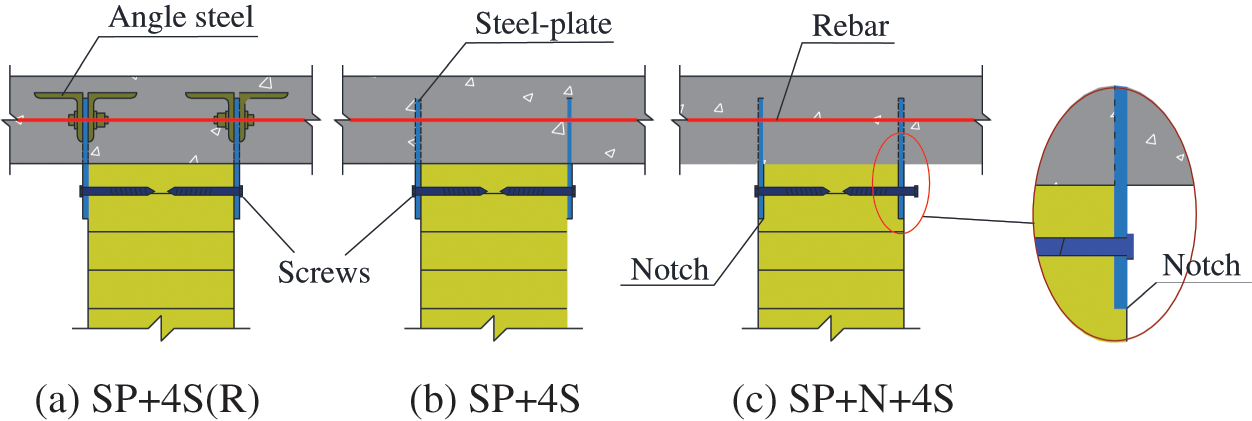
Figure 4: Configurations of the steel-plate connections

Figure 5: Photographs of the connecting region
Three samples for each group were prepared. According to European Standard EN 26891 [26], the loading procedure was determined as shown in Fig. 6a, and idealized load-slip curve was shown in Fig. 6b. Combined with the loading procedure, the slip moduli of the shear connection at different loading levels can be calculated by Eqs. (1)–(3), in which the Fmax denotes the maximum load; Fest is the estimated failure load; Ks denotes the slip modulus at the serviceability limit state, while K0.6 and K0.8 denote the slip moduli at the ultimate state and near collapse state, respectively. The value of the Fest for SP + 8S(R) specimens was 150 kN, while that for other groups was 80 kN.

Figure 6: Loading procedure and the idealized load-slip curve [26]
The push-out specimens were loaded by an actuator with the capacity of 300 kN. As shown in Fig. 7, the interfacial relative slip was measured by the linear voltage displacement transducers (LVDTs), and the relative slip displayed in this article was the average value recorded by P1∼P4 LVDTs.
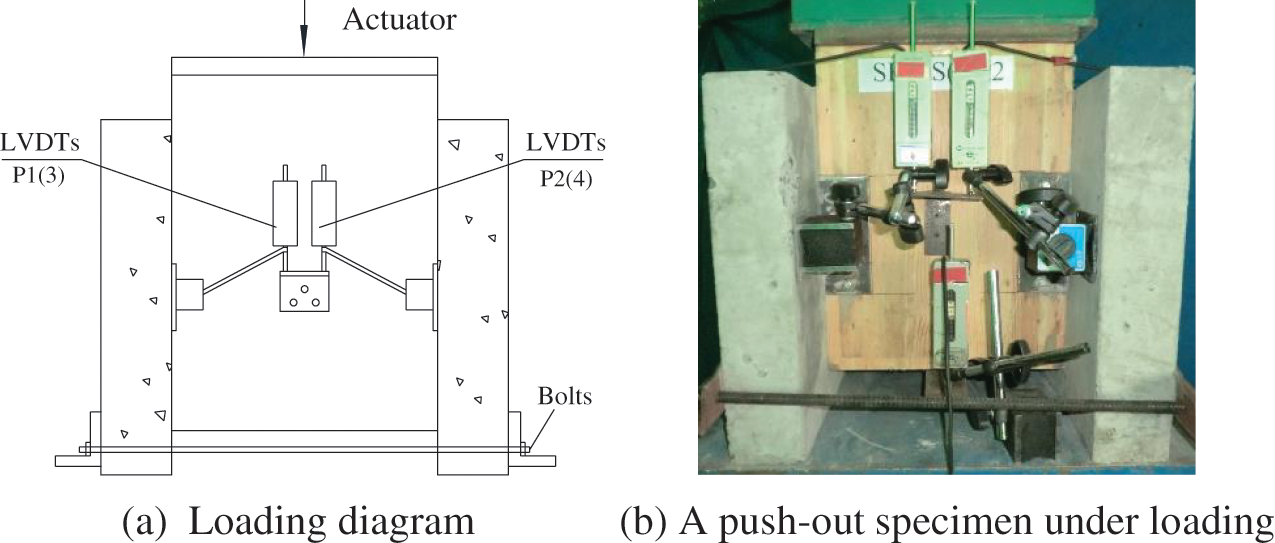
Figure 7: Loading and measuring methods
The typical failure modes of the developed connections were shown in Fig. 8. All of the specimens occurred slight interfacial relative slip between the timber block and the concrete slab at the initial loading stage, as shown in Figs. 8a–8b (Solid red line and broken white line refer to the original stage and later stage, respectively). While near the collapse state, the group SP + 8S(R) featured serious rotation of the steel-plate, as shown in Fig. 8c. As a comparison, the specimens in other groups showed no obvious rotation until failure, as shown in Figs. 8d–8e. The screws in different rows of group SP + 8S(R) occurred the plastic deformation with different degrees, leading to the serious rotation of steel-plates. As displayed in Fig. 8e, the specimen with shallow notches showed the embedment failure in the timber block near the collapse state, which is similar to the embedment splitting failure in dowel-type connections. Fig. 8f shows the deformation of the screws and surrounding timber of a failure specimen in group SP + N + 4S. The screws showed severe plastic bending, and the timer showed evident embedment failure. The ‘rope effect’ of the screws could be observed, which can provide a certain post-yielding bearing capacity for the shear connection.

Figure 8: Typical failure modes of the connections
3.2 Strengths and Interfacial Slip
The load-slip curves of all specimens are displayed in Fig. 9. The ultimate bearing capacity Fu and the corresponding interfacial relative slip su are summarized in Table 2. The values of Fu denote the total ultimate bearing capacity of the two shear planes for each specimen. Group SP + 4S was selected as the reference group to evaluate the improvement ratios of other groups.

Figure 9: The load-slip curves of steel-plate connections

The number of screws showed the great influence on the ultimate bearing capacity of the shear connection. As the screw number was doubled, the ultimate bearing capacity was improved by about 53.4%, by comparing group SP + 4S(R) with group SP + 8S(R). The angle steel has the slight improvement on the ultimate bearing capacity of the shear connection. Group SP + 4S without angle steel showed 8.2% decline in the ultimate bearing capacity compared with group SP + 4S(R). Comparing with groups SP + 4S(R) and SP + 4S specimens, it could be concluded that the average ultimate bearing capacity of group SP + N + 4S specimens was improved by 14.1% and 24.3%, respectively. It was supposed that the improvement was resulted from the application of the shallow notches, even though the screw length for group SP + N + 4S specimens was relatively shorter.
The proposed innovative steel-plate connections featured the significant deformability and post-yield bearing capacity. The maximum slip exceeded 15 mm, which meets the requirement of the connection in deformation ability [26]. The interfacial relative slip corresponding to the peak values of the testing loads was 8.3 mm∼15.0 mm. In Figs. 9b–9c, the testing load occurred abrupt decline for several specimens, which was caused by the fracture of the individual screws. The screw fracture failure was almost not observed in group SP + N + 4S specimens as shown in Figs. 8f and 9d. This was because that the timber shallow notch effectively restricted the deformation of the screws.
Table 2 summarizes the slip moduli of the steel-plate connections. Fig. 10 shows the comparison among different groups. Ks, K0.6, and K0.8 were calculated according to the Eqs. (1)–(3), respectively. The slip moduli in Table 2 and Fig. 10 include the contribution of the two shear planes for each push-out specimen.
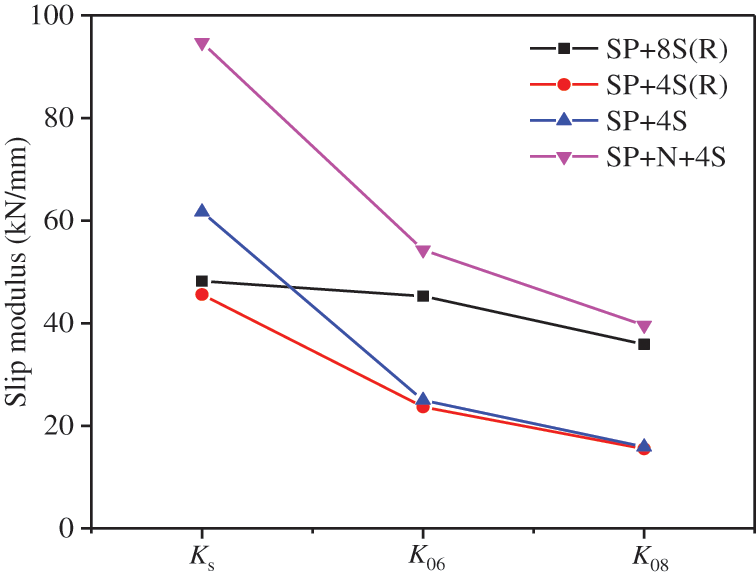
Figure 10: Slip modulus comparisons between difference connections
It can be found group SP + 8S(R) specimens showed the relatively lower value for the initial slip modulus Ks, compared with group SP + 4S(R) and group SP + 4S specimens. The steel-plate rotation shown in Fig. 8c may cause this result. In addition, the estimated ultimate bearing capacity (80 kN) for groups SP + 4S(R), SP + 4S, and SP + N + 4S was obviously smaller than their actual ultimate bearing capacities. This factor may cause the overestimation of the initial slip modulus Ks, due to the effect of the friction between the timber and the steel-plate as well as the pre-tightening force generated while the screw was drilled into the timber. Accordingly, the values of K0.6 and K0.8 showed the better reference significance while analyzing the effect of the screw number. Groups SP + 4S(R) and SP + 4S specimens showed different values in Ks. This may be caused by the individual material differences. Comparing with group SP + 4S specimens, the application of shallow notches in group SP + N + 4S specimens improved the initial slip modulus Ks by 53.5%. Moreover, the values of K0.6 and K0.8 for the SP + N + 4S specimens were also improved effectively, thanks to the constraint of the shallow notch.
It was considered that the bonding strength between the steel-plate and concrete was sufficient in the steel-plate connection. As shown in the Fig. 8, the typical failure of the steel-plate connections was the screw yielding and timber embedment failure. Thus, the ultimate strength of the screw connection in the timber was considered as the shear strength of the TCC connection in this article. According to the European yield method (EYM) [27,28], the shear resistance of the steel-timber connection with screws can be calculated by Eq. (4).
where, My is the yield moment of the screw, fh denotes the embedment strength of the timber, ds represents the diameter of the screw, fax denotes the withdrawal capacity of the screw, which was considered as the contribution of the rope effect of the screw.
Yurrita et al. [27] found that the EYM calculations in EN 1995–1–1 [28] provide conservative results comparing to experimental data, and proposed the correction factor as shown in Eq. (6).
For the connection with shallow notches, the embedment strength of the steel-plate in the timber block should be added into the resistance of the screwed connection of Eq. (6), as shown in Eq. (7).
where, fh,t denotes the embedment strength of the timber considering the effect of steel-plate thickness, which can be evaluated by Eq. (8) due to the relative small thickness; t denotes the width of the shallow notch, dt denotes the thickness of the steel-plate.
The comparisons between the testing results and theoretical ones are displayed in Table 3. It can be found the theoretical results based on the EYM calculations are basically consistent with the experimental results. The calculation models for the connection with shallow notches (Group SP + N + 4S) also showed acceptable accuracy by considering the contribution of embedding resistance of the shallow notch loaded by the steel-plate.

The initial slip modulus of the steel-plate connection can be evaluated based on the theory of the beam on the elastic foundation, which was initially developed by Kuenzi [29], and were demonstrated the feasibility and accuracy in screwed connections by existing investigations [30]. For the screw in the steel-plate connection, the differential equation and boundary conditions can be defined by Eqs. (9) and (10), respectively.
where, k is the foundation modulus of the timber, which was determined as 1320 MPa according to the summary of the Symons et al. [10], by adopting the foundation modulus value of the timber with similar density, moisture content, and elasticity modulus; EsIs is the bending stiffness of the screw, which was determined as 842 N⋅mm2 according the bending tests; l is the penetration depth of the screw.
where, F is the load sustained by the single screw.
The general solutions of Eq. (9) is
where, Ai and Bi (i = 1, 2) are the undetermined coefficients; and
Submitting Eq. (10) into Eq. (11), the relationship between the testing load and the interfacial slip can be obtained as shown in Eq. (13).
Therefore, the slip modulus of the steel-plate connection connected by screws can be estimated by Eq. (14).
For the steel-connection with shallow notches, the effects of the shallow notch on the slip modulus should be considered. Dias et al. [31] provided the design suggestion about the slip modulus of the notched connection depending on the notch width, and the slip modulus of 1000 N/mm per millimeter width was suggested for the notch depths between 20 mm and 30 mm. Similarly, Ben et al. [32] found the slip modulus of shallow notch (lower than 20 mm) were approximately 300 N/mm. Therefore, as the relatively shallow depth (5 mm) of the notch for the steel-plate, the 300 N/mm per millimeter width was adopted in this study. In addition, existing investigations [9,33] proposed the calculation models for the slip modulus of TCC shear connection based on the component method, and demonstrated the feasibility of the component method. Thus, the slip moduli of group SP + N + 4S specimens can be predicted by Eq. (15) considering the contribution of the screws and the shallow notches.
The comparisons between the testing results and analytical ones in the slip modulus are displayed in Table 3. It can be concluded that the predicted value of group SP + 8S(R) is slightly larger than the experimental one, which showed the acceptable accuracy. However, the analytical results of groups SP + 4S(R) and SP + 4S are obviously smaller than their experimental results. This is mainly because the experimental results in groups SP + 4S and SP + 4S(R) overestimated their actual slip moduli, due to that the estimated ultimate bearing capacities were greatly smaller than the maximum testing load. Thus, the initial slip modulus may be affected by the pre-tightening force caused by the screws and the friction between the timber and the steel-plate. This is also one of the reason that the slip moduli of groups SP + 4S(R) and SP + 4S specimens were larger than those of the SP + 8S(R) ones, at the precondition that the number of screws was halved. The values of K0.6 for groups SP + 8S(R), SP + 4S(R), and SP + 4S are consistent with the screw number, due to the ignorance of the effect of the interfacial friction and pre-tightening force caused by screws, demonstrating the feasibility of the prediction model in Eq. (14). For the connection with shallow notches, i.e., Group SP + N + 4S specimens, the analytical result predicted by Eq. (15) was also smaller than the testing results, which was also affected by the relatively small estimated ultimate bearing capacity. However, the K0.6 near the ultimate state was greatly smaller than the initial slip moduli Ks for group SP + N + 4S specimens. This phenomenon means that the shallow notch also lost the partial shear resistance near the ultimate state due to the appearance of the embedment failure of the timber. As a whole, the calculation models for the steel-plate connection with or without shallow notch show the acceptable prediction results compared with the experimental results.
This article presents the push-out experimental results of steel-plate connections for TCC beams. The main parameters included the screw number, the angle steel reinforcement, and the shallow notch for the steel-plate. The failure modes, shear strength, and slip moduli were discussed. Main conclusions can be summarised as following:
• The number of screws showed the significant influence on the ultimate bearing capacity. For the steel-plate with two rows of screws, the shear connection occurred the rotation deformation of steel-plate, which led to the decline of the ultimate bearing capacity and initial slip modulus.
• The application of the angle steel for improving the anchorage performance was unessential. The arrangement of rebar through the steel-plate was sufficient for ensuring the shear strength and slip modulus.
• The timber shallow notch for the steel-plate showed significant improvements in ultimate bearing capacity and slip modulus. Compared with Group SP + 4S, Group SP + N + S with shallow notches, showed the improvement of 53.5% in the initial slip modulus and 24.3% in the ultimate bearing capacity.
• The calculation models of ultimate bearing capacity and slip modulus for steel-plate connections with and without shallow notches showed acceptable accuracy.
Further investigations will focus on the long-term slip of this sort of shear connection. To provide the design guidance of the TCC beams considering the creep of component materials under the action of the long-term loads, the long-term slip and corresponding creep coefficient of the steel-plate connections should be researched further.
Funding Statement: This research was sponsored by the National Natural Science Foundation of China (Grant No. 51878344) and the Postdoctoral Foundation of Jiangsu Province (Grant No. 2021K128B).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Dias, A. M. P. G., Skinner, J., Crews, K., Tannert, T. (2016). Timber-concrete-composites increasing the use of timber in construction. European Journal of Wood and Wood Products, 74(3), 443–451. DOI 10.1007/s00107-015-0975-0. [Google Scholar] [CrossRef]
2. Deresa, S. T., Xu, J., Demartino, C., Minafò, G., Camarda, G. (2021). Static performances of timber-and bamboo-concrete composite beams: A critical review of experimental results. The Open Construction & Building Technology Journal, 15(1), 17–54. DOI 10.2174/1874836802115010017. [Google Scholar] [CrossRef]
3. Dias, A. M. P. G., Schänzlin, J., Dietsch, P. (2018). Design of timber-concrete composite structures (COST Action FP1402/WG 4). European Cooperation in Science and Technology (COSTBrussels, Belgium. [Google Scholar]
4. Sebastian, W. M., Piazza, M., Harvey, T., Webster, T. (2018). Forward and reverse shear transfer in beech LVL-concrete composites with singly inclined coach screw connectors. Engineering Structures, 175, 231–244. DOI 10.1016/j.engstruct.2018.06.070. [Google Scholar] [CrossRef]
5. Du, H., Hu, X., Xie, Z., Wang, H. (2019). Study on shear behavior of inclined cross lag screws for glulam-concrete composite beams. Construction and Building Materials, 224, 132–143. DOI 10.1016/j.conbuildmat.2019.07.035. [Google Scholar] [CrossRef]
6. Di Nino, S., Gregori, A., Fragiacomo, M. (2020). Experimental and numerical investigations on timber-concrete connections with inclined screws. Engineering Structures, 209, 109993. DOI 10.1016/j.engstruct.2019.109993. [Google Scholar] [CrossRef]
7. Marchi, L., Scotta, R., Pozza, L. (2017). Experimental and theoretical evaluation of TCC connections with inclined self-tapping screws. Materials and Structures, 50(3), 1–15. DOI 10.1617/s11527-017-1047-1. [Google Scholar] [CrossRef]
8. Appavuravther, E., Vandoren, B., Henriques, J. (2021). Behaviour of screw connections in timber-concrete composites using low strength lightweight concrete. Construction and Building Materials, 286, 122973. DOI 10.1016/j.conbuildmat.2021.122973. [Google Scholar] [CrossRef]
9. Dias, A. M. P. G. (2005). Mechanical behaviour of timber-concrete joints (Ph.D. Thesis). Delft University of Technology. [Google Scholar]
10. Symons, D., Persaud, R., Stanislaus, H. (2010). Slip modulus of inclined screws in timber-concrete floors. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 163(4), 245–255. DOI 10.1680/stbu.2010.163.4.245. [Google Scholar] [CrossRef]
11. Zhang, L., Chui, Y. H., Tomlinson, D. (2020). Experimental investigation on the shear properties of notched connections in mass timber panel-concrete composite floors. Construction and Building Materials, 234, 117375. DOI 10.1016/j.conbuildmat.2019.117375. [Google Scholar] [CrossRef]
12. Shi, B., Liu, W., Yang, H., Ling, X. (2020). Long-term performance of timber-concrete composite systems with notch-screw connections. Engineering Structures, 213, 110585. DOI 10.1016/j.engstruct.2020.110585. [Google Scholar] [CrossRef]
13. Martin-Gutierrez, E., Estevez-Cimadevila, J., Otero-Chans, D., Suarez-Riestra, F. (2020). Discontinuous π-form steel shear connectors in timber-concrete composites. An experimental approach. Engineering Structures, 216, 110719. DOI 10.1016/j.engstruct.2020.110719. [Google Scholar] [CrossRef]
14. Suárez-Riestra, F., Estévez-Cimadevila, J., Martin-Gutierrez, E., Otero-Chans, D. (2019). Perforated shear + reinforcement bar connectors in a timber-concrete composite solution. Analytical and numerical approach. Composites Part B: Engineering, 156, 138–147. DOI 10.1016/j.compositesb.2018.08.074. [Google Scholar] [CrossRef]
15. Lukaszewska, E., Johnsson, H., Fragiacomo, M. (2008). Performance of connections for prefabricated timber-concrete composite floors. Materials and Structures, 41(9), 1533–1550. DOI 10.1617/s11527-007-9346-6. [Google Scholar] [CrossRef]
16. Khorsandnia, N., Valipour, H., Schänzlin, J., Crews, K. (2016). Experimental investigations of deconstructable timber-concrete composite beams. Journal of Structural Engineering, 142(12), 04016130. DOI 10.1061/(ASCE)ST.1943-541X.0001607. [Google Scholar] [CrossRef]
17. Derikvand, M., Fink, G. (2021). Deconstructable connector for TCC floors using self-tapping screws. Journal of Building Engineering, 42, 102495. DOI 10.1016/j.jobe.2021.102495. [Google Scholar] [CrossRef]
18. Crocetti, R., Sartori, T., Tomasi, R. (2015). Innovative timber-concrete composite structures with prefabricated FRC slabs. Journal of Structural Engineering, 141(9), 04014224. DOI 10.1061/(ASCE)ST.1943-541X.0001203. [Google Scholar] [CrossRef]
19. Zhang, Y., Raftery, G. M., Quenneville, P. (2019). Experimental and analytical investigations of a timber-concrete composite beam using a hardwood interface layer. Journal of Structural Engineering, 145(7), 04019052. DOI 10.1061/(ASCE)ST.1943-541X.0002336. [Google Scholar] [CrossRef]
20. Hu, Y., Wei, Y., Chen, S., Yan, Y., Zhang, W. (2021). Experimental study on timber-lightweight concrete composite beams with ductile bolt connectors. Materials, 14(10), 2632. DOI 10.3390/ma14102632. [Google Scholar] [CrossRef]
21. Tao, H., Yang, H., Liu, W., Wang, C., Shi, B. et al. (2021). Experimental and nonlinear analytical studies on prefabricated timber-concrete composite structures with crossed inclined coach screw connections. Journal of Structural Engineering, 147(5), 04021043. DOI 10.1061/(ASCE)ST.1943-541X.0002988. [Google Scholar] [CrossRef]
22. Wei, Y., Wang, Z., Chen, S., Zhao, K., Zheng, K. (2021). Structural behavior of prefabricated bamboo-lightweight concrete composite beams with perforated steel plate connectors. Archives of Civil and Mechanical Engineering, 21(1), 1–21. DOI 10.1007/s43452-021-00176-9. [Google Scholar] [CrossRef]
23. GB/T 50329–2012 (2012). Standard for Test Methods of Timber Structures. China Building Industry Press (in Chinese). [Google Scholar]
24. ASTM F1575–17 (2017). Standard Test Method for Determining Bending Yield Moment of Nails. ASTM International. [Google Scholar]
25. Shi, B., Zhu, W., Yang, H., Liu, W., Tao, H. et al. (2020). Experimental and theoretical investigation of prefabricated timber-concrete composite beams with and without prestress. Engineering Structures, 204, 109901. DOI 10.1016/j.engstruct.2019.109901. [Google Scholar] [CrossRef]
26. EN 26891 (1991). Timber Structures–Joint Made with Mechanical Fasteners–General Principles for the Determination of Strength and Deformation Characteristics. European Committee for Standardization. [Google Scholar]
27. Jockwer, R., Fink, G., Köhler, J. (2018). Assessment of the failure behaviour and reliability of timber connections with multiple dowel-type fasteners. Engineering Structures, 172, 76–84. DOI 10.1016/j.engstruct.2018.05.081. [Google Scholar] [CrossRef]
28. EN 1995–1–1:2004 (2004). Eurocode 5: Design of Timber Structures–Part 1–1: General-Common Rules and Rules for Buildings. European Committee for Standardization. [Google Scholar]
29. Kuenzi, E. W. (1951). Theoretical design of a nailed or bolted joint under lateral load. Research Report No. D1951. Forest Products Laboratory (USA). [Google Scholar]
30. Wang, X. T., Zhu, E. C., Niu, S., Wang, H. J. (2021). Analysis and test of stiffness of bolted connections in timber structures. Construction and Building Materials, 303, 124495. DOI 10.1016/j.conbuildmat.2021.124495. [Google Scholar] [CrossRef]
31. Dias, A. M., Kuhlmann, U., Kudla, K., Mönch, S., Dias, A. M. A. (2018). Performance of dowel-type fasteners and notches for hybrid timber structures. Engineering Structures, 171, 40–46. DOI 10.1016/j.engstruct.2018.05.057. [Google Scholar] [CrossRef]
32. Ben, Q., Dai, Y., Chen, S., Shi, B., Yang, H. (2022). Shear performances of shallow notch connections for timber-concrete composite (TCC) floors. BioResources, 17(2), 3278–3290. 3278–3290. [Google Scholar]
33. Shi, B., Dai, Y., Tao, H., Yang, H. (2022). Shear performances of hybrid notch-screw connections for timber-concrete composite structures. BioResources, 17(2), 2259–2274. DOI 10.15376/biores.17.2.2259-2274. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |