Journal of Renewable Materials

DOI: 10.32604/jrm.2021.015193

ARTICLE

Bamboo Nail: A Novel Connector for Timber Assemblies

Yehan Xu, Zhifu Dong, Chong Jia, Zhiqiang Wang*and Xiaoning Lu*

College of Materials Science and Engineering, Nanjing Forestry University, Nanjing, 210037, China
*Corresponding Authors: Zhiqiang Wang. Email: tyzhan@njfu.edu.cn; Xiaoning Lu. Email: luxiaoning-nfu@126.com
Received: 30 November 2020; Accepted: 18 January 2021

1  Introduction

Facing on energetic and environmental challenges, sustainable materials for structural application have being worldwide used, such as wood and bamboo [1]. The applications of wood and bamboo have significant effect on the global environment, as wood and bamboo can absorb carbon dioxide from the atmosphere as they grow [2−4]. Wood and bamboo are also suitable for structural utilization with their excellent specific stiffness and strength, and ideal thermal insulating.

There are some kinds of engineered wood composites used in the construction and transportation fields, such as glued-laminated wood [5,6], cross-laminated timber [7], laminated veneer lumber [8,9], etc. The engineered wood products also include dimensional lumber. Normally, dimensional lumbers are assembled by bolted joints, tenon-mortise joints and nail/screw joints. Within these methods, nails represent the easiest and fastest method to connect timber members [10]. The earliest usage of nail is evidenced by Egyptian findings dating back to ca. 3400 BC [11]. Hand-operated hammer and air nail gun are widely used options to drive a nail into wood. When using a hammer, the nail is stepwise moved into wood with a velocity of about 1–2 m/s. In contrast, using machine nailing, the nail is driven into wood by one shot, in single step, with high velocity [12].

Steel nail is successful used in connecting wood members [13]. However, there are some disadvantages in some applications. Firstly, it is necessary to avoid the occurrence of decay concentration around steel nail in moist or high salinity environment. Secondly, Interface of steel nail and wood with tannic acids may cause black colored spots, affecting the visual performance. Thirdly, steel nail connected parts shall be treated afterwards by sawing, drilling or planning because of destructive interaction with the tool blades [12].

Alternative material sources might be wood nail [10,14]. Instead of steel nail, wood nail could be used for timber constructions exposed to wet environments. In addition, wood nail connected parts can easily be sawed, planned and drilled. From the sustainable point of view, wood nail connected parts is much more recyclable than steel nail connected one. Typically, some dense hardwood species are chosen as nail materials. To increasing density and mechanical properties of wood, hydro-thermal-mechanical treatment is an effective approach [15−17]. In the past few years, densified-wood nail and dowel-type fasteners are used to increase the tightness of the connection [10,18].

Bamboo has comparable density and mechanical properties to the densified wood. It is reasonable to produce bamboo nail substituting wood nail. However, limited studies describing the application of bamboo nail. Due to the intrinsic graded hierarchical structure [19,20], the property of bamboo nail should be concerned. In this study, bamboo nail was proposed as a novel connector for timber assemblies. The penetration depth of bamboo nail driven into wood was modelled and verified. The size parameters, such as length, radius and ogive radius, on penetration depth were investigated. Moreover, the effect of densification on penetration depth or mechanical properties was evaluated. The prospect of bamboo nail was discussed as well.

2  Penetration Model

Bamboo is a bio-composite material and its anatomy structure and mechanical properties are highly variable at different location with the stem. In view of the complicated inhomogeneous structure, some assumptions were established before constructing the penetration model. First of all, the bamboo nail was considered as non-compressible component, which had no deformation during penetration. Secondly, target wood was considered as isotropic materials with homogeneous structure [21]. Thirdly, no crack occurred during the penetration.

When the bamboo nail with an ogival nose penetrates a uniform wood surface, the motion and final depth can be calculated as penetration velocity (Vb) of the bamboo nail is known. The ogive radius (φ) is defined as:

φ=s2a (1)

where s and a are defined in Fig. 1.

The incremental ring force normal to the ogival nose (dFn) and in the axial direction (dFz) are expressed as [22]:

dFn=2πs2σn(Vb,φ)⋅[sinφ−(s−aa)]dφ (2a)

dFz=2πs2σn(Vb,φ)⋅[sinφ−(s−aa)]cosφdφ (2b)

where σn(Vb, φ) is the stress on the nose normal to the ogive surface from target resistance. Thus,

Fz=2πs2∫θ0π2σn(Vb,φ)⋅[sinφ−(s−aa)]cosφdφ (3a)

φ0=sin−1(s−aa) (3b)

For high enough Vb, a spherically symmetric cavity at constant velocity V produces plastic and elastic response regions (Fig. 2) [23]. In the plastic region [24]:

p=K(1−ρ0ρ)=Kη (4a)

p=σr+2σφ3 (4b)

σr−σφ=λp+τ;τ=[3−λ3]Y (4c)

where p is the pressure; ρ and ρ0 are densities of the undeformed and deformed material, respectively; η is the volumetric strain; K is the bulk modulus; σr and σφ are radial and circumferential Cauchy stress components, respectively; λ and τ define the pressure-dependent strength; and Y is the uniaxial compressive strength.

The particle velocity (v) at the interface of ogival nose and target is calculated on Vb:

v(Vb,φ)=Vbcosφ (5)

Luk et al. [22] introduced a dimensionless variable S to calculate the normal stress distribution around the nose as:

S(Vb,φ)=A+B(Vbcosφ)2 (6)

where A and B are variables associated with the mechanical properties of the target. They are defined as Eqs. (7a)−(7c):

A=23[1−lnη] (7a)

B=ρ0Yγ2[3YE+η(1−3Y2E)2+3η23−η(4−η)2(1−η)] (7b)

γ=[(1+Y2E)−(1−η)]13 (7c)

where E is Young’s modulus.

Substituting Eq. (6) into Eq. (3a) and integrating gives:

Fz=πa2Y[A+(8ψ−1)24ψ2BVb2] (8)

and transforms to

Fz=A′+B′Vb2 (9a)

A′=πa2YA (9b)

B′=πa2Y((8ψ−1)24ψ2)B (9c)

Based on Newton’s second law, Eq. (9a) transforms to

md2Ldt2=A′+B′Vb2 (10)

where m is mass of bamboo nail, L and t are theoretical penetration depth and time, respectively.

Eq. (10) becomes

dVbdL+1mB′Vb=−1mA′Vb−1 (11)

Dividing Vb–1 in Eq. (11), thus

dVbdL⋅Vb+1mB′Vb2=−1mA′ (12)

Setting Z = Vb2, and Eq. (12) becomes

dZdL+2mB′Z=−2mA′ (13)

Also, P = −2mB′ , Q = −2mA′ and dZdL=PZ+Q , thus Eq. (13) is written as

dZPZ+Q=dL (14)

Integrating gives:

L=1Pln|PZ+Q| (15)

Concerning that the bamboo nail is compressible during penetration, a correction factor (Kb) is introduced. Thus, a final penetration depth of bamboo nail in the target (Lb) is obtained as

Lb=KbL (16a)

Kb=EEs (16b)

where Es is the Young’s modulus of steel nail.

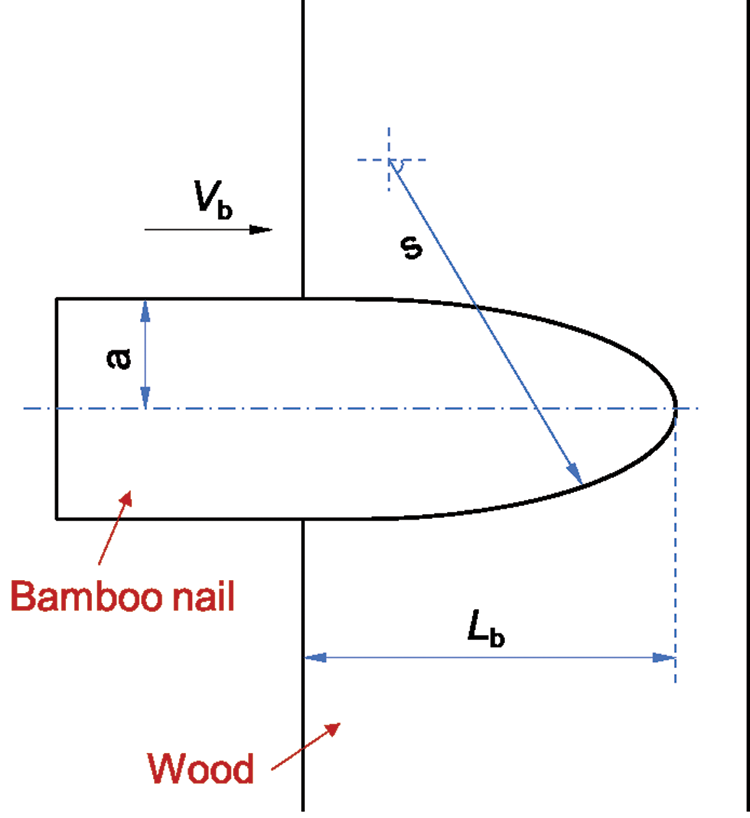
Figure 1: Penetration schematic of bamboo nail into wood

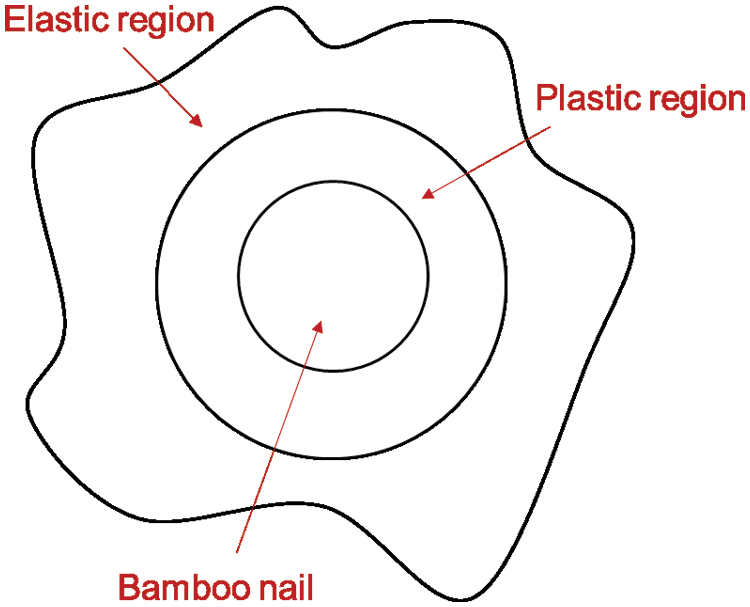
Figure 2: Elastic and plastic regions after penetration

3  Materials and Methods

3.1 Preparation of Bamboo Nail

Three years old moso bamboo culms were collected from a bamboo plantation located in Jiangsu Province in China. Bamboo blocks were cut from the third internode. The dimensions of the block were 100 mm (longitudinal) × 20 mm (radial) × 20 mm (tangential). The moisture content was about 12% after air-dried for 9 weeks. Then, a series of bamboo nails with different sizes (Groups 1–3 in Tab. 1) were prepared by using a micro machine tool (Fig. 3a). Different size of bamboo nail is shown in Fig. 3b.

Figure 3: Typical feature of bamboo nail (b) and its manufacturing (a)

Some densified bamboo nails were prepared as well. The above-mentioned blocks were immersed in water (80°C) for 3 h, and then densified by a hot press machine (140°C, 30 min). The densification pressure was adjusted to obtain a series of compression ratios. The bamboo was placed in the conditioning chamber (25°C, 60% RH) for 2 weeks after the densification. A series of densified bamboo nails were prepared with the density ranged from 0.82 to 1.16 g/cm3 (Group 4 in Tab. 1). The length, radius and the ogive radius of the densified bamboo nail was 40 mm, 4 mm and 3.1, respectively. Fifty replicates for each densification condition were performed.

3.2 Penetration Test

Air nail gun was operated (6.5 bar air pressure) as nailing machine. Target wood to nail in was Mongolian Scotch Pine (Pinussylvestris). The density of Mongolian Scotch Pine was 0.47 g/cm3. Bamboo nails were shot perpendicular to growth rings (radial direction) of wood.

After penetration, the final depth and the pull-out resistance were characterized. For evaluating the depth, the sample was cut alongside through the middle of the bamboo nail. The pull-out resistance force was determined by a universal testing machine. The modulus of rupture (MOR) of the target (two pieces of wood connected with bamboo nail) was tested according to the standard—GB/T 17657-2013. The statistical software, SPSS version 17.0, was used for data analysis. Significant effects of penetration depth, mechanical properties were analyzed by Duncan’s multiple comparison test (p = 0.05).

Penetration velocity (Vb) of bamboo nail was also tested. The scheme is shown in Fig. 4. A strain gauge was glued on the target surface, and the bamboo nail was shot towards the stain gauge. The distance (d) between strain gauge and the opening of the air nail gun was 5 cm. We recorded the response time (t) to calculate Vb as

Vb=dt (17)

In each condition, average value of Vb was calculated based on ten replicates.

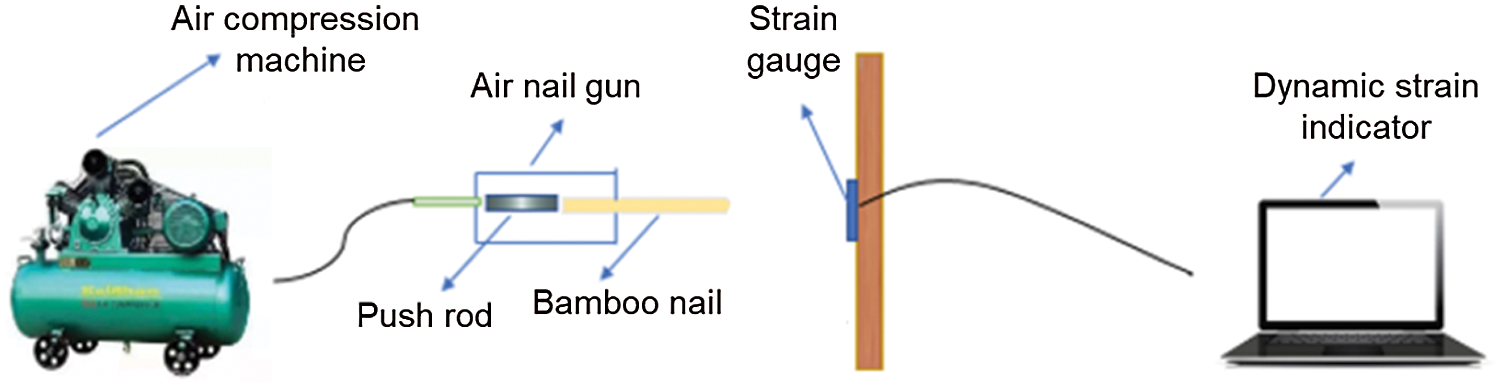
Figure 4: Schematic diagram of the determination of penetration velocity

Table 1: Size parameters of bamboo nail in different groups

4  Results and Discussion

4.1 Penetration Velocity (Vb)

Concerning the air resistance is neglectable, the velocity calculated based on Eq. (17) could represent the penetration velocity. Response time reflected by the strain gauge was about 0.0026 s, with no significant variation among different nail sizes. In hence, Vb was calculated as 19.23 m/s.

4.2 Effect of Nail Size

The tested penetration depth of bamboo nail with different length, radius and ogive radius are shown in Figs. 5−7. In addition, the predicted values derived from Eq. (16a) are displayed as well. According to Fig. 5, the penetration depth increased with the increasing nail length for both tested and predicted results. The predicted penetration depth was greater than real tested one. The gaps were more pronounced at longer lengths. During insertion, the nail with longer lengths were more easily to be deviated from the shooting direction. Fig. 6 shows the changes of actual or predicted penetration depth as a function of nail radius. Larger radius donated nail with more mass. At a given pressure (6.5 bar), the nail had more energy of motion to penetrate. The actual penetration depth was more than predicted one, especially at larger radius. Bamboo was a structurally graded material, vascular bundle distributed more sparser towards the center of the culm. In hence, the higher actual values of penetration depth may be attributed to greater density of bamboo nail with larger radius. In addition, the penetration depth increased with the increasing ogive radius of the bamboo nail (Fig. 7), which enhance the intensity of pressure at the interface of ogival nose and the target. The transverse tensile strength of the target (Pine wood) was significantly less than longitudinal one. More pressure at the interface caused cleavages of the target. In hence, the more penetration depth could be found at larger ogive radius.

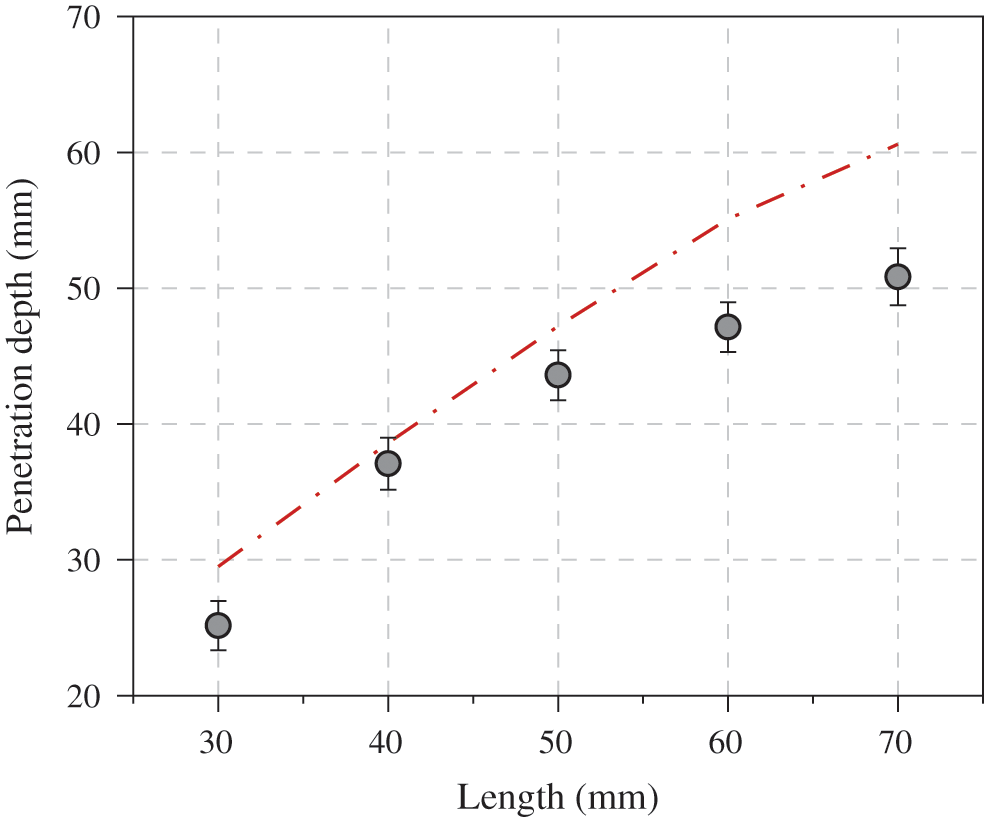
Figure 5: Effect of length of bamboo nail on the final penetration depth. Circle, real test data; Line, predicted data based on Eq. (16a)

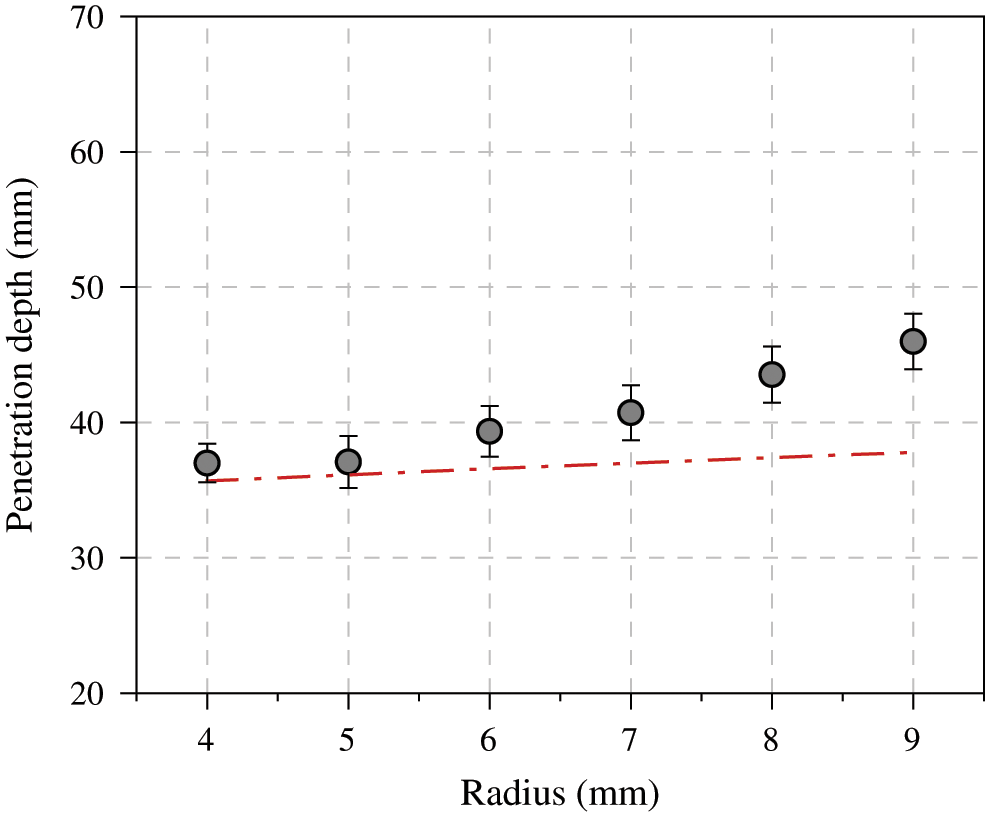
Figure 6: Effect of radius of bamboo nail on the final penetration depth. Circle, real test data; Line, predicted data based on Eq. (16a)

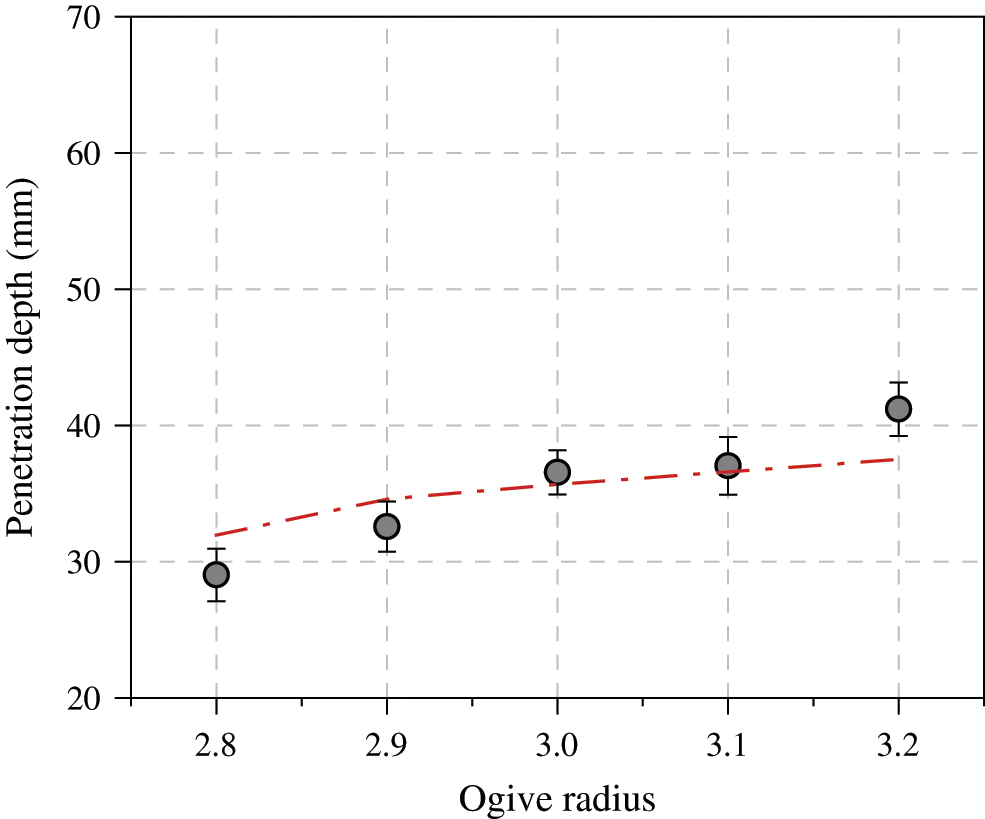
Figure 7: Effect of ogive radius of bamboo nail on the final penetration depth. Circle, real test data; Line, predicted data based on Eq. (16a)

4.3 Effect of Densification

The density of bamboo nail increased about 40% after densification, as shown in Fig. 8. With the combination effect of hydrothermal softening and mechanical pressing [25,26], bamboo is easily to be densified. As the density of bamboo nail increased to 1.12 g/cm3, the penetration depth was up to 46 mm compared to the un-densified one (37 mm) (Fig. 9). But it would decrease over 1.16 g/cm3, and had no significant difference with the un-densified nail. In hence, 1.12 g/cm3 could be seen as a critical value with respect to densification.

Hydro-thermal-mechanical treatment could enhance the density and mechanical properties of bamboo. Proper pressure could fully compress the space that cell lumens occupied [27]. However, when the pressure was too high, fiber cells would be collapsed. Thus, the stiffness of bulk bamboo would be diminished. In this study, when the compression ratio exceeded 30%, penetration depth declined significantly (Fig. 9), which may be attributed to the collapse of fiber cells.

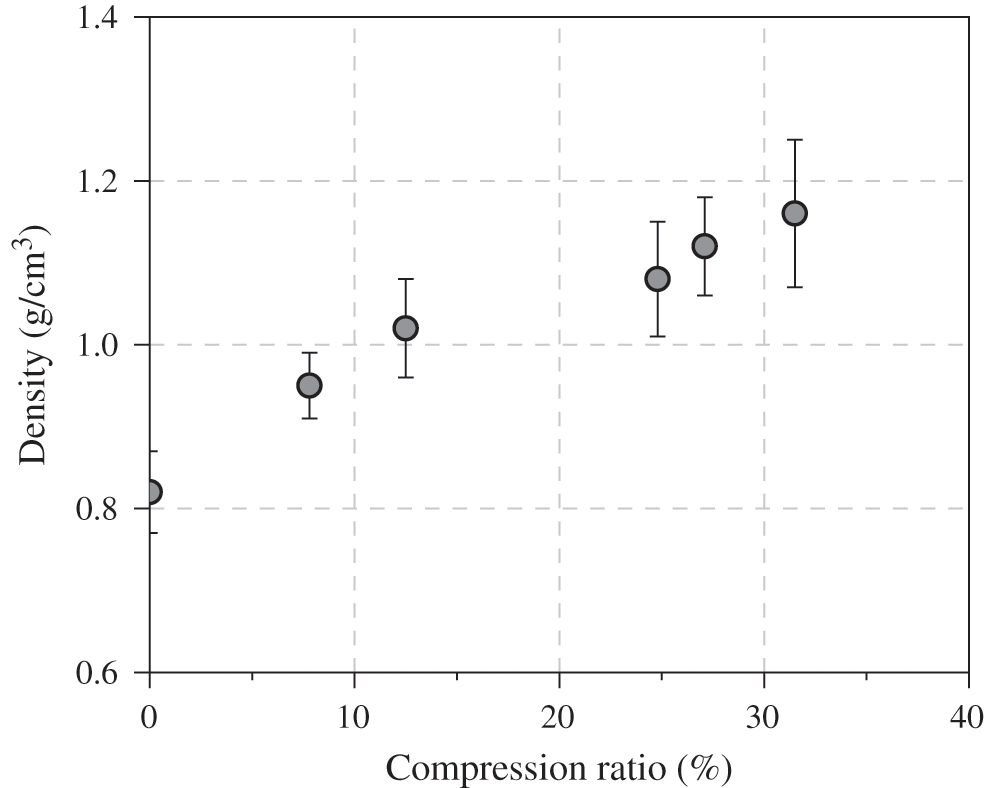
Figure 8: Relations of compression ratio and density

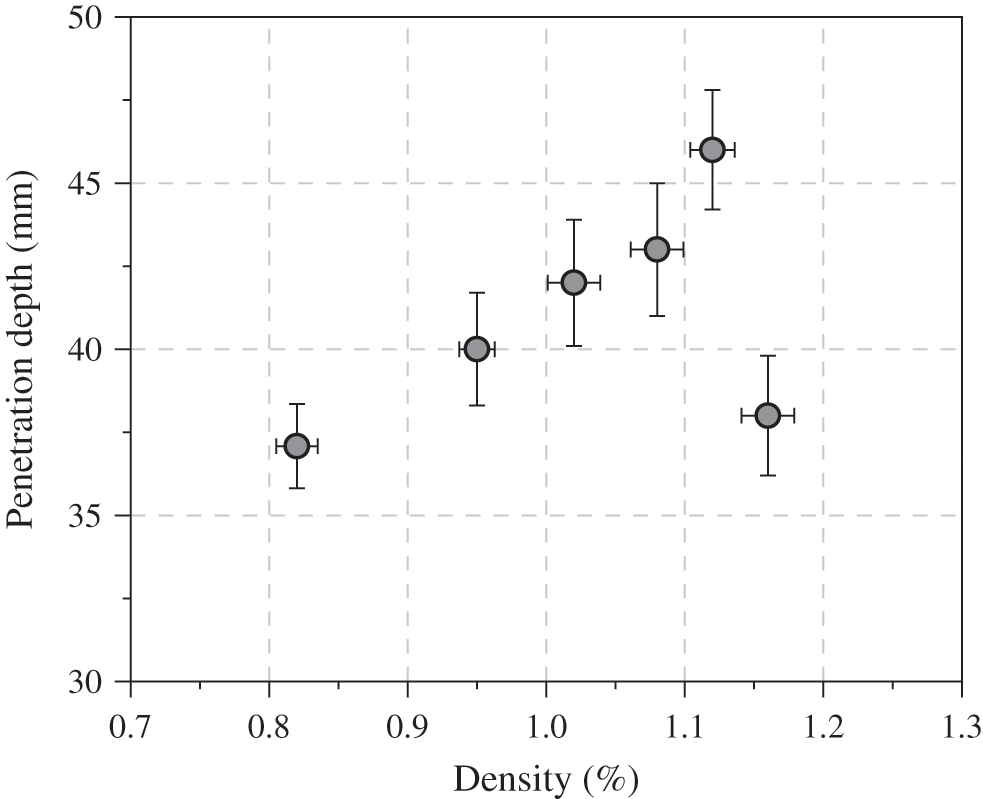
Figure 9: Influence of densification on penetration depth

The pull-out resistance of nail and the strength of wood were carried out to evaluate the densified performance. As shown in Fig. 10, the pull-out resistance of densified bamboo nail ranged from 387 to 395 N. The pull-out resistance was originated from the interface friction between wood and bamboo nail. Since the pull-out speed was constant, the interface friction was mostly related to the surface characteristics of wood and bamboo nail [28,29]. In hence, densified extent had no significant influence on the pull-out resistance. According to Fig. 11, highest MOR value of target connected with the densified nail was 202 MPa at the density of 1.12 g/cm3, which was obviously greater than the un-densified nail (150 MPa). Due to the probably collapse of fibers at over-high pressure, a decrement of MOR was observed when density reached as 1.16 g/cm3. Comparing to the previous study [A], the pull-out resistance of bamboo nail was not as perfect as the densified wood nail. The average pull-out resistance of densified wood nail was about 584 N.

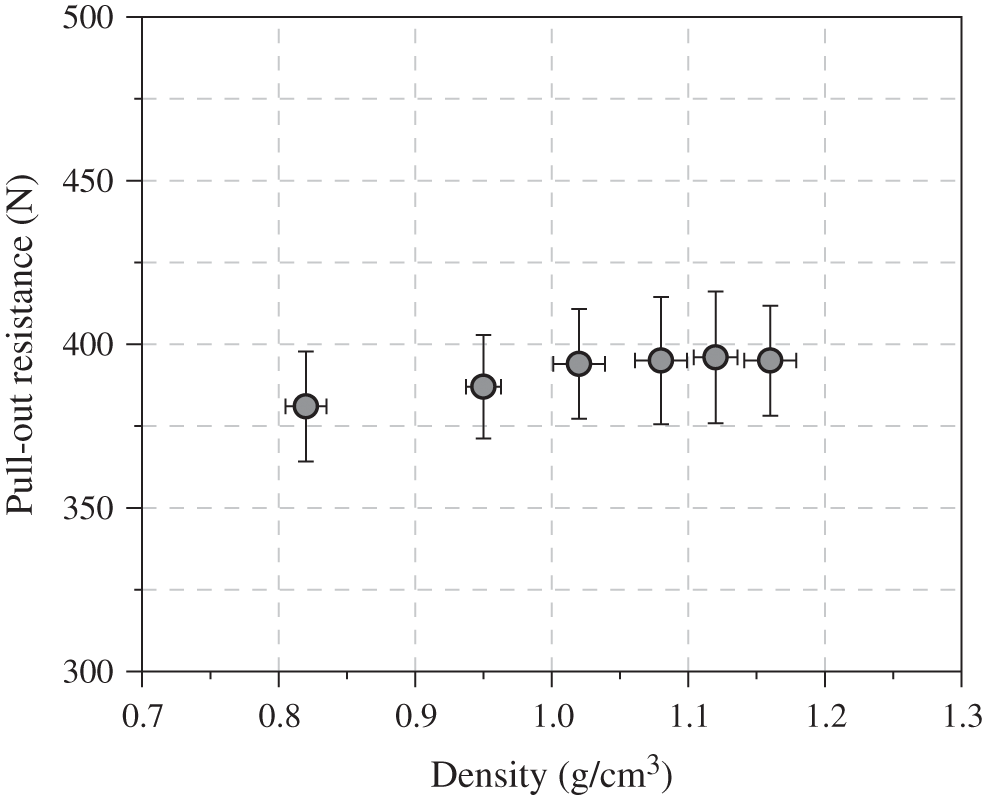
Figure 10: Influence of density on pull-out resistance of nail

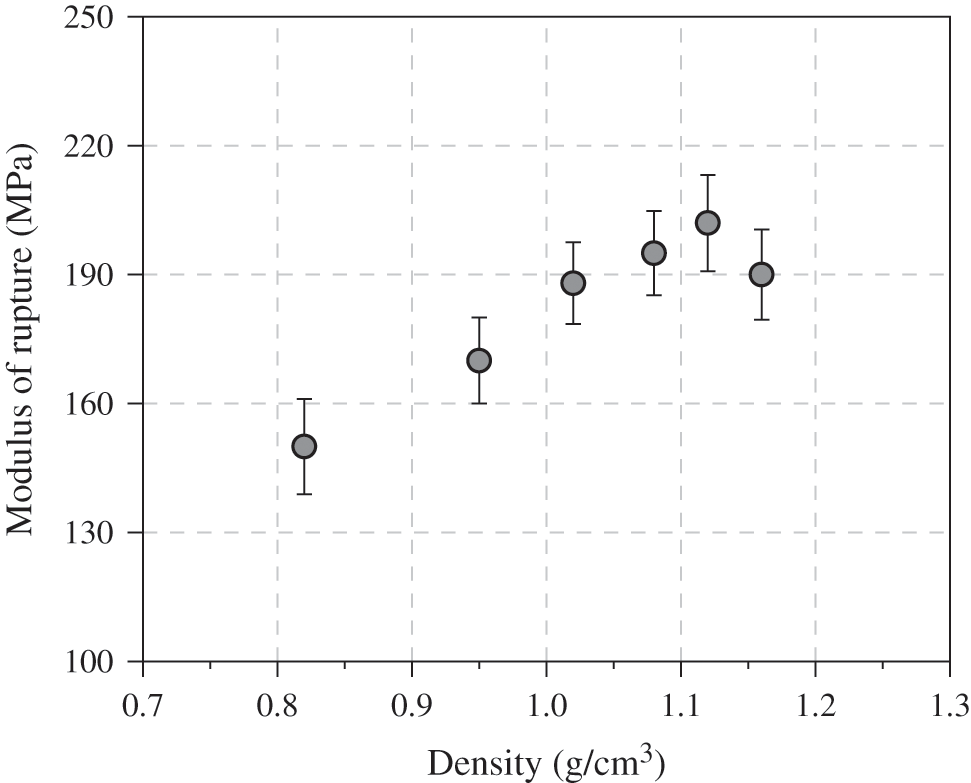
Figure 11: Influence of density on modulus of rupture of target

4.4 Prospect of Bamboo Nail

Bamboo is an intrinsically non-uniform material in both longitudinal and transverse directions. It is necessary to understandings the nail characteristics with respect to the structure of bamboo. Based on the penetration model established for steel nail [23,30], the related one of bamboo nail was proposed. In addition, the relationships between penetration depth of bamboo nail and its basic parameters were constructed.

Our tested results in Figs. 5–7 provided first hand data for selecting proper parameters during the actual uses of bamboo nail. Longer bamboo nail is better for penetration under the premise of that no bending of nail occur. Longer length could donate the nail with more motion of energy and more penetration depth. In terms of nail radius, large radius would expand the compressed region (illustrated as elastic region in Fig. 2), and increase the friction area among the interface.

Although the performance at ogive radius more than 3.2 was not done due to the machine limitation, we considered the strength of the taper nose would be declined. In addition, the different densified extents are also compared. 1.12 g/cm3 (or 30% compression ratio) is the critical density when densification is needed, because further increment of density would decrease the penetration depth of nail.

Comparing to steel nail, bamboo nail is much economically and environmental-friendly. Timber assemblies connected with bamboo nails are easily to be detached and recycled. With the application of bamboo nail, much manpower and metal resources can be saved. As a biomaterial, it is necessary to improve the durability and decay resistance of bamboo. Moreover, the time-dependent mechanical behavior (including pull-out, lateral resistances, relaxation) should be further investigated for effectively use of bamboo nail.

5  Conclusions

In this study, bamboo nail was proposed as a novel connector for timber assemblies. Penetration model of bamboo nail was established. Influence of nail parameters (length, radius and ogive radius) on penetration depth were verified. The penetration depth increased with the increasing nail length, radius or ogive radius for both tested and predicted results. The effect of densification on penetration depth or mechanical properties was evaluated. 1.12 g/cm3 was the critical density when densification was needed, and further increment of density would decrease the penetration depth of nail. The results of this study manifests that the proposed model is capable to predict the penetration depth of bamboo nail. These findings may provide new insight into efficiently utilization of bamboo resources.

Funding Statement: This work was financially supported by the National Natural Science Foundation of China (No. 32071700).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Zhan, T., Sun, F., Lv, C., He, Q., Wang, X. et al. (2019). Evaluation of moisture diffusion in lignocellulosic biomass in steady and unsteady states by a dynamic vapor sorption apparatus. Holzforschung, 73(12), 1113–1119. DOI 10.1515/hf-2019-0063. [Google Scholar] [CrossRef]

 2.  Sun, X., He, M., Li, Z. (2020). Novel engineered wood and bamboo composites for structural applications: State-of-art of manufacturing technology and mechanical performance evaluation. Construction and Building Materials, 249(6780), 118751. DOI 10.1016/j.conbuildmat.2020.118751. [Google Scholar] [CrossRef]

 3.  Li, H., Zhang, H., Qiu, Z., Su, J., Wei, D. et al. (2020). Mechanical properties and stress strain relationship models for bamboo scrimber. Journal of Renewable Materials, 8(1), 13–27. DOI 10.32604/jrm.2020.09341. [Google Scholar] [CrossRef]

 4.  Chen, C., Mo, M., Chen, W., Pan, M., Xu, Z. et al. (2018). Highly conductive nanocomposites based on cellulose nanofiber networks via NaOH treatments. Composites Science and Technology, 156(5), 103–108. DOI 10.1016/j.compscitech.2017.12.029. [Google Scholar] [CrossRef]

 5.  Okada, T., Kobori, H., Kojima, Y., Suzuki, S., Nishikido, K. et al. (2020). Evaluating the durability of structural glulam bonded with aqueous polymer-isocyanate adhesive by two kinds of accelerated aging treatments. European Journal of Wood and Wood Products, 78(1), 113–122. DOI 10.1007/s00107-019-01485-w. [Google Scholar] [CrossRef]

 6.  Guo, N., Xiong, H., Wu, M., Zuo, H., Jiang, F. et al. (2020). Long-term bending behaviour of prestressed glulam bamboo-wood beam based on creep effect. Structural Durability & Health Monitoring, 14(3), 229–248. [Google Scholar]

 7.  Brandner, R., Flatscher, G., Ringhofer, A., Schickhofer, G., Thiel, A. (2016). Cross laminated timber (CLTOverview and development. European Journal of Wood and Wood Products, 74(3), 31–351. DOI 10.1007/s00107-015-0999-5. [Google Scholar] [CrossRef]

 8.  Chen, F., Deng, J., Li, X., Wang, G., Smith, L. M. et al. (2017). Effect of laminated structure design on the mechanical properties of bamboo-wood hybrid laminated veneer lumber. European Journal of Wood and Wood Products, 75(3), 439–448. DOI 10.1007/s00107-016-1080-8. [Google Scholar] [CrossRef]

 9.  Chen, C., Wang, Y., Meng, T., Wu, Q., Fang, L. et al. (2019). Electrically conductive polyacrylamide/carbon nanotube hydrogel: Reinforcing effect from cellulose nanofibers. Cellulose, 26(16), 8843–8851. DOI 10.1007/s10570-019-02710-8. [Google Scholar] [CrossRef]

10. Riggio, M., Sandak, J., Sandak, A. (2016). Densified wooden nails for new timber assemblies and restoration works: A pilot research. Construction and Building Materials, 102(1), 1084–1092. DOI 10.1016/j.conbuildmat.2015.06.045. [Google Scholar] [CrossRef]

11. Wright, G. R. (2009). Ancient building technology. Volume 3: Construction. Leiden: Brill. [Google Scholar]

12. Korte, H., Koch, G., Krause, K. C., Koddenberg, T., Siemers, S. (2018). Wood nails to fix softwoods: Characterization of structural deformation and lignin modification. European Journal of Wood and Wood Products, 76(3), 979–988. DOI 10.1007/s00107-018-1288-x. [Google Scholar] [CrossRef]

13. Derikvand, M., Jiao, H., Kotlarewski, N., Lee, M., Chan, A. et al. (2019). Bending performance of nail-laminated timber constructed of fast-grown plantation eucalypt. European Journal of Wood and Wood Products, 77(3), 421–437. DOI 10.1007/s00107-019-01408-9. [Google Scholar] [CrossRef]

14. Wang, Y., Lee, S. H. (2018). A theoretical model developed for predicting nail withdrawal load from wood by mechanics. European Journal of Wood and Wood Products, 76(3), 973–978. DOI 10.1007/s00107-017-1227-2. [Google Scholar] [CrossRef]

15. Wang, J., Wang, X., Zhan, T., Zhang, Y., Lv, C. et al. (2018). Preparation of hydro-thermal surface-densified plywood inspired by the stiffness difference in sandwich structure of wood. Construction and Building Materials, 177(1–3), 83–90. DOI 10.1016/j.conbuildmat.2018.05.135. [Google Scholar] [CrossRef]

16. Zhan, T., Jiang, J., Lu, J., Zhang, Y., Chang, J. (2018). Influence of hygrothermal condition on dynamic viscoelasticity of Chinese fir (Cunninghamialanceolata). Part 1: Moisture adsorption. Holzforschung, 72(7), 567–578. DOI 10.1515/hf-2017-0129. [Google Scholar] [CrossRef]

17. Zhan, T., Jiang, J., Lu, J., Zhang, Y., Chang, J. (2018). Influence of hygrothermal condition on dynamic viscoelasticity of Chinese fir (Cunninghamialanceolata). Part 2: Moisture desorption. Holzforschung, 72(7), 579–588. DOI 10.1515/hf-2017-0130. [Google Scholar] [CrossRef]

18. Jung, K., Kitamori, A., Komatsu, K. (2008). Evaluation on structural performance of compressed wood as shear dowel. Holzforschung, 62(4), 461–467. DOI 10.1515/HF.2008.073. [Google Scholar] [CrossRef]

19. Zhan, T., Jiang, J., Lu, J., Zhang, Y., Chang, J. (2019). Frequency-dependent viscoelastic properties of Chinese fir (Cunninghamia lanceolata) under hygrothermal conditions. Part 1: Moisture adsorption. Holzforschung, 73(8), 727–736. DOI 10.1515/hf-2018-0208. [Google Scholar] [CrossRef]

20. Wang, X., Yuan, Z., Zhan, X., Li, Y., Li, M. et al. (2020). Multi-scale characterization of the thermal—Mechanically isolated bamboo fiber bundles and its potential application on engineered composites. Construction and Building Materials, 262(10), 120866. DOI 10.1016/j.conbuildmat.2020.120866. [Google Scholar] [CrossRef]

21. Kuai, B., Wang, X., Lv, C., Xu, K., Zhang, Y. et al. (2019). Orthotropic tension behavior of two typical Chinese plantation woods at wide relative humidity range. Forests, 10(6), 516. DOI 10.3390/f10060516. [Google Scholar] [CrossRef]

22. Luk, V. K., Forrestal, M. J. (1987). Penetration into semi-infinite reinforced-concrete targets with spherical and ogival nose projectiles. International Journal of Impact Engineering, 6(4), 291–301. DOI 10.1016/0734-743X(87)90096-0. [Google Scholar] [CrossRef]

23. Forrestal, M. J., Tzou, D. Y. (1997). A spherical cavity expansion penetration model for concrete targets. International Journal of Solids & Structures, 34(31–32), 4127–4146. DOI 10.1016/S0020-7683(97)00017-6. [Google Scholar] [CrossRef]

24. Forrestal, M. J., Longcope, D. B. (1990). Target strength of ceramic materials for high-velocity penetration. Journal of Applied Physics, 67(8), 3669–3672. DOI 10.1063/1.345322. [Google Scholar] [CrossRef]

25. Dixon, P. G., Semple, K. E., Kutnar, A., Kamke, F. A., Smith, G. D. et al. (2016). Comparison of the flexural behavior of natural and thermo-hydro-mechanically densified Moso bamboo. European Journal of Wood and Wood Products, 74(5), 633–642. DOI 10.1007/s00107-016-1047-9. [Google Scholar] [CrossRef]

26. Wang, J., Wang, X., He, Q., Zhang, Y., Zhan, T. (2020). Time-temperature-stress equivalence in compressive creep response of Chinese fir at high-temperature range. Construction and Building Materials, 235(6), 117809. DOI 10.1016/j.conbuildmat.2019.117809. [Google Scholar] [CrossRef]

27. Peng, H., Salmén, L., Jiang, J., Lu, J. (2020). Creep properties of compression wood fibers. Wood Science and Technology, 54(6), 1497–1510. DOI 10.1007/s00226-020-01221-1. [Google Scholar] [CrossRef]

28. Wang, Z., Li, H., Lorenzo, R., Corbi, I., Corbi, O. et al. (2020). Review on bond properties between wood and fiber reinforced polymer. Journal of Renewable Materials, 8(8), 993–1018. DOI 10.32604/jrm.2020.012488. [Google Scholar] [CrossRef]

29. Zhang, J., Zhang, Z., Tong, K., Wang, J., Li, S. (2020). Bond performance of adhesively bonding interface of steel-bamboo composite structure. Journal of Renewable Materials, 8(6), 687–702. DOI 10.32604/jrm.2020.09513. [Google Scholar] [CrossRef]

30. Forrestal, M. J., Luk, V. K. (1992). Penetration into soil targets. International Journal of Impact Engineering, 12(3), 427–444. DOI 10.1016/0734-743X(92)90167-R. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.