Phyton-International Journal of Experimental Botany

DOI: 10.32604/phyton.2022.019386

ARTICLE

Tree Height-Related Hydraulic Strategy to Cope with Freeze-Thaw Stress in Six Common Urban Tree Species in North China

Cunyang Niu, Wenkai Shou, Li Ma and Jianqiang Qian*

Department of Ecology, College of Forestry, Henan Agricultural University, Zhengzhou, 450002, China
*Corresponding Author: Jianqiang Qian. Email: qianfeng8582@163.com
Received: 22 September 2021; Accepted: 22 October 2021

1  Introduction

Frequent occurrence of extreme climatic events has been observed under the context of global climate change. People in cities are very vulnerable to extreme weather events, and the urban heat island effect exacerbates this adverse effect. Urban trees can effectively cool the air and surfaces [1] through shading effects and the evapotranspiration process [2,3]. However, urban forests are very sensitive to climate change [4]. The scale and effectiveness of ecosystem services provided by urban forests are determined by their size, structure, and species composition [4]. Urban trees can be damaged by extreme weather events, after which they cannot provide relevant services. Drought and freeze-thaw-induced hydraulic failure is an important factor that can cause tree dieback [5]. Urban trees with different heights contribute to the biodiversity of urban ecosystems, thereby enhancing the resistance of urban forests to climate change. Hence, exploring the hydraulic strategy of tree species with diverse heights to adapt to drought and freeze-thaw stress is of great significance to ecological function provision of urban forests under climate change.

Plant height is a key component of plant ecological strategies [6]. The maximum potential height has profound implications for photosynthesis, growth, and hydraulic conductance [7]. Many researchers have attempted to understand the underlying mechanisms that determine tree height growth. Dry-mass allocational allometry and hydraulic limitation, as mechanisms, have explained the universal patterns of plant height [8]. The widely accepted hypothesis of hydraulic limitation arises from the increased gravity of the water column constraining water transport from the root to the leaf along longer hydraulic pathways [9], which could induce hydraulic failure and limit plant growth.

In addition to the physiological limitations of plant height, environmental factors are also important in affecting plant height. For example, canopy leaves are often exposed to harsh environments (e.g., drought and cold), and they often have a strong stomatal control ability to reduce water loss and embolism induced by drought or cold stress, respectively, which in turn will decrease the photosynthetic and growth rates [8,10]. Water conduction through narrow vessels in the plant xylem system is a key link between plant height and climate change [8,11]. Drought or freeze-thaw stress can disrupt the conductive stream and block vessels with gas embolisms [12]. Abundant embolisms are often associated with branch dieback or even whole plant death [11]. Different tree species would have different strategies to adapt to embolism by adjusting hydraulic traits, which are tightly associated with tree height [8]. Numerous studies have found that tree height is a key predictor of mortality during extreme droughts [13,14]. However, few studies have been conducted to explore the tree height-related hydraulic strategies to respond to freeze-thaw stress under climate change.

In some warm temperate forests, freeze-thaw stress could interrupt the normal function of xylem water transport [15]. If the embolized vessels cannot recover in the next spring, they would inhibit the growth of trees. A previous study showed that freeze-thaw-induced embolism causes the death of large-scale trees in temperate forests [16]. Therefore, the study of hydraulic strategies in response to freeze-thaw stress of trees with different heights is helpful to understand the relationship between plant height and freeze-thaw stress under climate change. Co-occurring tree species often exhibit large variations in height within a given ecosystem, which indicates that different ecological strategies are involved in adapting to the microenvironment along the vertical height gradient within the ecosystem. The microenvironment differences from the tree canopy to the understory often have significant effects on stem and leaf physiological traits [17–19]. Stems and leaves in higher tree canopies are often exposed to increased radiation, strong winds, and low air temperature, and must cope with possible stem and leaf desiccation or frost, whereas the short plants experience relatively milder and wet microenvironments, that determine a lower irradiance, constant temperature, and higher humidity [19]. Tall and short trees should have different strategies to cope with environmental stress by regulating stem and leaf physiological traits.

Many studies have regarded stem hydraulic traits as proxies for understanding the water use strategies of species with different plant heights [20–22]. Traits, such as xylem anatomical structure, are essential metrics for vessels to maintain functionality and provide sufficient water to the canopy for plants growing taller. Vessel diameter is a key trait for xylem water transport efficiency, which is positively correlated with the fourth power of vessel diameter [23]. Previous studies have shown that xylem water transport efficiency is coordinated with transpiration, photosynthesis, and growth [24,25]. For a given sapwood area, fewer wider vessels provide higher transport conductivity than many small vessels, but wider vessels are more vulnerable to freeze-thaw stress [26], which can result in reduced growth or even diebacks [27]. Although small vessels are more resistant to freeze-thaw-induced embolism, they might limit the photosynthesis and growth of plants under favorable conditions [28]. Short plants, such as shrubs and small trees, often have narrow vessels and higher vessel and wood densities, suggesting a conservative water use strategy [22,29]. Furthermore, previous studies mainly focused on the relationship between plant height and functional traits in intraspecific comparisons [30,31], but the interspecific comparisons of relationships between tree height and hydraulic traits have often been ignored.

In this study, we examined nine stem hydraulic traits on six co-occurring tree species to compare different hydraulic strategies among tree species with different heights in urban forests of the Botanical Garden, Zhengzhou, Central China. The purpose of this study was to test the following hypothesis: 1) tall trees have wider vessels and higher hydraulic conductivity, but more winter embolism than short trees, and 2) trees of different heights can be well separated by multiple hydraulic functional traits, thus implying different hydraulic strategies.

2  Materials and Methods

2.1 Study Site and Plant Materials

This study was conducted in the Zhengzhou Botanical Garden, Henan Province, central China (112°42′−114°14E, 34°16′−34°58 N). It belongs to the northern temperate zone and has a continental monsoon climate with four distinct seasons and a frost-free period of 210 days. The mean annual air temperature and precipitation are 14.4°C and 640.9 mm, respectively. The zonal vegetation belongs to the broad-leaved temperate deciduous-evergreen mixed forest zone, and the flora belongs to the north-central temperate distribution and the East Asian distribution.

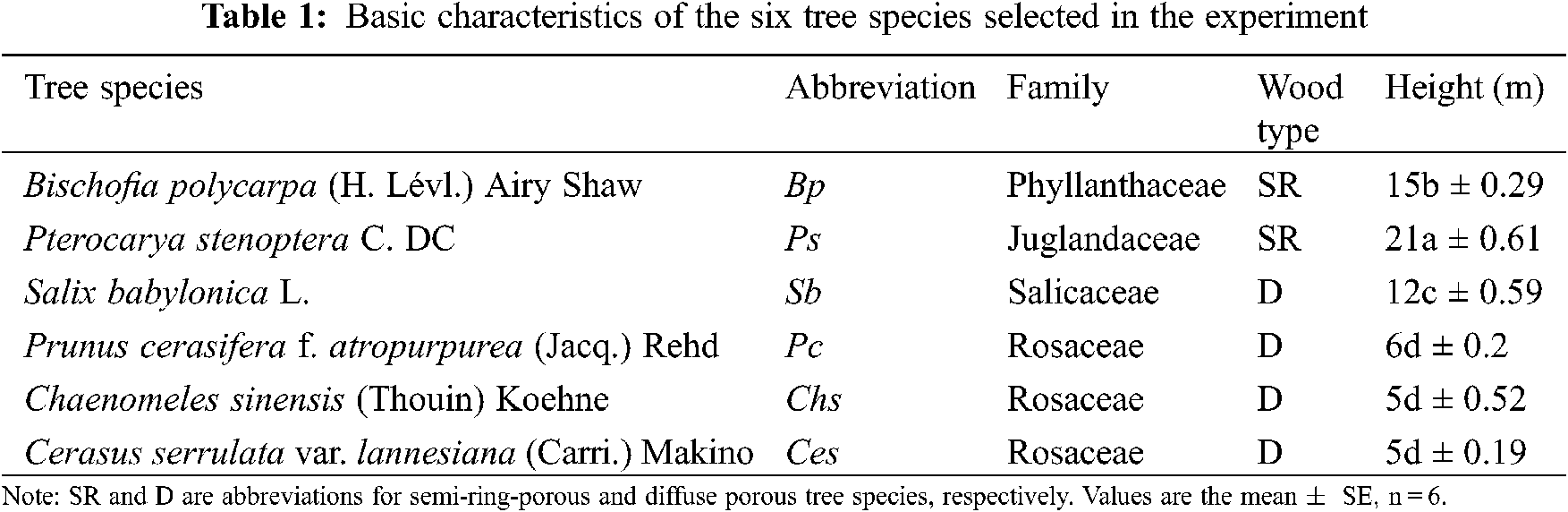
Six mature broad-leaf tree species, which are common urban trees in North China, were selected for this study. Species included Bischofia polycarpa (Bp), Pterocarya stenoptera (Ps), Salix babylonica (Sb), Prunus cerasifera (Pc), Chaenomeles sinensis (Chs), and Cerasus serrulate (Ces) (Table 1). For each species, six trees with similar ages and height were selected. The actual adult tree height was measured using a multifunctional tree height measuring instrument (LD6172). In the present study, trees differing in height were classified into two growth forms based on the system classification of plant life forms proposed by Christen Raunkier [32] as follows: Tall trees (height ranging from 12 to 21 m, including Bp, Ps, and Sb), and short trees (height ranging from 5 to 6 m, including Pc, Chs, and Ces) (Table 1). The hourly mean air temperature from October 2017 to October 2018 was obtained from the nearest meteorological station (Fig. S1). In addition, the botanical garden vegetation is not watered from mid-fall to the early next spring (i.e., from November to April in the following year).

2.2 Xylem Hydraulic Conductivity

We measured the xylem hydraulic conductivity (Kh) in February 2018 (late winter) and June 2018 (summer). Kh was measured for six stem segments on each tree species. Six branches of each species were cut before sunrise, which were approximately 1 m long, straight enough, and growing on the sun side. The branches were immediately placed in black plastic bags that were sprayed with water to keep the samples moist. The stem segment, approximately 20 cm long and 0.6 cm in diameter, was cut under water in the laboratory. We measured the xylem native Kh via gravimetric analysis using a degassed KCl solution (20 mmol L−1) filtered through a filter (0.2 μm in pore size) [33]. A 50 cm hydraulic head was used to generate stable low pressure, which was used to promote the flow of water and calculate the flow rate (Jv, kg s−1) of the liquid through the segments. The calculation formula for Kh (kg m s−1 MPa−1) was as follows:

Kh=Jv/(ΔP/ΔL) (1)

ΔP/ΔL (MPa m−1) is the pressure per unit length of the segment. Formula (1) was used to calculate the native Kh, and the maximum hydraulic conductivity (Khmax) was measured using the flush method [33]. The segments that were used to obtain the native Kh were flushed with degassed KCl solution (20 mmol L−1) filtered through a filter (0.2 μm in pore size) at 0.1 MPa for 20 min. Khmax was then determined using the maximum Jv of the segments.

The percent loss of hydraulic conductivity (PLC) per segment was obtained by the increase in native Kh after xylem embolism removal through the high-pressure flushing method [33]. The PLC formula was as follows:

PLC=100×(Khmax−Kh)/Khmax (2)

The xylem sapwood area was obtained using the dye method [34]. We selected both ends (c. 5 cm) of the segments that were used to determine Kh as the material. We infused the segments with basic fuchsin under low pressures of a 50 cm hydraulic head overnight. A sharp razor blade was used to cut a 50 μm cross section for each end of the segment. An optical scanner (LaserJet M1136 MFP, Hewlett-Packard Development Co., Beijing, China) was used to capture images of the stained sections. ImageJ (US National Institutes of Health, Bethesda, MD, USA) was used to calculate the sapwood area. The Kh divided by sapwood area was equal to the sapwood-specific hydraulic conductivity (Ks, kg m−1 s−1 MPa−1).

2.3 Anatomical Analysis

Six short stem segments (c. 2 cm) per tree species were selected to measure the wood density (ρwood). The stem bark and pith were removed and submerged in clean water overnight. The displacement method was used to measure wood volume [35]. The segments that were submerged in the water overnight were removed with dry paper towels to remove moisture from the wood surface. They were then submerged in a beaker of water and thereafter placed on a four-digit analytical balance (CPA225D, Sartorius Inc., Göttingen, Germany). The fresh segment volume was equal to the water mass replaced by the wood. The dry mass of the segment was obtained by oven drying at 75°C for 3 days. The dry mass divided by the fresh volume was the ρwood.

Six short fresh segments (c. 3 cm) per species were used to measure the sapwood moisture content (SMC). Stem bark and pith were removed, and the fresh mass was determined using a four-digit analytical balance. After that, the fresh segment was oven-dried at 75°C until a constant weight was reached. The constant weight represents the dry mass of the segment. The formula for SMC was as follows:

SMC=(freshmass−drymass)×100 (3)

The stem segments that were used to measure Kh were selected to determine the mean vessel diameter (Dv, μm), hydraulically weighed vessel diameter (Dh, μm), and vessel density (VD, No. per mm2). Stem bark and pith were removed, and a slicer was used to obtain cross sections (approximately 20 μm) of sapwood. A 0.1% toluidine blue solution was used to stain the sapwood cross-sections, and a light microscope (Leica ICC50, Wetzlar, Germany) with a digital camera was used to take photos at a magnification of 40×. The radial sectors with three recent growing rings were selected to take pictures. The lumen area of vessels was calculated as a circular shape using the Image-J program. The mean vessel diameter was determined using the circle diameter. The vessel fraction (F, %) was calculated as the proportion of the section occupied by the vessel lumen areas. The Dh was calculated using equation 2(Σr5/Σr4), where r is the radius of the conduit [34]. VD was calculated as the number of vessels per sapwood area.

2.4 Data Analysis

Trait differences between species were tested by one-way analysis of variance with LSD post-hoc tests. The trait differences between growth forms were tested using the independent samples test. The relationships between functional traits across all six species were determined by linear regression analyses with SigmaPlot 10.0 (Software, Inc., San Jose, CA, USA). All pairwise functional trait relationships were tested by Pearson correlation analysis. Multivariate associations among traits and species were determined using principal component analysis (PCA). All statistical analysis was implemented by SPSS Statistics (version 20.0; SPSS Inc., Chicago, IL, USA).

3  Results

3.1 Hydraulic Conductivity and Wood Anatomical Traits in Different Species and Growth Form

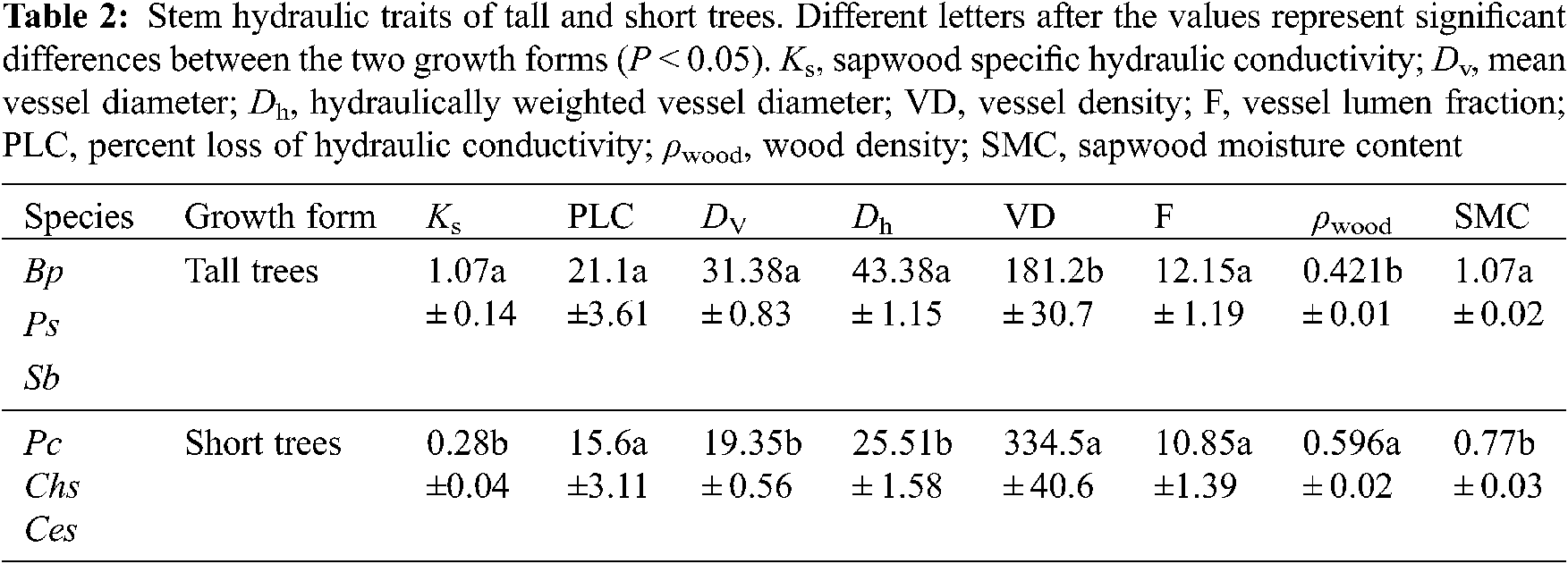
Significant differences in Ks were observed among the six tree species. The values of Ks ranged from 0.023 kg m−1 s−1 MPa−1 in P. cerasifera to 1.786 kg m−1 s−1 MPa−1 in P. stenoptera (Fig. 1). Ks in P. stenoptera, B. polycarpa and C. serrulata were significantly higher than that in S. babylonica, P. cerasifera and C. sinensis. Ks in S. babylonica was significantly higher than that in P. cerasifera. No significant difference in Ks was found between S. babylonica and C. sinensis (Fig. 1). In addition, wood anatomical traits showed significant differences among the six species (Fig. 2). Dv and Dh in P. stenoptera was significantly higher than that in the other five tree species (Figs. 2a, 2b). Dv in S. babylonica was significantly higher than that in three short tree species (Fig. 2a). No significant difference in Dv was found among three short tree species (Fig. 2a). Dh in B. polycarpa was significantly higher than that in three short tree species (Fig. 2b). No significant difference in Dv and Dh was found between B. polycarpa and S. babylonica Figs. 2a, 2b). VD in C. serrulata was significantly higher than that in the other five tree species (Fig. 2c). VD in P. cerasifera was significantly higher than that in C. sinensis and P. stenoptera. No significant difference in VD was found among B. polycarpa, S. babylonica and C. sinensis (Fig. 2c). F in C. sinensis was significantly lower than that in the other five tree species (Fig. 2d). No significant difference in F was found among B. polycarpa, S. babylonica and C. serrulata (Fig. 2d). The mean value of Ks, Dv and Dh of tall trees were higher than those of short trees, and VD was significantly lower in tall than short trees (Table 2, P < 0.05). In addition, there was no significant difference in F among tall and short trees (Table 2).

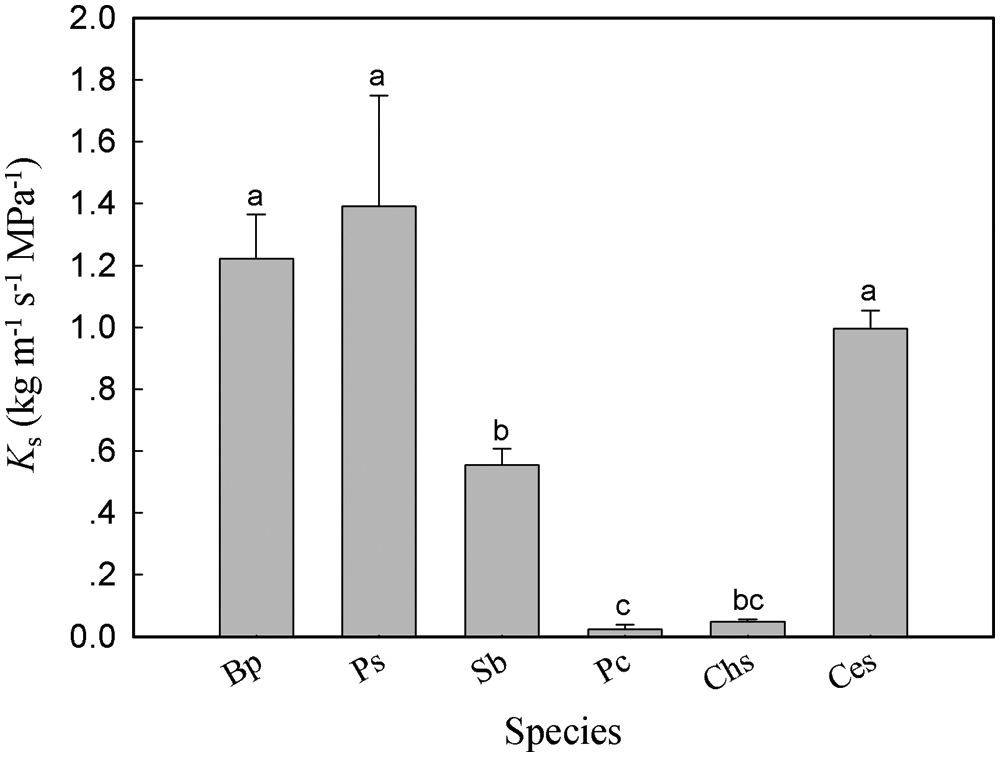
Figure 1: Sapwood-specific hydraulic conductivity of the six tree species. Each histogram represents the mean value of Ks and the vertical error bars show the standard errors (n = 4–6). Species abbreviations were defined in Table 1. Different lowercase letters on the histograms represent significant differences between tree species (P < 0.05)

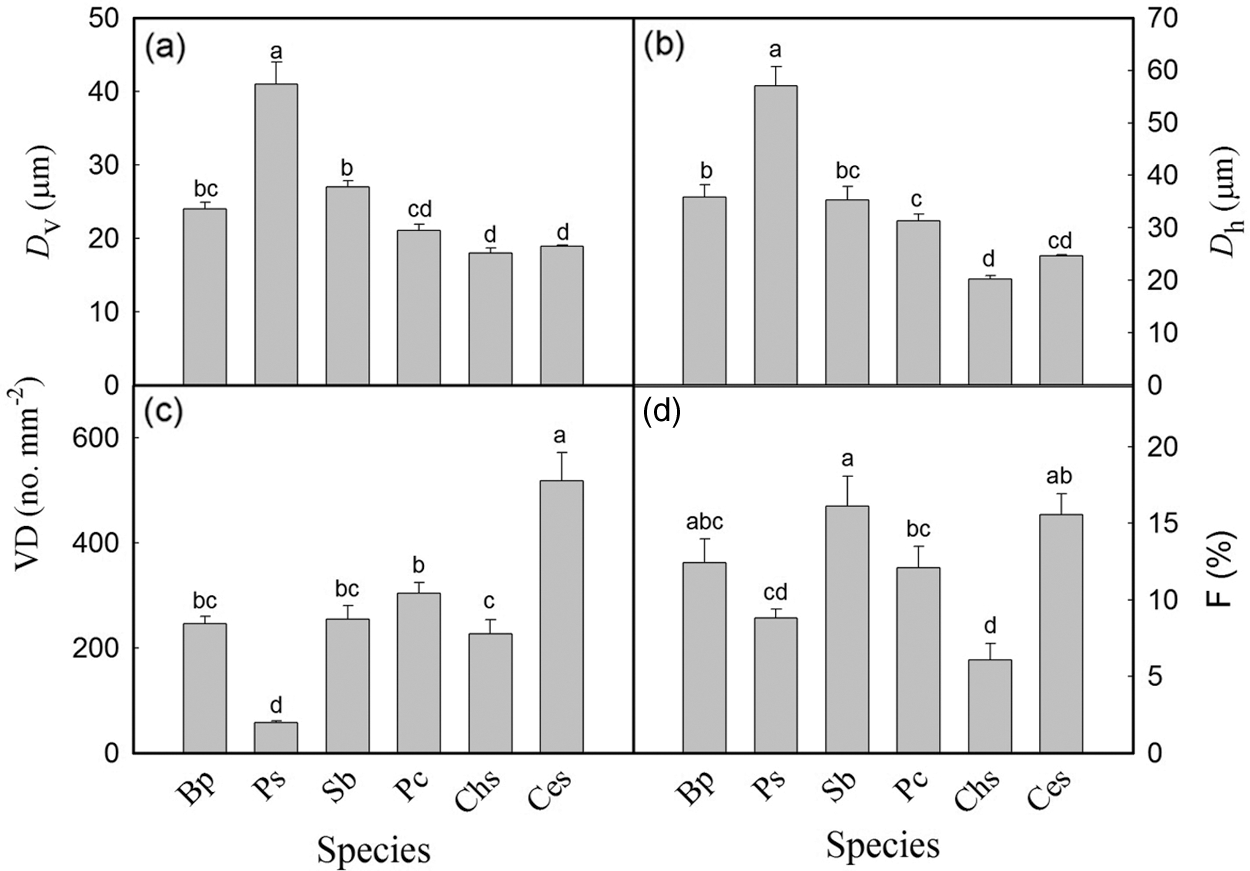
Figure 2: Mean vessel diameter (a), hydraulically weighted vessel diameter (b), mean vessel density (c), and vessel fraction (d) of six tree species. Each histogram represents the mean values of DV, Dh, VD and F, and the vertical error bars show the standard errors (n = 4–6). Species abbreviations were defined in Table 1. Different letters on the bars represent significant differences between tree species (P < 0.05)

3.2 Winter Embolism and Wood Density between Different Species

The PLC of the six tree species ranged from 5.4% to 31.9% (Fig. 3). PLC in P. stenoptera and P. cerasifera were significantly higher than that in the other tree species (Fig. 3). No significant difference in PLC was found between P. stenoptera and P. cerasifera. S. babylonica possessed the lowest PLC among the six tree species. No significant difference in PLC was found between B. polycarpa and C. serrulata. In addition, PLC in S. babylonica and C. sinensis was not significant different (Fig. 3). Although there was no significant difference in PLC between different growth forms (Table 2), the mean value of PLC from three tall tree species was higher than that from three short trees (Table 2).

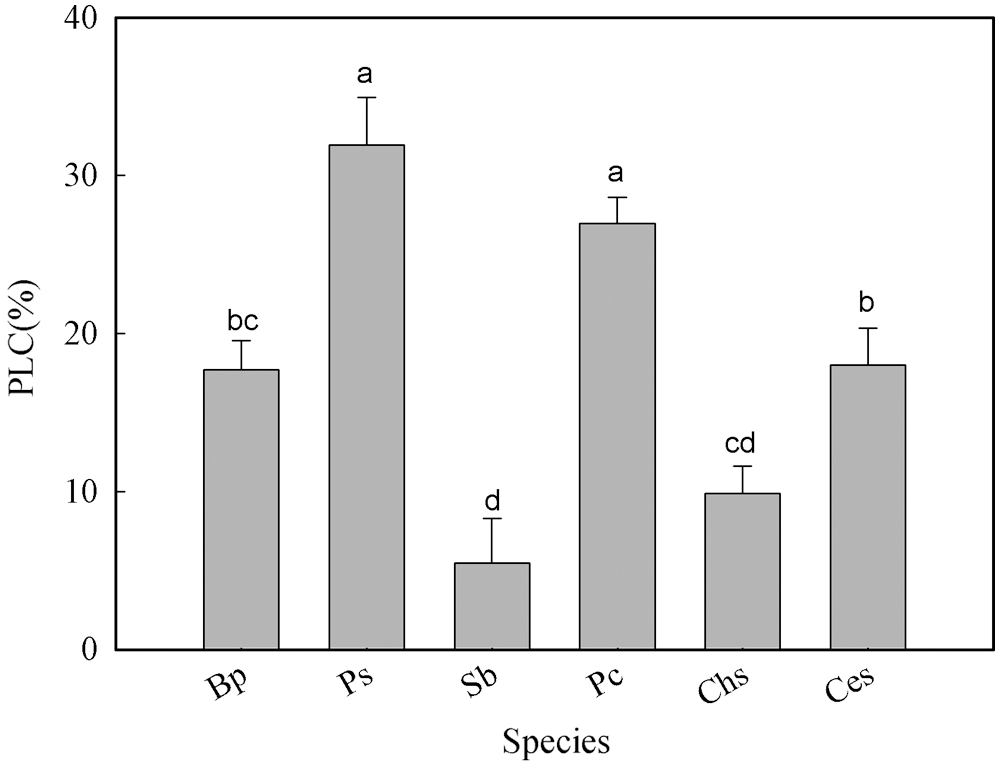
Figure 3: Percent loss of hydraulic conductivity among the six tree species. Species abbreviations were defined in Table 1

Wood density ranged from 0.393 g cm−3 (S. babylonica) to 0.648 g cm−3 (C. serrulata) (Fig. 4a). Wood density of three short trees was significantly higher than that of three tall trees (Fig. 4a, Table 2). In addition, SMC in B. polycarpa and S. babylonica was significantly higher than that in the other four tree species, and no significant difference was found between P. stenoptera and the other three short tree species (Fig. 4b). The mean value of SMC in three tall trees was significantly higher than that in three short tree species (Table 2).

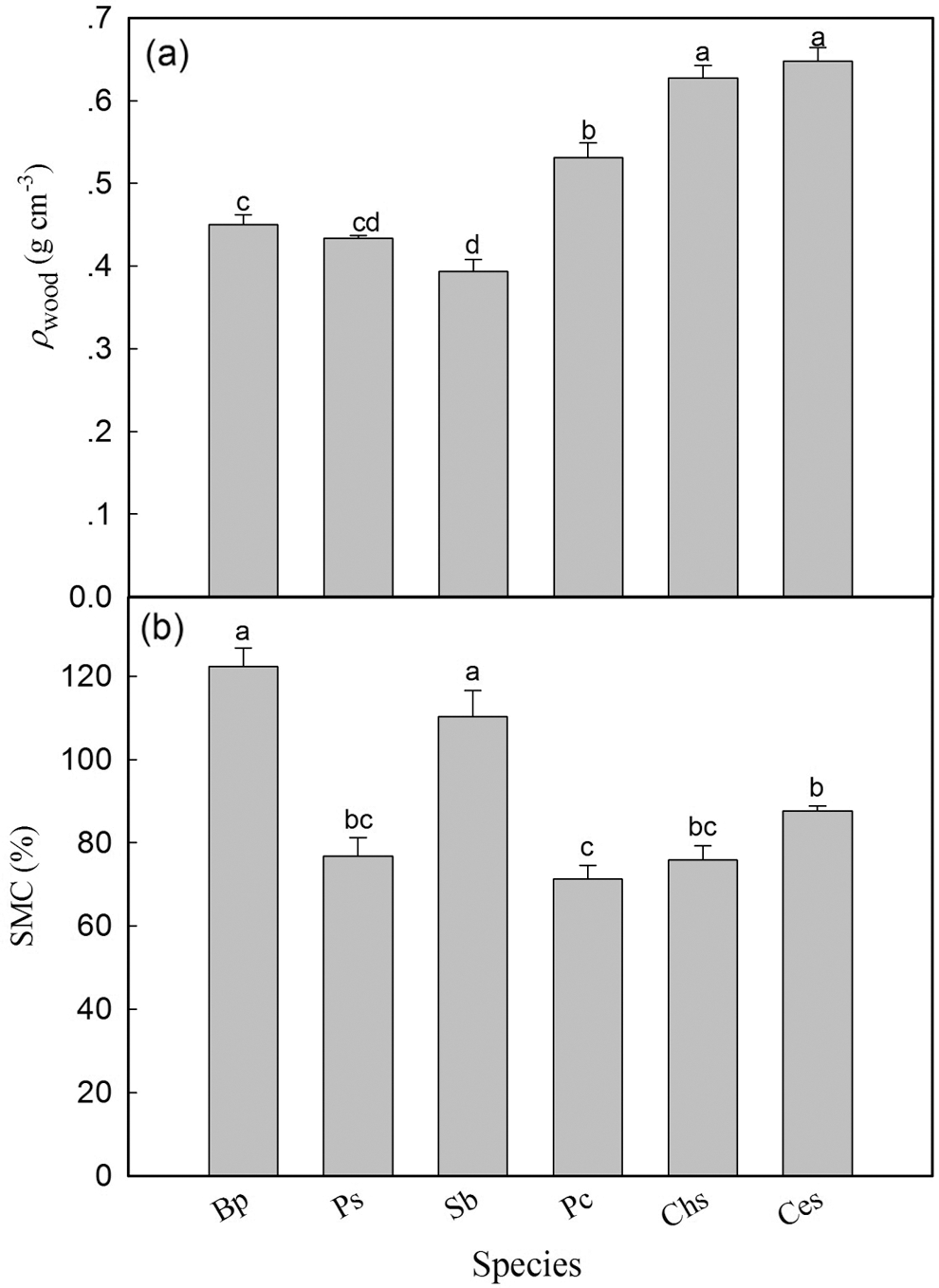
Figure 4: Wood density (a) and sapwood moisture content (b) of six tree species. Each bar represents the mean value of ρwood and SMC, and the error bars show standard error (n = 4–6). Species abbreviations were defined in Table 1. Different letters on the bars represent significant differences between tree species (P < 0.05)

3.3 Relationships among Functional Traits

According to the linear regression models, Dv and Dh were positively correlated with PLC (Figs. 5a, 5b; P < 0.05). Furthermore, Ks was positively correlated with Dv and Dh and negatively correlated with VD (Table 3; P < 0.05). In addition, tree height was positively correlated with PLC, Ks, Dh, and Dv (Fig. 6; Table 3; P < 0.05), but negatively correlated with VD and ρwood (Table 3; P < 0.05).

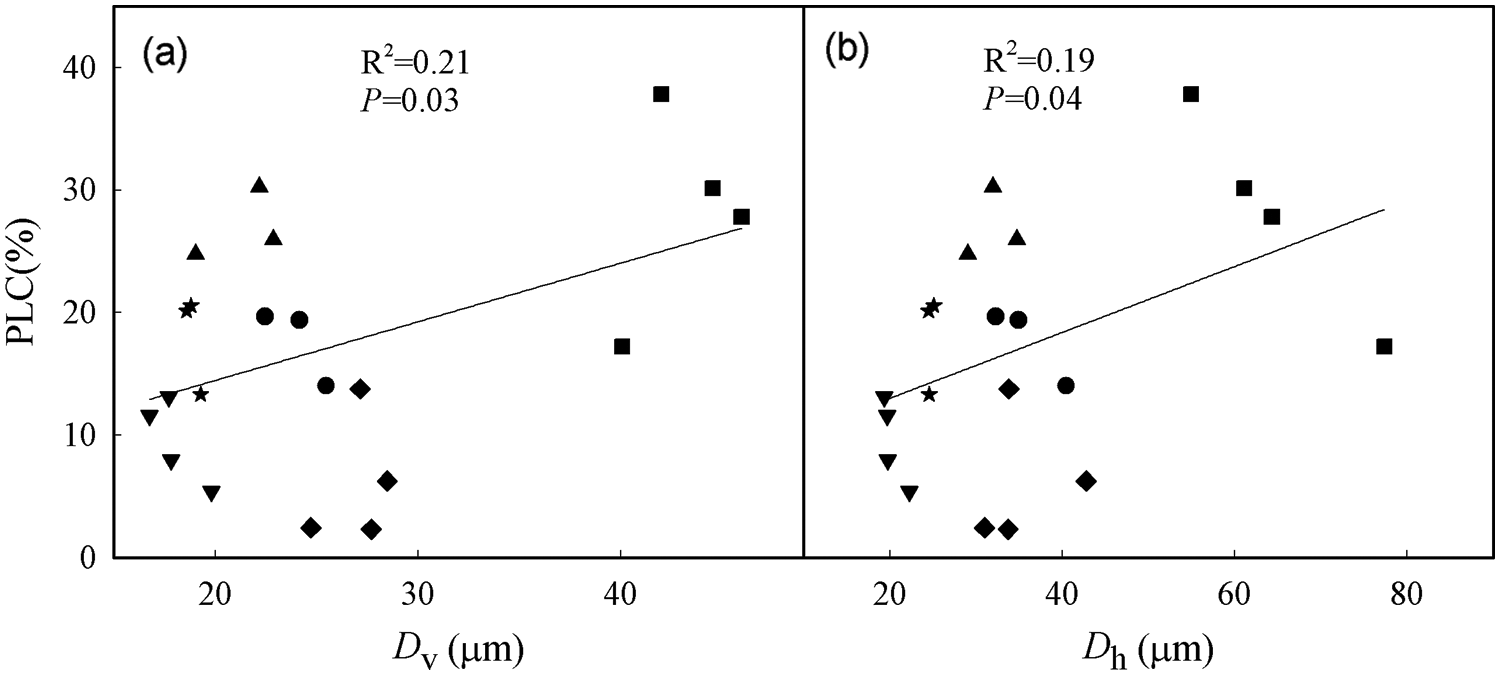
Figure 5: Relationships between percent loss of hydraulic conductivity (PLC) and (a) mean vessel diameter (Dv) and (b) hydraulically weighted vessel diameter (Dh). The filled black circle (●), square (▪), diamond (◆), triangle up (▴), triangle down (▾) and star (★) represent B. polycarpa, P. stenoptera, S. babylonica, P. cerasifera, C. sinensis, and C. serrulata, respectively

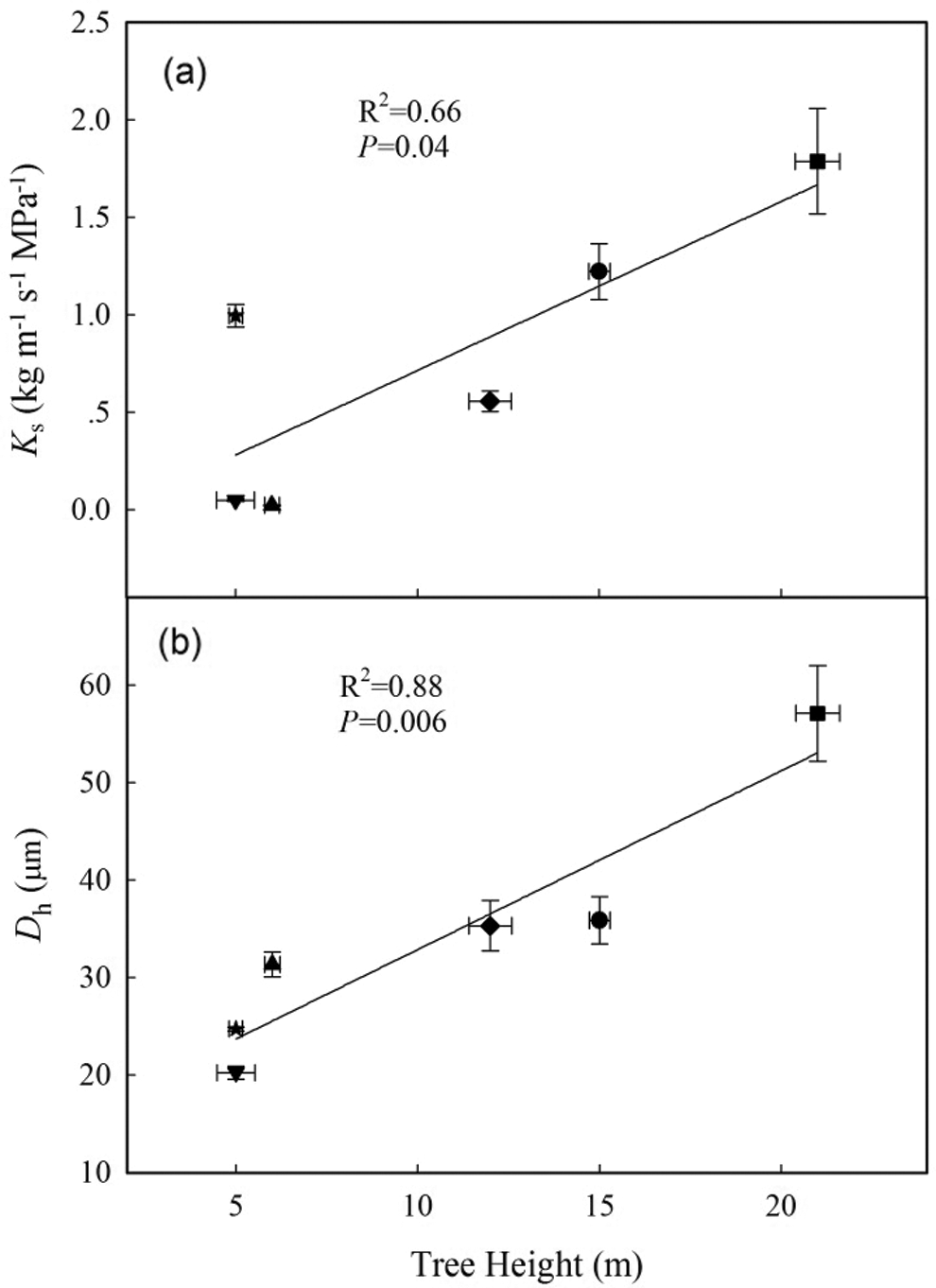
Figure 6: Relationship between tree height and (a) sapwood specific hydraulic conductivity (Ks) and (b) hydraulically weighted vessel diameter (Dh). Symbols are defined in Fig. 5. Error bars represent the standard error (n = 4–6)

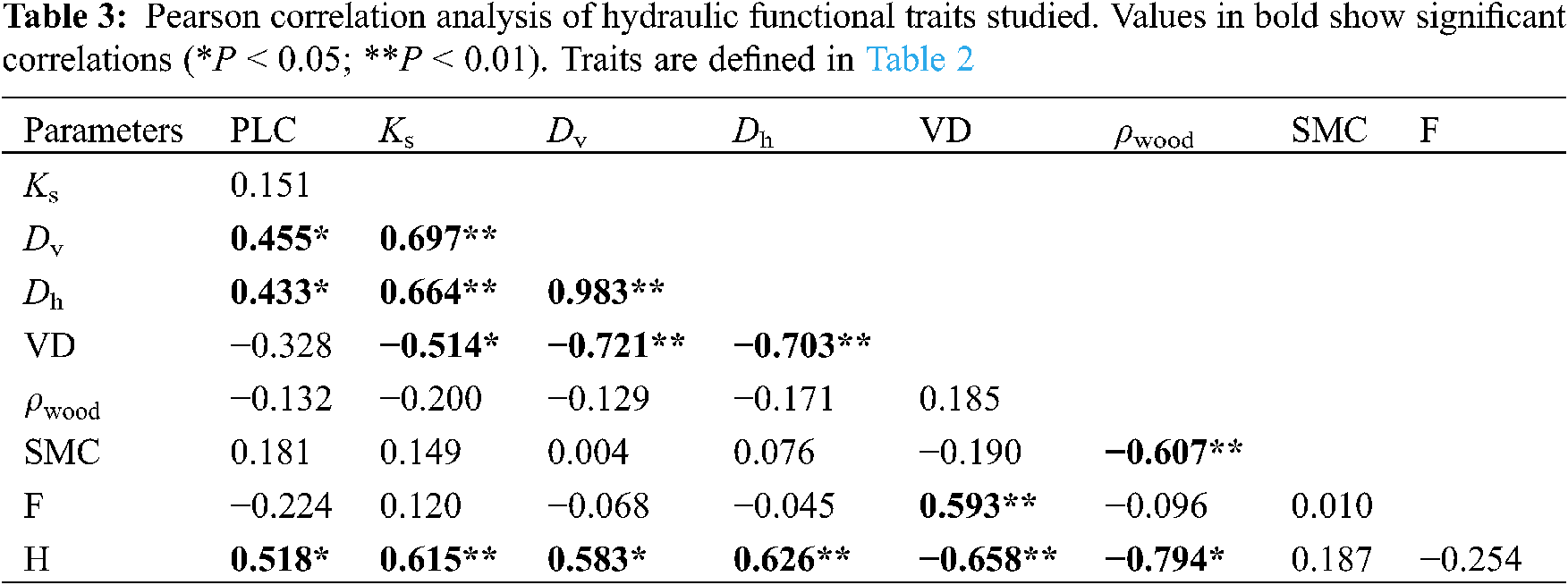
In addition, PCA axis 1 showed strong positive loadings for sapwood water transport efficiency (e.g., H, Ks, Dv, and Dh) and negative loadings for VD and ρwood (Fig. 7a). The SMC comprised positive loads of PCA axis 2, and ρwood comprised negative loads of PCA axis 2 (Fig. 7a). The three tall tree species (Ps, Bp, and Sb) and short tree species (Pc, Chs, and Ces) were well separated along PCA axis 1 (Fig. 7b).

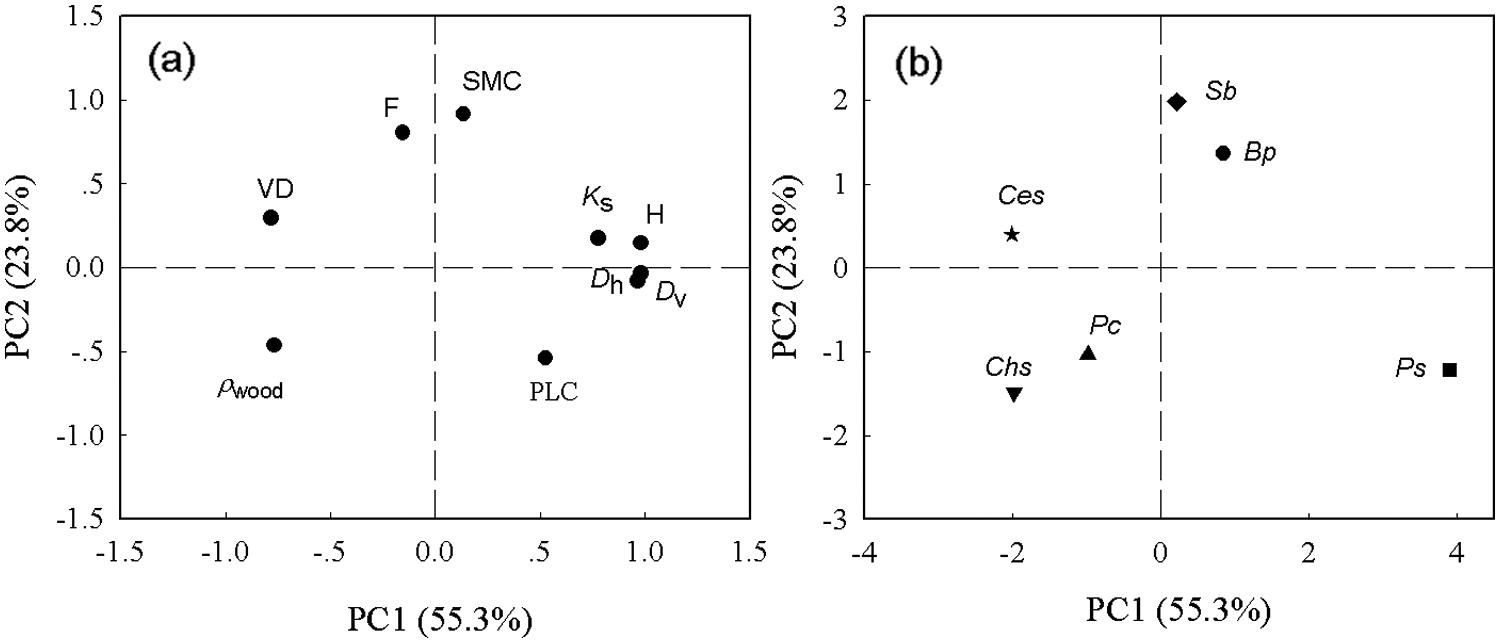
Figure 7: Principal component analysis (PCA) of all functional traits. (a) Arrangements of the functional traits; (b) species loading along PC axes 1 and 2. Functional traits are defined in Table 2. Species codes are defined in Table 1 and symbols are as defined in Fig. 5

4  Discussion

4.1 Different Tree Height-Associated Hydraulic Strategies in Response to Freeze-Thaw Stress

Ecologists found that tree height is the main driver of vessel diameter [36], and vessel diameter is an important trait influencing xylem water transport efficiency and vulnerability to embolism, and thus, plant adaptation to freeze-thaw stress inevitably involves tree height [36–39]. For example, in cold environments, narrow vessels are regarded as key adaptations because of their resistance to freezing-induced embolism [26]. However, the xylem vessels of trees with various heights in cold regions are not exceptionally narrow. Trees with different heights are often classified into different wood types based on differential wood anatomy, such as ring-porous [40] and diffuse-porous [41]. Trees with different heights employ different strategies to adapt to cold environments. Our study found that tall trees (B. polycarpa, P. stenoptera, and S. babylonica) and short trees (P. cerasifera, C. sinensis, and C. serrulata) were well separated by PC axis 1 (Fig. 7b), which suggests that tree height is an important trait that is tightly associated with hydraulic strategies to adapt to winter freeze-thaw stress. Previous studies found that there are three hypothetical solutions to cope with the winter embolism problems, avoidance, re-filling, and tolerance [34]. Short trees with relatively small vessels (Figs. 2a and 2b; Table 2) exhibited greater avoidance of embolism with lower PLC (Fig. 3, Table 2). In contrast, tall trees with fewer but wider vessels (Figs. 2a–2c; Table 2) exhibited higher PLC levels (Fig. 3, Table 2) in winter. Tall trees abandoned larger proportion of wider vessels in wither and relied on the new growing wider earlywood vessels and narrow vessels that not embolized in last winter to conduct water in the next growing season [42]. Short trees have narrow vessels to resist freeze-thaw induced embolism (Fig. 3; Table 2).

In addition, vessel diameter is an important trait for xylem water transport efficiency, which is positively correlated with the fourth power of vessel diameter [23]. Tall trees with wider vessels exhibited higher Ks (Fig. 1), which is necessary to obtain high photosynthetic rates for the fast growth of tall trees [43]. Furthermore, tree height was positively correlated with vessel diameter and hydraulic conductivity (Figs. 6a and 6b; P <0.05), which suggested a fast strategy for tall trees to move water rapidly and maintain high rates of resource acquisition during the growing season [44]. Meanwhile, the short trees with narrow vessels showed lower xylem water transport efficiency involving a slow-growing strategy during the growing season, which indicates a “fast-slow” strategy between tall and short trees [44].

There are also some other xylem structural differences between tall trees and short ones, which might be attributed to different strategies associated with plant height. For example, wood density can reflect the construction cost of wood. A low wood density means less resources to construct [45]. Trees with low wood density often have a high growth rate, but they often have a high rate of mortality owing to susceptibility to stem breakage or pathogens [45–47]. In our study, wood density was negatively correlated with tree height (Table 3), which suggested that short trees were more resistant to stem breakage and had a slower growth rate than tall trees. Furthermore, a previous study showed that dense wood is more resistant to embolism across species [48]. Our results are consistent with this. The results showed that short trees have higher wood density and lower PLC than tall trees, which indicates that short trees would be more resistant to extreme low-temperature weather caused by global climate change in the future.

4.2 Ecological Relationships between Tree Height and Hydraulic Traits

In this study, tree height was tightly correlated with xylem hydraulic traits (Table 3, Fig. 6). Tall trees had wider vessels and a lower vessel density than short ones (Fig. 2a, 2b), which is consistent with a previous study in which trees exhibited wider vessel diameters and lower vessel densities than shrubs [29]. The low vessel density and wider vessel diameter would allow trees to maintain strong mechanical support and defense [49]. In addition, the risk of cavitation increases with plant height because of the gravity of suspended water and greater fraction along water transport pathways [9], which could induce hydraulic failure and limit plant growth, especially under stressful conditions such as drought and frost. Hydraulic limitation is one of the mechanisms that determine tree height, and short trees with many narrow vessels are more resistant to freeze-thaw-induced embolism [50]. Tall trees require larger vessels to maintain fast growth but are also more vulnerable to freeze-thaw-induced embolism [36]. Consistent with this, our results showed that tree height was positively correlated with vessel diameter (Dv, Dh), hydraulic conductivity (Ks), and winter embolism (PLC) (Table 3, Fig. 6, P < 0.05), which indicated that tree height was aligned with the trade-off between hydraulic conductivity and resistance to freeze-thaw stress [51].

Moreover, a negative correlation was found between tree height and vessel and wood density, and a positive correlation was found between tree height and vessel diameter (Table 3), which suggested that tree height evolution is closely associated with trait integration. Tall trees invest more energy in sapwood water transport efficiency because the carbon fixation and water transfer required for rapid growth are closely coordinated. Meanwhile, the vessel diameter increases and the wood density decreases because of the lower investment in the cell wall material. In our study, the relationship between vessel diameter and wood density was weak (Table 3). Wood density is mainly determined by the fiber size, fiber wall thickness, and wall-to-lumen ratio [51]. Furthermore, sapwood moisture content was negatively correlated with wood density (Table 3, P < 0.05), and similar results have been reported in many tree species from diverse ecosystems [52].

The ecological correlation between tree height and hydraulic traits should be the result of long-term adaptation to selective pressure evolution [53]. It is more difficult for tall trees to transport water to upper leaves because the total path length resistance increases proportionately with increasing height [10]. Moreover, micro-environment differences might contribute to hydraulic trait variations between tall and short trees. For example, canopy stems and leaves of tall species are often exposed to higher radiation, stronger wind, and higher air temperature and must cope with possible stem and leaf desiccation or frost, whereas short plants experience relatively milder and wetter microenvironments, that is, lower irradiance, a constant temperature, and higher humidity. Consequently, tall trees would face a higher risk of embolism caused by drought or frost than short trees, unless this is compensated for by larger root systems or the enhanced narrowing of tapered vessels of stem segments in the canopy of tall trees [54,55].

5  Conclusion

Our study suggests that tree height is tightly correlated with xylem hydraulic functional traits; thus, different hydraulic strategies in response to freeze-thaw stress are inevitable with tree height. Tree height was positively correlated with vessel diameters and xylem hydraulic conductivity, but was negatively correlated with freeze-thaw induced embolism, which indicated that tree height was aligned with the trade-off between sapwood water transport efficiency and freeze-thaw-induced embolism. Short trees were more resistant to freeze-thaw stress and showed lower hydraulic conductivity, indicating a more conservative strategy in response to freeze-thaw stress than tall trees. Furthermore, tall trees and short trees could be well separated based on different xylem hydraulic functional traits, which indicate that differences in tree height resulted in different hydraulic strategies in response to freeze-thaw stress. Tall trees in urban cities might face large challenges to grow well, as global climate change results in more drought in the growing season and extremely low temperatures in winter. More attention should be paid to tall trees in urban garden tree management. It is also worth noting that future research should include the leaf gas exchange characteristics across tree species that differ in height, and future research should be carried out on a large number of common urban tree species that co-occur in North China.

Acknowledgement: The authors gratefully acknowledge the laboratory facilities provided by the Department of Ecology, Henan Agricultural University, for conducting this research. We would like to thank Editage (https://www.editage.cn) for English language editing.

Funding Statement: This work was financially supported by the National Natural Science Foundation of China (30900564, 41877542) and the Project of Henan Agricultural University Program for Fundamental Research (30900649).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding this study.

References

 1.  Meili, N., Manoli, G., Burlando, P., Carmeliet, J., Chow, W. T. et al. (2021). Tree effects on urban microclimate: Diurnal, seasonal, and climatic temperature differences explained by separating radiation, evapotranspiration, and roughness effects. Urban Forestry & Urban Greening, 58, 126970. DOI 10.1016/j.ufug.2020.126970. [Google Scholar] [CrossRef]

 2.  Rahman, M. A., Moser, A., Gold, A., Rötzer, T., Pauleit, S. (2018). Vertical air temperature gradients under the shade of two contrasting urban tree species during different types of summer days. Science of the Total Environment, 633, 100–111. DOI 10.1016/j.scitotenv.2018.03.168. [Google Scholar] [CrossRef]

 3.  Rahman, M. A., Moser, A., Rötzer, T., Pauleit, S. (2019). Comparing the transpirational and shading effects of two contrasting urban tree species. Urban Ecosystems, 22(4), 683–697. DOI 10.1007/s11252-019-00853-x. [Google Scholar] [CrossRef]

 4.  Santos, M. M., Lanzinha, J. C., Ferreira, A. V. (2021). Review on urbanism and climate change. Cities, 114, 103176. DOI 10.1016/j.cities.2021.103176. [Google Scholar] [CrossRef]

 5.  Nolan, R. H., Gauthey, A., Losso, A., Medlyn, B. E., Smith, R. et al. (2021). Hydraulic failure and tree size linked with canopy die-back in eucalypt forest during extreme drought. New Phytologist, 230(4), 1354–1365. DOI 10.1111/nph.17298. [Google Scholar] [CrossRef]

 6.  Moles, A. T., Warton, D. I., Warman, L., Swenson, N. G., Laffan, S. W. et al. (2009). Global patterns in plant height. Journal of Ecology, 97(5), 923–932. DOI 10.1111/j.1365-2745.2009.01526.x. [Google Scholar] [CrossRef]

 7.  McDowell, N. G., Bond, B. J., Dickman, L. T., Ryan, M. G., Whitehead, D. (2011). Relationships between tree height and carbon isotope discrimination. Size-and age-related changes in tree structure and function, pp. 255–286. Netherlands: Springer. [Google Scholar]

 8.  Givnish, T. J., Wong, S. C., Stuart-Williams, H., Holloway-Phillips, M., Farquhar, G. D. (2014). Determinants of maximum tree height in eucalyptus species along a rainfall gradient in Victoria, Australia. Ecology, 95(11), 2991–3007. DOI 10.1890/14-0240.1. [Google Scholar] [CrossRef]

 9.  Baret, M., Pepin, S., Pothier, D. (2018). Hydraulic limitations in dominant trees as a contributing mechanism to the age-related growth decline of boreal forest stands. Forest Ecology and Management, 427, 135–142. DOI 10.1016/j.foreco.2018.05.043. [Google Scholar] [CrossRef]

10. Munné-Bosch, S. (2018). Limits to tree growth and longevity. Trends in Plant Science, 23(11), 985–993. DOI 10.1016/j.tplants.2018.08.001. [Google Scholar] [CrossRef]

11. Anderegg, W. R., Klein, T., Bartlett, M., Sack, L., Pellegrini, A. F. et al. (2016). Meta-analysis reveals that hydraulic traits explain cross-species patterns of drought-induced tree mortality across the globe. Proceedings of the National Academy of Sciences, 113(18), 5024–5029. DOI 10.1073/pnas.1525678113. [Google Scholar] [CrossRef]

12. Hacke, U. G., Spicer, R., Schreiber, S. G., Plavcová, L. (2017). An ecophysiological and developmental perspective on variation in vessel diameter. Plant, Cell & Environment, 40(6), 831–845. DOI 10.1111/pce.12777. [Google Scholar] [CrossRef]

13. Bennett, A. C., McDowell, N. G., Allen, C. D., Anderson-Teixeira, K. J. (2015). Larger trees suffer most during drought in forests worldwide. Nature Plants, 1(10), 1–5. DOI 10.1038/nplants.2015.139. [Google Scholar] [CrossRef]

14. Stovall, A. E., Shugart, H., Yang, X. (2019). Tree height explains mortality risk during an intense drought. Nature Communications, 10(1), 1–6. DOI 10.1038/s41467-019-12380-6. [Google Scholar] [CrossRef]

15. Granda, E., Scoffoni, C., Rubio-Casal, A. E., Sack, L., Valladares, F. (2014). Leaf and stem physiological responses to summer and winter extremes of woody species across temperate ecosystems. Oikos, 123(11), 1281–1290. DOI 10.1111/oik.01526. [Google Scholar] [CrossRef]

16. Cox, R. M., Zhu, X. B. (2003). Effects of simulated thaw on xylem cavitation, residual embolism, spring dieback and shoot growth in yellow birch. Tree Physiology, 23(9), 615–624. DOI 10.1093/treephys/23.9.615. [Google Scholar] [CrossRef]

17. Iida, Y., Kohyama, T. S., Swenson, N. G., Su, S. H., Chen, C. T. et al. (2014). Linking functional traits and demographic rates in a subtropical tree community: The importance of size dependency. Journal of Ecology, 102(3), 641–650. DOI 10.1111/1365-2745.12221. [Google Scholar] [CrossRef]

18. Martin, A. R., Isaac, M. E. (2021). The leaf economics spectrum’s morning coffee: Plant size-dependent changes in leaf traits and reproductive onset in a perennial tree crop. Annals of Botany, 127(4), 483–493. DOI 10.1093/aob/mcaa199. [Google Scholar] [CrossRef]

19. McGregor, I. R., Helcoski, R., Kunert, N., Tepley, A. J., Gonzalez-Akre, E. B. et al. (2020). Tree height and leaf drought tolerance traits shape growth responses across droughts in a temperate broadleaf forest. New Phytologist, 231(2), 601–616. DOI 10.1111/nph.16996. [Google Scholar] [CrossRef]

20. Flo, V., Martínez-Vilalta, J., Mencuccini, M., Granda, V., Anderegg, W. R. et al. (2021). Climate and functional traits jointly mediate tree water-use strategies. New Phytologist, 231(2), 617–630. DOI 10.1111/nph.17404. [Google Scholar] [CrossRef]

21. Gleason, S. M., Butler, D. W., Ziemińska, K., Waryszak, P., Westoby, M. (2012). Stem xylem conductivity is key to plant water balance across Australian angiosperm species. Functional Ecology, 26(2), 343–352. DOI 10.1111/j.1365-2435.2012.01962.x. [Google Scholar] [CrossRef]

22. McCulloh, K. A., Johnson, D. M., Petitmermet, J., McNellis, B., Meinzer, F. C. et al. (2015). A comparison of hydraulic architecture in three similarly sized woody species differing in their maximum potential height. Tree Physiology, 35(7), 723–731. DOI 10.1093/treephys/tpv035. [Google Scholar] [CrossRef]

23. Zimmermann, M. H. (1983). Other functional adaptations. Xylem structure and the ascent of sap, pp. 83–95. Berlin, Heidelberg: Springer [Google Scholar]

24. Liu, Y. Y., Song, J., Wang, M., Li, N., Niu, C. Y. et al. (2015). Coordination of xylem hydraulics and stomatal regulation in keeping the integrity of xylem water transport in shoots of two compound-leaved tree species. Tree Physiology, 35(12), 1333–1342. DOI 10.1093/treephys/tpv061. [Google Scholar] [CrossRef]

25. Wang, A. Y., Han, S. J., Zhang, J. H., Wang, M., Yin, X. H. et al. (2018). The interaction between nonstructural carbohydrate reserves and xylem hydraulics in Korean pine trees across an altitudinal gradient. Tree Physiology, 38(12), 1792–1804. DOI 10.1093/treephys/tpy119. [Google Scholar] [CrossRef]

26. Davis, S. D., Sperry, J. S., Hacke, U. G. (1999). The relationship between xylem conduit diameter and cavitation caused by freezing. American Journal of Botany, 86(10), 1367–1372. DOI 10.2307/2656919. [Google Scholar] [CrossRef]

27. Liu, Y. Y., Wang, A. Y., An, Y. N., Lian, P. Y., Wu, D. D. et al. (2018). Hydraulics play an important role in causing low growth rate and dieback of aging Pinus sylvestris var. mongolica trees in plantations of northeast China. Plant, Cell & Environment, 41(7), 1500–1511. DOI 10.1111/pce.13160. [Google Scholar] [CrossRef]

28. Tedla, B., Dang, Q. L., Inoue, S. (2020). Freeze-thaw events delay spring budburst and leaf expansion while longer photoperiods have opposite effect under different [CO2] in white birch: Advance it under elevated but delay it under ambient [CO2]. Environmental and Experimental Botany, 173, 103982. DOI 10.1016/j.envexpbot.2020.103982. [Google Scholar] [CrossRef]

29. Apgaua, D. M., Tng, D. Y., Cernusak, L. A., Cheesman, A. W., Santos, R. M. et al. (2017). Plant functional groups within a tropical forest exhibit different wood functional anatomy. Functional Ecology, 31(3), 582–591. DOI 10.1111/1365-2435.12787. [Google Scholar] [CrossRef]

30. Kenzo, T., Inoue, Y., Yoshimura, M., Yamashita, M., Tanaka-Oda, A. et al. (2015). Height-related changes in leaf photosynthetic traits in diverse bornean tropical rain forest trees. Oecologia, 177(1), 191–202. DOI 10.1007/s00442-014-3126-0. [Google Scholar] [CrossRef]

31. Fang, L. D., Ning, Q. R., Guo, J. J., Gong, X. W., Zhu, J. J. et al. (2021). Hydraulic limitation underlies the dieback of populus pseudo-simonii trees in water-limited areas of Northern China. Forest Ecology and Management, 483, 118764. DOI 10.1016/j.foreco.2020.118764. [Google Scholar] [CrossRef]

32. Raunkiaer, C. (1907). The life forms of plants and their bearing on geography. In: Raunkiaer C. (EdThe life forms of plants and statistical plant geography, pp. 2–104. Oxford: Clarendon Press. [Google Scholar]

33. Sperry, J. S., Donnelly, J. R., Tyree, M. T. (1988). A method for measuring hydraulic conductivity and embolism in xylem. Plant, Cell & Environment, 11(1), 35–40. DOI 10.1111/j.1365-3040.1988.tb01774.x. [Google Scholar] [CrossRef]

34. Sperry, J. S., Nichols, K. L., Sullivan, J. E., Eastlack, S. E. (1994). Xylem embolism in ring-porous, diffuse-porous, and coniferous trees of northern utah and interior Alaska. Ecology, 75(6), 1736–1752. DOI 10.2307/1939633. [Google Scholar] [CrossRef]

35. Saranpää, P. (2003). Wood density and growth. In: Barnett, J. R., Jeronimidis, G. (Eds.Wood quality and its biological basis, biological sciences series A, pp. 87–117. Oxford: Blackwell Publishing & CRC Press. [Google Scholar]

36. Olson, M. E., Soriano, D., Rosell, J. A., Anfodillo, T., Donoghue, M. J. et al. (2018). Plant height and hydraulic vulnerability to drought and cold. Proceedings of the National Academy of Sciences, 115(29), 7551–7556. DOI 10.1073/pnas.1721728115. [Google Scholar] [CrossRef]

37. Niu, C. Y., Meinzer, F. C., Hao, G. Y. (2017). Divergence in strategies for coping with winter embolism among co-occurring temperate tree species: The role of positive xylem pressure, wood type and tree stature. Functional Ecology, 31(8), 1550–1560. DOI 10.1111/1365-2435.12868. [Google Scholar] [CrossRef]

38. Lintunen, A., Paljakka, T., Riikonen, A., Lindén, L., Lindfors, L. et al. (2015). Irreversible diameter change of wood segments correlates with other methods for estimating frost tolerance of living cells in freeze-thaw experiment: A case study with seven urban tree species in Helsinki. Annals of Forest Science, 72(8), 1089–1098. DOI 10.1007/s13595-015-0516-3. [Google Scholar] [CrossRef]

39. Fan, Z. X., Zhang, S. B., Hao, G. Y., Ferry Slik, J. W., Cao, K. F. (2012). Hydraulic conductivity traits predict growth rates and adult stature of 40 Asian tropical tree species better than wood density. Journal of Ecology, 100(3), 732–741. DOI 10.1111/j.1365-2745.2011.01939.x. [Google Scholar] [CrossRef]

40. Dai, Y., Wang, L., Wan, X. (2020). Frost fatigue and its spring recovery of xylem conduits in ring-porous, diffuse-porous, and coniferous species in situ. Plant Physiology and Biochemistry, 146, 177–186. DOI 10.1016/j.plaphy.2019.11.014. [Google Scholar] [CrossRef]

41. Jupa, R., Doubková, P., Gloser, V. (2019). Ion-mediated increases in xylem hydraulic conductivity: Seasonal differences between coexisting ring-and diffuse-porous temperate tree species. Tree Physiology, 39(8), 1313–1328. DOI 10.1093/treephys/tpz035. [Google Scholar] [CrossRef]

42. Savage, J. A., Chuine, I. (2021). Coordination of spring vascular and organ phenology in deciduous angiosperms growing in seasonally cold climates. New Phytologist, 230(5), 1700–1715. DOI 10.1111/nph.17289. [Google Scholar] [CrossRef]

43. Yang, D., Zhang, Y. J., Song, J., Niu, C. Y., Hao, G. Y. (2019). Compound leaves are associated with high hydraulic conductance and photosynthetic capacity: Evidence from trees in northeast China. Tree Physiology, 39(5), 729–739. DOI 10.1093/treephys/tpy147. [Google Scholar] [CrossRef]

44. Reich, P. B. (2014). The world-wide ‘fast-slow’ plant economics spectrum: A traits manifesto. Journal of Ecology, 102(2), 275–301. DOI 10.1111/1365-2745.12211. [Google Scholar] [CrossRef]

45. van der Sande, M. T., Poorter, L., Schnitzer, S. A., Engelbrecht, B. M., Markesteijn, L. (2019). The hydraulic efficiency–safety trade-off differs between lianas and trees. Ecology, 100(5), e02666. DOI 10.1002/ecy.2666. [Google Scholar] [CrossRef]

46. Greenwood, S., Ruiz-Benito, P., Martínez-Vilalta, J., Lloret, F., Kitzberger, T. et al. (2017). Tree mortality across biomes is promoted by drought intensity, lower wood density and higher specific leaf area. Ecology Letters, 20(4), 539–553. DOI 10.1111/ele.12748. [Google Scholar] [CrossRef]

47. Iida, Y., Poorter, L., Sterck, F., Kassim, A. R., Potts, M. D. et al. (2014). Linking size-dependent growth and mortality with architectural traits across 145 co-occurring tropical tree species. Ecology, 95(2), 353–363. DOI 10.1890/11-2173.1. [Google Scholar] [CrossRef]

48. Savi, T., Tintner, J., da Sois, L., Grabner, M., Petit, G. et al. (2019). The potential of mid-infrared spectroscopy for prediction of wood density and vulnerability to embolism in woody angiosperms. Tree Physiology, 39(3), 503–510. DOI 10.1093/treephys/tpy112. [Google Scholar] [CrossRef]

49. Hietz, P., Rosner, S., Hietz-Seifert, U., Wright, S. J. (2017). Wood traits related to size and life history of trees in a Panamanian rainforest. New Phytologist, 213(1), 170–180. DOI 10.1111/nph.14123. [Google Scholar] [CrossRef]

50. Götmark, F., Götmark, E., Jensen, A. M. (2016). Why be a shrub? A basic model and hypotheses for the adaptive values of a common growth form. Frontiers in Plant Science, 7, 1095. DOI 10.3389/fpls.2016.01095. [Google Scholar] [CrossRef]

51. Liu, H., Gleason, S. M., Hao, G., Hua, L., He, P. et al. (2019). Hydraulic traits are coordinated with maximum plant height at the global scale. Science Advances, 5(2), 1–14. DOI 10.1126/sciadv.aav1332. [Google Scholar] [CrossRef]

52. Oliva Carrasco, L., Bucci, S. J., di Francescantonio, D., Lezcano, O. A., Campanello, P. I. et al. (2015). Water storage dynamics in the main stem of subtropical tree species differing in wood density, growth rate and life history traits. Tree Physiology, 35(4), 354–365. DOI 10.1093/treephys/tpu087. [Google Scholar] [CrossRef]

53. Meinzer, F. C. (2003). Functional convergence in plant responses to the environment. Oecologia, 134(1), 1–11. DOI 10.1007/s00442-002-1088-0. [Google Scholar] [CrossRef]

54. Poorter, L., McDonald, I., Alarcón, A., Fichtler, E., Licona, J. C. et al. (2010). The importance of wood traits and hydraulic conductance for the performance and life history strategies of 42 rainforest tree species. New Phytologist, 185(2), 481–492. DOI 10.1111/j.1469-8137.2009.03092.x. [Google Scholar] [CrossRef]

55. Kong, D., Wang, J., Zeng, H., Liu, M., Miao, Y. et al. (2017). The nutrient absorption–transportation hypothesis: Optimizing structural traits in absorptive roots. New Phytologist, 213(4), 1569–1572. DOI 10.1111/nph.14344. [Google Scholar] [CrossRef]

Appendix

Figure S1: Hourly mean air temperature from October 2017 to October 2018

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.