
Health Monitoring

 | Structural Durability & Health Monitoring |  |
DOI: 10.32604/sdhm.2021.015644
ARTICLE
Artificial Neural Network (ANN) Approach for Predicting Concrete Compressive Strength by SonReb
LADS Laboratory, University of Bologna, Via dell’Università 50, Cesena, 47521, Italy
*Corresponding Author: Lucio Nobile. Email: lucio.nobile@unibo.it
Received: 01 January 2021; Accepted: 01 April 2021
Abstract: The compressive strength of concrete is one of most important mechanical parameters in the performance assessment of existing reinforced concrete structures. According to various international codes, core samples are drilled and tested to obtain the concrete compressive strengths. Non-destructive testing is an important alternative when destructive testing is not feasible without damaging the structure. The commonly used non-destructive testing (NDT) methods to estimate the in-situ values include the Rebound hammer test and the Ultrasonic Pulse Velocity test. The poor reliability of these tests due to different aspects could be partially contrasted by using both methods together, as proposed.in the SonReb method. There are three techniques that are commonly used to predict the compressive strength of concrete based on the SonReb measurements: computational modeling, artificial intelligence, and parametric multi-variable regression models. In a previous study the accuracy of the correlation formulas deduced from the last technique has been investigated in comparison with the effective compressive strengths based on destructive test results on core drilled in adjacent locations. The aim of this study is to verify the accuracy of Artificial Neural Approach comparing the estimated compressive strengths based on NDT measured parameters with the same effective compressive strengths. The comparisons show the best performance of ANN approach.
Keywords: Compressive concrete strength; destructive tests; non-destructive test; ultrasonic pulse velocity; rebound index; SonReb method; artificial neural network approach
List of abbreviations
| ANN: | Artificial Neural Network |
| DT: | Destructive Testing |
| FFN: | Feed-Forward Network |
| NDT: | Non-Destructive Testing |
| RI: | Rebound Index |
| RMSE: | Root Mean Squared error |
| V: | Ultrasonic Pulse Velocity |
Existing reinforced concrete structures were built according to standards and materials quite different to those available today. The evaluation of structural performance when seismic zones are concerned requires procedures and methods able to cover lack of data about mechanical material properties and reinforcement detailing. The structural assessment is more relevant when structural strengthening is necessary to prevent failures due to earthquakes.
Procedures and methods, such as detailed inspections and tests on materials, are mandatory to establish the performance levels in recent seismic codes. Accordingly, assessment of the in-situ concrete compressive strength is mainly based on cores drilled from the structure. This method is expensive and sometimes difficult to employ.
Non-destructive testing (NDT) of materials and structures is a testing and analysis technique without causing damage to the structure, aiming at maintenance and diagnosis [1–5]. A non-destructive evaluation procedure for determining the location and size of a crack in a structure has been proposed in Viola et al. [6–8]. This method is based on measured vibration frequencies and mode shapes. A global minimization approach is employed for identifying the cracked element in the discretized structure.
Fortunately, NDT can effectively supplement coring since the compressive strength can be cheaply evaluated throughout the whole structure. The procedure of NDT must be only used in conjunction with destructive testing according to both European and Italian Standards. Note that firstly steel reinforcements must be localized in order to perform properly a non-destructive test and/or destructive test method. To this end, a covermeter, a portable reinforcement bars detector instrument also called pachometer, can be easily used on-site. The critical step is to set reliable relationships between NDT results and actual concrete strength. Most codes suggest correlating the results of in-situ NDT with those of corresponding destructive test carried out on cores drilled at the same selected locations.
The commonly used NDT methods to predict concrete compressive strength include the rebound hammer test and the ultrasonic pulse Velocity (V) test. Ultrasonic method is a form of NDT and characterization of materials and structures in civil, mechanical, aerospace, automotive engineering. Concerning concrete structures, note that “This test method covers the determination of the propagation velocity of longitudinal stress wave pulses through concrete. This test method does not apply to the propagation of other types of stress waves through concrete” as reported in [9]. The test equipment consists of a pulse generator, a pair of transducers (transmitter and receiver), an amplifier, a time measuring circuit, a time display unit. The test is performed generating a series of pulses by means of the pulse generator. The transmitting transducer is characterized by the presence of a piezoelectric layer and a similar transducer acts as a receiver to monitor the arrival of the pulse. A timing circuit is used to measure the travel time of the pulse. It is possible to make measurements of ultrasonic pulse Velocity (V) by placing the two transducers on opposite faces (direct transmission), on adjacent faces (semi-direct transmission), or on the same face (indirect or surface transmission) of a concrete structure or specimen, even if the direct transmission is the most reliable. The V test result is affected by numerous factors, including the properties and proportion of the constituent materials, aggregate content and types, age of the concrete, presence of microcracks, water content, stresses in the concrete specimen, surface condition, temperature of the concrete, path length, shape and size of the specimen, presence of reinforcement, and so on, as confirmed in Diaferio et al. [10]. In their study, the results of an experimental campaign performed on an existing building in the area of Bari (Italy) are presented. The tests involved both destructive tests and V tests. The correlation curves have been evaluated for each one of the possible test conditions. Therefore, using the V test alone to predict compressive concrete strength is problematic.
The rebound hammer is a handheld instrument used for testing the quality of hardened concrete in an existing structure. The test device was developed in 1948 by Ernst Schmidt at the Swiss Federal Materials Testing and Experimental Institute in Zurich. The development of this “new” device originates from tests carried out to measure hardness of metals. For this reason, this test can be considered as an extension of the Scleroscope test, performed to evaluate the superficial hardness of a material. Due to its simplicity and low cost, the rebound hammer represents the most widely NDT method used for concrete evaluation. “This test method covers the determination of a rebound number of hardened concretes using a spring-driven steel hammer”, as reported in [11]. When the plunger of the rebound hammer is pushed against the surface and the latch is released, the spring-pulled mass rebounds back with a rebound distance. This distance is measured on a scale numbered from 10 to 100 and is recorded as the Rebound Index (RI). The rebound hammer test result is significantly influenced by the concrete type (aggregate size, water/cement ratio, admixtures, the type of cement, cement content, etc.) or by the conditions (moisture, concrete maturity, curing conditions, surface carbonation, etc.). Besides, important drawbacks of this test are the very limited area hit by the plunger and its interactions with irregularities such as voids and aggregates.
Many calibration curves have been proposed in literature with wide dispersion around the original Schmidt curve. The large deviation of curves raised a crucial question of whether the rebound hammer is effective or not in estimating the concrete strength [12]. Since the rebound hammer test might provide some information about the compressive strength only if it is calibrated on the specific concrete type, many codes limit its use. Therefore, using the rebound hammer test alone to predict compressive concrete strength is problematic.
The questionable reliability of both methods can be partially contrasted by using them together. One of the most employed NDT combined methods in practice is the SonReb method, developed by RILEM Technical Committees 7 NDT and TC-43 CND [13–15]. This combination technique is more reliable because the results obtained in the rebound hammer test provides information about the concrete strength near the surface, whereas the results obtained in the V test reflects the interior concrete properties.
The most used techniques to predict compressive concrete strength based on the SonReb measurements are computational modeling, artificial intelligence, and parametric multi-variable regression models. Computational modeling is based on the modeling of complex physical phenomena and thus is often not practical. Parametric multi-variable regression models, on the other hand, can be more easily implemented and used in practice for future applications, such as the reliability assessment of reinforcement concreste (RC) structures incorporating field data. Artificial intelligence including the Artificial Neural Network (ANN) approach is a nonparametric statistical tool without knowing the theoretical relationships between the input and the output. The parametric multi-variable regression model yielded accurate correlation formulas for the prediction of compressive strength in comparison with effective compressive strengths based on destructive test results on core drilled in adjacent locations [16–18]. In the former two studies, performances of the most used formulations in Italy for the estimation of the compressive strength of concrete utilizing NDT were analyzed. The comparison indicates the fair estimation potential of the proposed formulations in the evaluation of concrete compressive strength, starting only from the non-destructive parameters. ANN approach with feasible prediction has been employed to determine concrete compressive strength using input variables such as age, Portland cement, water, sand, etc. [19,20]. ANN approach has been already proposed for the evaluation of relationship between concrete compressive strength and V [21,22].
The aim of this paper is to verify the accuracy of ANN approach comparing the estimated compressive strength based on NDT measured parameters with the effective compressive strength based on destructive test results on cores drilled at adjacent locations. To this end, a relevant number of destructive tests and NDTs have been performed on many reinforced concrete structures [16,17].
ANN is an information processing system inspired by biological nervous system being constituted by many neurons connected in a complex network. The intelligent behavior arises from interactions among numerous interconnected neurons aggregated into layers, naming input layer, hidden layer and output layer. Some receive information from the external environment (i.e., input layer), some send responses in the environment (i.e., output layer), others communicate only with other units inside the network (i.e., hidden layer). In a standard neural network, signals travel from the input layer to the output layer along the hidden layer. Such systems learn from examples, generally without being programmed with any task-specific rules [23,24].
There are several types of ANN depending on the type of connections between the different layers, on the activation functions and learning algorithms. Depending on the type of connections between artificial neurons, Feed-Forward Network (FFN) (please provide the abbreviation) is the simplest and most used typology and is constituted by more than two layers of neurons. In other words, the input layer and output layer are bridged by one or more hidden layers. Each neuron is connected to all the neurons of the previous layer but has no connection with the neurons of its own layer and the signal propagates in a unidirectional way from input to output through the hidden layer. A schematic representation of a three-layer ANN is reported in Fig. 1.
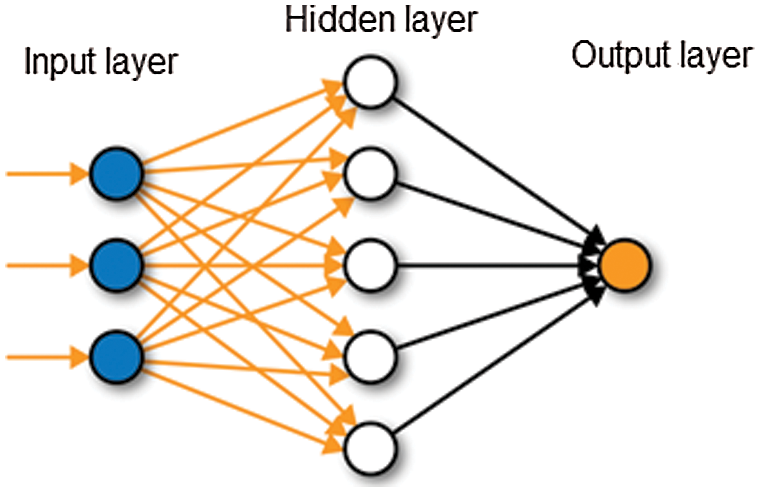
Figure 1: Schematic representation of a three-layer ANN
The fundamental building blocks of each neural networks, both biological and artificial, are represented by the neurons. These are an elementary information processing unit characterized by connections (synapses) able to transfer the signal (stimulus) into other neurons. Each neuron sums the weighted inputs emitting an y-output which varies according to the specific activation function choice. One of the most used activation functions is the sigmoid
where x is the input of the neuron.
The values of synaptic weights represent the first unknown parameter to be determined. In order to minimize the total error of the network, a process of learning (or training) must be carried out. In the supervised learning process, the aim is the prediction of the output value for each valid input data, based only on a limited number of examples of correspondence.
From a mathematical point of view the learning process consists of finding a minimum of a function in a n-dimensional space. This function is given by the variation of the error based on the weights of the network.
The most effective and widespread technique used in the learning with more supervision is the backpropagation error algorithm, which minimizes the total error of the network through the modification of the weights of the connections. In order to search for a minimum, it is usually used the gradient descent technique.
For our purpose, a feed-forward network composed of 3 layers (input, output, hidden layers), with sigmoid logistic activation function and supervised learning with backpropagation error algorithm has been employed (Fig. 2).
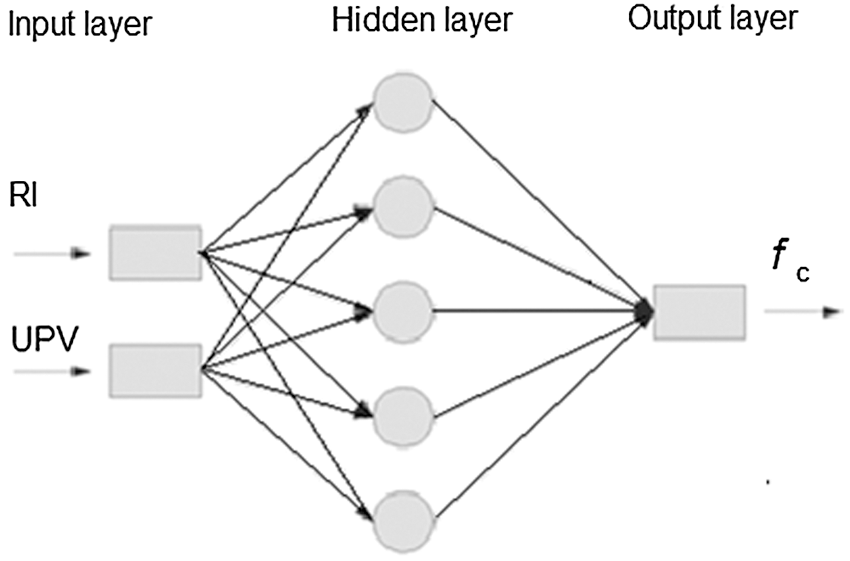
Figure 2: Schematic representation of a three-layer ANN with RI and V as input data
3 ANN-Based Prediction of Concrete Compressive Strength Using SonReb Method
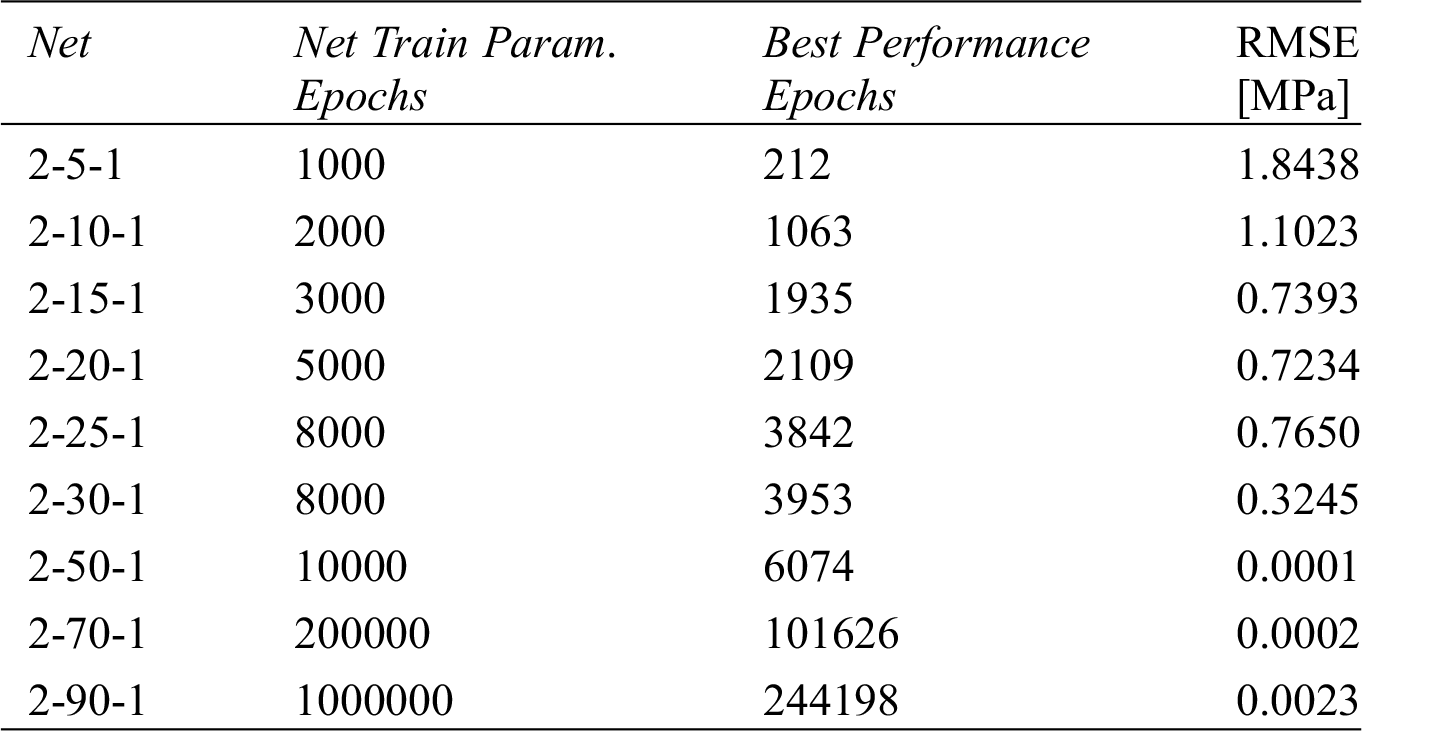
The effectiveness of the networks has been investigated as a function of the only variable parameter in their architecture: the number of neurons of the hidden layer. In order to understand the influence of the number of connections in a 3-layered feed-forward network with two non-destructive parameters (RI and V) input, nine ANNs were considered. The increment steps of the units in all the networks were established based on the efficiency-computational time ratio.
The principal data of all considered networks are reported in Tab. 1, where the Net and RMSE mean Network and Root Mean Squared error, respectively.
The in-situ compressive strengths, the SonReb parameters RI and V, the estimated compressive strengths in 16 locations are reported in Tab. 2.
It is worth mentioning that fck is the actual in-situ strength that can be determined from the core strength using the proposed following equation [25]:
where:
-fcore is the strength of a core specimen.
-CH/D is correction factor depending on the height/diameter ratio H/D, equal to 2 (1.5 + D/H).
-Cdia is correction factor depending on the diameter of core D, equal to 1.06, 1.00 and 0.98 for D equal to 50, 100 and 150 mm, respectively.
-Ca is correction factor depending on the presence of reinforcing bars, equal to 1 for no bars, and varying between 1.03 for small diameter bars and 1.13 for large diameter bars.
-Cd is correction factor depending on the damage due to drilling, equal to 1.20 for fcore < 20 MPa and 1.10 for fcore > 20 MPa.
The problem of conversion from cylinder to cube strength has been widely investigated in Indelicato et al. [26].
Nine different ANNs are considered to understand the influence of the number of units in a 3-layered feed-forward network with two non-destructive parameters RI and V as inputs.
To evaluate the accuracy of ANN approach, some of the estimated compressive strengths have been compared with the effective compressive strengths determined in DT on samples extracted in adjacent locations (Figs. 3–7).
Table 2: In-situ DT compression strength fck, RI, V and estimated NDTstrength fc in 16 locations according to nine different ANNs

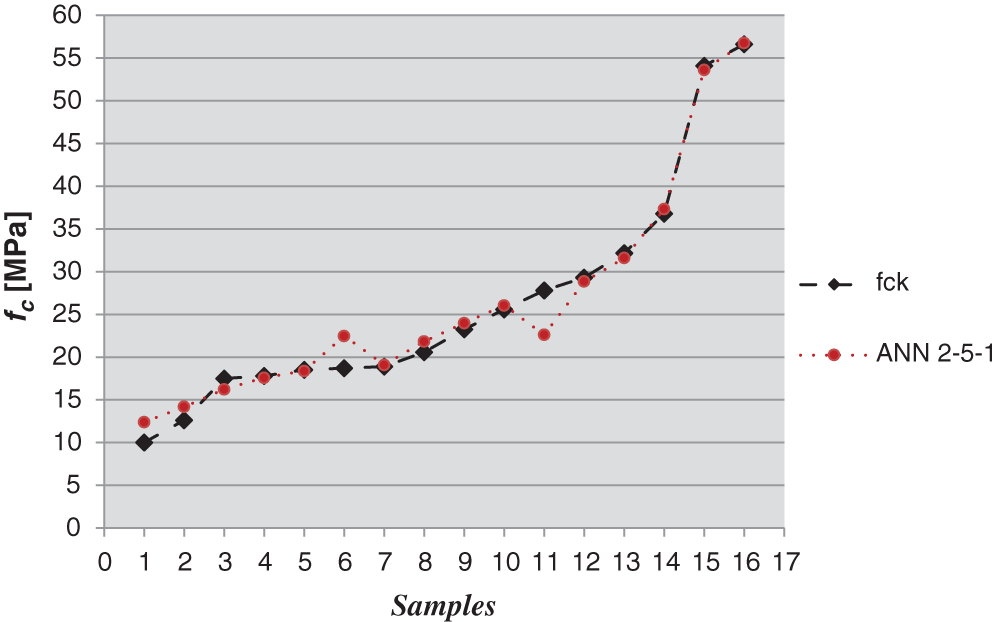
Figure 3: Comparison between DT fck- values and estimated NDT fc- values using ANN 2-5-1
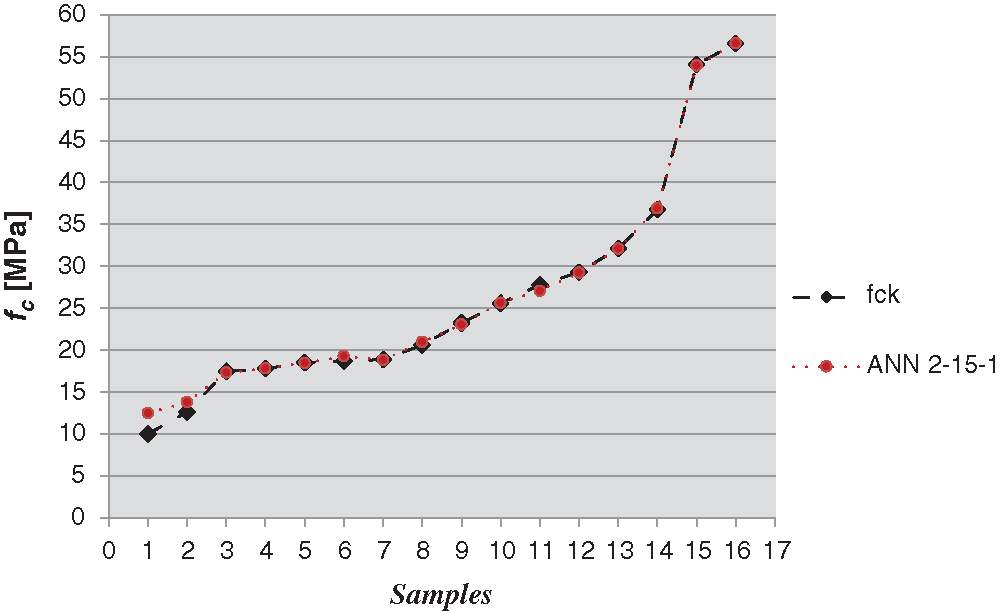
Figure 4: Comparison between DT fck- values and estimated NDT fc- values using ANN 2-15-1
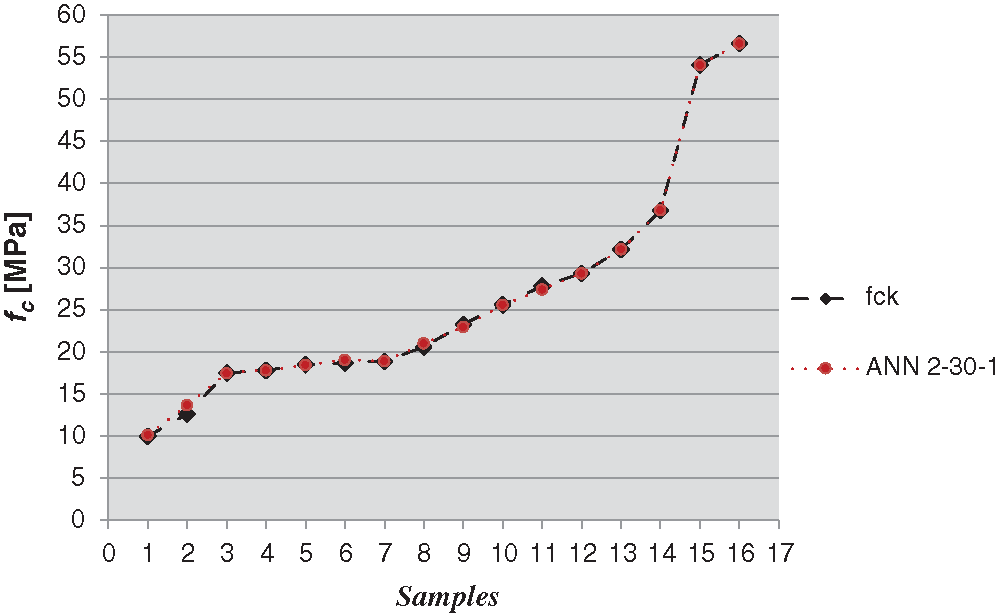
Figure 5: Comparison between DT fck- values and estimated NDT fc- values using ANN 2-30-1
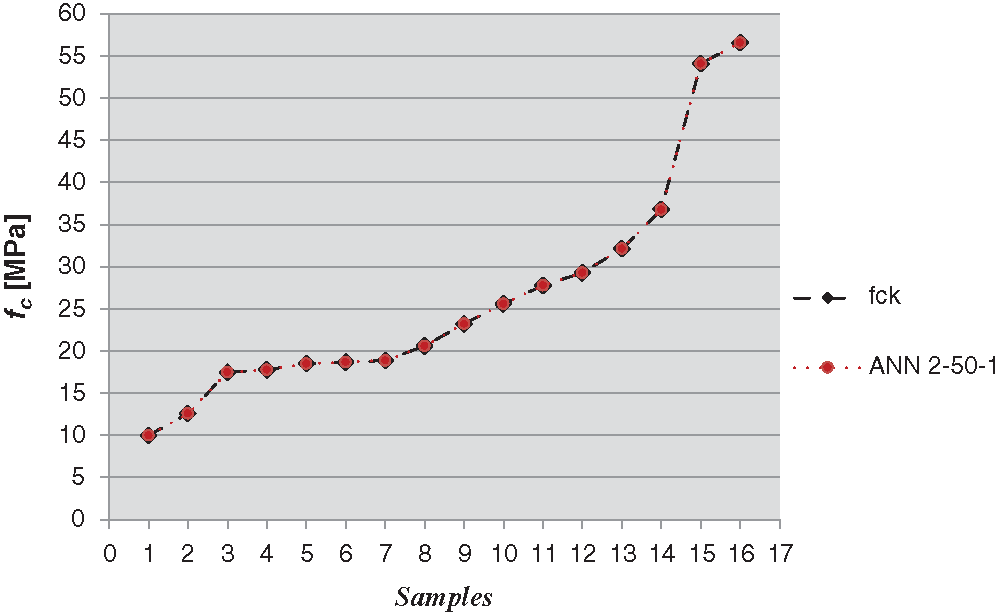
Figure 6: Comparison between DT fck- values and estimated NDT fc- values using ANN 2-50-1
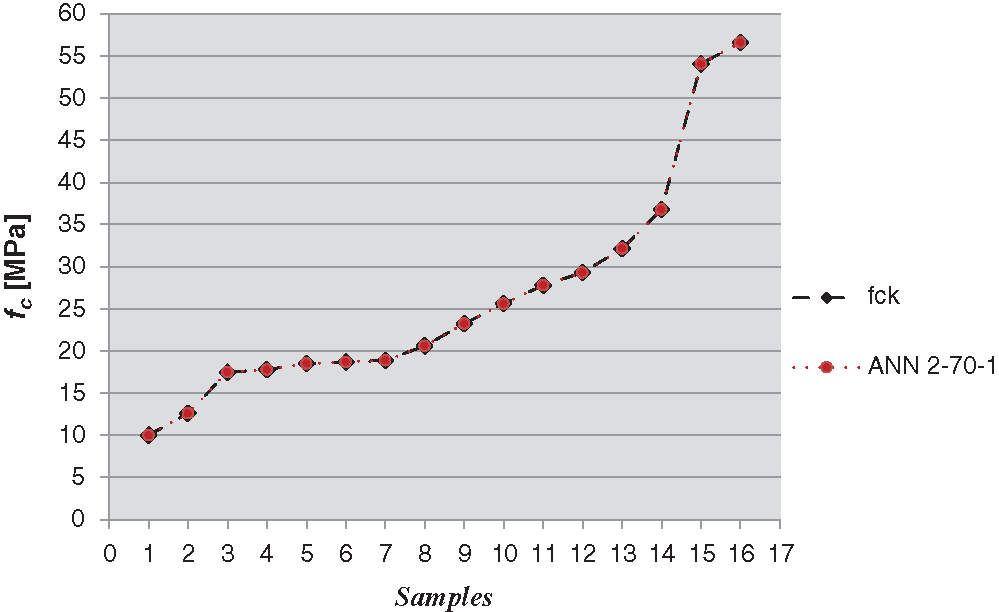
Figure 7: Comparison between DT fck- values and estimated NDT fc- values using ANN 2-70-1
Based on the results of the present research, it can be observed that the neurons of the hidden layer constitute the data processing unit of the system more susceptible to error and their quantity can extremely influence the final output. Therefore, using too few neurons in the hidden layer gives rise to a phenomenon known as underfitting. Underfitting occurs when the number of neurons in the hidden layers is not adequate to detect the complicated signals and transform them in a simpler data set. This condition occurs for the simpler structure of ANN until the best performance in terms of number of neurons is reached.
On the contrary too large number of hidden neurons would encourage another critical phenomenon known as overfitting, i.e., when the neural network has so much information processing capacity that the limited amount of information contained in the training set is not enough to train all the neurons in the hidden layers. This is the case of the ANNs with 70 and 90 neurons in the hidden layers and it can be detected analyzing the matrix of the synaptic weights in which some values are very close to zero. This condition results in an overall loss of information within the neural network with a consequent reduction of effectiveness in the precision of the estimation (Fig. 8).
It follows that Ann 2-50-1 can be considered the best performing for predicting the compressive concrete strength. The training and learning phases of this ANN with 50 neurons in the hidden layer are reported in Figs. 9 and 10.
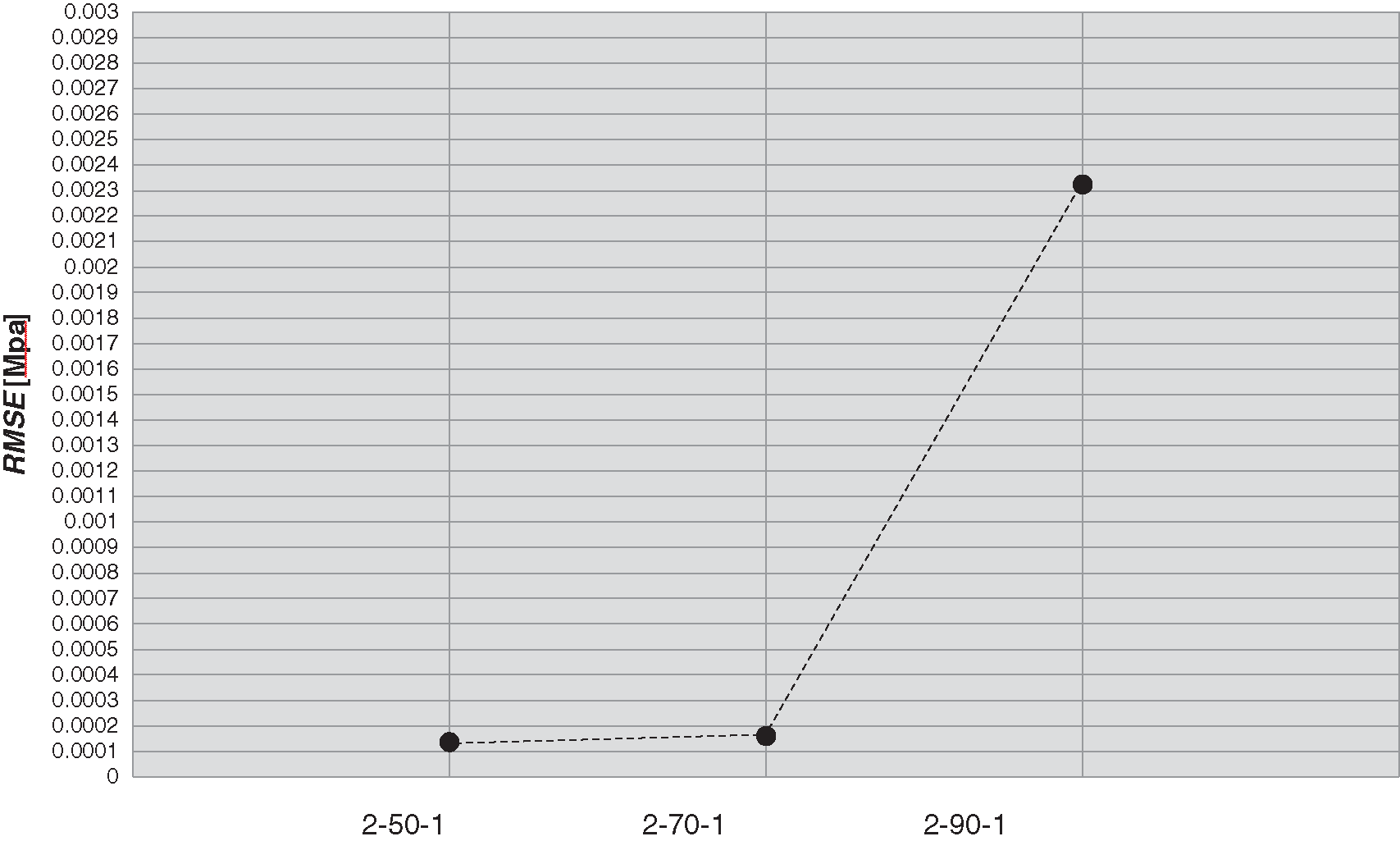
Figure 8: Comparison between the different last three ANNs with the most reliability in concrete strength assessment
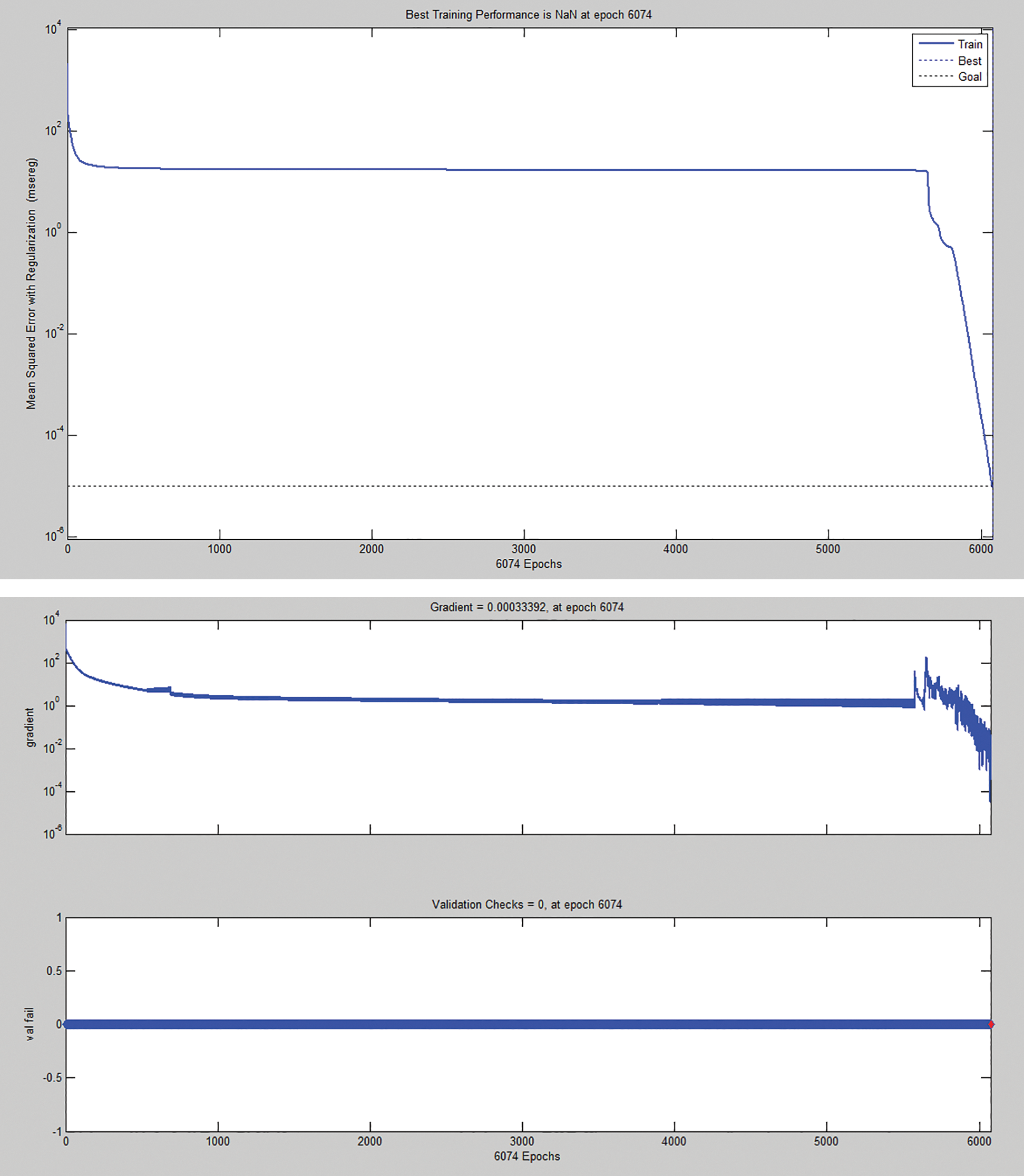
Figure 9: ANN behavior during training performance and gradient descendent
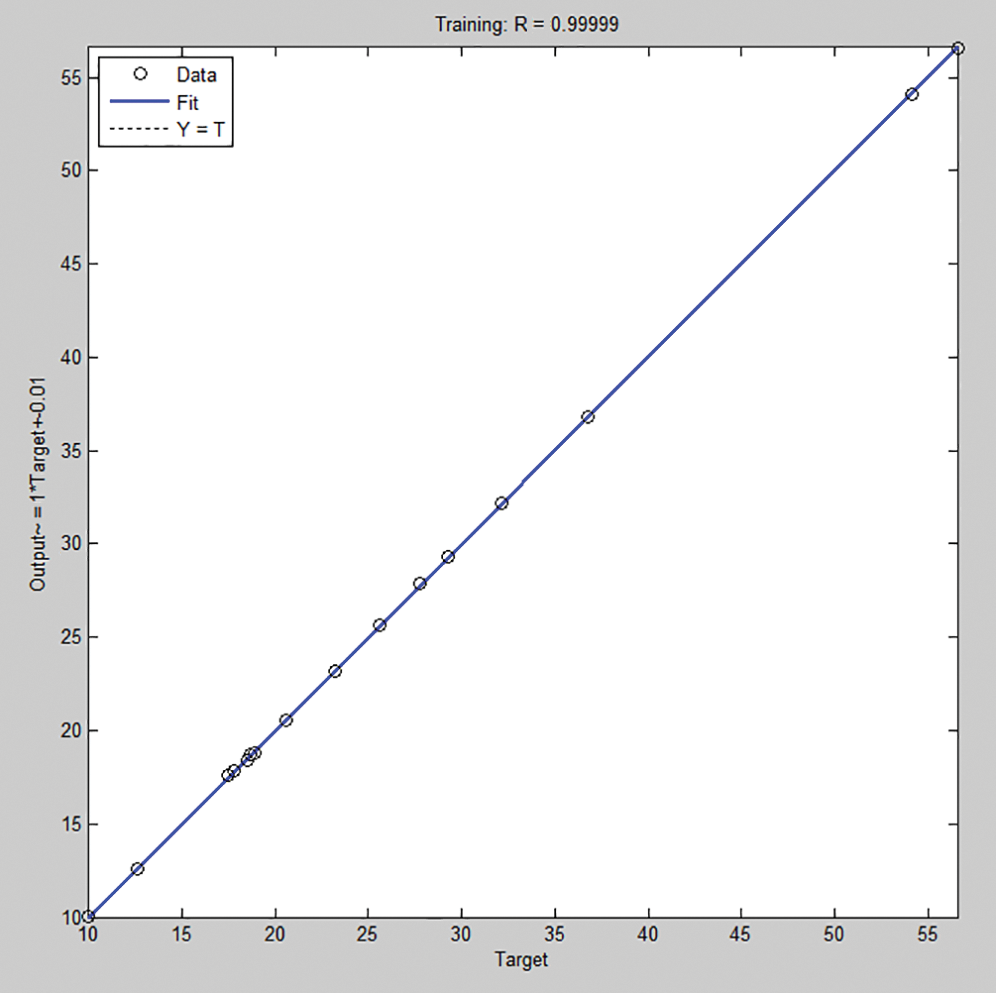
Figure 10: ANN training set
It is important to point out the better potential estimation of ANN present approach compared to parametric multi-variable regression approach [16,17]. In particular, Fig. 11 shows the comparison between fck values obtained during DT experimental campaign with respect to fc values calculated according to the latter approach using the following different correlation formulations suggested by Giacchetti et al. [27] (Eq. (3)), Di Leo et al. [28] (Eq. (4)), Gasparik [29] (Eq. (5)) and Standards of Tuscany Region [30].
According to the Standards of Tuscany Region fc is the average of the three values calculated using the previous correlation formulations (Eqs. (3)–(5)):
The comparative study of the above correlation formulas is shown in Fig. 11. A good approximation can be observed, but Ann 2-50-1 can be considered by far the best performing for predicting the compressive concrete strength a shown in Fig. 6.
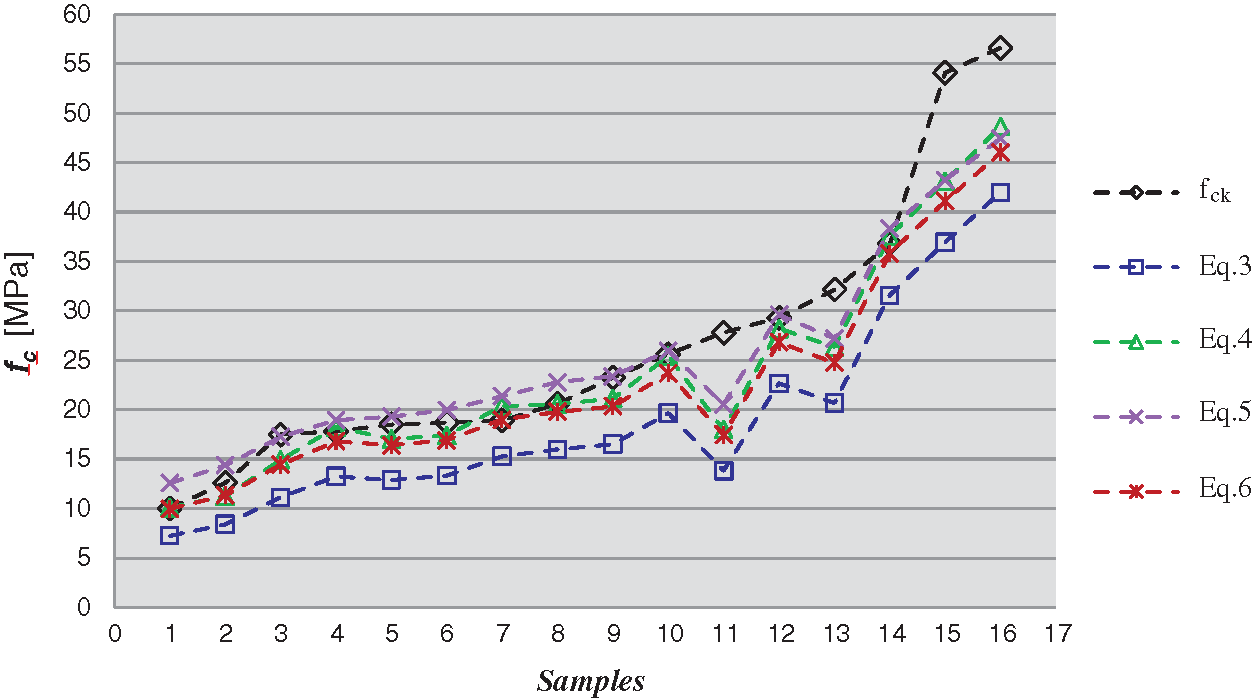
Figure 11: Comparison between DT fck- values and estimated NDT fc- values according to different formulations [16,17]
In general, most of the models used to study the on-site concrete compressive strength consist of mathematical rules and expressions that try to capture relationship between NDT parameters and concrete mechanical characteristics. Generally, these mathematical models based on experimental data are presented in regression forms. However, since these regression methods have shown less accuracy in concrete strength predictions, in the recent years new techniques, such as ANN, have been employed to approximate this non-linear and complex problem.
The results obtained from the study indicate the excellent estimation potential of a multilayer feed-forward neural network trained with backpropagation error algorithm in the evaluation of concrete compressive strength based only on non-destructive parameters. In fact, the calculated RMSE values are to be considered reasonably low in relation to those calculated with the regression formulas found in the literature, thus indicating the accuracy of the estimations.
Analyzing the results obtained for the neural networks characterized by two input parameters (i.e., RI and V value) it can be observed a significant improvement in the estimation of concrete compressive strength since for networks with 50 neurons into the hidden layer (RMSE = 0.00013 MPa, about 50000 times lower than that obtained with the regression formulas found in the literature).
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Kroworz, A., Katunin, A. (2018). Non-destructive testing of structures using optical and other methods: A review. Structural Durability & Health Monitoring, 12(1), 1–18. [Google Scholar]
2. Mishra, M., Bhatia, A. S., Maity, D. (2021). A comparative study of regression, neural network and neuro-fuzzy inference system for determining the compressive strength of brick-mortar masonry by fusing nondestructive testing data. Engineering with Computers, 37(1), 77–91. [Google Scholar]
3. van Dao, D., Ly, H. B., Trinh, S. H. E., Le, T. T. E., Pham, B. T. E. (2019). Artificial intelligence approaches for prediction of compressive strength of geopolymer concrete. Materials, 12/6(6), 983. [Google Scholar]
4. Rucka, M. (2020). Special issue: Non-destructive testing of structures. Materials, 13, 4996. DOI 10.3390/ma13214996. [Google Scholar] [CrossRef]
5. Balayssac, J. P., Garnier, V. (Eds.). (2017). Non-destructive testing and evaluation of civil engineering structures. ISTE Press-Elsevier. [Google Scholar]
6. Viola, E., Federici, L., Nobile, L. (2001). Detection of crack location using cracked beam element method for structural analysis. Theoretical and Applied Fracture Mechanics, 36, 23–35. [Google Scholar]
7. Viola, E., Nobile, L., Federici, L. (2002). Formulation of a cracked beam element for structural analysis. Journal of Engineering Mechanics, ASCE, 128, 220–230. [Google Scholar]
8. Nobile, L. (2001). Mixed mode crack growth in curved beams with edge crack. Theoretical and Applied Fracture Mechanics, 36, 61–68. [Google Scholar]
9. ASTM (2002a). Standard test method for pulse velocity through concrete, ASTM C 597. West Conshohocken, PA: ASTM International. [Google Scholar]
10. Diaferio, M., Vitti, M. (2021). Correlation curves to characterize concrete strength by means of UPV tests. Lecture Notes in Civil Engineering, 110, 209–218. [Google Scholar]
11. ASTM C805/C805M-08 Standard Test Method for Rebound Number of Hardened. [Google Scholar]
12. Kumavat, H. R., Chandak, N. R., Patil, I. T. (2021). Factors influencing the performance of rebound hammer used for non-destructive testing of concrete members: A review. Case Studies in Construction Materials,14, e00491. [Google Scholar]
13. Rilem Report TC43-CND (1983). Draft Recommendations for in situ Concrete Strength Determination by Combined Non-Destructive Methods. [Google Scholar]
14. Chandak, N. R., Kumavat, H. R. (2020). SonReb method for evaluation of compressive strength of concrete. IOP Conference Series: Materials Science and Engineering, 810(1), 012071. [Google Scholar]
15. Merzoug, W., Chergui, S., Cheikh Zouaoui, M. (2020). The impact of reinforced concrete on the modern-day architectural heritage of Algeria. Journal of Building Engineering, 30, 101210. [Google Scholar]
16. Nobile, L., Bonagura, M. (2014). Recent advances on non-destructive evaluation of concrete compression strength. International Journal of Microstructure and Materials Properties, 9(3/4/5), 413– 421. [Google Scholar]
17. Nobile, L. (2015). Prediction of concrete compressive strength by combined non-destructive methods. Meccanica, 50(2), 411–417. [Google Scholar]
18. Alwash, M., Breysse, D., Sbartaï, Z. M. (2015). Non-destructive strength evaluation of concrete: Analysis of some key factors using synthetic simulations. Construction and Building Materials, 99, 235–245. [Google Scholar]
19. Topcu, I. B., Sarıdemir, M. (2008). Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Computational Materials Science, 41(3), 305–311. [Google Scholar]
20. Nath, U. K., Goyal, M. K., Nath, T. P. (2011). Prediction of compressive strength of concrete using neural network. International Journal of Emerging Trends in Engineering and Development, 1(1), 32–43. [Google Scholar]
21. Trtnik, G., Kavcic, F., Turk, G. (2009). Prediction of concrete strength using ultrasonic pulse velocity and artificial neural networks. Ultrasonics, 49, 53–60. [Google Scholar]
22. Bilgehan, M., Turgut, P. (2010). Artificial neural network approach to predict compressive strength of concrete through ultrasonic pulse velocity. Research in Nondestructive Evaluation, 21(1), 1–17. [Google Scholar]
23. Rafiq, M. Y., Bugmann, G., Easterbrook, D. J. (2001). Neural network design for engineering applications. Computers & Structures, 79, 1541–1552. [Google Scholar]
24. Gurney, K. (2014). An introduction to neural networks. CRC Press. [Google Scholar]
25. Dolce, M., Masi, A., Ferrini, M. (2006). Estimation of the actual in-place concrete strength in assessing existing RC structures. The Second International Fib Congress, pp. 5–8. Naples, Italy. [Google Scholar]
26. Indelicato, F., Paggi, M. (2008). Specimen shape and the problem of contact in the assessment of concrete compressive strength. Materials and Structures, 41(2), 431–441. [Google Scholar]
27. Giacchetti, R., Lacquaniti, L. (1980). Controlli non distruttivi su impalcati da ponte in calcestruzzo armato. Nota Tecnica 04, Università di Ancona, Facoltà di Ingegneria, Istituto di Scienza e Tecnica delle Costruzioni (in Italian). [Google Scholar]
28. Di Leo, A., Pascale, G. (1994). Prove non distruttive sulle costruzioni in cemento armato. Proceeding of the Conference on Non Destructive Testing and Quality System for Reliability and Safety of Civil Structures. Bologna, SAIE’94(in Italian). [Google Scholar]
29. Gasparik, J. (1992). Prove non distruttive in edilizia.Quaderno Didattico A.I.P.N.D. Brescia (in Italian). [Google Scholar]
30. Regione Toscana (2004). Istruzioni Tecniche: Criteri per lo Svolgimento di Indagini Diagnostiche Finalizzate alla Valutazione della Qualita dei Materiali in Edifici Esistenti in Cemento Armato (in Italian). [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |