Structural Durability & Health Monitoring

DOI: 10.32604/sdhm.2021.015174

ARTICLE

Effect of Lead-Rubber Bearing Isolators in Reducing Seismic Damage for a High-Rise Building in Comparison with Normal Shear Wall System

Mahmoud Fakih1,*, Jaafar Hallal1, Hassan Darwich2 and Hala Damerji3

1Faculty of Engineering, Lebanese University, Beirut, Lebanon
2Laboratory of Composite Materials for Construction (LMC2), University of Lyon, Lyon, France
3Faculty of Engineering, Arts, Sciences and Technology University in Lebanon, Beirut, Lebanon
*Corresponding Author: Mahmoud Fakih. Email: mahmoud.fakih@ul.edu.lb
Received: 27 November 2020; Accepted: 25 December 2020

1  Introduction

Buildings and more precisely high buildings are very sensitive to earthquake ground motions. Since the 1960–1970’s, the study of structural behavior subjected to seismic motion has been developed and continues to evolve, after strong earthquakes that struck different urban regions around the world caused buildings destruction and loss of lives. These buildings should be protected against seismic motions in order to make their structures safer. Many researchers use the principle of energy dissipation by adding damping devices and other systems to the structure as protective systems [1–4]. These seismic protective devices have been developed to improve the seismic response of building structures against seismic vibrations. The base isolation technique is one of the most used seismic protection techniques in earthquake areas. This isolation technique consists of the separation concept between the structure and its foundation, where the reduction of interaction between the ground and the structure is expressed by the term ‘‘isolation’’, the term ‘‘base’’ means the foundation of the structure [5]. This tool is used to control the passive vibrations of the structure, and it reduces the damage in the structural and non-structural parts of the building subjected to an earthquake [6–8]. It is based on a separation system between the base and the structure which is made by fixing the isolators between the building and the foundation [9]. This provides flexibility and allows for energy dissipation which leads to reduce the seismic movement effect. The main difference between the conventional design approach and the seismic isolation concept is that the first one is based on the increasing of structure resistance (strengthening), whereas the second reduces the dynamic load produced by the seismic waves at the base of the structure [10].

Furthermore, the traditional design approach increases the stiffness of the building, i.e., increases the stiffness of the structural components. However, the non-structural components may be subjected to significant damages during a major earthquake. To reduce the inter-storey drifts, the storey accelerations and the storey displacements, the concept of base isolation is increasingly being adopted [11]. This acceleration reduction protects the non-structural elements, while the reduction in displacements should protect the structural and the non-structural elements during the earthquake with minor damages. Base isolators can be placed at the interface base-superstructure to reduce or filter out the forces transmitted from the ground to the whole structure, or at a specific level to isolate the above storeys. They adjust the dynamic response of the building so that the soil can move below the structures without transferring these seismic loads into the superstructures. In an ideal isolation system when the building achieves this flexibility, they will be a total separation. The increase of the seismic performance of the structure and its content arises from the dissipation of a part of the energy created by the extreme earthquake effect on the structure. The building can survive after an earthquake using the conventional methods, but it may not remain operational [12,13]. However, base isolation technique maintains the building functionality during an earthquake [14].

The application of isolators is well known and familiar in the literature, but there is no proper research for a tall irregular building using real floor plans. This study presents the seismic analysis for a high-rise building located in Beirut (Lebanon), which is irregular in shape using software package ETABS. It is the first implementation of this isolation technology (Lead Rubber Bearing) in this country. Hence, a non-linear time history analysis will be performed to understand the effect of seismic loading on the structural response throughout the loading period. In order to demonstrate the effectiveness of using LRB as an isolator system instead of a conventional shear wall system, a comparative analysis of the response results (such as the fundamental time period, storeys acceleration, storeys displacement, base shear force and inter-storey drift ratio) is accomplished for two structural models. In the following, Section 2 describes the type of isolator chosen for this work and its advantages. Section 3 describes the developed structural models with their properties. Section 4 presents the design of the isolators and their properties calculation. In Section 5, the results of the modeling for the two structural systems and the effect of isolator system on the dynamic behavior of the building are presented. Finally, Section 6 concludes the main findings of this work and opens a brief discussion of its possible extensions.

2  Selection of Base Isolation System

The development of isolation techniques has been progressed to provide more flexibility and damping to the structure during the seismic attack. Nowadays, lead rubber bearing (LRB) is one of the most used isolator types among all other categories. The first use of LRB was in New Zealand (1970’s) giving a new concept to the design of base isolated structures [15,16]. This technique has been extensively used in Japan and the United States [17], then China joined the group until recent days where the using of LRB has become much popular. From a construction point of view, the addition of a lead-plug which is press-fit into a central hole in the bearing is the difference between lead-rubber bearings and low-damping natural rubber bearings. Hence, this lead-plug deforms plastically under shear stresses, so the energy dissipation capabilities increase in comparison with the low-damping natural rubber bearing [18]. Moreover, LRB is an elastomeric bearing which is made by rubber layers with steel plates, cover plates and a lead core at the center.

Fig. 1 shows the composition of a typical LRB isolator [5]. The advantage of LRB is that it can combine the function of isolation and recentering in one element. Which gives structural support, horizontal flexibility and recentering force to the isolation system [16]. There are many isolation systems that provide sufficient isolation and self-centering too, like low damping rubber bearings and friction pendulum. The yielding of the lead core provides an energy dissipation which allows to achieve an equivalent viscous damping coefficient up to 30%, thereby reducing the horizontal isolator displacement effectively [19,20]. A high vertical stiffness can be obtained by these thin layers of rubber reinforced with steel plates in addition to damping. These characteristics permit the LRB system to carry a significant vertical load owing to its high vertical stiffness and to move laterally with relative lower stiffness than other isolation systems [21]. Therefore, one device can support a structure member vertically, providing a horizontal displacement and increasing the damping in the system to a desired value [6]. Several researchers [22–24] studied the behavior of base isolated building (LRB) under the action of seismic forces, and they compared the results with fixed base building. From these studies, they concluded a reduction in the lateral displacement and acceleration at the top storey. They also concluded that the base shear and the storey drifts are lower for base isolated buildings compared to fixed base buildings.

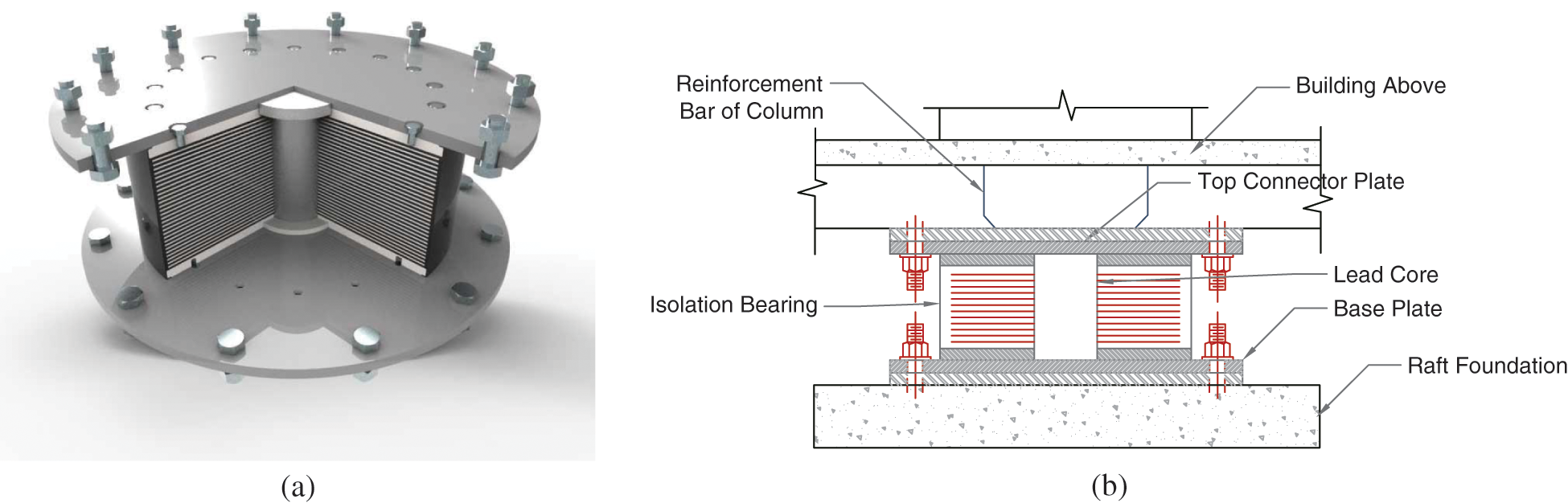
Figure 1: Lead rubber bearing

Dynamic Isolation System [25] is one of the leader companies in the manufacturing of lead rubber bearings. In this study, different types of lead rubber bearings have been examined based on their properties provided by the manufacturer’s website. The method of selection and calculation is detailed in the sections below. The hysteresis loop of the LRB isolator can be modelled as a bilinear curve as shown in Fig. 2, which provided the elastic stiffness (Ke) and the post-yield stiffness (Kd) for the material. The force-displacement relationship of a typical LRB is non-linear [26]. This curve is also given by the manufacturer’s website, depending on the material properties and the mechanical behavior of its LRB.

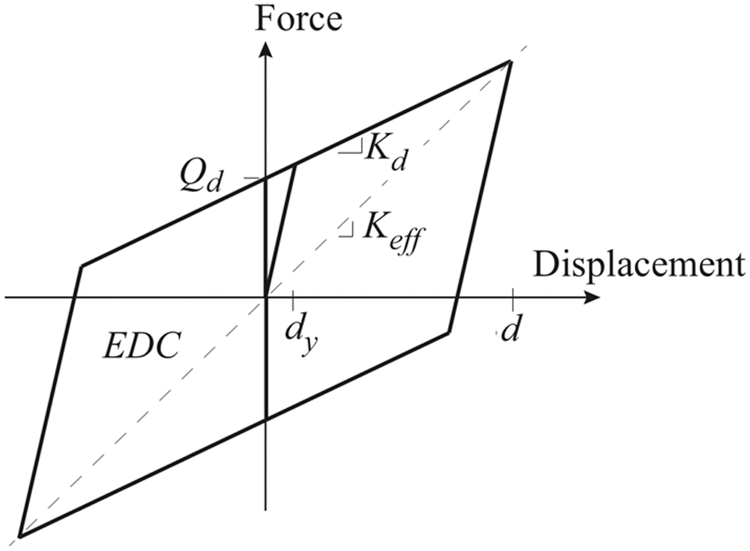
Figure 2: Hysteretic behavior of the LRB model

3  Structural System

In the present study, a 168.2 m height (44-storey, 3 basements, and a roof) high rise RC building has been modeled using software package ETABS. In order to proceed with the study two structural models has been designed. The first model is based on a shear wall system (1 m thickness) with fixed support at the base, as shown in Fig. 3a. While in the second model, the shear wall system is replaced with a frame resistance system (Fig. 3b), with the incorporation of the isolation system (LRB) near the base of the columns and while conserving the 3 core walls for the building. The building is subjected to a probability of 10% of exceedance seismic hazards in 50 years, corresponding to the design based earthquake (DBE) [27]. The response modification factor for the fixed base model (Model 1) was taken as the value of 4.5 consistent with shear wall system case according to UBC97 [28], and 8.5 for the moment frame system (Model 2) [29]. This factor should be modified to the value of 2 (R1 = 2) in Model 2, according to IBC isolation section [27] after the incorporation of the LRB isolators. The design of structural members is performed in accordance with ACI-318-14 [30]. LRB isolators are modeled on ETABS as explicit isolator elements with chosen properties.

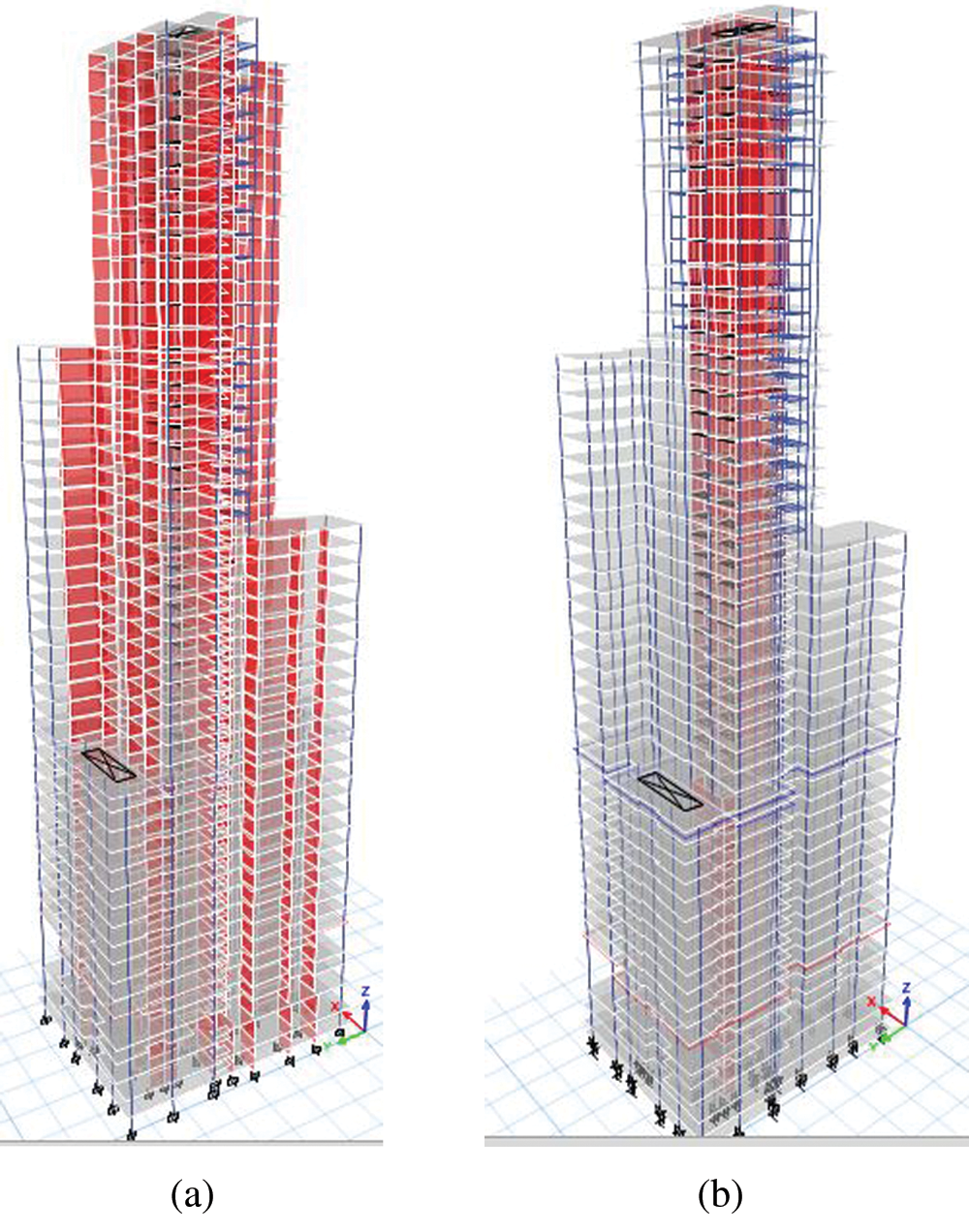
Figure 3: 3D view of the high-rise building (a) shear walls, (b) isolator system

Fig. 4 shows the two structural systems described above. In Fig. 4a, it has been noticed the positions of the shear walls of the Model 1. Whereas, Fig. 4b demonstrates the replacement of these shear walls by columns, with LRB isolators near the base of these columns. The shape irregularity of the studied high rise building is clearly demonstrated by the floor surface areas, presented in Tab. 1. The ground accelerations generate normally the seismic loads in a structure. A dynamic non-linear time history analysis has been performed on two building models. Such type of analysis allows to understand the dynamic performance of the structure under a real earthquake strike. The main objective of this study is to understand the effect of a base isolator, on the roof storey displacement, roof storey acceleration, base shear reaction and the inter-storey drift ratio of the structures. This analysis has been performed using the two seismic waves for El Centro array 6 earthquake [31], in both X and Y directions (the two perpendicular directions of the ground floor surface plan), as we can observe in Fig. 5. The ground motions were scaled using the gravity acceleration g = 9.81 m/s2. The ground motion processes during 39.1 s with 0.436 g as the peak ground acceleration for the two structural models. The soil acceleration vs. time record was available at a time step of 0.01 s. Fig. 6 shows the spectral accelerations for El Centro array 6 seismic waves in function of period domain. It has been noticed the maximum values of spectral accelerations occur at low period values i.e., at high frequencies. Buildings with a low natural period will be subject to high excitations under these seismic waves. There are several different versions of the El Centro record in existence [32,33]. The El-Centro ground motion is one of the earliest recorded and most widely used near-field ground motions. It does not contain pulses in the acceleration, velocity, or displacement histories. The peak values of ground acceleration, velocity, and displacement (PGA, PGV and PGD) for El Centro ground motion are available in the work of Malhotra et al. [34].

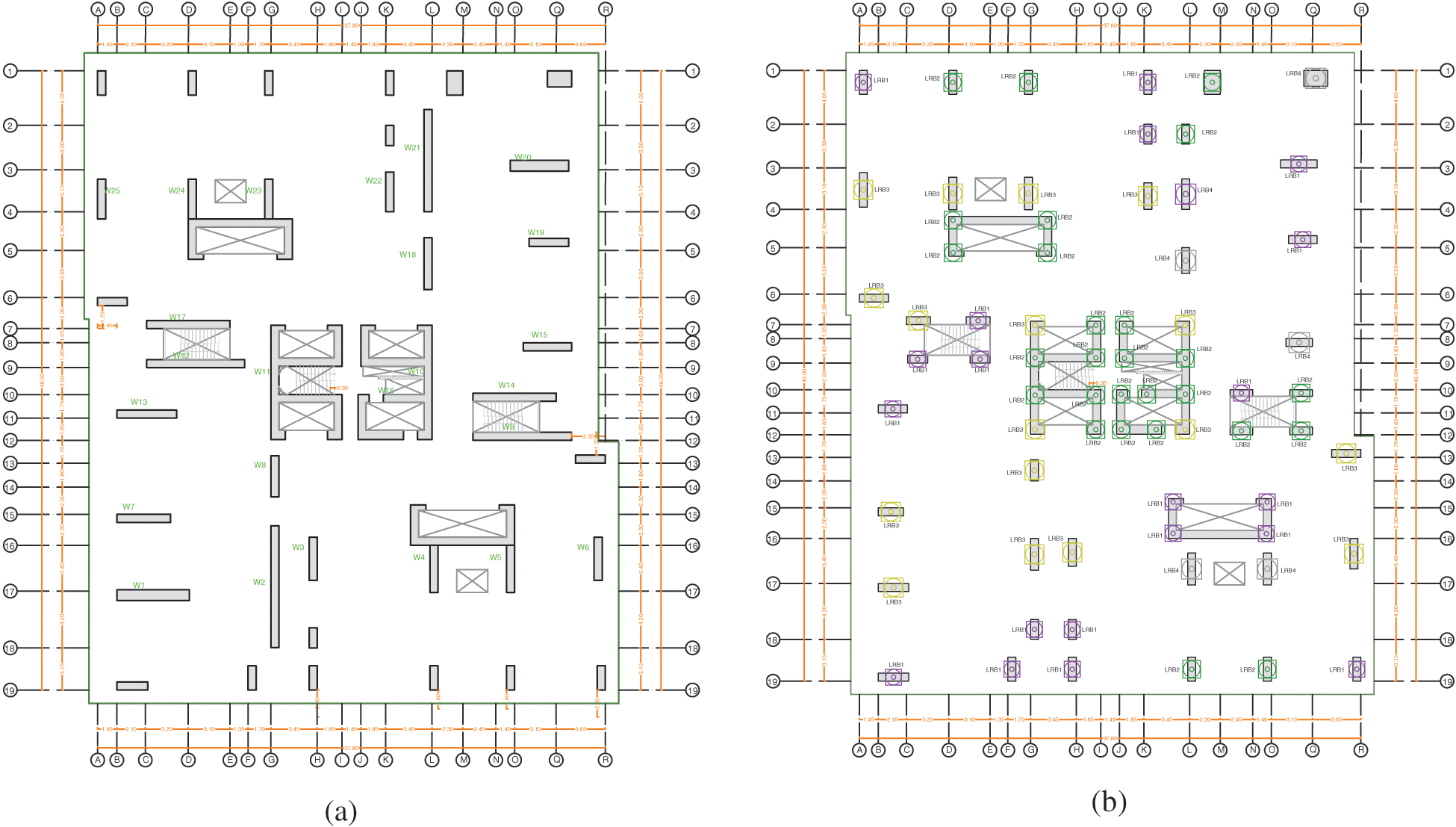
Figure 4: The plans of structural systems on the ground floor level (a) shear wall system, (b) isolator system

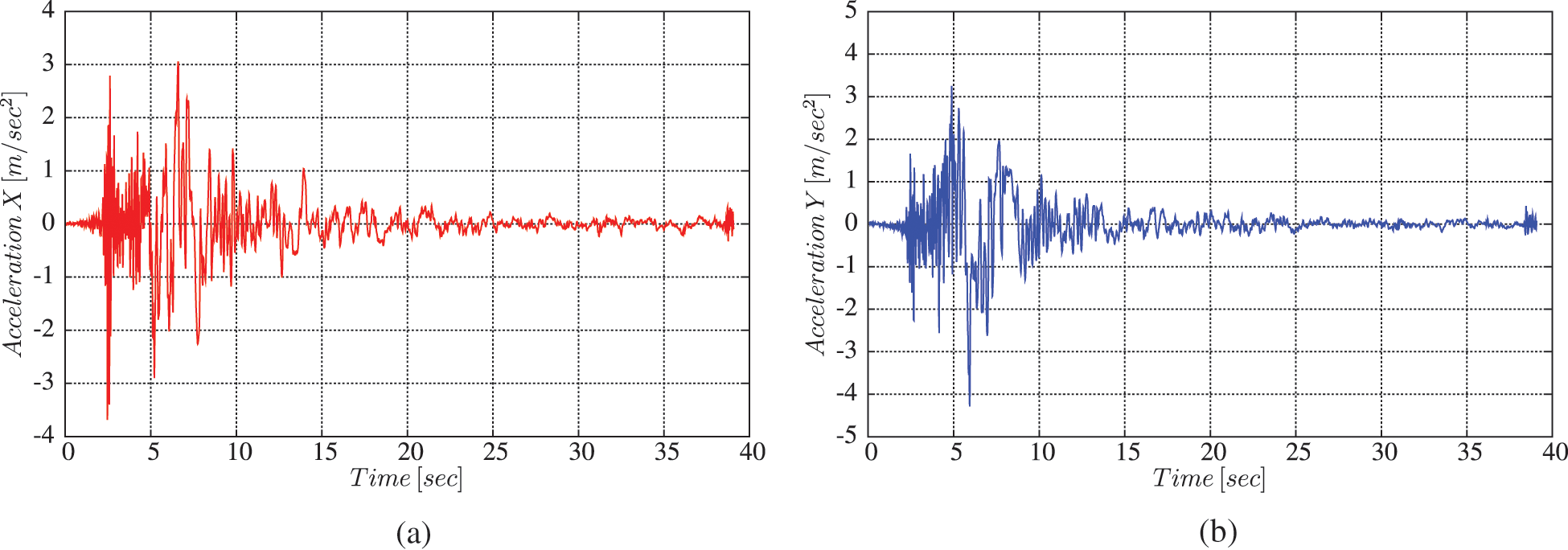
Figure 5: El-Centro-Array 6 time history [31] (a) acceleration in X direction, (b) acceleration in Y direction

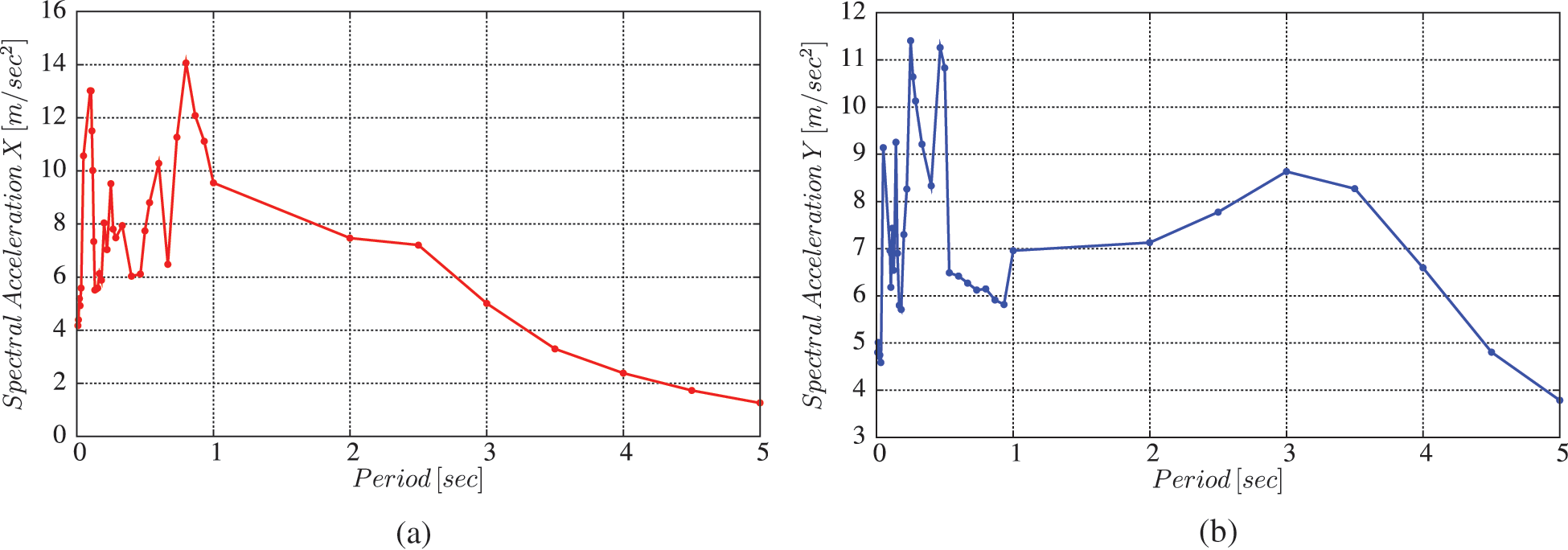
Figure 6: Spectral acceleration for El-Centro-Array 6 in period domain (a) acceleration in X direction, (b) acceleration in Y direction

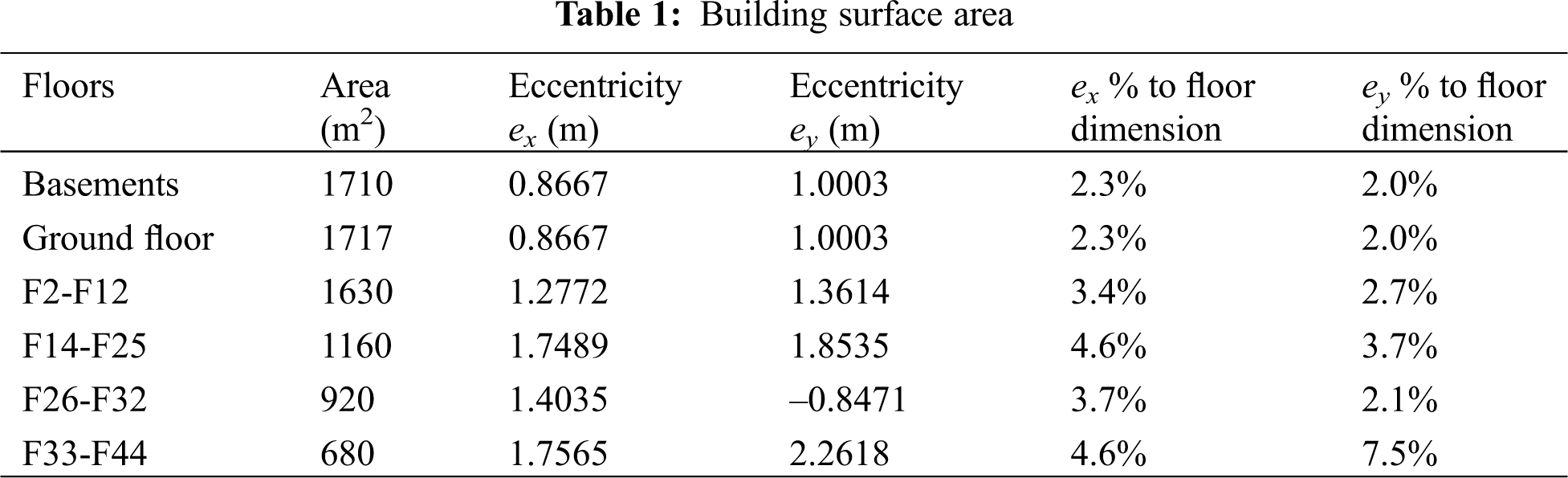
4  The Design and Characteristics of LRB System

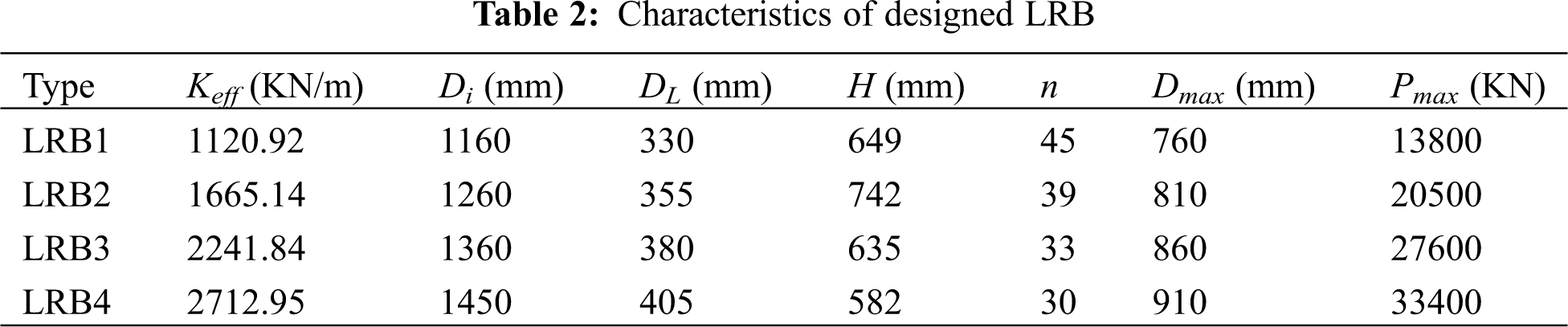
A static design of the high-rise building has been performed on ETABS, in order to calculate the vertical load acting on each isolator. This was the first step of LRB design. After that, the LRB isolators was divided into 4 types regarding the range of load acting on them, as shown in Fig. 4b. Two main factors which control the design of the LRB isolator system and affect its elastic forces are: the total effective stiffness and the maximum displacement of the bearing. These two parameters should be minimized in order to have an economical design. Using the design equations of IBC code-section 1623 for isolator design [27,35] and the data provided by the manufacturer [25], all design criteria of LRB have been calculated.

LRB isolators can be designed to carry different values of displacement by changing their diameter and their design parameters. The main parameters calculated for the four isolator types are: the effective stiffness Keff (the isolator force divided by the displacement), the effective damping (25%), the isolator diameter (Di), the lead diameter (DL), the isolator Height (H), and finally the number of layers (n). The elastic stiffness Ke and the yielding stiffness Kd (Fig. 2) are specific for each type and size of LRB isolator, regarding its Hysteretic behavior curve and represents the input parameter for the calculation of Keff. The design limit of rubber shear strain is 250%, and the rubber shear modulus is G = 0.7 MPa. The maximum horizontal displacement Dmax is the control parameter of each LRB isolator. After the time history analysis, the displacement calculated in each isolator should be less than the maximum displacement property provided in the manufacturer data, in order to have a safe design and avoid isolator failure. The design properties of the 4 isolator types are shown in Tab. 2. However, isolator stiffness was the same in both longitudinal and traversal directions of the building.

5  Results

The results of the non-linear time history analysis have been performed for the two structural models, for fixed base model (shear wall system) and for isolated model, in terms of the time history functions of storey responses (accelerations, displacements, base shear forces) and also storey responses in function of each level. These functions give better insight into the response behavior of the structure at each time step of the analysis. The following sub-sections detail these results.

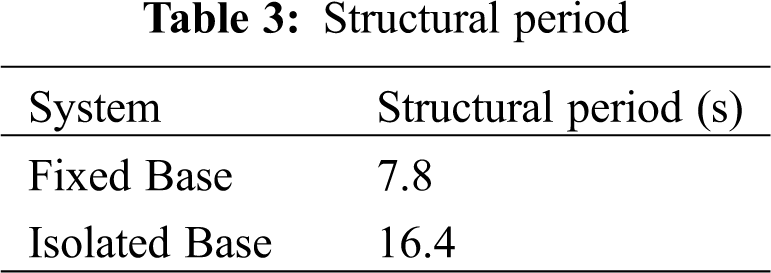
5.1 Comparison of Structural Period

The structural period is one of the most important factors in building seismic analysis. Structural period for both models was compared and presented in Tab. 3. In this study, the dynamic response was mainly affected by the role of rubber bearing isolators. The structural period increased in the base isolated structure between 2 to 3 times compared to the period of the fixed base structure [36,37]. For the fixed base structural system, the fundamental period was 7.8 s for Mode 1 (the high value of period is for the critical mode1). Whereas, for the base isolated structural system the fundamental period was 16.4 s for the same mode. The predominant time period has been lengthened for the seismic isolated building as logically expected. The important goal of a base isolation system is the increasing of the fundamental time period of the structure, which can reduce the destructive first shocks of an earthquake. Contrary to the base of the conventional RC structure, the increasing of structural period is not related to the structure softening. Moreover, the isolated base structure is stiffer than the conventional RC building, which is proved later in this section by the comparison of other dynamic properties between the two models.

5.2 Lateral Roof Acceleration

The increase of the fundamental time period length of a building structure causes a reduction of the induced storey acceleration, in other words a reduction of the earthquake induced inertia forces of the building. Fig. 7 shows an acceleration comparison at the roof storey of the structure for the two models. The isolation system decreases the acceleration transmitted to the superstructure, so it produces a lower effective stiffness with higher damping. The maximum acceleration of the fixed base system is 8.29 m/s2, whereas the maximum acceleration of the isolated base system is 3.71 m/s2, comparatively less than the first one. Then, the acceleration reduction at the roof storey is 55.24%. As seen in Fig. 8, it has been observed that the storey acceleration was almost stable in case of the isolated base (since soil-superstructure movement is separated). Whereas, it increases with storey height in case of the fixed base model. This is normal since the conventional fixed base structure acts as a cantilever. It can be observed that the storey acceleration has been reduced almost in all storeys due to the use of LRB as isolators, except in the first one (Basement 3).

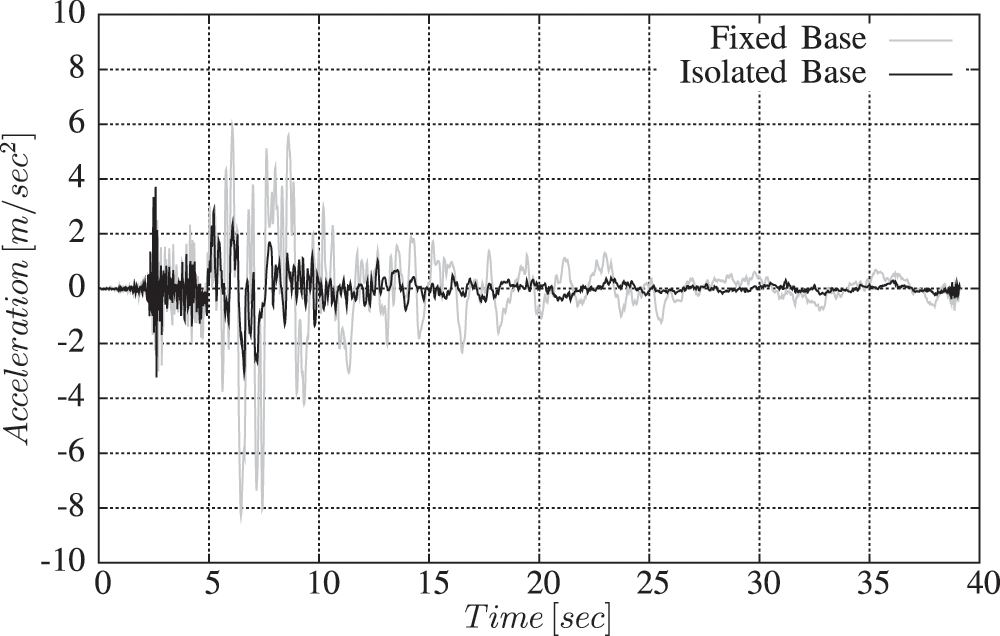
Figure 7: Joint acceleration at roof storey

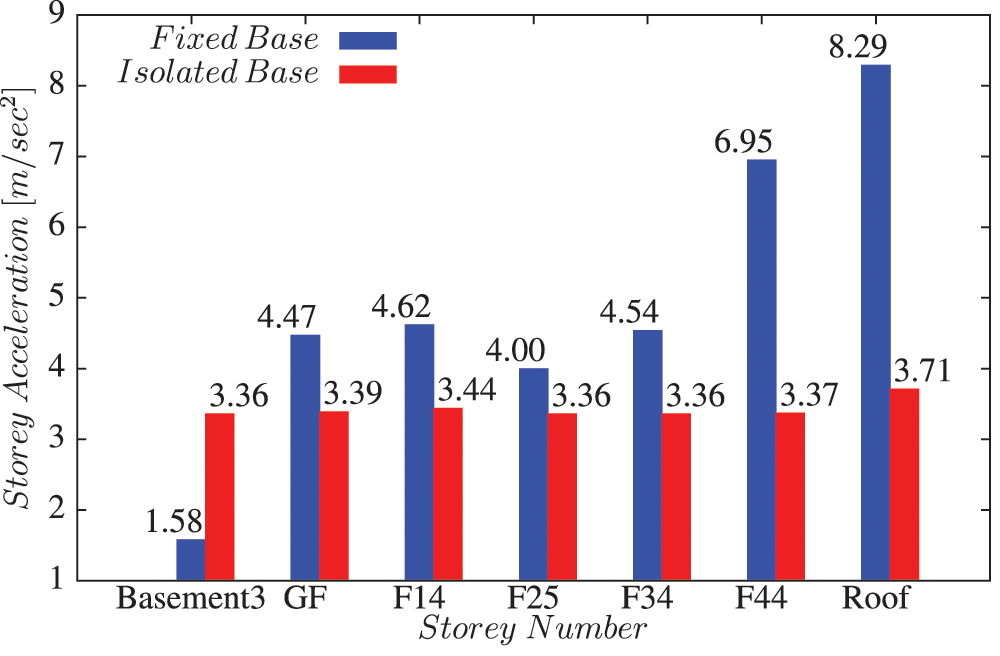
Figure 8: Storey acceleration vs. storey number

In other words, one of the main objectives of the seismic isolation system is to shift the fundamental frequency of a structure away from the dominant frequencies of an earthquake ground motion. Fig. 7 demonstrates that the acceleration was drastically reduced at roof storey when the rubber bearings were used. This acceleration reduction protects the non-structural components and reduces the damage inside the building. It seems to be lower than the reduction obtained in the case of low or medium rise building, which can reach 89% in the presence of rubber isolators at the bottom.

5.3 Lateral Roof Displacement

The displacements of the diaphragm centre of mass at each storey were reduced due to the use of the rubber bearings, which in turn reduced the impact of earthquakes on the structure. As seen in Fig. 9, the lateral displacement of the fixed base system is zero at the base and it increases with height since it has a cantilever behavior. Whereas, the lateral displacement of the isolated base has an important value at the base level, and it increases at a lower rate with height till a maximum at the roof level. The important difference between the displacements at the base level of the two models is related to the presence of an isolator system in the isolated base model [38]. At the highest storey levels the isolator system reduces the lateral displacement of the building. As seen in Fig. 10, the maximum value of joint displacement at the roof storey of the isolated building is 46.1 cm, which is less than the maximum allowable displacement Hbuilding/200 (16820 cm/200 = 84.1 cm) according to UBC-97. On the other hand, the maximum displacement value of 85.56 cm obtained for the fixed base building is more than the UBC maximum allowable displacement. This means that this building even with a high thickness of a shear wall system (1 m thickness) is not safe against an earthquake attack. However, the reduction in roof storey displacement is 46.11%. This gives evidence that the base isolation buildings are more flexible than fixed base buildings. The displacement reduction at roof storey joint is less than the reduction obtained in the case of low rise or medium rise buildings [39], and it remains lower than the maximum allowable displacement according to UBC-97 conditions. On the other hand, the maximum displacement at the base level in the lead rubber bearings is about 45 cm. It is lower than the minimum allowable displacement of the LRB types (76 cm for the first type, Tab. 2), therefore it will not undergo a fracture failure due to its horizontal displacement during the earthquake.

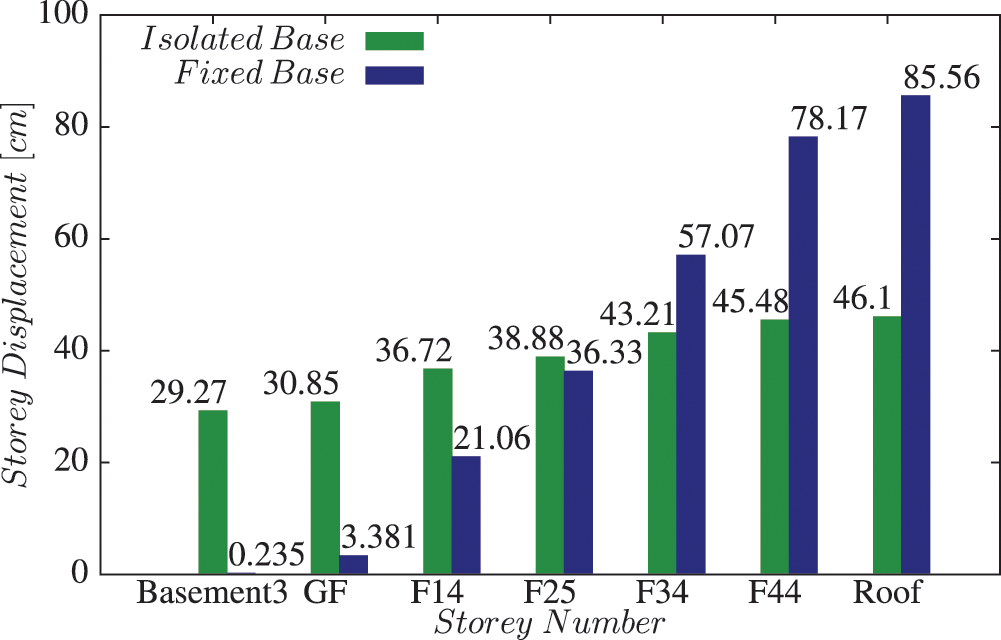
Figure 9: Storey displacement vs. Storey number

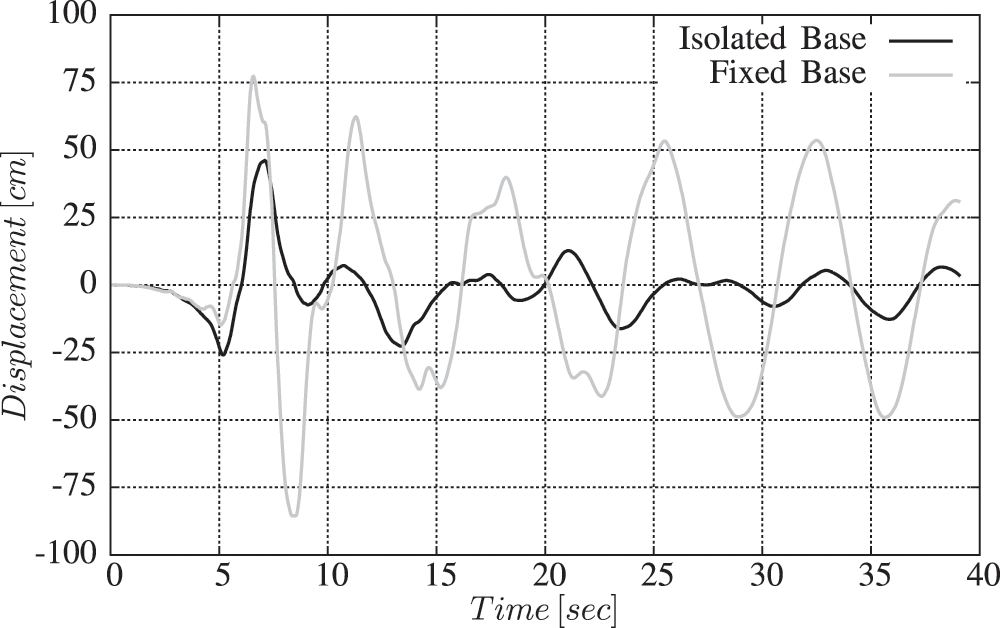
Figure 10: Joint displacement at the roof storey

5.4 Spectral Analysis

The spectral accelerations at roof storey for both models are shown in Fig. 11. The maximum values of spectral acceleration are: 24.39 m/s2 in case of the fixed base model and 1.68 m/s2 in case of the isolated base model. The value of spectral acceleration is greater in the fixed base model than in the isolated base model for the same building and seismic load case. It can be observed that the effect of high seismic excitations on low period values has been reduced due to the presence of the isolation system. On the other hand, the energy dissipation by the isolators and the forces developed within the isolators themselves are the two factors affecting the spectral displacement [40]. The time history of the spectral displacement at roof for the two models is shown in Fig. 12. The peak displacements of the roof are: 286.34 cm for the fixed base model and 44.11 cm for the second one. Therefore, the reduction in maximum spectral displacement is 84.6%. It can be noticed that the maximum spectral displacements for both models are obtained at the natural period of each one, whereas the lengthening of natural period for the isolated model decreases its excitations produced by the earthquake, so its maximum spectral displacement decreases.

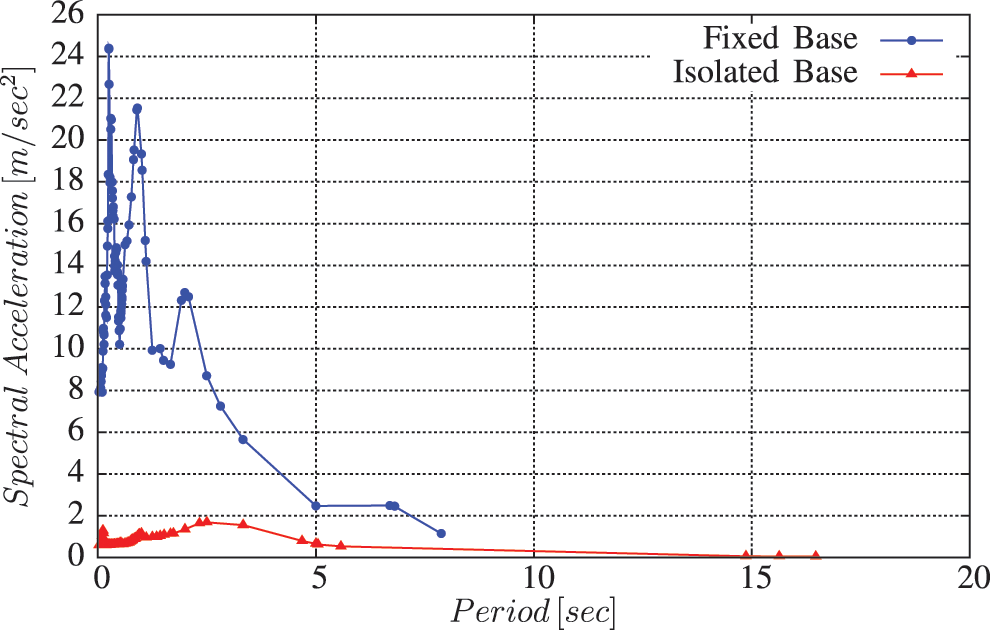
Figure 11: Spectral acceleration at the roof storey

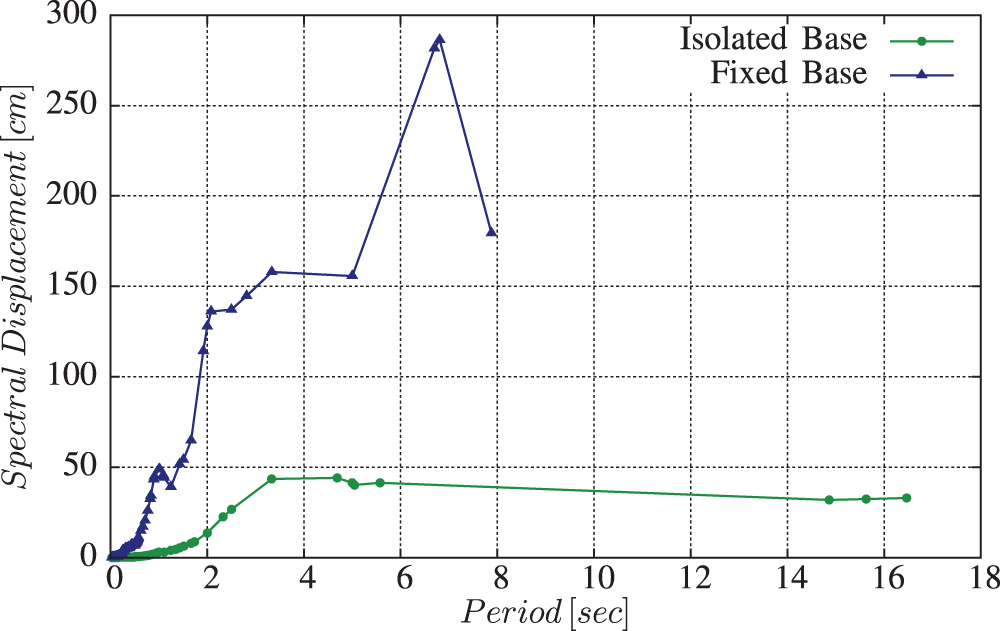
Figure 12: Spectral displacement at the roof storey

5.5 Base Shear Force

A The base shear force is also reduced due to the inducing of Rubber isolators during the vibration of an earthquake. Fig. 13 shows that the maximum value of base shear force of the isolated base structure is 1169 Ton, less than the maximum shear force value of 8368 Ton obtained from the fixed base structure. For the studied structure, the base shear has been reduced approximately by 86.03% due to the incorporation of the rubber isolators. The ratio of decreasing in base shear force of a high rise building is much greater than this ratio in low and medium rise building, when it is normally between 63% and 70% [41]. Therefore, this reduction in induced structural forces leads to minimizing the design of the structural components and then a notable reduction in the total weight of the structure, which reduces the construction costs. It also helps in reducing the repair costs after an earthquake.

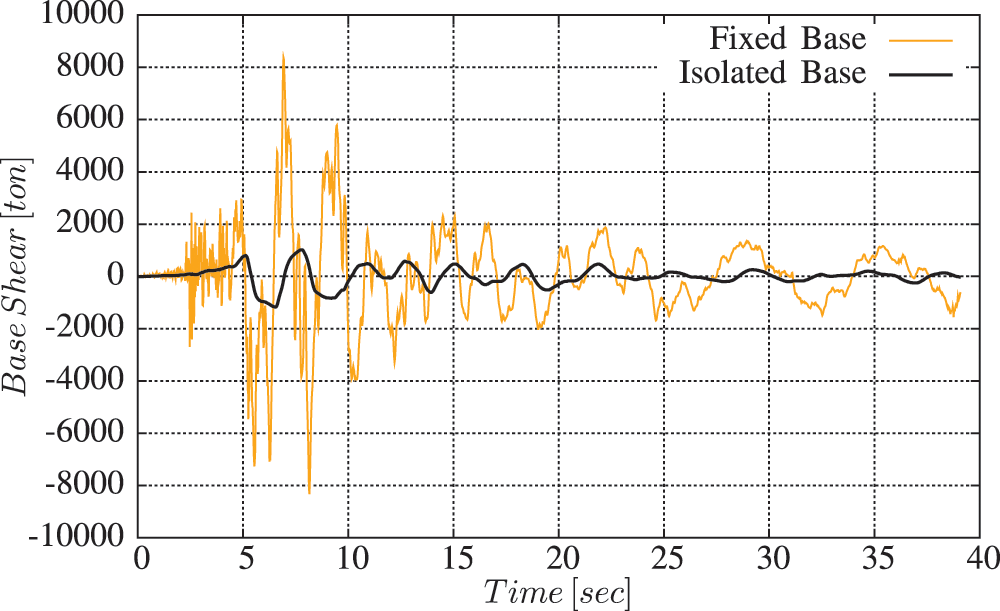
Figure 13: Base shear force at the bottom joint

5.6 Absolute Maximum Inter-Storey Drift

Figs. 14a and 14b show a comparison of inter-storey drift ratios for the two structural models in X and Y directions. It can be noticed that the storey drift ratio is higher at lower floors in case of isolator based model compared to the conventional model, then it has a constant value. This parameter proves the main objective of using the isolators at the ground level, by the separation between the ground movement and the superstructure movement. In the case of fixed base structure, the storey drift ratio starts at zero value at the ground level, then it increases with height in a non-linear manner. The mass irregularity can be observed clearly in these curves in the fixed base case, at floors F12, F25, and F32. The maximum inter-storey drift ratio for fixed base structure in X and Y directions is 0.01853, while the maximum drift evaluation according to UBC-97 is:

0.7×R×drift<0.02 (1)

The maximum drift evaluation in the fixed base case is 0.058 > 0.02. This means that this building is not safe in terms of drift damages during an earthquake. For the isolated model the maximum drift is 0.00317, that should be less than 0.02/R1 according to IBC isolated during time history analysis, Therefore, 0.00317 < 0.02/2 = 0.01. It is a safe design regarding the inter-storey drift ratio. The reduction in the maximum inter-storey drift ratio is 82.81% for isolated structural model compared with the fixed base structural model. This high reduction in the inter-storey drift ratio protects the structural and the non-structural elements during an earthquake.

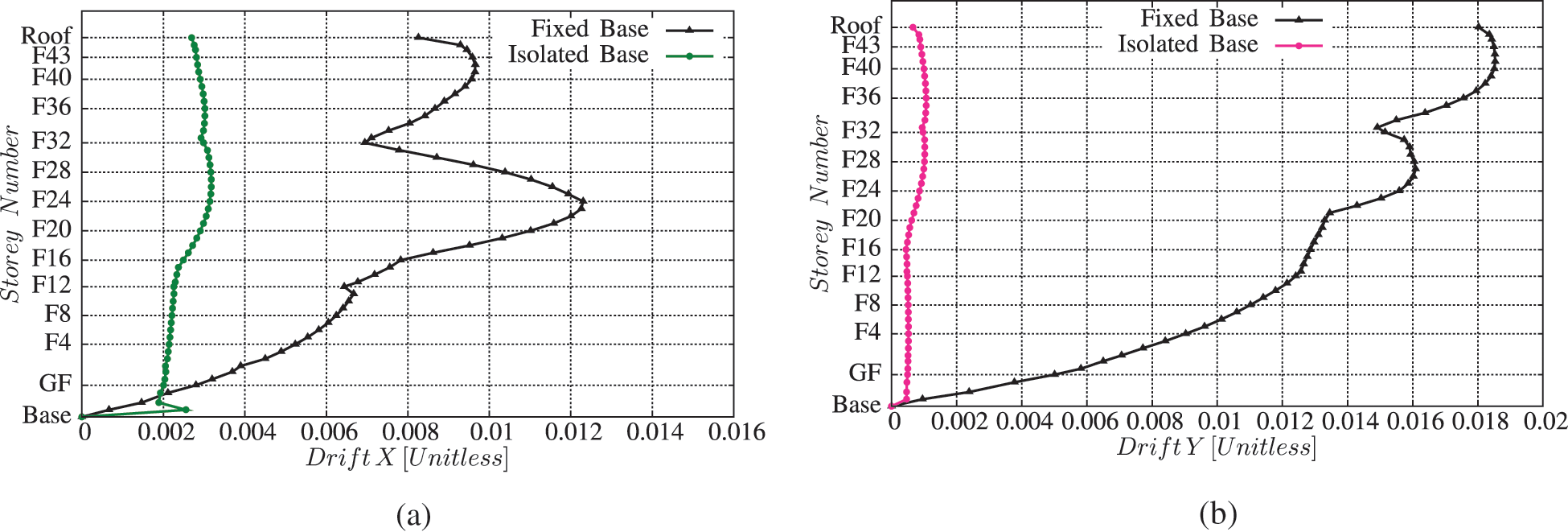
Figure 14: Maximum storey drifts vs. storey number (a) maximum storey drifts in X direction, (b) maximum storey drifts in Y direction

6  Conclusion and Discussions

In this study, a non-linear structural response analysis of high rise building in an active seismic region was performed by the incorporation of the innovative LRB isolators. The seismic analysis compared two structural models of the same high rise building. After providing LRB isolator system, the fundamental period of the isolated structure is increased by approximately 3 times compared with the fundamental period of the fixed base structure. We can also conclude by the comparison of the two models that:

•   The reduction in the energy dissipation, i.e., acceleration, at the roof storey is 55.24%.

•   There is increase in the storey acceleration at the first floor.

•   The lateral roof storey displacement is reduced by 46.11%, which gives evidences of the flexibility induced in the building.

•   The seismic excitations represented by the spectral acceleration history at roof level disappear in case of the isolated base model.

•   The spectral displacement at roof level decreases 84.6% with the use of the isolation system.

•   The base shear force is reduced from 8368 Ton in the fixed base, to 1169 Ton in the isolated base structure.

•   There is a decrease in the inter-storey drift ratio.

•   The lead rubber bearing can be used as an isolator system for high-rise buildings with efficient results.

Under seismic loading the response performance of a conventional fixed base structure is greatly improved by the incorporation of the LRB isolation system. The efficiency of this system depends on the characteristics of the seismic earthquake, its designed properties, and on the structural criteria. Therefore, it is important to perform a detailed analysis to make an efficient design of the rubber bearings according to the vibration data. The main goal of this isolation system is the gained flexibility in the structure and the reduced damages in the vibration movements of the structure. This study also proved also the feasibility of this system in high rise buildings. It should be mentioned that in this study, only one earthquake record has been used to find the optimum seismic response of the building. However, more generalized solutions can be achieved using additional records.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Whittaker, A. S., Bertero, V. V., Thompson, C. L., Alonso, L. J. (1991). Seismic testing of steel plate energy dissipation devices. Earthquake Spectra, 7(4), 563–604. DOI 10.1193/1.1585644. [Google Scholar] [CrossRef]

 2.  Pall, A. S., Marsh, C. (1982). Response of friction damped braced frames. Journal of the Structural Division, 108(6), 1313–1323. [Google Scholar]

 3.  Shen, K. L., Soong, T. T., Chang, K. C., Lai, M. L. (1995). Seismic behaviour of reinforced concrete frame with added viscoelastic dampers. Engineering Structures, 17(5), 372–380. DOI 10.1016/0141-0296(95)00020-8. [Google Scholar] [CrossRef]

 4.  Villaverde, R. (1994). Seismic control of structures with resonant appendages. Proceedings 9th World Conference of Structural Control. Los Angeles, CA, USA. [Google Scholar]

 5.  Win, N., Htun, Z. (2017). Comparative study on performance assessment of steel structure with lead rubber bearing system (Myanmar rubber) and fixed base. International Journal of Research in Chemical, Metallurgical and Civil Engineering, 4(1), 2349–1450. DOI 10.15242/IJRCMCE.AE1216304. [Google Scholar] [CrossRef]

 6.  Taywade, P. W. (2015). Sustainability of structure using base isolation techniques for seismic protection. International Journal Innovation Research in Science, Engineering and Technology, 4(3), 1215–1228. [Google Scholar]

 7.  Su, L., Ahmadi, G., Tadjbakhsh, G. (1991). Performance of sliding resilient-friction base-isolation system. Journal of Structural Engineering, 117, 1–165. DOI 10.1061/(ASCE)0733-9445(1991)117:. [Google Scholar] [CrossRef]

 8.  Shenton, H. W., Lin, A. N. (1993). Relative performance of fixed base and base isolated concrete frames. Journal of Structural Engineering, 119(10), 2952–2968. DOI 10.1061/(ASCE)0733-9445(1993)119:. [Google Scholar] [CrossRef]

 9.  Ismail, M., Rodellar, J., Ikhouane, F. (2010). An innovative isolation device for aseismic design. Engineering Structures, 32(4), 1168–1183. DOI 10.1016/j.engstruct.2009.12.043. [Google Scholar] [CrossRef]

10. Micheli, I., Cardini, S., Colaiuda, A., Turroni, P. (2004). Investigation upon the dynamic structural response of a nuclear plant on aseismic isolating devices. Nuclear Engineering and Design, 228(1), 319–343. DOI 10.1016/j.nucengdes.2003.06.028. [Google Scholar] [CrossRef]

11. Scawthorn, C., Chen, W. F. (2002). Earthquake engineering handbook. USA: CRC Press. [Google Scholar]

12. Liu, J., Zhang, L., Zhang, H., Liu, T. (2019). Seismic vulnerability analysis of single-story reinforced concrete industrial buildings with seismic fortification. Structural Durability & Health Monitoring, 13(2), 123–142. DOI 10.32604/sdhm.2019.04486. [Google Scholar] [CrossRef]

13. Zhou, J., Sun, C., Dai, X., Chen, G. (2019). Seismic reliability assessment of inelastic SDOF systems subjected to near-fault ground motions considering pulse occurrence. Structural Durability & Health Monitoring, 13(4), 361–378. DOI 10.32604/sdhm.2019.05171. [Google Scholar] [CrossRef]

14. Su, L., Ahmadi, G., Tadjbakhsh, I. G. (1989). A comparative study of performances of various base isolation systems, part I: Shear beam structures. Earthquake Engineering & Structural Dynamics, 18(1), 11–32. DOI 10.1002/eqe.4290180104. [Google Scholar] [CrossRef]

15. Robinson, W., Tucker, A. (1977). A lead-rubber shear damper. Bulletin of the New Zealand National Society For Earthquake Engineering, 10(3), 93–101. [Google Scholar]

16. Robinson, W. (1982). Lead-rubber hysteretic bearings suitable for protecting structures during earthquakes. Earthquake Engineering & Structural Dynamics, 10(4), 593–604. DOI 10.1002/eqe.4290100408. [Google Scholar] [CrossRef]

17. Reys, M. E. (1993). An introduction to seismic isolation by R.I. Skinner, W.H. Robinson and G.H. McVerry. Strain, 29(3), 99–100. DOI 10.1111/j.1475-1305.1993.tb00842.x. [Google Scholar] [CrossRef]

18. Warn, G. P., Ryan, K. L. (2012). A review of seismic isolation for buildings: Historical development and research needs. Buildings, 2(3), 300–325. DOI 10.3390/buildings2030300. [Google Scholar] [CrossRef]

19. Providakis, C. P. (2008). Effect of LRB isolators and supplemental viscous dampers on seismic isolated buildings under near-fault excitations. Engineering Structures, 30(5), 1187–1198. DOI 10.1016/j.engstruct.2007.07.020. [Google Scholar] [CrossRef]

20. Providakis, C. P. (2009). Effect of supplemental damping on LRB and FPS seismic isolators under near-fault ground motions. Soil Dynamics and Earthquake Engineering, 29(1), 80–90. DOI 10.1016/j.soildyn.2008.01.012. [Google Scholar] [CrossRef]

21. Seo, J., Hu, J. W. (2016). Seismic response and performance evaluation of self-centering LRB isolators installed on the CBF building under NF ground motions. Sustainability, 8, 109. DOI 10.3390/su8020109. [Google Scholar] [CrossRef]

22. Naimul Haque, M., Zisan, M., Bhuiyan, A. (2013). Seismic response analysis of base isolated building: Effect of lead rubber bearing characteristics. Malaysian Journal of Civil Engineering, 25, 154–167. [Google Scholar]

23. Santhosh, H. P. (2013). Seismic analysis of low to medium rise building for base isolation. International Journal of Research in Engineering and Technology, 2, 1–5. DOI 10.15623/ijret.2013.0213001. [Google Scholar] [CrossRef]

24. Shirule, P. A., Jagtap, L. P., Sonawane, K. R., Patil, T. D., Jadwanir, N. et al. (2012). Time history analysis of base isolated multi-storyed building. International Journal of Earth Sciences and Engineering, 5, 809–816. [Google Scholar]

25. Dynamic Isolation System (2019). http://www.dis-inc.com/index.html. [Google Scholar]

26. Furukawa, T., Ito, M., Izawa, K., Noori, M. N. (2019). System identification of base-isolated building using seismic response data. Journal of Engineering Mechanics, 131(3), 268–275. DOI 10.1061/(ASCE)0733-9399(2005)131. [Google Scholar] [CrossRef]

27. Naeim, F., James, S. E., Kelly, M. (1999). Design of seismic isolated structures: From theory to practice. New York: John Wiley. [Google Scholar]

28. Uniform Building Code (1997). International Conference of Building Officials, UK. [Google Scholar]

29. Lindeburg, M., McMullin, K. (2014). Seismic design of building structures. 11th ed. Professional Publications, Inc., USA. [Google Scholar]

30. ACI Committee 318. Building code requirements for structural concrete: (ACI 318-95); and commentary (ACI 318R-95) (1995). Farmington Hills, MI: American Concrete Institute. [Google Scholar]

31. Porcella, R., Matthiesen, R., Maley, R. (1982). Strong-motion data recorded in the United States. The Imperial Valley, California, Earthquake of October 15, 1979. U.S. Geology Survey, 1254, 289–318. [Google Scholar]

32. Trifunac, M. D., Lee, V. W. (1978). Uniformly processed strong earthquake ground accelerations in the Western United States of America for the period from 1933 to 1971: Corrected acceleration, velocity and displacement curves. Los Angeles, CA. [Google Scholar]

33. Chopra, A. K. (1995). Dynamics of structures: Theory and applications to earthquake engineering. Englewood Cliffs, NJ: Prentice-Hall. [Google Scholar]

34. Malhotra, P. K. (1999). Response of buildings to near-field pulse-like ground motions. Earthquake Engineering & Structural Dynamics, 28, 1309–1326. [Google Scholar]

35. Council, I. C. (2000). International building code. Falls Church, VA: International Code Council. [Google Scholar]

36. Chun, Y. S., Hur, M. W. (2015). Effects of isolation period difference and beam-column stiffness ratio on the dynamic response of reinforced concrete buildings. International Journal of Concrete Structures and Materials, 9(4), 439–451. DOI 10.1007/s40069-015-0120-9. [Google Scholar] [CrossRef]

37. Cancellara, D., de Angelis, F., Pasquino, M. (2013). A novel seismic base isolation system consisting of a lead rubber bearing in series with a friction slider. Part II: Application to a multi-storey RC building and comparison with traditional systems. Advances in civil engineering II, vol. 256, pp. 2174–2184. Trans Tech Publications, Ltd. [Google Scholar]

38. Xu, C., Chase, J. G., Rodgers, G. W. (2014). Physical parameter identification of nonlinear base-isolated buildings using seismic response data. Computers and Structures, 145, 47–57. [Google Scholar]

39. Tafheem, Z., Arafat, T., Chowdhury, A., Iqbal, A. (2017). Effect of base isolator on the structural response of reinforced concrete multistoried building under seismic loads. Journal of Civil Engineering, Science and Technology, 8, 49–56. DOI 10.33736/jcest.378.2017. [Google Scholar] [CrossRef]

40. Pietra, D., Pampanin, S., Mayes, R., Wetzel, N., Feng, D. (2015). Design of base-isolated buildings: An overview of international codes. Bulletin of the New Zealand Society for Earthquake Engineering, 48, 118–135. DOI 10.5459/bnzsee.48.2.118-135. [Google Scholar] [CrossRef]

41. Chandak, N. (2013). Effect of base isolation on the response of reinforced concrete building. Journal of Civil Engineering Research, Scientific and Academic Publishing, 3, 135–142. DOI 10.5923/j.jce.20130304.02. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.