Structural Durability & Health Monitoring

DOI: 10.32604/sdhm.2022.020418

ARTICLE

The Coupled Effect of Temperature Changes and Damage Depth on Natural Frequencies in Beam-Like Structures

Tareq Al-hababi1,2, Nizar Faisal Alkayem1,3, Li Cui4, Shixiang Zhang5, Cong Liu6 and Maosen Cao1,2,*

1Anhui Provincial International Joint Research Center of Data Diagnosis and Smart Maintenance on Bridge Structures, Chuzhou University, Chuzhou, 239000, China
2Department of Engineering Mechanics, Hohai University, Nanjing, 210098, China
3College of Civil and Transportation Engineering, Hohai University Nanjing, 210098, China
4College of Civil and Architecture Engineering, Chuzhou University, Chuzhou, 239000, China
5China Design Group Co., Ltd., Nanjing, 210014, China
6Jiangsu Zhongqiao Technology Research Co., Ltd., Nantong, 226000, China
*Corresponding Author: Maosen Cao. Email: cmszhy@hhu.edu.cn
Received: 22 November 2021; Accepted: 28 December 2021

1  Introduction

In recent years, a large number of useful approaches have been employed for damage detection and localization. These approaches rely on measuring changes in structures’ dynamic properties before and after damage occurs, such as natural frequencies and mode shapes. An inclusive survey of vibration-based SHM and damage detection methods for various mechanical and civil engineering structures has been conducted in [1]. The methods employed to detect structural damage through natural frequencies and damping change were reviewed in [2,3]. Methods concerning structural health monitoring of composite materials were discussed in [4]. Various methods of extracting temperature effects from modal parameters have been shown in the literatures [5–7].

Through the literature review, it has been found that there are mainly three types of studies about damage detection: analytical, numerical, and experimental studies [8–12]. The previous research of damage detection focused on aluminum alloys, steel alloys, conventional composites, functionally graded materials [13], and concrete structures.

Real civil constructions are susceptible to changing environmental and operational conditions like temperature. These topics have always been under investigation and continuous development of structural health monitoring in light of environmental changes and have become a popular research subject in the scope of civil engineering [14,15]. Wang et al. [16] examined the influences of ambient temperature changes on reinforced concrete (RC) slabs’ modal properties. The results demonstrated that the effect of temperature changes led to a significant change in natural frequencies compared to damping and mode shapes. Xia et al. [17] introduced a literature survey and a case study of temperature variation effect on vibration characteristics. In their conclusion, the effect of temperature increase on structural frequencies is more apparent than that on the mode shapes. The changes in structural frequencies are produced due to the variation in the modulus of materials under varying temperatures. Through an optimization problem, Ashwear et al. [18] studied the influence of changes in environmental temperatures on a cable-strut structure’s dynamic properties. They found that the first natural frequencies are less susceptible to temperature variations. Kita et al. [19] examined the impact of temperature changes on a historical building’s static and dynamic responses in Italy. The findings confirmed that an increase in temperature causes a clear and sometimes nonlinear decrease in natural frequencies. Also, the decrease in temperature below 0°C led to an increase in natural frequencies. Liu et al. [20] analyzed the effects of temperature differences on modal frequencies of an RC slab and beam. Ralbovsky et al. [21] measured the effect of temperature loads on the structural responses as damage indicators of two bridges.

Many mechanical engineering structures operate under different thermal conditions, such as spacecraft, engines, turbines, etc. The change of these conditions leads to changes in the material properties and the stress state, and thus, this will affect the static and dynamic performance during operation. Towards safety and productivity, in order to keep the machines in a healthy state, the effect of such parameters, especially temperature, must be recognized and taken into account. Several studies have examined the effect of temperature changes on the natural frequencies of structures in this regard. Karsh et al. [22] studied the effect of temperature changes on the first three natural frequencies of a functionally graded materials plate. Using the finite element method, Esfarjani et al. [23] studied the simultaneous effect of temperature changes and multiple damages on natural frequencies of an aluminum alloy beam. Sha et al. [24] examined the influence of temperature differences on natural frequencies of beam structures without and with damping. They found that the natural frequencies and damping ratios decreased linearly with increasing temperature. Qian et al. [25] numerically and experimentally studied the effect of thermal loading on dynamic and acoustic responses of a clamped aluminum plate. Dan et al. [26] considered the effect of temperature on guided wave propagation and frequencies drift of an aluminum alloy plate. Gupta et al. [27] examined the effect of the thermal gradient (an exponential temperature distribution) on the first three modes of natural frequencies of a rectangular plate. Talebian et al. [28] investigated the effects of temperatures on an electrostatically actuated microplate’s mechanical behavior. The findings show that the first natural frequency of the microplate greatly depends on the state of the design requirements. This indicates that the positive changes in temperature reduce the first natural frequency and vice versa. Ding et al. [29] numerically and experimentally studied a damage identification of a steel plate and beam under temperature variations effects. Also, they show the relationship between temperature change and Young’s modulus of the material properties, which led to a change in modal properties. Oh et al. [30] analyzed the effect of temperature variations on the turbine blades under thermal loading conditions. The results show that the increase in blade surface temperatures causes a decrease in the first natural frequency and an increase in blade length due to the thermal expansion. Abdus et al. [31] numerically and experimentally investigated the influence of pre-load and temperature changes on the natural frequencies of bolted joints. The results indicate that the temperature rise reduces the overall stiffness and thus decreases the natural frequencies. Talai et al. [32] investigated the effect of frictional temperature evolution on the natural frequencies of steel cantilever beam-like structures. Wang et al. [33] studied the effects of temperature elevation on the mechanical attributes of high-strength alloy steels. The results show that the steel stiffness and strength degrade with an increase in temperature, and the speed of degradation depends on the chemical composition of the steel alloys. Quan et al. [34] numerically investigated the effect of thermal loads (under a steady-state temperature) on the natural frequency of a steel alloy spur gear. The results show that the main cause of the shift in natural frequencies is thermal stress due to temperature changes. Recently, Gillich et al. [35] proposed mathematical expressions in order to study the effect of temperature variations on the natural frequencies of healthy and damaged beams. They performed experimental and numerical investigations on beams exposed to an axial force due to temperature variations. All these investigations show that changes in natural frequencies can be utilized as indicators for damage detection.

Beams are one of the most commonly used structural elements that can be seen in civil and mechanical engineering constructions. In most damage detection techniques, modal parameters are assessed considering constant environmental conditions. In real cases, many structures are susceptible to varying operational and environmental conditions that must be considered, like temperature variations leading to early state damage. Otherwise, incorrect data is obtained, and vibration-based damage estimation becomes inaccurate.

Beams fixed at one end and free on another are among the most used beams because the end support is not restricted and free to shift and is less affected by axial loads due to the thermal expansion caused by the increase in temperature. In practice, therefore, beams fixed at one end are typically used. In contrast, beams fixed at both ends are influenced mainly by temperature variations due to the generated axial loads resulting from thermal expansion. So, this kind of beam is usually avoided in practice [35]. More research is needed to understand the relationship between temperature effect and damage depth on natural frequencies in beam-like structures. The present investigations deal with two types of boundary conditions, cantilever beam and cantilever, simply supported beam.

In this paper, intensive numerical simulations are made to investigate the coupled effect of temperature changes and damage depth on the natural frequencies for intact and damaged steel beams. The main contribution of this paper is the use of the 3D representation of the relationship between the effect of temperature and damage depth on natural frequencies making it easy for modes to be compared and selected for accurate detection of damage. First, the effect of temperature on the natural frequency of intact beams is performed. Second, besides the effect of temperature, transverse damages with different depths are studied. Then, the findings are compared with similar research areas by introducing two examples from the literature. The validation results confirm that the present work using ANSYS is in good agreement with those from the literature.

The paper is structured as follows. Starting from the equation of motion of the free vibration given by the Euler-Bernoulli beam theory, Section 2 formulates the concept of the natural frequencies of a uniform beam and the influence of temperature on the mechanical properties of structural materials. Section 3 displays the numerical simulation and modeling of beam-like structures. Section 4 shows the numerical results of the different studied cases using ANSYS software. Section 5 introduces two examples from literature in order to validate the present work. In Section 6, the discussions. Finally, in Section 7, the paper was concluded.

2  Fundamentals

This section provides an overview of the basics of vibrations in beams and the effect of temperature on the mechanical properties of structural materials.

2.1 Vibration of Beams

Consider a uniform beam shown in Fig. 1, the equation of motion of the free vibration is introduced by the well-known Euler-Bernoulli beam theory (thin beam theory) [36] as follows:

EIρA∂4v∂x4+∂2v∂t2=0 (1)

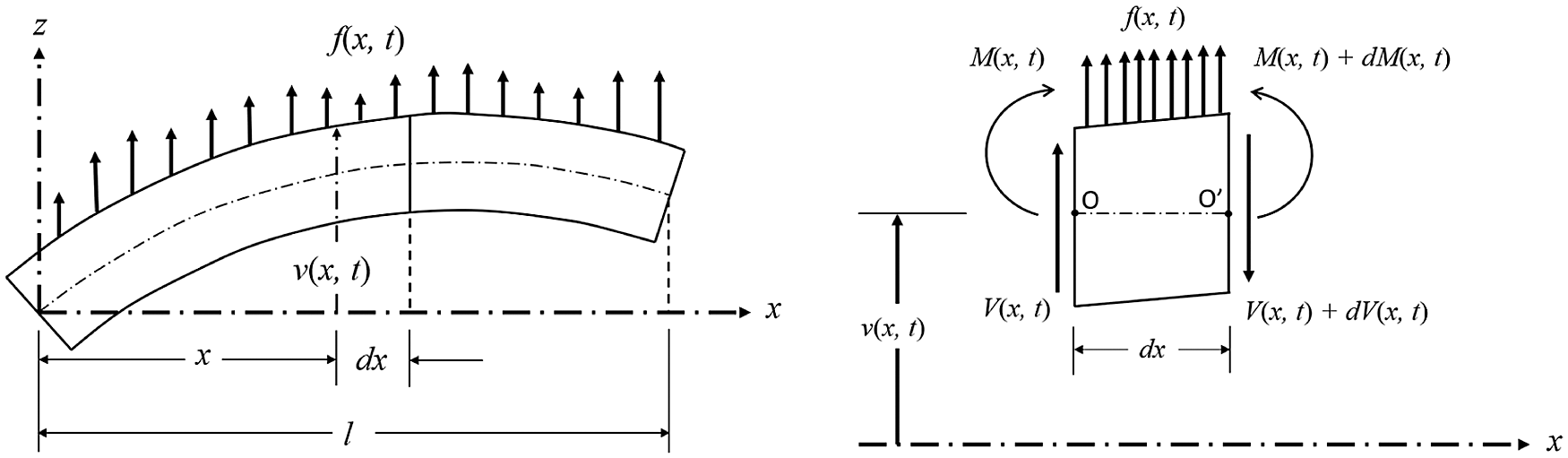
Figure 1: A beam in bending [37]

where E is Young’s modulus, ρ is mass density, and I is the moment of inertia of the cross-sectional area. And v is the displacement in the vertical direction at a distance x calculated from the fixed end. Recognizing that v is dependent on time t and distance x , and the evolution in time is harmonic, the displacement expression becomes:

(x,t)=ϕ(x)⋅y(t)=ϕ(x)⋅sin⁡(ωt+), (2)

By deriving Eq. (2) and substituting in Eq. (1), we get:

ϕiv(x)sin⁡(ωt+)−ρAω2EIϕ(x)sin⁡(ωt+)=0, (3)

and, after simplification by sin⁡(ωt+) :

ϕiv(x)−ρAω2EIϕ(x)=0, (4)

The solution of Eq. (4) can be expressed as:

ϕ(x)=A∗sin⁡αx+B∗cos⁡αx+C∗sinh⁡αx+D∗cosh⁡αx, (5)

where A∗,B∗,C∗ and D∗ are different unknown constants that can be determined from the initial conditions.

ρAω2EI=α4, (6)

By deriving the Eq. (5) three times, one obtains:

{ϕ(x)=A∗sin⁡αx+B∗cos⁡αx+C∗sinh⁡αx+D∗cosh⁡αxϕi(x)=α(A∗cos⁡αx−B∗sin⁡αx+C∗cosh⁡αx+D∗sinh⁡αx)ϕii(x)=α2(−A∗sin⁡αx−B∗cos⁡αx+C∗sinh⁡αx+D∗cosh⁡αx)ϕiii(x)=α3(−A∗cos⁡αx+B∗sin⁡αx+C∗cosh⁡αx+D∗sinh⁡αx) (7)

The above expressions are proportional to the vertical displacement v(x) , shear force T(x) , deflection θ(x) , and bending moment M(x) . For a clamped cantilever beam, the boundary conditions are:

ϕ(0)=ϕi(0)=ϕii(L)=ϕiii(L)=0, (8)

The transcendental equation in order to obtain the previous constants is:

1+cos⁡λ⋅cosh⁡λ=0, (9)

with λ=α⋅L , Eq. (8) allows determining λi values for any i vibrations mode. The mathematical relationship representing the natural frequencies is then can be obtained from Eq. (6) as:

fi=λi22πEIρAL4, (10)

The following function gives the mode shapes for the cantilever beam:

ϕi(x)=(cosh⁡αix−cos⁡αix)−(cos⁡αiL+cosh⁡αiL)(sin⁡αiL+sinh⁡αiL)(sinh⁡αix−sin⁡αix). (11)

2.2 The Influence of Temperature on the Mechanical Properties of Structural Materials

Consider an exponential temperature distribution in a longitudinal plate that is, in the x-direction [27]:

T=T0e−exe−1, (12)

where T is the excessed temperature over the reference temperature TRef. at any point, at a distance, X=x/a and T0 is the excessed temperature over the reference temperature at the end, i.e., x=a . The dependence relationship of the modulus of elasticity on temperature for a wide range of engineering materials was introduced by Nowacki [38]:

E(T)=E0(1−γT), (13)

where E0 is Young’s modulus at the TRef.=0 , and γ is the slope of variation of E with T . Considering the reference temperature and temperature at x=a , the modulus of elasticity according to Eqs. (12) and (13) is given as:

E(x)=E0(1−αe−exe−1), (14)

and

α=γT0(0−α<1). (15)

where α is known as the constant of the temperature.

Most previous studies show that an increase in temperature leads to decreased natural frequencies and vice versa. Also, it was found that these changes rely on temperature range and the properties of the materials, especially the modulus of elasticity.

The section presented some basics of vibrations in beam-like structures considering the effect of temperature changes on mechanical properties. Numerical investigations and validation results pertaining to a cantilever beam and a cantilever simply supported beam under temperature and damage depths changes are reported in the following sections.

3  Numerical Simulations

This section investigates the coupled effect of temperature variations and damage depth on natural frequencies of the carbon steel (ASTM A36) beam. A 3-D FE model has been created using ANSYS, shown in Fig. 2. The specimen used in the numerical simulation has the following geometrical characteristics: length (L), width (B), and height (H). The material properties of the carbon steel (ASTM A36) beam are listed in Table 1. The damage is located at xc=0.249m from the fixed end.

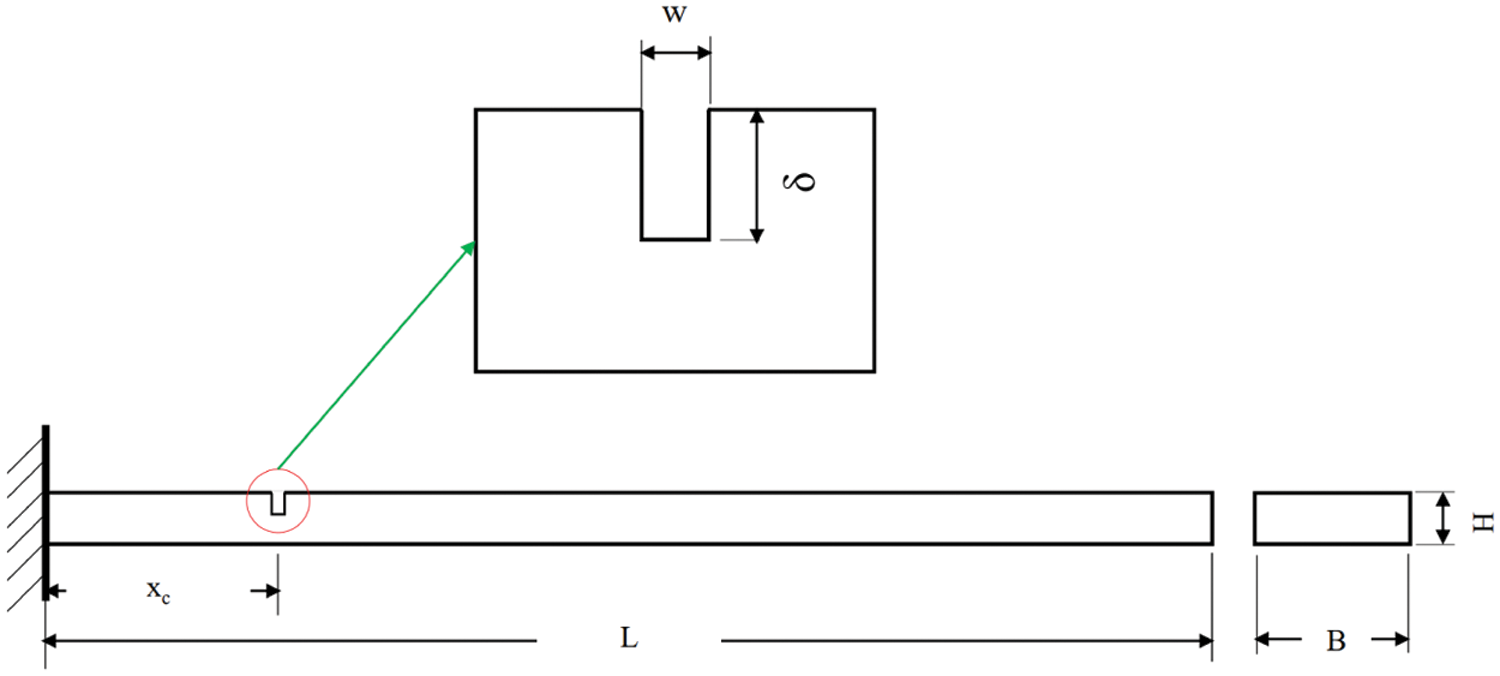
Figure 2: Geometry of the cantilever beam and damage location

Two cases are investigated here, intact beams and damaged beams. Two types of beams are studied, a cantilever and cantilever, simply supported beams. All numerical investigations are conducted using ANSYS. The first investigation was conducted under the influence of temperature changes on two intact beams; a cantilever beam and a cantilever simply supported beam. Secondly, damage depth has been introduced in ten levels in addition to the effects of temperature.

3.1 Healthy Beam

This subsection studies the effect of temperature variations on natural frequencies. Both intact beams, cantilever and cantilever simply supported beams, are investigated. Moreover, in order to study the effect of the support type, two kinds of supports are simulated to detect the effect of temperature on the natural frequencies. The first attempt is made to investigate the effect of temperature on both types of intact beams. Modal analysis for beams at temperatures between 0°C and 50°C with a step of 5°C is carried out. The simulation findings are exploited for the frequency analysis made for all studied temperature cases.

3.2 Damaged Beam

As mentioned before, the second attempt is performed to examine the coupled effect of temperature and damage depth on natural frequencies of damaged beams for each temperature in the range between 0°C and 50°C with a step of 5°C. For analyzing the impact of the damage depth, ten depth levels are simulated separately, where the damage is located at a distance x=0.249m from the fixed left end. All damage scenarios have the same width w=2mm and a depth ranging from δ=0.35mm to 3.5mm , which means a small loss of masses.

4  Numerical Results

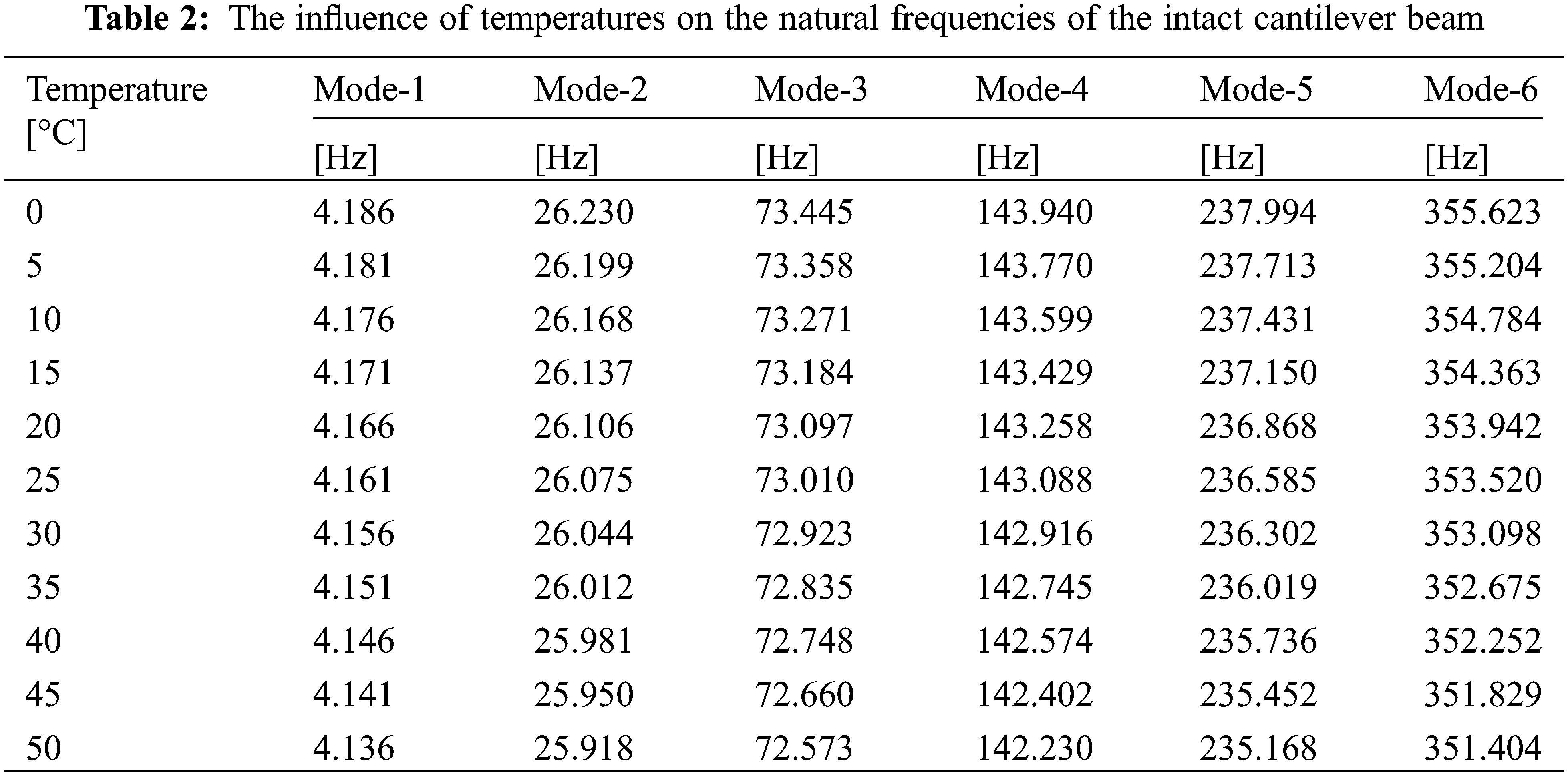
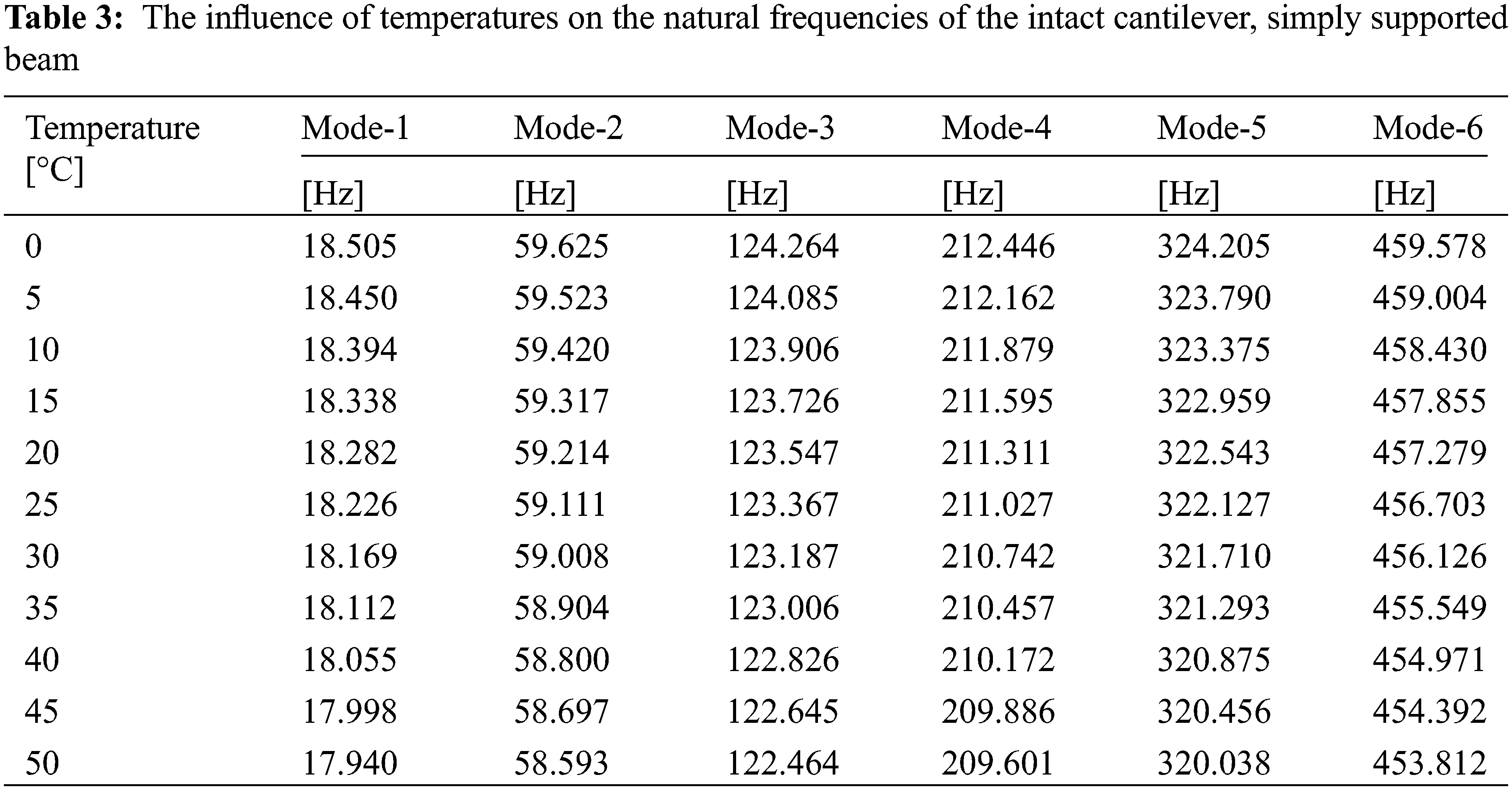
This section summarizes and discusses the important findings of the present work. The first six mode shapes of vibration of the intact cantilever and a cantilever, simply supported beams, are displayed in Fig. 3. The natural frequencies under the effect of temperature for an intact cantilever beam and cantilever simply supported beam are presented in Tables 2 and 3, respectively. The first six natural frequencies of the steel beams are illustrated as a function of temperature in Fig. 4, and it can be found that temperature is an important factor affecting the natural frequencies. The results prove that there is a significant linear negative relationship between temperature changes and natural frequencies.

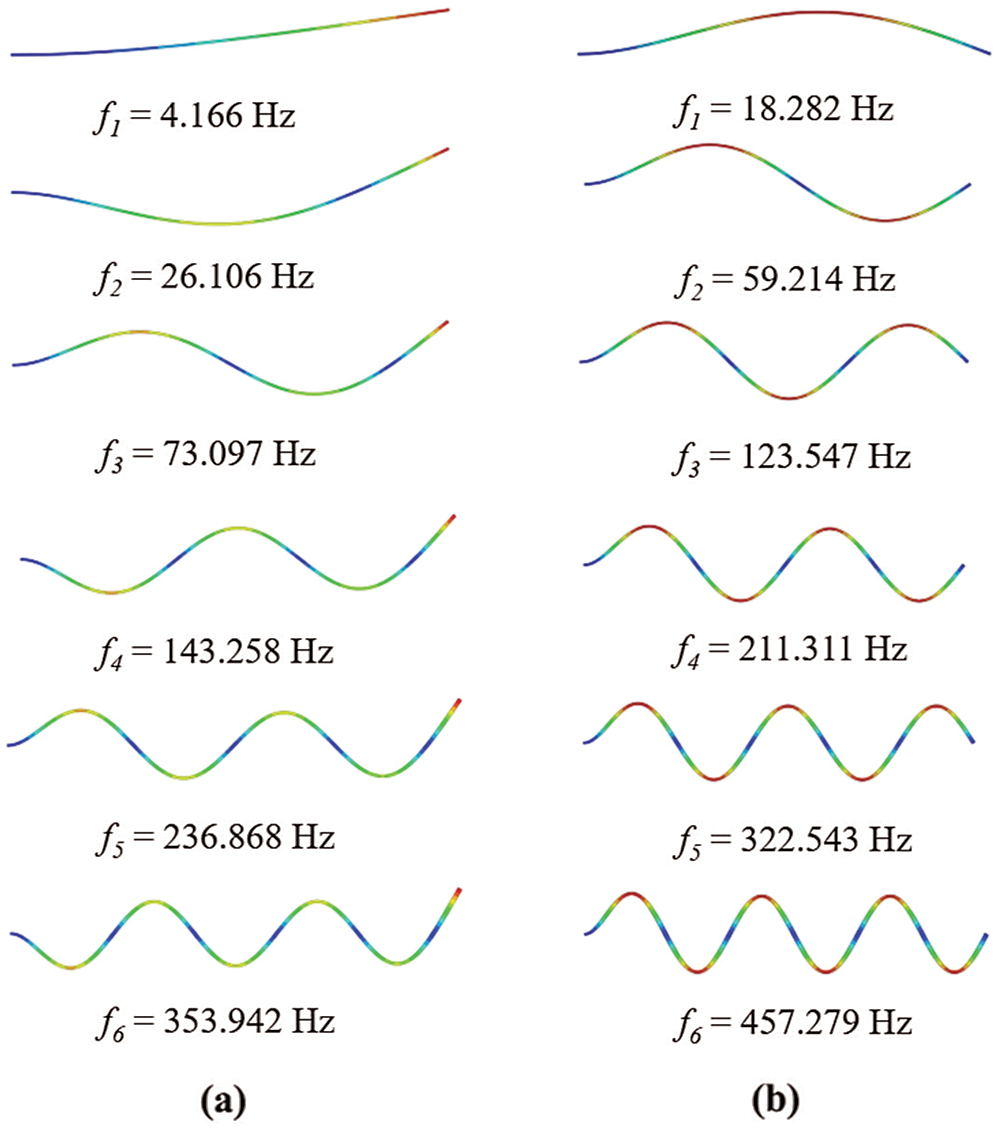
Figure 3: The first six mode shapes of vibration of the undamaged steel beams, (a) a cantilever beam, (b) a cantilever, simply supported beam (at 20oC)

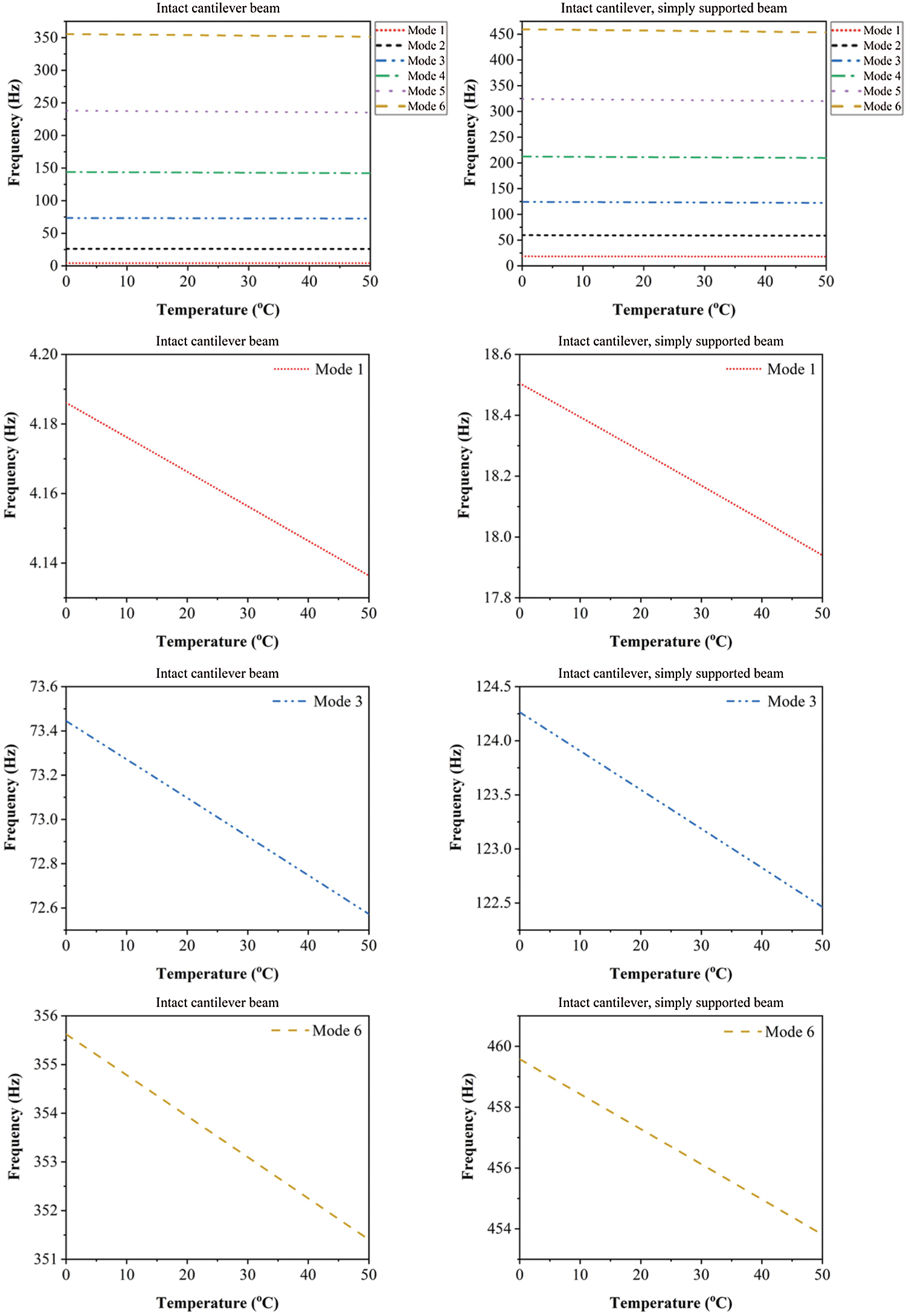
Figure 4: Frequency shifts of the first six bending modes of vibration of the intact cantilever beam (Left side) and the cantilever, simply supported beam (Right side)

Frequency changes as a function of temperature and damage depth of the first six bending modes for the damaged cantilever and cantilever simply supported beams are presented in Figs. 5 and 6, respectively. The three-dimensional illustrations of natural frequency curves charted for the cantilever beam and cantilever simply supported beam for damage depth between 0.35 mm and 3.5 mm are shown in Figs. 7 and 8, respectively.

Fig. 7 shows that Mode-2 is more susceptible to temperature changes than Modes-5 and 6, where the influence of temperature changes is more significant than the influence of damage depth on the natural frequencies of a cantilever beam. Mode-1 is less affected by temperature changes. Also, Modes-3 and 4 are moderately affected by temperature and damage depth changes. Therefore, Modes-1, 3, and 4 can be selected for damage evaluation. Fig. 8 shows that Modes-1 and 5 are the most affected by temperature changes. Modes-2, 4, and 6 are moderately affected by temperature and the damage depth changes. While Mode-3 is less affected by temperature changes. Therefore, Modes-2, 3, and 6 can be chosen for damage evaluation.

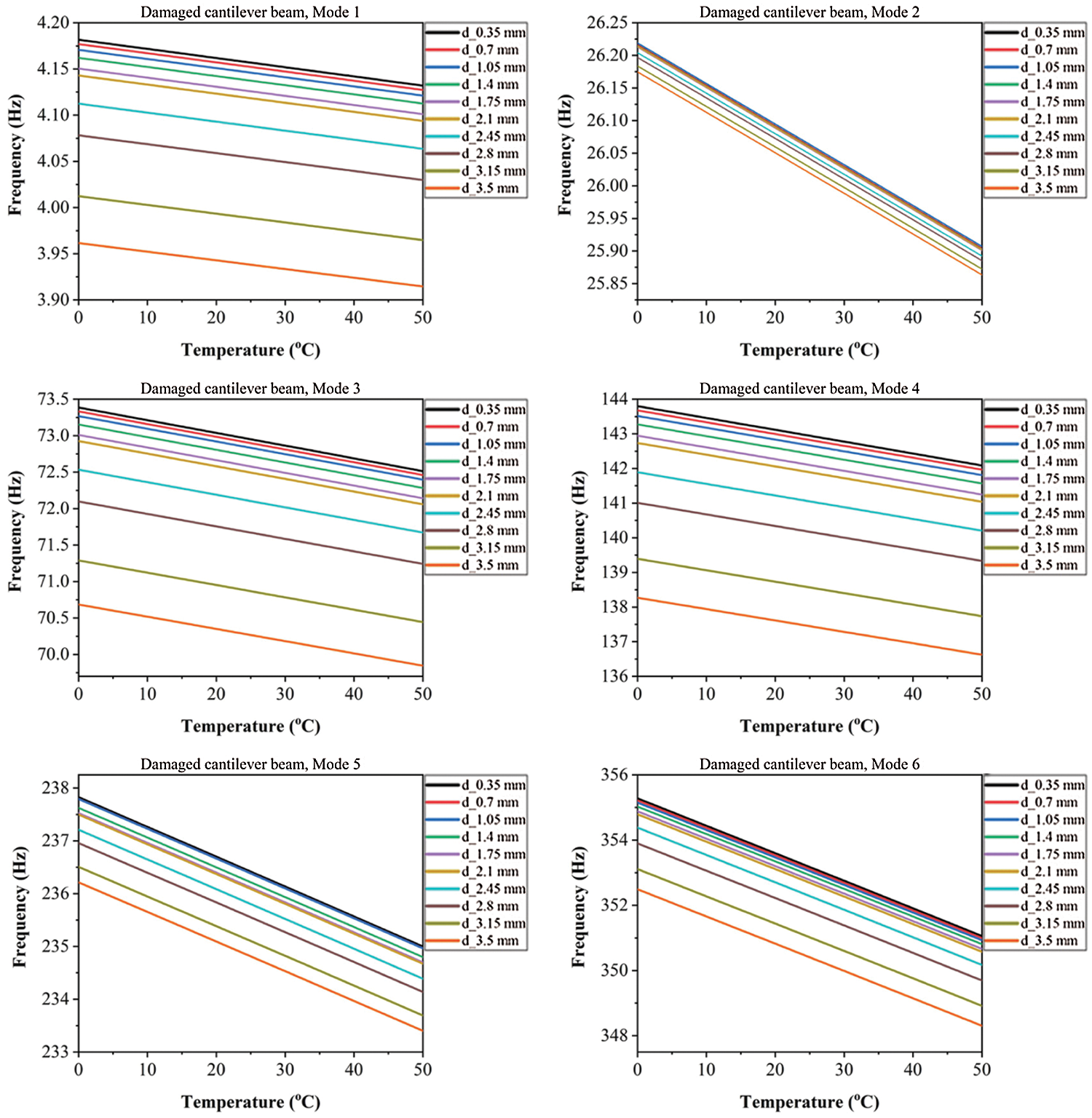
Figure 5: Frequency shifts as a function of temperature and damage depth for the first six bending modes of the damaged cantilever beam

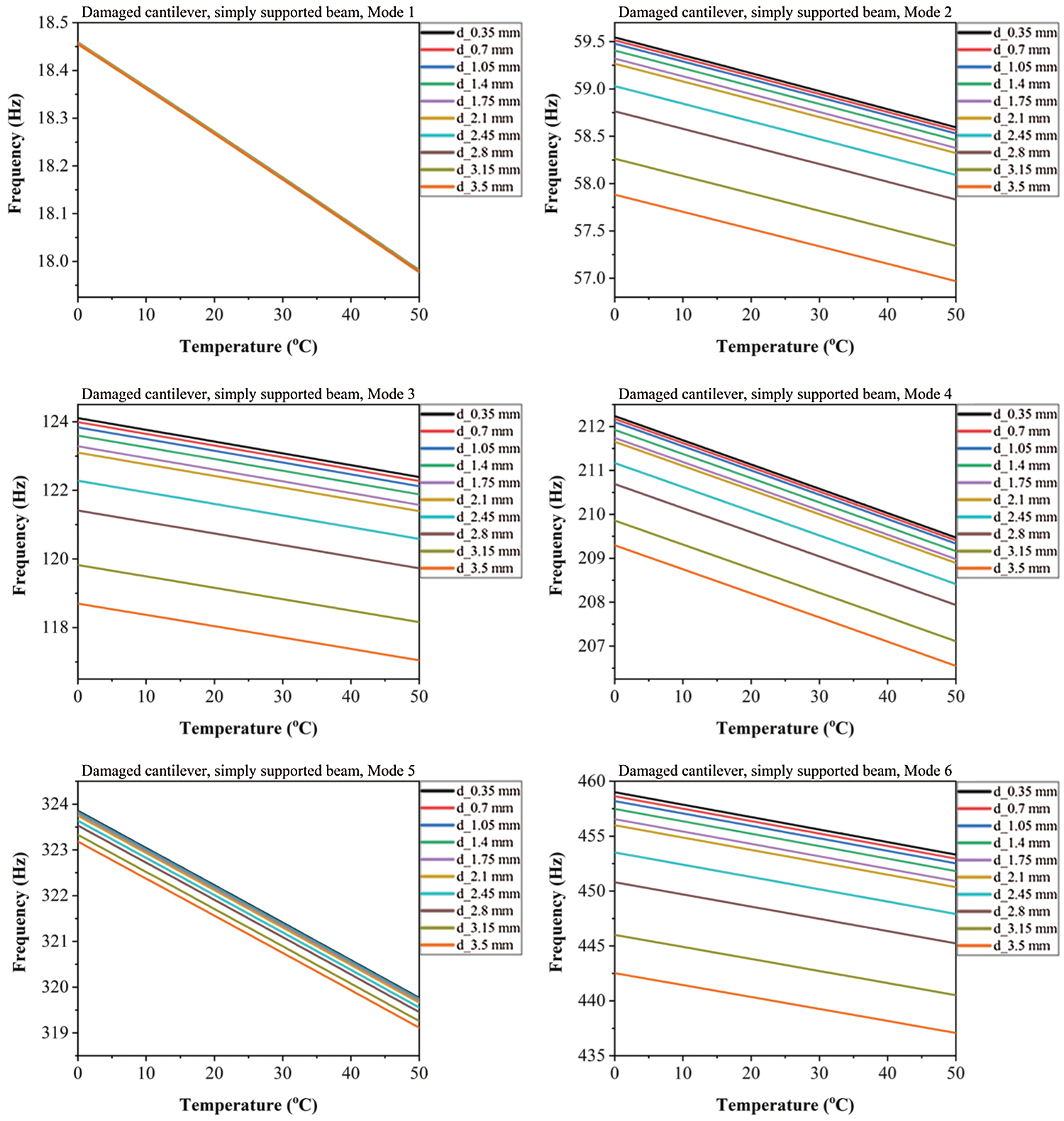
Figure 6: Frequency shifts as a function of temperature and damage depth for the first six bending modes of the damaged cantilever, simply supported beam

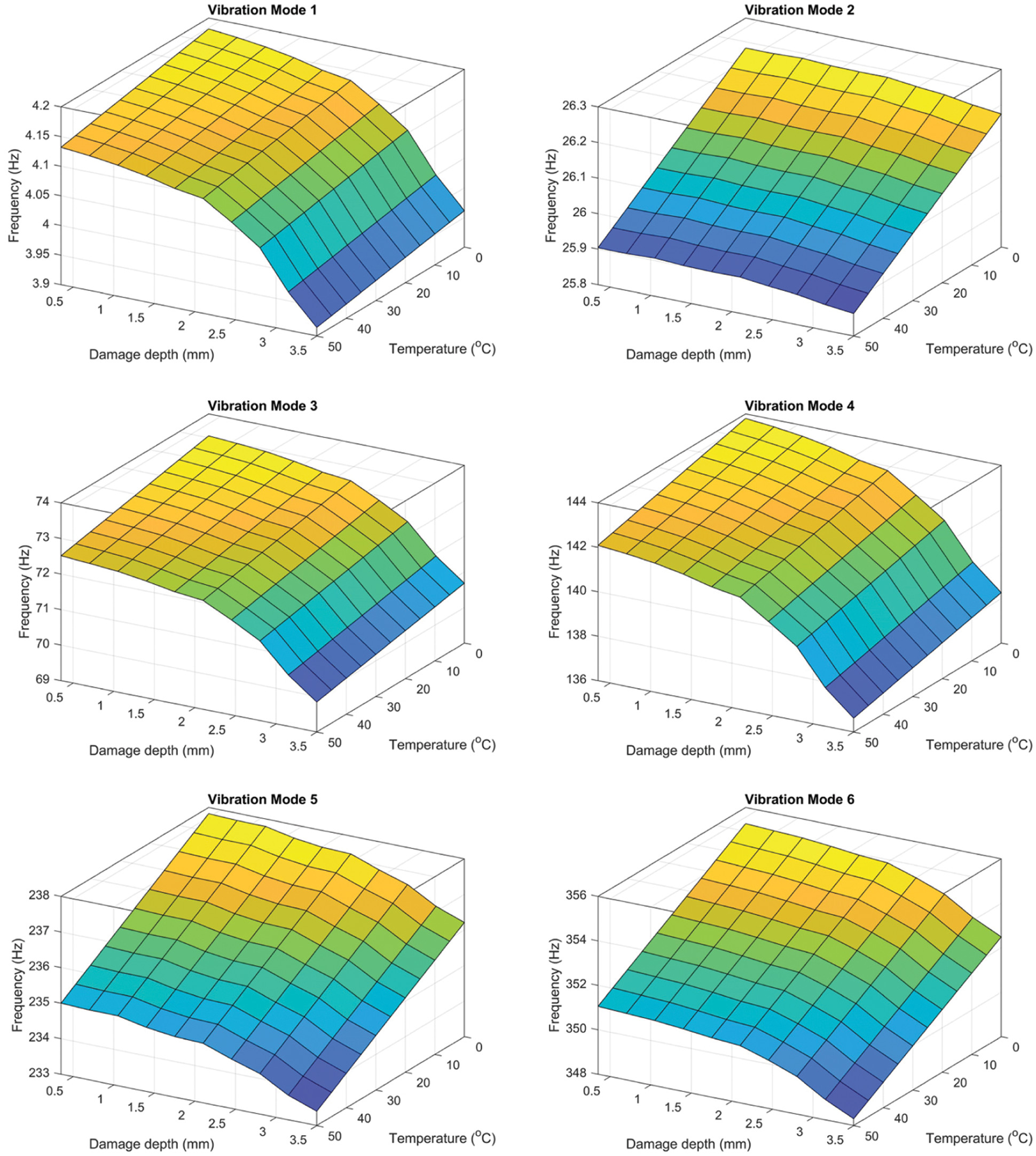
Figure 7: A 3D representation of the frequency changes of the first six bending modes of the damaged cantilever beam

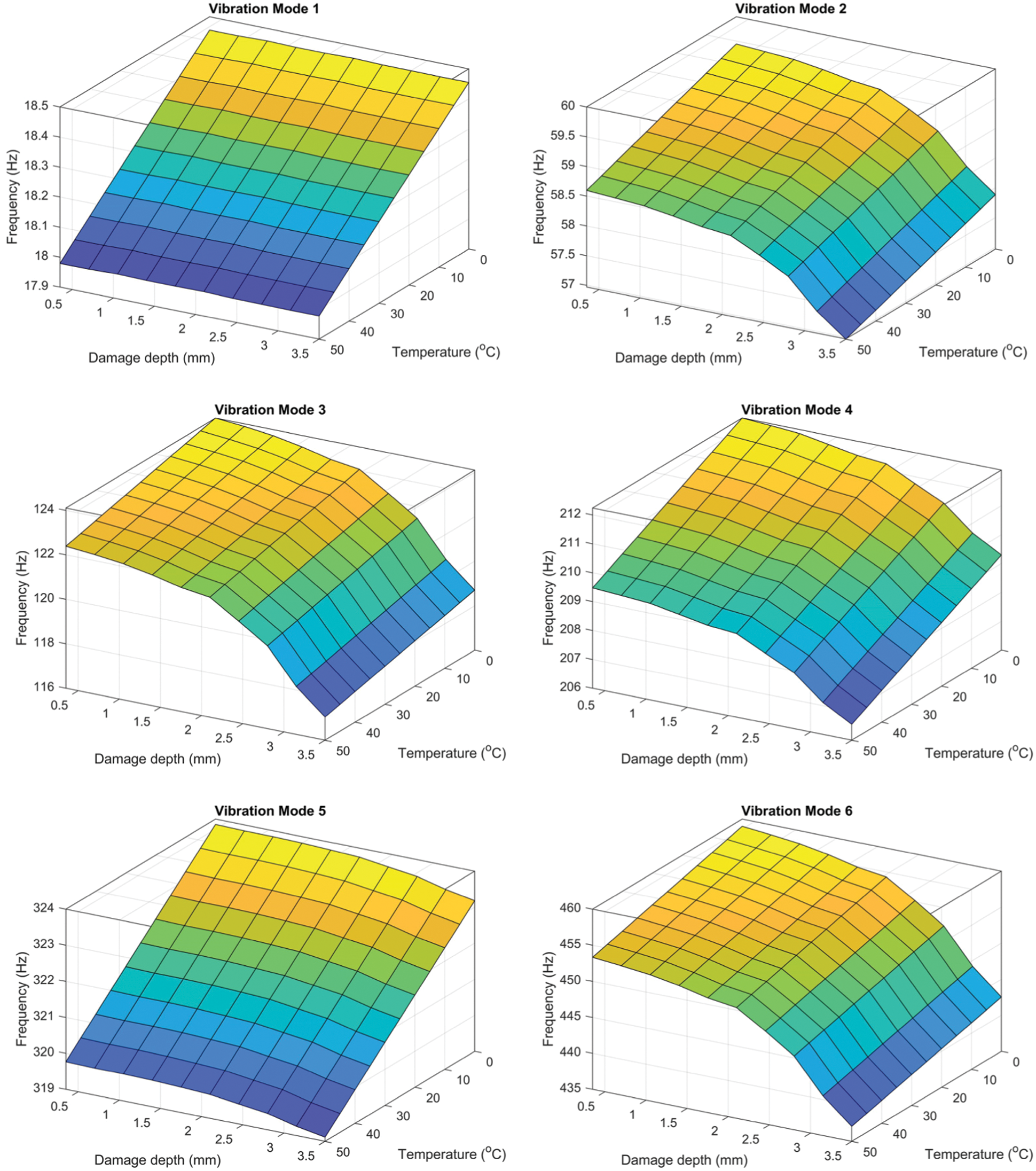
Figure 8: A 3D representation of the frequency changes of the first six bending modes of the damaged cantilever, simply supported beam

In Fig. 9, one can see that the highest relative shifts of the damaged cantilever beam are for Mode-1 and moderate for Modes-3 and 4, while Modes-2, 5, and 6 have slight relative frequency shifts. Also, it can be seen that the most significant relative frequency shifts are for the damage depth 3.5 mm for each mode.

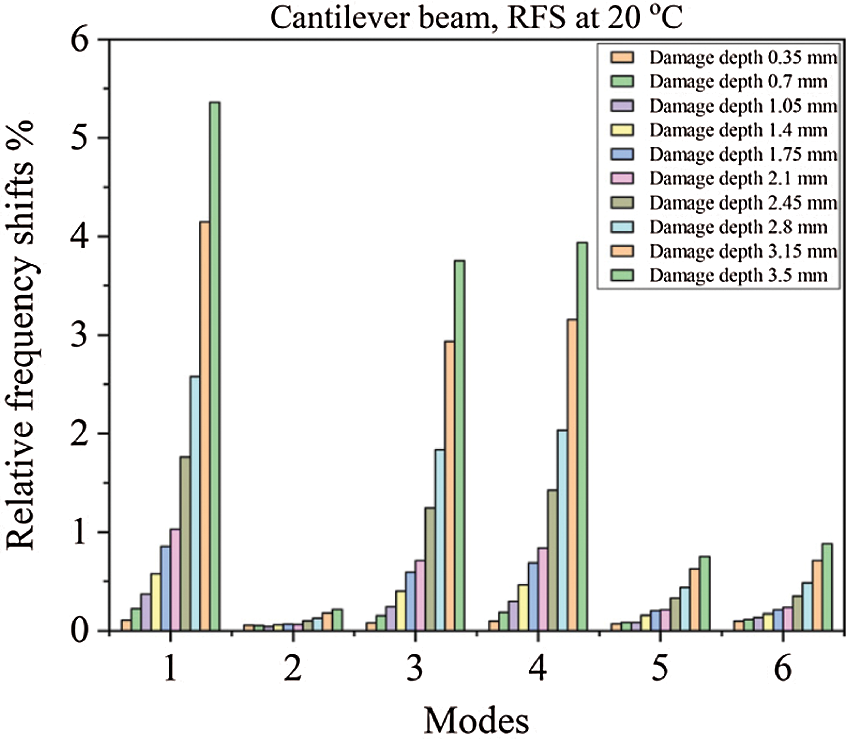
Figure 9: Represents the relative frequency shifts (RFS) of a cantilever beam at 20oC

In Fig. 10, it can be found that for the damaged cantilever simply supported beam, the highest relative shifts are for Mode-3 and intermediate values achieved for Modes-2, 4, and 6, while Mode-1 has the smallest relative shift of frequencies. Also, it can be found that the largest relative frequency shifts are for the damage depth 3.5 mm for each mode. So, the appropriate vibration modes should be selected correctly in the damage estimation process.

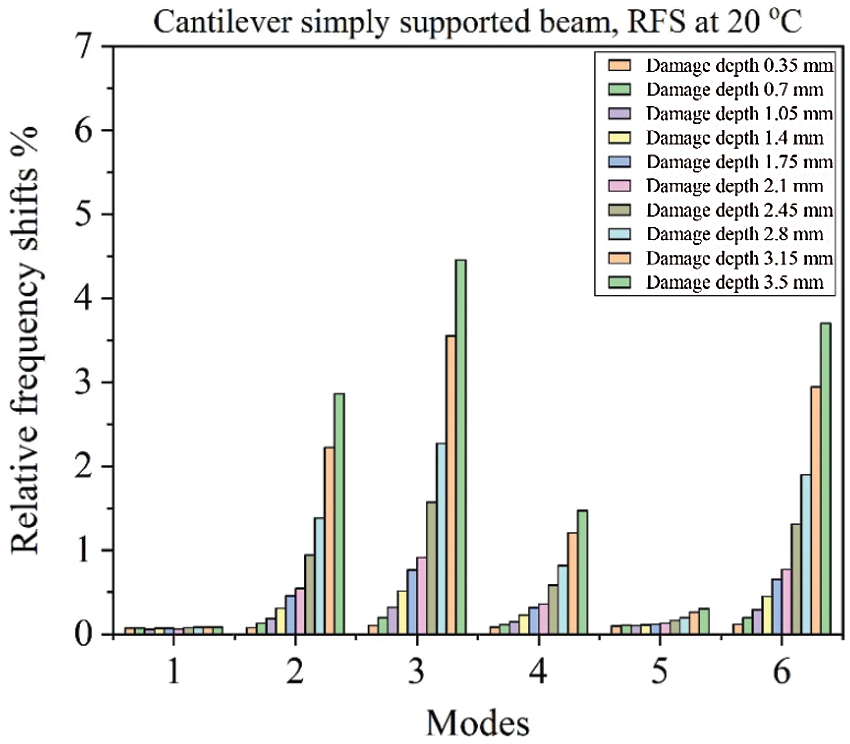
Figure 10: Represents the relative frequency shifts (RFS) of a cantilever simply supported beam at 20oC

The relative frequency shifts (RFS) of any vibration mode obtained from the analyses are indicators of damage presence, severity, and location. This is determined using the mathematical expression [35]:

RFSi=fiU−fiDfiU

where fiU represents the frequency of an intact beam for the ith bending mode of vibration and fiD is the frequency of the beam containing the damage.

5  Validation

In this section, two examples have been introduced in order to validate the present work. The first example shows the temperature’s influence on the natural frequencies of intact and damaged steel beams clamped at both ends. The second example presents the influence of damage depth on the natural frequencies of healthy and damaged steel beams fixed at one end.

5.1 Example 1

The validation shown here was based on the numerical investigation of Gillich et al. [35]. They used the SolidWorks simulation software in order to investigate the effect of temperatures on intact and damaged steel beams. In this example, ANSYS finite element software is used.

In order to validate the present work, two cases are considered here; an intact beam and a damaged beam with completely fixed ends. The damaged beam has a transverse crack with a width w=1mm and a depth a=4mm and is located at a distance xc=235mm from the left end. The temperature was in the range of 0°C to 50°C. The thermal and mechanical parameters of the investigated beams are shown in Table 4. Modal analysis was performed to obtain the natural frequencies for the damaged and intact beams. A comparison of the results obtained using SolidWorks in the [35] and the present work using ANSYS to show the relationship between frequencies and temperatures for the first six bending vibration modes are listed in Tables 5 and 6 and displayed in Fig. 11.

One can notice that, for the damaged case, the highest relative shifts are for Mode-3, and there are no relative shifts for Modes-1 and 5. Therefore, the appropriate vibration modes should be selected carefully in the damage evaluation process. The first vibration mode should be excluded at high temperatures, and higher-order vibration modes should be used instead [35].

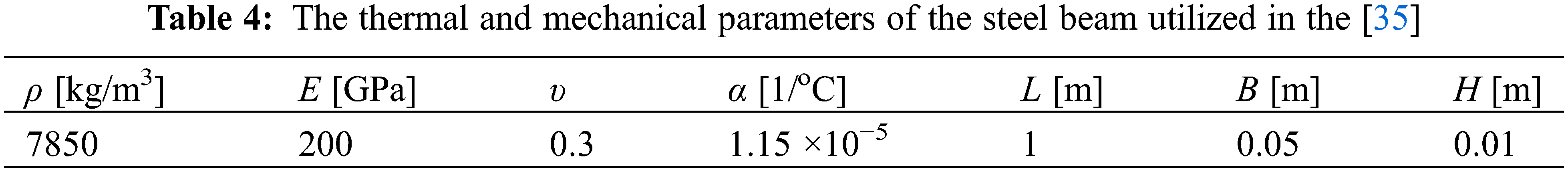
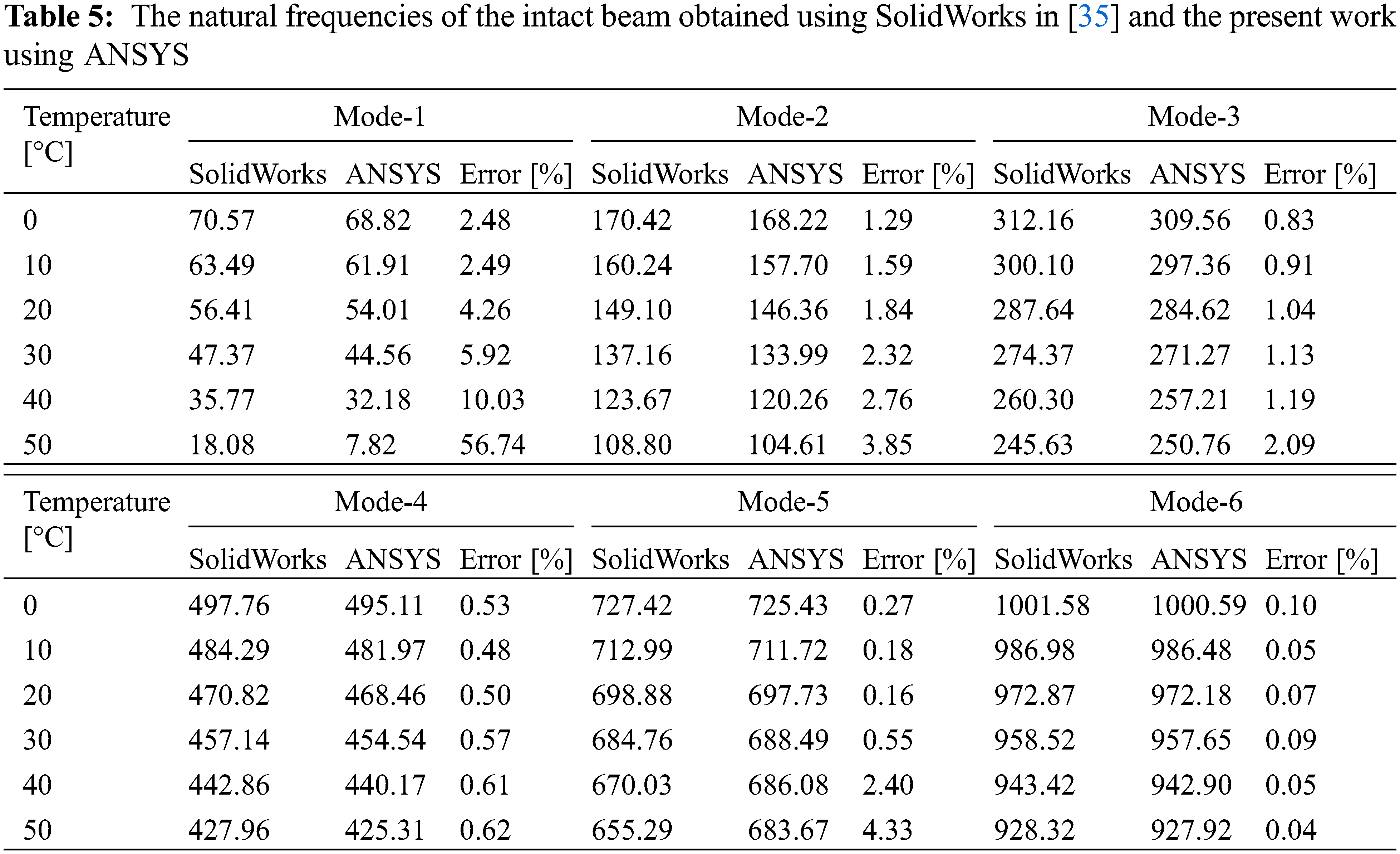
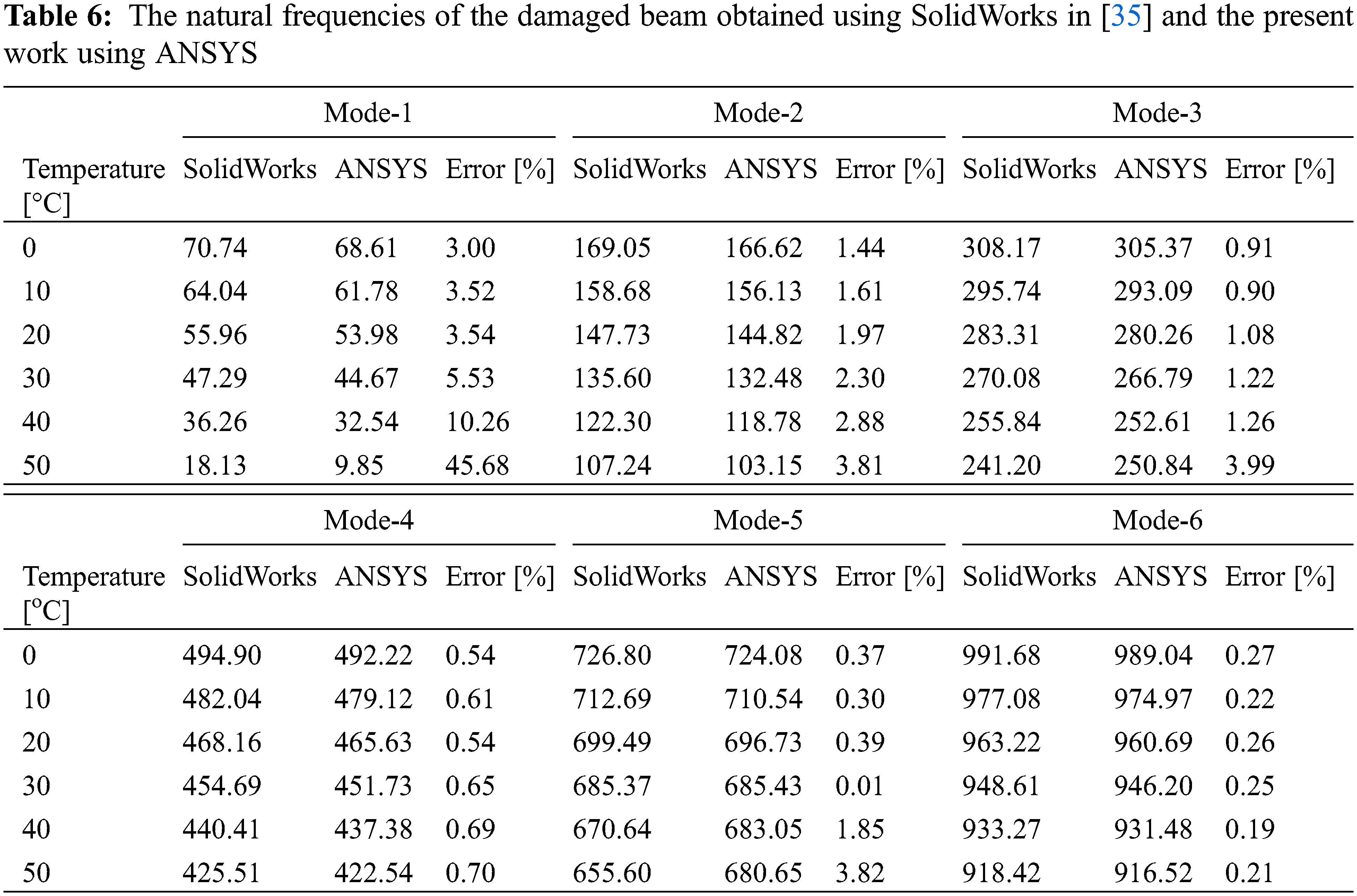
Figure 11: Relationship between temperature and natural frequencies obtained using SolidWorks in the [35] and the present work using ANSYS of the intact and damaged steel beams under the effect of temperature

5.2 Example 2

This example is based on the experimental work provided by Nedelcu et al. [39] that was conducted in order to detect small changes in frequencies in beam-­like structures. The specimen is a steel cantilever beam with a length (L), width (B), and thickness (H). The dimensions and mechanical parameters of the steel beam utilized in this example are presented in Table 7.

Investigations were performed on an intact beam and damaged beam at four damage depth levels. The natural frequencies of the first five bending modes of vibration found using the work in [39] through experimental work and those obtained using ANSYS and ABAQUS are listed in Table 8 and charted in Fig. 12. The results agree well with those reported by [39], where the maximum error was within 1.5%.

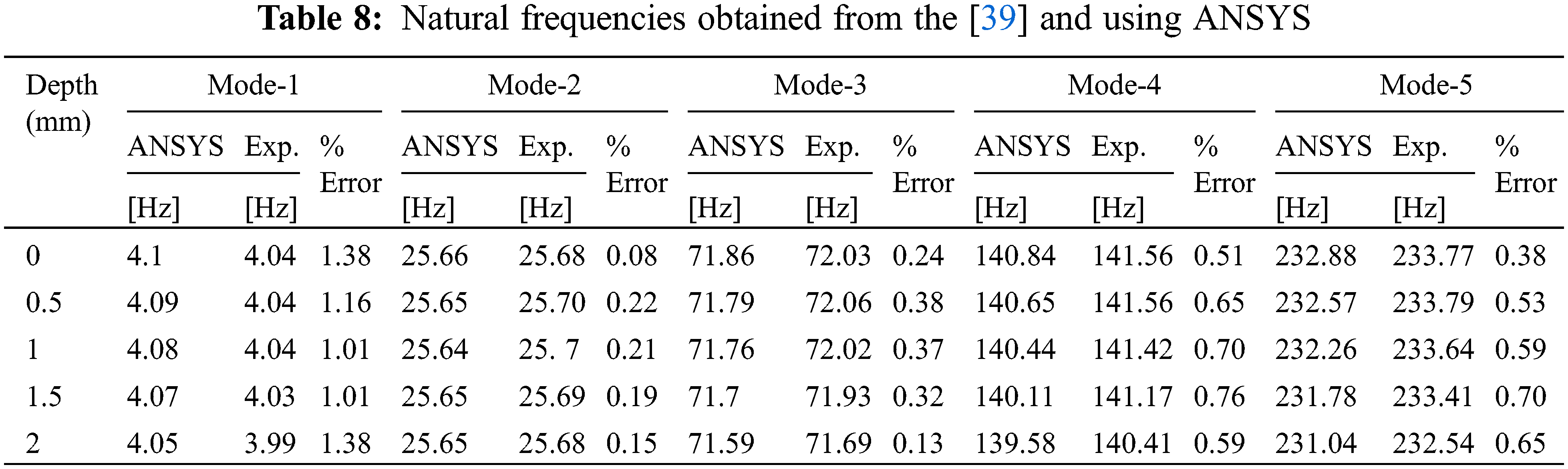
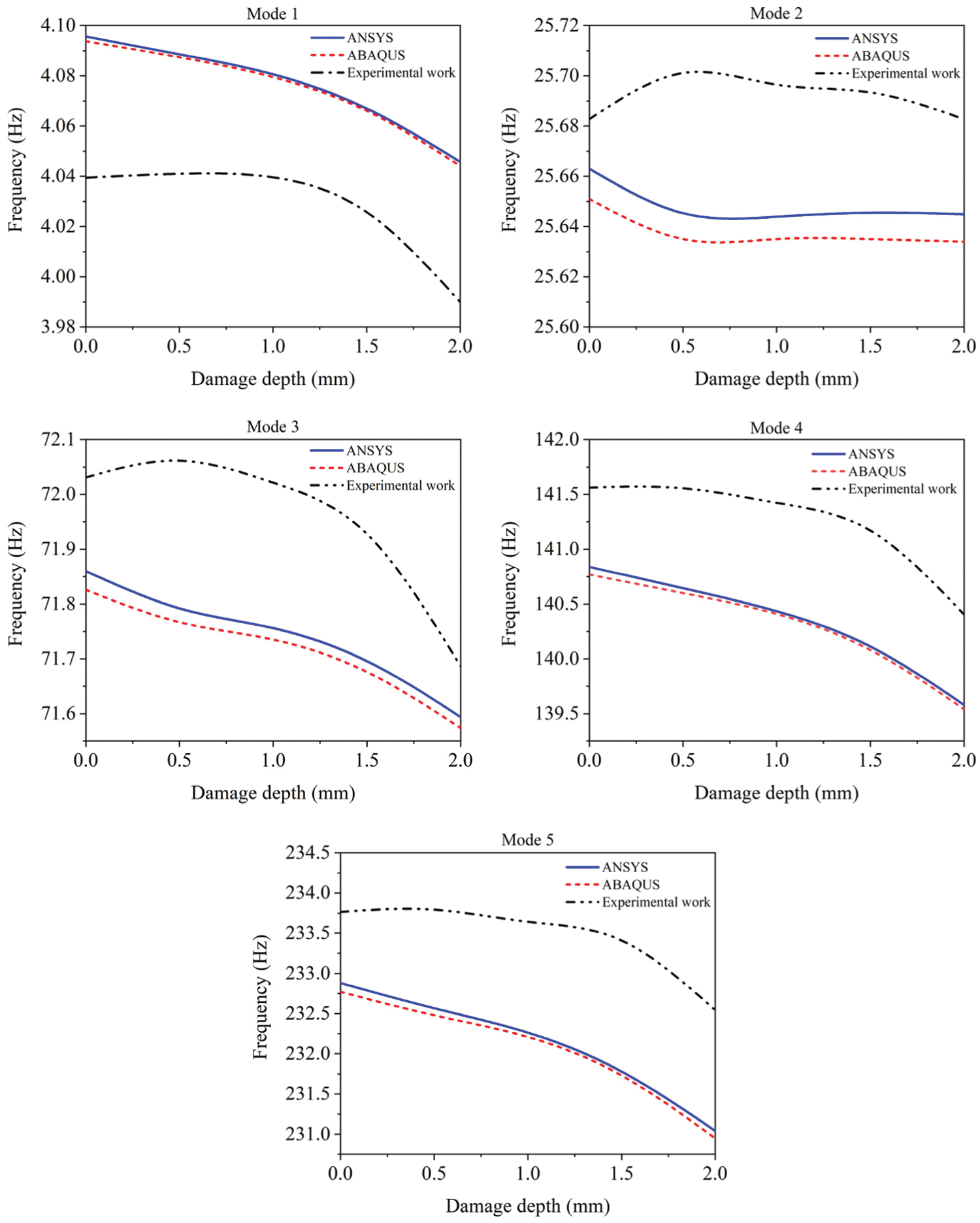
Figure 12: Represents the natural frequencies evolution curves as a function of damage depth obtained from ANSYS and ABAQUS and compared with results from [39]

The reason for the slight difference in the results between SolidWorks in the [35] and ANSYS is that both programs are designed for different purposes, as SolidWorks is used to create parts and CAD almost more than for analysis. ANSYS is a program designed primarily for the purpose of analysis for a wide variety of finite element applications and is used in the analysis of forces, thermal, vibration, etc. The ANSYS program has the advantage of providing better results for thermal analysis investigations [40]. ANSYS is the solution of elastic mechanics, and SolidWorks is the solution of mechanics of materials. The theory of elasticity interests itself mainly with more mathematical analysis to determine the exact distributions of strain and stress in a loaded body. The mechanics of materials concentrates primarily on the more or less approximate solutions to practical problems. It can be concluded that the difference between these approaches is mainly in the nature of the simplifying assumptions used. More details about this subject can be found in [41].

6  Discussions

This section discusses the effect of temperature changes, damage depth, and boundary conditions on natural frequencies changes in beam-like structures.

First, the modal analysis was performed on intact steel specimens with different boundary conditions using ANSYS software. Modal analysis of the beams was performed at temperatures between 5°C and 50°C, with a step of 5°C. The analysis results show that the natural frequencies decrease with increasing temperature, as shown in Tables 2 and 3 and Fig. 4.

Second, the modal analysis was performed on steel specimens containing open cracks at different depths and under temperatures ranging from 0°C to 50°C with a step of 5°C and different boundary conditions. The results indicate that the changes in temperatures, crack depths, and boundary conditions affect the natural frequencies. This analysis concluded that the effects resulting from temperature changes must be taken into account when evaluating the damage in beam-like structures based on natural frequencies changes. Also, it was found that the change of dynamic features caused by the damage may be less than the change of dynamic properties due to temperature change. Furthermore, the result shows that choosing an appropriate vibration mode is necessary for damage assessment as was observed in the case of the cantilever beam where Modes-1, 3, and 4 are most appropriate, and in the case of the cantilever, simply supported beam the Modes-2, 3 and 6 are also more appropriate to get better results.

Finally, in order to validate the current work, numerical simulations were performed using two examples from the literature to study the effect of crack depth and temperature changes. The validation results confirm that the present work using ANSYS agrees well with that in the literature.

7  Conclusions

Damage detection based on structural dynamics features, such as natural frequencies and mode shapes, is an important research field. In the measurement process, obtaining accurate results for structural dynamics properties is challenging. Operational and environmental conditions such as temperature variations caused by seasonal weather or radiation from sunlight lead to changes in structures’ dynamic characteristics. An interesting observation is that dynamic features change caused by damage may be lower than dynamic properties change due to temperature variations. Also, damage can affect the frequency response. In this study, the coupled effect of the damage depth and temperatures on the natural frequencies of the carbon steel (ASTM A36) beam is assessed numerically. The ANSYS finite element software is used for numerical analysis. Modal analysis is used to analyze natural frequencies obtained from the numerical simulations. In addition, damage signatures at temperatures ranging from 0°C to 50°C have been obtained. The study was also conducted at different damage depths, starting from 0.35 mm to 3.5 mm in ten levels. The numerical results demonstrated that an increase in temperature reduces the structural frequency. The assessment of the influence of damage depth on natural frequency displays that when damage depth is increased, there is a considerable decrease in the natural frequency. It is expected that the decrease in natural frequencies at higher temperatures will be higher.

The study demonstrated that choosing an appropriate vibration mode is necessary for damage assessment. The effect of temperature must be taken into account when measurements are carried out in changing environmental conditions. The relative frequency shifts (RFS) of any vibration mode obtained from investigations can be used to indicate the existence, severity, and location of the damage. The future work is intended to study the effect of temperature on the dynamic characteristics of a beam containing fatigue-breathing crack in beam-like structures. The temperature range can be expanded to provide a better analysis under high temperature conditions. Moreover, the coupled effect of temperature-crack depth can be studied for various materials and the effect of various kinds of practical cracks, i.e., V-, U- and rectangular- shape cracks can be evaluated. Also, the effect of crack geometry, depth, and location on the beam stiffness can be discussed.

Funding Statement: This work is partially supported by the Anhui Provincial International Joint Research Center of Data Diagnosis and Smart Maintenance on Bridge Structures (No. 2021AHGHZD01), the Nanjing Science and Technology Project (No. 202002014), and the Nantong Science and Technology Opening Cooperation Project in 2021 (No. BW2021001).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Doebling, S. W., Farrar, C. R., Prime, M. B. (1998). A summary review of vibration-based damage identification methods. Shock and Vibration Digest, 30(2), 91–105. DOI 10.1177/058310249803000201. [Google Scholar] [CrossRef]

 2.  Salawu, O. S. (1997). Detection of structural damage through changes in frequency: A review. Engineering Structures, 19(9), 718–723. DOI 10.1016/S0141-0296(96)00149-6. [Google Scholar] [CrossRef]

 3.  Al-Hababi, T., Cao, M., Saleh, B., Alkayem, N. F., Xu, H. (2020). A critical review of nonlinear damping identification in structural dynamics: Methods, applications, and challenges. Sensors, 20(24), 7303. DOI 10.3390/s20247303. [Google Scholar] [CrossRef]

 4.  Montalvao, D., Maia, N. M. M., Ribeiro, A. M. R. (2006). A review of vibration-based structural health monitoring with special emphasis on composite materials. Shock and Vibration Digest, 38(4), 295–324. DOI 10.1177/0583102406065898. [Google Scholar] [CrossRef]

 5.  Azadi, M. (2011). Free and forced vibration analysis of FG beam considering temperature dependency of material properties. Journal of Mechanical Science and Technology, 25(1), 69–80. DOI 10.1007/s12206-010-1015-y. [Google Scholar] [CrossRef]

 6.  Hios, J. D., Fassois, S. D. (2014). A global statistical model based approach for vibration response-only damage detection under various temperatures: A proof-of-concept study. Mechanical Systems and Signal Processing, 49(1–2), 77–94. DOI 10.1016/j.ymssp.2014.02.005. [Google Scholar] [CrossRef]

 7.  Deraemaeker, A., Preumont, A., Kullaa, J. (2006). Modeling and removal of environmental effects for vibration based SHM using spatial filtering and factor analysis. Proceedings of IMAC XXIV, S.E.M., St. Louis, USA. [Google Scholar]

 8.  Alkayem, N. F., Shen, L., Asteris, P. G., Sokol, M., Xin, Z. et al. (2021). A new self-adaptive quasi-oppositional stochastic fractal search for the inverse problem of structural damage assessment. Alexandria Engineering Journal, 61(3), 1922–1936. DOI 10.1016/j.aej.2021.06.094. [Google Scholar] [CrossRef]

 9.  Wah, W. S. L., Chen, Y. T., Owen, J. S. (2021). A regression-based damage detection method for structures subjected to changing environmental and operational conditions. Engineering Structures, 228(1851), 111462. DOI 10.1016/j.engstruct.2020.111462. [Google Scholar] [CrossRef]

10. Soo Lon Wah, W., Xia, Y. (2021). Elimination of outlier measurements for damage detection of structures under changing environmental conditions. Structural Health Monitoring, 571(1). DOI 10.1177/1475921721998476. [Google Scholar] [CrossRef]

11. Chinka, S. S. B., Putti, S. R., Adavi, B. K. (2021). Modal testing and evaluation of cracks on cantilever beam using mode shape curvatures and natural frequencies. Structures, 32(8), 1386–1397. DOI 10.1016/j.istruc.2021.03.049. [Google Scholar] [CrossRef]

12. Alkayem, N. F., Cao, M., Ragulskis, M. (2019). Damage localization in irregular shape structures using intelligent FE model updating approach with a new hybrid objective function and social swarm algorithm. Applied Soft Computing, 83(1), 105604. DOI 10.1016/j.asoc.2019.105604. [Google Scholar] [CrossRef]

13. Saleh, B., Jiang, J., Fathi, R., Al-hababi, T., Xu, Q. et al. (2020). 30 years of functionally graded materials: An overview of manufacturing methods, applications and future challenges. Composites Part B: Engineering, 201, 108376. DOI 10.1016/j.compositesb.2020.108376. [Google Scholar] [CrossRef]

14. Huang, M., Lei, Y., Li, X., Gu, J. (2021). Damage identification of bridge structures considering temperature variations-based SVM and MFO. Journal of Aerospace Engineering, 34(2), 04020113. DOI 10.1061/(ASCE)AS.1943-5525.0001225. [Google Scholar] [CrossRef]

15. Peeters, B., de Roeck, G. (2001). One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthquake Engineering & Structural Dynamics, 30(2), 149–171. DOI 10.1002/(ISSN)1096-9845. [Google Scholar] [CrossRef]

16. Wang, Z., Huang, M. (2020). Temperature effects on vibration-based damage detection of a reinforced concrete slab. Applied Sciences, 10(8), 2869. DOI 10.3390/app10082869. [Google Scholar] [CrossRef]

17. Xia, Y., Chen, B., Weng, S. (2012). Temperature effect on vibration properties of civil structures: A literature review and case studies. Journal of Civil Structural Health Monitoring, 2(1), 29–46. DOI 10.1007/s13349-011-0015-7. [Google Scholar] [CrossRef]

18. Ashwear, N., Elderrat, H., Eljaarani, M. A. (2020). Overcoming effects from environmental temperature on the natural frequencies of cable-strut structures. Journal of Engineering Research and Reports, (4), 22–30. DOI 10.9734/jerr/2020/v13i417110. [Google Scholar] [CrossRef]

19. Kita, A., Cavalagli, N., Ubertini, F. (2019). Temperature effects on static and dynamic behavior of Consoli Palace in Gubbio, Italy. Mechanical Systems and Signal Processing, 120(4), 180–202. DOI 10.1016/j.ymssp.2018.10.021. [Google Scholar] [CrossRef]

20. Liu, H., Wang, X., Jiao, Y. (2016). Effect of temperature variation on modal frequency of reinforced concrete slab and beam in cold regions. Shock and Vibration, 2016(6), 1–17. DOI 10.1155/2016/4792786. [Google Scholar] [CrossRef]

21. Ralbovsky, M., Santos, J., Kwapisz, M., Dallinger, S., Catarino, J. M. (2014). Damage detection based on structural response to temperature changes and model updating. EWSHM-7th European Workshop on Structural Health Monitoring, Nantes, France. [Google Scholar]

22. Karsh, P. K., Mukhopadhyay, T., Dey, S. (2020). A stochastic investigation of effect of temperature on natural frequencies of functionally graded plates. In: Advances in structural engineering and rehabilitation, pp. 41–53, Springer, Singapore. DOI 10.1007/978-981-13-7615-3_3. [Google Scholar] [CrossRef]

23. Esfarjani, S. M., Salehi, M., Ghassemi, A. (2017). Effect of the multiple damages and temperature changes on the natural frequency. Journal of Theoretical and Applied Mechanics, 55(3), 813–822. DOI 10.15632/jtam-pl.55.3.813. [Google Scholar] [CrossRef]

24. Sha, G., Radzieński, M., Cao, M., Ostachowicz, W. (2019). A novel method for single and multiple damage detection in beams using relative natural frequency changes. Mechanical Systems and Signal Processing, 132, 335–352. DOI 10.1016/j.ymssp.2019.06.027. [Google Scholar] [CrossRef]

25. Geng, Q., Wang, D., Liu, Y., Li, Y. (2015). Experimental and numerical investigations on dynamic and acoustic responses of a thermal post-buckled plate. Science China Technological Sciences, 58(8), 1414–1424. DOI 10.1007/s11431-015-5838-8. [Google Scholar] [CrossRef]

26. Dan, C. A., Kudela, P., Radzienski, M., Ostachowicz, W. (2014). Temperature effects compensation strategy for guided wave based structural health monitoring. 6th International Symposium on NDT in Aerospace, Madrid, Spain. [Google Scholar]

27. Moughty, J. J., Casas, J. R. (2017). A state of the art review of modal-based damage detection in bridges: Development, challenges, and solutions. Applied Sciences, 7(5510. DOI 10.3390/app7050510. [Google Scholar] [CrossRef]

28. Talebian, S., Rezazadeh, G., Fathalilou, M., Toosi, B. (2010). Effect of temperature on pull-in voltage and natural frequency of an electrostatically actuated microplate. Mechatronics, 20(6), 666–673. DOI 10.1016/j.mechatronics.2010.07.009. [Google Scholar] [CrossRef]

29. Ding, Z. H., Fu, K. S., Deng, W., Li, J., Lu, Z. R. (2020). A modified Artificial Bee Colony algorithm for structural damage identification under varying temperature based on a novel objective function. Applied Mathematical Modelling, 88(16), 122–141. DOI 10.1016/j.apm.2020.06.039. [Google Scholar] [CrossRef]

30. Oh, Y., Yoo, H. H. (2020). Thermo-elastodynamic coupled model to obtain natural frequency and stretch characteristics of a rotating blade with a cooling passage. International Journal of Mechanical Sciences, 165(2), 105194. DOI 10.1016/j.ijmecsci.2019.105194. [Google Scholar] [CrossRef]

31. Abdus, S., Cheng, X., Cheng, Y., Hu, R., Muhammad, A. (2021). Dynamic properties of single and multi-bolted composite joints at different bolt-loads and elevated temperature. Australian Journal of Mechanical Engineering, 19(4), 406–413. DOI 10.1080/14484846.2019.1629188. [Google Scholar] [CrossRef]

32. Talai, S. M., Desai, D. A., Heyns, S. P. (2016). Experimentally validated structural vibration frequencies’ prediction from frictional temperature signatures using numerical simulation: A case of laced cantilever beam-like structures. Advances in Mechanical Engineering, 9(1). DOI 10.1177/1687814016685001. [Google Scholar] [CrossRef]

33. Wang, W. Y., Liu, B., Kodur, V. (2013). Effect of temperature on strength and elastic modulus of high-strength steel. Journal of Materials in Civil Engineering, 25(2), 174–182. DOI 10.1061/(ASCE)MT.1943-5533.0000600. [Google Scholar] [CrossRef]

34. Yuan, H. Q., Ri, C. N. (2012). Modal analysis of gear considering temperature based on ANSYS. In: Advanced materials research, vol. 482–484, pp. 1209–1212.Trans Tech Publications, Ltd. DOI10.4028/www.scientific.net/AMR.482-484.1209. [Google Scholar] [CrossRef]

35. Gillich, G., Furdui, H., Abdel, M., Korka, Z. (2019). A robust damage detection method based on multi-modal analysis in variable temperature conditions. Mechanical Systems and Signal Processing, 115(9), 361–379. DOI 10.1016/j.ymssp.2018.05.037. [Google Scholar] [CrossRef]

36. Gillich, G. R., Praisach, Z. I. (2014). Modal identification and damage detection in beam-like structures using the power spectrum and time-frequency analysis. Signal Processing, 96(2), 29–44. DOI 10.1016/j.sigpro.2013.04.027. [Google Scholar] [CrossRef]

37. Rao, S. S. (2012). Mechanical vibrations: Fifth edition in SI units. Pearson, USA. [Google Scholar]

38. Nowacki, W. (1962). Thermoelasticity. Polish Science Publishers, Oxford, Warszawa. [Google Scholar]

39. Nedelcu, D., Gillich, G. R. (2021). A structural health monitoring Python code to detect small changes in frequencies. Mechanical Systems and Signal Processing, 147(5), 107087. DOI 10.1016/j.ymssp.2020.107087. [Google Scholar] [CrossRef]

40. Zhang, H., Li, T., Li, Z. (2009). Modeling in solid works and analysis of temperature and thermal stress during construction of intake tower. Water Science and Engineering, 2(1), 95–102. DOI 10.3882/j.issn.1674-2370.2009.01.009. [Google Scholar] [CrossRef]

41. Ugural, A. C., Fenster, S. K. (2011). Advanced Mechanics of Materials and Applied Elasticity (6th edition) Pearson Education, Prentice Hall, New Jersey. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.