Sound & Vibration

DOI: 10.32604/sv.2021.014157

ARTICLE

Modeling of Dark Solitons for Nonlinear Longitudinal Wave Equation in a Magneto-Electro-Elastic Circular Rod

Hulya Durur1, Asıf Yokuş2, Doğan Kaya3 and Hijaz Ahmad4,*

1Department of Computer Engineering, Faculty of Engineering, Ardahan University, Ardahan, Turkey
2Department of Mathematics, Faculty of Science, Firat University, Elazig, Turkey
3Department of Mathematics, Istanbul Commerce University, Istanbul, Turkey
4Department of Basic Sciences, University of Engineering and Technology, Peshawar, Pakistan
*Corresponding Author: Hijaz Ahmad. Email: hijaz555@gmail.com
Received: 03 September 2020; Accepted: 28 September 2020

1  Introduction

Nonlinear evolution equations (NLEEs) are used in various fields such as biological sciences, plasma physics, quantum mechanics, fluid dynamics and engineering. Many methods have been used to obtain solutions of NLEEs from past to present.

In particular, (1/G′)− expansion method that we will consider in this study produces hyperbolic type traveling wave solution, while the sub equation method produces dark solitons. Generally, dark solitons are solutions that contain tangent function.

We know that solitons have an important place in wave theory. There are many solitons that offer a mathematical perspective to many physical phenomena. Some of these are dark soliton, bright soliton, peaked solitary, topological soliton, non-topological soliton, singular soliton and so on. The mathematical expressions of these solitons appear as a solution of NLEEs.

It is very difficult to obtain the analytical solution of NLEEs. However, with the help of classical wave transformation, traveling wave solutions can be obtained by converting to ordinary differential equations. Traveling wave solutions, which have an important place in wave theory and contain many physical events, are important for mathematics. Different types of traveling wave solutions are available with different methods. Some of these methods are auxiliary equation method [1], (G′/G)− expansion method [2], Homotopy perturbation method [3], sumudu transform method [4], (1/G′)− expansion method [5,6], finite element method [7], variational iteration method (VIM) and modified VIM algorithms [8–15], Meshless methods [16], Homotopy analysis, Homotopy-Pade methods [17], decomposition method [18], the first integral method [19], Clarkson–Kruskal direct method [20], residual power series method [21], collocation method [22], F-expansion method [23], homogeneous balance method [24], the auto-Bäcklund transformation method [25], new sub equation method [26,27], Exp-function method [28] and so on [29–38].

Let’s take the LWE in a magneto-electro-elastic circular rod [39]

utt−η2uxx−(η2u2+qutt)xx=0, (1)

where η is the linear longitudinal wave velocity and q is the dispersion parameter for a magneto-electro-elastic circular rod, all of which depend on the material property and geometry [40].

The real-world physical response of a magneto-electro-elastic circular rod LWE is the combination of piezomagnetic and piezoelectric BaTiO3 [39]. The solutions offered especially for those working in this field are important. It will become more important with the physical meaning of the constants in the solution.

In this study, some researchers have examined the physically precious LWE. In the study of Iqbal et al. wave solutions have been obtained with extended auxiliary equation mapping and extended direct algebraic mapping methods [39]. Ilhan et al. have provided solutions including complex, hyperbolic and trigonometric functions with sine-Gordon expansion method [40]. Baskonus et al. have been presented topological, non-topological and singular soliton solutions using the extended sinh-Gordon equation expansion method [41]. Also, Baskonus et al. have obtained hyperbolic, complex and complex hyperbolic function solutions with the modified exp expansion function method [42]. In their study, Yang et al. achieved solitary wave solutions that peaked using direct integration with the boundary condition and symmetry condition [43]. Younis et al. have been presented dark, bright and singular solitons solutions with the solitary wave ansatz method [44].

In this study, we will present different solutions from the solutions presented in the literature. In particular, we offer a different solution than the dark solitons that Younis et al. present in their work.

2  Sub-Equation Method

Consider the sub-equation method for the solving NLEEs. Regard the NLEEs as

ℵ(u,ut,ux,utt,uxx,...)=0. (2)

Applying the wave transmutation

U(ξ)=u(x,t),ξ=kx+wt, (3)

Eq. (2) converts into ODE

T(U,U′,U′′,...)=0, (4)

where w is arbitrary constant. In the form it is supposed that Eq. (4) has a solution

U(ξ)=∑i=0naiϕi(ξ),an≠0, (5)

in here ai,(0≤i≤n) are constants to be determined, n is a positive integer value which is going to be attained in Eq. (4) by balancing term is found according to the principle of balance and the solution of Riccati equation is ϕ(ξ)

ϕ′(ξ)=μ+(ϕ(ξ))2, (6)

where μ is an arbitrary constant. Some exclusive solutions are given of the Riccati equation in (6) as follows:

ϕ(ξ)={−−μtanh⁡(−μξ),μ<0−−μcoth⁡(−μξ),μ<0μtan⁡(μξ),μ>0−μcot⁡(μξ),μ>0−1ξ+r,μ=0(risacons.) (7)

In Eq. (4), if we apply the Eqs. (6) and (5), we attained the new polynomial with respect φ(ξ) a nonlinear algebraic equation system in ai,(i=0,1,...,n) setting all the coefficients of to zero yields ϕi(ξ),(i=0,1,...,n). To find solutions in nonlinear algebraic equations to we determine constants μ,τ,k,r,ai,(i=0,1,...,n). Substituting attained constants from this system and by the aid of the formulas (7) the solutions of Eq. (6) into Eq. (5). Then, we obtain analytic solutions for Eq. (2).

Using this analytical method, trigonometric provides solutions of hyperbolic and algebraic type. These solutions are in Eq. (7) formats. Especially our tanh solution contains dark soliton feature [45]. This method is a reliable, effective and powerful analytical method in obtaining the analytical solution of many differential equations.

3  The (1/G’)-Expansion Method

Consider a general form of NLEEs,

Ω(u,∂u∂t,∂u∂x,∂2u∂x2,...)=0. (8)

Let u=U(ξ)=u(x,t),ξ=kx+wt,w≠0, where w is a constant and the speed of the wave. We can convert it into the following nODE for U(ξ) :

℧(U,kU′,τU′,k2U′′,...)=0. (9)

The solution of Eq. (9) is assumed to have the form

U(ξ)=a0+∑i=1nai(1G′)i, (10)

where ai,i=0,1,...,n are constants, n is the balancing term that we need to calculate based on the homogeneous balance principle. G=G(ξ) provides the following second order IODE:

G′′+λG′+δ=0, (11)

where λ and δ are constants to be determined after,

1G′(ξ)=1−δλ+Bcosh⁡(ξλ)−Bsinh⁡(ξλ), (12)

where B is integral constant.

After calculating the n balancing term, the structure of the solution function of the assumed Eq. (10) emerges. The necessary derivatives of this solution are taken and replaced in the Eq. (9), and after some algebraic operations, a polynomial that accepts the expression (1/1G′G′)i,(i=0,1,2,...,n) as a variable can be created. Considering the zero polynomial property, the coefficients of the variable are equal to zero and an algebraic system of equations is obtained. We can reach the solution of the algebraic equation system using ready-made package programs. These solutions are the coefficients of the solution function of the default Eq. (10). When these coefficients are replaced in Eq. (10), there is a solution of Eq. (9). Finally, the classical wave transformation is reversed and the solution of Eq. (8) is reached.

4  Application of Sub-Equation Method

If we apply the transform in the Eq. (3) to the Eq. (1), we find

w2U′′−η2k2U′′−η2(U2)′′−qw2U(4)=0, (13)

or

(w2−η2k2)U′′−η2(U2)′′−qw2U(4)=0. (14)

If we take the integral twice according to ξ to the Eq. (14) and neglecting the integration constant with zero, we obtain

(w2−η2k2)U−η2(U2)−qw2U′′=0, (15)

In Eq. (15), we get n=2 from the balance principle and in Eq. (5), the following situation is obtained

U(ξ)=a0+a1ϕ(ξ)+a2(ϕ(ξ))2, (16)

If the equation given by (16) is placed in the Eq. (15) and the necessary arrangements are made, we can write the following equation system:

(ϕ(ξ))0:w2a0−k2η2a0−12k2ηa02−2k2qw2μ2a2=0,(ϕ(ξ))1:w2a1−k2η2a1−2k2qw2μa1−k2ηa0a1=0,(ϕ(ξ))2:−12k2ηa12+w2a2−k2η2a2−8k2qw2μa2−k2ηa0a2=0,(ϕ(ξ))3:−2k2qw2a1−k2ηa1a2=0,(ϕ(ξ))4:−6k2qw2a2−12k2ηa22=0.} (17)

a0,a1,a2 and μ constants are attained from Eq. (17) system with the aid of packet program.

Case 1: If μ<0,

a0=−w2+k2η2k2η,a1=0,a2=−12qw2η,μ=w2−k2η24k2qw2, (18)

Substituting values (18) into (16), we can also present the dark soliton for Eq. (1) using the classical wave transformation inverse, that is, using the ξ=kx+wt , as follows:

u1(x,t)=−w2+k2η2k2η+3(w2−k2η2)tanh⁡[12(tw+kx)−w2−k2η2k2qw2]2k2η. (19)

Case II: If μ<0,

a0=−w2+k2η2k2η,a1=0,a2=−12qw2η,μ=w2−k2η24k2qw2, (20)

Substituting values (20) into (16), we can also present the singular for Eq. (1) using the classical wave transformation inverse, that is, using the ξ=kx+wt , as follows:

u2(x,t)=−w2+k2η2k2η+3(w2−k2η2)coth⁡[12(tw+kx)−w2−k2η2k2qw2]2k2η. (21)

Case III: If μ>0,

a0=−w2+k2η2k2η,a1=0,a2=−12qw2η,μ=w2−k2η24k2qw2, (22)

Substituting values (22) into (16), we attain trigonometric soliton for Eq. (1)

u3(x,t)=−w2+k2η2k2η−3(w2−k2η2)tan⁡[12(tw+kx)w2−k2η2k2qw2]2k2η. (23)

Case IV: If μ>0,

a0=−w2+k2η2k2η,a1=0,a2=−12qw2η,μ=w2−k2η24k2qw2, (24)

Substituting values (24) into (16), we attain trigonometric soliton for Eq. (1)

u4(x,t)=−w2+k2η2k2η−3(w2−k2η2)cot⁡[12(tw+kx)w2−k2η2k2qw2]2k2η. (25)

Case V: If μ=0,

w=k2η2,a0=−w2+k2η2k2η,a1=0,a2=−12qw2η,μ=w2−k2η24k2qw2, (26)

Substituting values (26) into (16), we attain rational traveling wave solution for Eq. (1)

u5(x,t)=−12k2qη(r+kx+tk2η2)2. (27)

5  Application of (1/G’)-Expansion Method

Considering Eq. (15), we get balancing term n=2 and in Eq. (10), the following situation is obtained:

u(ξ)=a0+a1(1G′)+a2(1G′)2,a2≠0. (28)

Replacing Eq. (28) into Eq. (15) and the coefficients of the algebraic Eq. (1) are equal to zero, can find the following algebraic equation systems:

Const:w2a0−k2η2a0−12k2ηa02=0,(1G′[ξ])1:w2a1−k2η2a1−k2qw2λ2a1−k2ηa0a1=0,(1G′[ξ])2:−3k2qw2λδa1−12k2ηa12+w2a2−k2η2a2−4k2qw2λ2a2−k2ηa0a2=0,(1G′[ξ])3:−2k2qw2δ2a1−10k2qw2λδa2−k2ηa1a2=0,(1G′[ξ])4:−6k2qw2δ2a2−12k2ηa22=0. (29)

Case 1.

a0=−2k2qηλ21+k2qλ2,a1=−12k2qηλδ1+k2qλ2,a2=−12k2qηδ21+k2qλ2,w=kη1+k2qλ2, (30)

Replacing values Eq. (30) into Eq. (28) and we have the following hyperbolic type solutions for Eq. (1):

6  Results and Discussion

In this study, the LWE of a magneto-electro-elastic circular rod has been successfully produced using two different analytical methods. These solutions are emphasized to be hyperbolic, rational, dark soliton and trigonometric type traveling wave solutions. Generating the solutions of this equation is mathematically valuable as much in terms of physical meaning. The u solutions presented in this article represent the electrostatic potential of the magneto-electro-elastic circular rod. Also, using this potential, a different physical perspective can be presented. If we represent the pressure of this physical event with P, the P pressure can be calculated for different analytical solutions as follows:

P(x,t)=−ρ∂u(x,t)∂t, (32)

The potential u calculated here and the P pressure magneto-electro-elastic circular rod can offer different interpretations and different perspectives on the physical event [46–49].

The figures presented in this work are the graphs of solitons representing the standing wave. Fig. 1 represents the dark soliton, Fig. 2 represents the singular soliton, Figs. 3 and 4 represent the trigonometric solitons, Fig. 5 represents the rational soliton, and Fig. 6 represents the graphics of hyperbolic type solitons.

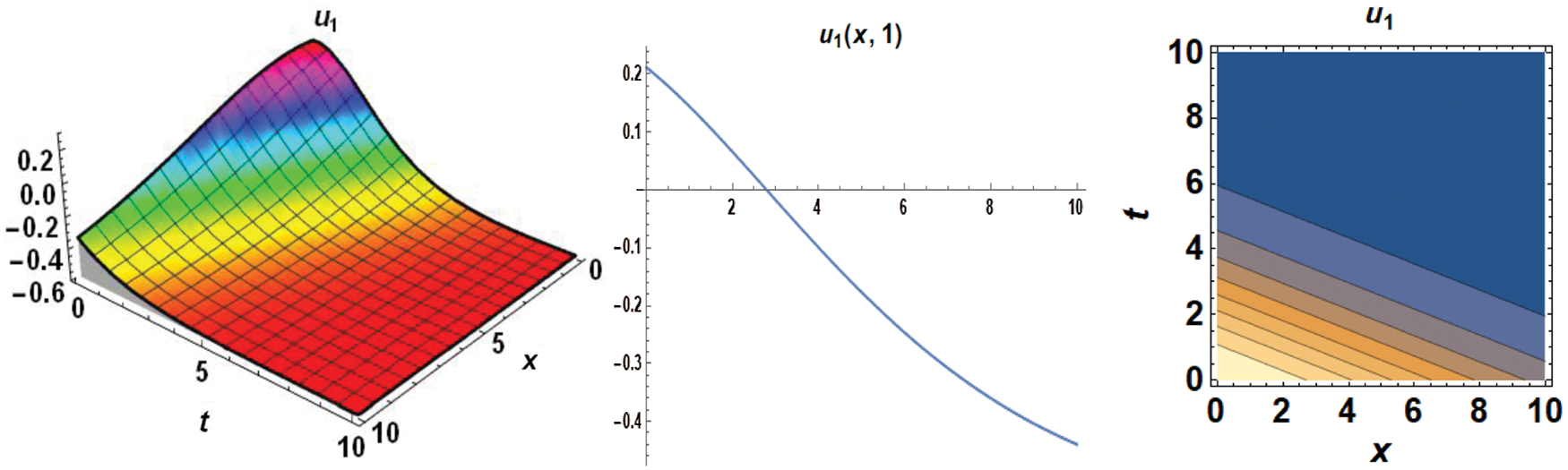
Figure 1: 3D, 2D and contour graphs respectively for w=0.5,η=2.65,q=2,k=0.2 values of Eq. (19)

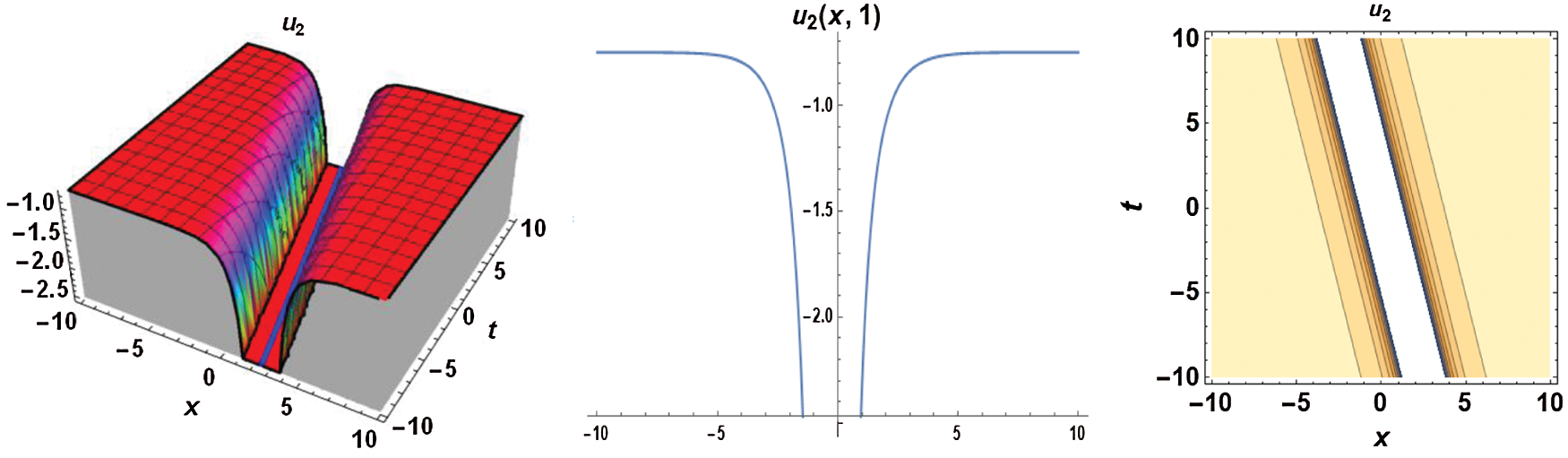
Figure 2: 3D, 2D and contour graphs respectively for w=0.5,η=0.5,q=2,k=2 values of Eq. (21)

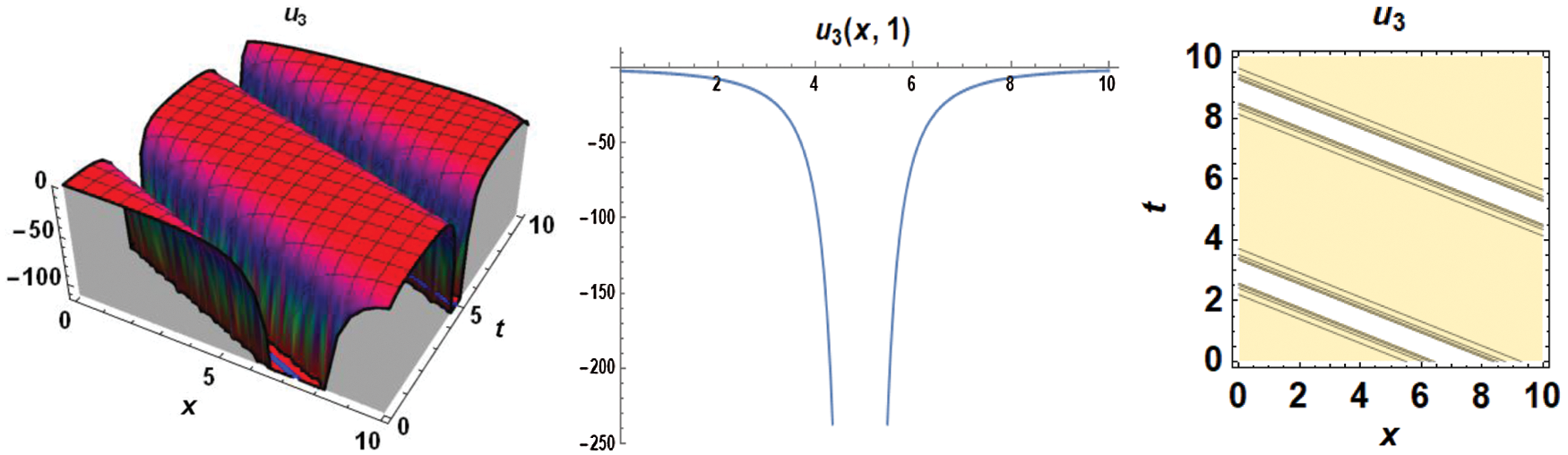
Figure 3: 3D, 2D and contour graphs respectively for w=0.5,η=2,q=2,k=0.2 values of Eq. (23)

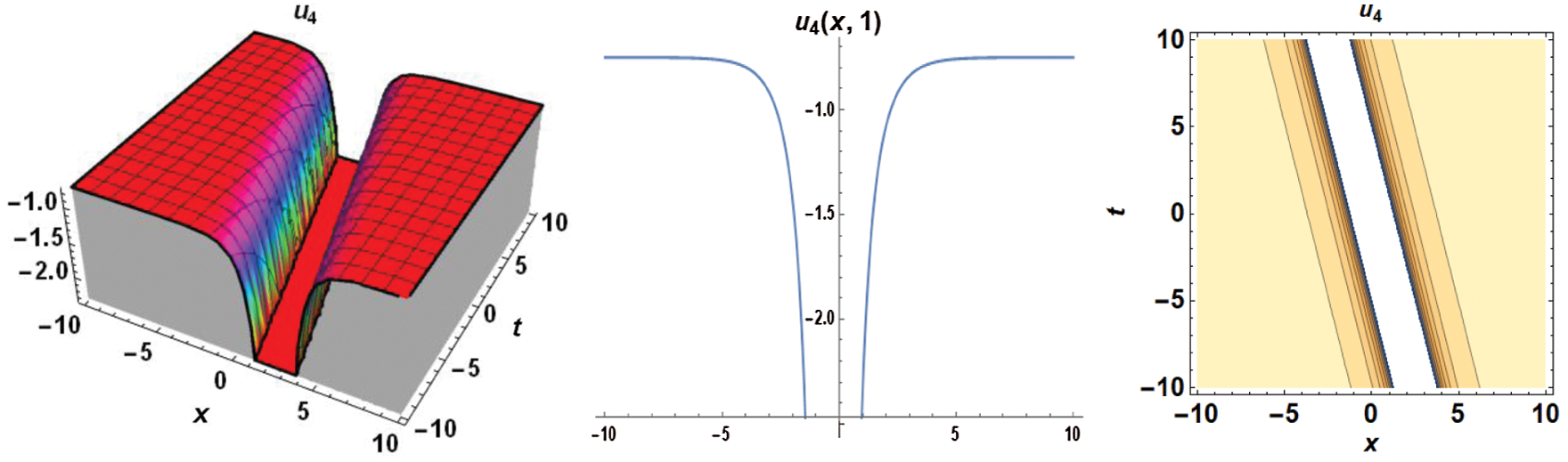
Figure 4: 3D, 2D and contour graphs respectively for w=0.5,η=0.5,q=2,k=2 values of Eq. (25)

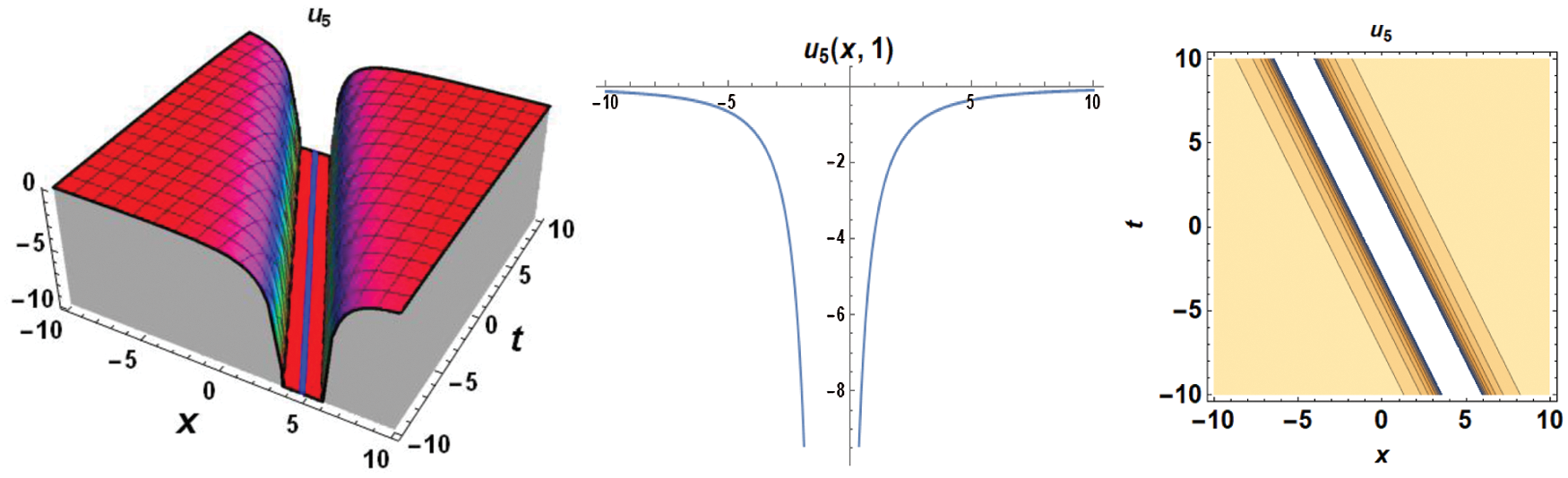
Figure 5: 3D, 2D and contour graphs respectively for r=0.5,η=0.5,q=2,k=2 values of Eq. (27)

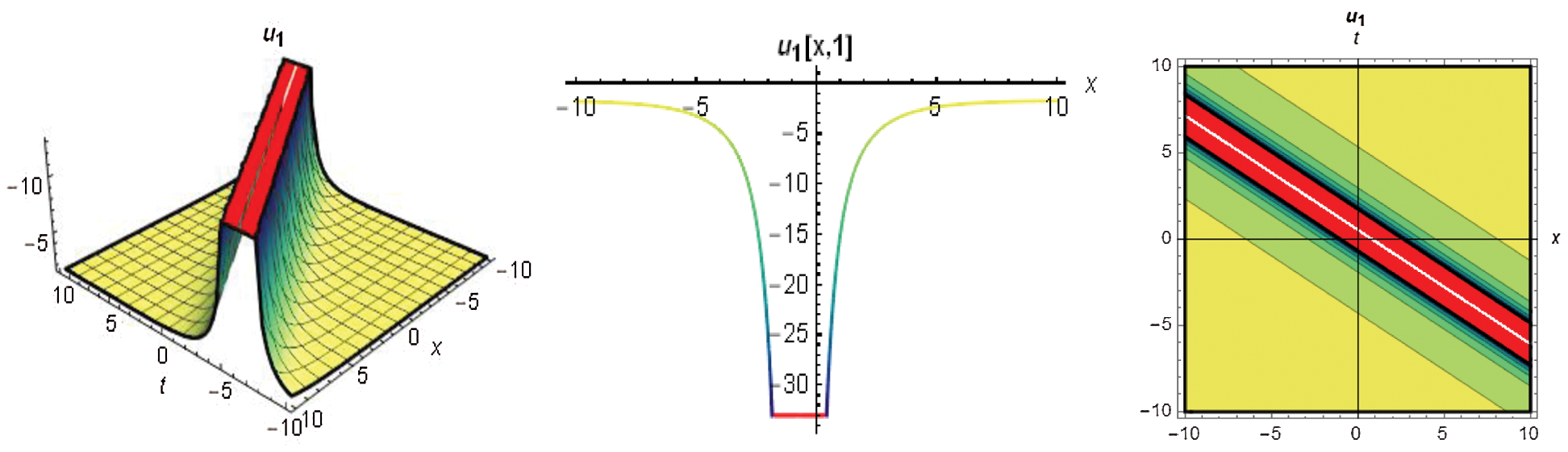
Figure 6: 3D, 2D and contour graphs respectively for c1=0.9,δ=0.3,λ=0.5,q=3,k=1,η=2 values of Eq. (31)

7  Conclusions

In this study, we have achieved hyperbolic, rational, dark soliton and trigonometric traveling wave solutions for the LWE in a magneto-electro-elastic circular rod using sub equation method and (1/G′) -expansion method. By giving arbitrary values to the constants in the solution obtained, 3D, 2D and contour graphics of the solution representing the stationary wave are presented. It has been observed that the methods used are easy, effective and powerful, and solutions of NLEEs can be obtained. It would be even more valuable to add a physical meaning to these solutions in the future. Computer package program was used in the construction of these solutions.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Durur, H., Tasbozan, O., Kurt, A. (2020). New analytical solutions of conformable time fractional bad and good modified Boussinesq equations. Applied Mathematics and Nonlinear Sciences, 5(1), 447–454. [Google Scholar]

 2.  Durur, H. (2020). Different types analytic solutions of the (1+1)-dimensional resonant nonlinear Schrödinger’s equation using (G’/G)-expansion method. Modern Physics Letters B, 34(3), 2050036. [Google Scholar]

 3.  He, J. H., El-Dib, Y. O. (2020). Homotopy perturbation method for Fangzhu oscillator. Journal of Mathematical Chemistry, 58(10), 2245–2253. [Google Scholar]

 4.  Yokuş, A., Durur, H. (2019). Complex hyperbolic traveling wave solutions of Kuramoto-Sivashinsky equation using (1/G’) expansion method for nonlinear dynamic theory. Journal of Balıkesir University Institute of Science and Technology, 21(2), 590–599. [Google Scholar]

 5.  Durur, H., Yokuş, A. (2019). Hyperbolic traveling wave solutions for Sawada-Kotera equation using (1/G’)-expansion method. Afyon Kocatepe Üniversitesi Fen ve Mühendislik Bilimleri Dergisi, 19(3), 615–619. [Google Scholar]

 6.  Ali, K. K., Yilmazer, R., Yokus, A., Bulut, H. (2020). Analytical solutions for the (3+1)-dimensional nonlinear extended quantum Zakharov-Kuznetsov equation in plasma physics. Physica A: Statistical Mechanics and its Applications, 548, 124327. [Google Scholar]

 7.  Yokus, A., Durur, H., Ahmad, H., Thounthong, P., Zhang, Y. F. (2020). Construction of exact traveling wave solutions of the Bogoyavlenskii equation by (G’/G, 1/G)-expansion and (1/G’)-expansion techniques. Results in Physics, 19, 103409. [Google Scholar]

 8.  Zhang, J. J., Shen, Y., He, J. H. (2019). Some analytical methods for singular boundary value problem in a fractal space. Applied and Computational Mathematics, 18(3), 225–235. [Google Scholar]

 9.  He, J. H., Latifizadeh, H. (2020). A general numerical algorithm for nonlinear differential equations by the variational iteration method. International Journal of Numerical Methods for Heat and Fluid Flow, 30(11), 4797–4810. DOI 10.1108/HFF-01-2020-0029. [Google Scholar] [CrossRef]

10. Ahmad, H., Khan, T. A., Stanimirovic, P. S., Ahmad, I. (2020). Modified variational iteration technique for the numerical solution of fifth order KdV-type equations. Journal of Applied and Computational Mechanics, 6, 1220–1227. [Google Scholar]

11. Ahmad, H., Seadawy, A. R., Khan, T. A., Thounthong, P. (2020). Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. Journal of Taibah University for Science, 14(1), 346–358. [Google Scholar]

12. Ahmad, H., Khan, T. A., Cesarano, C. (2019). Numerical solutions of coupled Burgers’ equations. Axioms, 8(4), 119. [Google Scholar]

13. Ahmad, H., Khan, T. A. (2020). Variational iteration algorithm I with an auxiliary parameter for the solution of differential equations of motion for simple and damped mass-spring systems. Noise & Vibration Worldwide, 51(1–2), 12–20. [Google Scholar]

14. Bazighifan, O., Ahmad, H., Yao, S. W. (2020). New oscillation criteria for advanced differential equations of fourth order. Mathematics, 8(5), 728. [Google Scholar]

15. Ahmad, H., Seadawy, A. R., Khan, T. A. (2020). Study on numerical solution of dispersive water wave phenomena by using a reliable modification of variational iteration algorithm. Mathematics and Computers in Simulation, 177, 13–23. [Google Scholar]

16. Nawaz Khan, M., Ahmad, I., Ahmad, H. (2020). A radial basis function collocation method for space-dependent inverse heat problems. Journal of Applied and Computational Mechanics, 6, 1187–1199. DOI 10.22055/JACM.2020.32999.2123. [Google Scholar] [CrossRef]

17. Kaya, D., Yokus, A. (2002). A numerical comparison of partial solutions in the decomposition method for linear and nonlinear partial differential equations. Mathematics and Computers in Simulation, 60(6), 507–512. [Google Scholar]

18. Kaya, D., Yokus, A. (2005). A decomposition method for finding solitary and periodic solutions for a coupled higher-dimensional Burgers equations. Applied Mathematics and Computation, 164(3), 857–864. [Google Scholar]

19. Yavuz, M., Özdemir, N. (2018). A quantitative approach to fractional option pricing problems with decomposition series. Konuralp Journal of Mathematics, 6(1), 102–109. [Google Scholar]

20. Qian, S. P., Tian, L. X. (2007). Modification of the Clarkson-Kruskal direct method for a coupled system. Chinese Physics Letters, 24(10), 2720. [Google Scholar]

21. Durur, H., Şenol, M., Kurt, A., Taşbozan, O. (2019). Zaman-kesirli Kadomtsev-Petviashvili denkleminin conformable türev ile yaklaşık çözümleri. Erzincan University Journal of the Institute of Science and Technology, 12(2), 796–806. [Google Scholar]

22. Aziz, I., Šarler, B. (2010). The numerical solution of second-order boundary-value problems by collocation method with the Haar wavelets. Mathematical and Computer Modelling, 52(9–10), 1577–1590. [Google Scholar]

23. Gao, W., Silambarasan, R., Baskonus, H. M., Anand, R. V., Rezazadeh, H. (2020). Periodic waves of the non dissipative double dispersive micro strain wave in the micro structured solids. Physica A: Statistical Mechanics and its Applications, 545, 123772. [Google Scholar]

24. Rady, A. A., Osman, E. S., Khalfallah, M. (2010). The homogeneous balance method and its application to the Benjamin-Bona–Mahoney (BBM) equation. Applied Mathematics and Computation, 217(4), 1385–1390. [Google Scholar]

25. Kaya, D., Yokuş, A., Demiroğlu, U. (2020). Comparison of exact and numerical solutions for the Sharma-Tasso–Olver equation. Numerical solutions of realistic nonlinear phenomena, pp. 53–65. Cham: Springer. [Google Scholar]

26. Kurt, A., Tasbozan, O., Durur, H. (2019). The exact solutions of conformable fractional partial differential equations using new sub equation method. Fundamental Journal of Mathematics and Applications, 2(2), 173–179. [Google Scholar]

27. Tasbozan, O., Kurt, A., Durur, H. (2019). Implementation of new sub equation method to time fractional partial differential equations. International Journal of Engineering Mathematics & Physics, 1, 1–12. [Google Scholar]

28. He, J. H., Wu, X. H. (2006). Exp-function method for nonlinear wave equations. Chaos, Solitons & Fractals, 30(3), 700–708. [Google Scholar]

29. Yavuz, M., Yokus, A. (2020). Analytical and numerical approaches to nerve impulse model of fractional-order. Numerical Methods for Partial Differential Equations, 36(6), 1348–1368. [Google Scholar]

30. Akbar, M. A., Akinyemi, L., Yao, S. W., Jhangeer, A., Rezazadeh, H. et al. (2021). Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results in Physics, 25, 104228. [Google Scholar]

31. Ahmad, H., Rafiq, M., Cesarano, C., Durur, H. (2020). Variational iteration algorithm-I with an auxiliary parameter for solving boundary value problems. Earthline Journal of Mathematical Sciences, 3(2), 229–247. [Google Scholar]

32. Ahmad, H., Khan, T. A., Yao, S. W. (2020). An efficient approach for the numerical solution of fifth-order KdV equations. Open Mathematics, 18(1), 738–748. [Google Scholar]

33. Durur, H., Kurt, A., Tasbozan, O. (2020). New travelling wave solutions for KdV6 equation using sub equation method. Applied Mathematics and Nonlinear Sciences, 5(1), 455–460. [Google Scholar]

34. Ahmad, H., Khan, T. A., Durur, H., Ismail, G. M., Yokus, A. (2021). Analytic approximate solutions of diffusion equations arising in oil pollution. Journal of Ocean Engineering and Science, 6(1), 62–69. [Google Scholar]

35. Rezazadeh, H., Kumar, D., Neirameh, A., Eslami, M., Mirzazadeh, M. (2020). Applications of three methods for obtaining optical soliton solutions for the Lakshmanan-Porsezian–Daniel model with Kerr law nonlinearity. Pramana, 94(1), 39. [Google Scholar]

36. Ahmad, H., Seadawy, A. R., Khan, T. A., Thounthong, P. (2020). Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. Journal of Taibah University for Science, 14(1), 346–358. [Google Scholar]

37. Yokus, A., Durur, H., Ahmad, H., Yao, S. W. (2020). Construction of different types analytic solutions for the Zhiber-Shabat equation. Mathematics, 8(6), 908. [Google Scholar]

38. Yokus, A., Durur, H., Ahmad, H. (2020). Hyperbolic type solutions for the couple Boiti-Leon-Pempinelli system. Facta Universitatis, Series: Mathematics and Informatics, 35(2), 523–531. [Google Scholar]

39. Iqbal, M., Seadawy, A. R., Lu, D. (2019). Applications of nonlinear longitudinal wave equation in a magneto-electro-elastic circular rod and new solitary wave solutions. Modern Physics Letters B, 33(18), 1950210. [Google Scholar]

40. İlhan, O. A., Bulut, H., Sulaiman, T. A., Baskonus, H. M. (2019). On the new wave behavior of the Magneto-Electro-Elastic (MEE) circular rod longitudinal wave equation. An International Journal of Optimization and Control: Theories & Applications, 10(1), 1–8. [Google Scholar]

41. Ahmad, I., Ahmad, H., Abouelregal, A. E., Thounthong, P., Abdel-Aty, M. (2020). Numerical study of integer-order hyperbolic telegraph model arising in physical and related sciences. European Physical Journal Plus, 135(9), 1–14. [Google Scholar]

42. Bulut, H., Sulaiman, T. A., Baskonus, H. M. (2018). On the solitary wave solutions to the longitudinal wave equation in MEE circular rod. Optical and Quantum Electronics, 50(2), 1–10. [Google Scholar]

43. Baskonus, H. M., Bulut, H., Atangana, A. (2016). On the complex and hyperbolic structures of the longitudinal wave equation in a magneto-electro-elastic circular rod. Smart Materials and Structures, 25(3), 035022. [Google Scholar]

44. Yang, S., Xu, T. (2017). 1-Soliton and peaked solitary wave solutions of nonlinear longitudinal wave equation in magneto-electro–elastic circular rod. Nonlinear Dynamics, 87(4), 2735–2739. [Google Scholar]

45. Younis, M., Ali, S. (2015). Bright, dark, and singular solitons in magneto-electro-elastic circular rod. Waves in Random and Complex Media, 25(4), 549–555. [Google Scholar]

46. Mandi, A., Kundu, S., Pati, P., Pal, P. (2019). Love wave propagation in a fiber-reinforced layer with corrugated boundaries overlying heterogeneous half-space. Journal of Applied and Computational Mechanics, 5(5), 926–934. [Google Scholar]

47. Zargaripoor, A., Daneshmehr, A., Nikkhah Bahrami, M. (2019). Study on free vibration and wave power reflection in functionally graded rectangular plates using wave propagation approach. Journal of Applied and Computational Mechanics, 5(1), 77–90. [Google Scholar]

48. Anjum, N., Ain, Q. T. (2020). Application of He’s fractional derivative and fractional complex transform for time fractional Camassa-Holm equation. Thermal Science, 24(5A), 3023–3030. [Google Scholar]

49. Ain, Q. T., He, J. H., Anjum, N., Ali, M. (2020). The fractional complex transform: A novel approach to the time-fractional Schrödinger equation. Fractals–An Interdisciplinary Journal on the Complex Geometry of Nature, 28(7), 2050141–2055578. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.